Effect of Residual Stress on Mode-I Stress Intensity Factor: A Quantitative Evaluation and a Suggestion of an Estimating Equation
Abstract
1. Introduction
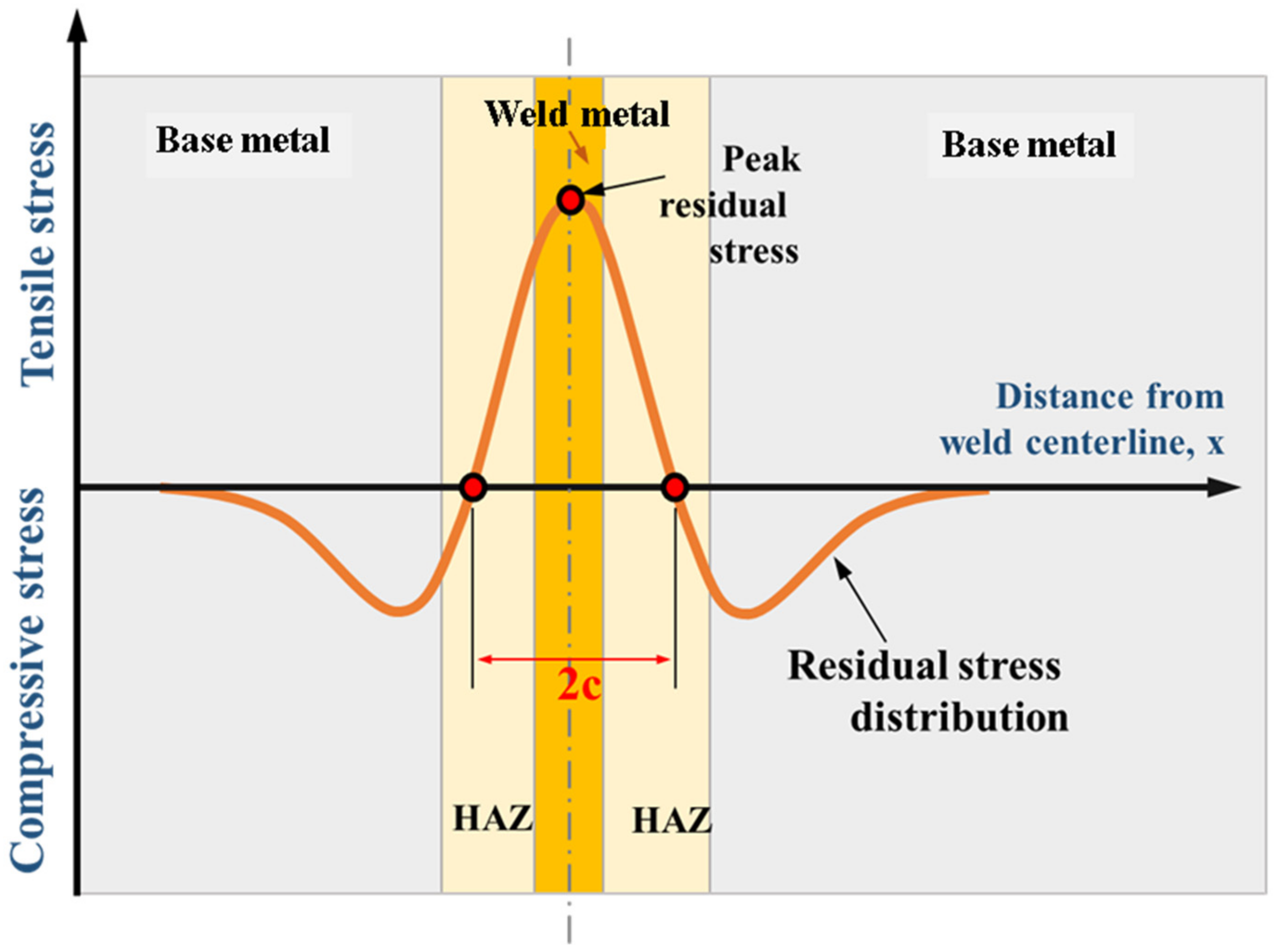
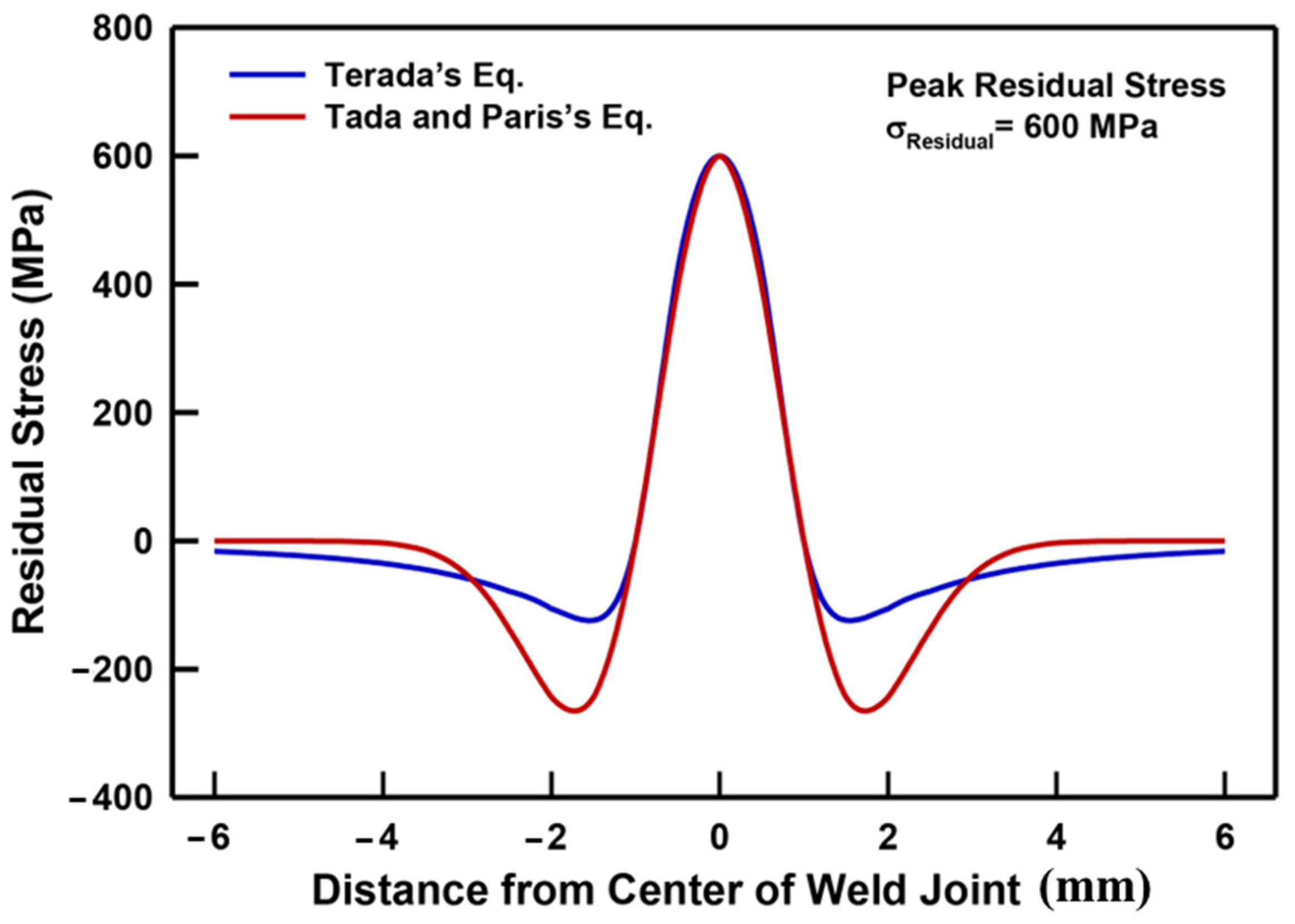
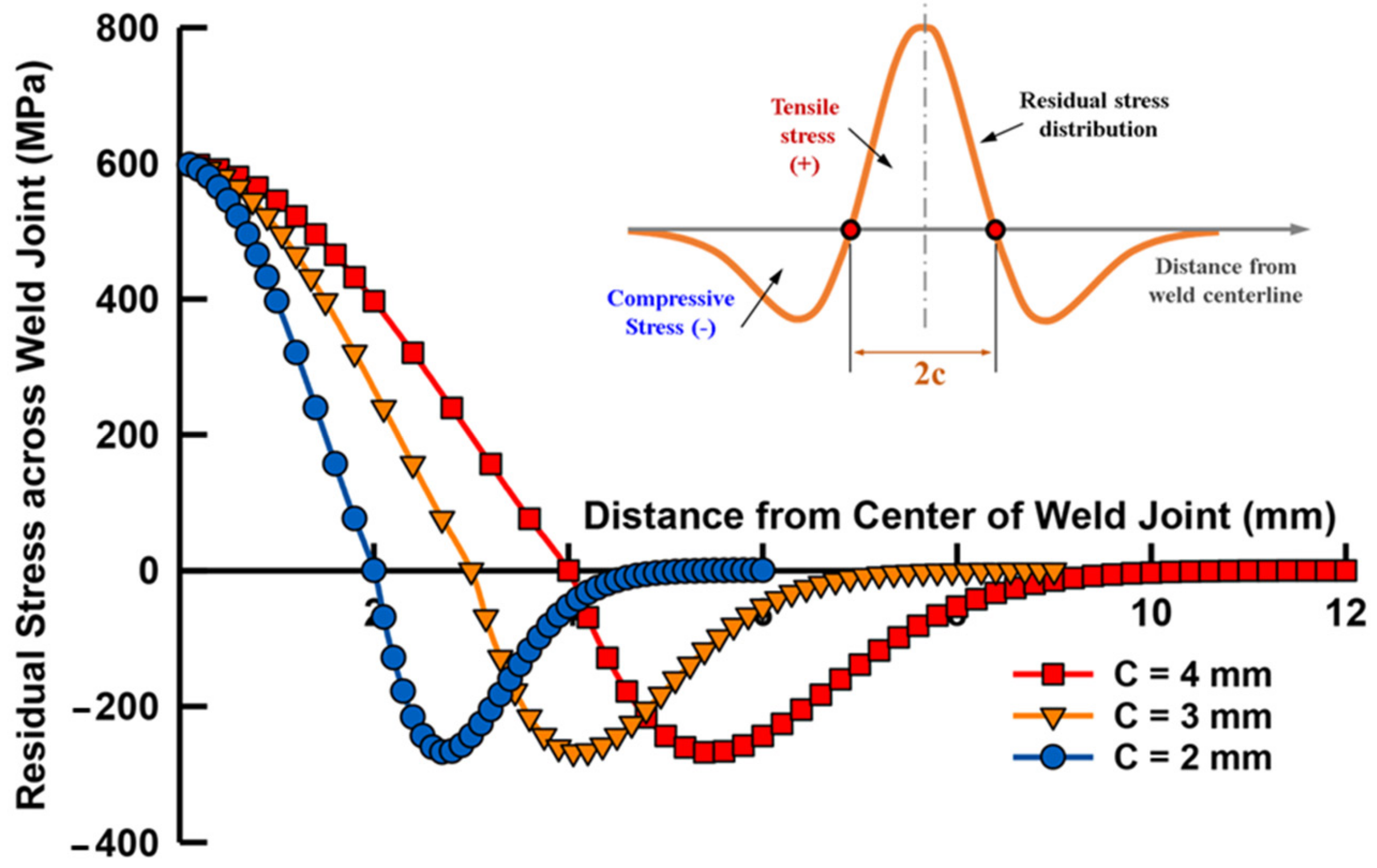
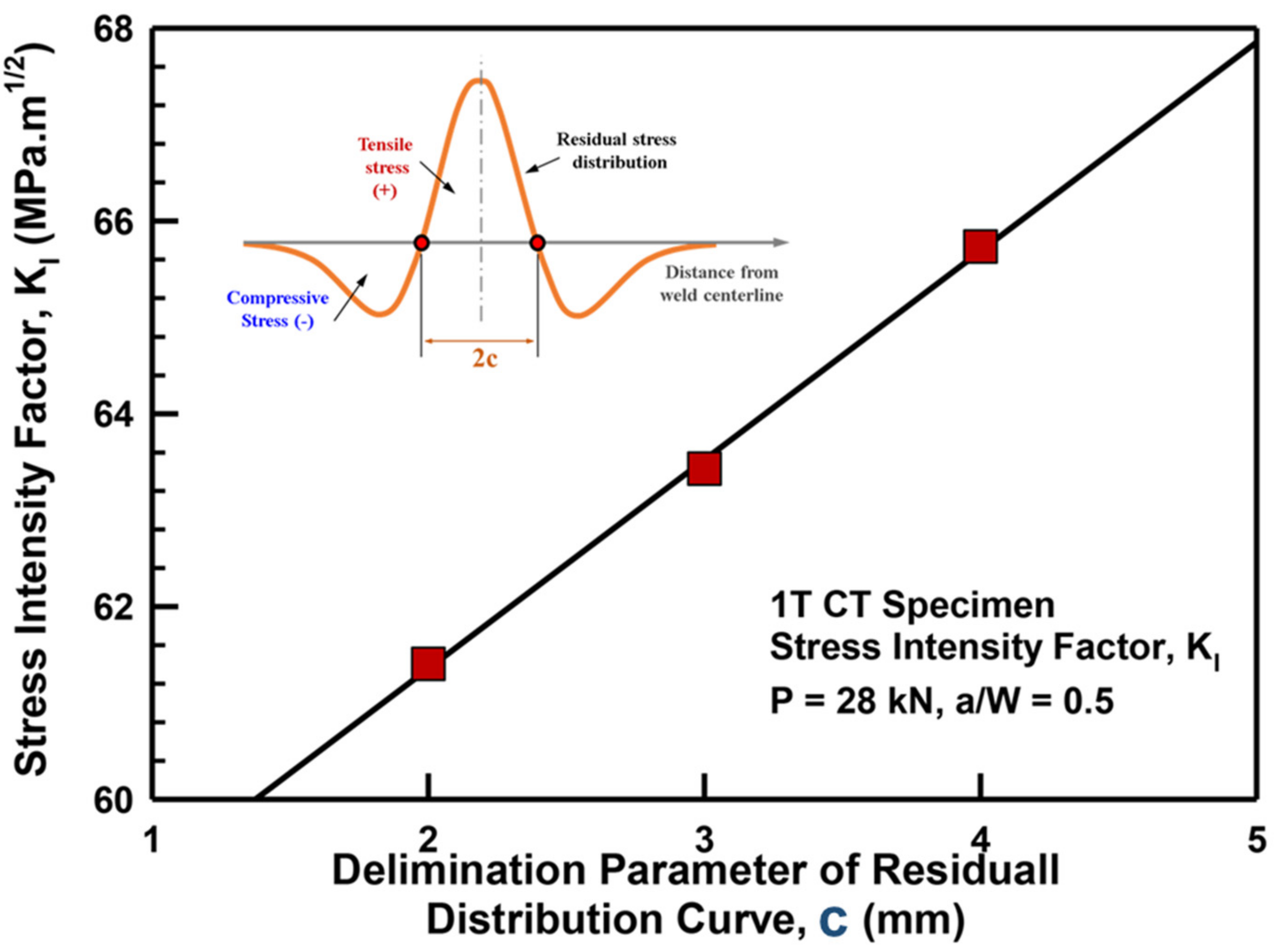
2. Residual Stress Distribution: A Review
3. Finite Element Analyses
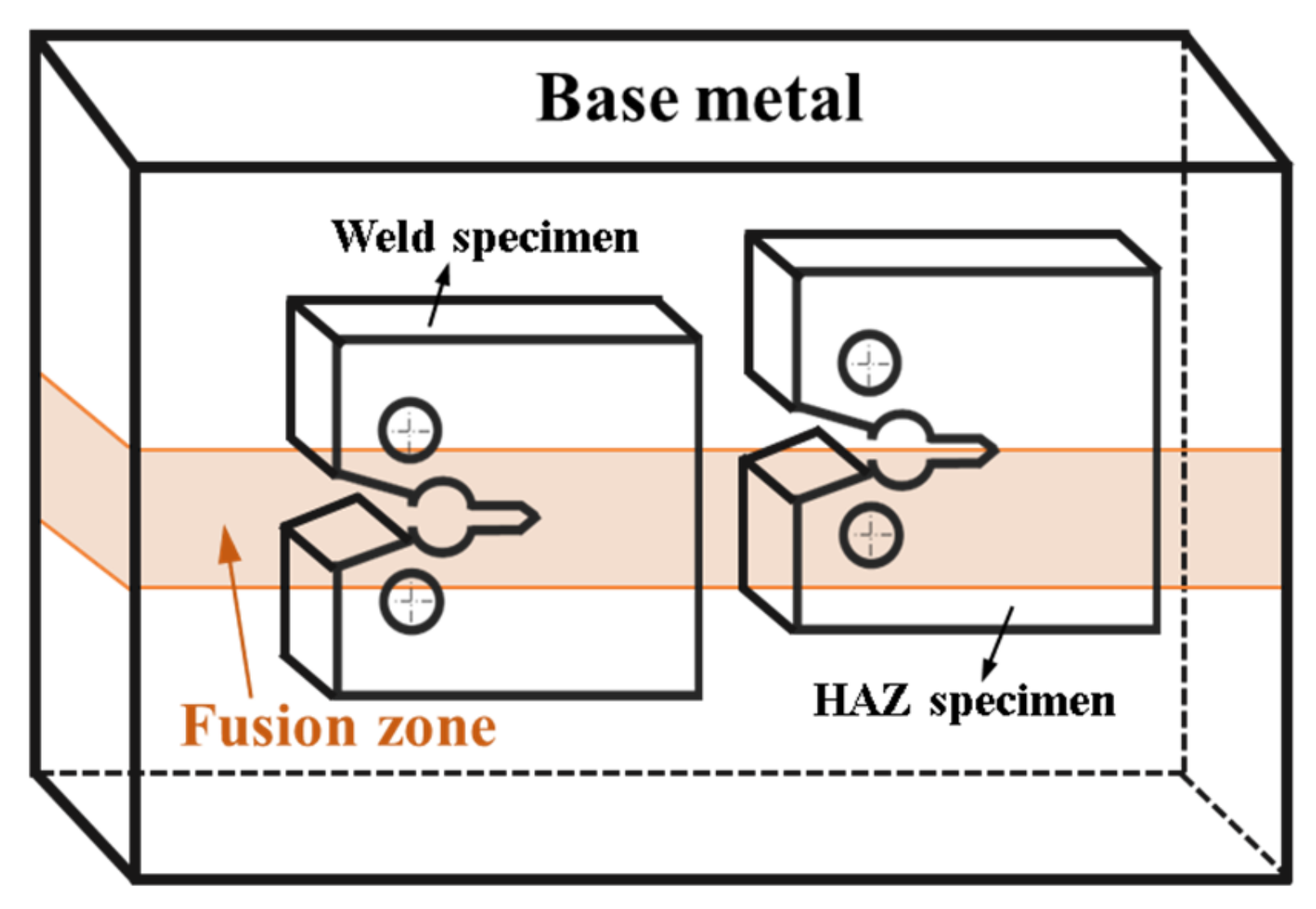
3.1. Materials, Specimen Geometries, and Boundary Conditions
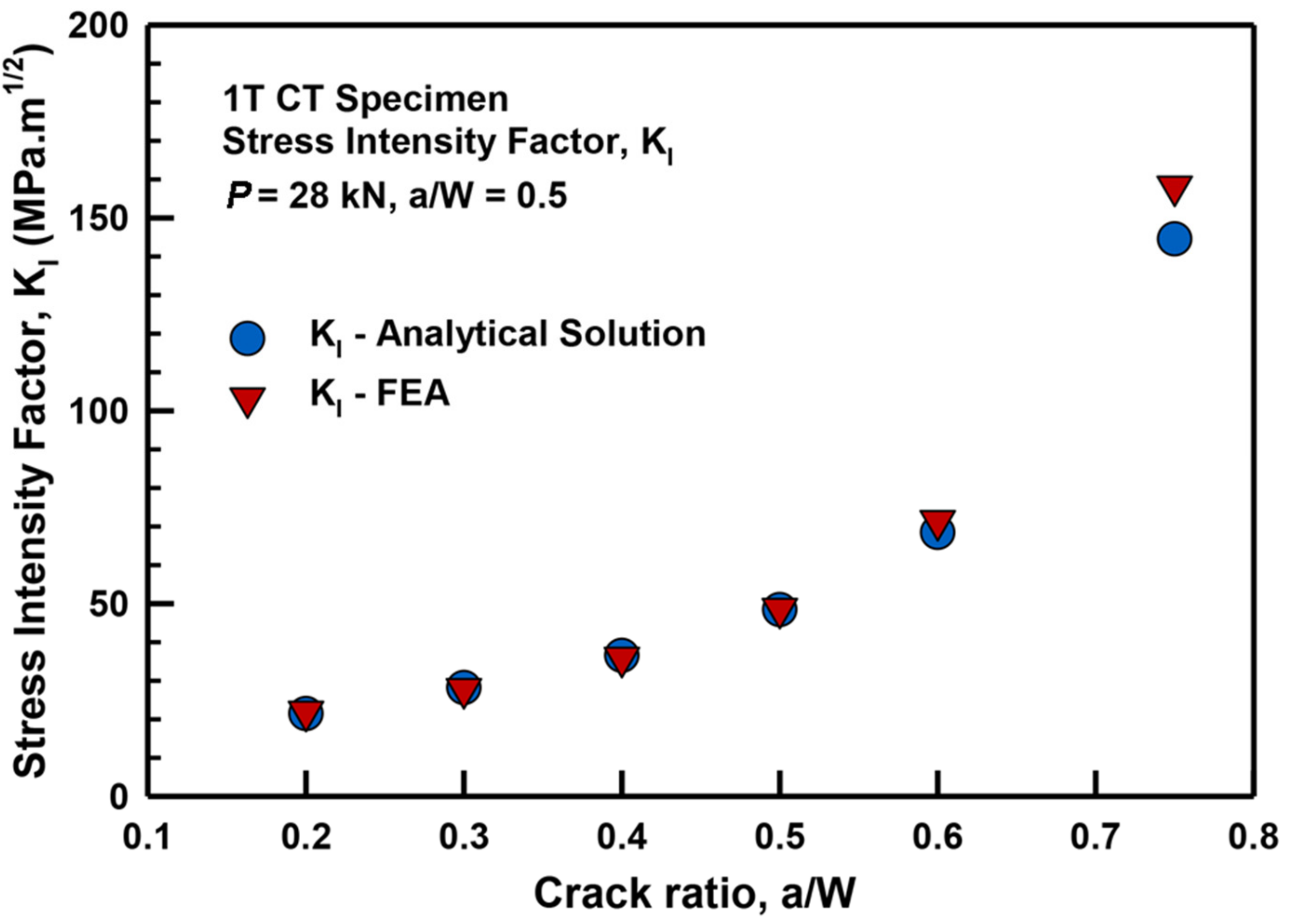
3.2. Estimation of Stress Intensity Factor using FEA
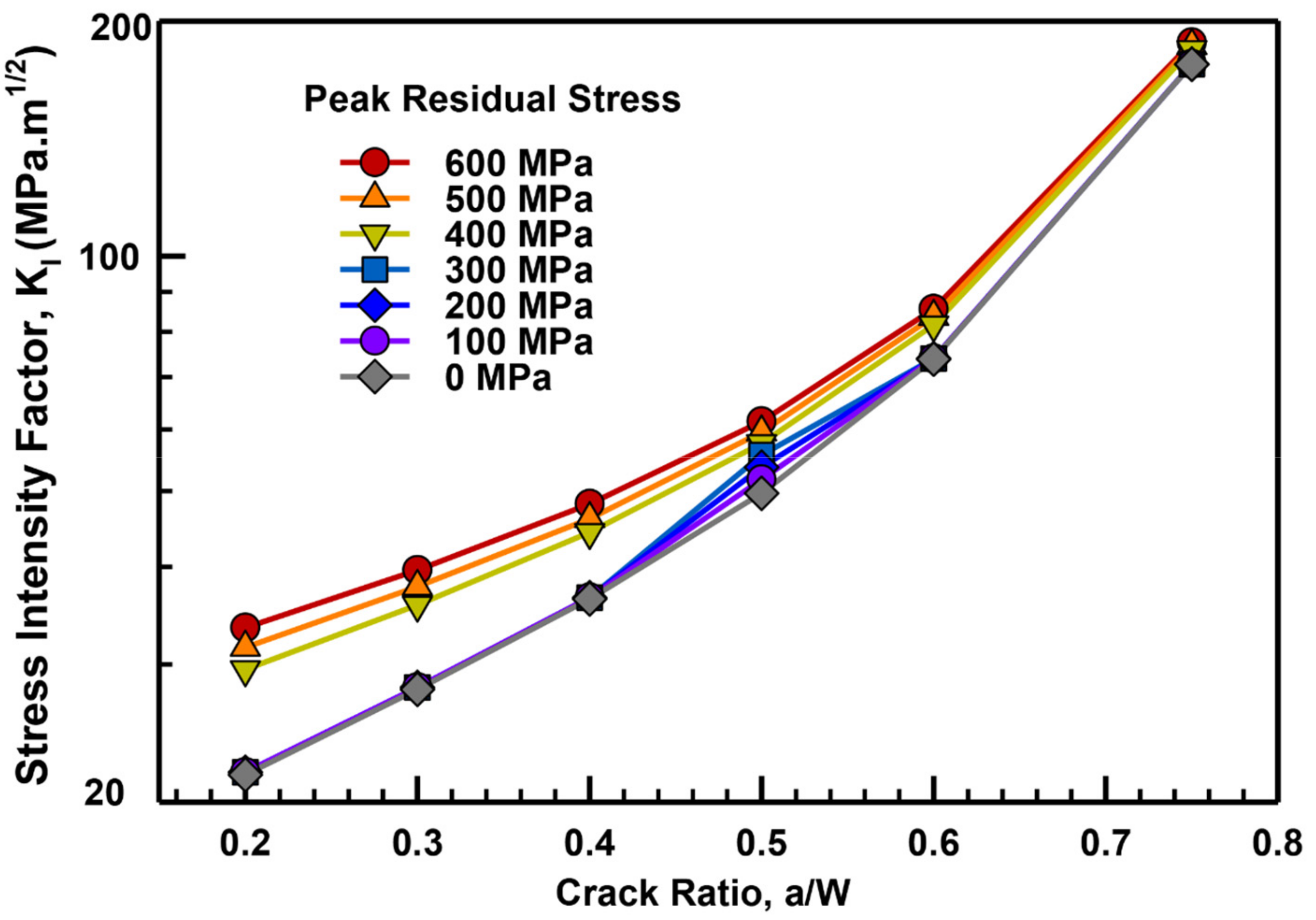
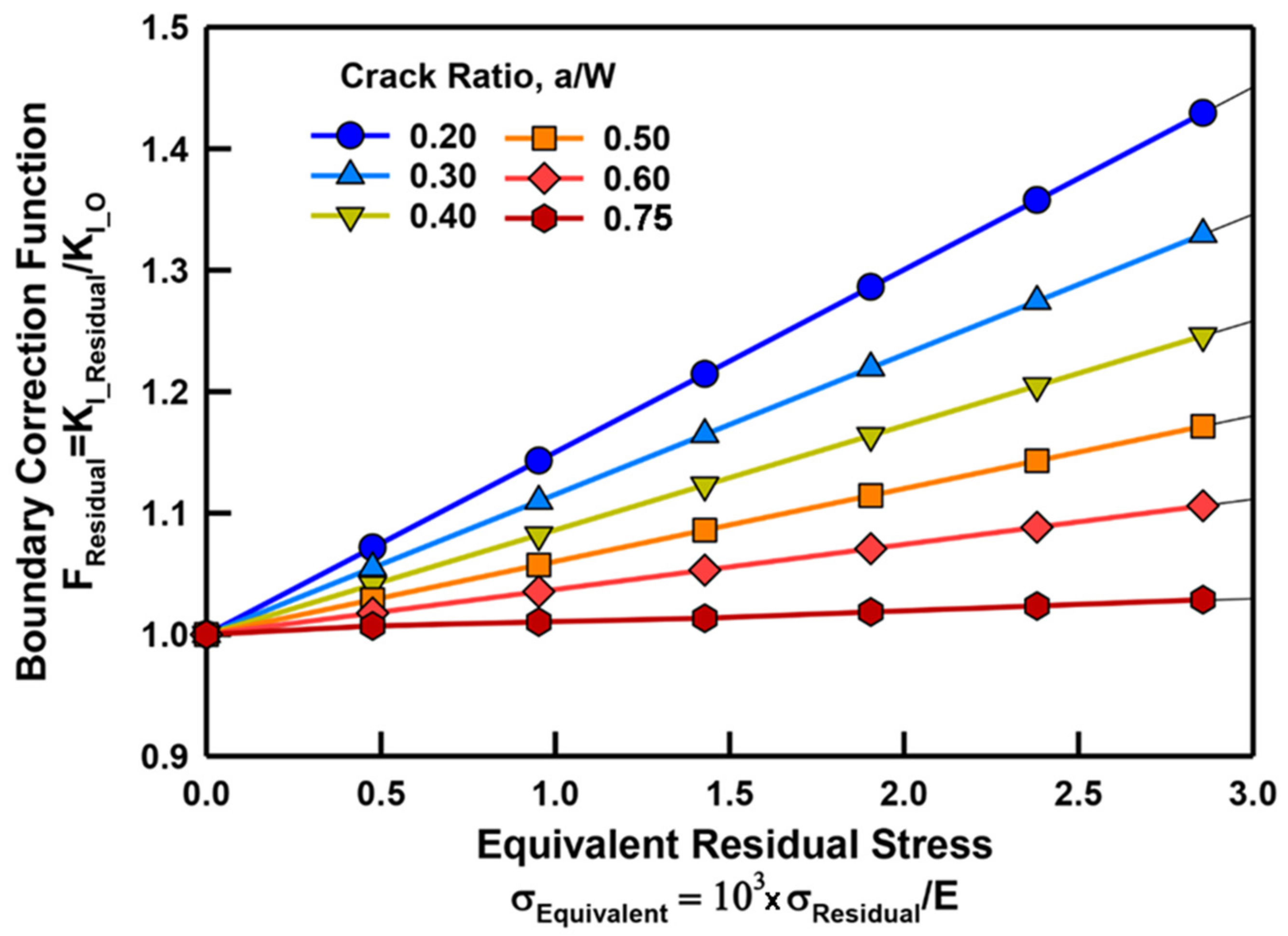
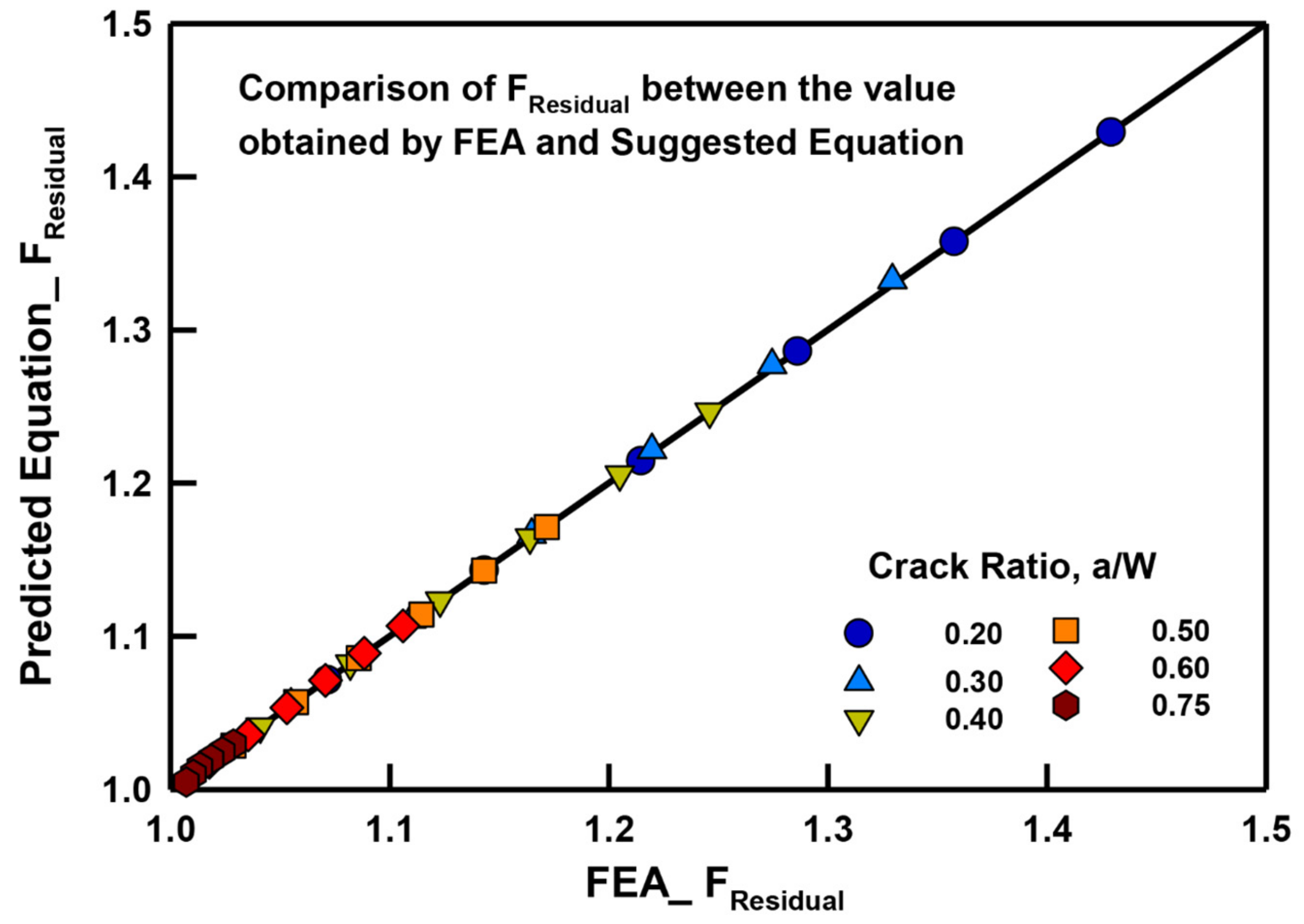
3.3. Suggested Equation for Stress Intensity Factor under the Effect of RS
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, K.M.; Shin, Y.C. Prospects of laser welding technology in the automotive industry: A review. J. Mater. Process. Technol. 2017, 245, 46–69. [Google Scholar] [CrossRef]
- Little, R.L. Welding and Welding Technology; McGraw-Hill Book Co.: New York, NY, USA, 1973. [Google Scholar]
- Katayama, S. Handbook of Laser Welding Technologies; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Ma, S.; Li, B.; Ma, Y.; Zhang, P.; Xu, P. Effect of Brazing Filler Metals and Welding Parameters on Laser Welding-Brazing Joints of WC-Co to S1045. Metals 2022, 12, 1780. [Google Scholar] [CrossRef]
- Krishnan, S.A.; Nikhil, R.; Sasikala, G.; Moitra, A.; Albert, S.K.; Bhaduri, A.K.; Raghava, G. Evaluation of fracture resistance of AISI type 316LN stainless steel base and welded pipes with circumferential through-wall crack. Int. J. Press. Vessel. Pip. 2019, 178, 104008. [Google Scholar] [CrossRef]
- Cavaliere, P.; Campanile, G.; Panella, F.; Squillace, A. Effect of welding parameters on mechanical and microstructural properties of AA6056 joints produced by friction stir welding. J. Mater. Process. Technol. 2006, 180, 263–270. [Google Scholar] [CrossRef]
- Bagheri, B.; Sharifi, F.; Abbasi, M.; Abdollahzadeh, A. On the role of input welding parameters on the microstructure and mechanical properties of Al6061-T6 alloy during the friction stir welding: Experimental and numerical investigation. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 236, 299–318. [Google Scholar] [CrossRef]
- Abbasi, M.; Abdollahzadeh, A.; Bagheri, B.; Ostovari Moghaddam, A.; Sharifi, F.; Dadaei, M. Study on the effect of the welding environment on the dynamic recrystallization phenomenon and residual stresses during the friction stir welding process of aluminum alloy. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1809–1826. [Google Scholar] [CrossRef]
- Bagheri, B.; Abbasi, M.; Sharifi, F. Study on Microstructure Evolution and Mechanical Properties of Al5083 Joint Obtained from Friction Stir Spot Welding: Effect of Vibration and Plunge Depth. In Engineering Principles: Welding and Residual Stresses; IntechOpen: London, UK, 2022; p. 133. [Google Scholar]
- Bagheri, B.; Abbasi, M.; Abdollahzadeh, A. Microstructure and mechanical characteristics of AA6061-T6 joints produced by friction stir welding, friction stir vibration welding and tungsten inert gas welding: A comparative study. Int. J. Miner. Metall. Mater. 2021, 28, 450–461. [Google Scholar] [CrossRef]
- Abdollahzadeh, A.; Bagheri, B.; Abassi, M.; Kokabi, A.H.; Moghaddam, A.O. Comparison of the weldability of AA6061-T6 joint under different friction stir welding conditions. J. Mater. Eng. Perform. 2021, 30, 1110–1127. [Google Scholar] [CrossRef]
- Kong, D.; Wu, Y.; Long, D.; Zhou, C. Tension fracture behaviors of welded joints in X70 steel pipeline. Theor. Appl. Mech. Lett. 2011, 1, 031008. [Google Scholar] [CrossRef]
- Bukovská, Š.; Moravec, J.; Solfronk, P.; Pekárek, M. Assessment of the Effect of Residual Stresses Arising in the HAZ of Welds on the Fatigue Life of S700MC Steel. Metals 2022, 12, 1890. [Google Scholar] [CrossRef]
- Cao, J.; Ma, W.; Pang, G.; Wang, K.; Ren, J.; Nie, H.; Yao, T. Failure analysis on girth weld cracking of underground tee pipe. Int. J. Press. Vessel. Pip. 2021, 191, 104371. [Google Scholar] [CrossRef]
- Ramakokovhu, U.; Desai, D.; Snedden, G.; Jamiru, T. Significance of residual stresses in fatigue life prediction of micro gas turbine blades. Eng. Fail. Anal. 2021, 120, 105092. [Google Scholar] [CrossRef]
- Vaara, J.; Kunnari, A.; Frondelius, T. Literature review of fatigue assessment methods in residual stressed state. Eng. Fail. Anal. 2020, 110, 104379. [Google Scholar] [CrossRef]
- Gadallah, R.; Osawa, N.; Tanaka, S.; Tsutsumi, S. Critical investigation on the influence of welding heat input and welding residual stress on stress intensity factor and fatigue crack propagation. Eng. Fail. Anal. 2018, 89, 200–221. [Google Scholar] [CrossRef]
- Francis, J.A.; Bhadeshia, H.K.D.H.; Withers, P.J. Welding residual stresses in ferritic power plant steels. Mater. Sci. Technol. 2007, 23, 1009–1020. [Google Scholar] [CrossRef]
- Leggatt, R.H. Residual stresses in welded structures. Int. J. Press. Vessel. Pip. 2008, 85, 144–151. [Google Scholar] [CrossRef]
- Withers, P.J.; Bhadeshia, H.K.D.H. Residual stress. Part 2—Nature and origins. Mater. Sci. Technol. 2001, 17, 366–375. [Google Scholar] [CrossRef]
- Yukio, U.E.D.A.; Chul, K.Y.; Gang, Y.M. A predicting method of welding residual stress using source of residual stress (report I): Characteristics of inherent strain (source of residual stress) (mechanics, strength & structural design). Trans. JWRI 1989, 18, 135–141. [Google Scholar]
- Nguyen, T.T.; Yoon, K.B.; Vu, T.T.; Park, J.; Baek, U.B. On the changes in the low-cycle-fatigue life and cracking mechanism of P91 cross-weld specimens at elevated temperatures. Int. J. Fatigue 2022, 159, 106833. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Beak, U.B.; Park, J.; Nahm, S.H.; Tak, N. Hydrogen environment assisted cracking in X70 welding heat-affected zone under a high-pressure hydrogen gas. Theor. Appl. Fract. Mech. 2020, 109, 102746. [Google Scholar] [CrossRef]
- Ghaini, F.M.; Ebrahimnia, M.; Gholizade, S. Characteristics of cracks in heat affected zone of ductile cast iron in powder welding process. Eng. Fail. Anal. 2011, 18, 47–51. [Google Scholar] [CrossRef]
- Karadeniz, E.; Ozsarac, U.; Yildiz, C. The effect of process parameters on penetration in gas metal arc welding processes. Mater. Des. 2007, 28, 649–656. [Google Scholar] [CrossRef]
- Ren, S.R.; Ma, Z.Y.; Chen, L.Q. Effect of welding parameters on tensile properties and fracture behavior of friction stir welded Al–Mg–Si alloy. Scr. Mater. 2007, 56, 69–72. [Google Scholar] [CrossRef]
- Shakil, M.; Tariq, N.H.; Ahmad, M.; Choudhary, M.A.; Akhter, J.I.; Babu, S.S. Effect of ultrasonic welding parameters on microstructure and mechanical properties of dissimilar joints. Mater. Des. 2014, 55, 263–273. [Google Scholar] [CrossRef]
- ISO 12108; 2012 Metallic Materials—Fatigue Testing—Fatigue Crack Growth Method. British Standards Institution: London, UK, 2012.
- John, R.; Jata, K.V.; Sadananda, K. Residual stress effects on near-threshold fatigue crack growth in friction stir welds in aerospace alloys. Int. J. Fatigue 2003, 25, 939–948. [Google Scholar] [CrossRef]
- Beghini, M.; Bertini, L. Fatigue crack propagation through residual stress fields with closure phenomena. Eng. Fract. Mech. 1990, 36, 379–387. [Google Scholar] [CrossRef]
- Ma, Y.E.; Staron, P.; Fischer, T.; Irving, P.E. Size effects on residual stress and fatigue crack growth in friction stir welded 2195-T8 aluminium–Part II: Modelling. Int. J. Fatigue 2011, 33, 1426–1434. [Google Scholar] [CrossRef]
- Moshayedi, H.; Sattari-Far, I. The effect of welding residual stresses on brittle fracture in an internal surface cracked pipe. Int. J. Press. Vessel. Pip. 2015, 126, 29–36. [Google Scholar] [CrossRef]
- LaRue, J.E.; Daniewicz, S.R. Predicting the effect of residual stress on fatigue crack growth. Int. J. Fatigue 2007, 29, 508–515. [Google Scholar] [CrossRef]
- Muñoz, J.A.; Dolgach, E.; Tartalini, V.; Risso, P.; Avalos, M.; Bolmaro, R.; Cabrera, J.M. Microstructural Heterogeneity and Mechanical Properties of a Welded Joint of an Austenitic Stainless Steel. Metals 2023, 13, 245. [Google Scholar] [CrossRef]
- Ronevich, J.A.; Song, E.J.; Feng, Z.; Wang, Y.; D’Elia, C.; Hill, M.R. Fatigue crack growth rates in high pressure hydrogen gas for multiple X100 pipeline welds accounting for crack location and residual stress. Eng. Fract. Mech. 2020, 228, 106846. [Google Scholar] [CrossRef]
- Lam, Y.C.; Lian, K.S. The effect of residual stress and its redistribution of fatigue crack growth. Theor. Appl. Fract. Mech. 1989, 12, 59–66. [Google Scholar] [CrossRef]
- Srivastava, B.K.; Tewari, S.P.; Prakash, J. A review on effect of preheating and/or post weld heat treatment (PWHT) on mechanical behavior of ferrous metals. Int. J. Eng. Sci. Technol. 2010, 2, 625–631. [Google Scholar]
- Carone, S.; Corigliano, P.; Epasto, G.; Moramarco, V.; Palomba, G.; Pappalettera, G.; Casavola, C. Innovative Approach for the Evaluation of the Mechanical Behavior of Dissimilar Welded Joints. Metals 2022, 12, 2039. [Google Scholar] [CrossRef]
- Prabakaran, M.P.; Kannan, G.R. Effects of post-weld heat treatment on dissimilar laser welded joints of austenitic stainless steel to low carbon steel. Int. J. Press. Vessel. Pip. 2021, 191, 104322. [Google Scholar] [CrossRef]
- Jiang, W.; Luo, Y.; Zeng, Q.; Wang, J.; Tu, S.T. Residual stresses evolution during strip clad welding, post welding heat treatment and repair welding for a large pressure vessel. Int. J. Press. Vessel. Pip. 2021, 189, 104259. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, J.X.; Xue, C.B. Numerical investigation on residual stress distribution and evolution during multipass narrow gap welding of thick-walled stainless-steel pipes. Fusion Eng. Des. 2011, 86, 288–295. [Google Scholar] [CrossRef]
- Wang, X.; Gong, J.; Zhao, Y.; Wang, Y.; Ge, Z. Numerical simulation to study the effect of arc travelling speed and welding sequences on residual stresses in welded sections of new ferritic p92 pipes. High Temp. Mater. Process. 2016, 35, 121–128. [Google Scholar] [CrossRef]
- Deng, D. FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects. Mater. Des. 2009, 30, 359–366. [Google Scholar] [CrossRef]
- Farajian, M. Welding residual stress behavior under mechanical loading: Henry Granjon prize competition 2012 winner category C: Design and structural integrity. Weld. World 2013, 57, 157–169. [Google Scholar] [CrossRef]
- Terada, H. An Analysis of the Stress Intensity Factor of a Crack Perpendicular to the Welding Bead. Eng. Fract. Mech. 1976, 8, 441–444. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.C. The Stress Intensity Factor for a Crack Perpendicular to the Welding Bead. Int. J. Fract. 1983, 21, 279–284. [Google Scholar] [CrossRef]
- Srawley, J.E. Wide Range Stress Intensity Factor for ASTME399 Standard Fracture Toughness Specimens. Int. J. Fract. 1976, 12, 475–476. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook; Paris Productions & Del Research Corp.: Saint Louis, France, 1985. [Google Scholar]
- Paris, P.C.; Erdogen, F. A critical analysis of crack propagation laws. Trans. ASME. Ser. D J. Basic Eng. 1963, 85, 528–534. [Google Scholar] [CrossRef]
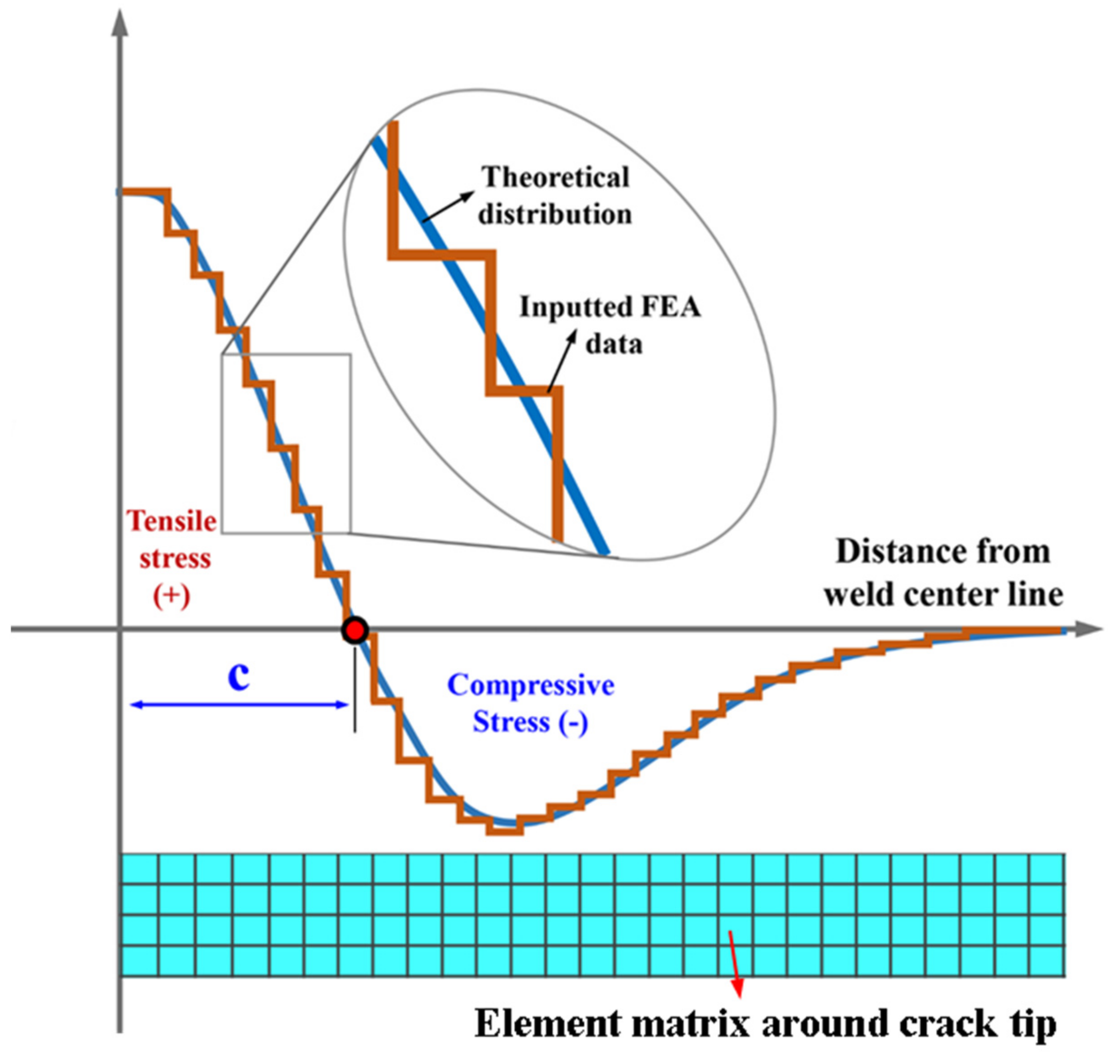
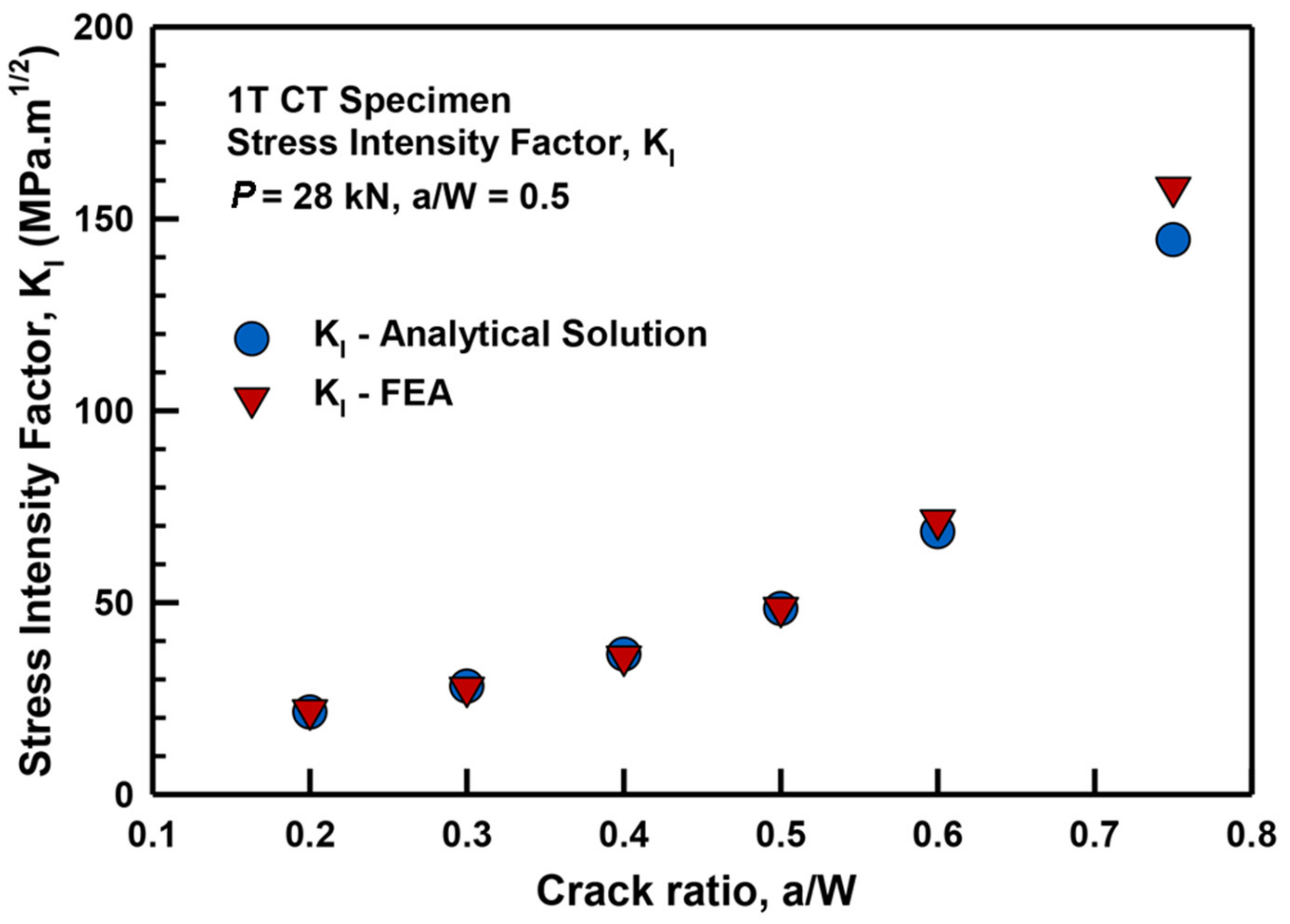
| Material | Welded Joint Geometry | Residual Stress Distribution Behavior | Ref. |
|---|---|---|---|
| Stainless steel | Thick-walled pipe | The value of tensile RS on the outer is significantly higher than that at the inner surfaces | [41] |
| Ferritic P92 steel | Thin-walled pipe | The peak values of tensile RS on the outer and inner surfaces are nearly identical | [42] |
| Low-carbon steel (S15C), Medium-carbon steel (S45C) | Plate | Insignificant RS exists in the weld joint of low-carbon steel (S15C)–low strength material, while a considerable RS is present in the weld zone of medium-carbon steel (S45C)–higher strength material | [43] |
| Different steels: S235JRG2, S355J2G3, P460NL, S690QL, S960QL, and S1100QL | Plate | Peak tensile RS is proportional to the yield strength of materials | [44] |
| Peak RS (MPa) | Crack Ratio, a/W | |||||
|---|---|---|---|---|---|---|
| 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.75 | |
| 600 | 1.55 | 1.43 | 1.33 | 1.24 | 1.16 | 1.07 |
| 500 | 1.46 | 1.36 | 1.27 | 1.2 | 1.14 | 1.06 |
| 400 | 1.37 | 1.29 | 1.22 | 1.16 | 1.11 | 1.05 |
| 300 | 1.28 | 1.22 | 1.17 | 1.12 | 1.09 | 1.04 |
| 200 | 1.19 | 1.15 | 1.11 | 1.09 | 1.06 | 1.03 |
| 100 | 1.1 | 1.08 | 1.06 | 1.05 | 1.03 | 1.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.T.; Pham, V.S.; Tran, H.A.; Nguyen, D.H.; Nguyen, T.H.; Dinh, H.B. Effect of Residual Stress on Mode-I Stress Intensity Factor: A Quantitative Evaluation and a Suggestion of an Estimating Equation. Metals 2023, 13, 1132. https://doi.org/10.3390/met13061132
Nguyen TT, Pham VS, Tran HA, Nguyen DH, Nguyen TH, Dinh HB. Effect of Residual Stress on Mode-I Stress Intensity Factor: A Quantitative Evaluation and a Suggestion of an Estimating Equation. Metals. 2023; 13(6):1132. https://doi.org/10.3390/met13061132
Chicago/Turabian StyleNguyen, Thanh Tuan, Van Son Pham, Hoang Anh Tran, Duc Huy Nguyen, Thu Huong Nguyen, and Hong Bo Dinh. 2023. "Effect of Residual Stress on Mode-I Stress Intensity Factor: A Quantitative Evaluation and a Suggestion of an Estimating Equation" Metals 13, no. 6: 1132. https://doi.org/10.3390/met13061132
APA StyleNguyen, T. T., Pham, V. S., Tran, H. A., Nguyen, D. H., Nguyen, T. H., & Dinh, H. B. (2023). Effect of Residual Stress on Mode-I Stress Intensity Factor: A Quantitative Evaluation and a Suggestion of an Estimating Equation. Metals, 13(6), 1132. https://doi.org/10.3390/met13061132





