Microstructural Characterization of Reactor Pressure Vessel Steels
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. Microstructure Characterization of the Unirradiated Material
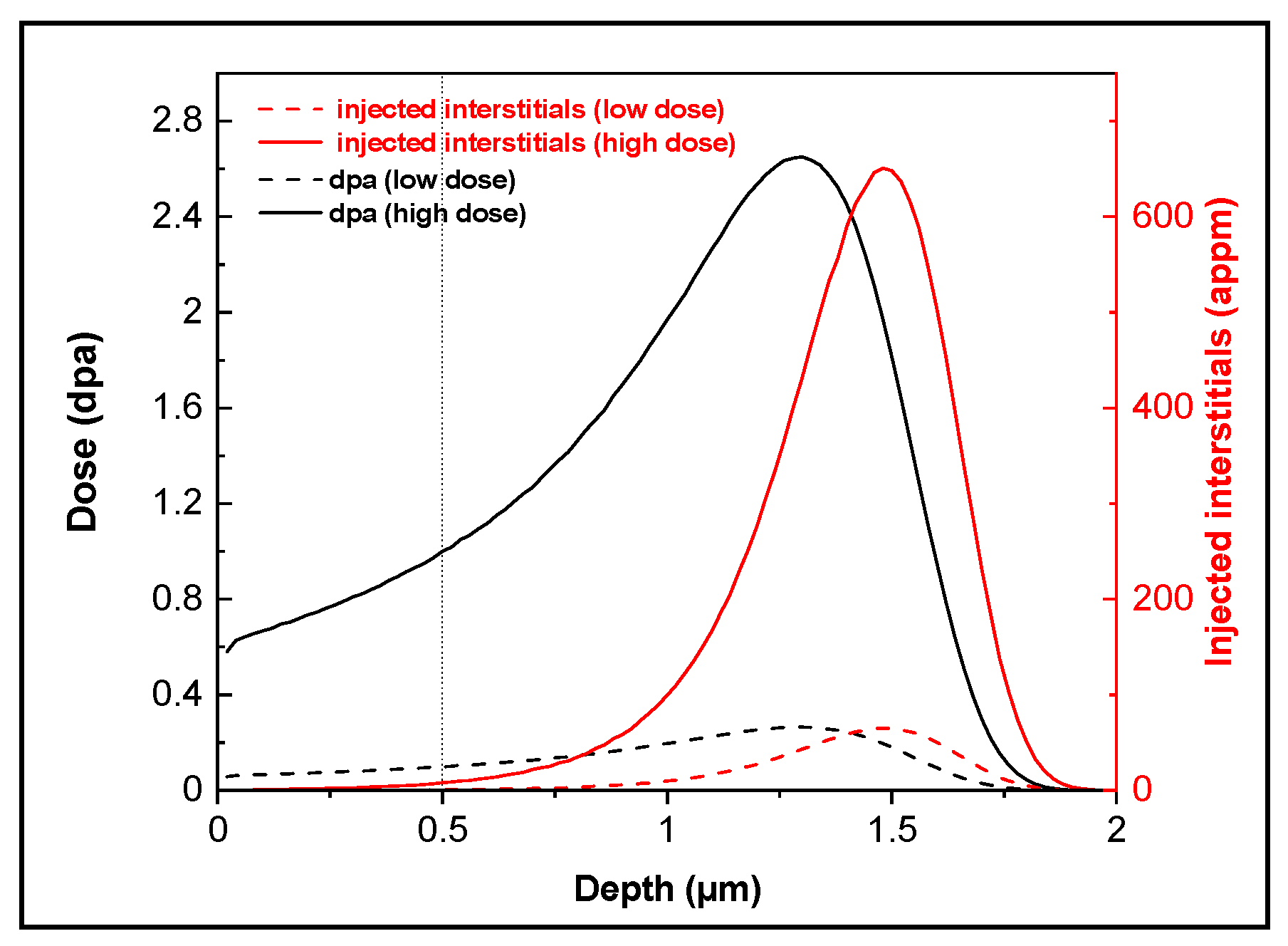
2.4. Ion Irradiation
2.5. STEM Study of Irradiation-Induced Defects
2.6. Effect of PIA
3. Results
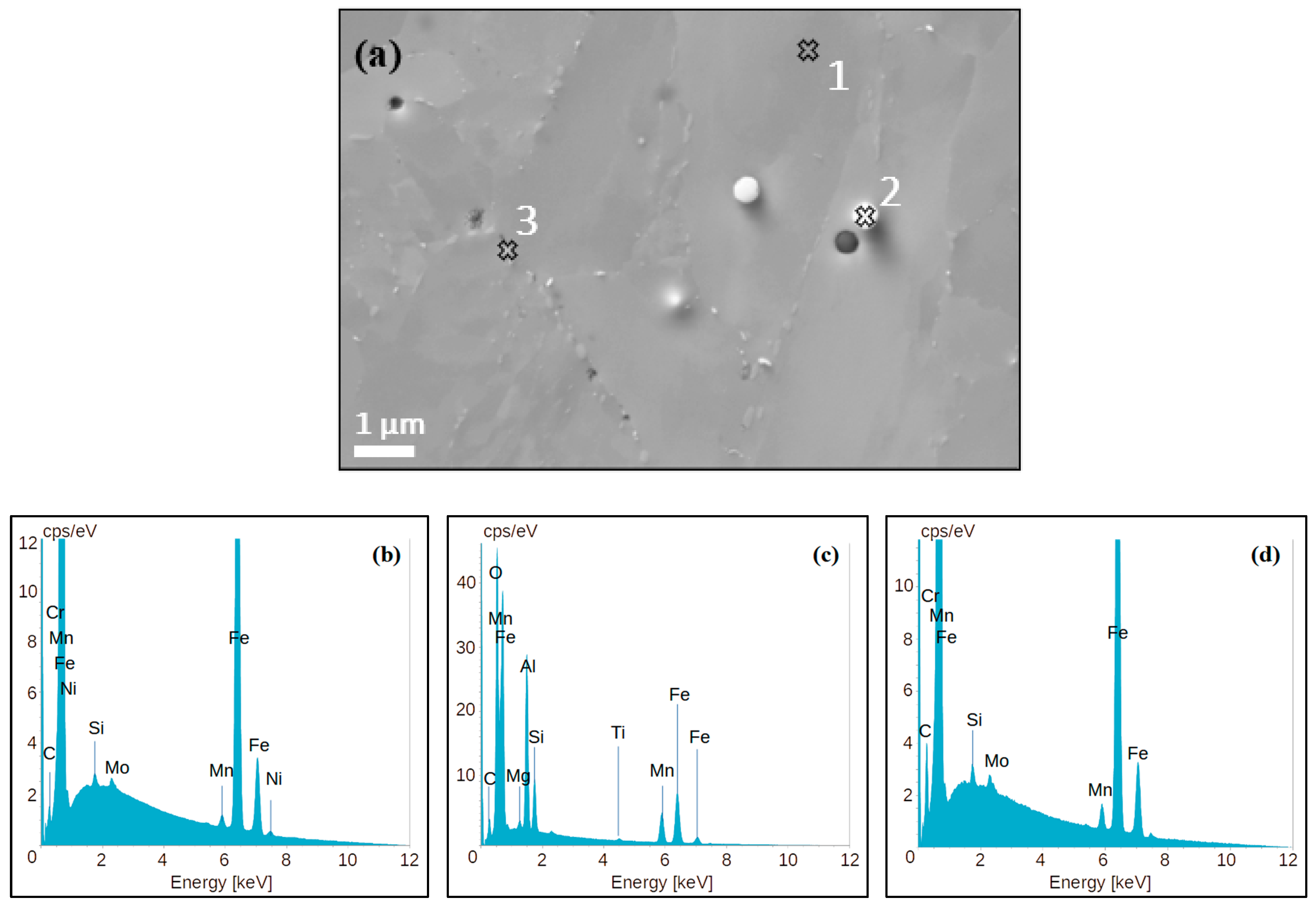
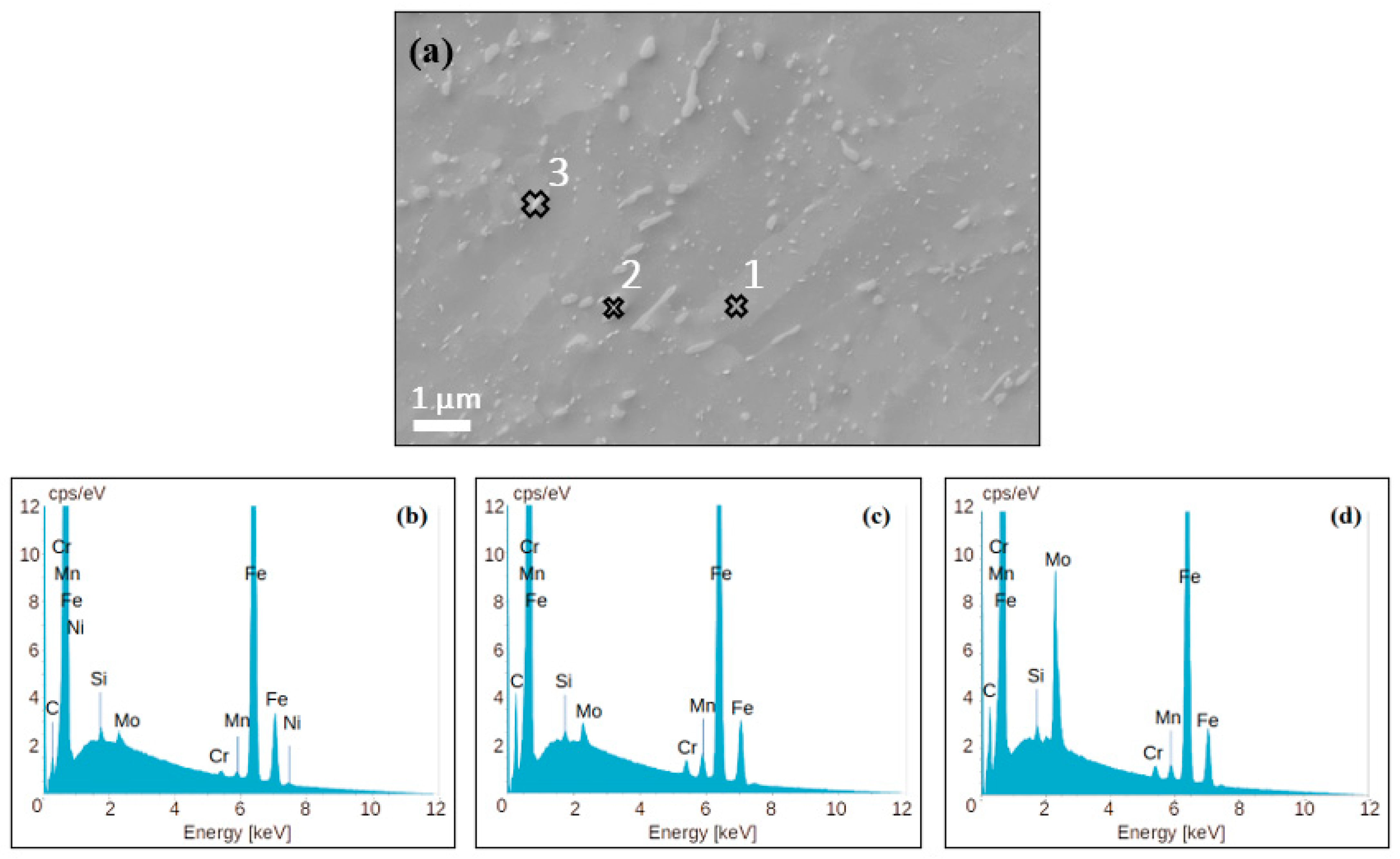
3.1. Unirradiated Microstructure
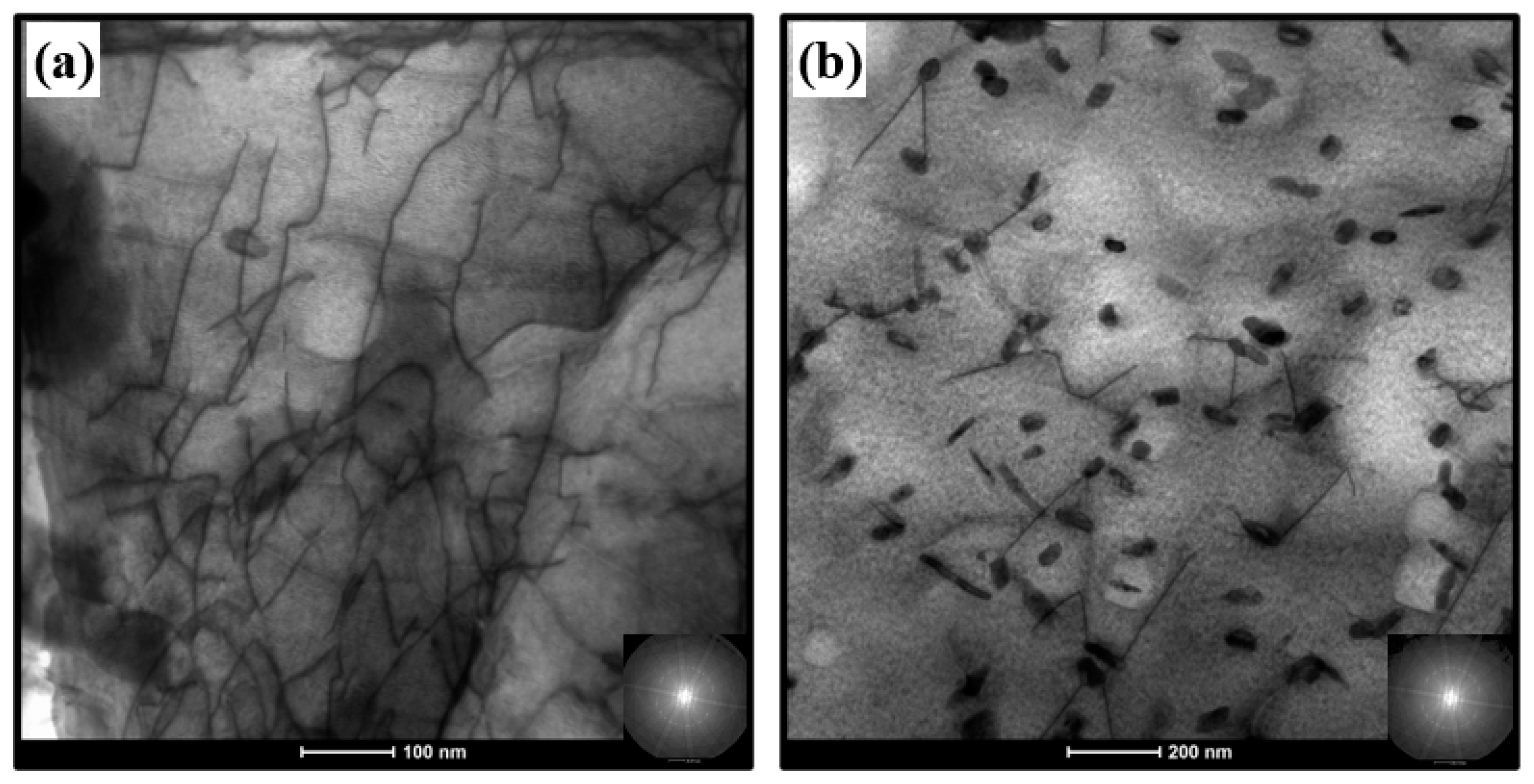
3.2. Ion-Irradiation Effect
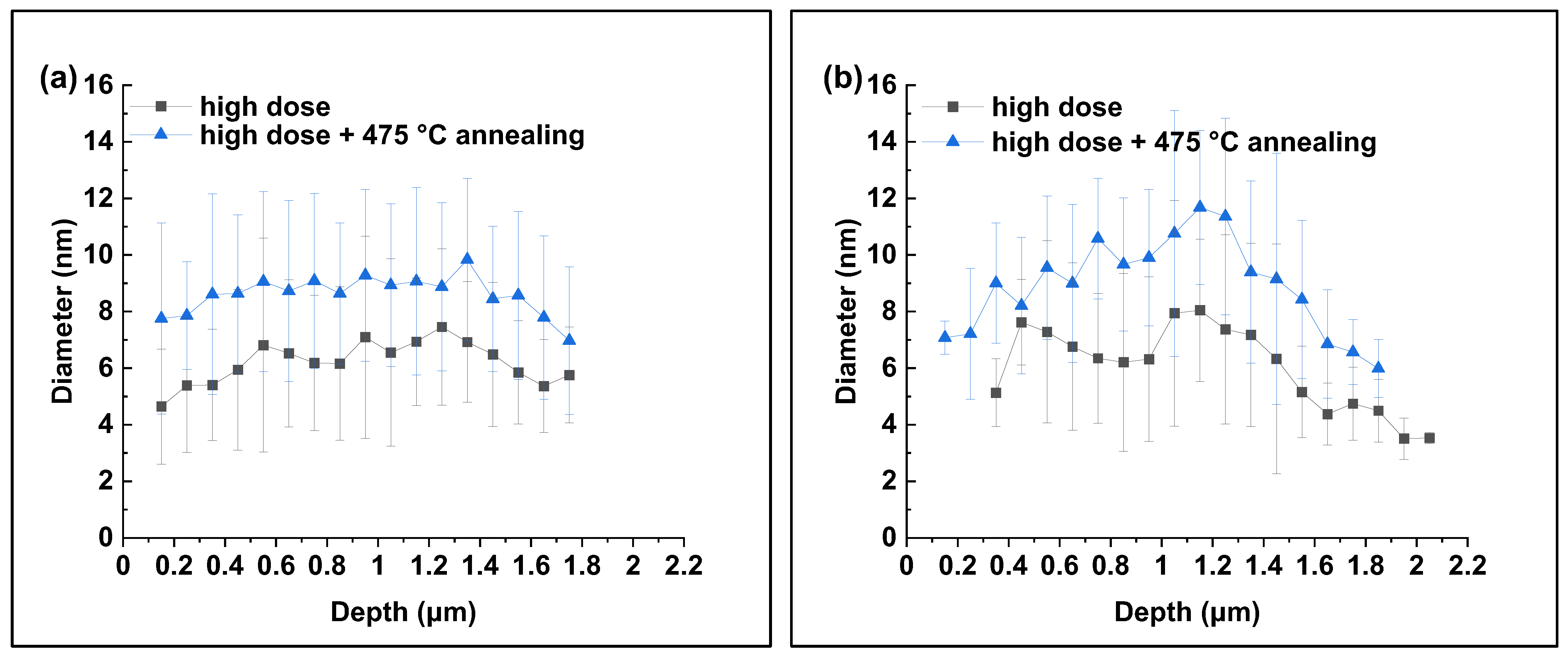
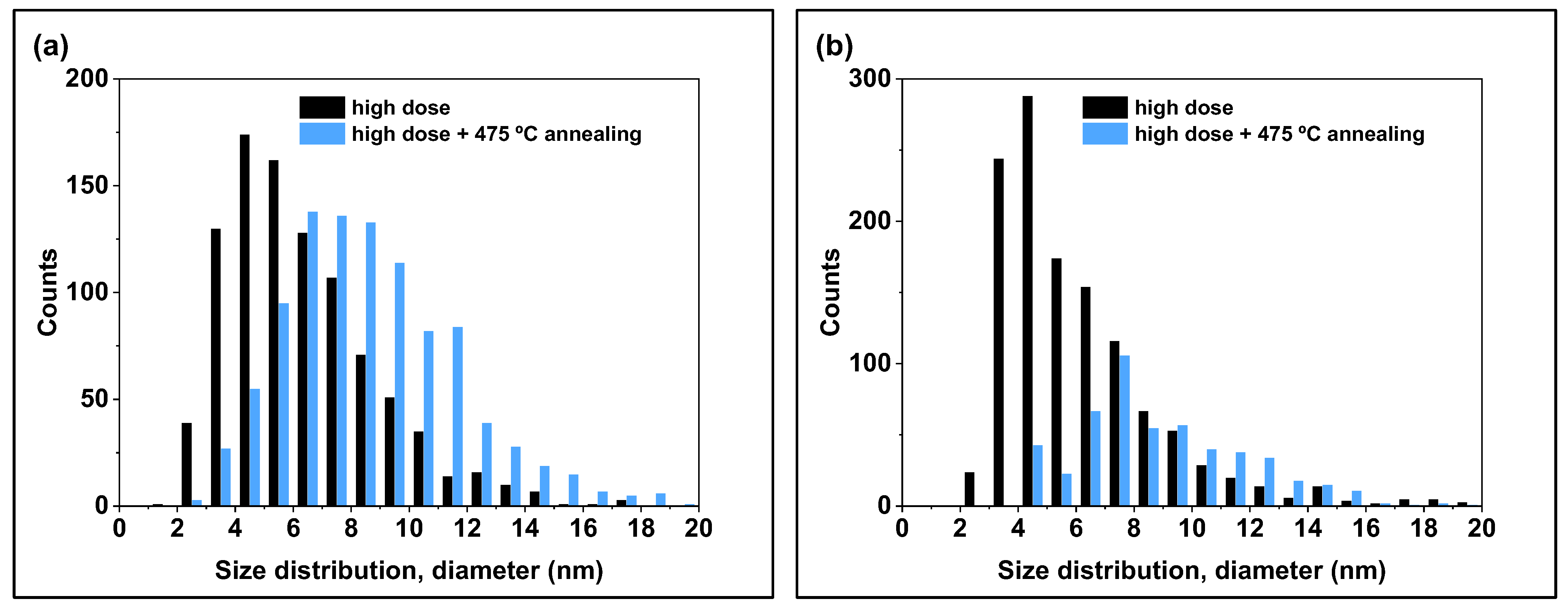
3.3. Effect of PIA
3.4. Determination of Burgers Vector of Loops
4. Discussion
4.1. Correlation between Initial Microstructure and Yield Stress
4.2. Effect of Dose
4.3. Comparison between ANP-6 and ANP-10
4.4. Effect of PIA
4.5. Comparison between Ion and Neutron Irradiation
5. Conclusions
- The yield stress calculated from the measured initial dislocation density, grain size, and number density of particles agrees well with the measured yield stress for both ANP-6 (~1% deviation) and ANP-10 (~10% deviation).
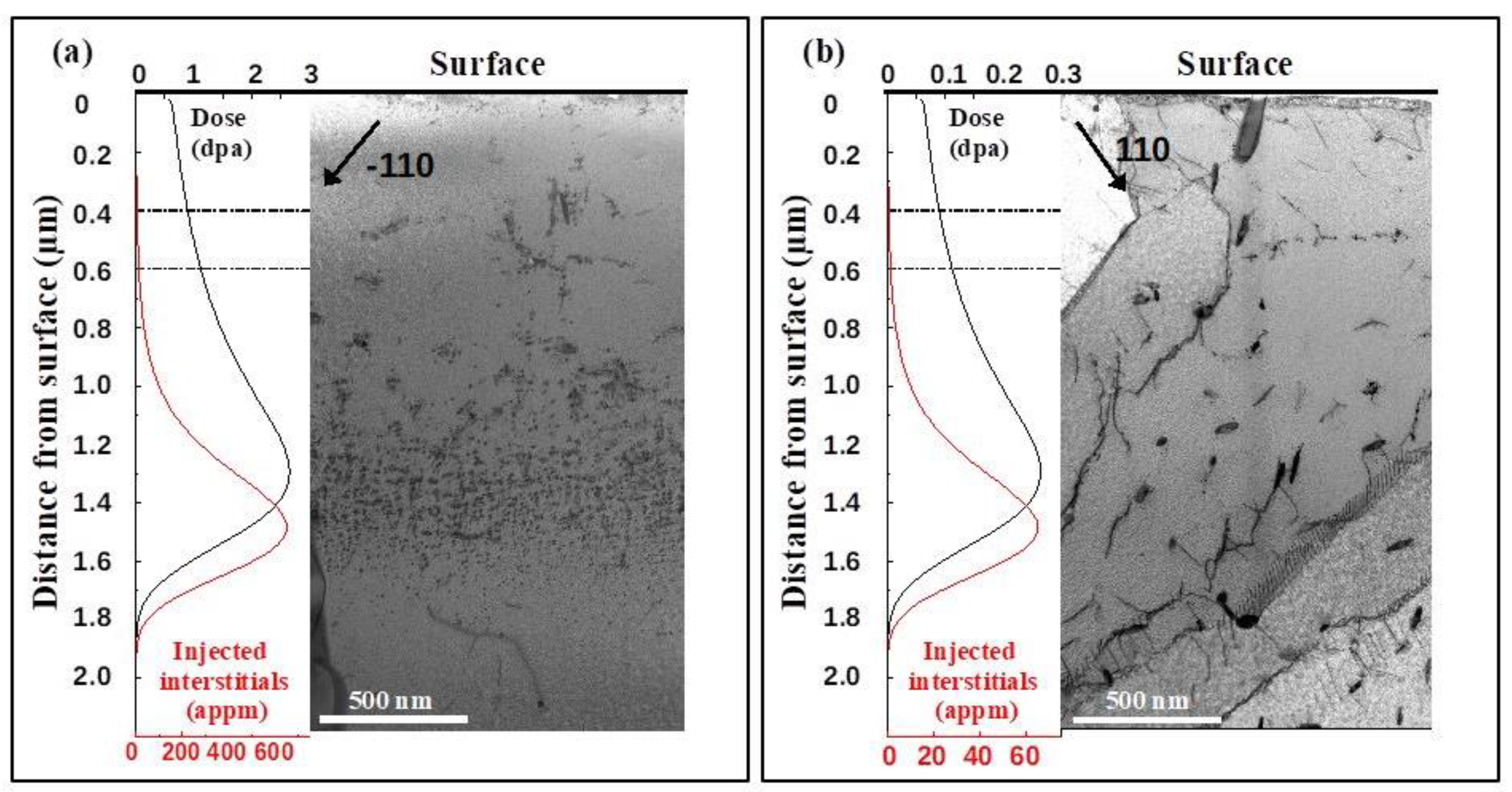
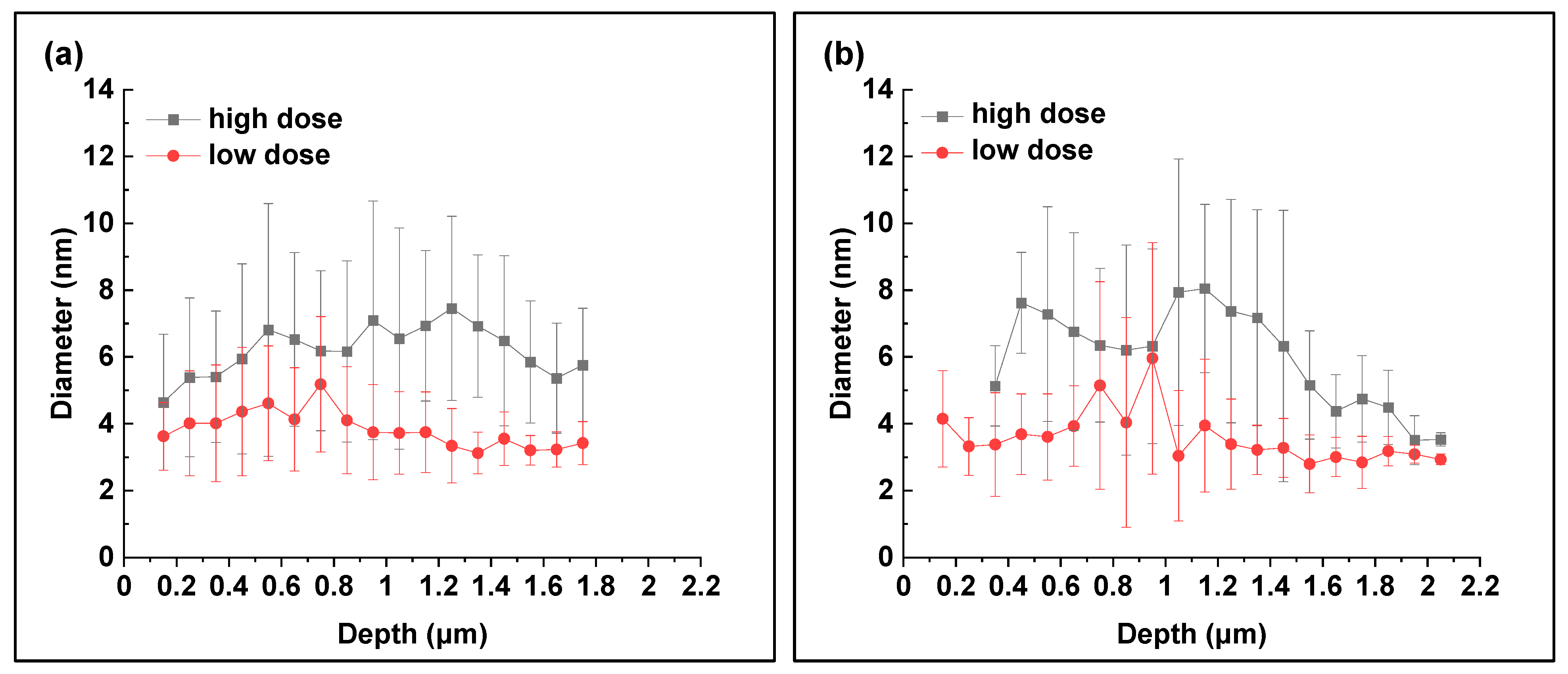
- The number densities of irradiation-induced loops peak close to the depths of maximum injected interstitials. The regions around the peaks have a band-like appearance. In the depth range between the surface and the band, loops are preferentially located close to point-defect sinks (line dislocations, grain boundaries, precipitates). The loop size does not strongly depend on depth.
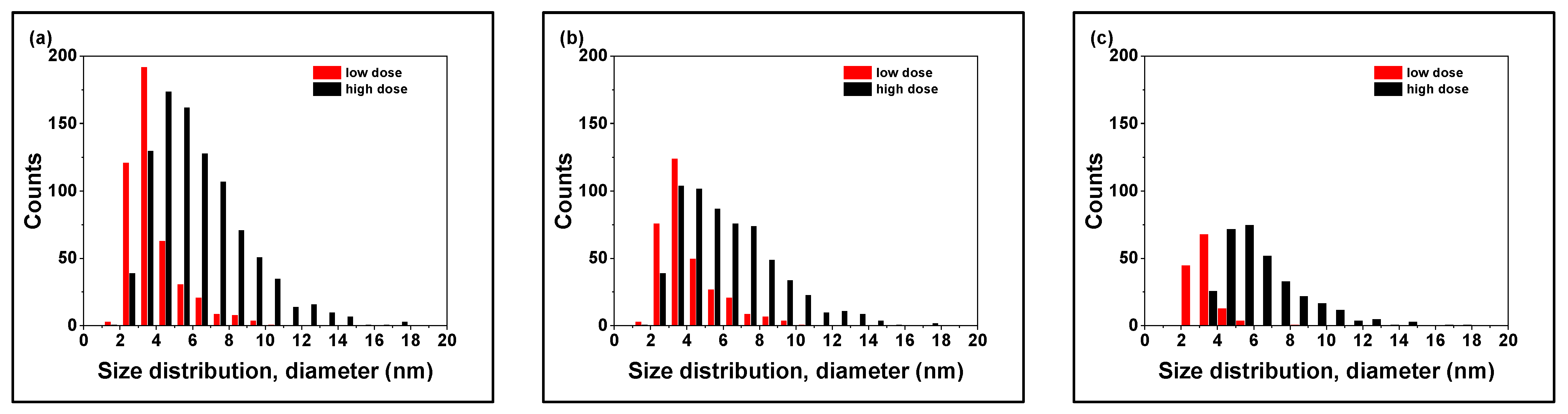
- Both the number density and size of irradiation-induced loops increase as functions of dose in such a way that the number density of point defects constituting the loops is linearly related to dose.
- For the 1 dpa irradiations of both materials, we have found ½ <111>- and <001>-type loops. In both materials, <001>-type loops are dominant representing approximately 70% of all loops.
- The total sink strengths calculated from the initial microstructures for ANP-6 and ANP-10 are both small (as compared to ODS steels) and comparable, which is consistent with the observation of similar irradiation-induced microstructures.
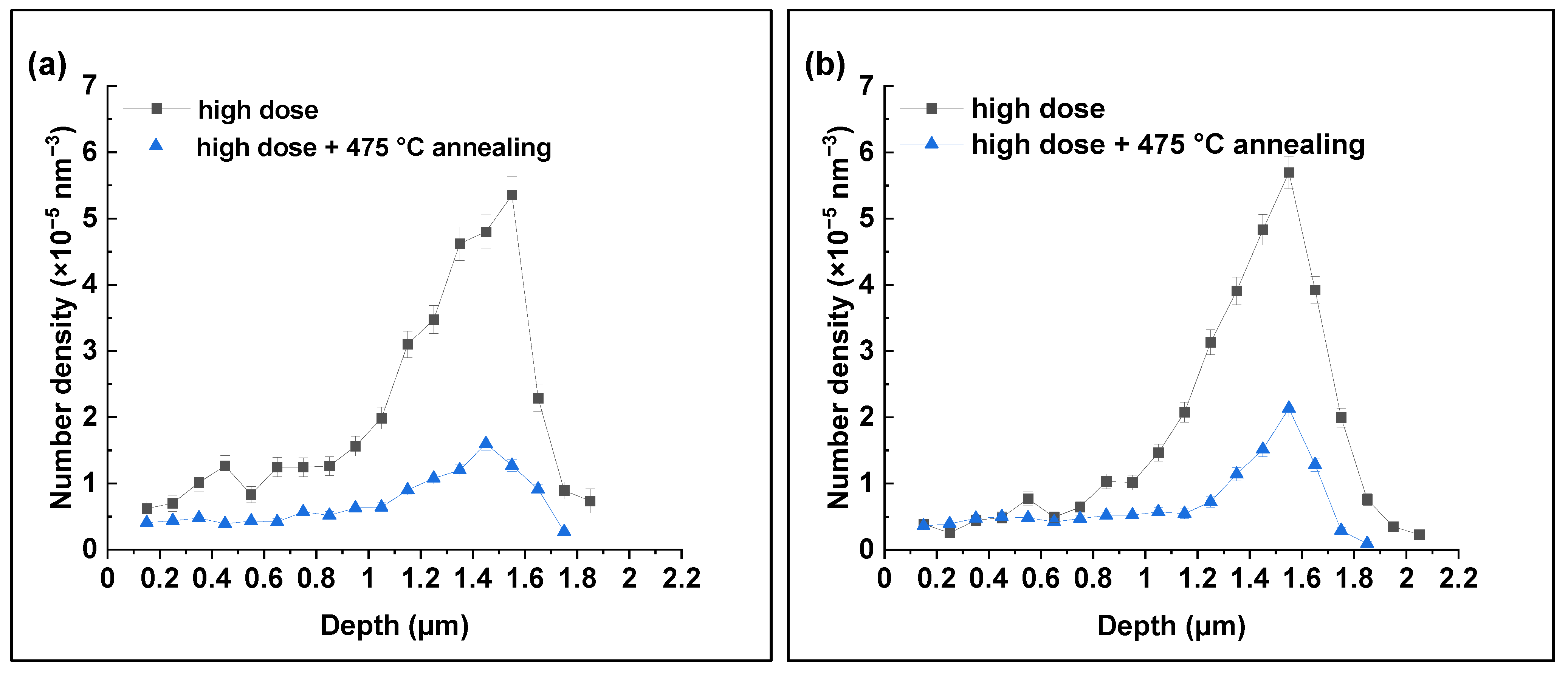
- PIA at 475 °C for 3 h leads to a reduction in the number density but an increase in the average diameter of loops for both materials in such a way that the total number of point defects constituting the loops decreases. PIA at 550 °C for 3 h carried out for ANP-10 completely removes irradiation-induced loops.
- The number density and size of loops representative of the zone between the surface and the band (safe zone) were compared with results reported for the same materials irradiated with neutrons. At comparable dose levels, the size of dislocation loops is almost the same for ion and neutron irradiation. The number density of loops for the ion-irradiated samples is significantly higher (by at least one order of magnitude) than for the neutron-irradiated samples. This is related to the higher dose rate of ion irradiation as compared to neutron irradiation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ballesteros, A.; Brumovský, M.; Davies, L.M.; Debarberis, L.; Jumel, S.; Kang, K.S.; Kryukov, A.; Kupca, L.; Langer, R.; Lott, R.; et al. Integrity of Reactor Pressure Vessels in Nuclear Power Plants: Assessment of Irradiation Embrittlement Effects in Reactor Pressure Vessel Steels; International Atomic Energy Agency: Vienna, Austria, 2009. [Google Scholar]
- Was, G.S. Fundamentals of Radiation Materials Science: Metals and Alloys; Springer: New York, NY, USA, 2016. [Google Scholar]
- Yuya, H.; Yabuuchi, K.; Kimura, A. Radiation embrittlement of clad-HAZ of RPV of a decommissioned BWR plant. J. Nucl. Mater. 2021, 557, 153300. [Google Scholar] [CrossRef]
- Rabung, M.; Kopp, M.; Gasparics, A.; Vértesy, G.; Szenthe, I.; Uytdenhouwen, I.; Szielasko, K. Micromagnetic characterization of operation-induced damage in charpy specimens of RPV steels. Appl. Sci. 2021, 11, 2917. [Google Scholar] [CrossRef]
- Kolluri, M.; ten Pierick, P.; Bakker, T.; Straathof, B.; Magielsen, A.; Szaraz, Z.; D’Agata, E.; Ohms, C.; Martin, O. Influence of Ni-Mn contents on the embrittlement of PWR RPV model steels irradiated to high fluences relevant for LTO beyond 60 years. J. Nucl. Mater. 2021, 553, 153036. [Google Scholar] [CrossRef]
- Hata, K.; Takamizawa, H.; Hojo, T.; Ebihara, K.; Nishiyama, Y.; Nagai, Y. Grain-boundary phosphorus segregation in highly neutron-irradiated reactor pressure vessel steels and its effect on irradiation embrittlement. J. Nucl. Mater. 2021, 543, 152564. [Google Scholar] [CrossRef]
- Kočík, J.; Keilova, E.; Čížek, J.; Prochazka, I. TEM and PAS study of neutron irradiated VVER-type RPV steels. J. Nucl. Mater. 2002, 303, 52–64. [Google Scholar] [CrossRef]
- Meslin, E.; Lambrecht, M.; Hernández-Mayoral, M.; Bergner, F.; Malerba, L.; Pareige, P.; Radiguet, B.; Barbu, A.; Gómez-Briceño, D.; Ulbricht, A. Characterization of neutron-irradiated ferritic model alloys and a RPV steel from combined APT, SANS, TEM and PAS analyses. J. Nucl. Mater. 2010, 406, 73–83. [Google Scholar] [CrossRef]
- Hernández-Mayoral, M.; Gómez-Briceño, D. Transmission electron microscopy study on neutron irradiated pure iron and RPV model alloys. J. Nucl. Mater. 2010, 399, 146–153. [Google Scholar] [CrossRef]
- Sprouster, D.; Sinsheimer, J.; Dooryhee, E.; Ghose, S.; Wells, P.; Stan, T.; Almirall, N.; Odette, G.; Ecker, L. Structural characterization of nanoscale intermetallic precipitates in highly neutron irradiated reactor pressure vessel steels. Scr. Mater. 2016, 113, 18–22. [Google Scholar] [CrossRef] [Green Version]
- Fujita, T.; Hirabayashi, J.; Katayama, Y.; Kano, F.; Watanabe, H. Contribution of dislocation loop to radiation-hardening of RPV steels studied by STEM/EDS with surveillance test pieces. J. Nucl. Mater. 2022, 572, 154055. [Google Scholar] [CrossRef]
- Carter, M.; Gasparrini, C.; Douglas, J.O.; Riddle, N.; Edwards, L.; Bagot, P.A.; Hardie, C.D.; Wenman, M.R.; Moody, M.P. On the influence of microstructure on the neutron irradiation response of HIPed SA508 steel for nuclear applications. J. Nucl. Mater. 2022, 559, 153435. [Google Scholar] [CrossRef]
- Naziris, F.; Kolluri, M.; Bakker, T.; Hageman, S.; Petrosyan, V.; Petrosyan, A.; Sevikyan, G. Mechanical properties and microstructure of VVER 440 RPV steels irradiated to extremely high fluences and the effect of recovery annealing. J. Nucl. Mater. 2021, 551, 152951. [Google Scholar] [CrossRef]
- Kolluri, M.; Martin, O.; Naziris, F.; D’Agata, E.; Gillemot, F.; Brumovsky, M.; Ulbricht, A.; Autio, J.; Shugailo, O.; Horvath, A. Structural MATerias research on parameters influencing the material properties of RPV steels for safe long-term operation of PWR NPPs. Nucl. Eng. Des. 2023, 406, 112236. [Google Scholar] [CrossRef]
- Jiao, Z.; Michalicka, J.; Was, G. Self-ion emulation of high dose neutron irradiated microstructure in stainless steels. J. Nucl. Mater. 2018, 501, 312–318. [Google Scholar] [CrossRef]
- Xu, S.; Yao, Z.; Jenkins, M. TEM characterisation of heavy-ion irradiation damage in FeCr alloys. J. Nucl. Mater. 2009, 386, 161–164. [Google Scholar] [CrossRef]
- Taller, S.; VanCoevering, G.; Wirth, B.D.; Was, G.S. Predicting structural material degradation in advanced nuclear reactors with ion irradiation. Sci. Rep. 2021, 11, 2949. [Google Scholar] [CrossRef] [PubMed]
- Was, G.; Jiao, Z.; Getto, E.; Sun, K.; Monterrosa, A.; Maloy, S.; Anderoglu, O.; Sencer, B.; Hackett, M. Emulation of reactor irradiation damage using ion beams. Scr. Mater. 2014, 88, 33–36. [Google Scholar] [CrossRef]
- Bai, X.; Han, Y.; Liaw, P.K.; Wei, L. Effect of Ion Irradiation on Surface Microstructure and Nano-Hardness of SA508-IV Reactor Pressure Vessel Steel. J. Mater. Eng. Perform. 2022, 31, 1981–1990. [Google Scholar] [CrossRef]
- Iwata, K.; Takamizawa, H.; Ha, Y.; Shimodaira, M.; Okamoto, Y.; Honda, M.; Katsuyama, J.; Nishiyama, Y. EXAFS studies for atomic structural change induced by ion irradiation of a reactor pressure vessel steel. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2022, 511, 143–152. [Google Scholar] [CrossRef]
- Gasparrini, C.; Xu, A.; Short, K.; Wei, T.; Davis, J.; Palmer, T.; Bhattacharyya, D.; Edwards, L.; Wenman, M. Micromechanical testing of unirradiated and helium ion irradiated SA508 reactor pressure vessel steels: Nanoindentation vs in-situ microtensile testing. Mater. Sci. Eng. A 2020, 796, 139942. [Google Scholar] [CrossRef]
- Zinkle, S.; Snead, L. Opportunities and limitations for ion beams in radiation effects studies: Bridging critical gaps between charged particle and neutron irradiations. Scr. Mater. 2018, 143, 154–160. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, Q.; Song, L.; Zhang, W.; She, M.; Zhu, F. Microstructure Evolution of Reactor Pressure Vessel A508-3 Steel under High-Dose Heavy Ion Irradiation. Crystals 2022, 12, 1091. [Google Scholar] [CrossRef]
- Ding, Z.; Han, X.; Yang, Y.; Chen, Y.; Zhang, X.; Niu, M.; Zhang, C.; Liu, X.; Xue, F. Characterization of microstructures and mechanical property of Fe-ion-irradiated China A508-3 steel. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2021, 504, 14–20. [Google Scholar] [CrossRef]
- Fujii, K.; Fukuya, K. Characterization of defect clusters in ion-irradiated A533B steel. J. Nucl. Mater. 2005, 336, 323–330. [Google Scholar] [CrossRef]
- Watanabe, H.; Masaki, S.; Masubuchi, S.; Yoshida, N.; Kamada, Y. Radiation induced hardening of ion irradiated RPV steels. J. Nucl. Mater. 2011, 417, 932–935. [Google Scholar] [CrossRef]
- Stoller, R.E.; Toloczko, M.B.; Was, G.S.; Certain, A.G.; Dwaraknath, S.; Garner, F.A. On the use of SRIM for computing radiation damage exposure. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2013, 310, 75–80. [Google Scholar] [CrossRef]
- Eyre, B.; Bullough, R. On the formation of interstitial loops in bcc metals. Philos. Mag. 1965, 12, 31–39. [Google Scholar] [CrossRef]
- Hernández-Mayoral, M.; Heintze, C.; Oñorbe, E. Transmission electron microscopy investigation of the microstructure of Fe–Cr alloys induced by neutron and ion irradiation at 300 °C. J. Nucl. Mater. 2016, 474, 88–98. [Google Scholar] [CrossRef]
- Hein, H. Deliverable of Euratom Project SOTERIA, D3.5—Set of Guidelines on Use of Experiments Carried Out in WP3, Grant Agreement No. 661913, 2019. Framatome GmbH, Erlangen, Germany.
- Iza-Mendia, A.; Gutiérrez, I. Generalization of the existing relations between microstructure and yield stress from ferrite–pearlite to high strength steels. Mater. Sci. Eng. A 2013, 561, 40–51. [Google Scholar] [CrossRef]
- Chauhan, A.; Bergner, F.; Etienne, A.; Aktaa, J.; De Carlan, Y.; Heintze, C.; Litvinov, D.; Hernandez-Mayoral, M.; Oñorbe, E.; Radiguet, B. Microstructure characterization and strengthening mechanisms of oxide dispersion strengthened (ODS) Fe-9% Cr and Fe-14% Cr extruded bars. J. Nucl. Mater. 2017, 495, 6–19. [Google Scholar] [CrossRef]
- Dadé, M.; Malaplate, J.; Garnier, J.; De Geuser, F.; Barcelo, F.; Wident, P.; Deschamps, A. Influence of microstructural parameters on the mechanical properties of oxide dispersion strengthened Fe-14Cr steels. Acta Mater. 2017, 127, 165–177. [Google Scholar] [CrossRef] [Green Version]
- Monnet, G. Multiscale modeling of irradiation hardening: Application to important nuclear materials. J. Nucl. Mater. 2018, 508, 609–627. [Google Scholar] [CrossRef]
- Praud, M.; Mompiou, F.; Malaplate, J.; Caillard, D.; Garnier, J.; Steckmeyer, A.; Fournier, B. Study of the deformation mechanisms in a Fe–14% Cr ODS alloy. J. Nucl. Mater. 2012, 428, 90–97. [Google Scholar] [CrossRef]
- Ghosh, G.; Olson, G. The isotropic shear modulus of multicomponent Fe-base solid solutions. Acta Mater. 2002, 50, 2655–2675. [Google Scholar] [CrossRef]
- Stoller, R.; Zinkle, S. On the relationship between uniaxial yield strength and resolved shear stress in polycrystalline materials. J. Nucl. Mater. 2000, 283, 349–352. [Google Scholar] [CrossRef]
- Foreman, A.; Makin, M. Dislocation movement through random arrays of obstacles. Philos. Mag. 1966, 14, 911–924. [Google Scholar] [CrossRef]
- Zinkle, S.J.; Snead, L.L. Designing radiation resistance in materials for fusion energy. Annu. Rev. Mater. Res. 2014, 44, 241–267. [Google Scholar] [CrossRef]
- Odette, G.; Alinger, M.; Wirth, B. Recent developments in irradiation-resistant steels. Annu. Rev. Mater. Res. 2008, 38, 471–503. [Google Scholar] [CrossRef]
- Duan, B.; Heintze, C.; Bergner, F.; Ulbricht, A.; Akhmadaliev, S.; Oñorbe, E.; de Carlan, Y.; Wang, T. The effect of the initial microstructure in terms of sink strength on the ion-irradiation-induced hardening of ODS alloys studied by nanoindentation. J. Nucl. Mater. 2017, 495, 118–127. [Google Scholar] [CrossRef]
- Chauhan, A.; Yuan, Q.; Dethloff, C.; Gaganidze, E.; Aktaa, J. Post-irradiation annealing of neutron-irradiated EUROFER97. J. Nucl. Mater. 2021, 548, 152863. [Google Scholar] [CrossRef]
- Yuan, Q.; Chauhan, A.; Gaganidze, E.; Aktaa, J. Direct observation of dislocation loops shrinkage upon annealing neutron-irradiated Fe–9Cr alloy. J. Nucl. Mater. 2020, 542, 152401. [Google Scholar] [CrossRef]
- Ulbricht, A.; Hernandez-Mayoral, M.; Onorbe, E.; Etienne, A.; Radiguet, B.; Hirschmann, E.; Wagner, A.; Hein, H.; Bergner, F. Effect of Neutron Flux on an Irradiation-Induced Microstructure and Hardening of Reactor Pressure Vessel Steels. Metals 2022, 12, 369. [Google Scholar] [CrossRef]
- Mansur, L. Correlation of neutron and heavy-ion damage: II. The predicted temperature shift if swelling with changes in radiation dose rate. J. Nucl. Mater. 1978, 78, 156–160. [Google Scholar] [CrossRef]
- Mansur, L. Theory of transitions in dose dependence of radiation effects in structural alloys. J. Nucl. Mater. 1993, 206, 306–323. [Google Scholar] [CrossRef]
- Duparc, A.H.; Moingeon, C.; Smetniansky-de-Grande, N.; Barbu, A. Microstructure modelling of ferritic alloys under high flux 1 MeV electron irradiations. J. Nucl. Mater. 2002, 302, 143–155. [Google Scholar] [CrossRef]










| Material | C | Mn | Si | Cr | Ni | Mo | V | P | Cu |
|---|---|---|---|---|---|---|---|---|---|
| ANP-6 | 0.05 | 1.41 | 0.15 | 0.07 | 1.69 | 0.46 | 0.004 | 0.012 | 0.08 |
| ANP-10 | 0.18 | 0.81 | 0.15 | 0.40 | 0.96 | 0.53 | <0.01 | 0.006 | 0.09 |
| Ion Type | Energy (MeV) | Flux (cm−2/s) | Fluence (cm−2) | Irradiation Time (h) | Temperature (°C) | Dose at Depth of 0.5 µm (dpa) |
|---|---|---|---|---|---|---|
| Fe2+ | 5 | 1.25 × 1011 | 2.67 × 1014 | 0.6 | 300 | 0.1 |
| Fe2+ | 5 | 1.25 × 1011 | 2.67 × 1015 | 6 | 300 | 1 |
| b | ½ [11] | ½ [11] | ½ [11] | ½ [111] | [100] | [010] | [001] | |
|---|---|---|---|---|---|---|---|---|
| g | ||||||||
| [10] | V | V | 0 | 0 | V | V | 0 | |
| [110] | 0 | 0 | V | V | V | V | 0 | |
| Properties | ANP-6 | ANP-10 |
|---|---|---|
| Grain size (µm) by EBSD | 2.9 | 5.5 |
| Initial dislocation density (m−2) by STEM | 3.2 × 1014 | 5.2 × 1013 |
| Mean size of oxide particles (nm) | 300 | - |
| Mean size of carbide particles (nm) | 65 | 67 |
| Number density of oxide particles (m−3) | 2.7 × 1017 | - |
| Number density of carbide particles (m−3) | 8.6 × 1019 | 2.9 × 1020 |
| Yield stress (MPa) | 555 | 422 |
| Material | Peak Positions (μm) for: | |||
|---|---|---|---|---|
| Dose | Injected Interstitials | Nd for Low Dose | Nd for High Dose | |
| ANP-6 | 1.3 | 1.48 | 1.35 | 1.55 |
| ANP-10 | 1.3 | 1.48 | 1.45 | 1.55 |
| Sample | Number Density (×10−5 nm−3) | Diameter (nm) |
|---|---|---|
| ANP-6, low dose | 1.4 ± 0.2 | 3.8 ± 1.2 |
| ANP-6, high dose | 5.4 ± 0.3 | 6.2 ± 2.5 |
| ANP-10, low dose | 1.3 ± 0.1 | 3.6 ± 1.4 |
| ANP-10, high dose | 5.7 ± 0.2 | 6.0 ± 2.3 |
| Sample | Number Density at Peak Position (×10−5 nm−3) | Diameter (nm) |
|---|---|---|
| ANP-6, high dose | 5.4 ± 0.3 | 6.2 ± 2.5 |
| ANP-6, high dose + 475 °C annealing | 1.6 ± 0.1 | 8.6 ± 3.0 |
| ANP-10, high dose | 5.7 ± 0.2 | 6.0 ± 2.3 |
| ANP-10, high dose + 475 °C annealing | 2.1 ± 0.1 | 8.9 ± 2.5 |
| ANP-10, high dose + 550 °C annealing | No loops | - |
| Type of Loops | ANP-6 (High Dose) | ANP-10 (High Dose) |
|---|---|---|
| <001> | 63 ± 7% (147) | 72 ± 8% (105) |
| ½ <111> | 37 ± 7% (85) | 28 ± 8% (41) |
| Material | Experimental Yield Stress σy (MPa) | Grain Size (µm) | Initial Dislocation Density (m−2) | Carbides Number Density (m−3) | σg (MPa) | σd (MPa) | σp (MPa) | Calculated Yield Stress σy (MPa) |
|---|---|---|---|---|---|---|---|---|
| ANP-6 | 555 | 2.9 | 3.20 × 1014 | 8.62 × 1019 | 157 | 384 | 122 | 547 |
| ANP-10 | 422 | 5.5 | 5.20 × 1013 | 2.93 × 1020 | 114 | 155 | 229 | 381 |
| Material | ƒe | ƒn | ƒd | ƒp |
|---|---|---|---|---|
| ANP-6 | 10 | 3.9 ± 0.6 | 1.6 ± 0.8 | 10.0 ± 10.4 |
| ANP-10 | 10 | 4.4 ± 0.4 | 1.7 ± 0.9 | 12.7 ± 13.9 |
| Material | Total Sink Strength, Stotal (×1014 m−2) | Sink strength of Dislocations, Sd (×1014 m−2) | Sink Strength of Particles, Sp (×1014 m−2) | Sink Strength of Grain Boundaries, Sg (×1014 m−2) |
|---|---|---|---|---|
| ANP-6 | 4.7 | 3.8 | 0.4 | 0.5 |
| ANP-10 | 2.0 | 0.6 | 1.2 | 0.2 |
| ODS alloys | 30–80 | 0.6–6 | 27–63.6 | 2.7–12.3 |
| ANP-6 (Neutron) | ANP-6 (Ion) | ANP-10 (Neutron) | ANP-10 (Ion) | |
|---|---|---|---|---|
| Neutron fluence (cm−2) | 5.3 × 1019 | - | 3.4 × 1019 | - |
| Doses (dpa) | 0.080 | 0.1 (at 0.5 µm) | 0.051 | 0.1 (at 0.5 µm) |
| Dose rate (dpa/s) | 3.5 × 10−9 | 4.63 × 10−5 | 7 × 10−11 | 4.63 × 10−5 |
| Temperature (°C) | 285 | 300 | 300 | 300 |
| Number density of loops (×10−5 nm−3) | 0.017 ± 0.005 | 0.61 ± 0.11 | 0.002 ± 0.003 | 0.39 ± 0.03 |
| Average diameter of loops (nm) | 3.8 ± 0.1 | 4.5 ± 1.8 | 4.0 ± 0.2 | 3.7 ± 1.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, L.; Chekhonin, P.; Akhmadaliev, S.; Brandenburg, J.-E.; Bergner, F. Microstructural Characterization of Reactor Pressure Vessel Steels. Metals 2023, 13, 1339. https://doi.org/10.3390/met13081339
Lai L, Chekhonin P, Akhmadaliev S, Brandenburg J-E, Bergner F. Microstructural Characterization of Reactor Pressure Vessel Steels. Metals. 2023; 13(8):1339. https://doi.org/10.3390/met13081339
Chicago/Turabian StyleLai, Libang, Paul Chekhonin, Shavkat Akhmadaliev, Jann-Erik Brandenburg, and Frank Bergner. 2023. "Microstructural Characterization of Reactor Pressure Vessel Steels" Metals 13, no. 8: 1339. https://doi.org/10.3390/met13081339
APA StyleLai, L., Chekhonin, P., Akhmadaliev, S., Brandenburg, J.-E., & Bergner, F. (2023). Microstructural Characterization of Reactor Pressure Vessel Steels. Metals, 13(8), 1339. https://doi.org/10.3390/met13081339







