Investigation on the Effect of Mesomixing on Crystal Quality during Antisolvent Crystallization of Nd2(SO4)3·8H2O
Abstract
1. Introduction
2. Experimental Setup and Procedure
2.1. Thermodynamic Modelling
2.2. Leach Liquor Preparation
2.3. Measurement Techniques
2.4. Experimental Procedures
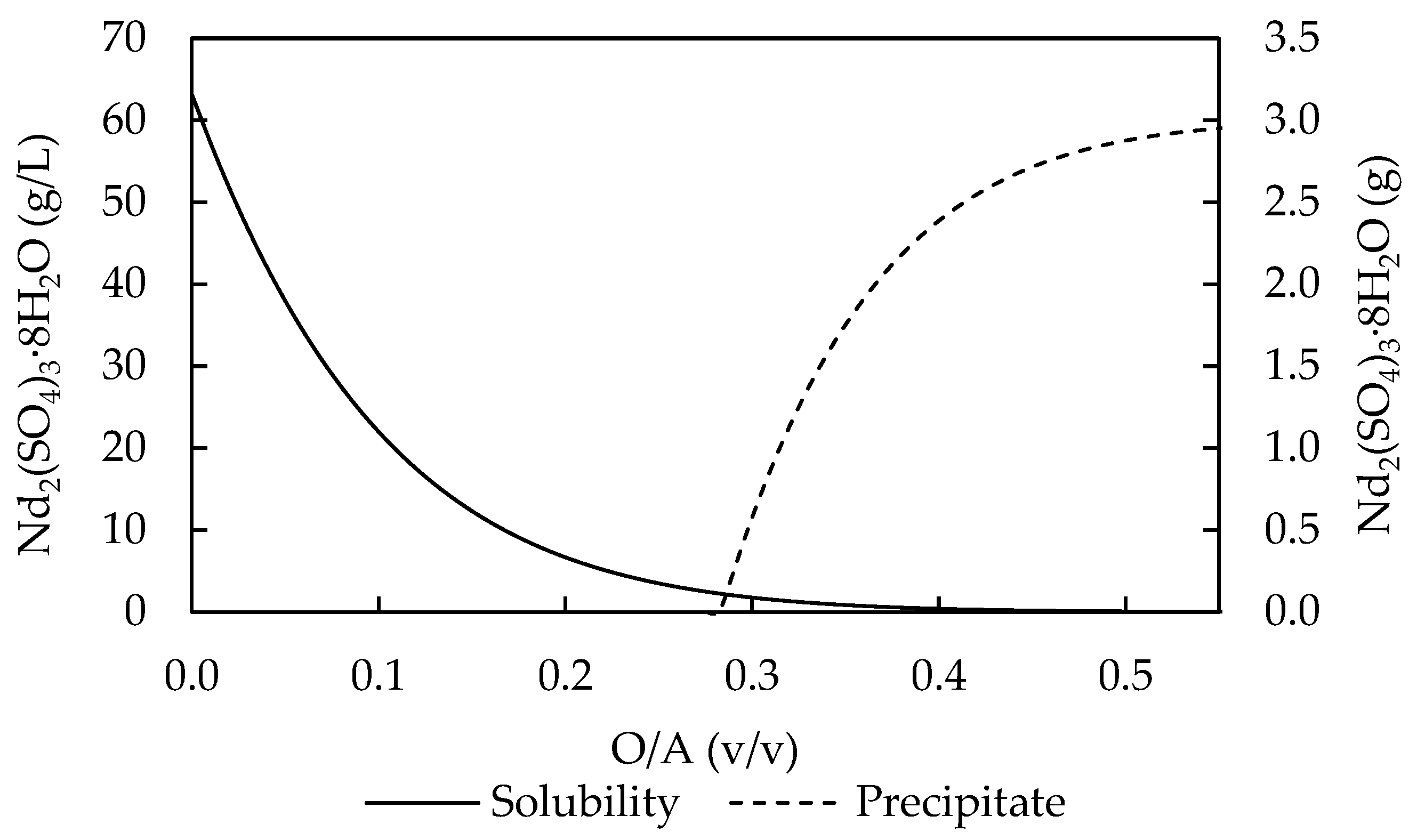
2.4.1. Equilibrium Studies
2.4.2. Effect of Mixing Intensity in the Non-Confined Impinging Jet Mixer (NCIJM) Coupled with Secondary Mixing in the Stirred Batch Crystallizer on Crystal Quality
2.4.3. Effect of Mixing Intensity in the NCIJM on Crystal Quality
3. Results and Discussion
3.1. Thermodynamic Modelling and Equilibrium Studies
3.2. Effect of Mixing Intensity on Crystal Quality
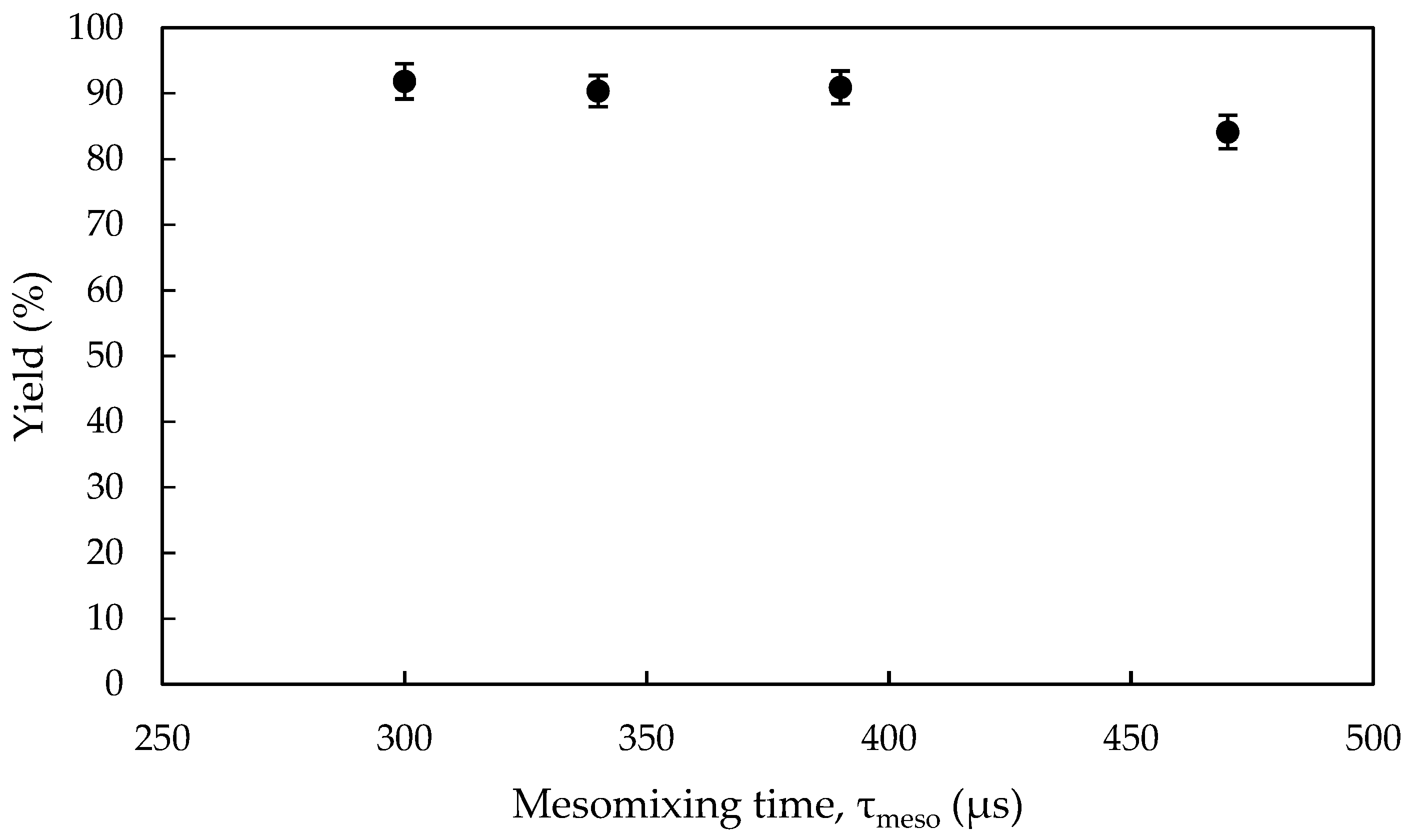
3.2.1. Effect of Power Input on Mixing Time Constants
3.2.2. Effect of Mixing Intensity in the NCIJM and Secondary Mixing in the Stirred Batch Crystallizer on Crystal Quality
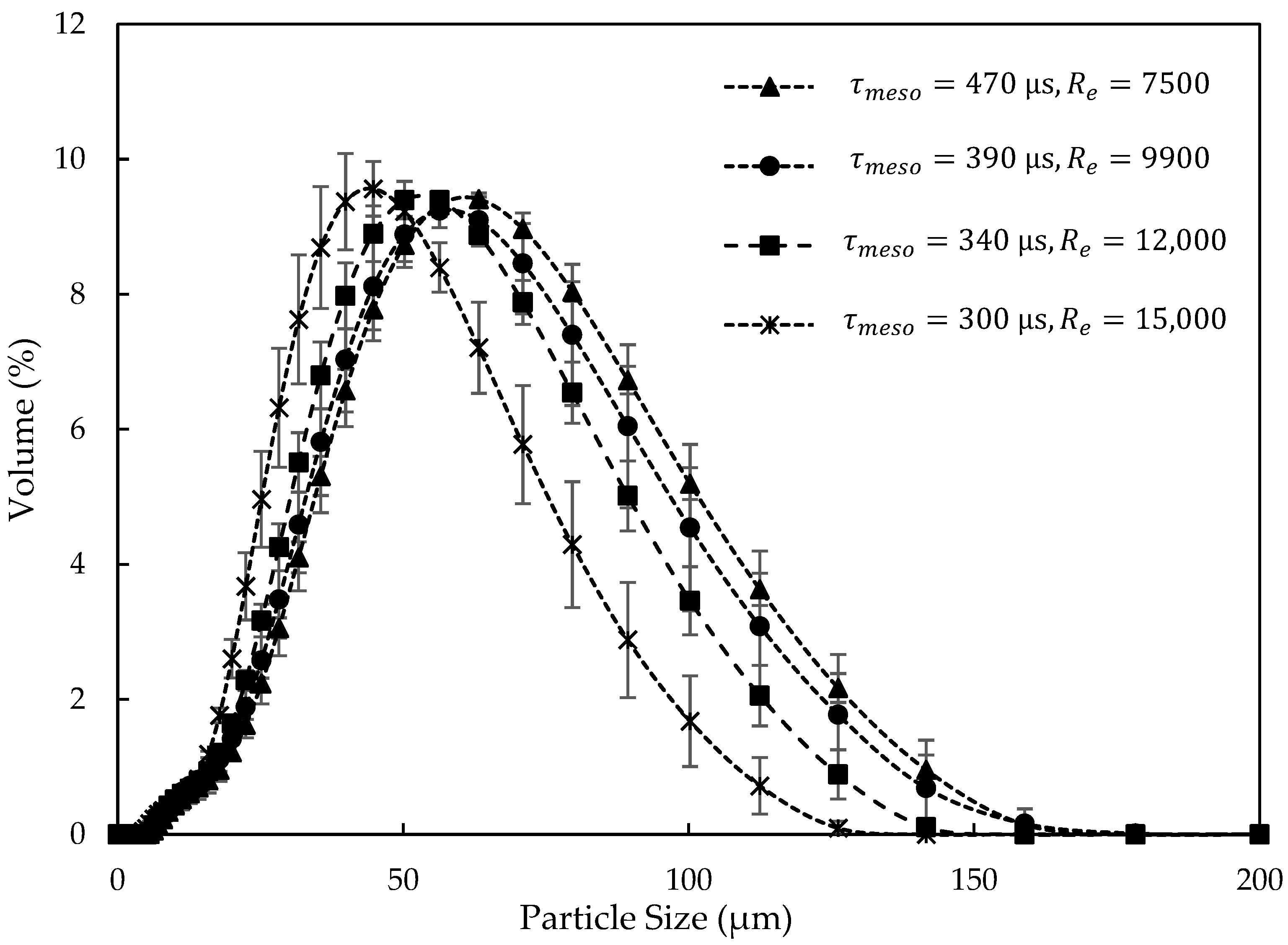
3.2.3. Effect of Mixing Intensity in the NCIJM on Crystal Quality
3.2.4. Effect of Mixing Intensity in the NCIJM on Crystal Morphology
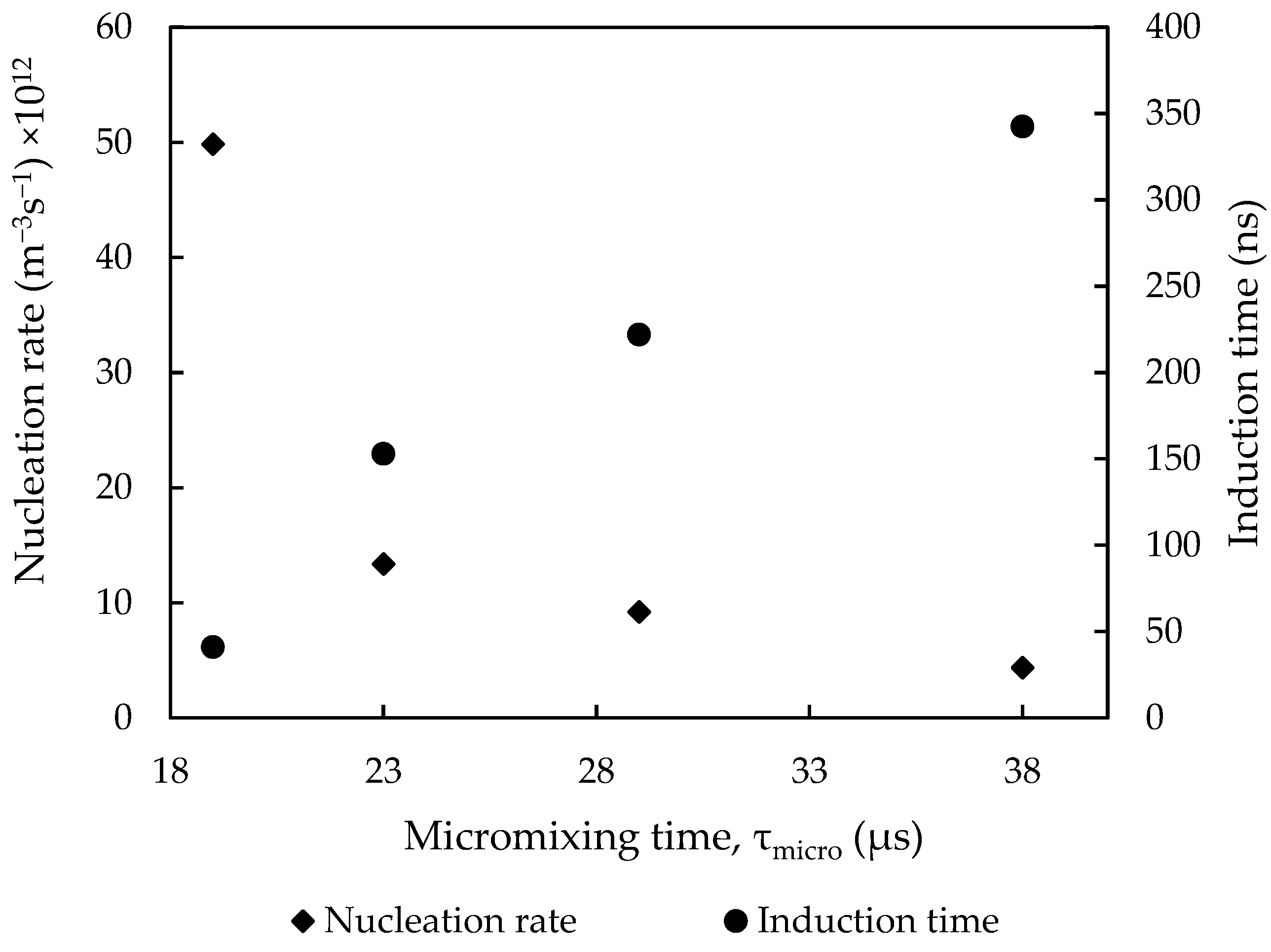
3.2.5. Effect of Mixing Intensity on Nucleation and Induction Time
4. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Habashi, F. Extractive metallurgy of rare earths. Can. Metall. Q. 2013, 52, 224–233. [Google Scholar] [CrossRef]
- Shecterle, R. BSG Ranks Global Supply Risks of Rare Earth Elements and Other Minerals. 2011. Available online: https://www.industryweek.com/finance/article/22011199/bsg-ranks-global-supply-risks-of-rare-earth-elements-and-other-minerals (accessed on 25 May 2021).
- Binnemans, K.; Jones, P.T.; Blanpain, B.; Van Gerven, T.; Pontikes, Y. Towards zero-waste valorisation of rare-earth-containing industrial process residues: A critical review. J. Clean. Prod. 2015, 99, 17–38. [Google Scholar] [CrossRef]
- Korkmaz, K.; Alemrajabi, M.; Rasmuson, Å.C.; Forsberg, K.M. Separation of valuable elements from NiMH battery leach liquor via antisolvent precipitation. Sep. Purif. Technol. 2020, 234, 115812. [Google Scholar] [CrossRef]
- Korkmaz, K.; Alemrajabi, M.; Rasmuson, Å.; Forsberg, K. Sustainable Hydrometallurgical Recovery of Valuable Elements from Spent Nickel–Metal Hydride HEV Batteries. Metals 2018, 8, 1062. [Google Scholar] [CrossRef]
- Lewis, A.; Seckler, M.; Kramer, H.; Rosmalen, G.v. Industrial Crystallization: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Baldyga, J.; Bourne, J.R.; Hearn, S.J. Interaction between chemical reactions and mixing on various scales. Chem. Eng. Commun. 1996, 52, 457–466. [Google Scholar] [CrossRef]
- Baldyga, J.; Bourne, J.R. A Fluid Mechanical Approach to Turbulent Mixing and Chemical Reaction Part II Micromixing in the Light of Turbulence Theory. Chem. Eng. Commun. 1983, 28, 243–258. [Google Scholar] [CrossRef]
- Alvarez, A.J.; Myerson, A.S. Continuous Plug Flow Crystallization of Pharmaceutical Compounds. Cryst. Growth Des. 2010, 10, 2219–2228. [Google Scholar] [CrossRef]
- Mahajan, A.J.; Kirwan, D.J. Micromixing Effects in a Two-Impinging-Jets Precipitator. AIChE 1996, 42, 1801–1814. [Google Scholar] [CrossRef]
- Charmolune, H.; Rousseau, R.W. L-Serine Obtained by Methanol Addition in Batch Crystallization. AIChE 1991, 37, 1121–1128. [Google Scholar] [CrossRef]
- Yu, Z.Q.; Tan, R.B.H.; Chow, P.S. Effects of operating conditions on agglomeration and habit of paracetamol crystals in anti-solvent crystallization. J. Cryst. Growth 2005, 279, 477–488. [Google Scholar] [CrossRef]
- Ramisetty, K.A.; Pandit, A.B.; Gogate, P.R. Ultrasound-Assisted Antisolvent Crystallization of Benzoic Acid: Effect of Process Variables Supported by Theoretical Simulations. Ind. Eng. Chem. Res. 2013, 52, 17573–17582. [Google Scholar] [CrossRef]
- Meyer, T.; David, R.; Renken, A.; Villermaux, J. Micromixing in a static mixer and an empty tube by a chemical method. Chem. Eng. Sci. 1988, 43, 1955–1960. [Google Scholar] [CrossRef]
- Davey, R.; Garside, J. From Molecules to Crystallizers; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Midler, M.J.; Liu, P.D.; Paul, E.L.; Futran, M.; Whittington, E.F. A Crystallization Method to Improve Crystal Structure and Size. US5314506A, 24 May 1994. [Google Scholar]
- OLI Systems Inc. OLI Studio Stream Analyzer, v11.5 (Build 1.7) 15-Sep-2022; OLI Systems Inc.: Morris Plains, NJ, USA, 2022. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Baldyga, J.; Bourne, J.R. Interactions between mixing on various scales in stirred tank reactors. Chem. Eng. Sci. 1991, 47, 1839–1848. [Google Scholar] [CrossRef]
- Hendrik, R.; Michel, B.; Mathias, K. A new scale-up method for competitive chemical model reactions based on complete similarity. Chem. Eng. J. 2020, 400, 125763. [Google Scholar] [CrossRef]
- Baldyga, J.; Bourne, J.R. Simplification of micromixing calculations. I. Derivation and application of new model. Chem. Eng. J. 1989, 42, 83–92. [Google Scholar] [CrossRef]
- Vicum, L.; Ottiger, S.; Mazzotti, M.; Makowski, Ł.; Bałdyga, J. Multi-scale modeling of a reactive mixing process in a semibatch stirred tank. Chem. Eng. Sci. 2004, 59, 1767–1781. [Google Scholar] [CrossRef]
- Johnson, B.K.; Prud’homme, R.K. Chemical Processing and Micromixing in Confined Impinging Jets. AIChE 2003, 49, 2264–2282. [Google Scholar] [CrossRef]
- Demyanovich, R.J.; Bourne, J.R. Rapid micromixing by the impingement of thin liquid sheets. 2. Mixing study. Ind. Eng. Chem. Res. 1989, 28, 830–839. [Google Scholar] [CrossRef]
- Ottino, J.M. Description of mixing with diffusion and reaction in terms of the concept of material surfaces. J. Fluid Mech. 1982, 114, 83–103. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Nobbmann, U. D90, D50, D10, and Span—for DLS? 2016. Available online: https://www.materials-talks.com/d90-d50-d10-and-span-for-dls/ (accessed on 29 August 2022).
- Sunagawa, I. Crystals Growth, Morphology, and Perfection; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
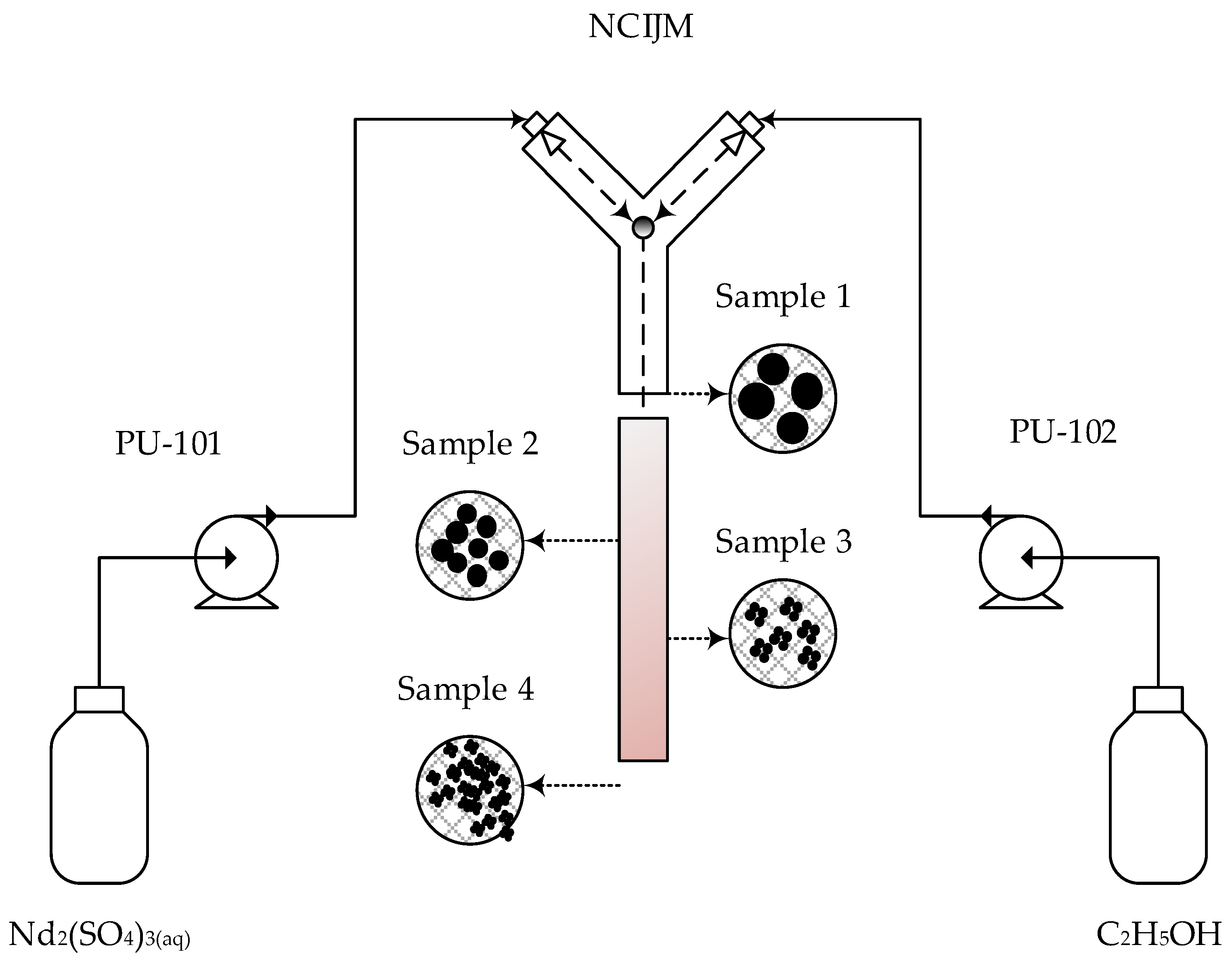






| Neodymium Sulphate PU-101 | Ethanol PU-102 | |
|---|---|---|
| Exp No. | uA (m/s) | uO (m/s) |
| 1 | 10 | 11 |
| 2 | 13 | 15 |
| 3 | 16 | 19 |
| 4 | 20 | 22 |
| Diffusivities | m2/s |
|---|---|
| 1 × 10−9 | |
| 7 × 10−10 | |
| 5 × 10−10 | |
| 2 × 10−10 |
| Exp No. | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| (m/s) | 10 | 13 | 16 | 20 |
| (m/s) | 11 | 15 | 19 | 22 |
| 7500 | 9900 | 12,000 | 15,000 | |
| 5600 | 7400 | 9200 | 11,000 | |
| P (W) | 110 | 190 | 290 | 410 |
| ε (W/kg) | 2.4 × 105 | 4.1 × 105 | 6.4 × 105 | 9.2 × 105 |
| (µm) | 1.6 | 1.4 | 1.2 | 1.1 |
| (s) | 2.1 × 10−4 | 1.8 × 10−4 | 1.5 × 10−4 | 1.4 × 10−4 |
| (s) | 2.6 × 10−4 | 2.1 × 10−4 | 1.8 × 10−4 | 1.6 × 10−4 |
| (s) | 3.8 × 10−5 | 2.9 × 10−5 | 2.3 × 10−5 | 1.9 × 10−5 |
| (s) | 3.7 × 10−6 | 2.8 × 10−6 | 2.2 × 10−6 | 1.9 × 10−6 |
| (s) | 2.6 × 10−11 | 1.7 × 10−11 | 1.2 × 10−11 | 9.2 × 10−12 |
| (s) | 4.7 × 10−4 | 3.9 × 10−4 | 3.4 × 10−4 | 3.0 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baloyi, T.O.; Chivavava, J.; Lewis, A.E. Investigation on the Effect of Mesomixing on Crystal Quality during Antisolvent Crystallization of Nd2(SO4)3·8H2O. Metals 2023, 13, 1378. https://doi.org/10.3390/met13081378
Baloyi TO, Chivavava J, Lewis AE. Investigation on the Effect of Mesomixing on Crystal Quality during Antisolvent Crystallization of Nd2(SO4)3·8H2O. Metals. 2023; 13(8):1378. https://doi.org/10.3390/met13081378
Chicago/Turabian StyleBaloyi, Tinjombo Octavious, Jemitias Chivavava, and Alison Emslie Lewis. 2023. "Investigation on the Effect of Mesomixing on Crystal Quality during Antisolvent Crystallization of Nd2(SO4)3·8H2O" Metals 13, no. 8: 1378. https://doi.org/10.3390/met13081378
APA StyleBaloyi, T. O., Chivavava, J., & Lewis, A. E. (2023). Investigation on the Effect of Mesomixing on Crystal Quality during Antisolvent Crystallization of Nd2(SO4)3·8H2O. Metals, 13(8), 1378. https://doi.org/10.3390/met13081378







