Two-Step Spin Forming of Thin-Walled Heads with Lateral Normal Flanged Holes

Abstract

A thin-walled head with a lateral normal flanged hole is a key part of a propellant tank, and its low-cost and high-precision forming process is very challenging. In this paper, a two-step method is proposed to preform the head via marginal-restraint mandrel-free spinning and then to realize the flanging of the lateral normal hole using a punching–spinning method. Finite element analysis of round-hole punching–spinning flanging shows that the larger the thinning ratio and the roller fillet radius, the lower the rebound and contour rise amount; the larger the feed ratio, the lower the rebound and the higher the contour rise amount. Further study on the effects of round-hole punching–spinning flanging on the secondary deformation of thin-walled heads shows that the deformation of the head in the area around the flanging hole is less severe than that of the flat blank, and the deformation in the circumferential direction is different from that in the busbar direction. Finally, it is verified through experiments that the two-step method can realize the spin forming of thin-walled heads with lateral normal flanged holes.

1. Introduction

Propellant tank heads need to have a liquid (gas) port and connect with a pipeline, and it is often necessary to install a lateral normal flanged hole on the side wall of the head [1,2,3], which is characterized by the direction of the orifice, which points outwards, parallel to the flanged position, i.e., with normal side characteristics, as shown in Figure 1. It is a greater challenge to form lateral normal flanged holes, and the most common flanged hole forming methods at home and abroad are mainly stamping forming [4], progressive forming round-hole flanging [5], single-point incremental forming [6], thermoplastic round-hole flanging [7,8], electromagnetic forming round-hole flanging [9,10], and spin flanging [11]. Traditional round-hole stamping flanging often results in insufficient flanging height [12], necking of the straight section of the flanged hole [13,14], and cracking of the hole [15].

Traditionally, large propellant tank heads are mainly formed by means of melon flap assembling and welding, where the melon flaps are first formed by stamping, creep, or deep drawing, and then the whole head is obtained through assembly and welding [16,17]. At present, integral head forming is mainly realized via center-constrained spinning, and thick blanks are mainly used for spinning in order to solve the instability problem [18,19]. References [20,21] explored numerical simulation methods for heads, references [22,23] described the influence of process parameters on the quality of spinning and forming, and references [24,25] investigated the phenomenon of instability susceptibility to destabilization in the spinning process of heads. In response to the instability phenomenon of the traditional center-constrained spinning of thin-walled heads using thin-walled blanks, Li et al. [26,27,28,29] proposed a marginal-restraint mandrel-free spinning method. Reference [30] explores the role of low temperature on spinning when using a marginal-restraint mandrel-free spinning process for aluminum alloy heads. As shown in Figure 2, the blank is fixed circumferentially on the cylindrical support fixture to rotate with the table, and the deformation is controlled by controlling the motion trajectory of the roller, which successfully realizes the marginal-restraint mandrel-free spinning forming of a thin-walled head.

The traditional forming process for heads with a lateral normal flanged hole shown in Figure 3 is difficult to carry out with precision and presents other problems. This paper considers the structural characteristics of thin-walled heads with a lateral normal flanged hole and proposes a two-step method to perform the forming of a thin-walled head with a lateral normal flanged hole. The marginal-restraint mandrel-free spinning method is employed for head spinning and the flanging hole is then obtained by adopting a new punching–spinning flanging process combining the characteristics of stamping and spinning. The finite element method is employed to study the influence of different process parameters on the forming accuracy of punching–spinning flanging. The effect of punching–spinning flanging on the accuracy of spun thin-walled head contour is further investigated. Finally, the feasibility of the two-step method is verified through experiments.

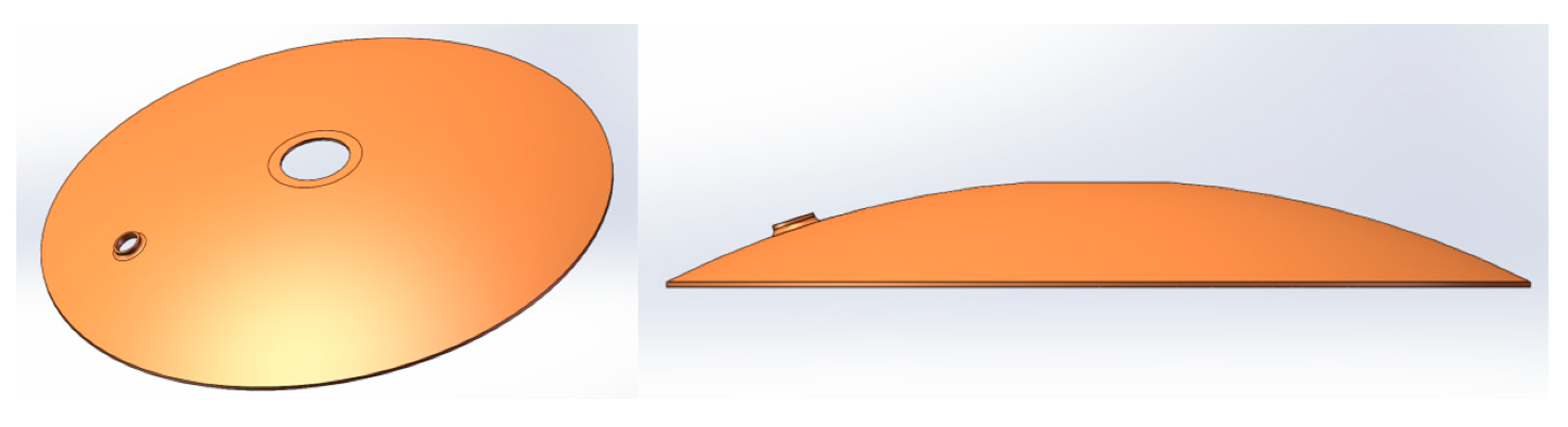
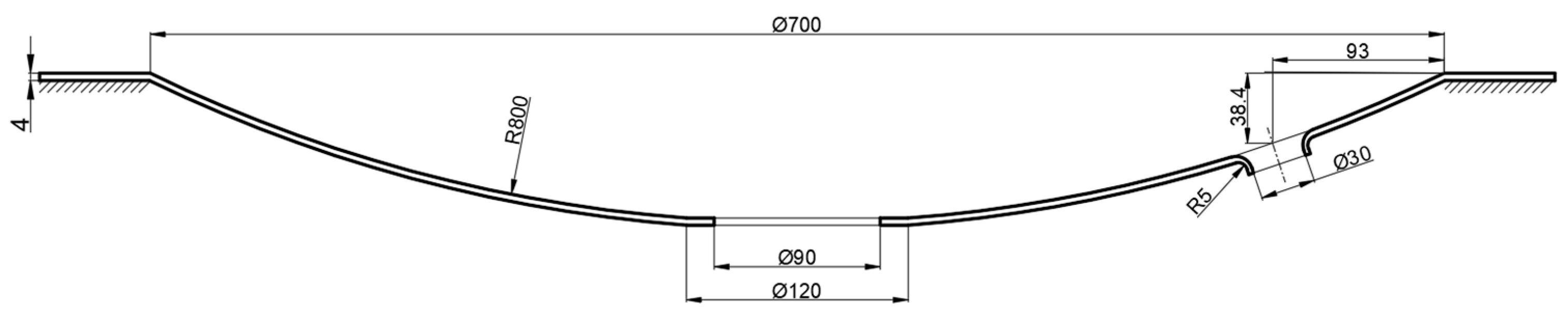
2. A Two-Step Spinning Method for Thin-Walled Heads with Lateral Normal Flanged Holes

A two-step method of head forming and round-hole flanging is proposed as shown in Figure 4. As shown in Figure 4a, the first step adopts the marginal-restraint mandrel-free spinning method to achieve accurate forming of head by spinning. In this process, the blank is fixed on the cylindrical support fixture by the blank-hold ring and rotates with the table, and the roller moves in a curve to realize the head spinning and forming. As shown in Figure 4b, the second step will machine the preformed holes of the preformed head, and then use the concave mold and stamping roller to achieve the lateral normal hole flanging.

The first step of precise head forming by marginal-restraint mandrel-free spinning has been studied in detail. However, the precise forming of lateral normal hole flanging in the second step is more difficult, and this paper proposes a punching–spinning flanging process. In this paper, the flanging of round holes in flat blanks is the first object of study, and then extended to the flanging of round holes in circular arc blanks to achieve flanging forming on the head. As shown in Figure 5, the process is divided into two stages: the first stage of bending–expansion, which achieves flanging through a material flow process similar to stamping; and the second stage of spinning–thinning, which ensures the accurate forming of the inner contour and height of the flanging hole. The control of the deformation process is regulated by the shape of the roller, which reduces the inhomogeneous deformation caused by the dynamic effect in the stamping process. Under the joint action of the roller and the concave mold, the thinning of the wall thickness of the flanging hole lengthens the length of the straight section.

In order to perform the above deformation, this paper proposes a stamping roller structure, as shown in Figure 6. It is designed in one piece and consists of four parts: the punch, transition section, roller, and connecting section. The front end of the spherical punch is flat, and after the punch feed is completed, a transition section with a height of 4 mm is reserved to avoid interference in the flanging area when the roller comes into contact with the flanging area too early. The diameter of the transition section is the same as the maximum diameter of the punch. The transition section is connected to the roller. The roller shape directly affects the forming size and accuracy of the flanged hole and determines the contact area between the roller and the blank, as well as the forming load. The main design dimensions of the stamping roller are shown in

Table 1. Main design dimensions of the stamping roller.

Material	Forming Angle $\mathit{\alpha }$	Roller Fillet Radius ${\mathit{\rho }}_{\mathit{R}}$	Exit Angle $\mathit{\beta }$	Flange Diameter $\mathbf{ø}$
Cr12MoV	15°	2–4 mm	3°	30 mm

.

3. Development and Verification of the Finite Element Model (FEM)

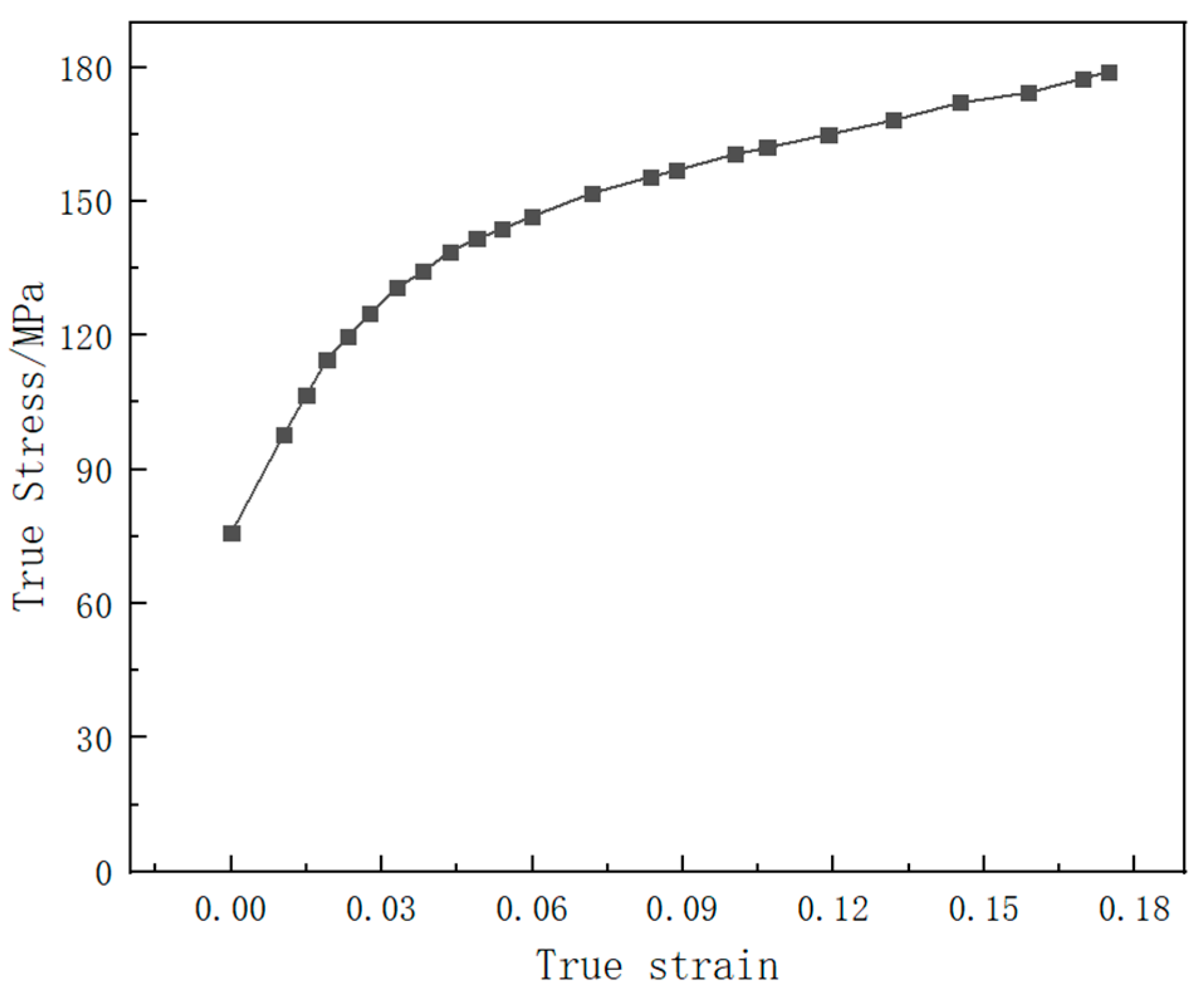
3.1. Development of the FEM

The FEM of the punching–spinning flanging model established by using MSC.MARC MENTAT software 2020 (Hexagon, Stockholm, Sweden) is shown in Figure 7, which mainly consists of a stamping roller, a concave mold, a blank, and a blank-hold ring, where the stamping roller rotates with the machine spindle and moves downward to perform punching–spinning flanging of the blank and the concave mold fixed on the working table.

The blank is a circular shape of 2219-O aluminum alloy with a diameter of 110 mm, a central prefabricated hole of 20 mm, and a thickness of 3 mm, for which the material properties are shown in

Table 2. 2219-O material performance parameters.

Elastic Modulus E/MPa	Poisson’s Ratio μ	Density ρ/(kg·m−3)	Tensile Strength /MPa	Yield Strength /MPa	Elongation /%
73,100	0.33	2840	179	75.8	18

[29], and the true stress–strain curve is shown in Figure 8. The edge of the blank is kept in the same position relative to the mold under the action of the blank-hold ring, and the contact area between the part inside the blank-hold ring and the mold changes all the time as the flanging process proceeds. The cell thickness direction is refined to a five-layer grid, because the blank does not deform in the circumferential constraint position and the main deformation region is the cell around the prefabricated holes, so a radial offset coefficient of 0.2 is introduced in the cell refinement, which makes the cell near the prefabricated holes denser, and the cell near the edge of the slab is relatively sparse, which takes into account the efficiency of the computation and the accuracy of the simulation. After the unit refinement, the four-node quadrilateral element is expanded into an eight-node hexahedral element, and the total number of divided elements is 14,400. The stamping roller, concave mold, and blank-hold ring are defined as the analytic rigid body, and the blank is defined as the deformed body. The contact relationship between the stamping roller and the blank is Touching, and the other contact relationships are set to GLUE. The friction coefficient of the contact relationship between the stamping roller and the blank is set to 0.02. The simulation process parameters are: feed ratio $f=0.2 \mathrm{m}\mathrm{m}/\mathrm{r}$, roller fillet radius ${\rho }_R=2 \mathrm{m}\mathrm{m}$, rotation speed $n=30 \mathrm{r}/\mathrm{m}\mathrm{i}\mathrm{n}$ (revolutions per minute).

From Figure 9, it can be seen that the equivalent effect stress in the deformation zone during the punching–spinning flanging process is uniformly distributed in the circumferential direction of the belt. As shown in Figure 9a, the equivalent stress in the bending–expansion process gradually becomes larger from the edge of the blank to the prefabricated hole, and the maximum equivalent stress is located at the outer edge of the prefabricated hole. As shown in Figure 9b, after the bending–expansion is completed, the stress is mainly concentrated in the flanged hole transition fillet, and the overall stress is more uniform. Figure 9c indicates that at the beginning of spinning–thinning, the maximum equivalent stress is located in the annular area where the roller is in contact with the blank. As the thinning ratio increases, the equivalent stress increases and reaches the maximum value after entering the linear section and stabilizes. Figure 9d shows that at the end of the spinning–thinning section, the roller gets closer to the free end of the flanged hole, the resistance to material flow gradually decreases, and the equivalent stress gradually decreases until the roller is completely detached.

3.2. Verification of the FEM Model

As shown in Figure 10, the flat blank with prefabricated holes is fixed on the concave mold with fixing bolts, the concave mold is fixed on the machine without moving, and the stamping roller actively rotates and moves down to realize the punching–spinning of the flanged holes. The same process parameters as in the simulation are used for the punching–spinning experiment, and the experimental piece shown in Figure 11 is obtained.

The contour data and wall thickness data of the experimental piece are extracted by using the 3D scanner (Smart 3D Technology(Suzhou) Ltd., Suzhou, China) and ultrasonic thickness gauge (Dakota Ultrasonics, Scotts Valley, CA, USA) in Figure 12. The specific measurement path is shown in Figure 11b, which is the inner surface bus of the center axis section of the flanged hole, and the measurement direction starts from the edge of the flanged hole toward the outer edge of the experimental piece.

The simulated result and the experimental result of the thickness and clearance are shown in Figure 13. The wall thickness remains about 2.1 mm from the edge of the flanged hole, and then rises rapidly following nonlinear variation and converges to the thickness of the blank, respectively. That is, it corresponds to the straight edge section, the arc section, and the blank section of the flanged hole, respectively. The wall thickness of the arc section rises rapidly near the straight edge section and rises slowly near the blank wall thickness. The minimum wall thickness is 2.08 mm in the straight section of the flanged hole. Figure 13b shows the comparison of the contour accuracy between the experimental and simulated pieces, which shows that the mold gap is small in the straight section of the flanged hole, and the minimum mold gap reaches about 0 mm in the arc section, and then the mold gap increases rapidly to a maximum of 0.278 mm, which means the contour rising phenomenon occurs.

From the comparison between the simulation and experimental results, it can be seen that the maximum difference between the experimental and simulated wall thicknesses occurs in the arc near the blank, and the maximum deviation is 0.04 mm. The maximum deviation between the experimental and simulated contours occurs at the contour rising of the blank, and the maximum deviation is 0.015 mm. The flanging height of the experimental piece is 10.82 mm, the flanging height of the simulated piece is 10.9 mm, and the flanging height error is 0.07 mm. All of them are within the allowable error range, so the FEM is considered reliable.

4. Results and Discussion

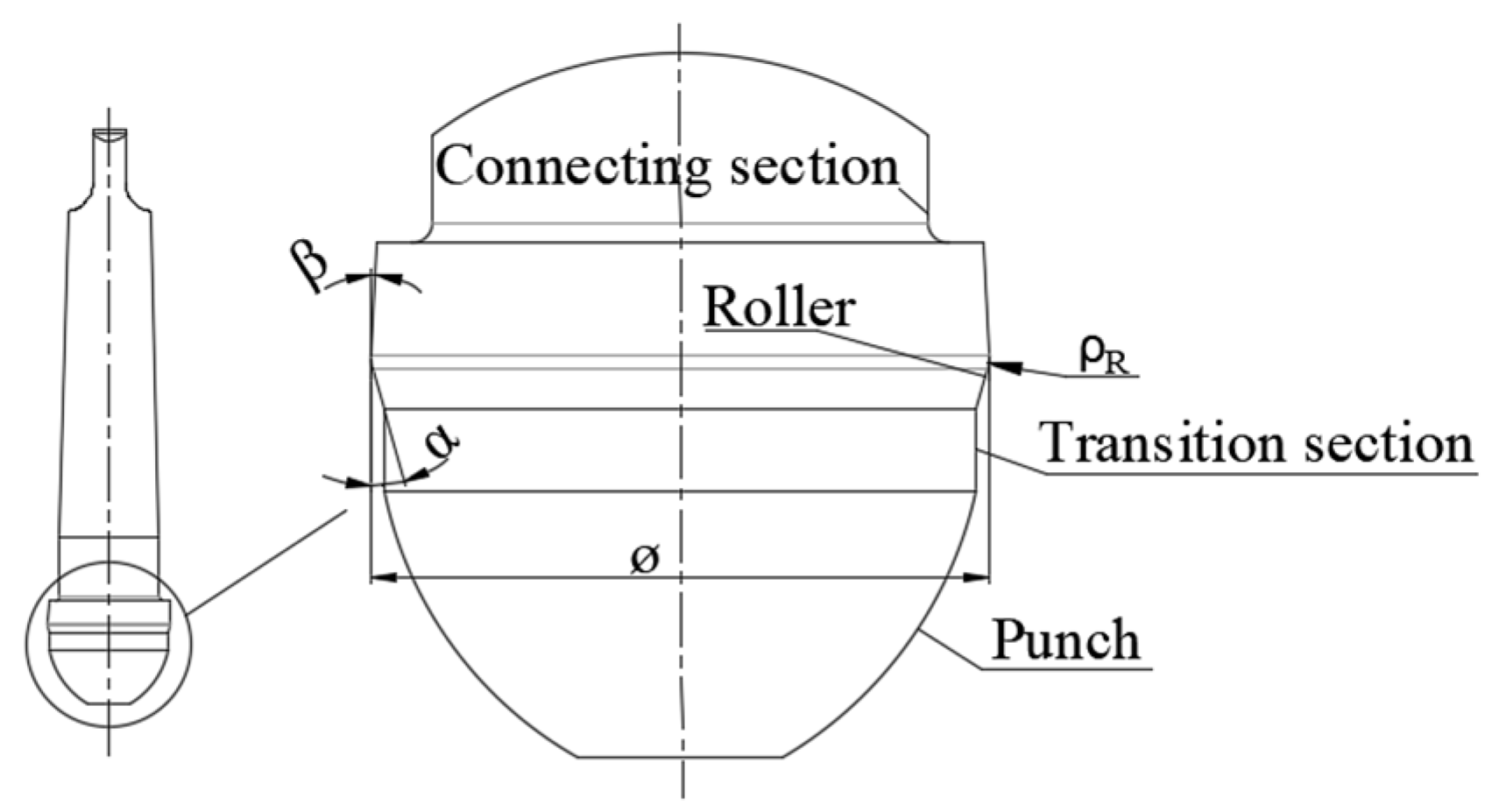
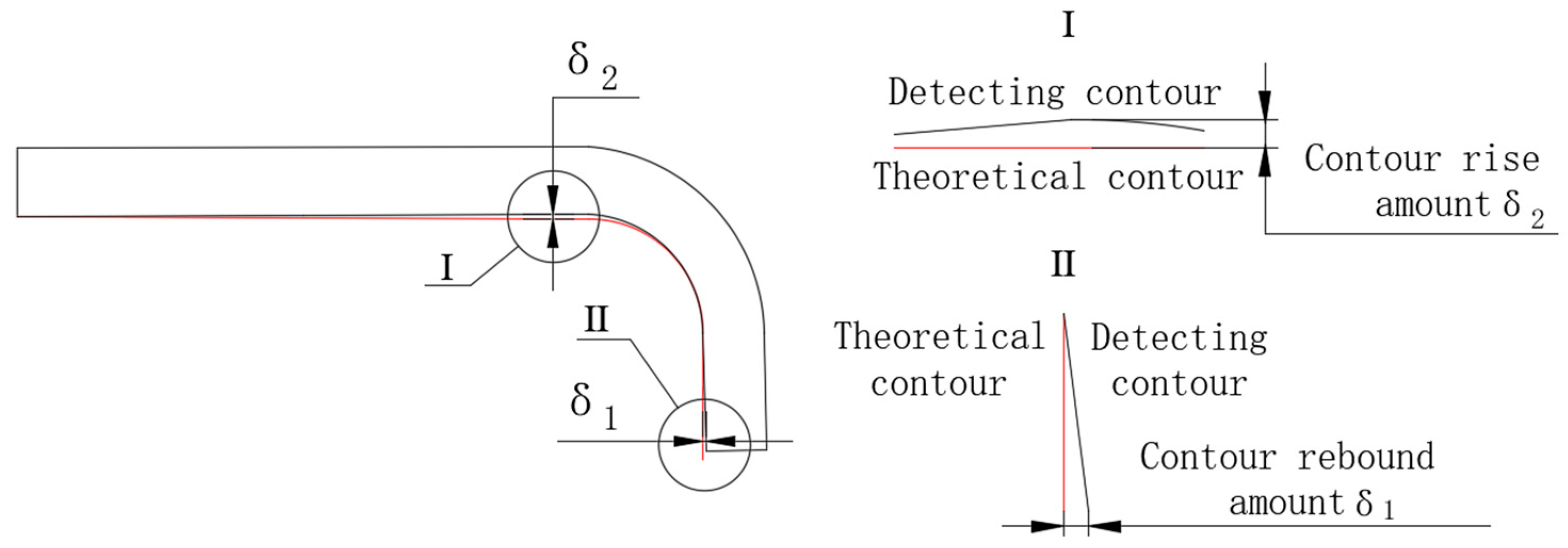
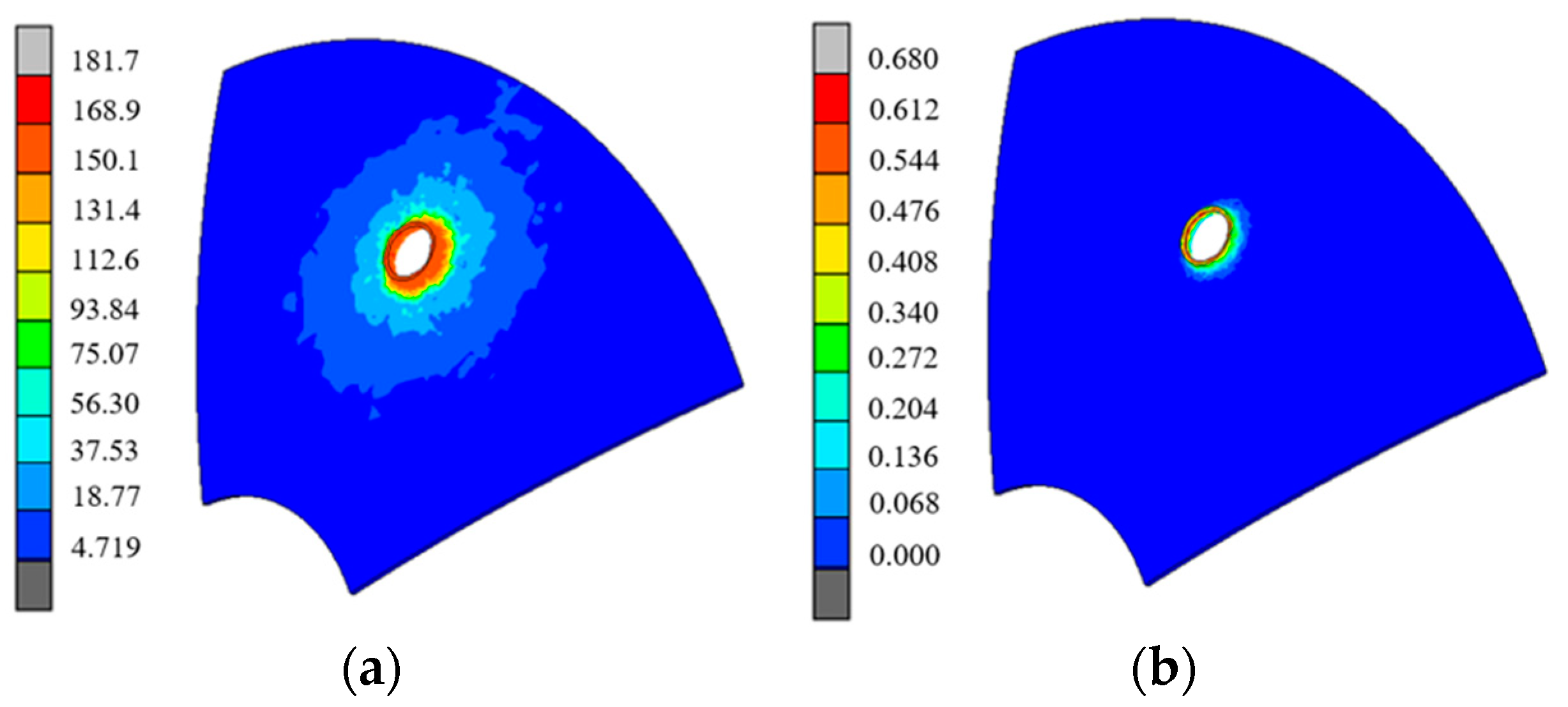
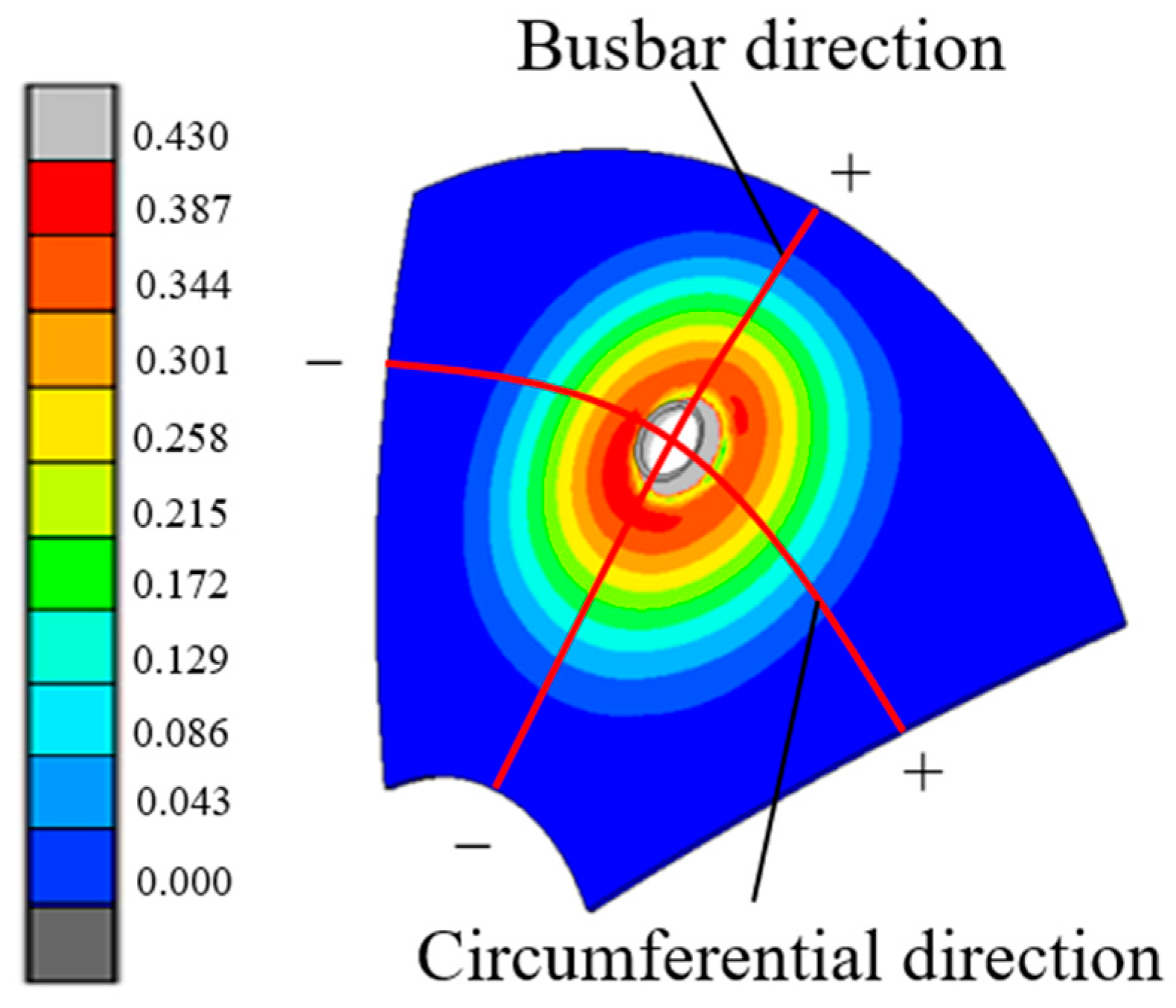
4.1. Evaluation Index of Punching–Spinning Flanging Accuracy

From the above experimental results, it can be seen that the local contour rising phenomenon occurs and the corner is the area where the maximum error is prone to occur. Therefore, the main accuracy evaluation index of punching–spinning flanging is defined as follows: contour rebound amount ${\delta }_1$ and contour rise amount ${\delta }_2$, as shown in Figure 14. ${\delta }_1$ and ${\delta }_2$ are employed to describe the shaping result.

From Figure 15, it can be seen that the contour rise amount of the blank is the largest near the corner of the concave mold, and the contour rise amount decreases rapidly near the flanged hole. Away from the flanged hole, the contour rise amount is gradually reduced, and it is almost zero near the edge of the blank.

As shown in Figure 16, the maximum contour rise amount starts to grow rapidly and reaches the maximum value when the straight section is about to be formed in the flanged hole. After the roller starts to spin and thin, the material flow to the edge of the flanged hole under the action of the roller, and the area after the spin, are subjected to large surface tensile stress, which makes the material tend to flow to the edge of the hole, and the contour rise amount also decreases slowly until the roller is completely disengaged.

4.2. Influence of the Punching–Spinning Flanging Process Parameters on the Forming Accuracy

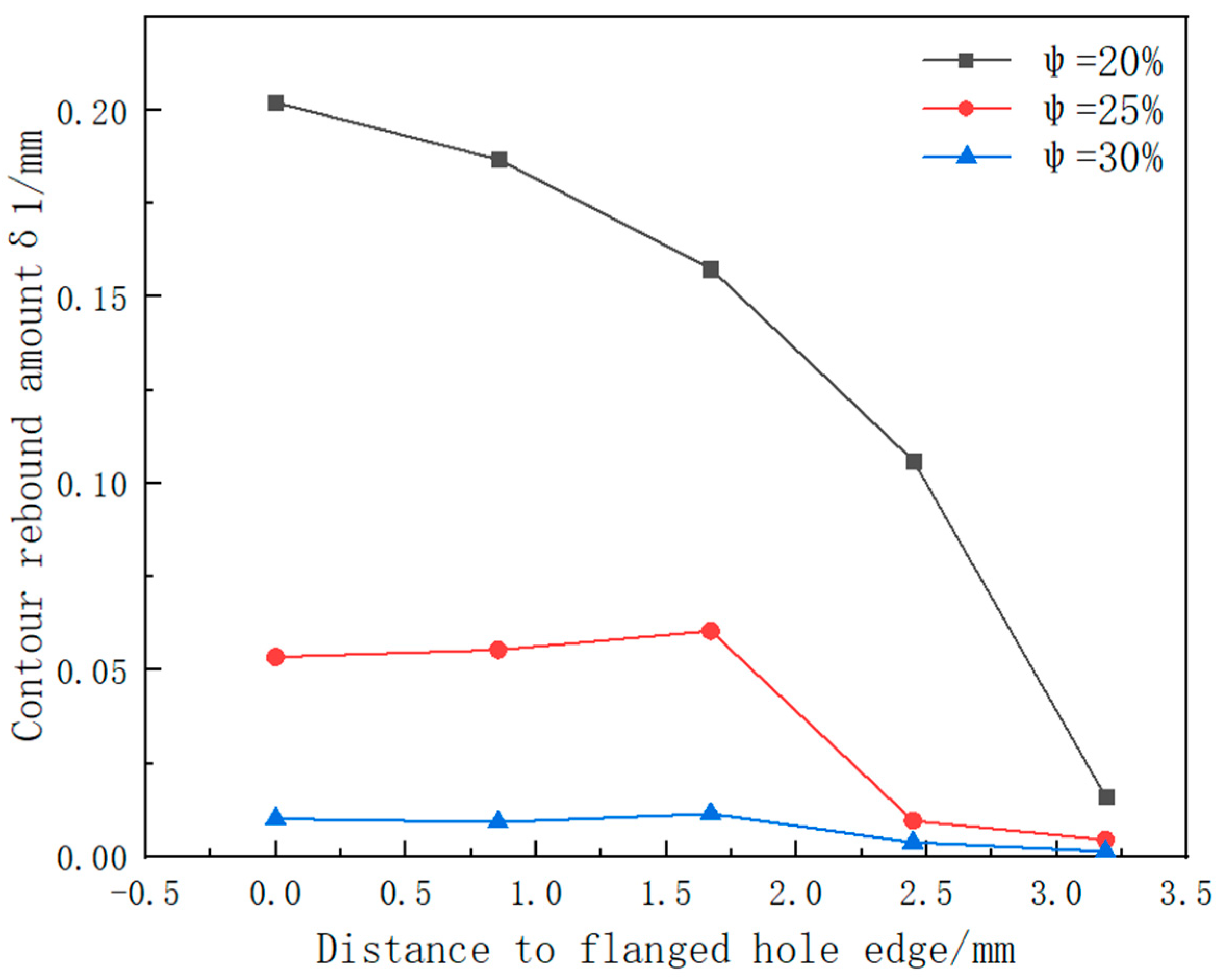
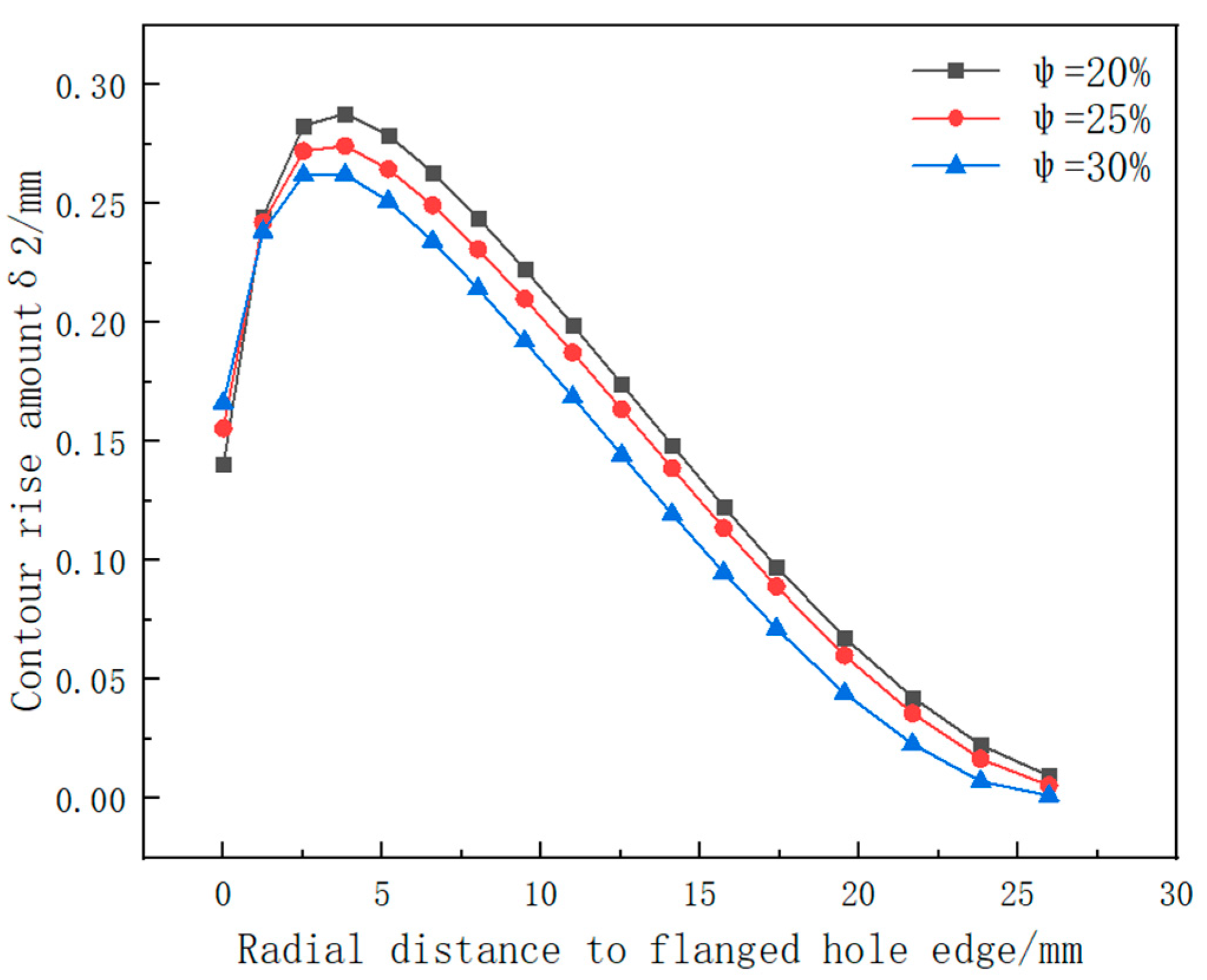
4.2.1. Effect of the Thinning Ratio on the Forming Accuracy

The thinning ratio $\psi$ is the ratio of spinning–thinning to the wall thickness of the blank.

$$\psi =\frac{t_0-t_1}{t_0}$$

(1)

where $t_0$ is the blank wall thickness and t₁ is the wall thickness after spinning–thinning.

The effect of thinning ratio $\psi$ of 20%, 25%, and 30% on the flanging forming accuracy is studied under the premise that the roller fillet radius is ${\rho }_R=2 \mathrm{m}\mathrm{m}$ and the feed ratio $f=0.2 \mathrm{m}\mathrm{m}/\mathrm{s}$ are constant.

As can be seen from Figure 17, the maximum contour rebound amount occurs at the edge of the flanged hole, and the further away from the edge of the flanged hole, the smaller the amount of contour rebound amount is, and at the rounded position of the concave mold, the contour rebound amount is completely adhered to the mold. The smaller the thinning ratio is, the larger the contour rebound amount is. When the thinning ratio is 20%, the contour rebound amount of the edge of the flanged hole is 0.2 mm, and when the thinning ratio is 30%, the contour rebound amount of the flanged hole position is 0.01 mm. Increasing the thinning ratio can significantly improve the contour rebound amount of the edge of flanging hole, but it has less effect on the contour rebound amount of the straight edge section which is more than 3 mm away from the edge of the flanged hole. At a 30% thinning ratio, the mold adhesion of the straight section is relatively uniform, and the contour rebound amount at different height positions of the flanging hole is not much different. The blank is rapidly molded in the area near the rounded corner of the concave mold, causing the contour rebound amount to reduce to zero.

As shown in Figure 18, the contour rise amount tends to increase and then decrease as the distance from the edge of the flanged hole increases, and the maximum contour rise amount occurs near the corner of the mold. The larger the thinning ratio is, the smaller the maximum contour rise amount is. The maximum contour rise amount is 0.29 mm when the thinning ratio is 20%, and 0.26 mm when the thinning ratio is 30%, where the contour rise amount is always the smallest when the thinning ratio is larger, and the trend changes after the contour rise amount reaches the maximum. Overall, the effect of the thinning ratio on the contour rise amount is limited.

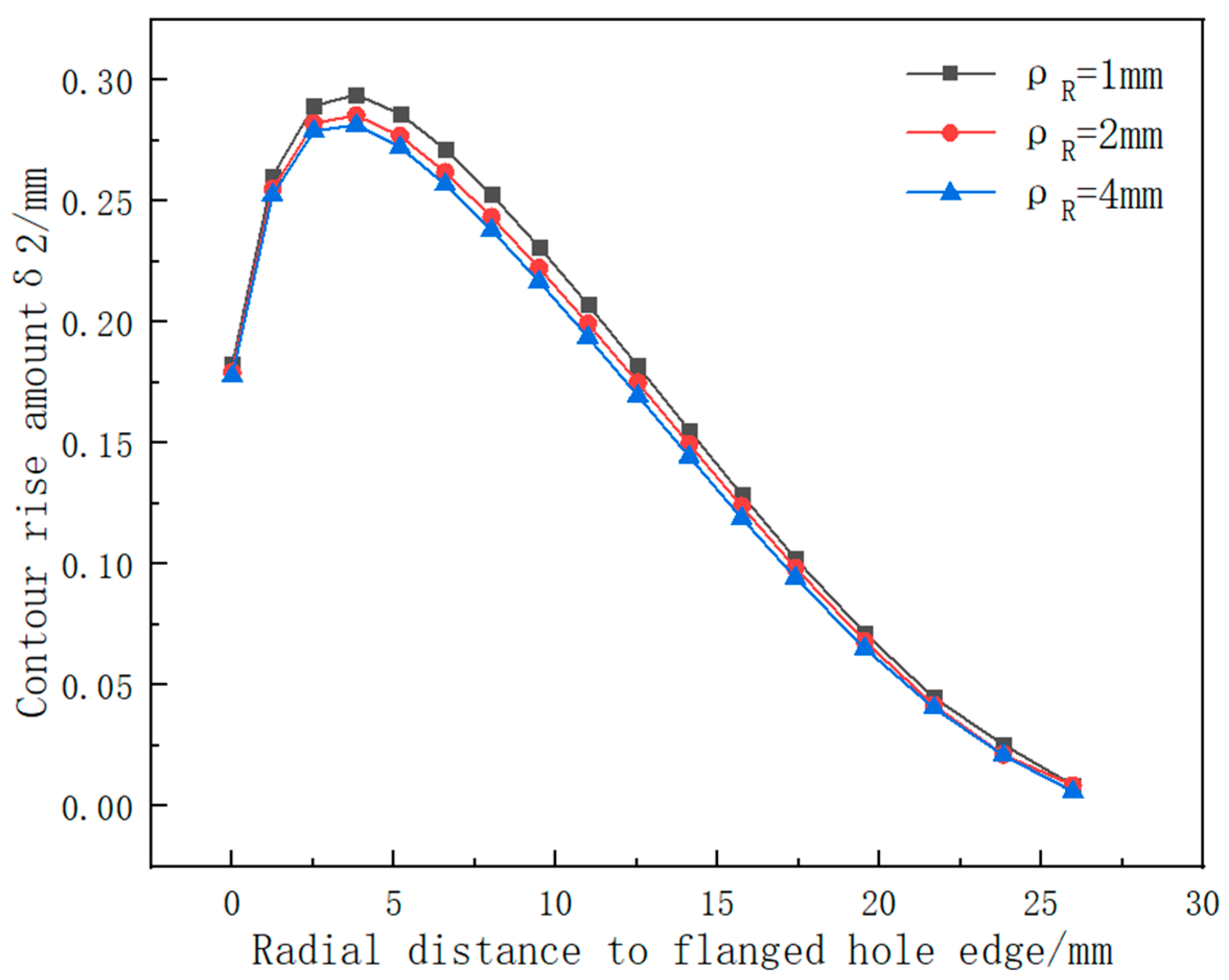
4.2.2. Influence of the Roller Fillet Radius on the Forming Accuracy

Under the premise that the feed ratio $f=0.2 \mathrm{m}\mathrm{m}/\mathrm{s}$ and the thinning ratio $\psi =25\mathrm{\%}$ are constant, the effect on the flanging forming accuracy is studied when the roller fillet radius ${\rho }_R$ is taken as 1 mm, 2 mm, and 4 mm, respectively.

As shown in Figure 19, the further away from the edge of the flanged hole, the smaller the contour rebound amount, and the maximum contour rebound amount appears at the edge of the flanged hole. The larger the roller fillet radius, the smaller the contour rebound amount, and the maximum contour rebound amount is 0.055 mm when the roller fillet radius is 1 mm, and 0.051 mm when the roller fillet radius is 4 mm. Although the change in the roller fillet radius has little effect on the maximum contour rebound amount, it has a significant effect on the average contour rebound amount, especially when the overall contour rebound amount at the roller fillet radius is 1 mm, which is significantly larger than that at the large roller fillet radius. Once the roller fillet radius reaches 2 mm, its impact on the contour rebound amount becomes limited.

According to Figure 20, the contour rise amount increases and then decreases as the distance from the edge of the flanged hole increases, with the maximum contour rise amount occurring close to the corner of the concave mold. As the roller fillet radius increases, the maximum contour rise amount decreases gradually. The maximum contour rise amount is 0.294 mm when the roller fillet radius is 1 mm, and 0.281 mm when the roller fillet radius is 4 mm. The change in the roller fillet radius has a limited effect on the contour rise amount.

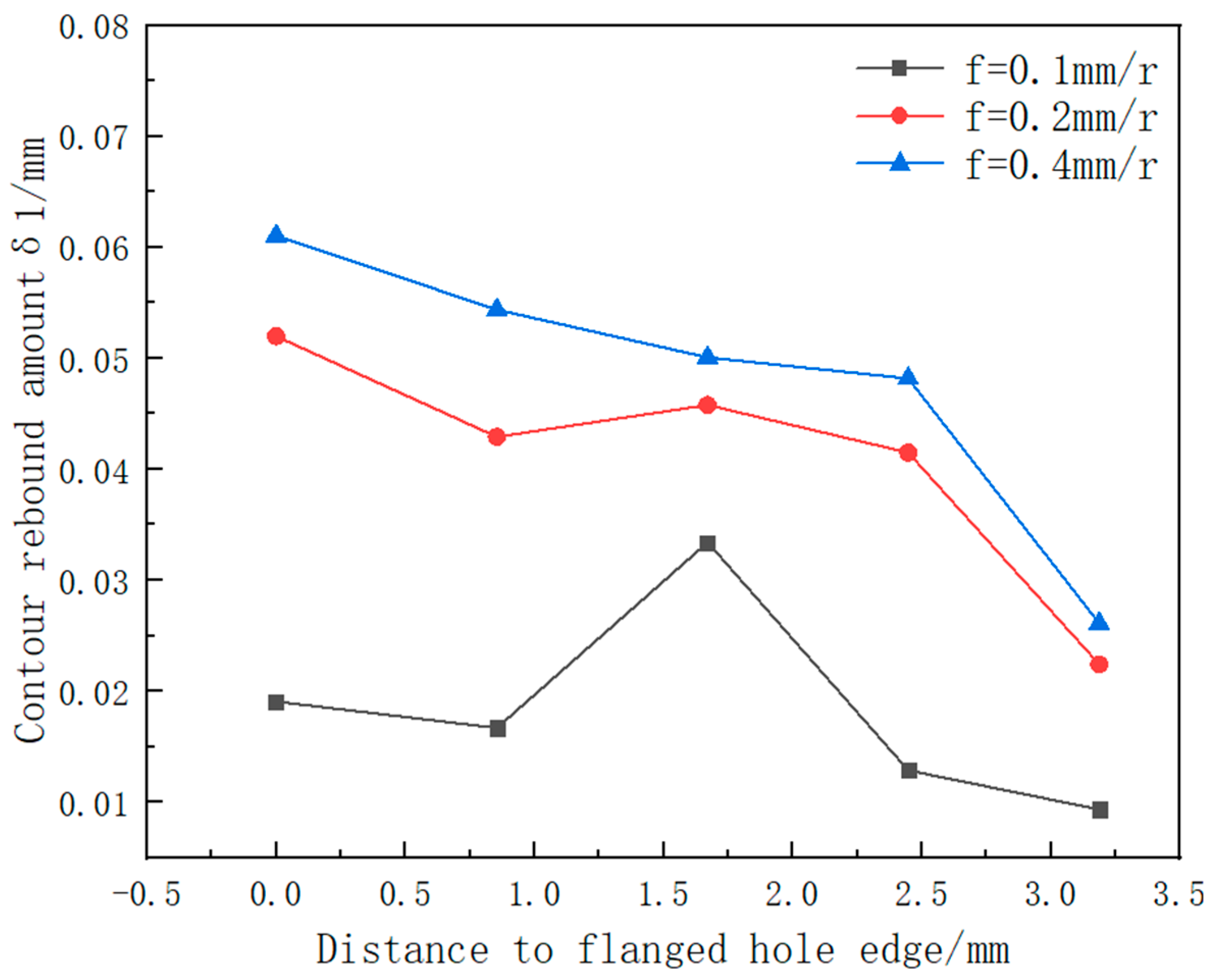
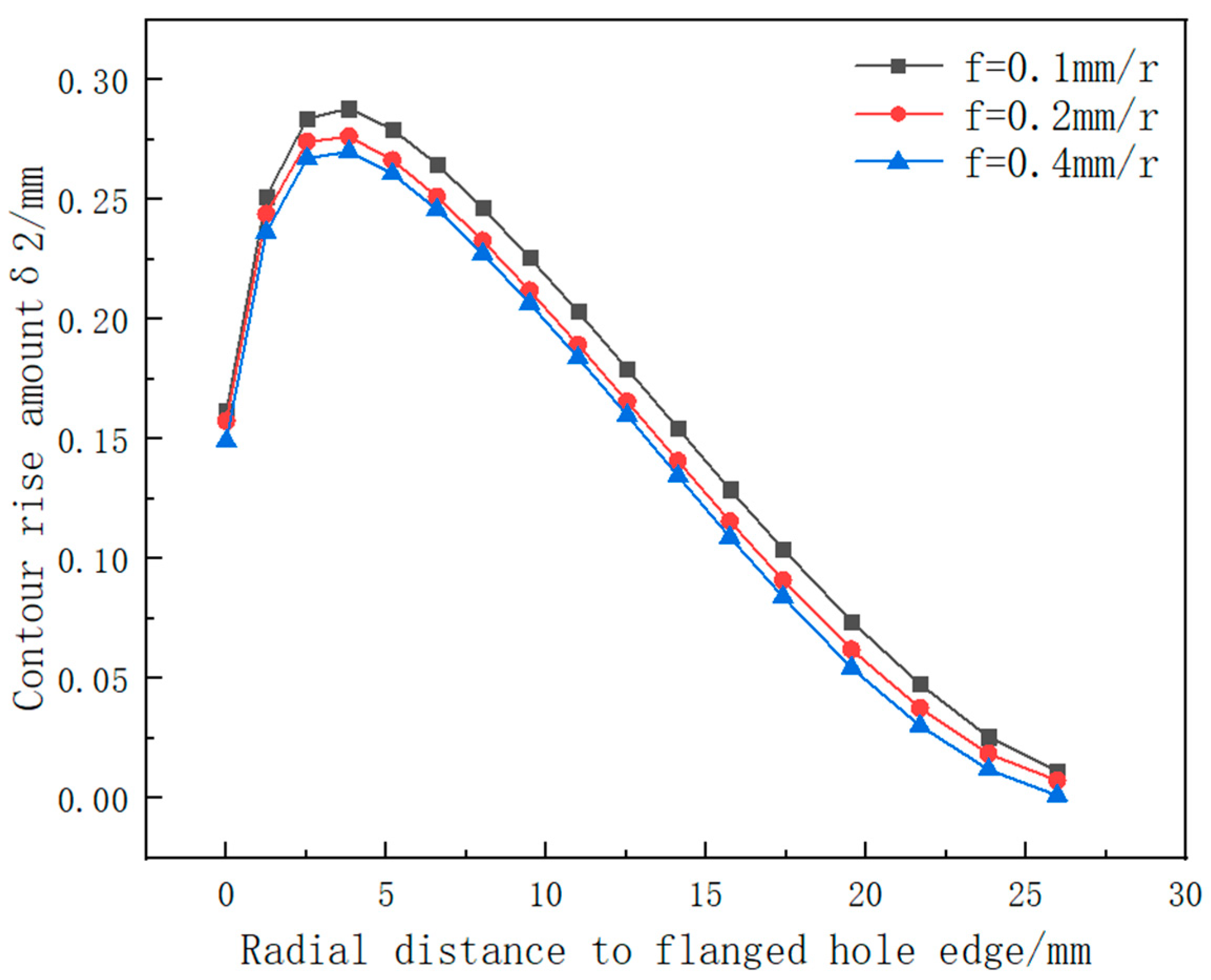
4.2.3. Influence of the Feed Ratio on the Forming Accuracy

This study analyzes the effect of the feed ratio $f$ on the flanging forming accuracy while keeping the roller fillet radius ${\rho }_R=2 \mathrm{m}\mathrm{m}$ and the thinning ratio $\psi =25\%$ constant. The selected values for the feed ratios investigated in this study are 0.1 mm/r, 0.2 mm/r, and 0.4 mm/r.

An analysis of Figure 21 reveals that the maximum contour rebound amount occurs at the location of the edge of the flanged hole, and the further away from the edge of the flanged hole, the smaller the contour rebound amount. The larger the feed ratio, the larger the contour rebound amount. When the feed ratio is 0.1 mm/r, the maximum contour rebound amount is 0.033 mm, and when the feed ratio is 0.4 mm/r, the maximum contour rebound amount is 0.061 mm. The feed ratio has a large influence on the contour rebound amount, and a smaller feed ratio can improve the forming accuracy.

According to Figure 22, the maximum contour rise amount occurs after the rounded area, and a higher feed ratio, results in a smaller rise amount. For a feed ratio of 0.1 mm/r, the maximum contour rise amount is 0.288 mm, whereas for a feed ratio of 0.4 mm/r, it is only 0.269 mm. The change in feed ratio has a limited effect on the contour rise amount.

Figure 23 shows the obvious cracks on the edge of the flanged hole at a feed ratio of 0.8 mm/r. Increasing the feed ratio helps to improve the efficiency of punching–spinning flanging, but too high a feed ratio increases fracture tendency and leads to hole cracking. The surface quality of the flanged hole is significantly improved in a relatively small feed speed.

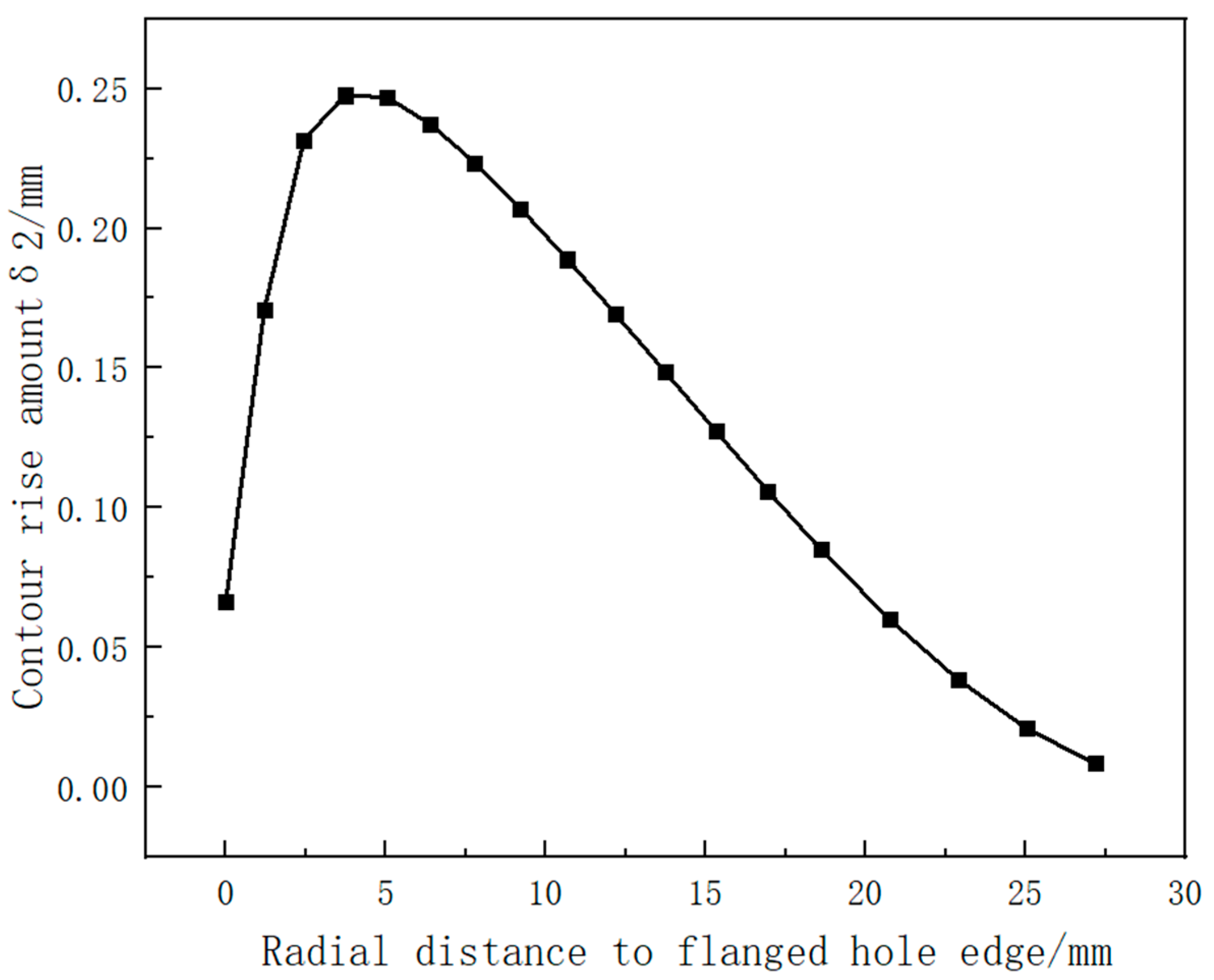
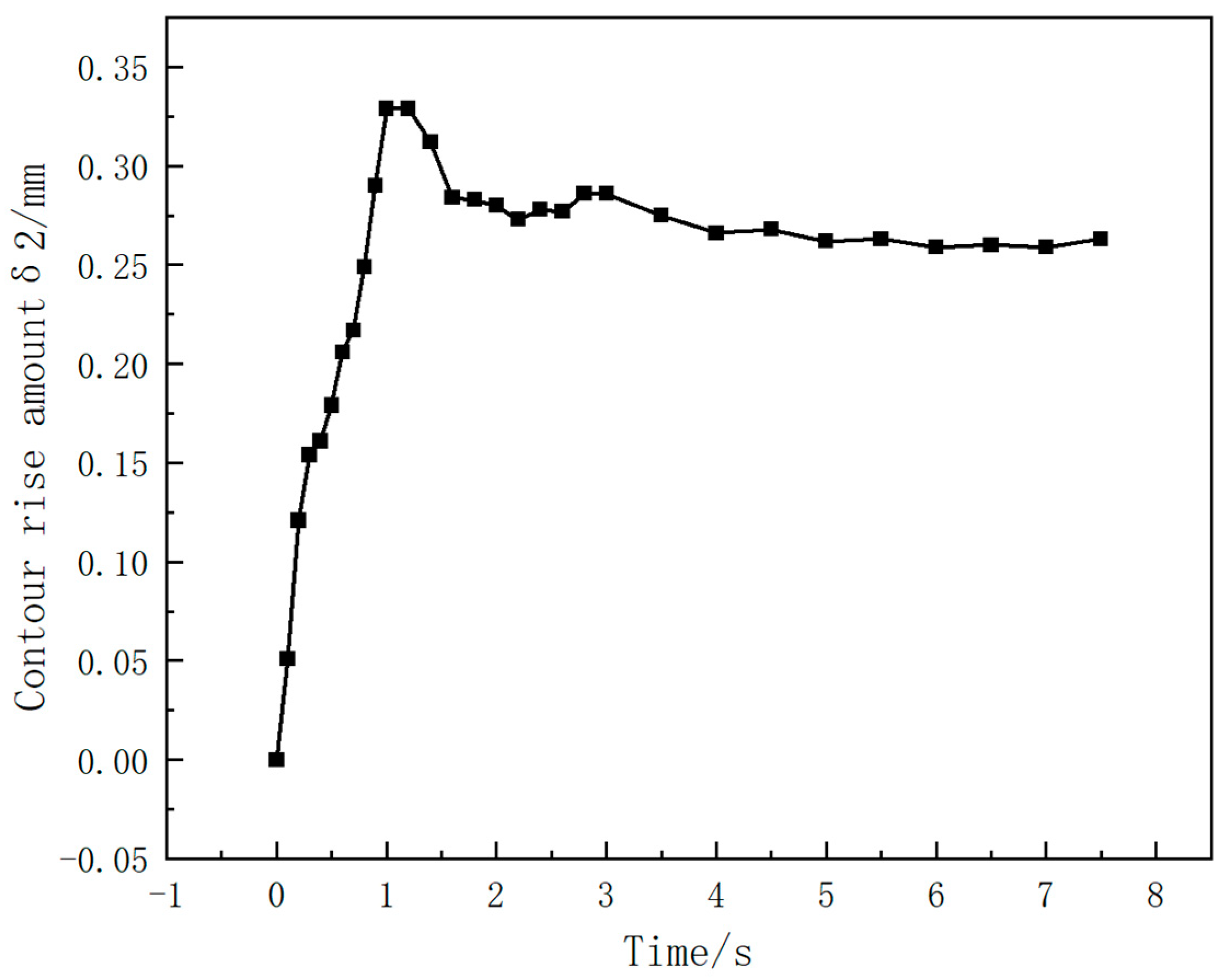
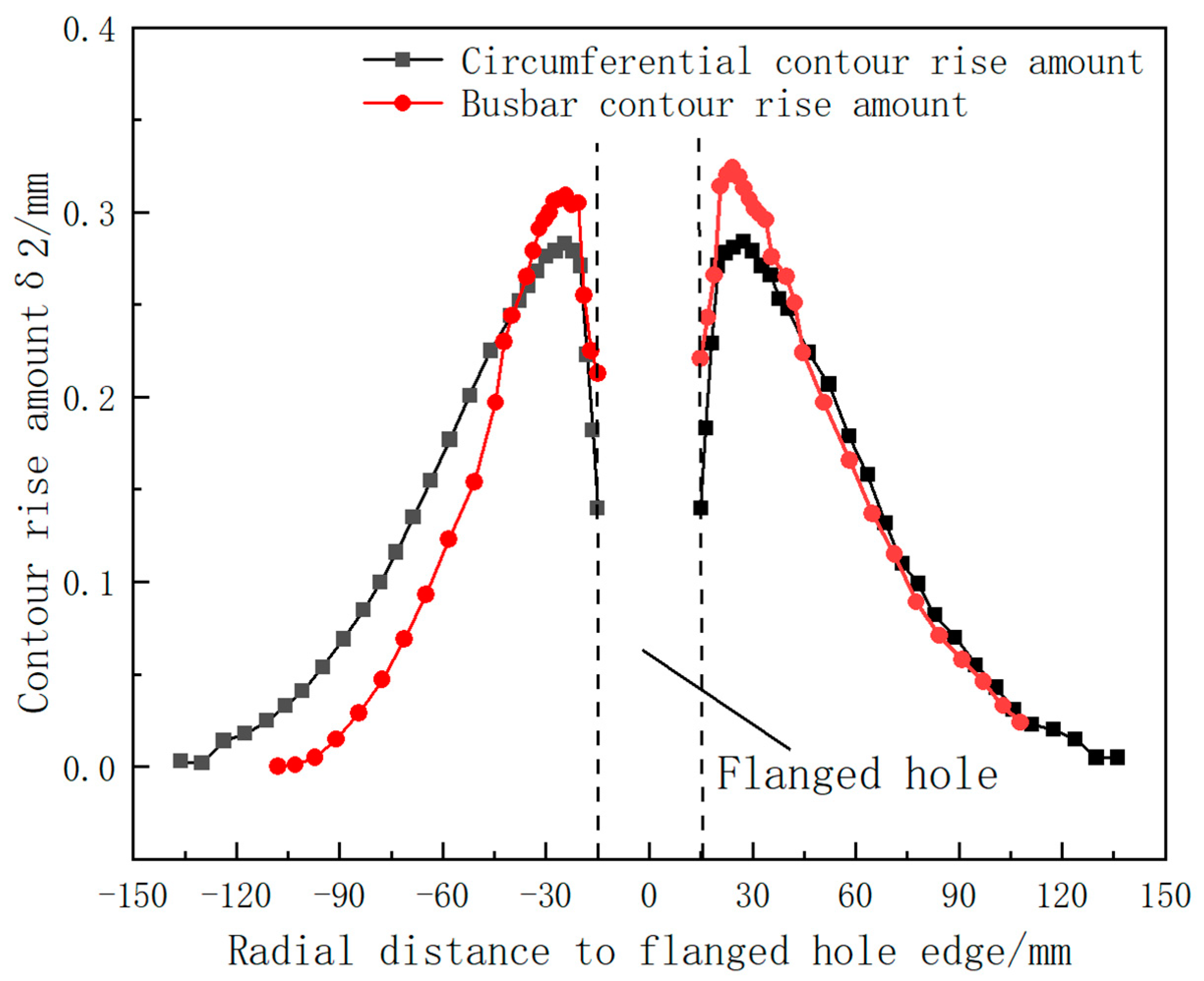
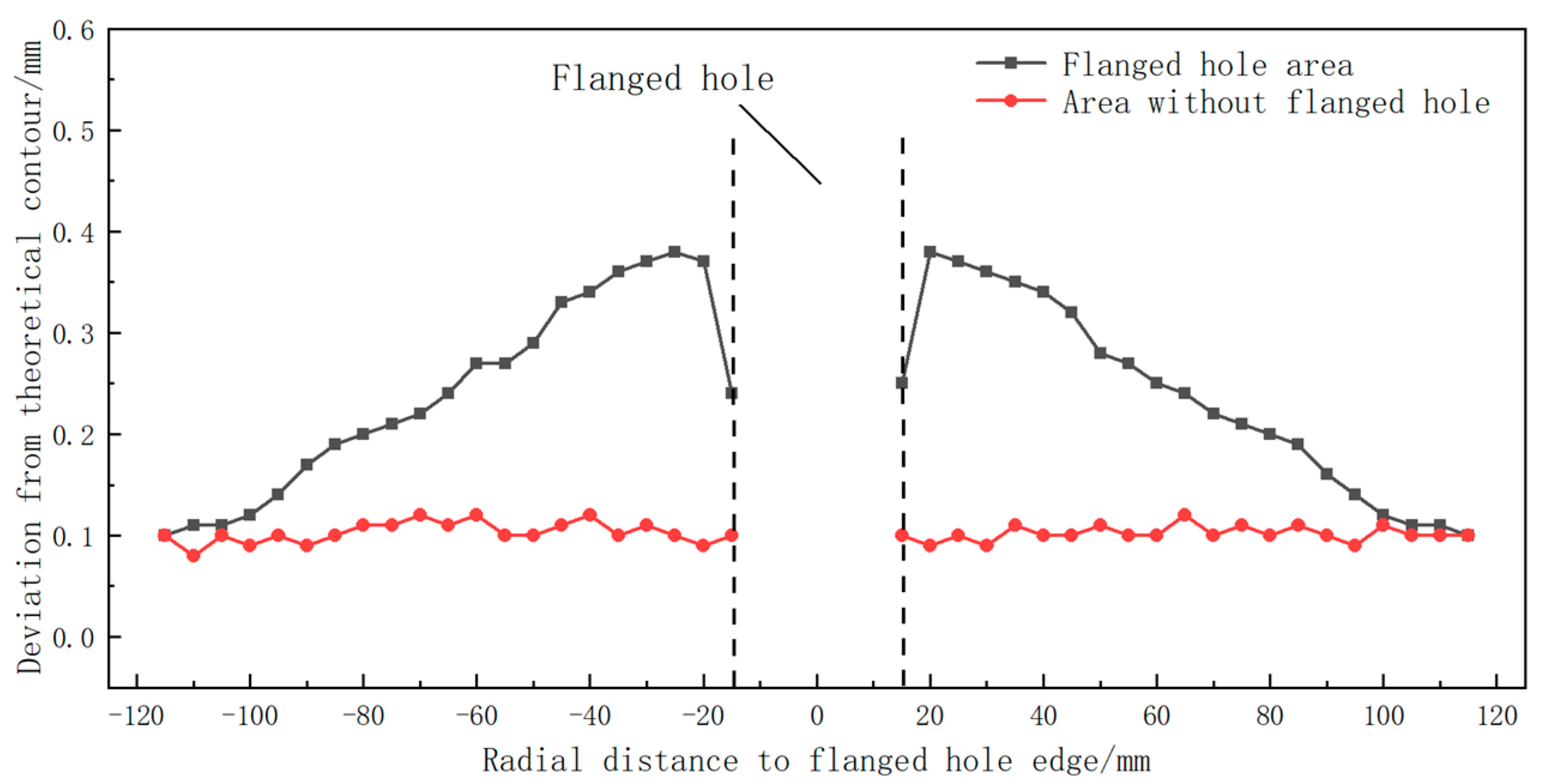
4.3. The Influence of Punching–Spinning Flanging on the Accuracy of the Thin-Walled Head Contour

Different from punching–spinning flanging on a flat blank, the flanging area of the head is irregularly curved, and the edge of the prefabricated hole is formed by flanging along the opposite direction of its curvature center, which is a kind of concave curved internal flanging. A propellant tank head with lateral normal flanged hole is used as the manufacturing objective, and the main dimensional parameters are shown in Figure 24.

The flanged holes on the surface of the head are of the same height at both ends along the circumference of the head, and the height difference between the two ends along the busbar line is 1.05 mm. Since the punching–spinning flanging only affects the local area of the flanged holes, a part of the head with flanged holes is selected as the object of study. From the above analysis, it can be seen that the larger the thinning ratio, the smaller the feed ratio, and the smaller the roller fillet radius, the better the flanging accuracy. Therefore, we chose a 30% thinning ratio, 0.1 mm/r feed ratio, and 4 mm roller fillet radius to study the effect of punching–spinning flanging on the surface accuracy of the head.

Figure 25a shows the equivalent stress distribution of curved surface of head after partial punching–spinning flanging. It can be seen that, unlike the flat blank which has a circular band stress distribution, the equivalent stress distribution of the curved surface punching–spinning flanging also has a band distribution, and the closer to the flanging hole, the higher the stress is, but the stress distribution in the busbar line direction and circumferential direction of the head is not uniform. The circumferential stress band is narrower, the stress band in the busbar direction is wider, and the stress distribution is more concentrated on the side of the busbar near the edge of the flanged head. Figure 25b shows the strain distribution of head punching–spinning flanging, which shows that the material strain is mainly distributed in the area near the flanging hole, the material strain outside the flanging area is smaller, and its distribution is basically consistent with the stress distribution.

The displacement distribution diagram of head punching–spinning flanging shown in Figure 26 reflects the head deformation caused by punching–spinning flanging. The displacement distribution in the area near the flanging hole is band-like as a whole, there is not much difference in the displacement distribution along the circumference of the head, and there is some difference along the busbar line direction.

Figure 27 shows that punching–spinning flanging affects the contour accuracy of the head, especially in the flanged hole area. The maximum contour rise amount is located at the round corner of the flanged hole. In contrast to the flat blank, the contour rise amount is unevenly distributed along both the head busbar line and the circumferential direction of the head. The maximum contour rise amount in the circumferential direction is 0.24 mm, and the maximum contour rise amount in the busbar line direction is 0.28 mm, which is caused by the different curvature of the contour in the two directions of the head, resulting in different rigidity, thus reducing the contour rise amount on the sides with higher curvature.

The contour rise amount is distributed more evenly on both sides of the circumference, and the further away from the flanged hole, the smaller the contour rise amount is, and if the deformation of the head contour is within 0.1 mm at a distance of 50 mm, the forming accuracy is hardly affected. This is because both sides are symmetrical and the curvature change in the surface contour remains the same, so the circumferential contour rise amount is distributed symmetrically. The maximum contour rise amount near the edge of the head is smaller than that near the center of the head, and the overall trend is that the contour rise amount is smaller the farther away from the flanged hole it is, and the decline trend is faster on one side near the center of the head than the other side. The greater the surface curvature is, the better the surface rigidity is, and the harder the deformation is.

The above study on punching–spinning flanging of specific curved surfaces of the head shows that some deformation occurs in the area around the flanging hole of the head, the amount of deformation is smaller than that of the flat blank, and the amount of deformation in its circumferential direction is somewhat different from that in the busbar line direction, but the overall deformation law is basically the same as that of the flat blank.

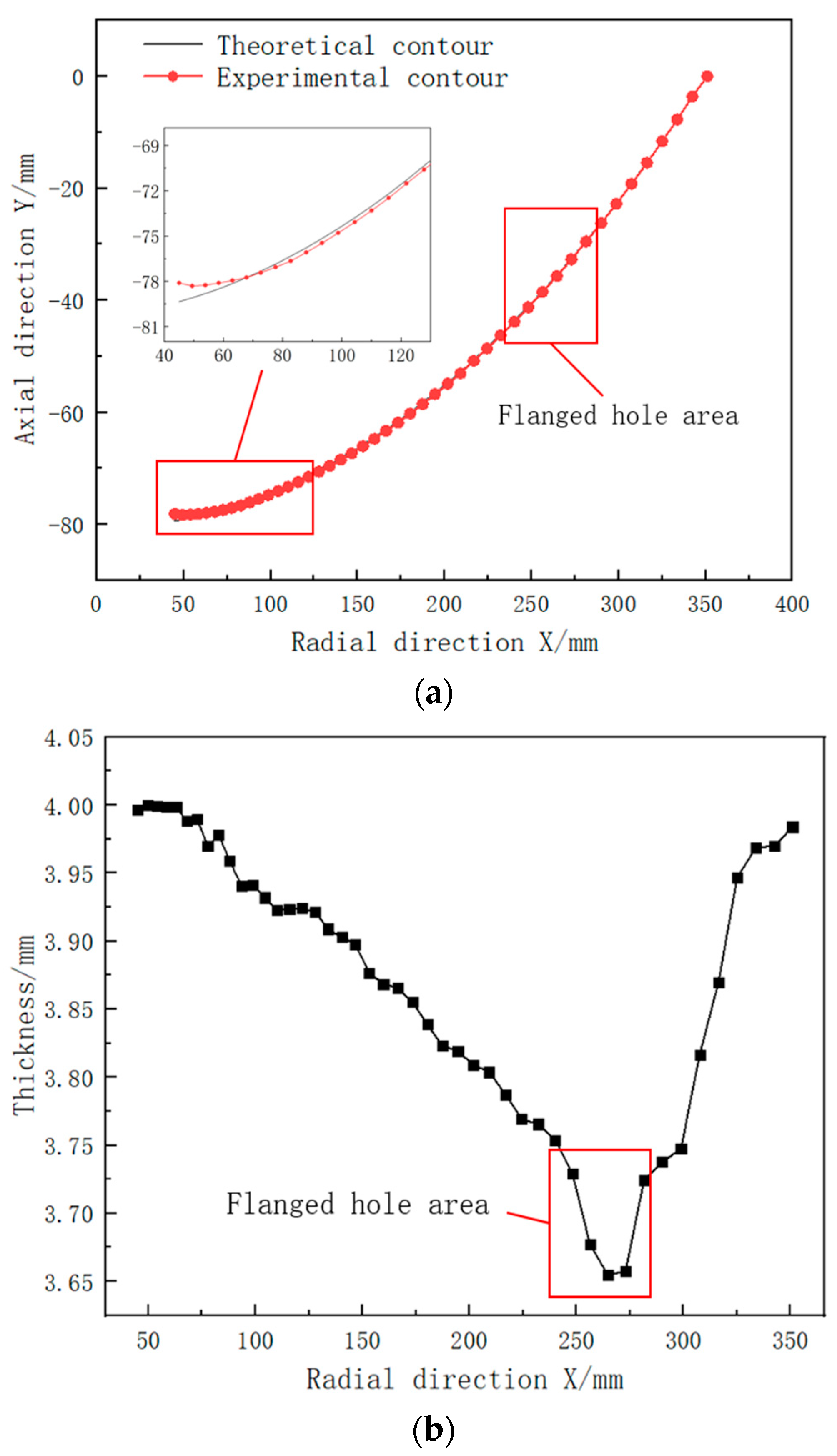
4.4. Experimental Verification

Pre-spinning forming of the head is first carried out, as illustrated in Figure 28, using the marginal-restraint mandrel-free spinning method. The cylindrical support fixture is attached to the machine table and the blank is fixed onto it. The blank is then formed using a single roller in one step. For the experiments, a 2219-O state aluminum alloy plate measuring 820 × 820 mm was used. It had a 4 mm thickness and a prefabricated center hole of 90 mm. The rotation speed was set to $n=15 \mathrm{r}/\mathrm{m}\mathrm{i}\mathrm{n}$, the feed ratio was $f=2 \mathrm{m}\mathrm{m}/\mathrm{s}$, and the roller fillet radius was ${\rho }_R=60 \mathrm{m}\mathrm{m}$. The resulting preformed head is depicted in Figure 29, and the forming effect is deemed satisfactory.

The wall thickness and contour accuracy of the head were inspected after marginal-restraint mandrel-free spin forming, and the results are illustrated in Figure 30. The contour accuracy is good in the flanged hole area, with the error within 0.11 mm, and the wall thickness value is approximately 3.7 mm. A milling head was utilized to finish the machining of the lateral normal preformed hole with 20 mm diameter. The process data, such as rotation speed of 30 r/min, feed ratio of 0.1 mm/r, thinning ratio of 30%, and roller fillet radius of 4 mm, were used for punching–spinning flanging as in Figure 31. The whole formed prototype of head with lateral normal flanging hole and the local features of flanging hole are shown in Figure 32.

A 3D scanner was used to measure the contour of the flanged hole area of the experimental piece, and the contour deviation near the flanged hole area was obtained as shown in Figure 33 and Figure 34. From Figure 33 and Figure 34, it can be seen that there are obvious contour deviations in the flanged hole area of the head with lateral normal flanged hole, and the contour deviations in the flanged hole area show a changing pattern of increasing and then decreasing from the flanged hole. The maximum contour deviation occurs at the flanged corner. The circumferential contour deviation is smaller than the busbar contour deviation, and the circumferential contour deviation is basically symmetrical with respect to the flanged hole. The maximum deviation of the busbar is larger near the edge of the head than near the center of the head, the maximum circumferential contour deviation is 0.38 mm, the maximum busbar deviation is 0.42 mm near the edge of the head, and the maximum busbar deviation is 0.44 mm near the edge of the head. For the area without the flanged hole, the contour deviation is more uniform, the difference between the circumferential and busbar contour deviation is very small, and the maximum contour deviation is 0.11 mm.

The analysis of the above results reveals that the two-step forming process can achieve the target head form by first preforming the head through marginal-restraint mandrel-free spinning followed by flanging the lateral normal hole via punching–spinning. Additionally, the maximum contour deviation present in the flanged hole area measures 0.44 mm, which complies with the head contour tolerance forming accuracy requirement (0~+1 mm).

5. Conclusions

A head with lateral normal flanged hole is a key component of a launch vehicle propellant tank. This paper proposes a two-step method for the integral forming of the head with a lateral normal flanged hole for these kinds of parts and their flanged holes. A FEM with good accuracy is established, and the influence law of different process parameters on the forming accuracy of flanged holes is discussed to study the influence of normal hole flanging on the forming accuracy of the head. Finally, the forming of a head with a lateral normal flanged hole is realized. The main conclusions are as follows:

(1) Combining the characteristics of punching flanging and the spin forming process, a two-step method is proposed for the overall forming of the head with a lateral normal flanging hole, and the new process of punching–spinning flanging with a round hole to ensure the forming of the punching–spinning flanging of the lateral normal hole;

(2) While punching–spinning flanging of a round hole, the larger the thinning ratio and the roller fillet radius, the lower the contour rebound amount and contour rise amount; and the larger the feed ratio, the smaller the contour rebound amount and the less the contour rise amount increases;

(3) The two-step method can be used to achieve accurate forming of the head with a lateral normal flanging hole. For the first step of the marginal-restraint mandrel-free spinning preforming process, the following parameters are used: rotation speed of 15 r/min, feed ratio of 2 mm/r, and roller fillet radius of 60 mm. For the second step of the punching–spinning flanging process, the parameters used: rotation speed of 30 r/min, feed ratio of 0.1 mm/r, thinning ratio of 30%, and roller fillet radius of 4 mm.