Two-Scale Computational Analysis of Deformation and Fracture in an Al-Si Composite Material Fabricated by Electron Beam Wire-Feed Additive Manufacturing
Abstract
:1. Introduction
2. Experimental Evidence
2.1. Materials and Experimental Set-Up
2.2. Microstructure of the Additively Manufactured Alloy
3. Computational Analysis
3.1. Formulation of the Problem
3.2. Aluminum–Silicon Composites at the Eutectic Scale and Homogenization
3.3. Thermomechanical Behavior of the Dendritic Structures
4. Conclusions
- The volume fractions of dendrites (VFD) were found to be 56%, 47% and 31% in the bottom, middle and top parts of the printed sample in the building direction, respectively. In the eutectics, the particles are of spherical, ellipsoidal or toothed shapes and about 400 nm in size on average.
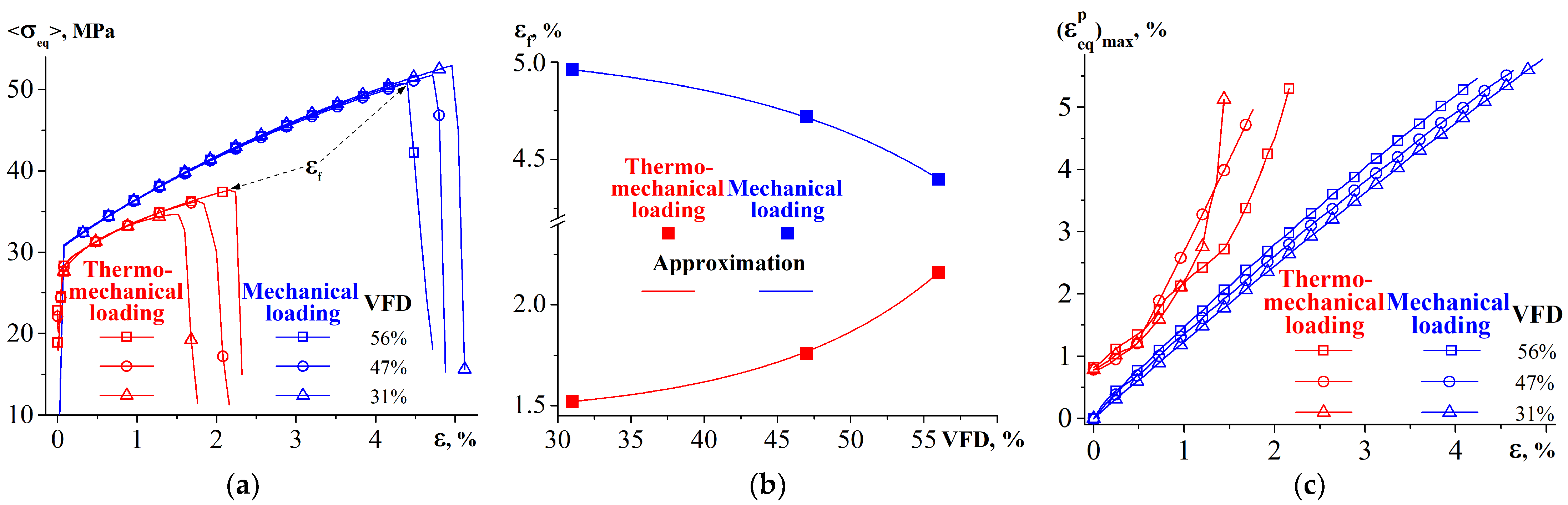
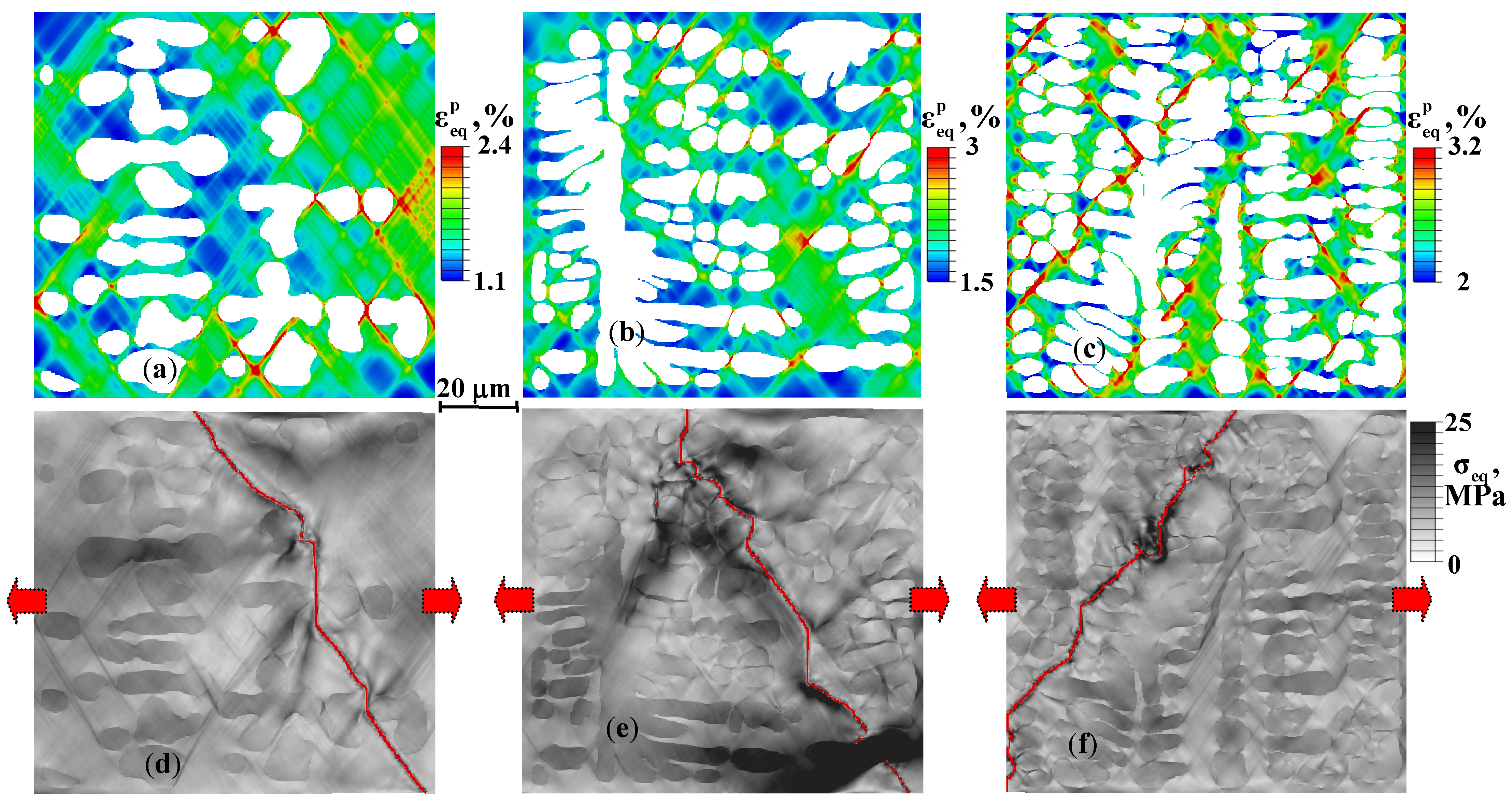
- After cooling of the composite, the silicon particles are entirely subjected to bulk compressive stresses, while the matrix is experiencing both bulk compression and tension. The higher the volume fraction of silicon particles, the larger the value of compressive stresses in the particles and tensile stresses in the matrix, and the earlier the main crack forms in the composite during its tension.
- During cooling of the composites, the aluminum dendrites experience bulk tension, while the eutectic matrix undergoes both bulk tension and compression. Fracture occurs in the eutectic network of the dendritic structures, where the main crack propagates along the dendrite boundaries at an angle of 60 degrees to the loading application direction.
- The residual stresses (RSs) change the plastic strain localization behavior and detrimentally affect the macroscopic strength of the composites subjected to tension. With increasing VFD, the crack develops earlier in the M case and later in the TM case, which is due to nonlinear accumulation of localized plastic strain in the latter case.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, N.; Parthasarathy, M.; Patil, S.; Coates, D.; Myers, K.; Zhu, H.; Li, W. Direct additive manufacturing of metal parts for automotive applications. J. Manuf. Syst. 2023, 68, 368–375. [Google Scholar] [CrossRef]
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Mardaras, J.; Emile, P.; Santgerma, A. Airbus approach for F&DT stress justification of Additive Manufacturing parts. Procedia Struct. Integr. 2017, 7, 109–115. [Google Scholar] [CrossRef]
- Leal, R.; Barreiros, F.M.; Alves, L.; Romeiro, F.; Vasco, J.C.; Santos, M.; Marto, C. Additive manufacturing tooling for the automotive industry. Int. J. Adv. Manuf. Technol. 2017, 92, 1671–1676. [Google Scholar] [CrossRef]
- Kaur, I.; Singh, P. Critical evaluation of additively manufactured metal lattices for viability in advanced heat exchangers. Int. J. Heat Mass Transf. 2021, 168, 120858. [Google Scholar] [CrossRef]
- Nugraha, A.D.; Ruli; Supriyanto, E.; Rasgianti; Prawara, B.; Martides, E.; Junianto, E.; Wibowo, A.; Sentanuhady, J.; Muflikhun, M.A. First-rate manufacturing process of primary air fan (PAF) coal power plant in Indonesia using laser powder bed fusion (LPBF) technology. J. Mater. Res. Technol. 2022, 18, 4075–4088. [Google Scholar] [CrossRef]
- Kolubaev, E.A.; Rubtsov, V.E.; Chumaevsky, A.V.; Astafurova, E.G. Micro-, Meso- and Macrostructural Design of Bulk Metallic and Polymetallic Materials by Wire-Feed Electron-Beam Additive Manufacturing. Phys. Mesomech. 2022, 25, 479–491. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Rahito; Wahab, D.A.; Azman, A.H. Additive manufacturing for repair and restoration in remanufacturing: An overview from object design and systems perspectives. Processes 2019, 7, 802. [Google Scholar] [CrossRef] [Green Version]
- Verma, R.P.; Pandey, K.N.; András, K.; Khargotra, R.; Singh, T. Difficulties and redressal in joining of aluminium alloys by GMA and GTA welding: A review. J. Mater. Res. Technol. 2023, 23, 2576–2586. [Google Scholar] [CrossRef]
- Qbau, N.; Nam, N.D.; Hien, N.T.; Ca, N.X. Development of light weight high strength aluminum alloy for selective laser melting. J. Mater. Res. Technol. 2020, 9, 14075–14081. [Google Scholar] [CrossRef]
- Zhang, J.; Song, B.; Wei, Q.; Bourell, D.; Shi, Y. A review of selective laser melting of aluminum alloys: Processing, microstructure, property and developing trends. J. Mater. Sci. Technol. 2019, 35, 270–284. [Google Scholar] [CrossRef]
- Kumar, S.N.N.; Devarajaiah, R.M.; Ram Prabhu, T. Review on aluminium based functionally graded composites. Mater. Today Proc. 2021, 39, 1743–1749. [Google Scholar] [CrossRef]
- Mathers, G. 3—Material standards, designations and alloys. In The Welding of Aluminium and Its Alloys; Mathers, G., Ed.; Woodhead Publishing Series in Welding and Other Joining Technologies; Woodhead Publishing: Sawston, UK, 2002; pp. 35–50. ISBN 978-1-85573-567-5. [Google Scholar]
- Dash, S.S.; Chen, D. A Review on Processing–Microstructure–Property Relationships of Al-Si Alloys: Recent Advances in Deformation Behavior. Metals 2023, 13, 609. [Google Scholar] [CrossRef]
- Choudhary, C.; Sahoo, K.L.; Mandal, D. Microstructure and mechanical properties of Al-Si alloys processed by strain induced melt activation. Mater. Today Proc. 2018, 5, 27107–27111. [Google Scholar] [CrossRef]
- Barrirero, J. Eutectic Modification of Al-Si Casting Alloys; Saarland University: Saarbrücken, Germany, 2019; ISBN 9789175190075. [Google Scholar]
- Dahle, A.; Nogita, K.; McDonald, S.D.; Dinnis, C.; Lu, L. Eutectic modification and microstructure development in Al–Si Alloys. Mater. Sci. Eng. A 2005, 413–414, 243–248. [Google Scholar] [CrossRef]
- Alkahtani, S.A.; Elgallad, E.M.; Tash, M.M.; Samuel, A.M.; Samuel, F.H. Effect of rare earth metals on the microstructure of Al-Si based alloys. Materials 2016, 9, 45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suarez, C.E. Light Metals 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–1407. [Google Scholar] [CrossRef]
- Xu, W. Direct Additive Manufacturing Techniques for Metal Parts: SLM, EBM, Laser Metal Deposition. In Encyclopedia of Materials: Metals and Alloys; Caballero, F.G., Ed.; Elsevier: Oxford, UK, 2022; pp. 290–318. ISBN 978-0-12-819733-2. [Google Scholar]
- Bae, C.-J.; Diggs, A.B.; Ramachandran, A. Quantification and certification of additive manufacturing materials and processes. In Additive Manufacturing; Zhang, J., Jung, Y.-G., Eds.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 181–213. ISBN 978-0-12-812155-9. [Google Scholar]
- Siddique, S.; Imran, M.; Wycisk, E.; Emmelmann, C.; Walther, F. Influence of process-induced microstructure and imperfections on mechanical properties of AlSi12 processed by selective laser melting. J. Mater. Process. Technol. 2015, 221, 205–213. [Google Scholar] [CrossRef]
- Ponnusamy, P.; Rahman Rashid, R.A.; Masood, S.H.; Ruan, D.; Palanisamy, S. Mechanical Properties of SLM-Printed Aluminium Alloys: A Review. Materials 2020, 13, 4301. [Google Scholar] [CrossRef] [PubMed]
- Rashid, R.; Masood, S.H.; Ruan, D.; Palanisamy, S.; Rahman Rashid, R.A.; Elambasseril, J.; Brandt, M. Effect of energy per layer on the anisotropy of selective laser melted AlSi12 aluminium alloy. Addit. Manuf. 2018, 22, 426–439. [Google Scholar] [CrossRef]
- Baitimerov, R.; Lykov, P.; Zherebtsov, D.; Radionova, L.; Shultc, A.; Prashanth, K.G. Influence of Powder Characteristics on Processability of AlSi12 Alloy Fabricated by Selective Laser Melting. Materials 2018, 11, 742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lykov, P.A.; Baitimerov, R.M. Selective laser melting of AlSi12 powder. Solid State Phenom. 2018, 284 SSP, 667–672. [Google Scholar] [CrossRef]
- Weaver, J.; Barton, T.J.; Jenkins, D.; Linn, J.; Miles, M.; Smith, R. Quantifying Accuracy of Metal Additive Processes through a Standardized Test Artifact. In Proceedings of the 2017 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 7–9 August 2018. [Google Scholar]
- Jackson, M.A.; Van Asten, A.; Morrow, J.D.; Min, S.; Pfefferkorn, F.E. A Comparison of Energy Consumption in Wire-based and Powder-based Additive-subtractive Manufacturing. Procedia Manuf. 2016, 5, 989–1005. [Google Scholar] [CrossRef] [Green Version]
- Köhler, M.; Fiebig, S.; Hensel, J.; Dilger, K. Wire and arc additive manufacturing of aluminum components. Metals 2019, 9, 608. [Google Scholar] [CrossRef] [Green Version]
- Langelandsvik, G.; Horgar, A.; Furu, T.; Roven, H.J.; Akselsen, O.M. Comparative study of eutectic Al-Si alloys manufactured by WAAM and casting. Int. J. Adv. Manuf. Technol. 2020, 110, 935–947. [Google Scholar] [CrossRef]
- Hauser, T.; Reisch, R.T.; Breese, P.P.; Lutz, B.S.; Pantano, M.; Nalam, Y.; Bela, K.; Kamps, T.; Volpp, J.; Kaplan, A.F.H. Porosity in wire arc additive manufacturing of aluminium alloys. Addit. Manuf. 2021, 41, 101993. [Google Scholar] [CrossRef]
- Osipovich, K.; Kalashnikov, K.; Chumaevskii, A.; Gurianov, D.; Kalashnikova, T.; Vorontsov, A.; Zykova, A.; Utyaganova, V.; Panfilov, A.; Nikolaeva, A.; et al. Wire-Feed Electron Beam Additive Manufacturing: A Review. Metals 2023, 13, 279. [Google Scholar] [CrossRef]
- Balokhonov, R.R.; Romanova, V.A.; Schmauder, S.; Emelianova, E.S. A Numerical Study of Plastic Strain Localization and Fracture across Multiple Spatial Scales in Materials with Metal-Matrix Composite Coatings. Theor. Appl. Fract. Mech. 2019, 101, 342–355. [Google Scholar] [CrossRef]
- Balokhonov, R.R.; Romanova, V.A.; Buyakova, S.P.; Kulkov, A.S.; Bakeev, R.A.; Evtushenko, E.P.; Zemlyanov, A.V. Deformation and Fracture Behavior of Particle-Reinforced Metal Matrix Composites and Coatings. Phys. Mesomech. 2022, 25, 492–504. [Google Scholar] [CrossRef]
- Balokhonov, R.R.; Kulkov, A.S.; Zemlyanov, A.V.; Romanova, V.A.; Evtushenko, E.P.; Gatiyatullina, D.D.; Kulkov, S.N. Evolution of Residual Stresses and Fracture in Thermomechanically Loaded Particle-Reinforced Metal Matrix Composites. Phys. Mesomech. 2021, 24, 503–512. [Google Scholar] [CrossRef]
- Balokhonov, R.; Romanova, V.; Schwab, E.; Zemlianov, A.; Evtushenko, E. Computational Microstructure-Based Analysis of Residual Stress Evolution in Metal-Matrix Composite Materials during Thermomechanical Loading. Facta Univ. Mech. Eng. 2021, 19, 241–252. [Google Scholar] [CrossRef]
- Utyaganova, V.R.; Filippov, A.V.; Shamarin, N.N.; Vorontsov, A.V.; Savchenko, N.L.; Fortuna, S.V.; Gurianov, D.A.; Chumaevskii, A.V.; Rubtsov, V.E.; Tarasov, S.Y. Controlling the porosity using exponential decay heat input regimes during electron beam wire-feed additive manufacturing of Al-Mg alloy. Int. J. Adv. Manuf. Technol. 2020, 108, 2823–2838. [Google Scholar] [CrossRef]
- Thermoelasticity. Available online: https://www.sciencedirect.com/topics/physics-and-astronomy/thermoelasticity (accessed on 14 August 2023).
- Balokhonov, R.; Zemlianov, A.; Gatiyatullina, D.; Romanova, V. Computational Analysis of the Influence of Residual Stress on the Strength of Composites with Different Aluminum Matrices and Carbide Particles. Metals 2023, 13, 724. [Google Scholar] [CrossRef]
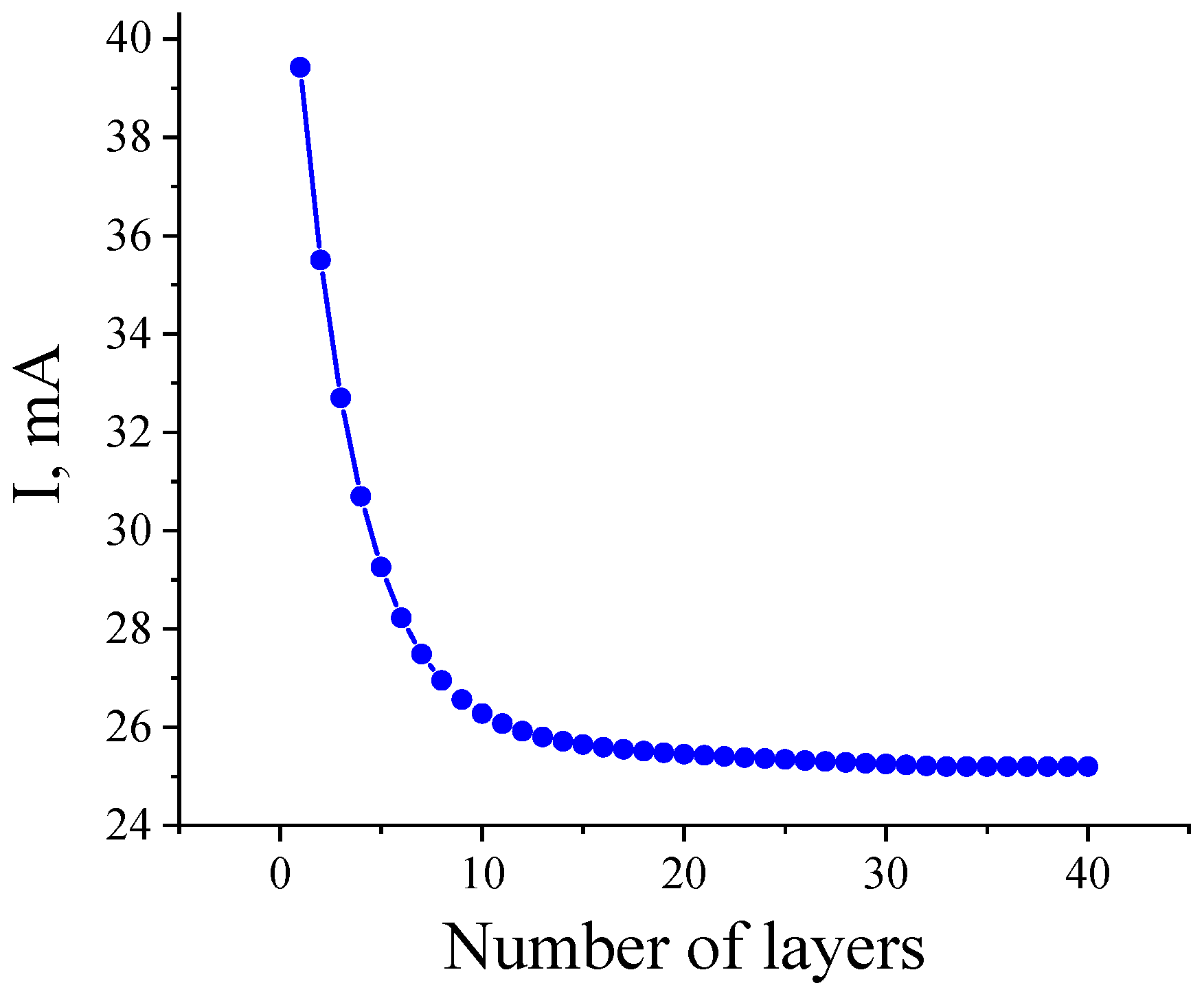




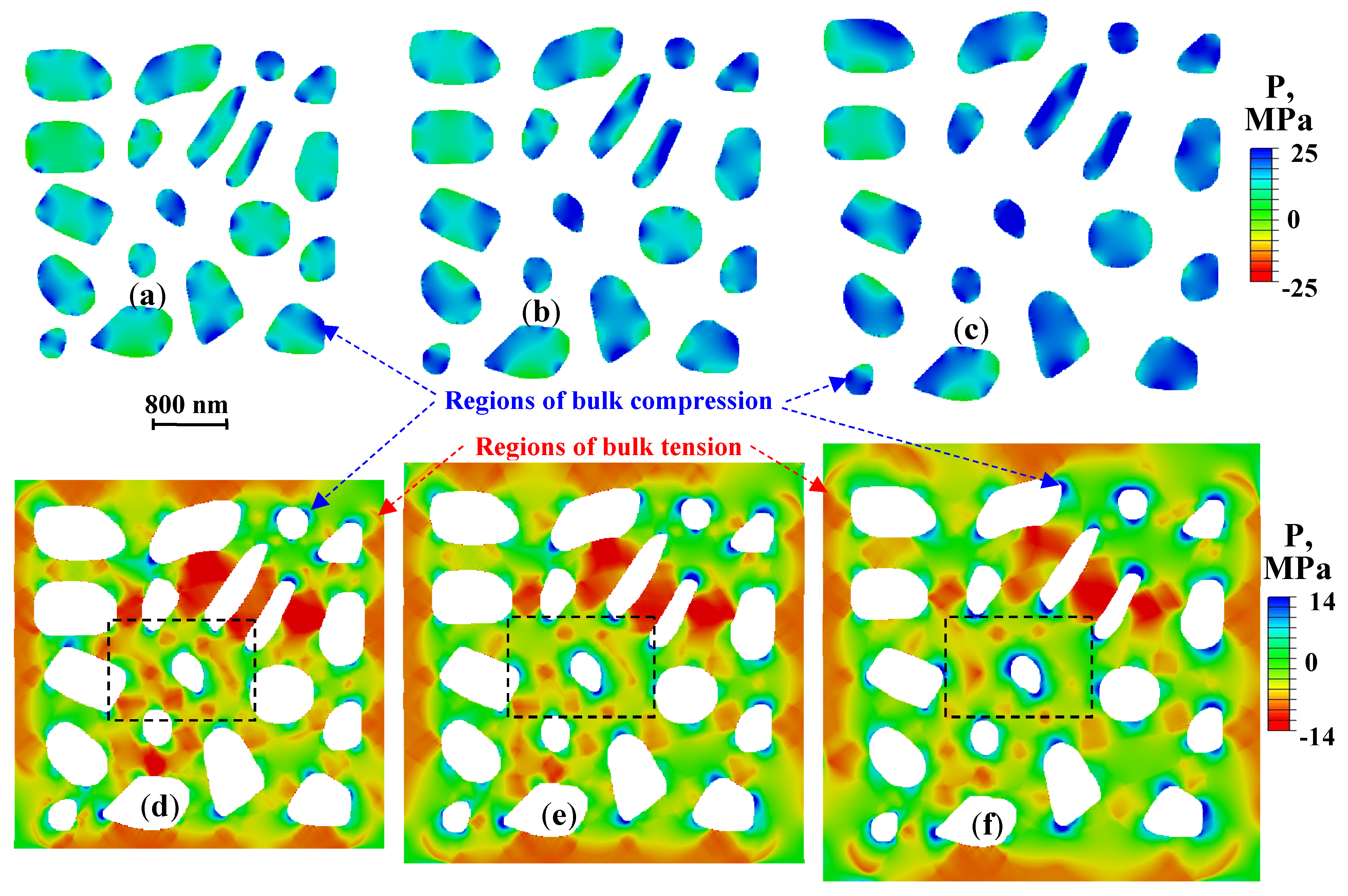

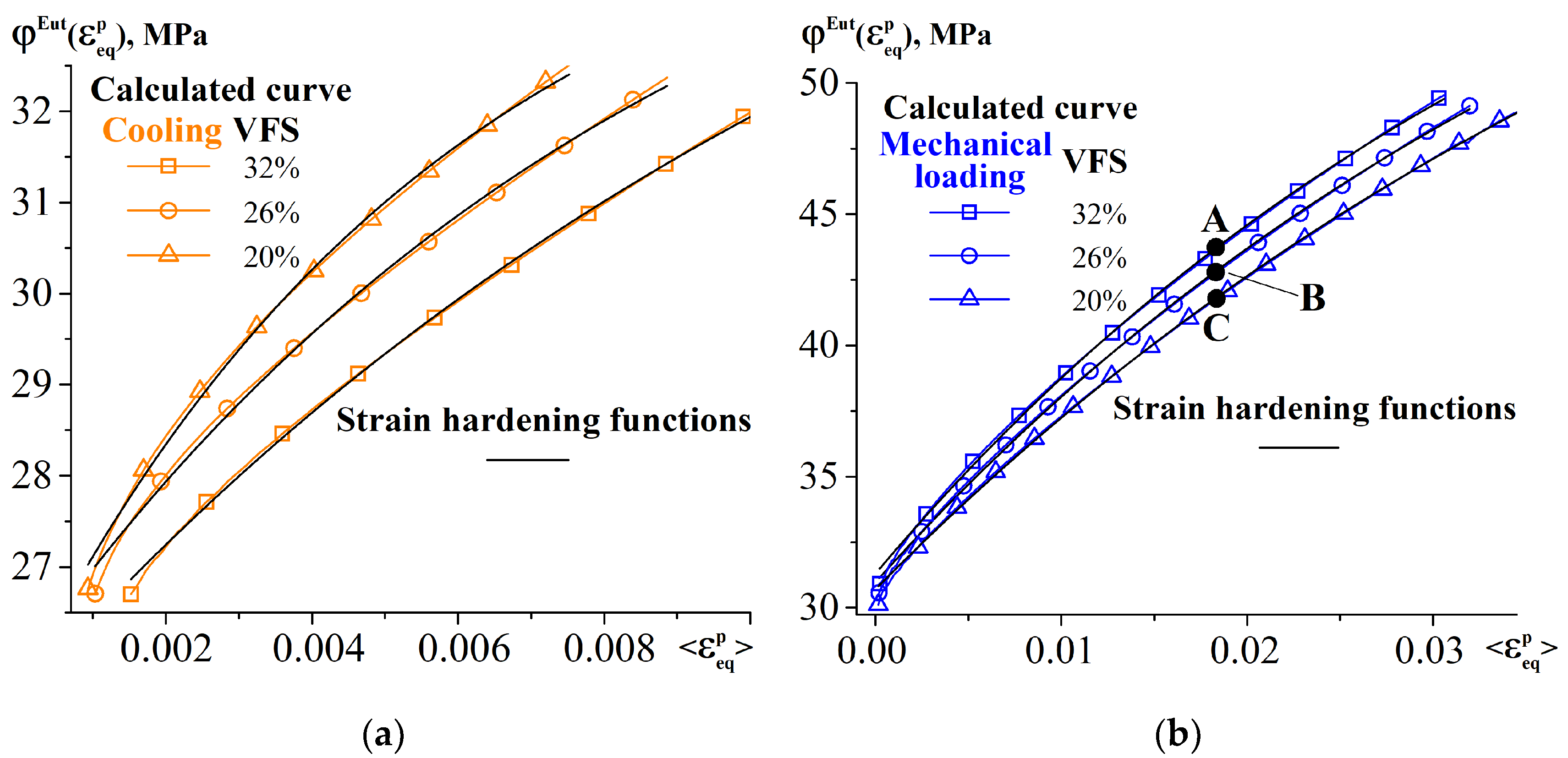
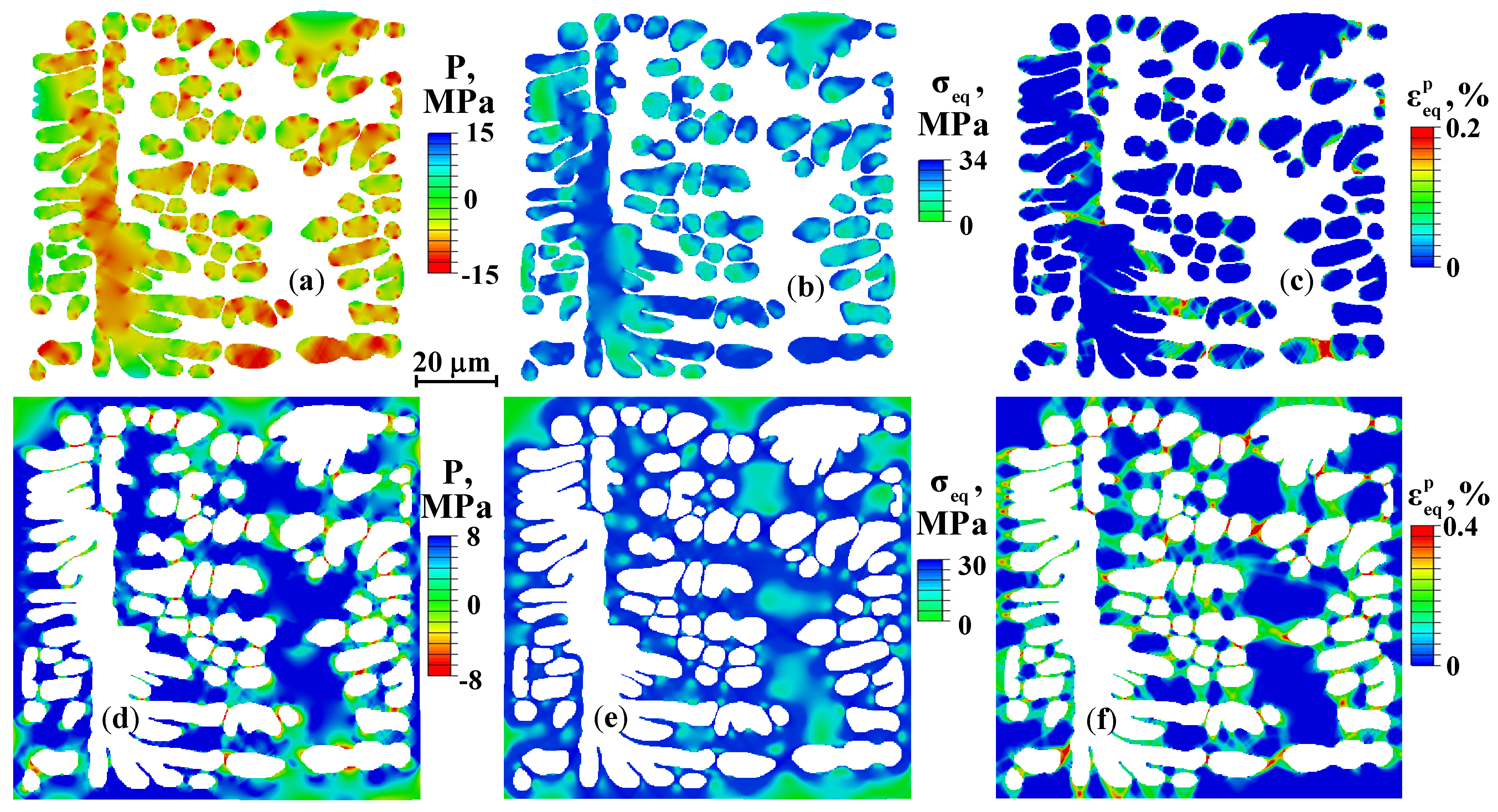
| Alloy | Al, % | Mg, % | Si, % | Mn, % | Fe, % | Cr, % | Ti, % | Zn, % | V, % | Zr, % |
|---|---|---|---|---|---|---|---|---|---|---|
| AlMg5 | balance | 5.21 | 0.41 | 0.48 | 0.43 | 0.23 | 0.11 | 0.16 | - | - |
| AlSi12 | - | 13.3 | - | 0.11 | 0.08 | 0.03 | - | 0.035 | 0.005 |
| Accelerating Voltage, kV | Number of Layers | Beam Spot Type | Table Motion Velocity, mm/min | Beam Spot Diameter, mm | Wire Diameter, mm |
|---|---|---|---|---|---|
| 30 | 40 | Spiral from center | 540 | ~4 | 1.2 |
| Volume Fraction of Si, % | ρ, g/cm3 | K, GPa | µ, GPa | α, 10−6 °C−1 | σS, MPa | σ0, MPa | εpr, % | εpf, % | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | M | C | M | C | M | M | |||||
| 20 | 2.63 | 72 | 34 | 18 | 35 | 68 | 25.7 | 30.5 | 0.6 | 5 | 5.8 |
| 26 | 2.6 | 74 | 36 | 17 | 36 | 66 | 26 | 31 | 0.9 | 4.5 | 5.6 |
| 32 | 2.58 | 76 | 38 | 16 | 38 | 65.6 | 25.6 | 31.3 | 1.3 | 4 | 5.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balokhonov, R.; Zemlianov, A.; Utyaganova, V.; Gatiyatullina, D.; Romanova, V. Two-Scale Computational Analysis of Deformation and Fracture in an Al-Si Composite Material Fabricated by Electron Beam Wire-Feed Additive Manufacturing. Metals 2023, 13, 1465. https://doi.org/10.3390/met13081465
Balokhonov R, Zemlianov A, Utyaganova V, Gatiyatullina D, Romanova V. Two-Scale Computational Analysis of Deformation and Fracture in an Al-Si Composite Material Fabricated by Electron Beam Wire-Feed Additive Manufacturing. Metals. 2023; 13(8):1465. https://doi.org/10.3390/met13081465
Chicago/Turabian StyleBalokhonov, Ruslan, Aleksandr Zemlianov, Veronika Utyaganova, Diana Gatiyatullina, and Varvara Romanova. 2023. "Two-Scale Computational Analysis of Deformation and Fracture in an Al-Si Composite Material Fabricated by Electron Beam Wire-Feed Additive Manufacturing" Metals 13, no. 8: 1465. https://doi.org/10.3390/met13081465
APA StyleBalokhonov, R., Zemlianov, A., Utyaganova, V., Gatiyatullina, D., & Romanova, V. (2023). Two-Scale Computational Analysis of Deformation and Fracture in an Al-Si Composite Material Fabricated by Electron Beam Wire-Feed Additive Manufacturing. Metals, 13(8), 1465. https://doi.org/10.3390/met13081465







