Abstract
In this study, we review some aspects of the application of free randomly moving (RM) electron density and its probability density function distribution to the main free electron transport characteristics of elemental metals. It is shown that metal atom thermal vibrations not only produce free RM electrons, but also produce the same number of electronic defects (weakly shielded ions). The general expressions for the drift mobility, diffusion coefficient, and mean free path of randomly moving electrons are presented. It is shown that the scattering of free RM electrons is mainly due to electronic defects, which cause the distortion of the periodic potential (or the charge density) distribution in the periodic lattice. The resistivity of the elemental metal is caused by electronic defect scattering, taking into account the exchange in the thermal energies between phonons and free RM electrons. Special attention is paid to the analysis of the Hall effect measurement data: the Hall coefficient is presented for two types of RM electrons and holes, taking into account electron-like and hole-like densities of states. The paramagnetism and diamagnetism of the free RM electrons are simply explained using the definition of free RM electron density.
1. Introduction
The foundations of electron transport were laid at the beginning of the last century by the Drude–Lorentz–Sommerfeld free electron theory [1,2,3]. The main achievement of the Drude–Lorentz theory was the prediction of the Wiedemann–Franz law. Sommerfeld solved the electronic heat capacity problem by considering the Fermi–Dirac statistics of electrons in metals. The main limitations of the Sommerfeld model of free electrons are related to the suggestion that all of the valence electrons in the metal are free, as a result of which the estimates of the free electron density, their mobility, the Hall coefficient, and the Fermi-level energy are not correct. Later, very important works on the electron theory of metals were published [4,5,6,7,8,9,10,11,12,13,14,15,16,17], but they did not solve the mentioned limitations. Even recently [18], explanations of electrical conductivity in metals have been proposed based on the Drude–Sommerfeld model in which all valence electrons are free, which is completely inapplicable to metals.
According to quantum mechanics, in the ideal periodic lattice of a metal with periodic potential energy distribution, free electrons can move without any scattering by lattice atoms as Bloch waves [5,12]. The scattering of the free electrons can take place in spots of chemical and structural imperfection. These defects cause the metal’s residual resistivity at very low temperatures. It is a well-known fact that at temperatures above the Debye temperature, the resistivity of elemental metals changes linearly with temperature, while it usually changes as T−5 below it [11]. This has been thought to be caused by lattice atom vibrations [6,8,9], but this cannot explain why the real electron mean free path is many orders of magnitude greater than the interatomic distance. As shown in [19,20,21,22,23], the lattice vibrations play another role. In this study, the estimation of the density of free randomly moving (RM) electrons and their probability density distribution as a function of electron energy and the applications of these characteristics to free electron transport in elemental metals are presented.
Section 2 deals with free electron effective density and the probability density distribution of free electrons on energy; Section 3 deals with the mean free path of free RM electrons and resistivity temperature dependences of elemental metals; Section 4 deals with the Hall effect in elemental metals; Section 5 deals with the magnetic properties caused by free RM electrons in elemental metals; and Section 6 deals with the plasma frequency of free RM electrons.
2. The Effective Density of Free RM Electrons and Their Probability Density Distribution as a Function of Energy
As shown in [19,20,21,22,23], the effective density neff of the free RM electrons can be expressed as
where g(E) is the density of states (DOS) in the conduction band; f(E) is the Fermi distribution function; and f1(E) = 1 − f(E) is the probability that at a given temperature T, an electron can be thermally scattered or change its energy state due to the external field.
Such a description of free RM electrons is valid for any degree of degeneracy of the electron gas in materials, and it is valid for semiconductors, metals and superconductors in the normal state. From Equation (1), it follows that the function
is the probability density function of the free RM electron distribution as a function of energy, which fulfils all the requirements of probability theory [24,25] and is consistent with the Pauli exclusion principle. It should be noted that the probability density function allows us to determine the average value of any random function x(E) as a function of energy:
For materials that have a non-degenerate electron gas, the probability f1(E) = 1 − f(E) ≈ 1, and Equation (1) adopts the classical view. Thus, all electrons in the conduction band n are free and participate in conduction:
Equation (4) is not appropriate for describing free RM electrons in metals. For metals, the probability density function p(E) has a sharp maximum at the Fermi energy E = EF. Under these conditions, Equation (1) becomes
where g(EF) = g(E) at E = EF. The DOS at Fermi-level energy g(EF) can be obtained from the electronic heat capacity data for elemental metals [7]. The DOS g(EF) values of the elemental metal distribution in the periodic table are shown in Figure 1. As can be seen from Figure 1, the smallest g(EF) values are those for Be and alkali metals, while the largest ones are those for V, Ni, Pd, and Nb.
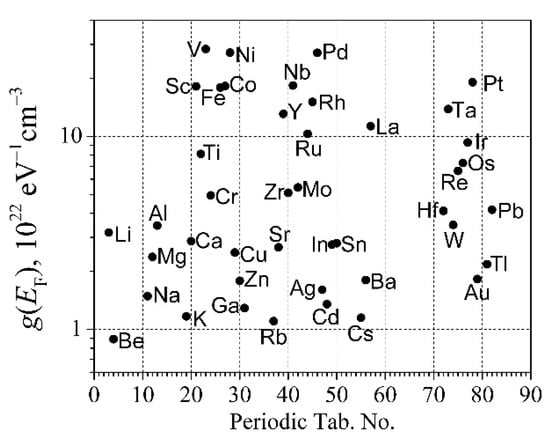
Figure 1.
The DOS g(EF) values of elemental metal distribution in the periodic table.
Figure 2 provides a schematic hypothetical illustration of the DOS for noble- and transition-group metals at room temperature, as described in [26]. In the case of noble metals (Figure 2a), the area beneath the curve gs(E)f(E) in yellow is obtained using Equation (4) and represents the total density of valence electrons in the conduction band; the red area corresponds to the effective density of free RM electrons evaluated using Equation (1). It can be seen that the d-band is not created in noble metals, because this band is lower by 2 eV than the Fermi-level energy. For transition metals, the d-band is not entirely filled, and the total effective density of the free RM electrons can be described as = , where is obtained from the electronic heat measurements. As can be seen from Figure 1, the DOS g(EF) at the Fermi surface for transition-group metals is much larger than that for alkali and noble metals.
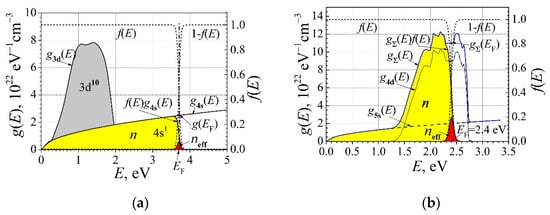
Figure 2.
Schematic illustration of the energy dependence of the functions g(E), g(E)f(E), and g(E)f(E){1 − f(E)] for noble (a) and transition-group (b) metals at room temperature. The yellow area represents the total density n of valence electrons in the conduction band and the red area represents the effective density neff of free RM electrons; gΣ(E) = g5s(E) + g4d(E).
Since only free RM electrons neff electrons participate in the conduction of metals, the other parts of the valence electrons (n − neff) cannot change their energy because all neighbor energy levels are occupied, and also because of the Pauli exclusion principle. Therefore, those parts of the electrons have a constant energy and can only move around the native ions. It is essential to emphasize that free RM electrons in equilibrium conditions do not interact with these (n − neff) electrons as they cannot change their energy.
The valence electrons of a given elemental metal are distributed in the conduction band from 0 to the Fermi level energy EF. Those atoms whose valence electrons have energies close to the Fermi level energy due to lattice thermal vibrations can be excited and leave the native atoms, becoming free and able to move randomly. The atoms that lose their valence electrons partially are shielded by the valence electrons of neighboring atoms. Such partially shielded ions, which are referred to as electronic defects, cause a distortion of the periodic potential in the periodic lattice. Therefore, thermal vibrations of lattice atoms produce free RM electrons and the same number of electronic defects, as well as the local distortion spots in the potential periodicity. In Figure 3, there is presented a schematic illustration of a two-dimensional lattice pattern of metal atoms. The waves of valence electrons partially overlap with those of neighboring atoms, and they move in the field of a central force of the native ions [27]. When a particular atom, due to its thermal vibration, excites a free RM electron, as shown in Figure 3A in the row (b), it also produces a distortion of the potential U(x) periodicity, as shown schematically in Figure 3B in case (b). Therefore, atoms that produce free RM electrons produce the same number of ionic spots (electronic defects), which are not completely screened by the neighbor valence electrons. Considering that the density of free RM electrons is equal to neff = g(EF)kT, this means that the average density of electronic defects can be estimated as [23]:
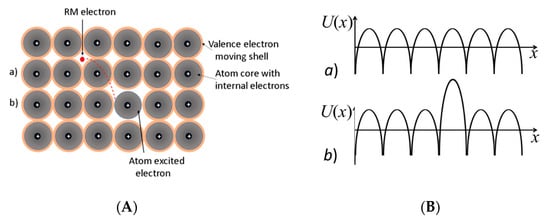
Figure 3.
(A) Schematic representation of a two-dimensional pattern of metal atoms, and (B) a schematic potential U(x) distribution. In row (b) one atom excites the RM electron, causing the distortion of the potential periodicity in row (b) in Figure 3B.
The other parts of the atoms (N − Neff) (where N is the total atom density) do not have enough vibrational (phonon) energy to produce free RM electrons close to the Fermi level energy. It is worth pointing out that the thermal vibrations of the lattice atoms play another role, as described in [4,6,7,8,9,10,11,12].
As shown in [19,20,21,22,23], the conductivity σ of a homogeneous material can be expressed as
where q is the electron charge, D is the diffusion coefficient, and μdrift is the drift mobility of free RM electrons. From this expression follows the Einstein relation D/= kT/q, which is valid for materials with any degree of the degeneration of electron gas with one type of free charge carriers (electrons and holes). The relationship between the electrical conductivity and both the diffusion coefficient and the drift mobility is described by Equation (7) and is shown in Figure 4. Considering that values of the electrical conductivity and the electronic heat capacity are well known and are available from the Handbook [28], values of the diffusion coefficient and the drift mobility of free RM electrons were calculated using Equations (6) and (7).
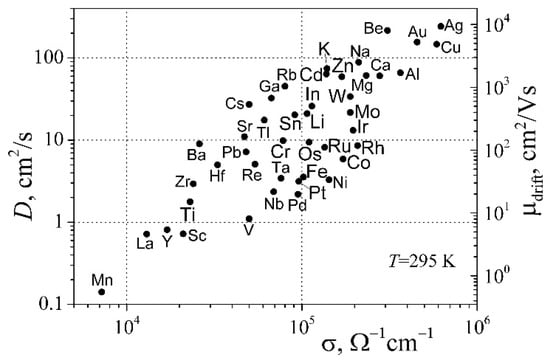
Figure 4.
The diffusion coefficient and the drift mobility relation with the conductivity of elemental metals at room temperature (the right scale has been chosen to correspond to the left scale, so that the positions of the points in the pattern are the same for both scales).
Accounting for the total effective density of free RM electrons being equal to = , and free charge carriers at the Fermi surface having the same Fermi energy, the same diffusion coefficients and the same velocities and relaxation times, thus, each quasi-particle (electron or hole) carries in the same contribution to the electronic heat capacity and conductivity. Moreover, each quasi-particle makes the same contribution to the energy fluctuation variance:
where
and here, ɛ = E/kT. Then,
This result is consistent with the theory of energy fluctuations of free randomly moving particles [29]. It also shows that quasi-particle scattering in metals is an inelastic process. Therefore, the term free electron can be used here as a quasi-particle.
3. The Mean Free Path of RM Electrons and the Temperature Dependence of the Resistivity of the Elemental Metals
The mean free path is the most important parameter characterizing the scattering mechanism of randomly moving charge carriers [30].
The mean free path of free RM electrons in metals can be estimated as
and the average relaxation time as
where σeff is the effective scattering cross-section of free RM electrons by electronic defects. It should be noted that above the Debye temperature, the effective electron scattering cross-section σeff is temperature independent. Thus, the statement that the scattering cross-section is proportional to temperature in the mentioned temperature range [4,5,6,7,11,12] contradicts the probability density function of free RM electrons. Equation (11) directly shows that the electron mean free path at temperatures above the Debye temperature is inversely proportional to both the temperature and the DOS at the Fermi surface.
The electron-scattering cross-section of elemental metal distribution on DOS at the Fermi level is shown in Figure 5a at room temperature. The product , where is the volume for one free RM electron. The dependence of the volume on the periodic table is shown in Figure 5b at room temperature. The largest volume has Be and alkali metals and the smallest one has V, Ni, and Pd.
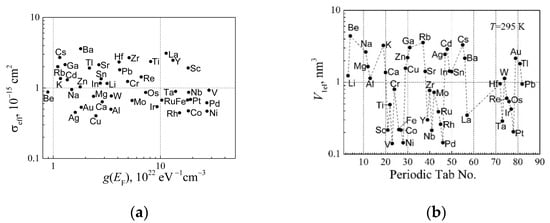
Figure 5.
(a) The effective scattering cross-section σeff of free RM electrons caused by electronic defects and the relation with DOS at the Fermi surface at room temperature; (b) the volume for one free RM electron distribution on the periodic table at room temperature.
Figure 6 shows the electric resistivity of Al, Cu, and Pd as a function of temperature from 1 K to 1000 K. As has been mentioned, the resistivity at temperatures above the Debye temperature is proportional to temperature T, and it is not related to the scattering cross-section dependence on temperature. What are the effects that cause a steep resistivity decrease with temperatures below the Debye temperature Θ? The electric resistivity below 10 K is independent and caused by the scattering of free RM electrons by chemical and structural imperfections. Since each free electron absorbs or excites one phonon during scattering, the scattering cross-section depends on the ratio of the thermal energy exchange between free RM electrons and electronic defects.
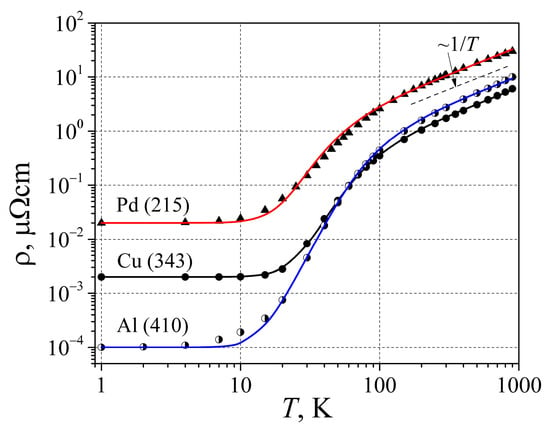
Figure 6.
The resistivity dependence on temperature for Pd, Cu, and Al. The points are experimental data taken from [28], the number in brackets near the chemical symbol is the Debye temperature Θ in K used to calculate resistivity, and the solid lines are calculated with Equation (22).
The average thermal energy [5] of the free electrons estimated for one free RM electron is:
The average phonon thermal energy at T > Θ is 3kT because all the lattice vibration waves are excited, but at T < Θ only the low-frequency phonons become excited. The average thermal energy of a single phonon accounting for the excitation and annihilation of the phonon can be described as [12,23,31,32]:
Then,
where
is the phonon mediation factor for free RM electron scattering. Then, the resultant scattering cross-section σres of free RM electrons can be described as
where σeff can be obtained from Equation (11) at room temperature.
At temperatures above the Debye temperature, the resistivity of the elemental metal is given by
where T0 = 300 K, and ]. The resultant relaxation time τres of the free RM electrons now can be expressed as
where
and
where is the average scattering cross-section of the residual defects (impurities), and Ndef is their density. Thus, the resistivity of elemental metals in the temperature range from 1 K to 1000 K can be expressed as
The calculated resistivity dependences on temperature by Equation (22) are shown in Figure 6 as solid lines with T0 = 300 K. Here, the calculations have been performed using the constant Debye temperature values Θ. Considering that the Debye temperature is not completely constant [29], there may be a small difference between calculated and experimental data in some temperature ranges. It can be seen that Equation (22) describes the resistivity temperature dependence well enough, though the metals presented have very different Fermi surfaces and different DOS at the Fermi surface.
4. Hall Effect of Metals
The Hall coefficient RH, when the direct current flows in the x-direction and the magnetic field is directed along the z-axis, is given by
where jx is the direct current density in the x-direction, Bz is the magnetic flux density in the z-direction, Ey = EH = UH/w, and here UH is the Hall voltage in a material plate with dimensions d × w × l (thickness × width × length). Ex = Ux/l is the applied electric field strength in the x-direction, and σ is the conductivity of the material wafer. The Hall effect for the small direct current and weak magnetic fields can also be characterized by the Hall angle φ:
On the other hand, the Hall angle can be expressed in terms of the electron cyclotron angular frequency [33]:
where is the Hall factor, which depends on the free charge carrier scattering mechanism. For highly degenerate electron gas , it can be noted that is independent of the kinetic energy of the particle, and it does not depend on the radius of motion of the electrons and on their velocity.
Such a general expression for materials with one type of the free charge carriers follows from Equations (23)–(25):
Considering that the quantity has the same dimension as the drift mobility of the free charge carriers, it is called Hall mobility. Equation (26) is valid for both non-degenerate and degenerate electron gas materials with one type of the free RM charge carriers.
In the general case, the absolute value of the drift mobility for one type of charge carriers can be described as
where the coefficient indicates by how many times the average kinetic energy <E> of the free RM electron is higher than the classical particle thermal energy (3/2)kT. Accounting that the conductivity can be described by such a general expression:
then the Hall coefficient is described by the following general relationship:
which is valid for any degree of degeneration of the electron gas with one type of free charge carrier. In the case of a material with non-degenerate electron gas, and the Hall coefficient takes the classical form:
Considering that for metals rH = 1, and , the Hall coefficient for metals with one type of free randomly moving charge carrier can be expressed as [20,21,22,23]:
For an ideal spherical Fermi surface, the product = 3n/2 [5], and one can obtain the classical relation , where n is the total density of electrons in the conduction band, but this does not mean that all the electrons in the conduction band are free, and can move randomly and participate in conduction. Many elemental metals do not have spherical Fermi surfaces; they have very complex Fermi surfaces [5,7,26].
The experimental data of the Hall coefficient distribution in the periodic table for elemental metals at room temperature is shown in Figure 7a.
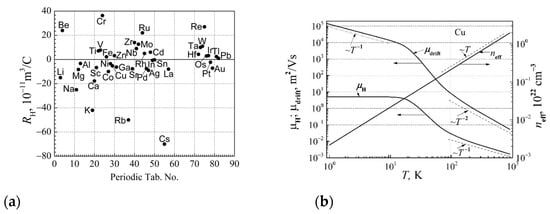
Figure 7.
(a) The Hall coefficient distribution on location in the periodic table for elemental metals at room temperature. Data are taken from [7,34,35]. (b) The free RM electron density neff, and their drift mobility μdrift and Hall mobility (absolute values) as a function of temperature for copper.
The magnetic flux density during the Hall coefficient measurement was in the range (0.5–1.3) T. As can be seen from Figure 7a, the Hall coefficient for different elemental metals has different signs, i.e., in different elemental metals prevail in electronic-type or hole-type charge carriers.
The general expressions for conductivity and the Hall coefficient for two types of free charge carriers (electrons and holes) can be described as [12,36]:
Here, the relation is fulfilled for each type of charge carrier. The total density of DOS obtained from the electronic heat capacity results is equal to ) = , where and are the DOS components caused by electron-like and hole-like DOS at the Fermi surface, respectively. The electrical conductivity, the electronic heat capacity, and the thermal noise measurements [37] show that they do not depend on the quasi-particle origin (electron or hole); all these particles move randomly with the Fermi velocity.
Considering that the Fermi energy for a given elemental metal is the same for free RM electrons and for free RM holes, this means that the average velocity and the average relaxation time at the Fermi surface are the same for all free RM charge carriers. Then, the absolute value of the drift mobility for each type of free RM charge carrier can be expressed as
From this expression, it can be seen that for elemental metals the drift mobility of free RM charge carriers does not depend on the effective mass of the charge carrier, and changes with temperature as 1/T2, because . Therefore, the absolute value of the Hall mobility for free RM charge carriers can be expressed as
The Hall mobility is determined by the relaxation time and is independent of the energy of free charge carriers. An illustration of the effective density of free RM electrons, and their absolute values of the drift and Hall mobility as a function of temperature for copper, is shown in Figure 7b.
At temperatures higher than room temperature, the free RM electron density increases with temperature as ~T, and the drift mobility decreases as ~1/T2, causing the resistivity to increase with temperature as ~T. As can be seen from Figure 7b, the absolute value of the drift mobility in copper at cryogenic temperatures exceeds the Hall mobility by three orders.
It follows from Equations (27) and (35) that the Hall mobility for a single type of free charge carriers can also be expressed as . The absolute values of the Hall mobilities of the free RM charge carriers of elemental metals’ distribution in the periodic table are shown in Figure 8a at room temperature. The Hall mobility values are distributed in the range 10–70 cm2/Vs. The highest Hall mobilities have Ag, Be, and Au, and the lowest ones have La, Sc, Y, and V. The absolute values of the drift mobilities of free RM charge carriers of the elemental metal distribution in the periodic table are shown in Figure 8b at room temperature. The drift mobility values for different elemental metals are distributed in a very wide range, from 30 cm2/Vs to 104 cm2/Vs, and this causes the very wide distribution of the conductivity values of elemental metals. The highest values of drift mobility have Ag, Be, Au, and Cu, and the lowest ones have Sc, Y, La, and V.
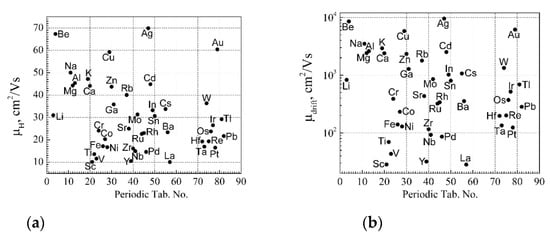
Figure 8.
(a) The absolute value of the Hall mobilities for a single type of free RM charge carrier of elemental metal distribution in the periodic table at room temperature; (b) the absolute value of the drift mobilities for a single type of free RM charge carriers of elemental metal distribution in the periodic table at room temperature.
Since metals have electrons and holes, free RM charge carrier densities neff and peff can be expressed as follows:
then, taking into account Equations (34) – (37), Equations (32) and (33) can be rewritten as
where gtotal (EF) = gel (EF)+ ghole (EF), and RH1 = 3/[2qgtoal (EF)EF] is the Hall coefficient in the case of only a single type of randomly moving charge carriers in the sample, and
is the quantity that plays the role of compensation in Hall voltages caused by electrons and holes in the Hall effect measurement. Thus, from the Hall coefficient RH2 data of metals (Figure 7a) and Equation (31) for RH1, it is possible to determine the compensation quantity η and the relative parts of electron-like or hole-like densities of states at the Fermi surface. The relative electron-like and hole-like DOS parts are shown in Figure 9a,b, respectively.
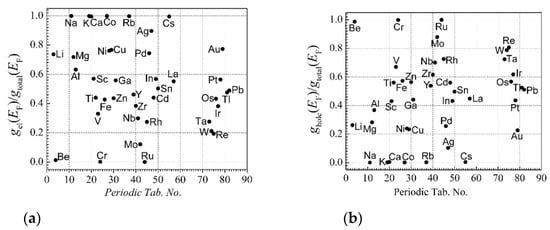
Figure 9.
(a) Relative electron-like DOS part at the Fermi surface distribution in the periodic table of elemental metals; (b) relative hole-like DOS part at the Fermi surface distribution in the periodic table of elemental metals. The relative hole-like DOS part is determined as ghole(EF)/gtotal(EF) = 1 − gel(EF)/gtotal(EF).
From Figure 9a,b, it can be seen that electronic-like DOS at the Fermi surface prevails for alkali metals, Ca, and Co. On the other hand, the hole-like DOS at the Fermi surface prevails for Be, Cr, and Ru.
The measurement results of the Hall coefficient show that its value depends on the magnetic field strength [38]. Figure 10a shows the Hall coefficient RH2 dependence of the magnetic field strength for aluminum, where the parameter of the magnetic field strength is expressed by the cyclotron frequency , where B is the magnetic flux density and τ is the charge carrier mean free flight time. It can be seen that at low magnetic field strengths () the Hall coefficient is negative and electrons are the dominant free charge carriers, but with a high magnetic field the Hall coefficient is positive and holes are the dominant free charge carrier.
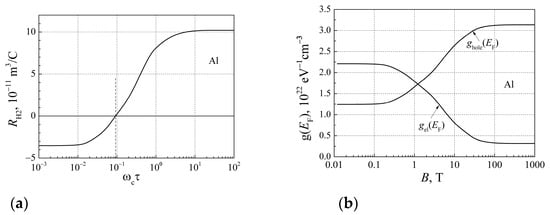
Figure 10.
(a) The dependence of the Hall coefficient on for aluminum (prepared with respect to data from [37]); (b) the dependences of the electron-like gel(EF) and hole-like ghole(EF) DOS on the magnetic field for aluminum.
This means that the Fermi surface nonuniformity is affected by the magnetic field due to changes in the energy derivative at the Fermi surface. It causes the redistribution between electron-like and hole-like DOS at the Fermi surface.
Thus, the measurement of the Hall coefficient does not give the total density of the electrons in the conduction band, either at low or at high magnetic field strengths. Using Equations (31) and (39), and g(EF) for Al, we have estimated the electron-like and hole-like DOS dependences on the magnetic field strength, which are shown in Figure 10b. It can be seen that these DOS densities are strongly dependent on the magnetic field strength, and that there is no relationship with the total electron density in the conduction band.
Equation (39) also allows us to explain the Hall mobility and the Hall coefficient measurement results in the normal state superconductor Yba2Cu3 O7−δ [39,40].
5. Magnetic Susceptibility of Free RM Electrons
The magnetic susceptibility is defined as
where is the relative permeability, and · H/m is the magnetic constant. The magnetization of the material is given by
where B is the magnetic flux density and H is the magnetic field strength. Thus, the electron behaves as a two-state system with energies of (where is the Bohr magneton), and the single electron partition function is given by
The partition function for n free electrons per unit volume is
Then, the free energy F of the system is equal to [41]:
The total magnetic moment M of the n free electron system can be obtained by calculating the derivative:
For a small magnetic field , the paramagnetic susceptibility is
The conduction band electrons can be expected to make a Curie-type paramagnetic contribution to the magnetization of the metal [9,42]:
This formula is valid for free electrons. Considering the observed data of the M of the elemental non-ferromagnetic metals, the magnetization is almost independent of temperature, and it has been concluded that the Curie-type law is not valid for free electrons in metals. However, this erroneous conclusion has been reached by considering that all valence electrons are free, but only RM electrons are free, whose density is equal to = g(. Therefore, the Curie-type law is fulfilled if the real density of the free RM electrons is taken into account. Then, the paramagnetic susceptibility of the free RM electrons for non-ferromagnetic metals is given by
It is known that when electrons are freely moving in a magnetic field, in addition to the paramagnetic effect of their spin, they exhibit a diamagnetic effect due to their motion. In accordance with Lenz′s law this yields a magnetic field that is the opposite to the direction of an applied magnetic field. Considering that the rotational energy of the free randomly moving electron in a perpendicular magnetic field is , where is the electron cyclotron frequency, one can write an analogous expression for the electron partition function, taking into account the electron spin (1/2):
Then, the diamagnetic susceptibility, taking into account the diamagnetic effect yielding a magnetic field opposed to the direction of the applied magnetic field, can be expressed as
because the effective density of free RM electrons in the plane perpendicular to the magnetic field is equal to 3). The absolute value of Landau diamagnetism is thus equal to one-third that of Pauli paramagnetism in the free-electron model [9,42]. Therefore, it produces diamagnetic susceptibility:
Then, the resulting magnetic susceptibility of free RM electrons for non-ferromagnetic metals is equal to:
Though the magnetic susceptibility of free RM electrons is proportional to the DOS at the Fermi surface (Equation (53)), as for the electronic heat capacity, it cannot be used as a suitable quantity for evaluating the DOS at the Fermi surface because the magnetic susceptibility measurement results also depend on the susceptibilities of the neutral atoms and ions (Figure 11).
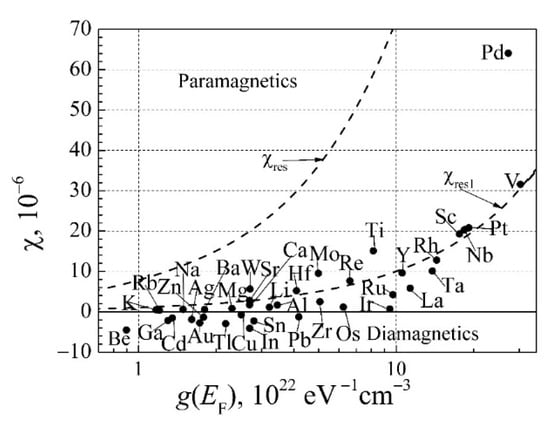
Figure 11.
Magnetic susceptibility dependence on the DOS at the Fermi surface for non-ferromagnetic metals: the points are the experimental data from [35], the dashed curve χres is calculated with Equation (53), and the curve χres1 = (1/7)χres is plotted as an average value.
In addition, diamagnetism is also present in all atoms and molecules, and in gases of atoms and molecules that do not carry permanent magnetic moments. This leads to an additional diamagnetism of the ions, comparable to the Landau diamagnetism. There are therefore three temperature-independent contributions to the magnetic susceptibility of non-ferromagnetic metals: the free electron Pauli paramagnetism, the Landau diamagnetism, and the diamagnetism of the metal ions.
Therefore, the free RM electron model allows a very simple explanation of the diamagnetism and paramagnetism of non-ferromagnetic elemental metals.
6. Plasma Frequency of the Free RM Electrons in Elemental Metals
A.C. conductivity σ(ω) is usually presented in the following form [5]:
and the relative permittivity at ω<τ> >> 1 as
where
where ωp is the free electron oscillation plasma frequency. Taking into account Equation (28) for the d.c. conductivity, the plasma frequency for elemental metals can be described as:
It can be seen that the plasma frequency does not depend on the temperature. The dependence of the plasma frequency fp = ωp/2π on the DOS g(EF) at the Fermi surface for elemental metals is shown in Figure 12a. It can be seen that there is no correlation between plasma frequency and DOS at the Fermi surface for different metals.
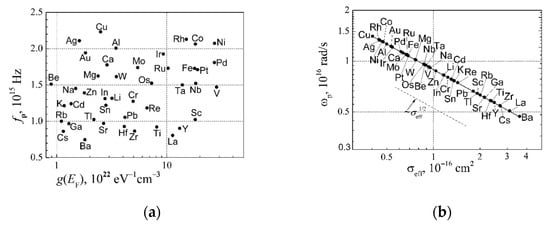
Figure 12.
(a) The dependence of the plasma frequency fp on the DOS g(EF) for elemental metals; (b) the dependence of the plasma frequency on the free electron effective scattering cross-section for elemental metals (Figure 5a).
7. Conclusions
A study of the main transport characteristics of the free electrons on the basis of the stochastic definition of the effective density of free RM electrons in elemental metals is presented. It is shown that thermal vibrations of the lattice atoms play a different role than has been explained in many publications: the thermal vibrations of the atom not only excite the free RM electrons, but also produce the same number of electronic defects (weakly shielded ions). The temperature dependence of the resistivity over a very wide temperature range is explained by the scattering of free RM electrons by the electronic defects accounting for the thermal energy exchange between the phonon and the free RM electron. The Hall coefficient of metals is explained by using electron-like and hole-like densities of states at the Fermi surface. The definition of the density of the free RM electrons allows a very simple explanation of the paramagnetism and diamagnetism of the free RM electron. It is shown that different values of the plasma frequency are caused by different values of the effective scattering cross-sections of different elemental metals.
Author Contributions
Conceptualization, V.P.; methodology and software, V.P. and V.J.; validation, V.P. and V.J.; investigation, V.P. and V.J.; writing-original draft preparation V.P.; review and editing V.P. and V.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are provided in the figures in the article. All data generated and analyzed during this study are included in the presented manuscript, and are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Drude, P. Zur Elektronentheorie der Metale. Ann. Phys. 1900, 306, 441–624. [Google Scholar] [CrossRef]
- Lorentz, H.A. The Theory of Electrons, 1st ed.; The Columbia University Press: New York, NY, USA, 1909. [Google Scholar]
- Sommerfeld, A.; Bethe, H. Elektronentheorie der Metals; Springer: Berlin, Germany, 1967. [Google Scholar]
- Abrikosov, A.A. Fundamentals of the Theory of Metals; Dover Publ.: Mineola, NY, USA, 2017. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; HRW Int. Ed.: New York, NY, USA, 1976. [Google Scholar]
- Kaveh, M.; Wisser, N. Electron-electron scattering in conducting materials. Adv. Phys. 2001, 33, 257–372. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; John Wiley and Sons: New York, NY, USA, 1976. [Google Scholar]
- Lundstrom, M. Fundamentals of the Carrier Transport; Cambridge Univ. Press Online: Cambridge, UK, 2014. [Google Scholar]
- Mizutani, U. Introduction to the Electron Theory of Metals; Cambridge Univ. Press Online: Cambridge, UK, 2014. [Google Scholar]
- Schulze, G.E.R. Metallphysik; Akademie: Berlin, Germany, 1967. [Google Scholar]
- Sondheimer, E.H. The mean free path of electrons in metals. Adv. Phys. 2001, 50, 499–537. [Google Scholar] [CrossRef]
- Ziman, J.M. Principles of the Theory of Solids; Cambridge Univ. Press: Cambridge, UK, 1972. [Google Scholar]
- Sander, L.M. Advanced Condensed Matter Physics; Cambridge Univ. Press Online: Cambridge, UK, 2014. [Google Scholar]
- Rossiter, P.L. The Electrical Resistivity of Metals and Alloys; Cambridge Univ. Press Online: Cambridge, UK, 2014. [Google Scholar]
- Alloul, H. Introduction of the Physics of Electrons in Solids; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Sólyom, J. Fundamentals of the Physics of Solids; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ibach, H.; Lüth, H. Solid State Physics, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Belashchenko, D.K. The relationship between electrical conductivity and electromigration in liquid metals. Dynamics 2023, 3, 405–424. [Google Scholar] [CrossRef]
- Palenskis, V. A Novel View to Free Electron Theory; LAP LAMBERT Acad. Publ.: Berlin, Germany, 2013. [Google Scholar]
- Palenskis, V. Drift mobility, diffusion coefficient of randomly moving charge carriers in metals and other materials with degenerate electron gas. World J. Cond. Matt. Phys. 2013, 3, 73–81. [Google Scholar] [CrossRef]
- Palenskis, V. The effective density of randomly moving electrons and related characteristics of materials with degenerate electron gas. AIP Adv. 2014, 4, 047119. [Google Scholar] [CrossRef]
- Palenskis, V.; Žitkevičius, E. Study of the Transport of Charge Carriers in Materials with Degenerate Electron Gas, 123–186. In Electron Gas: An Overview; NOVA Science Publ., Inc.: New York, NY, USA, 2019. [Google Scholar]
- Palenskis, V.; Žitkevičius, E. Summary of new insight into electron transport in metals. Crystals 2021, 11, 622. [Google Scholar] [CrossRef]
- Stirzaker, D.R. Elementary Probability; Cambridge Univ. Press Online: Cambridge, UK, 2014. [Google Scholar]
- Grimmet, G.R.; Stirzaker, D.R. Probability and Random Processes; Oxford Univ. Press: Oxford, UK, 2020. [Google Scholar]
- Cracknell, A.P.; Wong, K.C. The Fermi Surfaces: Its Concept, Determination, and Use in the Physics of Metals; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Blokhintsev, D.L. Quantum Mechanics; Reidel Publ. Comp.: Dordrecht, The Netherlands, 1964. [Google Scholar]
- Lide, D.R. (Ed.) Handbook of Chemistry and Physics, 84th ed.; CRC Press LLC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Kittel, C. Thermal Physics; John Wiley and Sons: New York, NY, USA, 1969. [Google Scholar]
- Gall, D. Electron mean free path in elemental metals. J. Appl. Phys. 2016, 119, 085101. [Google Scholar] [CrossRef]
- Palenskis, V. Free electron characteristic peculiarities caused by lattice vibrations in metals. World J. Cond. Matt. Phys. 2022, 12, 9–17. [Google Scholar] [CrossRef]
- Palenskis, V.; Žitkevičius, E. Analysis of transport properties of the randomly moving electrons in metals. Matt. Sci. (Medžiagotyra) 2020, 26, 147–153. [Google Scholar] [CrossRef]
- Smith, R.A. Semiconductors, 2nd ed.; Cambridge Univ. Press: Cambridge, UK, 1987. [Google Scholar]
- Gray, D.E. AIP Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Grigoryev, I.S.; Meilihkov, E.Z. (Eds.) Handbook of the Physical Quantities; Energoatomizdat: Moscow, Russia, 1991. [Google Scholar]
- Markiewicz, R.S. Simple model for the Hall effect inYBa2Cu3O7-δ. Phys. Rev. B 1988, 38, 5010–5011. [Google Scholar] [CrossRef] [PubMed]
- Palenskis, V.; Pralgauskaitė, S.; Maknys, K.; Matulionis, A. Thermal Noise and Drift Mobility of Randomly Moving Electrons in Homogeneous Material with Highly Degenerate Electron Gas. In Proceedings of the IEEE of the 22nd Conference ICNF, Montpellier, France, 23–28 June 2013. [Google Scholar]
- Lüc, K.R. Zur Temperatur- und Feldabhängigheit der galvanomagnetischen Eigenschaften von Aluminium und Indium. Phy. Stat. Sol. 1966, 18, 49–56. [Google Scholar] [CrossRef]
- Palenskis, V. Transport characteristics of charge carriers in normal state superconductor YBa2Cu3O7-δ. World J. Cond. Matt. Phys. 2015, 5, 118–128. [Google Scholar] [CrossRef][Green Version]
- Palenskis, V. Description of the Transport Characteristic in Normal State Superconductor YBa2Cu3O7-δ, 52–64. In New Insights into Physical Science. Book Publ. Inter.: India. 2020. Available online: https://digiwire.co.in/description-of-the-transport-characteristics-of-charge-carriers-in-normal-state-superconductor-yba2cu3o7-%EF%81%A41/ (accessed on 1 July 2023).
- Simon, S.H. The Oxford Solid State Basics; Clarendon Press: Oxford, UK, 2015. [Google Scholar]
- Cottingham, W.N.; Greenwood, D.A. Electricity and Magnetism; Cambridge Univ. Press Online: Cambridge, UK, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).