An Optimized Design Method and Experimental Study of Belt-Type Ultra-High-Pressure Dies
Abstract
:1. Introduction
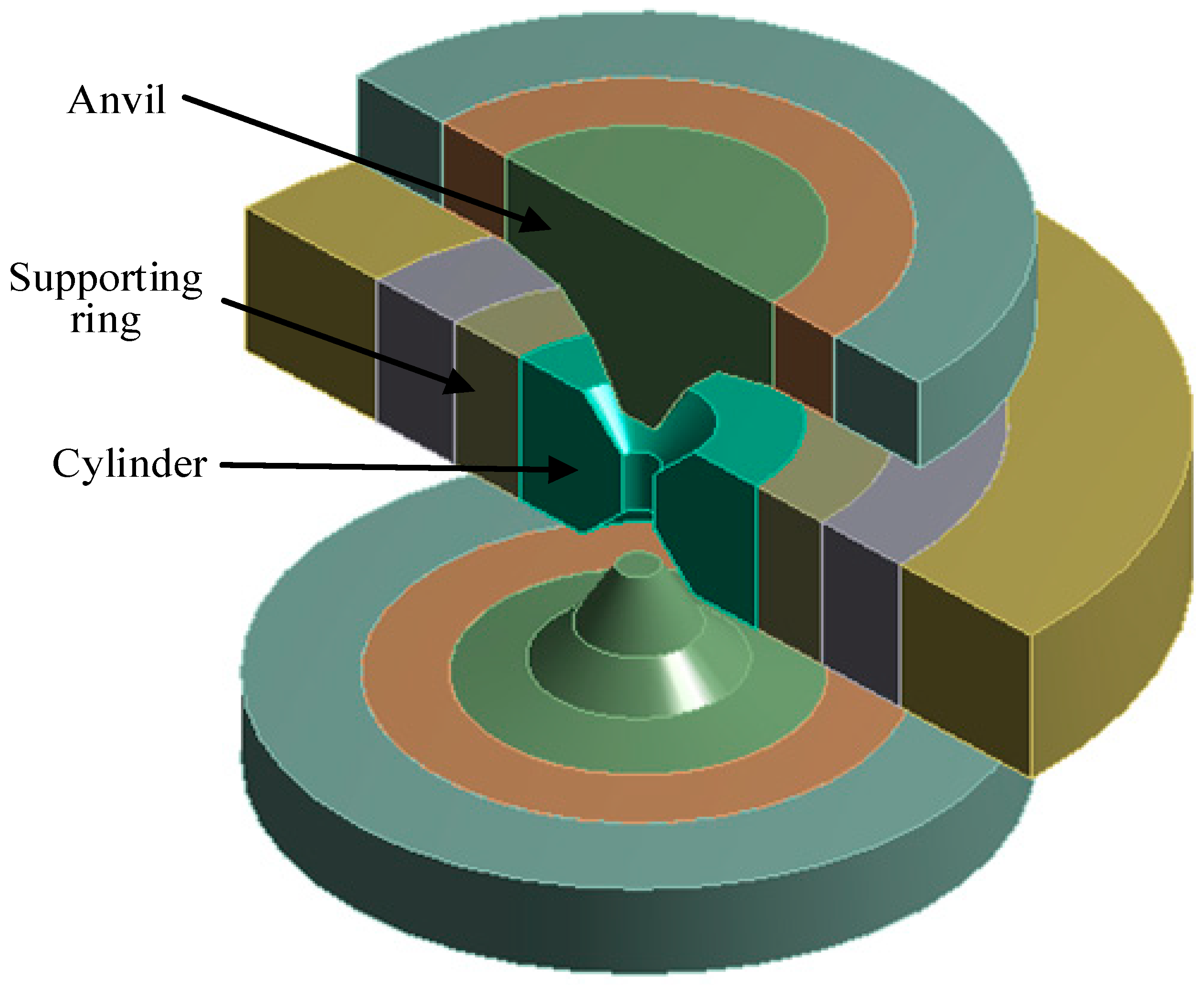
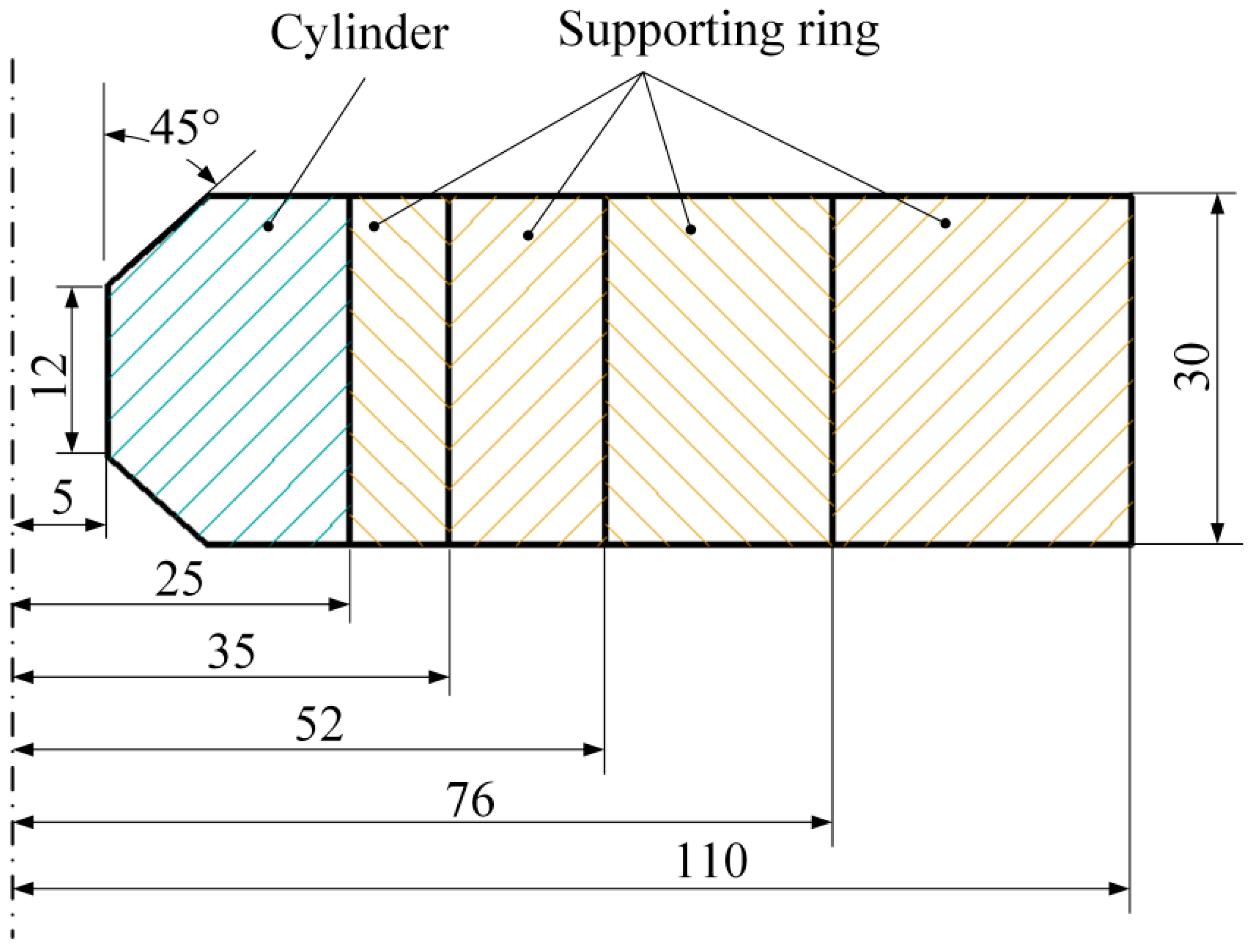
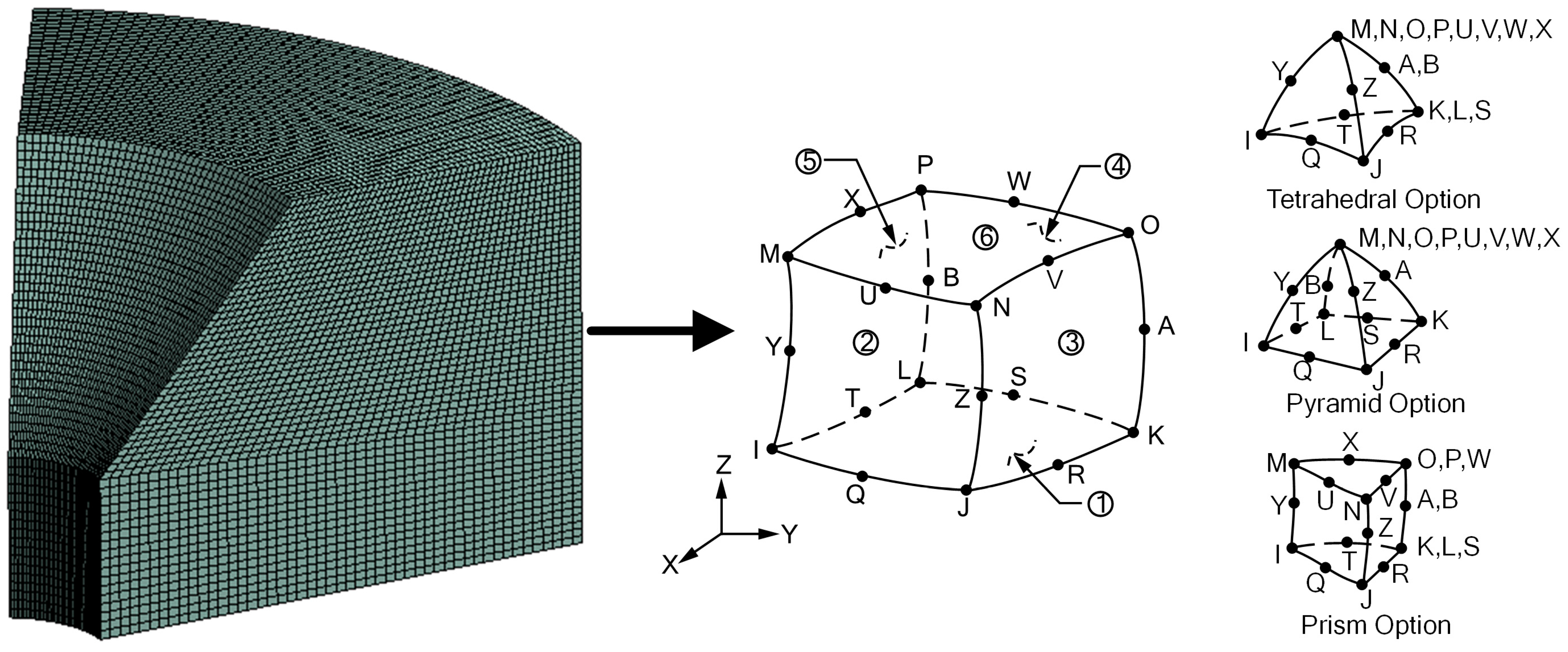
2. Finite Element Model
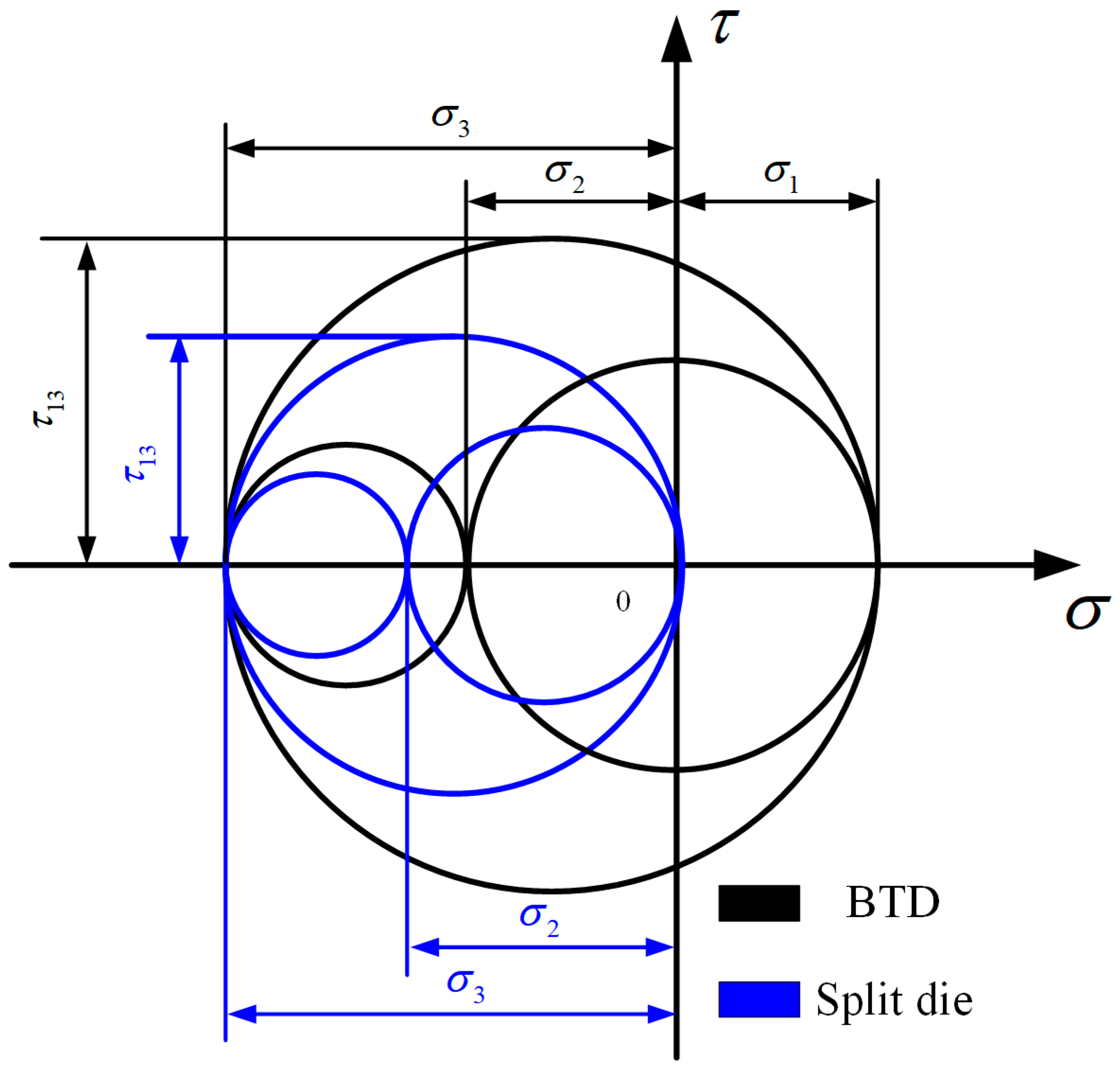
3. Theoretical Analysis
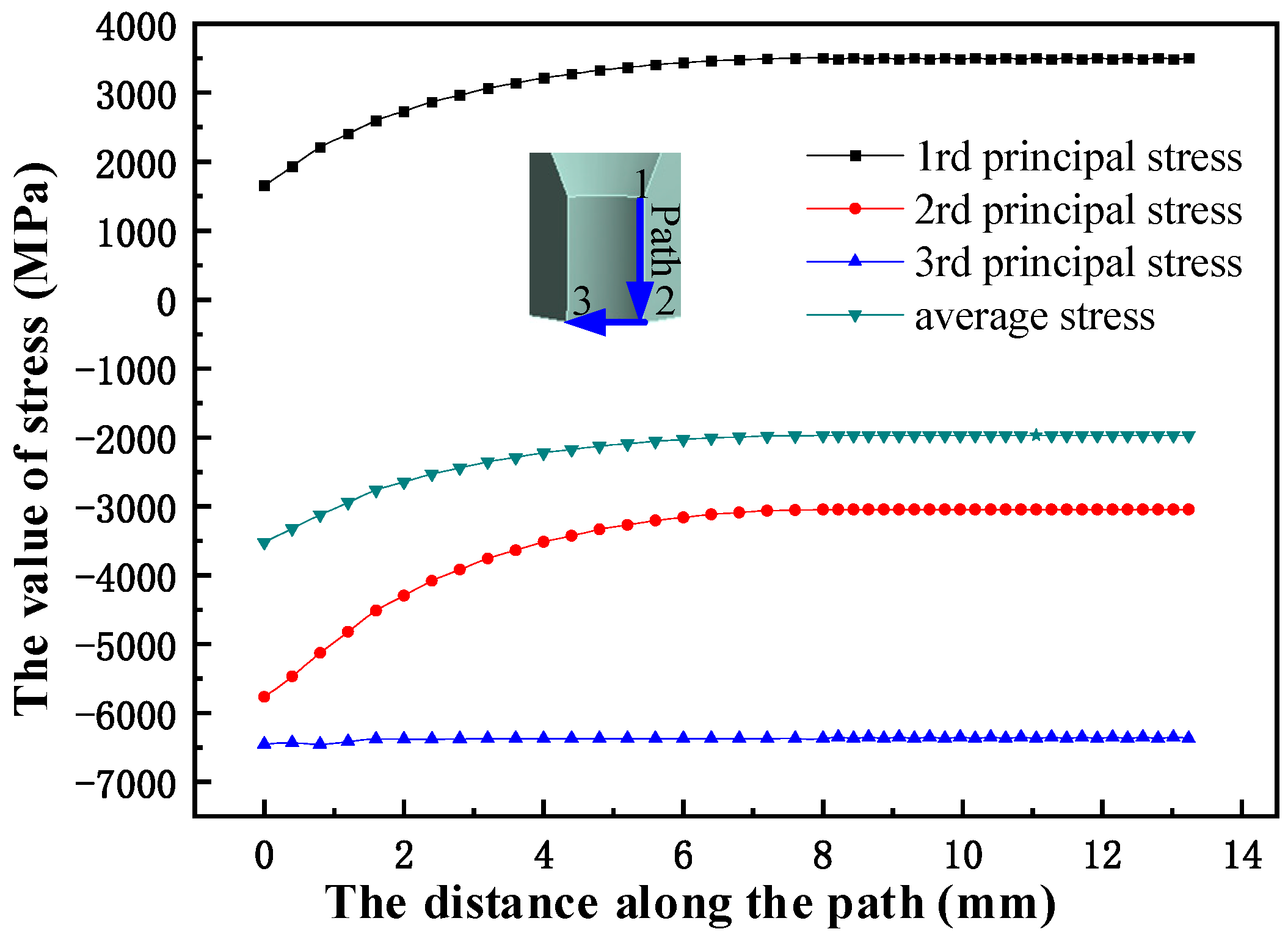
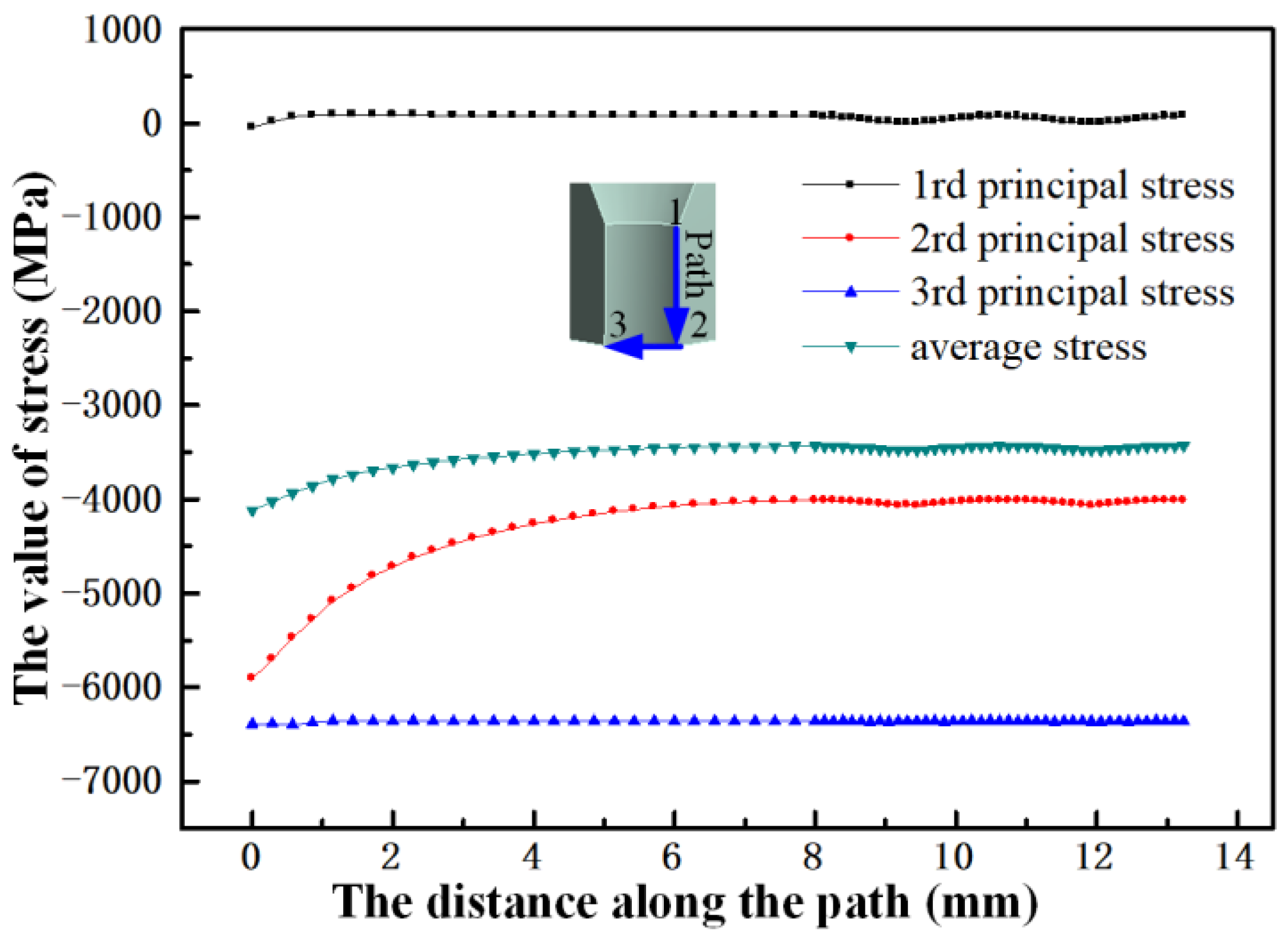
4. Results and Discussion
4.1. The Belt-Type Die
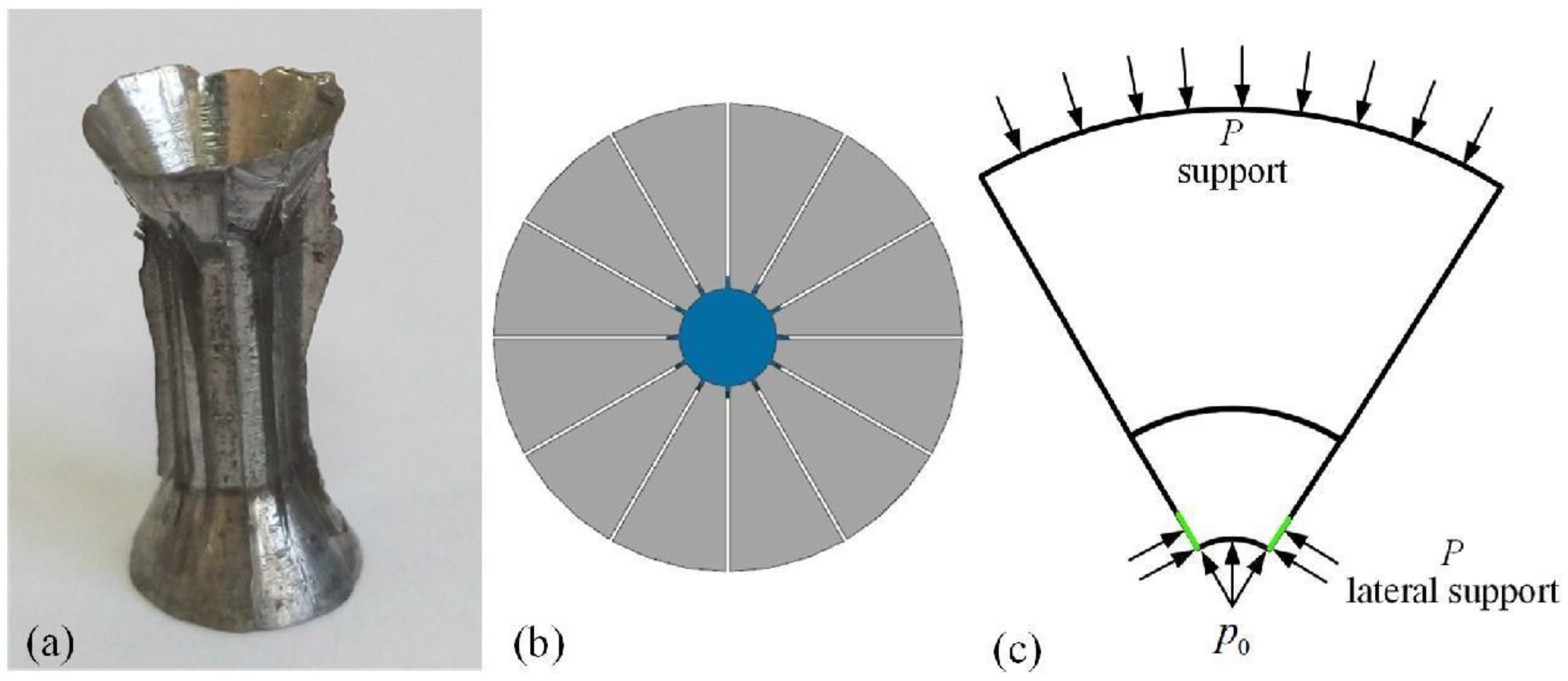
4.2. The Split Die
4.3. The Tangential Split Die
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hall, H.T. Ultra-High-Pressure, High-Temperature Apparatus: The “Belt”. Rev. Sci. Instrum. 1960, 31, 125–131. [Google Scholar] [CrossRef]
- Bridgman, P.W. The Resistance of 72 Elements, Alloys and Compounds to 100,000 kg/cm2; Papers 169–199; Harvard University Press: Cambridge, MA, USA, 1964; pp. 4113–4197. [Google Scholar]
- Li, S.H.; Li, J.L.; Ge, J.Z.; Gao, X. Design and Research of Double-Layered Cemented Carbide Novel High-Pressure Die. Int. J. Eng. Res. Afr. 2021, 53, 42–52. [Google Scholar] [CrossRef]
- Guan, W.; Gao, G.; Yu, Y.; Zhuo, T. Theoretical, experimental and numerical investigations on the energy absorption of splitting multiple circular tubes under impact loading. Thin-Walled Struct. 2020, 155, 106916. [Google Scholar] [CrossRef]
- Kawai, N.; Endo, S. The generation of ultrahigh hydrostatic pressures by a split sphere apparatus. Rev. Sci. Instrum. 1970, 41, 1178–1181. [Google Scholar] [CrossRef]
- Hall, H.T. High pressure apparatus: Ram-in-tie-bar multianvil presses. Rev. Phys. Chem. Jpn. 1967, 37, 63–71. [Google Scholar]
- Hall, H.T. Some high-pressure, high-temperature apparatus design considerations: Equipment for use at 100,000 atmospheres and 3000 C. Rev. Sci. Instrum. 1958, 29, 267–275. [Google Scholar] [CrossRef]
- Yang, Y.; Li, M.; Wang, B. Study on stress distribution of tangent split high pressure apparatus and its pressure bearing capacity. Diam. Relat. Mater. 2015, 58, 180–184. [Google Scholar] [CrossRef]
- Xu, B.; Tian, Y. Superhard materials: Recent research progress and prospects. Sci. China Mater. 2015, 58, 132–142. [Google Scholar] [CrossRef]
- Zhao, L.; Li, M.; Li, R.; Qu, E.; Wang, L.; Yi, Z.; Zheng, C. Stress analysis of the multi-layer stagger-split die for synthesizing gem quality large single crystal diamond. Diam. Relat. Mater. 2018, 83, 54–59. [Google Scholar] [CrossRef]
- Bassett, W.A. Diamond anvil cell, 50th birthday. High Press. Res. 2009, 29, 163–186. [Google Scholar] [CrossRef]
- Liebermann, R.C. Multi-anvil, high pressure apparatus: A half-century of development and progress. High Press. Res. 2011, 31, 493–532. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, N.; Li, M.; Liang, X.; Gu, Z. Stress analysis and experiment on a split-type ultra-high-pressure die for synthesizing diamond. Rev. Sci. Instrum. 2021, 92, 103903. [Google Scholar] [CrossRef]
- Katsura, T.; Funakoshi, K.; Kubo, A.; Nishiyama, N.; Tange, Y.; Sueda, Y.-I.; Kubo, T.; Utsumi, W. A large-volume high-pressure and high-temperature apparatus for in situ X-ray observation,‘SPEED-Mk. II’. Phys. Earth Planet. Inter. 2004, 143, 497–506. [Google Scholar] [CrossRef]
- Xu, J.A.; Mao, H.K.; Bell, P.M. High-pressure ruby and diamond fluorescence: Observations at 0.21 to 0.55 terapascal. Science 1986, 232, 1404–1406. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Lei, T.; He, X.; Jin, W. Numerical optimization of billet diameter in the wide-spread and split extrusion process. J. Phys. Conf. Ser. 2023, 2483, 012001. [Google Scholar] [CrossRef]
- Qiang, W.; Fang, H.; Wei, L.; Li, D.; Wang, Z.R. Strength analysis and optimization for both the cylinder and the anvil of a BELT-type ultra-high-pressure apparatus by FEM. J. Mater. Process. Technol. 1995, 55, 5–10. [Google Scholar] [CrossRef]
- Ichida, Y.; Ohfuji, H.; Irifune, T.; Kunimoto, T.; Kojima, Y.; Shinmei, T. Synthesis of coarse-grain-dispersed nano-polycrystalline cubic boron nitride by direct transformation under ultrahigh pressure. Diam. Relat. Mater. 2017, 77, 25–34. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Zheng, J.; Xue, Y. Radially loading rotary extrusion for manufacturing large-size conical cylinders with inner transverse high ribs. Chin. J. Aeronaut. 2023, 36, 582–594. [Google Scholar] [CrossRef]
- Moss, W.C.; Goettel, K.A. The stability of a sample in a diamond anvil cell. J. Appl. Phys. 1987, 61, 4951–4954. [Google Scholar] [CrossRef]
- Yi, Z.; Fu, W.; Li, M.; Li, R.; Zhao, L.; Wang, L.Y. Numerical simulation and experimental verification of a novel double-layered split die for high-pressure apparatus used for synthesizing superhard materials. Int. J. Miner. Metall. Mater. 2019, 26, 377–385. [Google Scholar] [CrossRef]
- Choi, J.; Choi, J.; Lee, K.; Hur, N.; Kim, N. Fatigue Life Prediction Methodology of Hot Work Tool Steel Dies for High-Pressure Die Casting Based on Thermal Stress Analysis. Metals 2022, 12, 1744. [Google Scholar] [CrossRef]
- Liu, X.Y. High pressure synthesis and preparation of inorganic materials. In Modern Inorganic Synthetic Chemistry; Elsevier: Amsterdam, The Netherlands, 2017; pp. 105–141. [Google Scholar]
- Vrbka, J.; Knesl, Z. High Pressure Geoscience and Material Synthesis; Akademie-Verlag: Berlin, Germany, 1988; p. 234. [Google Scholar]
- Vrbka, J.; Knésl, Z. Philosophy and reality of strength design of the BELT chamber by finite element method. In High Pressure Geoscience and Material Synthesis; Akademie-Verlag: Berlin, Germany, 1988; pp. 234–239. [Google Scholar]
- Xu, S.; Zhao, D.; Gao, X.; Liu, C.; Huang, W.; Meng, X. Numerical simulation and research of the split ultrahigh pressure cylinder. IOP Conf. Ser. Mater. Sci. Eng. 2020, 768, 042043. [Google Scholar] [CrossRef]
- Longjian, X.; Artem, C.; Takayuki, I.; Bondar, D.; Nishida, K.; Chen, Z.; Bhat, S.; Farla, R.; Higo, Y.; Tange, Y.; et al. Simultaneous generation of ultrahigh pressure and temperature to 50 GPa and 3300 K in multi-anvil apparatus. Rev. Sci. Instrum. 2021, 92, 103902. [Google Scholar]
- Klünsner, T.; Wurster, S.; Supancic, P.; Ebner, R.; Jenko, M.; Glätzle, J.; Püschel, L.; Pippan, R. Effect of specimen size on the tensile strength of WC–Co hard metal. Acta Mater. 2011, 59, 4244–4252. [Google Scholar] [CrossRef]
- Xiao, S.; Luan, X.; Liang, Z.; Wang, X.; Zhou, T.; Ding, Y. Fracture Analysis of Ultrahigh-Strength Steel Based on Split Hopkinson Pressure Bar Test. Metals 2022, 12, 628. [Google Scholar] [CrossRef]
- Wang, B.; Mingzhe, L.I.; Liu, Z.; Han, X. A Novel Tangential Split-Belt Ultrahigh Pressure Apparatus. Gaoya Wuli Xuebao/Chin. J. High Press. Phys. 2019, 33, 64–69. [Google Scholar]
- Xinyu, H.; Guangdong, Z.; Tong, D. Improved Optimization of a Coextrusion Die with a Complex Geometry Using the Coupling Inverse Design Method. Polymers 2023, 15, 3310. [Google Scholar]
- Wang, B.; Li, M.; Liu, Z.; Han, X. Numerical Simulation and Experiment on New Multilayer Stagger-Split Die of Ultra-High Pressure Apparatus. Gaoya Wuli Xuebao/Chin. J. High Press. Phys. 2018, 32, 27–32. [Google Scholar]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Wang, B.; Li, M. An Optimized Design Method and Experimental Study of Belt-Type Ultra-High-Pressure Dies. Metals 2023, 13, 1593. https://doi.org/10.3390/met13091593
Shi Z, Wang B, Li M. An Optimized Design Method and Experimental Study of Belt-Type Ultra-High-Pressure Dies. Metals. 2023; 13(9):1593. https://doi.org/10.3390/met13091593
Chicago/Turabian StyleShi, Zhou, Bolong Wang, and Mingzhe Li. 2023. "An Optimized Design Method and Experimental Study of Belt-Type Ultra-High-Pressure Dies" Metals 13, no. 9: 1593. https://doi.org/10.3390/met13091593
APA StyleShi, Z., Wang, B., & Li, M. (2023). An Optimized Design Method and Experimental Study of Belt-Type Ultra-High-Pressure Dies. Metals, 13(9), 1593. https://doi.org/10.3390/met13091593





