Lithography-Based Metal Manufacturing of Copper: Influence of Exposure Parameters on Green Part Strength
Abstract
:1. Introduction
2. Materials and Methods
2.1. Source Materials Used in This Work
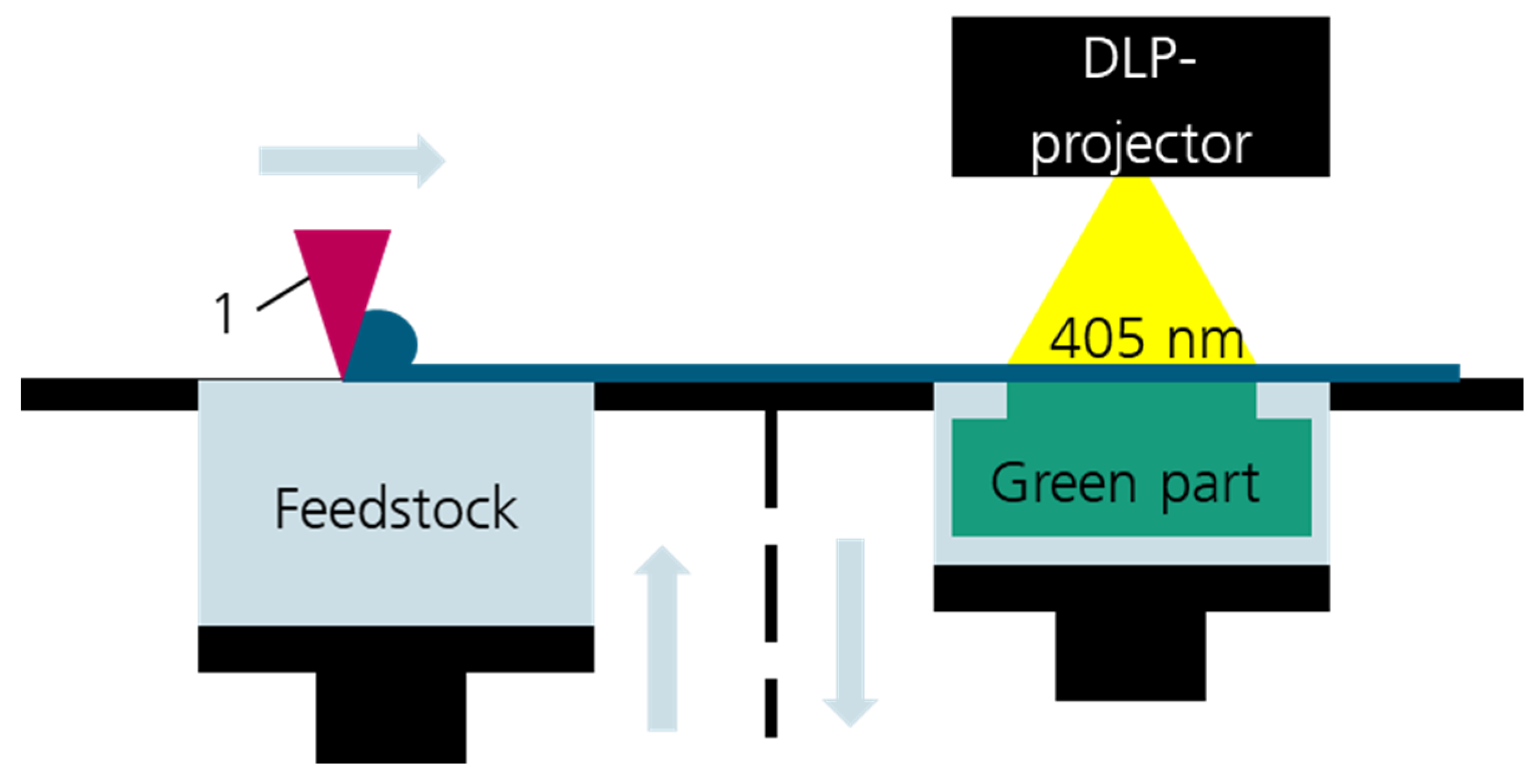
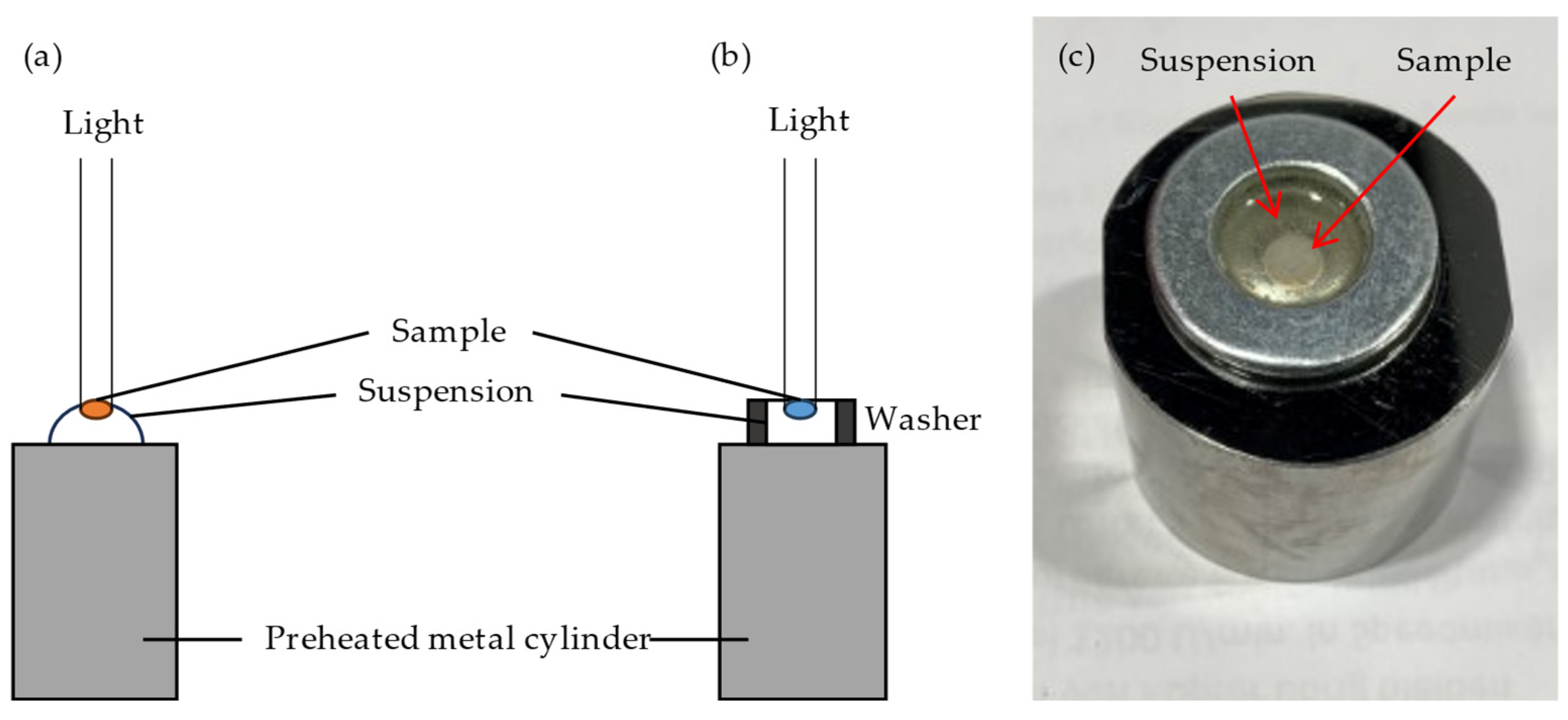
2.2. Single-Layer Exposure for Working Curve Determination
2.3. Green Parts and Green Strength Measurement
2.4. Heat Treatment and Sintering
2.5. Characterization of Sintered Samples
3. Results
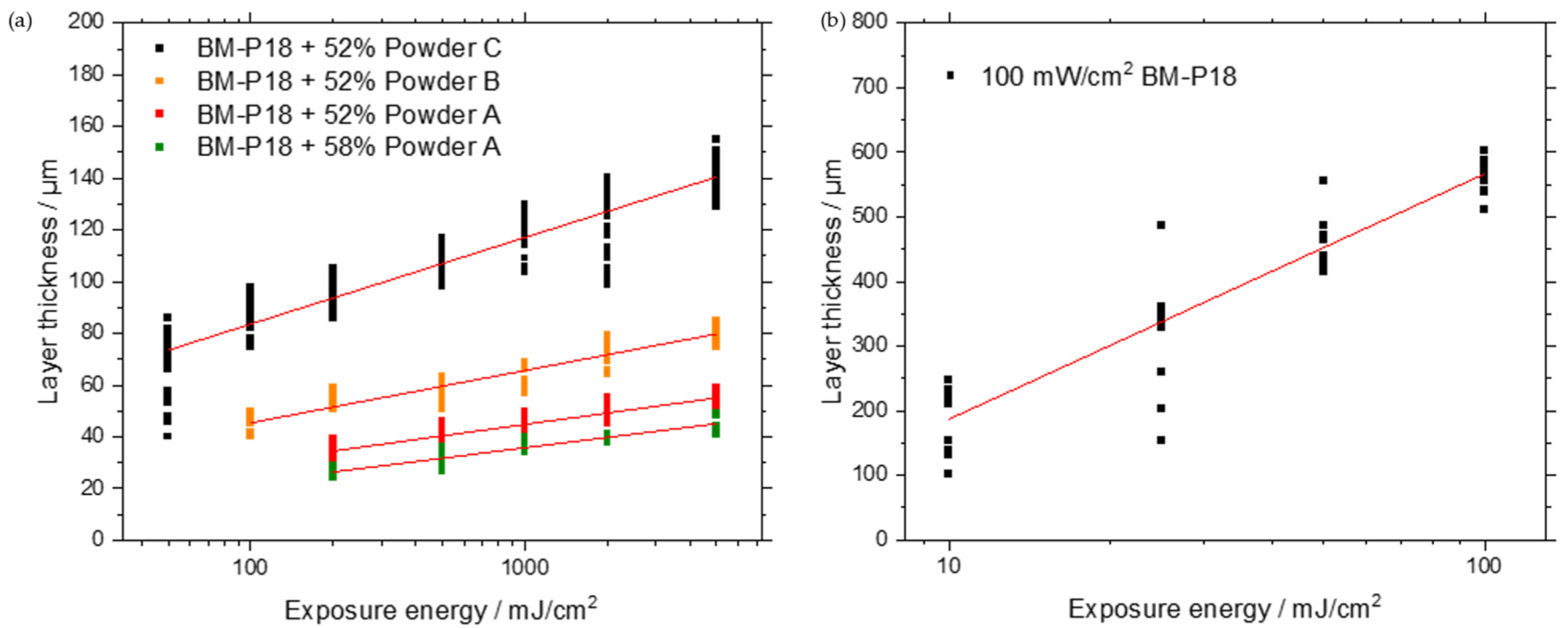
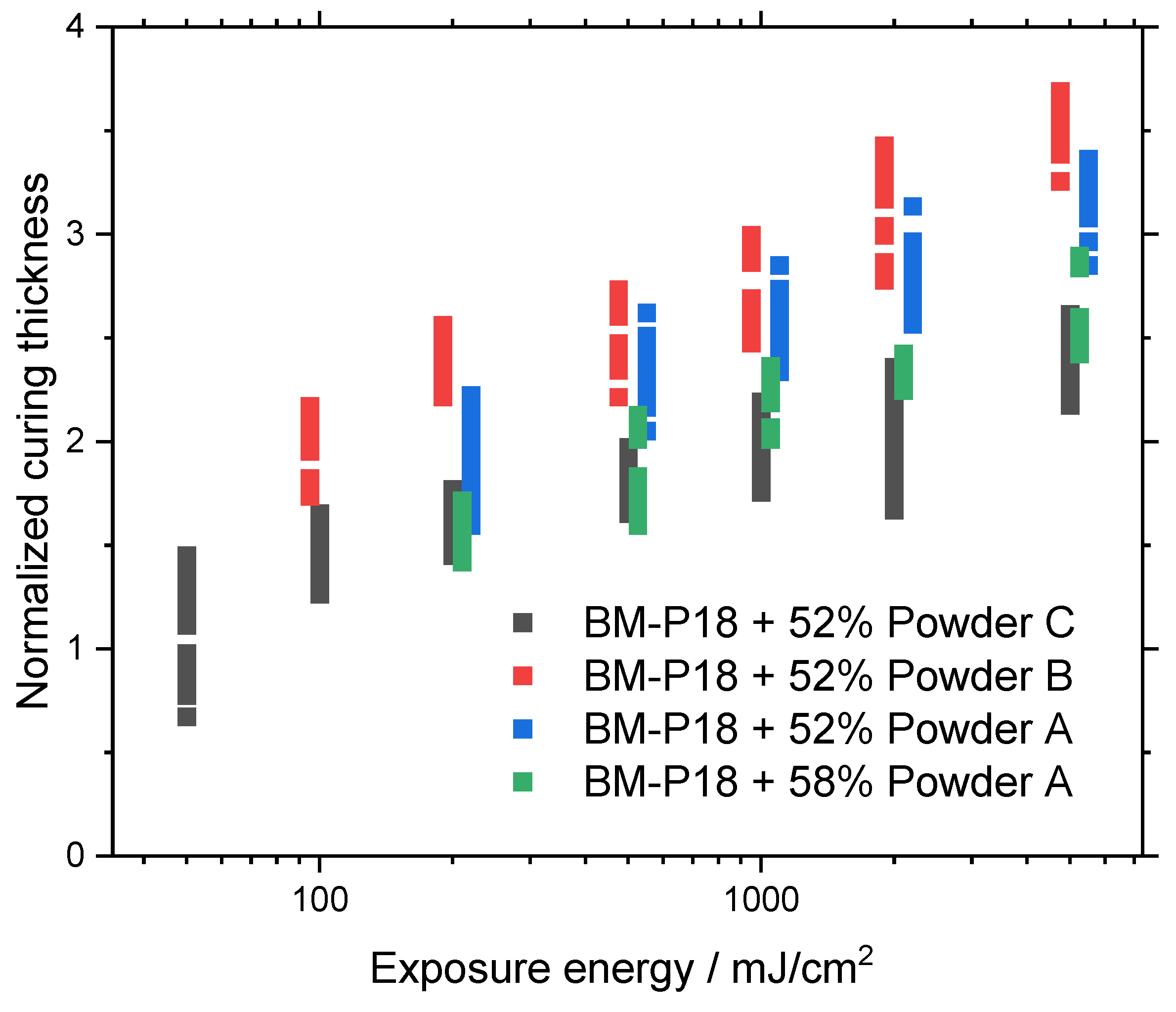
3.1. Single-Layer Exposure for Working Curve Determination
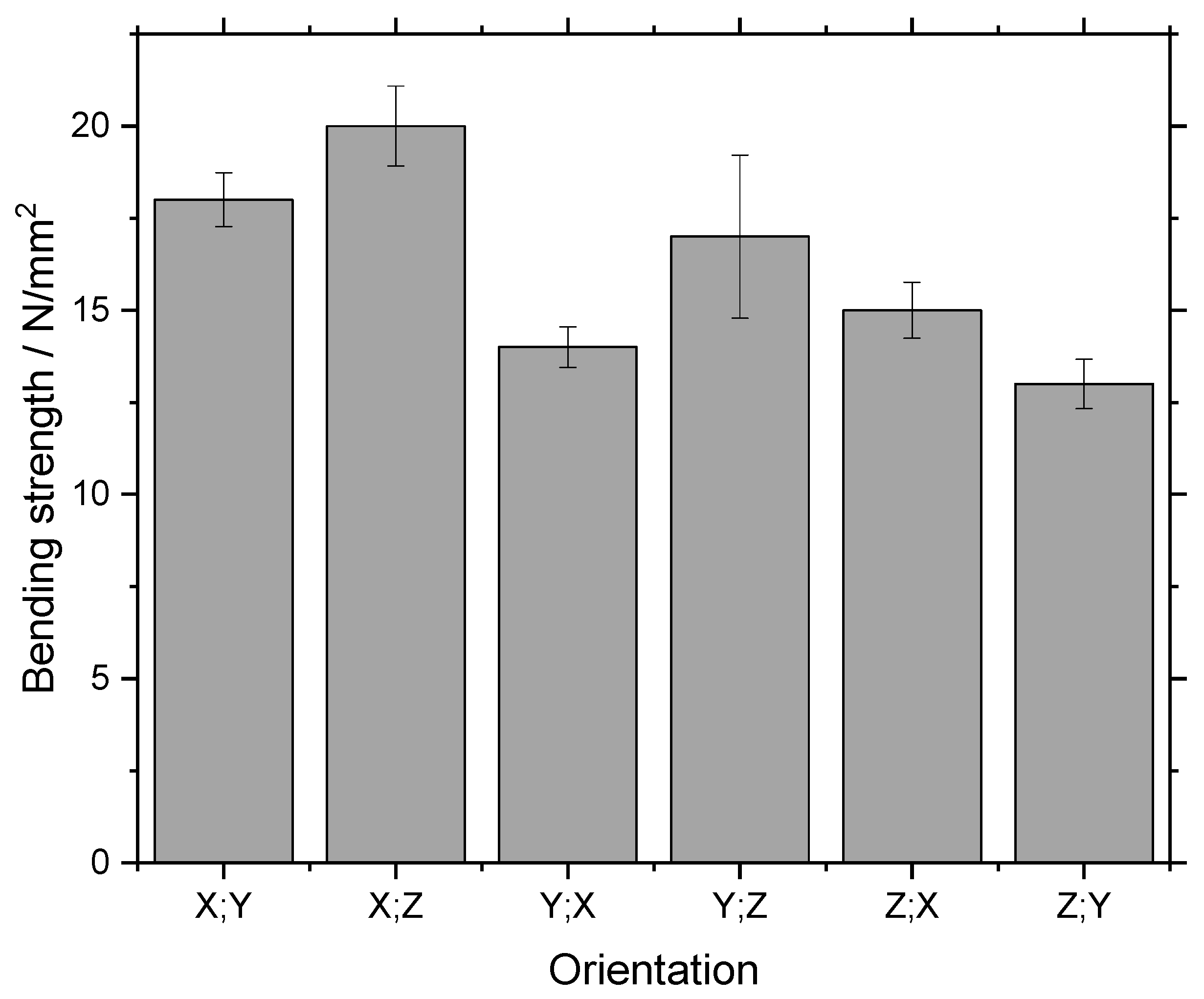
3.2. Green Strength Measurement
3.3. Properties of Sintered Samples
4. Discussion
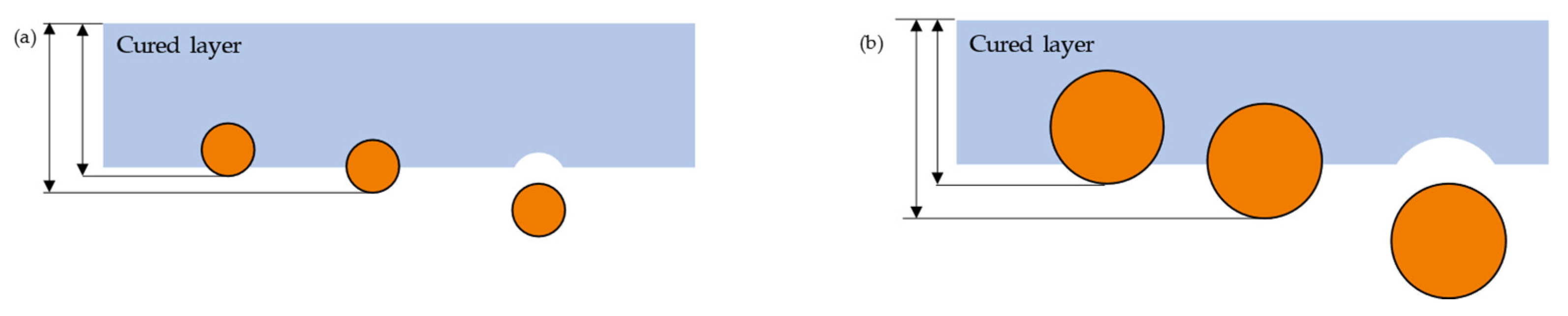
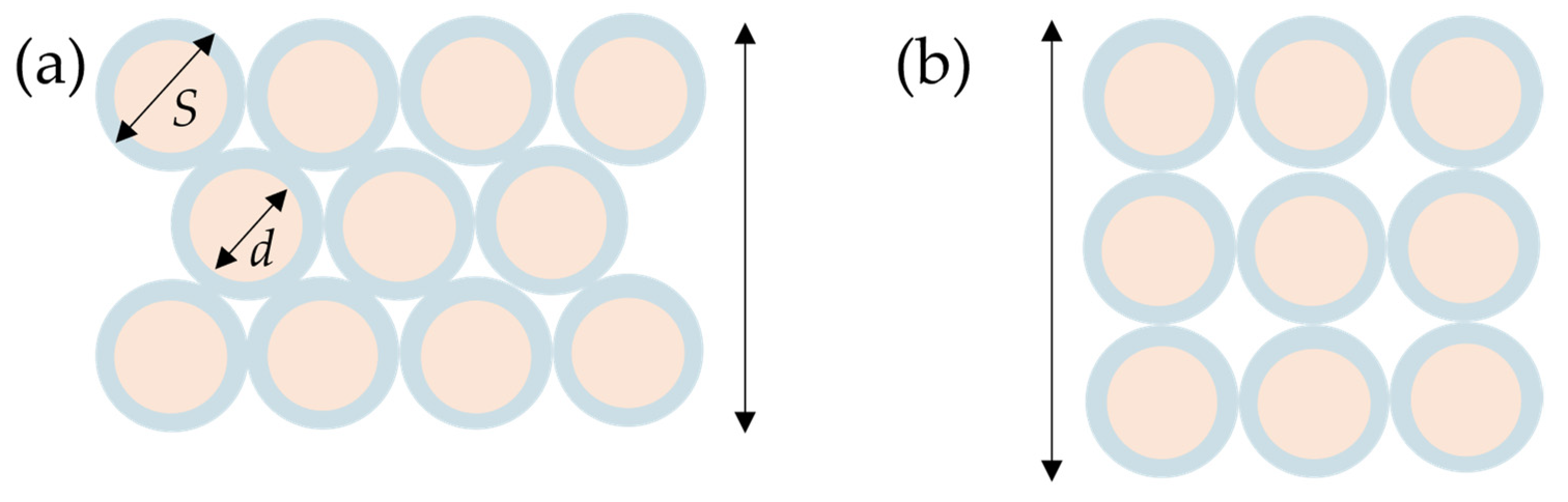
4.1. Influencing Factors on Working Curves
4.2. Modeling of Working Curves
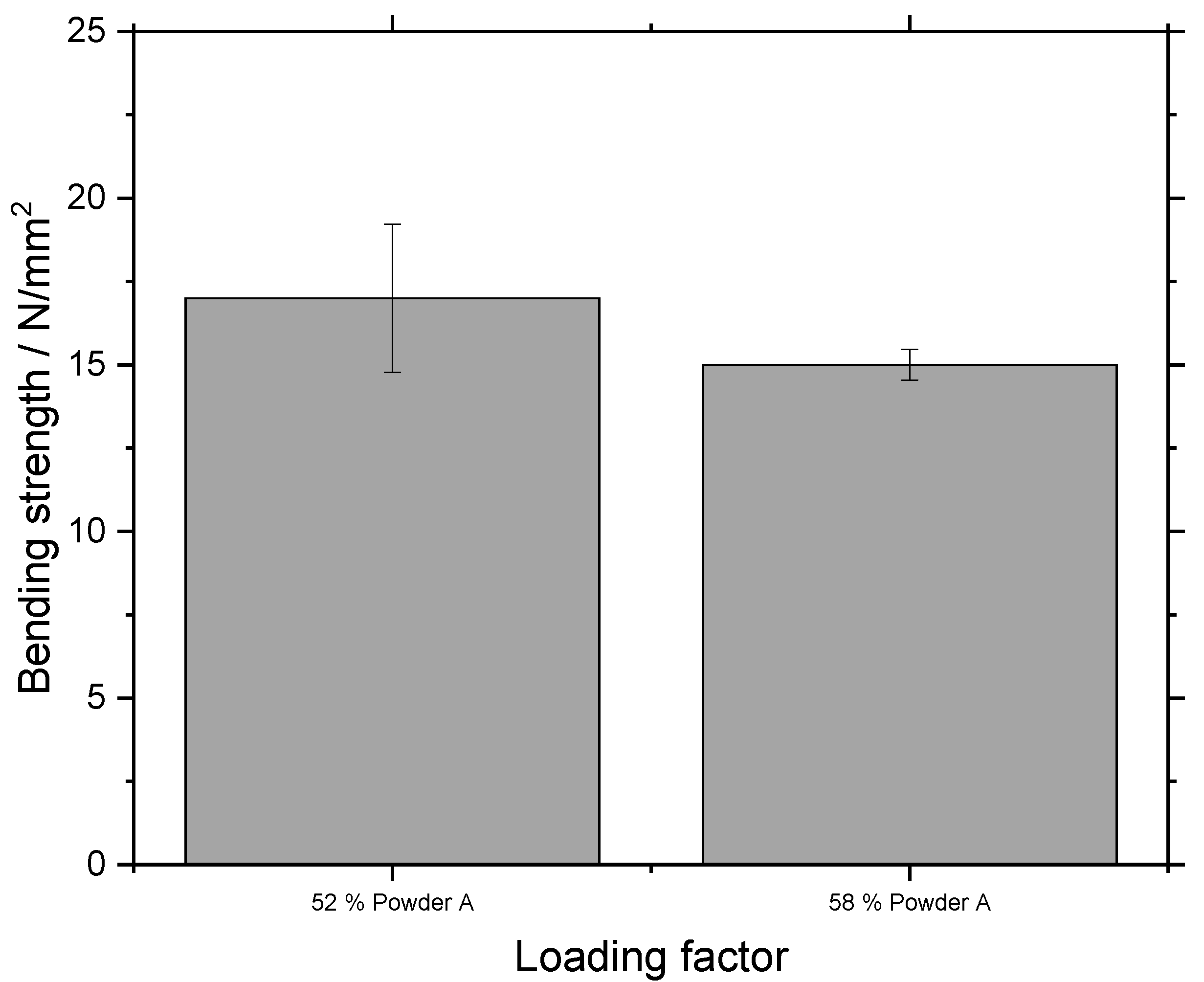
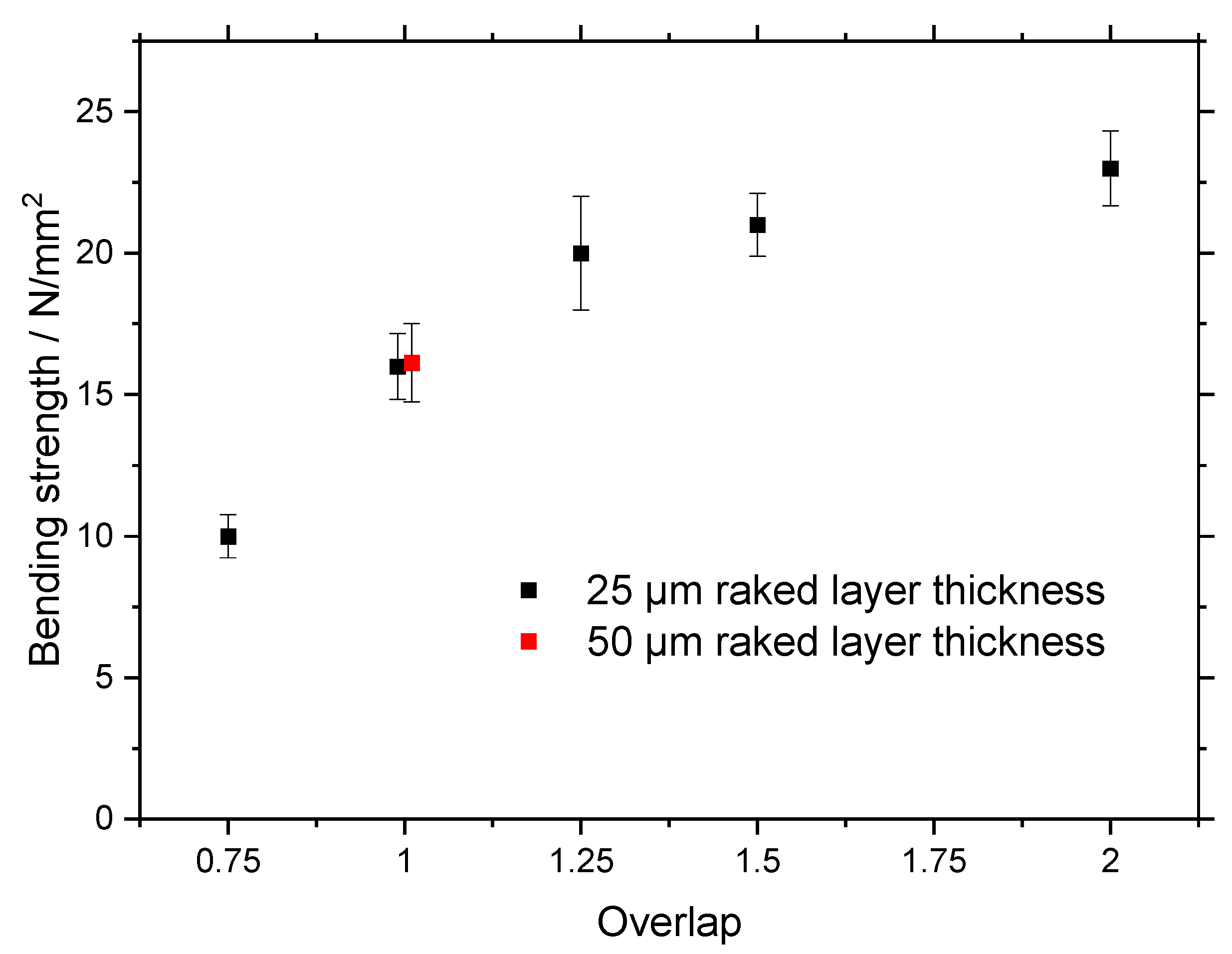
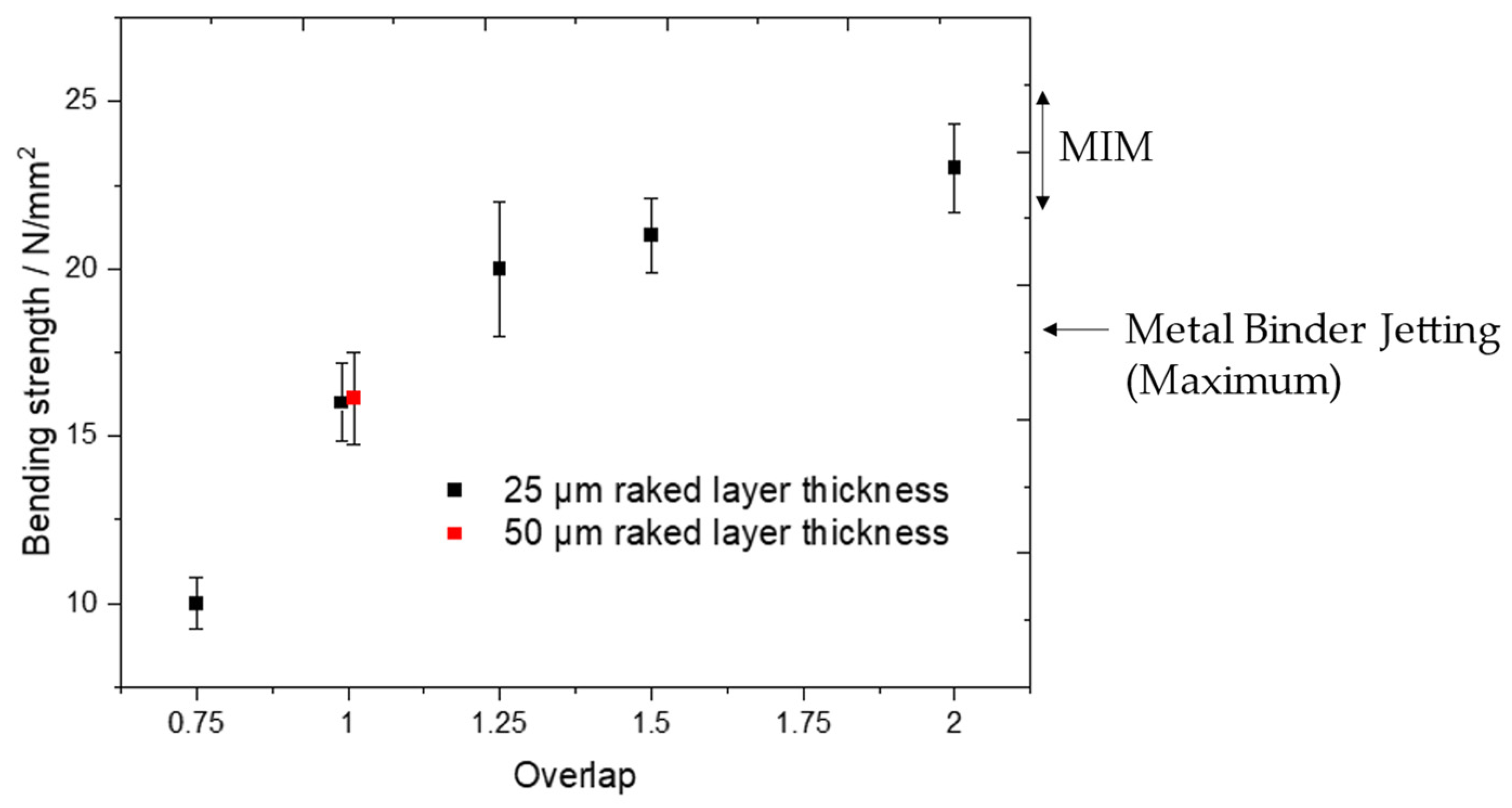
4.3. Green Strength
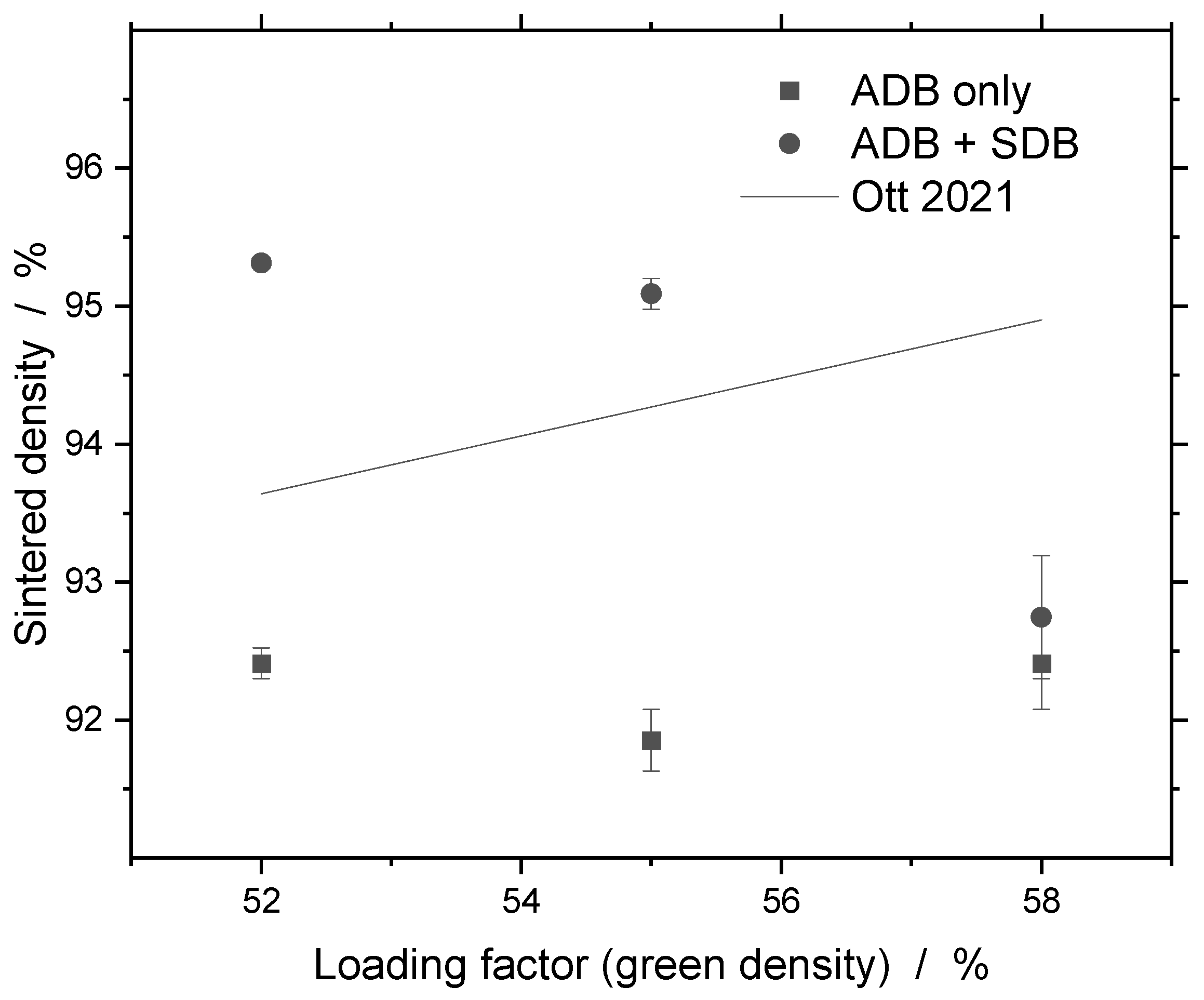
4.4. Sintering Behavior
5. Conclusions
- The reflectivity of copper is low in the 400 nm wavelength range and high in the 1 µm wavelength range [20]. Both worsen the productivity for additive manufacturing by LMM (405 nm wavelength) or laser-based AM processes (1 µm wavelength), respectively.
- The applicability of Jacobs working curve theory for filled suspensions is limited. Therefore, the coated-sphere-layer model is proposed. Future research will prove if this model is applicable to other powder materials and loading factors.
- The study reaffirmed that curing thickness increases with higher exposure energy, a finding that contradicts previous research. The use of larger powder particles also results in thicker cured layers, although this comes with an increased scatter of measured values.
- Green strength can be increased to 23 N/mm2 by increasing layer overlap or reducing loading factor. It is possible to achieve the green strength of MIM and surpass the green strength of Metal Binder Jetting. Green strength is lower when the longest sample dimension is aligned with the z-axis. A reduced loading factor increases green strength.
- A sintered density of about 92% is reached. With additional solvent debinding, increasing density to 95% is possible for certain loading factors. The results suggest that incomplete debinding may hinder densification, highlighting the need for optimizing the time–temperature profile and binder composition to ensure the complete removal of binder residues.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Joseph, G. (Ed.) Copper: Its Trade, Manufacture, Use, and Environmental Status; 1. Printing; ASM International: Materials Park, OH, USA, 1999; ISBN 0871706563. [Google Scholar]
- Grohol, M.; Veeh, C. Study on the Critical Raw Materials for the EU 2023: Final Report; Publications Office of the European Union: Luxembourg, Germany, 2023; ISBN 978-92-68-00414-2. [Google Scholar]
- DIN Deutsches Institut für Normung e. V. Additive Fertigung:—Grundlagen—Terminologie (ISO/ASTM 52900:2021); Deutsche Fassung EN ISO/ASTM 52900:2021; (52900:2022-03); Beuth Verlag GmbH: Berlin, Germany, 2021. [Google Scholar]
- Braasch, K.; Teplyuk, A.; Miek, D.; Scheibler, J.; Weißgärber, T.; Zhong, C.; Höft, M. Additive Manufacturing of a Copper Elliptical Corrugated Horn Antenna in the Sub-Terahertz Regime. In Proceedings of the 2024 IEEE/MTT-S International Microwave Symposium—IMS 2024, Washington, DC, USA, 16–21 June 2024; IEEE: New York, NY, USA, 2024; pp. 509–512, ISBN 979-8-3503-7504-6. [Google Scholar]
- Tran, T.Q.; Chinnappan, A.; Lee, J.K.Y.; Loc, N.H.; Tran, L.T.; Wang, G.; Kumar, V.V.; Jayathilaka, W.A.D.M.; Ji, D.; Doddamani, M.; et al. 3D Printing of Highly Pure Copper. Metals 2019, 9, 756. [Google Scholar] [CrossRef]
- Siva Prasad, H.; Brueckner, F.; Volpp, J.; Kaplan, A.F.H. Laser metal deposition of copper on diverse metals using green laser sources. Int. J. Adv. Manuf. Technol. 2020, 107, 1559–1568. [Google Scholar] [CrossRef]
- Dadbakhsh, S.; Zhao, X.; Chinnappan, P.K.; Shanmugam, V.; Lin, Z.; Hulme, C. Process and geometrical integrity optimization of electron beam melting for copper. CIRP Ann. 2022, 71, 201–204. [Google Scholar] [CrossRef]
- Zamorano Reichold, A.; Baufeld, B. The potential of wire electron beam additive manufacturing of copper. Prog. Addit. Manuf. 2024, 9, 1417–1423. [Google Scholar] [CrossRef]
- Dicandia, F.A.; Fonseca, N.J.G.; Bacco, M.; Mugnaini, S.; Genovesi, S. Space-Air-Ground Integrated 6G Wireless Communication Networks: A Review of Antenna Technologies and Application Scenarios. Sensors 2022, 22, 3136. [Google Scholar] [CrossRef] [PubMed]
- Melentiev, R.; Harakály, G.; Stögerer, J.; Mitteramskogler, G.; Wagih, A.; Lubineau, G.; Grande, C.A. High-resolution metal 3D printing via digital light processing. Addit. Manuf. 2024, 85, 104156. [Google Scholar] [CrossRef]
- Allonas, X.; Hammouda, B.; Métral, B.; Goldbach, E.; Schuller, A.-S.; Ley, C.; Croutxé-Barghorn, C. Controlling photopolymerization reaction in layer-by-layer photopolymerization in 3D printing. Appl. Res. 2024, 3, e202400004. [Google Scholar] [CrossRef]
- Vogel, L.; Ali Khan, Q.; Zimmermann, M.; Burkhardt, C. Impact of Printing Parameters on Green Density Homogeneity in Lithography-based Metal Manufacturing. In Proceedings of the World PM2022, Lyon, France, 9–13 October 2022. [Google Scholar] [CrossRef]
- Jacobs, P.F. Fundamentals of Stereolithography, Valencia, California. 1992. Available online: https://repositories.lib.utexas.edu/handle/2152/64400 (accessed on 31 May 2023).
- Nguyen, H.X.; Suen, H.; Poudel, B.; Kwon, P.; Chung, H. Development of an innovative, high speed, large-scaled, and affordable metal additive manufacturing process. CIRP Ann. 2020, 69, 177–180. [Google Scholar] [CrossRef]
- Resch, A.; Benayad, A.; Roumanie, M.; Croutxé-Barghorn, C. Lithography based Metal Manufacturing (LMM): Influence of particle size and composition of copper powder on UV light penetration. Mater. Today Commun. 2023, 35, 105595. [Google Scholar] [CrossRef]
- Ott, J. Druckloses Sintern von Cu für Hochleistungsanwendungen. Ph.D. Dissertation, Universität des Saarlandes, Saarbrücken, Germany, 2021. [Google Scholar]
- Roumanie, M.; Flassayer, C.; Resch, A.; Cortella, L.; Laucournet, R. Influence of debinding and sintering conditions on the composition and thermal conductivity of copper parts printed from highly loaded photocurable formulations. SN Appl. Sci. 2021, 3, 55. [Google Scholar] [CrossRef]
- DIN Deutsches Institut für Normung e. V. Sintermetalle, Ausgenommen Hartmetalle: Ermittlung der Biegebruchfestigkeit; Beuth Verlag GmbH: Berlin, Germany, 2002. [Google Scholar]
- DIN Deutsches Institut für Normung e. V. Hochleistungskeramik: Bestimmung der Dichte und der scheinbaren Porosität; Beuth Verlag GmbH: Berlin, Germany, 2022. [Google Scholar]
- Enghag, P. Encyclopedia of the Elements: Technical Data, History, Processing, Applications; Wiley-VCH: Weinheim, Germany, 2004; ISBN 3527306668. [Google Scholar]
- Melentiev, R.; Wagih, A.; Lagerweij, A.; Mitteramskogler, G.; Lubineau, G.; Grande, C.A. Unlocking multiscale metallic metamaterials via lithography additive manufacturing. Virtual Phys. Prototyp. 2024, 19, e2339368. [Google Scholar] [CrossRef]
- Bowman, R.L.; Jack, J.R.; Spisz, E.W.; Weigand, A.J. Solar Absorptances and Spectral Reflectances of 12 Metals for Temperatures Ranging from 300 to 500 K; National Aeronautics and Space Administration (NASA): Moffett Field, CA, USA, 1969; Available online: https://api.semanticscholar.org/CorpusID:136918277 (accessed on 22 September 2024).
- Giardino, M.; Gobber, F.S.; Pennacchio, A.; Lupi, G.; Casati, R.; Actis Grande, M. Study of surface oxidation in metal powders by means of optical spectroscopy. Powder Technol. 2024, 443, 119883. [Google Scholar] [CrossRef]
- Schatt, W. Pulvermetallurgie: Technologien und Werkstoffe; VDI-Verlag: Dusseldorf, Germany, 1994; ISBN 3540633561. [Google Scholar]
- Reineke, L.; Barthel, B.; Hein, S.B. Analysis of powder characteristics and powder-binder interaction for process parameter prediction in Metal Binder Jetting. In Developing the Powder Metallurgy Future: Powder Production, Consolidation Technologies, Materials, Applications, Tools for Improving PM, Proceedings of the World PM2022 Congress & Exhibition, Lyon Convention Centre, Lyon, France, 9–13 October 2022; European Powder Metallurgy Association (EPMA): Shrewsbury, UK, 2022; ISBN 9781899072552. [Google Scholar]
- Contreras, J.M.; Jiménez-Morales, A.; Torralba, J.M. Fabrication of bronze components by metal injection moulding using powders with different particle characteristics. J. Mater. Process. Technol. 2009, 209, 5618–5625. [Google Scholar] [CrossRef]
- Oh, J.-W.; Nahm, S.; Kim, B.; Choi, H. Anisotropy in Green Body Bending Strength due to Additive Direction in the Binder-Jetting Additive Manufacturing Process. Korean J. Met. Mater. 2019, 57, 227–235. [Google Scholar] [CrossRef]
- Mezger, T. Das Rheologie Handbuch: Für Anwender von Rotations- und Oszillations-Rheometern, 5., Vollständig überarbeitete Auflage; Vincentz Network: Hannover, Germany, 2016; ISBN 978-3-74860-012-1. [Google Scholar]
- Singh, G.; Missiaen, J.-M.; Bouvard, D.; Chaix, J.-M. Copper additive manufacturing using MIM feedstock: Adjustment of printing, debinding, and sintering parameters for processing dense and defectless parts. Int. J. Adv. Manuf. Technol. 2021, 115, 449–462. [Google Scholar] [CrossRef]
- Ajjarapu, K.P.K.; Barber, C.; Taylor, J.; Pelletiers, T.; Jackson, D.; Beamer, C.; Atre, S.V.; Kate, K.H. Advancements in 3D printing and hot isostatic pressing of copper: Bridging the gap between green and sintered states for enhanced mechanical and electrical properties. Prog. Addit. Manuf. 2024, 9, 2343–2350. [Google Scholar] [CrossRef]





| Powder Name | d10/µm | d50/µm | d90/µm |
|---|---|---|---|
| A | 9 | 16 | 25 |
| B | 11 | 20 | 40 |
| C 1 | 15 | 53 | 111 |
| Sample Name | Loading Factor/% | Exposure Energy/mJ/cm2 | Raked Layer Thickness/µm | Overlap |
|---|---|---|---|---|
| O-0.75 | 52 | 28 | 25 | 0.75 |
| O-1 | 52 | 60 | 25 | 1 |
| O-1.25 | 52 | 128 | 25 | 1.25 |
| O-1.5 | 52 | 275 | 25 | 1.5 |
| O-2 | 52 | 1262 | 25 | 2 |
| R-1 | 52 | 1262 | 50 | 1 |
| S-52 1 | 52 | 200 | 25 | 1.40 |
| S-58 | 58 | 200 | 25 | 0.97 |
| Suspension | Penetration Depth/µm | Critical Exposure Energy/mJ/cm2 | Minimum Examined Exposure Energy/mJ/cm2 | R2 |
|---|---|---|---|---|
| BM-P18 + 52% Powder C | 14.5 | 0.3 | 50 | 0.86 |
| BM-P18 + 52% Powder B | 8.3 | 0.4 | 100 | 0.84 |
| BM-P18 + 52% Powder A | 8.2 | 3.2 | 200 | 0.89 |
| BM-P18 + 58% Powder A | 5.8 | 2.1 | 200 | 0.88 |
| Unfilled BM-P18 | 165.0 | 3.2 | 10 | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scheibler, J.; Kosmehl, A.S.; Studnitzky, T.; Zhong, C.; Weißgärber, T. Lithography-Based Metal Manufacturing of Copper: Influence of Exposure Parameters on Green Part Strength. Metals 2024, 14, 1268. https://doi.org/10.3390/met14111268
Scheibler J, Kosmehl AS, Studnitzky T, Zhong C, Weißgärber T. Lithography-Based Metal Manufacturing of Copper: Influence of Exposure Parameters on Green Part Strength. Metals. 2024; 14(11):1268. https://doi.org/10.3390/met14111268
Chicago/Turabian StyleScheibler, Jakob, Alina Sabine Kosmehl, Thomas Studnitzky, Chongliang Zhong, and Thomas Weißgärber. 2024. "Lithography-Based Metal Manufacturing of Copper: Influence of Exposure Parameters on Green Part Strength" Metals 14, no. 11: 1268. https://doi.org/10.3390/met14111268
APA StyleScheibler, J., Kosmehl, A. S., Studnitzky, T., Zhong, C., & Weißgärber, T. (2024). Lithography-Based Metal Manufacturing of Copper: Influence of Exposure Parameters on Green Part Strength. Metals, 14(11), 1268. https://doi.org/10.3390/met14111268






