Fracture and Fatigue Crack Growth Behaviour of A516 Gr 60 Steel Welded Joints

Abstract

The facture and fatigue behaviour of welded joints made of A516 Gr 60 was analysed, bearing in mind their susceptibility to cracking, especially in the case of components which had been in service for a long time period. With respect to fracture, the fracture toughness was determined for all three zones of a welded joint, the base metal (BM), heat-affected zone (HAZ) and weld metal (WM), by applying a standard procedure to evaluate K_Ic via based on J_Ic values (ASTM E1820). With respect to fatigue, the fatigue crack growth rates were determined according to the Paris law by the standard procedure (ASTM E647) to evaluate the behaviour of different welded joint zones under amplitude loading. The results obtained for A516 Gr. 60 structural steel showed why it is widely used in the case of static loads, since the minimum value of fracture toughness (185 MPa√m) provides relatively large critical crack lengths, whereas its behaviour under amplitude loading indicated a need for further improvement in WM and HAZ, since the crack growth rate reached values as high as 4.58 × 10⁻⁴ mm/cycle. In addition, risk-based analysis was applied to assess the structural integrity of a pressure vessel, including comparison with the high-strength low-alloy (HSLA) steel NIOVAL 50, proving once again its superior behaviour under static loading.

1. Introduction

Welded joints are of crucial importance for structural integrity in all welded constructions due to their crack sensitivity, caused by material heterogeneity (base metal—BM; heat-affected zone—HAZ; and weld metal—WM), as well as eventual stress concentrations in the case of geometry imperfections [1,2,3]. As shown recently, not only are welded joints typically accompanied by defects, but often multiple defects play an important role [3]. This was shown even for common carbon structural steels (S235, S275), which were examined with respect to their fracture behaviour in the presence of cracks, revealing somewhat surprising results, [3]. On the other had, it is well known that HSLA steels are prone to cracking [1,2,4,5,6] requiring so-called undermatching welded joint design as opposed to more common overmatching design. In both cases, welded joint mismatching is designed to prevent fracture under service loading.

This issue is especially important for components which have been service for a long time period, not only due to the inevitable damage of the material under loading, but also due to the fact that early generations of this steel, and steels in general, were not of the same high quality as they are now. In particular, the contents of phosphorus and sulphur were significantly higher couple of decades ago, making steels more susceptible to cracking than they are nowadays. In addition, the quality of welded joints was also significantly lower than that today. One well-known example of welded joints cracking is the history of problems with Nioval 50 back in 1980s [7].

With respect to A516 steels, few studies can be found in the literature, but they are worth considering, [8,9,10,11]. In [8], a SA516 Gr. 70 steel welded joint was analysed with a focus on the effect of the submerged arc welding speed on strength, microstructure, hardness and impact toughness in the WM and in the HAZ. Mechanisms of fracture were correlated with the impact toughness values using SEM fractography. As expected, the highest hardness values were in the coarse-grained HAZ followed by the WM, with the lowest hardness in the BM.

In [9], the objective was to quantify the effect of loading rate temperature dependence of cleavage fracture toughness data of SA516 Gr. 70 steel (P265GH according to EN standards) on the ductile-to-brittle transition temperature (DBTT) regime. For integrity analysis in a radioactive environment, the concept of a master curve according to ASTM E1921 [10] was used and the reference temperature T₀ was evaluated. Toward this aim, a specially designed test setup was made to carry out tests using sub-sized single-edged notched-bend specimens. It was found that the median fracture toughness value, as well as its scatter, increases with temperature in the DBTT regime.

In [11], fracture toughness determination was crucial for the design phase of pressure vessels made of ASTM A516 Gr. 70 steel [12]. Tensile properties and the J_Ic values were evaluated, taking into account rolling parallel and transverse orientations, to evaluate the effect of perlite banding. Additionally, as for J_Ic determination, the differences were associated with the different blunting line slope estimations in different standards, indicating the need to use a work-hardening-based blunting line.

In [13], the growth of a semi-elliptical crack in the walls of thick-walled cylindrical pressure vessels made of A516 steel was investigated numerically using 3D FEM models to estimate fatigue life, based on the experimentally evaluated fatigue crack growth rate, using a new proposed specimen. Hardness, tensile properties and Charpy impact toughness were also determined experimentally, but fracture toughness was not.

The research presented in [8,9,11,13] provides good insight into properties and behavioural of A516 steel in the presence of cracks, including its welded joints. Although generally accepted as a material which is not susceptible to cracking and brittle fracture, A516 Gr. 60 steel and its welded joints may still face problems with cracking, especially under fatigue loading, which is not addressed thoroughly in the literature. Therefore, in this paper, A516 Gr. 60 steel is considered a typical carbon structural steel with a somewhat increased level of manganese to improve its strength and to keep its weldability and ductility at a sufficient level [14,15].

This research is focused on A516 Gr. 60 steel welded joints’ resistance to fracture and fatigue crack growth under different types of loading (static, amplitude), bearing in mind its use for pressure vessels (PVs) in the chemical and petrochemical industry, including the transportation of gas and oil, both at ambient and low temperatures. As already mentioned, the main reason for this research was the need to obtain precise data about A516 Gr. 60 steel crack resistance in order to determine the structural integrity of critical components which have been in service for a long time. To assess the structural integrity of a PVs, taken as an example, a recently introduced risk-based procedure is applied, using risk assessment by a risk matrix, [16,17,18], including a comparison of two steels, one being HSLA steel NIOVAL 50 and the other one being A516 Gr. 60.

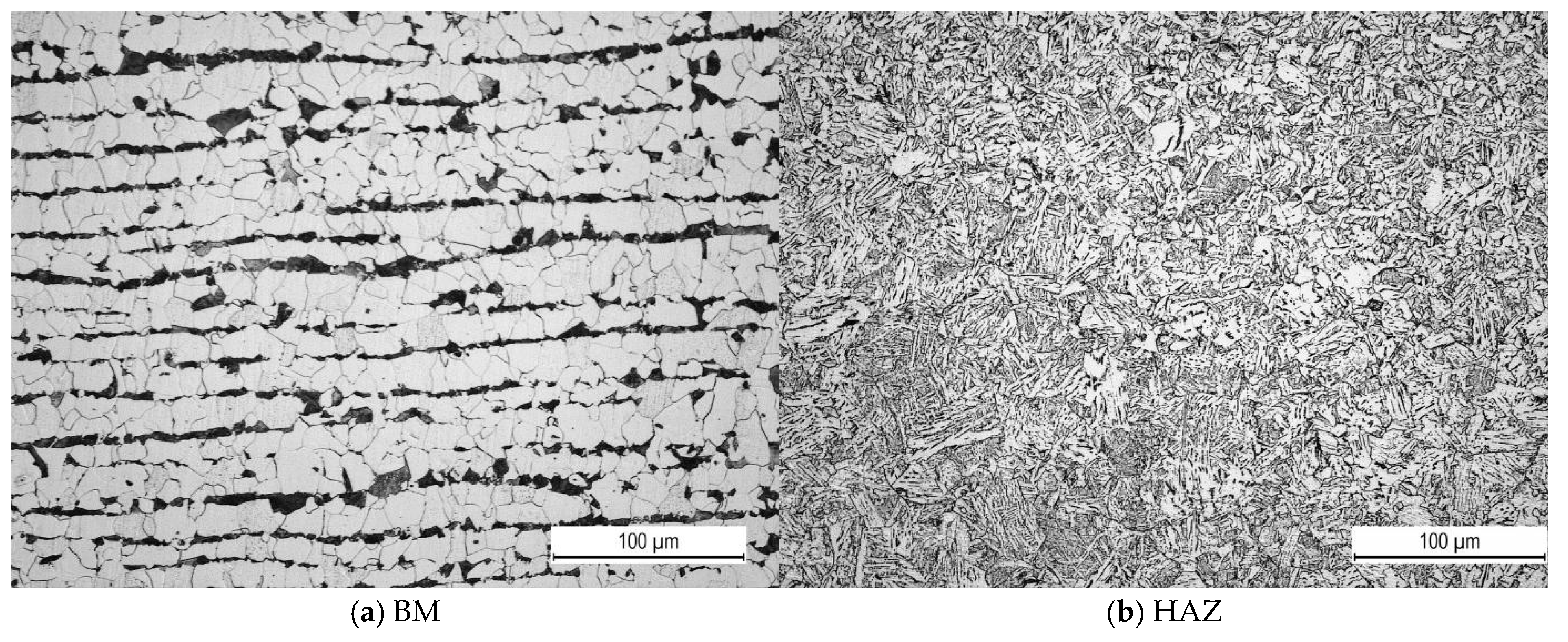
2. Materials and Methods

A516 Gr. 60 steel belongs to a group of carbon structural steels mainly used for the manufacturing of pressure vessels (spherical tanks, gas tanks, liquid–gas tanks) due to its good mechanical properties at lower temperatures [14,15]. Its yield stress is min. 255 MPa, and its guaranteed impact toughness is at −40 °C is 41 kJ/m². Plates with a thickness of 15 mm were available for experimental tests which were a part of the presented research. Experimental research consisted of basic material testing such as tests on chemical composition and tensile properties, as well as fracture mechanics (K_Ic via J_Ic) and fatigue crack growth rate testing.

The chemical composition of steel A516 Gr. 60 was determined and is shown in

Table 1. Chemical composition—BM, [14].

Element, %wt.
C	Si	Mn	P	S	Cu	Al	Cr	Mo	Ni	N
0.22	0.20	0.86	0.007	<0.001	0.24	0.038	0.12	0.05	0.15	0.005

, [14]. Tensile properties are shown in

Table 2. Tensile properties, min. BM, [14].

Material	Upper Yield Stress, ReH, MPa	Lower Yield Stress, ReL, MPa	Tensile Strength Rm, MPa	Elongation A, %	Elasticity Module E, GPa
BM (A516 Gr. 60)	365.9	350.4	483.1	40.8	211.7
NIOVAL 50	527	505	650	22.6	205.0

as the minimum values of strength measured on 3 specimens [14]. Table 2 also gives the mechanical properties of NIOVAL 50, for comparison purposes.

Welding was performed by the manual metal arc welding (MMAW) process, with EVB Ni electrode as the filler material, [14], using a groove prepared as shown in Figure 1. The chemical composition of the filler material is given in

Table 3. Chemical composition of the filler material, EVB 50 [14].

Filler Material	Element, %wt.
	C	Si	Mn	Ni	P	S	N
EVB Ni	0.07	0.50	1.40	1.1	0.009	0.011	0.012

, whereas its mechanical properties are shown in

Table 4. Mechanical properties of the filler material, EVB 50 [14].

Filer Material	Yield Stress Rp0.2, MPa, min.	Tensile Strength Rm, MPa	Elongation A, %, min.	Impact Energy, KV, J нa −40 °C, min.
EVB Ni	460	560–720	22	47

.

The root pass (mark 1, Figure 2) and fill passes (marks 2–7, Figure 2) were made with the electrode EVB Ni, diameter 2,5 mm, while fill passes 8–9, shown in Figure 2, were made with the same electrode, diameter 3.25 mm. Preheating was also applied at 120 °C in each pass. Figure 3 shows a macrographic view of the welded joint. The microstructure of the welded joint is shown in Figure 4, Figure 5, Figure 6 and Figure 7, indicating typical ferrite–perlite bands in the BM, shown in Figure 4a, transformed into different shapes in the HAZ, shown Figure 4b, the fusion line (FL), shown in Figure 4c, and the WM, shown in Figure 4d. Microstructures were determined using SEM, with the specimen previously etched using 3% Nital solution.

2.1. Fracture Toughness

To determine fracture toughness, K_Ic, standard three-point bending specimens—SE(B)—were used and their geometry was defined in accordance with ASTM E1820-20 “Standard Test Method for Measurement of Fracture Toughness” [19], as shown in Figure 5. Three groups of specimens were made, I-III, depending on the fatigue crack tip position in the welded joint, BM, WM and HAZ, respectively; see Figure 6a. Instrumentation for crack tip opening displacement (CTOD) measurement is shown in Figure 6b. Three specimens were made, since this is the minimum required for testing to ensure result accuracy and repeatability.

In the case of relatively ductile material, such as A516 Gr. 60 steel, the standard procedure includes data collection from the servohydraulic system (load cell, displacement and COD extensometer), to construct the J–Δa curve and to evaluate J_Ic, where J and Δa represent the J integral and increments of crack length, respectively. Values of the critical stress intensity factor (fracture toughness) in the plane strain can be calculated using Equation (1), [20,21,22,23]:

$$J_{Ic}={\displaystyle \frac{\left(1-{\nu }^2\right)\cdot K_{Ic}^2}{E}}$$

(1)

To calculate K_Ic, the elastic modulus E was determined by tensile tests performed on welded joint specimens at room temperature using E = 211.7 GPa; see Table 2. Now, it is possible to calculate the critical crack length value by applying the basic formula of fracture mechanics:

$$K_{Ic}={\sigma }_c\cdot \sqrt{\pi \cdot a_c}$$

(2)

where σ_c can be replaced with the yield stress, R_p0,2, to obtain its minimum value. One should notice that this as just an approximation valid for the wide plate with a central crack, since no geometry factor Y(a/W) is taken into account. Anyhow, it will be useful for comparison purposes, based on different K_Ic values in different welded joint zones. One should notice that linear elastic fracture mechanics is used here as a conservative approach, with inevitable plasticity as a prevention of failure.

2.2. Determining of Fatigue Crack Growth Parameters

Analysis of the stress/strain state at the fatigue crack tip based on linear–elastic fracture mechanics (LEFM) principles led to the formulation of the well-known Paris equation, which relates the fatigue crack growth rate with the stress intensity factor range at the crack tip [24]:

$${\displaystyle \frac{da}{dN}}=C\cdot {\left(\Delta K\right)}^m$$

(3)

To evaluate material parameters C and m, ASTM E647-15e1, “Standard Test Method for Measurement of Fatigue Crack Growth Rates” [25], can be used, including the procedure for measuring of fatigue crack growth rate da/dN, along with the calculation of the stress intensity factor range, K. One common option to achieve this aim is to use standard Charpy specimens via a three-point bending method on a RUMUL FRACTOMAT device, shown in Figure 7. Similarly to the previous test, a total of three specimens were used for fatigue tests.

Prior to testing, specimens were machined and measuring tapes—foils—which were used to monitor the growth of the crack, were glued to them. RMF A-5 measuring foils with a measuring length of 5 mm were used. In order to monitor the fatigue crack growth in this manner, the FRACTOMAT crack growth registration device was used [26]. The crack growth measuring system, the FRACTOMAT, and the measuring foil work by registering the change in the electrical resistance of the foils. As the fatigue crack grows below the measuring foil, it deforms following the fatigue crack tip and provides a change in foil resistance that varies linearly with the change in crack length. The scheme of operation of the system for measuring crack growth, FRACTOMAT-measuring film, is shown in Figure 8.

2.3. Risk-Based Analysis—FAD

Steels used for welded joints are commonly not susceptible to brittle fracture, but static failure still can appear in combination with plastic collapse. Thus, a more general approach is needed, as provided by the failure analysis diagram (FAD), based on the simple yield strip model and corresponding limit curve [27,28]:

$${\displaystyle \frac{K_{eff}}{K_I}}={\displaystyle \frac{{\sigma }_c}{\sigma }}{\left[{\displaystyle \frac{8}{{\pi }^2}}\ln \sec {\displaystyle \frac{\pi }{2}}{\displaystyle \frac{\sigma }{{\sigma }_c}}\right]}^{1/2}$$

(4)

where K_I = σ√πa. As a final step, non-dimensional variables S_r = σ/σ_c and K_r = K_I/K_Ic are defined, where K_eff is replaced by fracture toughness K_Ic to construct the limit curve in dimensionless coordinates (K_r, S_r):

$$K_r=S_r{\left[{\displaystyle \frac{8}{{\pi }^2}}\ln \sec \left({\displaystyle \frac{\pi }{2}}{S}_r\right)\right]}^{-1/2}$$

(5)

Now, for a component under analysis, one should know the stress and stress intensity factor K_I, corresponding to the loading and geometry, including a crack, to evaluate the coordinates in the FAD, if material properties are known as well (critical stress c and fracture toughness K_Ic). If a point is below the limit curve, a component is safe. Moreover, using the position of this point in relation to the limit curve, one can estimate the likelihood as the representative of the probability of failure and combine it with the consequence of failure to estimate the risk. The reasoning behind this approach is presented and discussed in detail in [14]. Finally, a risk matrix can be used to present the result and to provide all data needed for the decision making process, also presented in detail in [16,17,18].

A more detailed description of this approach is given in [29], as a part of the SINTAP, which is more efficient to use in the case of complex geometry.

3. Results

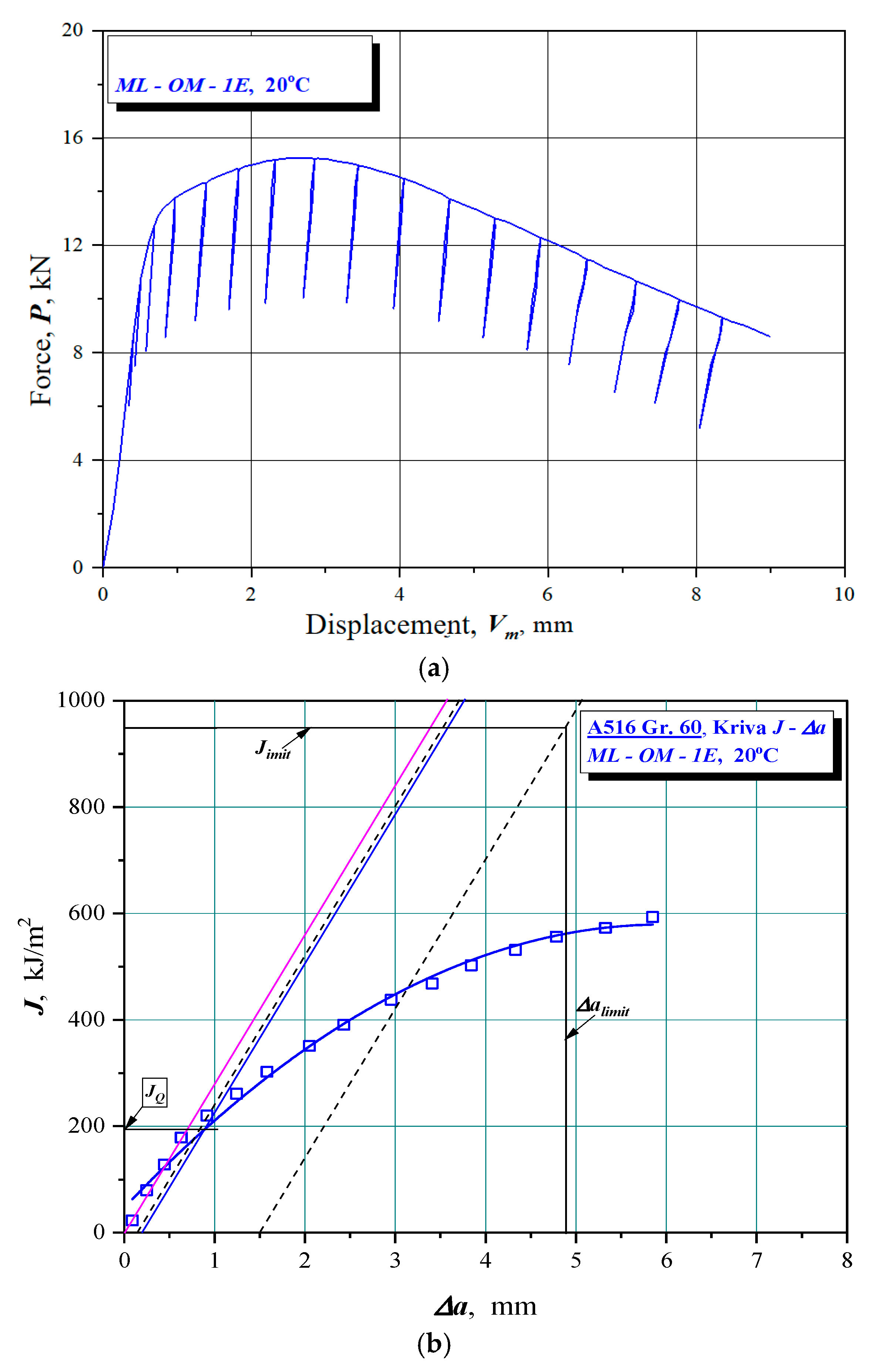
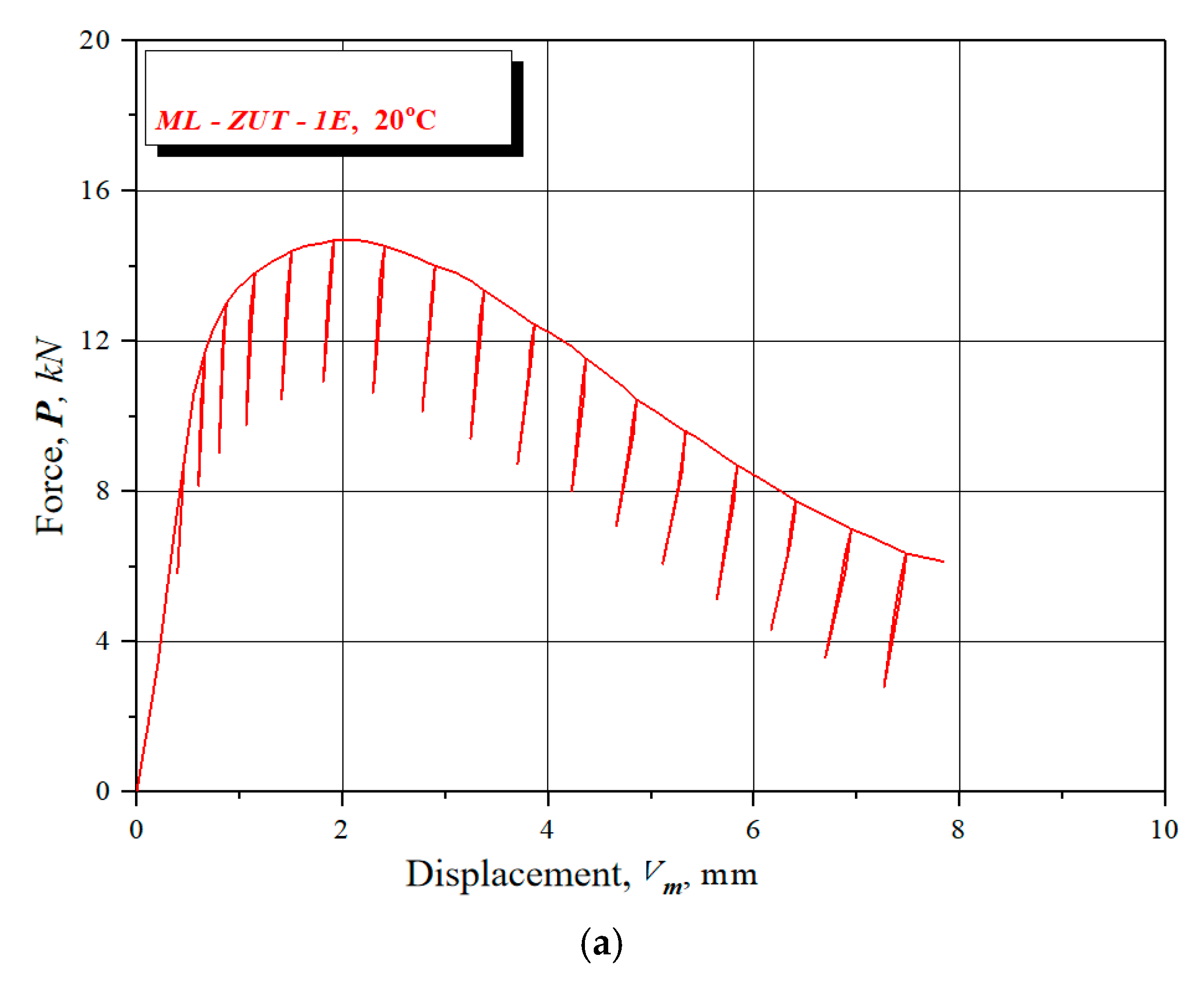
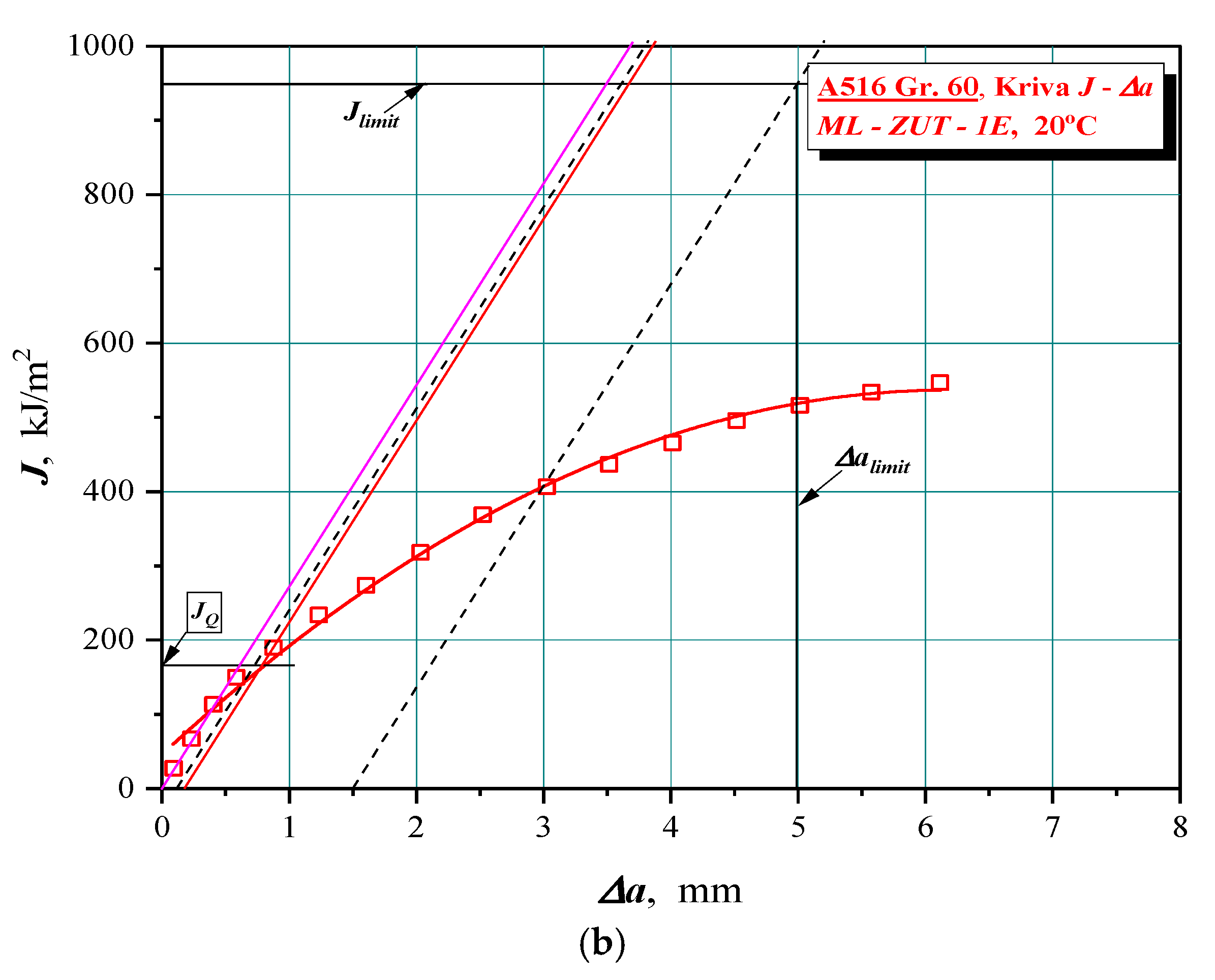
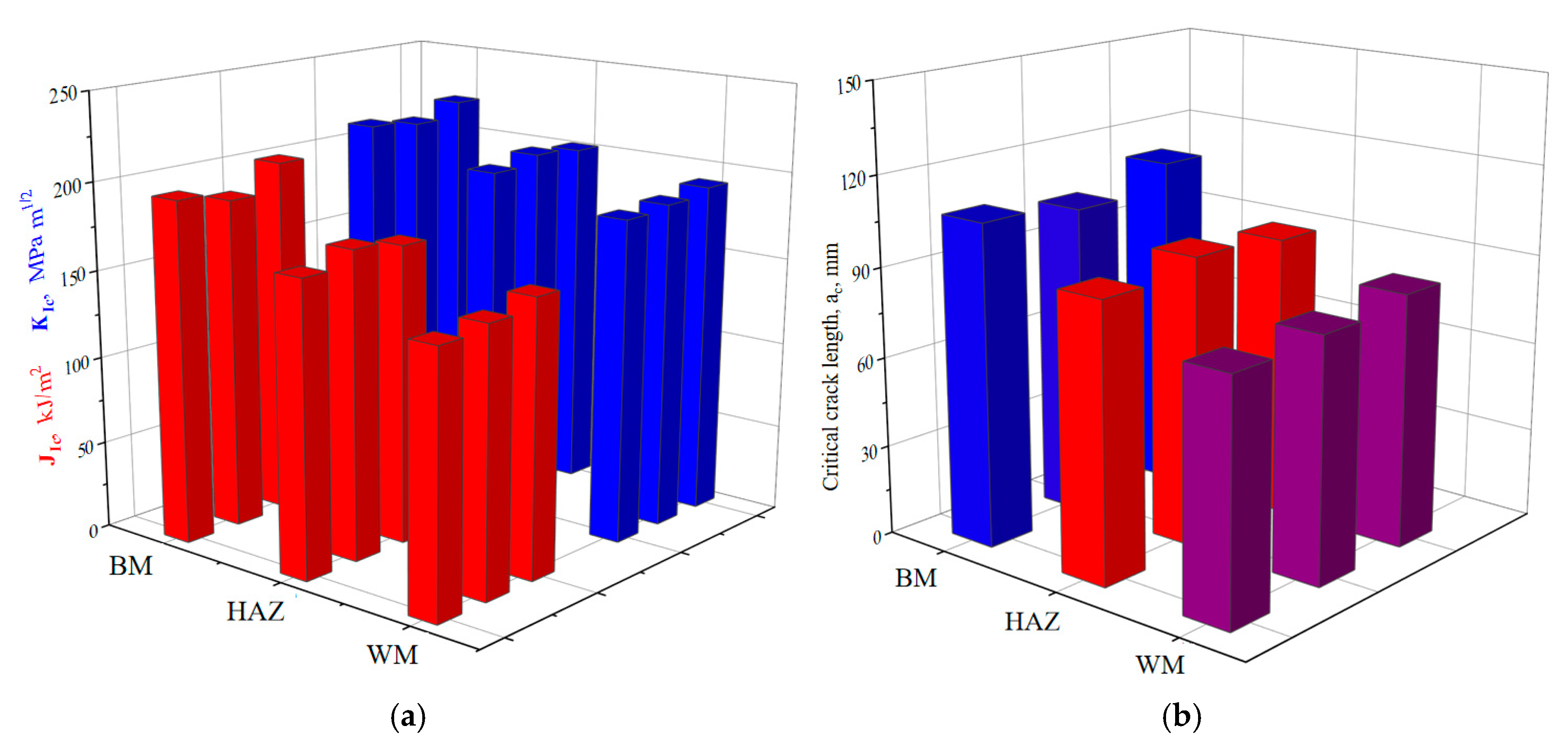
3.1. J–R Curves and Calculation of J_Ic and K_Ic

Force–displacement and J–Δa diagrams for specimens denoted as BM 1–3 (crack tip in the BM), HAZ 1–3 (crack tip in the HAZ) and WM 1–3 (crack tip in the WM) are shown in Figure 9, Figure 10 and Figure 11, respectively. In these figures, the boxes in the corner contain the designation of used specimens and the test temperature. The calculated values of K_Ic for specimens are shown in

Table 5. Values of K_Ic for specimens for all three groups.

Specimen Designation	Critical J-Integral, JIc, kJ/m2	Fracture Toughness, KIc, MPa√m	Critical Crack Length, ac, mm
BM 1	195.3	215.1	107.6
BM 2	189.2	211.7	104.3
BM 3	204.5	220.1	112.7
HAZ 1	167.2	199.0	92.2
HAZ 2	175.4	203.9	96.7
HAZ 3	170.8	201.2	94.1
WM 1	147.8	185.0	79.6
WM 2	151.2	187.1	81.4
WM 3	157.4	190.9	84.8

, as well as the critical crack length, obtained by using Equation (2).

In the J–Δa diagrams in these figures, the blue curve represents the so-called regresion line, and the dotted blue line is defined by crack length of Δa = 0.2 mm, and the point on the regression line which corresponds to J_Q, and slope of this line is proportional to twice the value of yield stress. Other dotted lines are simply obtained by offsetting this line to the coordinate system origin (red) and the intersection between J_limit and Δa_limit lines.

One can see from Figure 9, Figure 10 and Figure 11 and Table 5 the typical elastic–plastic behaviour of a common structural steel welded joint, such as A516 Gr. 60, with relatively high values of fracture toughness and, consequently, high values of critical crack length. Indeed, the minimum value of fracture toughness is 185 MPa√m (specimen WM 1) and the corresponding critical crack length is 79.6 mm, which is easily detectable with standard NDT examination. Another important aspect is the relatively small difference between the maximum and minimum fracture toughness values (220.1–185.0 MPa√m), indicating the high crack resistance of the whole welded joint under static loading.

Figure 12a shows the effects of the crack tip position, in terms of welded joint regions, on the critical values of fracture mechanics parameters J_Ic and K_Ic. Figure 12b shows the same effect on the values of critical crack length.

3.2. Risk Assessment of Pressure Vessels in RHPP Bajina Basta

Pressure vessels in the Reversible Hydropower Plant (RHPP) Bajina Basta in Serbia are used as storage for compressed air under a pressure of 78 bar. They were made of HSLA steel of the old generation (Nioval 50), back in the 1980s, with a history of cracking problems in welded joints ever since 1998 [7].

Inspection and testing of pressure vessels was performed by different ultrasonic NDTs, conventional and advanced ones [30], according to EN ISO 11666 2018 [31]. Out of nine tested PVs, vessel 977 is briefly presented here (pressure p = 78 bar, thickness t = 42 mm, mean diameter D = 1958 mm). Ultrasonic testing was conducted on two vertical welded joints, and three circular welded joints. A crack-like defect, marked 2.5, was found in the central circular welded joint, with a length of 170 mm and ranging from 28 to 42 mm in depth, [18,30], far above the acceptance level [31].

To assess the structural integrity of PV 977, the FAD was used. The fracture toughness K_Ic for the weld metal was taken as 50 MPa√m [32]. In the case of defect 2.5 in vessel 977, the stress intensity factor for the edge surface defect (2c = 170 mm, a = 14 mm) was calculated using Equation (6):

K_I = Y(a/W)(pR/2t)√πa

(6)

where Y(a/W) is the geometry factor equal to [26]

Y(a/W) = 1.12 − 0.26(a/W) + 10.52(a/W)² − 21.66(a/W)³ + 30.31(a/W)⁴

(7)

for a/W = 0.33, resulting in Y(a/W) = 1.78, K_I = 32.5 MPa√m and K_I/K_Ic = 0.65.

The ratio of critical cross-section stress to critical stress (the half-sum of yield stress, 500 MPa, and tensile strength, 650 MPa, [18]) is as follows: S_R = σ_n/σ_F = 132/575 = 0.23.

The coordinates of the point in the FAD (0.23; 0.65) are in the safe area, in Figure 13, at the level of fracture probability of approximately 0.66. The safe area is defined by the limit curve given by the following formula:

$$K_{\mathrm{r}}\left(S_{\mathrm{r}}\right)={\displaystyle \frac{1-0.1S_{\mathrm{r}}^2+0.1S_{\mathrm{r}}^4}{1+3S_{\mathrm{r}}^4}}$$

(8)

In the case of A516 Gr. 60 steel, the fracture toughness K_Ic for the weld metal is taken as 185 MPa√m, [12], so that the ratio defining Y coordinate is K_I/K_Ic = 0.175, whereas the ratio defining the X coordinate is S_R = S_n/S_c = 132/460 = 0.29, where S_c = (360 + 560)/2 = 460 MPa.

The coordinates of the point in the FAD (0.29; 0.175) correspond to A516 Gr. 60 steel. It is also in the safe area in Figure 13 at the level of fracture probability of approximately 0.30.

Now, one can construct the risk matrix, as shown in

Table 6. Risk matrix for defect 2.5.

		Consequence Category
		1 Very Low	2 Low	3 Medium	4 High	5 very High	Risk Level
Probability Category	≤0.2 very low						Very low
	0.2–0.4 low					A516 Gr. 60	Low
	0.4–0.6 medium						Medium
	0.6–0.8 high					Nioval 50	High
	0.8–1.0 very high						Very high

. The consequence category of PVs in RHPP Bajina Basta is the highest one, since they can bring the whole plant down. As one can see, different steels pose different risks in the case of defect 2.5 in the analysed PV; in other words, their welded joints present a significant difference: A516 Gr. 60 is located in the medium-risk area, whereas Nioval 50 is in the very-high-risk area. Probability is determined based on the location of the point in the FAD, by dividing its distance from the origin by the distance from the origin of the point on the limit curve, which is obtained by drawing a line through the origin and the point, and finding its intersection with the curve.

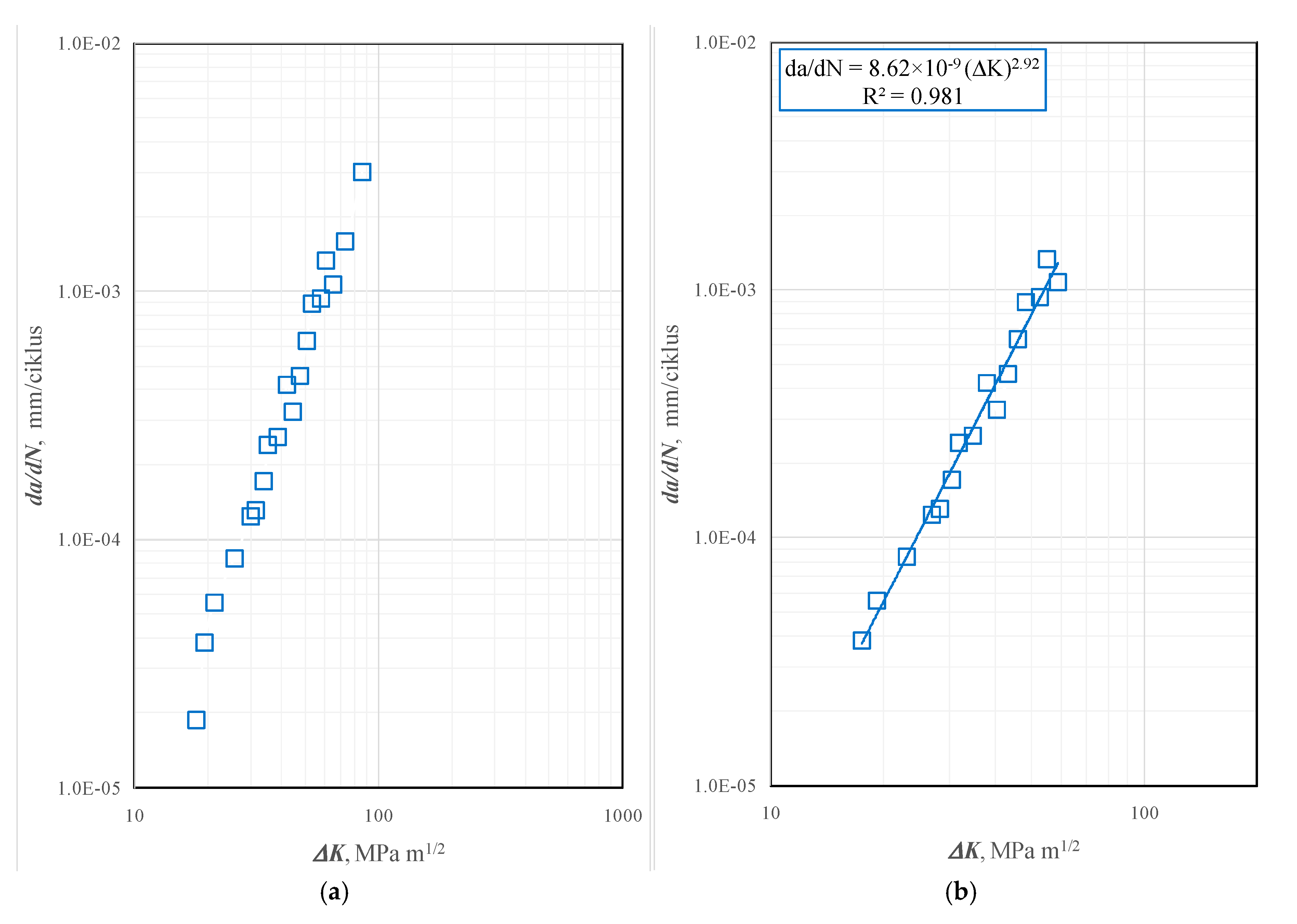
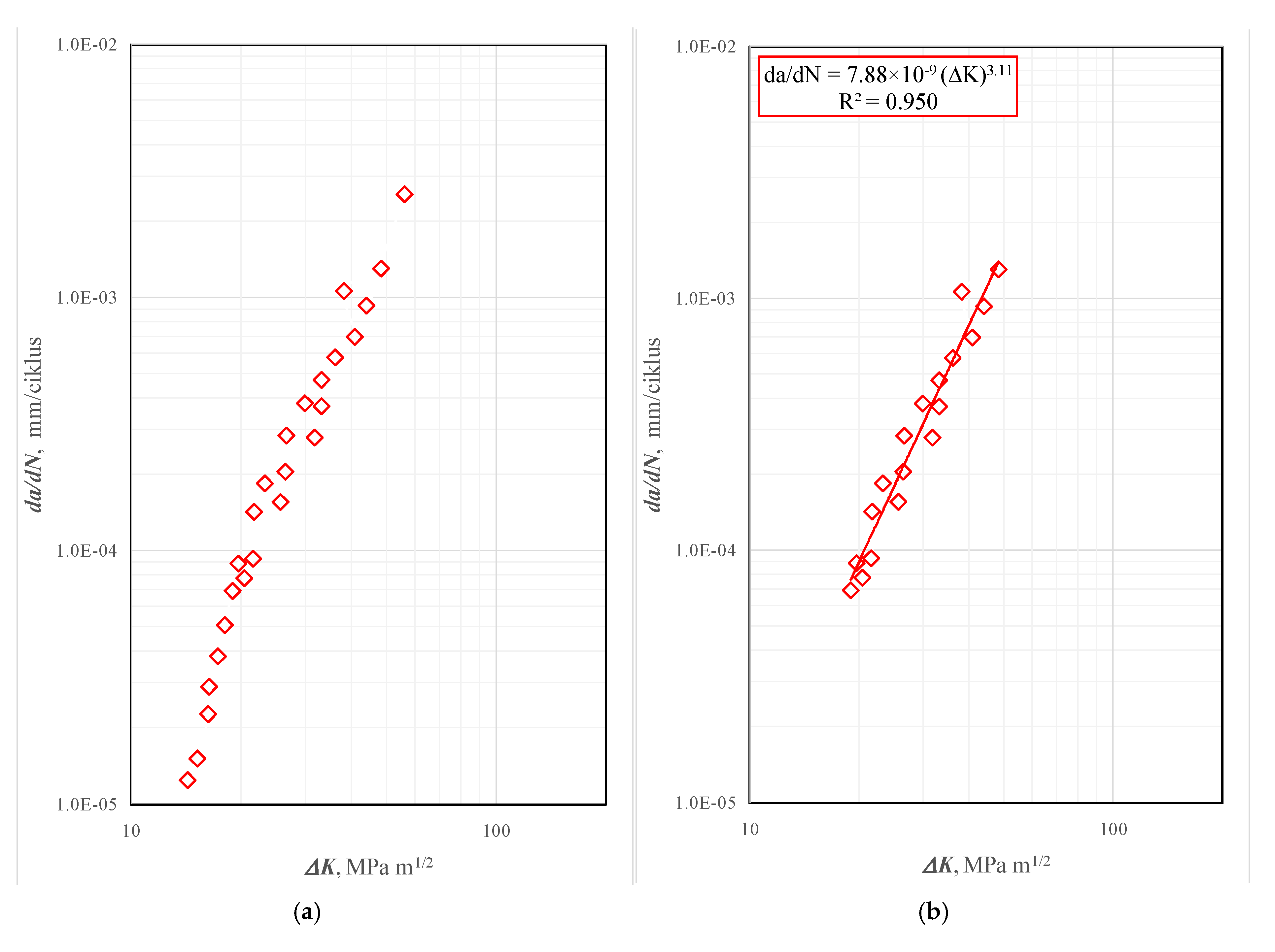
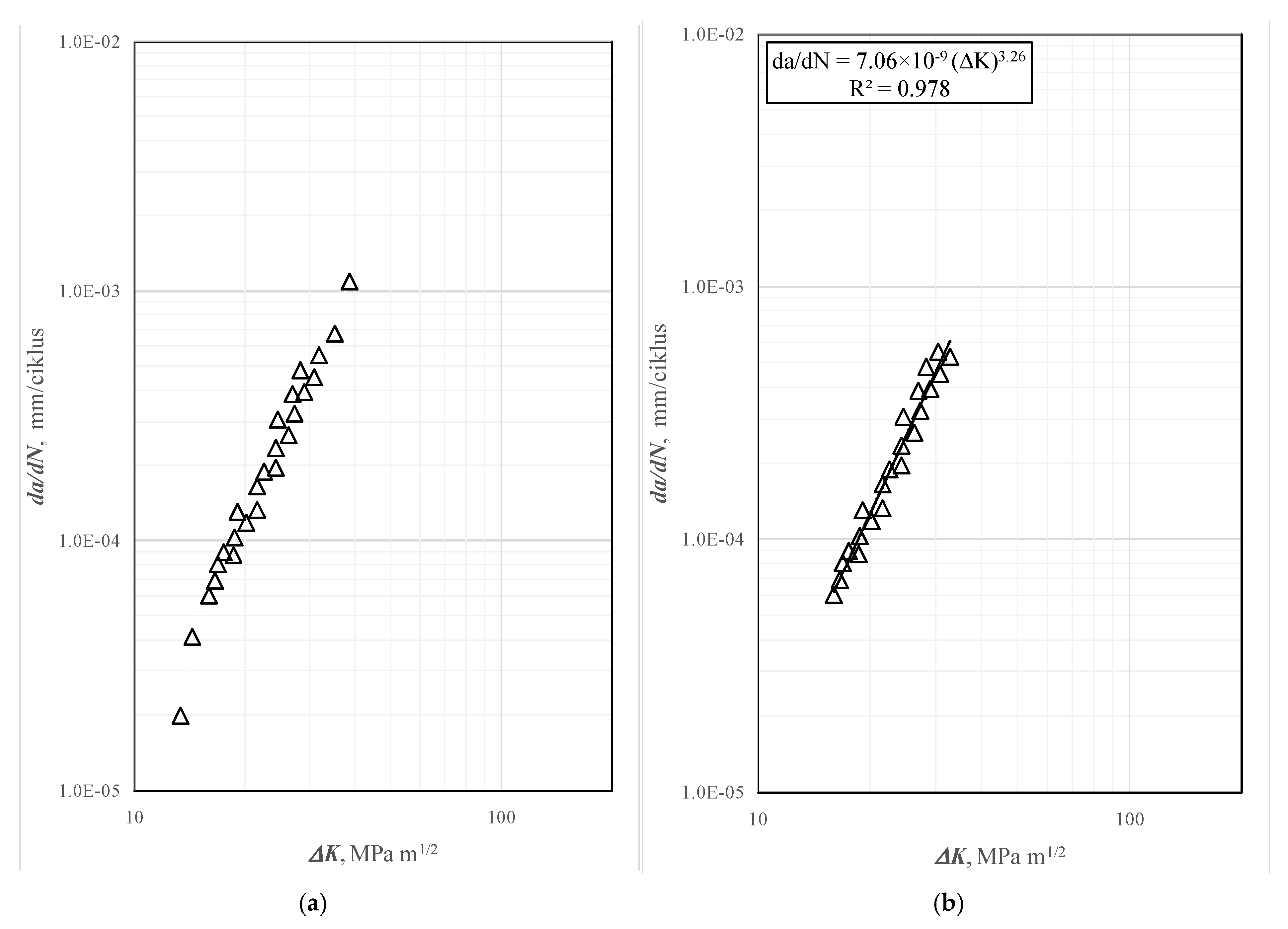
3.3. Fatigue Crack Growth (FCG)

The results of FCG testing are shown in

Table 7. Parameters for fatigue crack growth for specimens with notches in PM, WM and HAZ.

Crack Tip Position	Coefficient, C	Exponent, m	da/dN, mm/cycl, for ΔK = 30 MPa√m
BM 1	8.62 × 10−9	2.92	1.77 × 10−4
BM 2	2.49 × 10−9	3.19	1.28 × 10−4
BM 3	3.65 × 10−8	2.36	1.12 × 10−4
HAZ 1	7.88 × 10−9	3.11	3.09 × 10−4
HAZ 2	2.84 × 10−9	3.36	2.61 × 10−4
HAZ 3	1.23 × 10−8	2.92	2.52 × 10−4
WM 1	7.06 × 10−9	3.26	4.58 × 10−4
WM 2	2.21 × 10−9	3.56	4.01 × 10−4
WM 3	3.18 × 10−10	4.10	3.62 × 10−4

for specimens with crack tips in the BM, WM and HAZ, for ΔK = 30 MPa√m.

Typical da/dN-ΔK diagrams are shown in Figure 14, Figure 15 and Figure 16 for specimens BM 1, HAZ 1 and WM 1, respectively. On the left side, the whole diagram is shown, while on the right side, only a part of the diagram, used to evaluate C and m, is shown.

4. Discussion

Specimens with a crack in the parent material (PM) showed the best resistance to static crack growth. The obtained values of fracture toughness, K_Ic, were in the range from 211.7 to 220.1 MPa√m. Slightly lower values of K_Ic (up to 6%) were obtained for HAZ, from 199.1 to 203.9 MPa√m. The lowest values of K_Ic were in the WM 185.2 to 190.9 MPa√m range, i.e., up to 12%. Therefore, one can see that these differences are relatively small, certainly smaller than in the case of HSLA steels [32]. As a consequence, the critical crack length, a_c, was the largest for PM (104 mm), medium for the HAZ (92 mm) and the lowest for the WM (80 mm); see Table 5. Once again, the differences are relatively small and the values certainly appear large. One should bear in mind that these values are given here for comparison purposes only, and are not realistic, since the geometry parameter Y(a/W) was not taken into account. More realistic values for a long crack would be around half of the thickness in depth, a_c = 21 mm.

More realistic analysis is given in the following text using risk-based analysis of a pressure vessel presented in this paper. As one can see, the replacement of common carbon steel (A516 Gr. 60) with HSLA steel Nioval 50 (of the old generation, with low fracture toughness) raises the risk level from low to high; see Table 6. Therefore, the question arises as to why one should use a design based on safety factors (174/500 = 35% of YS for Nioval 50 vs. 174/360 = 49% of YS for A516 Gr. 60) when at the same time there is a raised risk of failure from low to high in the presence of cracks. In other words, what is the reason and logic for using larger safety factors when they actually increase the risk of failure in the case of a material replacement’s with a stronger one?

For the analysis of fatigue crack growth behaviour, the stress intensity factor range value of ΔK = 30 MPa√m was adopted. This value corresponds to the parts of the da/dN—ΔK diagrams which are located in the stable crack growth region, i.e., where the Paris law applies. The fatigue crack growth rate ranges from 1.12 × 10⁻⁴ mm/cycle to 1.77 × 10⁻⁴ mm/cycle for specimens with a notch in the PM. In the case of specimens with a fatigue crack tip in the HAZ, the fatigue crack growth rate is from 2.52∙× 10⁻⁴ mm/cycle to 3.09∙× 10⁻⁴ mm/cycle, meaning that fatigue crack in the HAZ grows almost twice as fast in comparison to that in the BM. The highest speed of fatigue crack growth, i.e., the worst resistance to crack propagation under the effect of variable load, was observed in specimens with a fatigue crack tip in the WM, and it ranged from 3.62∙× 10⁻⁴ mm/cycle to 4.58 × 10⁻⁴ mm/cycle, as shown in Figure 17, together with values for the HAZ and PM. Obviously, differences between different welded joint zones are much more significant in the case of amplitude loading and fatigue crack growth behaviour. Taking coefficient m = 3 (just for a comparison), one can estimate that the number of cycles in the BM would be about 8 times larger compared to HAZ and 27 times larger than in the WM. Therefore, if fatigue loading becomes important, one should carefully analyse differences in welded joint zones and calculate fatigue life as precisely as possible, either analytically [33] or by using numerical methods such as XFEM, as described in a couple of recently published papers [34,35,36].

Different microstructures in the WM, HAZ and BM, as shown and described in [14], are more sensitive to fatigue crack growth than to static loading and ductile crack growth. These differences strongly depend on the welding process and parameters, which have to be defined carefully in order to not make microstructural differences too big. In the case analysed here, microstructures are basically ferrite–perlite, with differences not being too pronounced.

With respect to the FAD and risk-based analysis, it should be noted that a simple engineering approach was used here to obtain a conservative estimate of the structural integrity of a chosen PV example. More complex analysis can be conducted in the scope of a R6 procedure [37] and SINTAP [29]. In any case, the comparison between two steels (A516 Gr. 60 and Nioval 50) revealed the important difference in the level of risk, this being much lower in the case of A 516 Gr. 60. In practical terms, this means that the safety factor when designing A516 Gr. 60 components can be lower, thereby reducing the disadvantage of having a lower yield stress.

5. Conclusions

Based on the presented results and discussion, one can conclude the following:

• The heterogeneity of the welded joint microstructure of a common carbon structural steel, such as A516 Gr. 60, causes different crack growth behaviours in the BM, WM and HAZ, which are not significant for static loading, but may become important in the case of fatigue loading, since the analysis presented here showed that the crack growth rate in the least favourable region, the WM, can be 2.5 to 3.2 times greater than that in the BM.
• The effectiveness of replacing a common carbon structural steel such as A516 Gr. 60 with HSLA steel Nioval 50 is questionable because of the low static crack resistance of the later one. This was confirmed via a risk matrix, which indicated that A516 Gr. 60 was in the low-risk zone, as opposed to Nioval 50, which was in the high-risk zone, with a much greater probability of failure. Nevertheless, modern HSLA steels not only have higher strength, but also significantly better crack resistance, including both static and fatigue resistance, due to their more favourable microstructure.
• The risk-based procedure presented and applied here is a practical tool to assess structural integrity and is especially useful in the case of components which have been in service for a long time.
• More advanced methods for structural integrity assessment are needed, such as SINTAP, in the case of a component with a more complex geometry, including numerical analysis of the stress state by the finite element method.