Experimental and Numerical Investigation of Forming Limit Diagrams during Single Point Incremental Forming for Al/Cu Bimetallic Sheets
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Incremental Forming
2.3. Mechanical Study
2.4. Microstructure Investigation
2.5. Finite Element Model
3. Results and Discussion
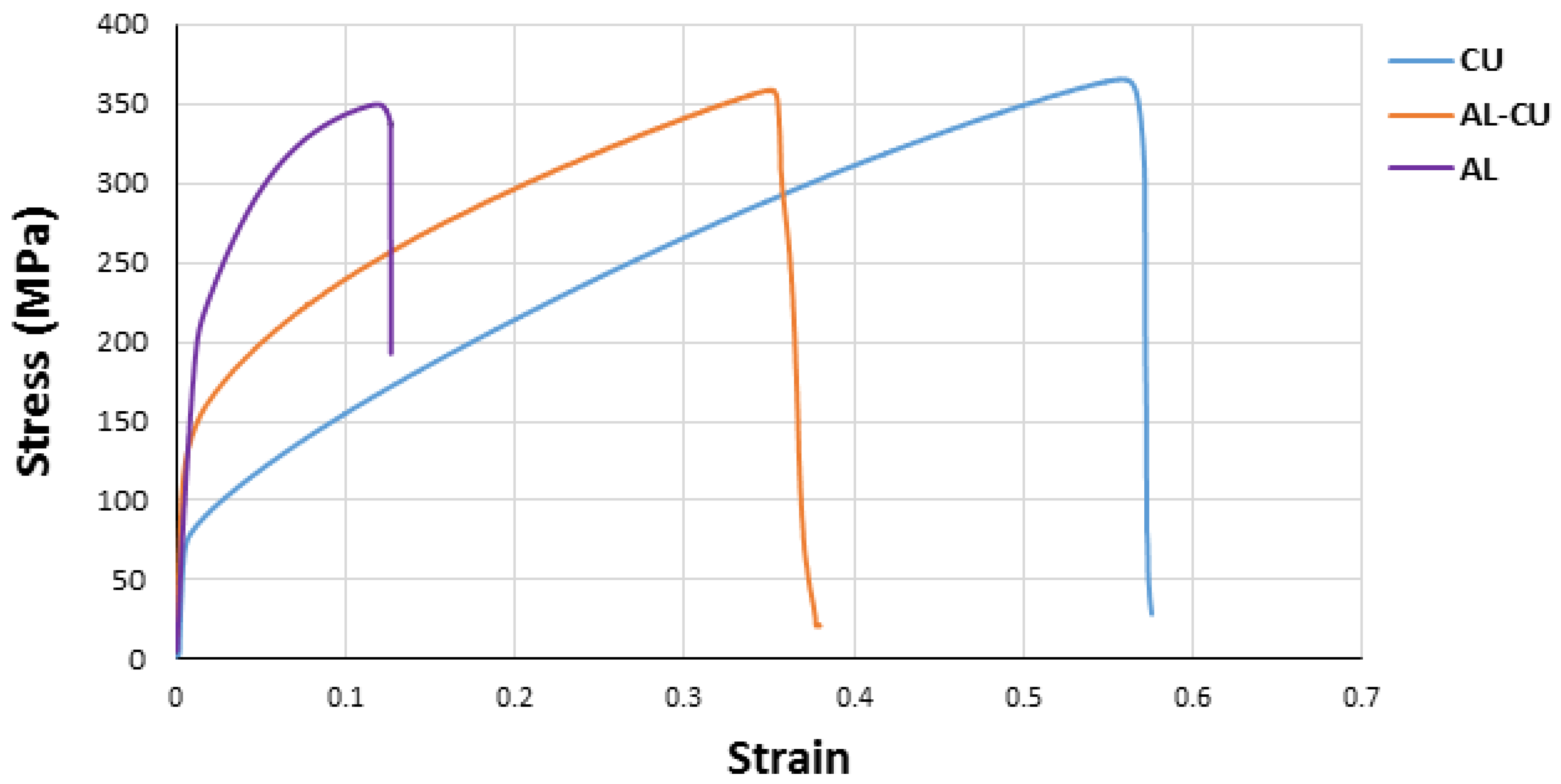
3.1. Mechanical Results
3.2. Microstructure Analysis
3.3. Intermetallic Study
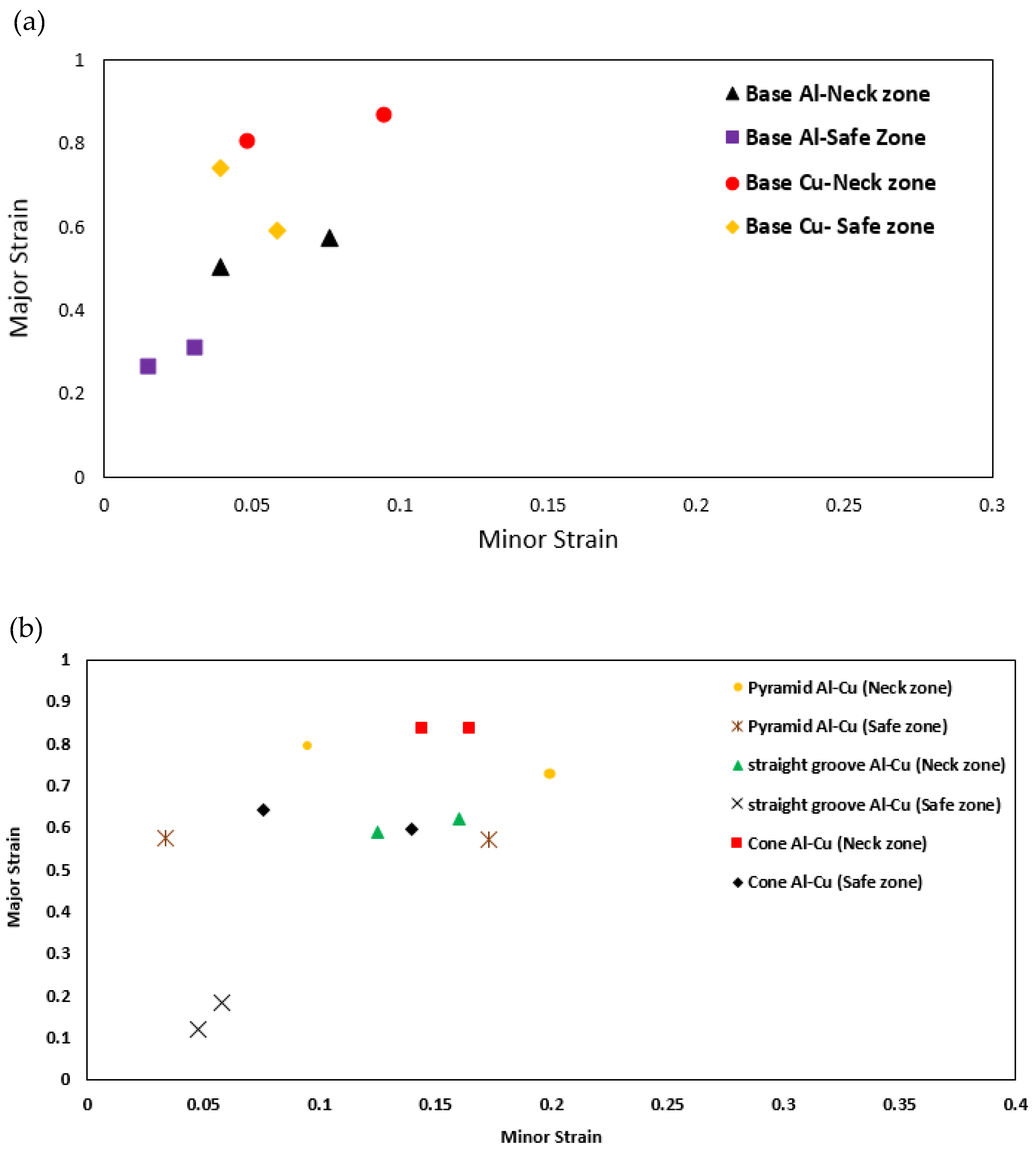
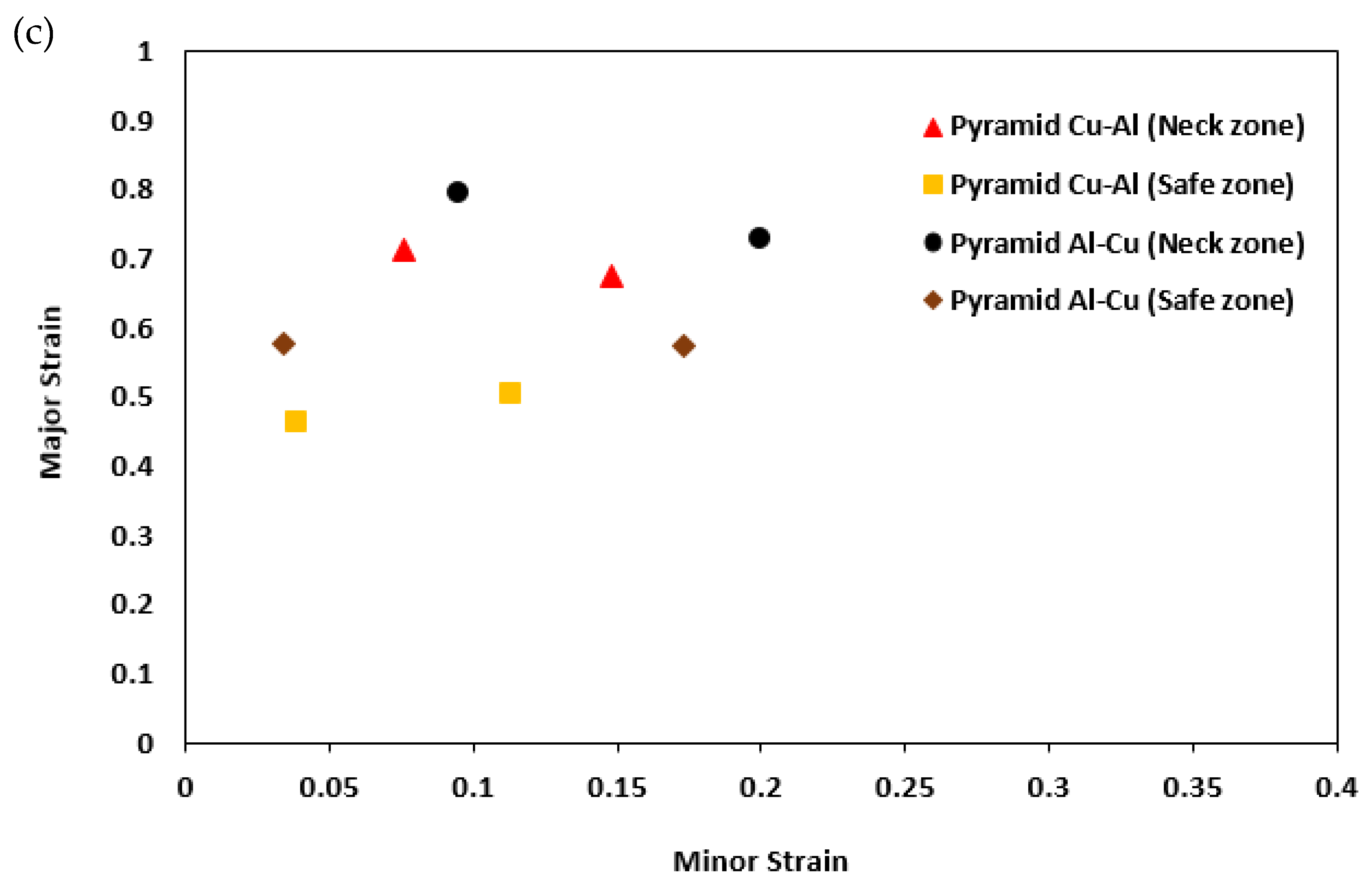
3.4. Incremental Forming Results
3.5. FEM Results
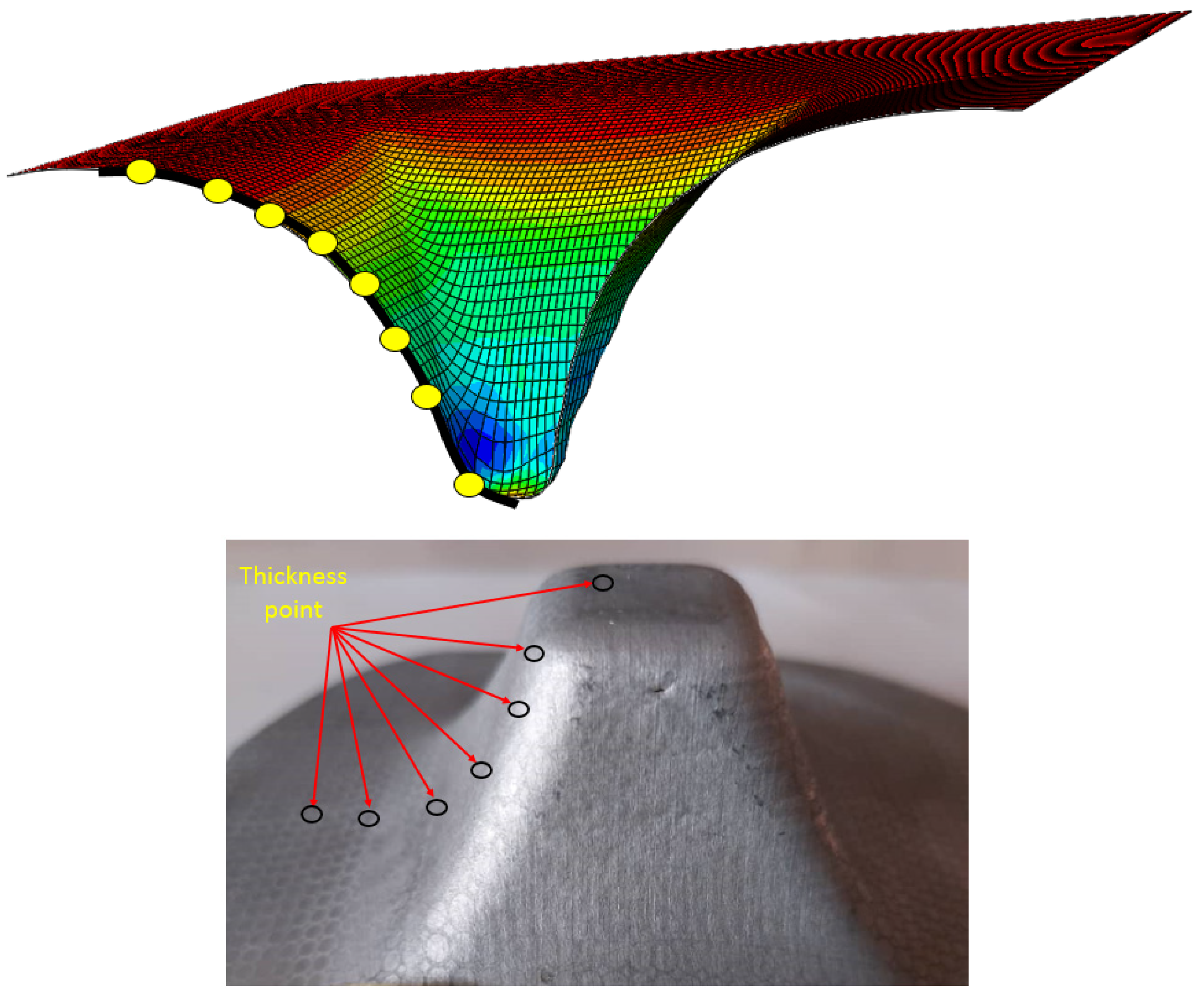
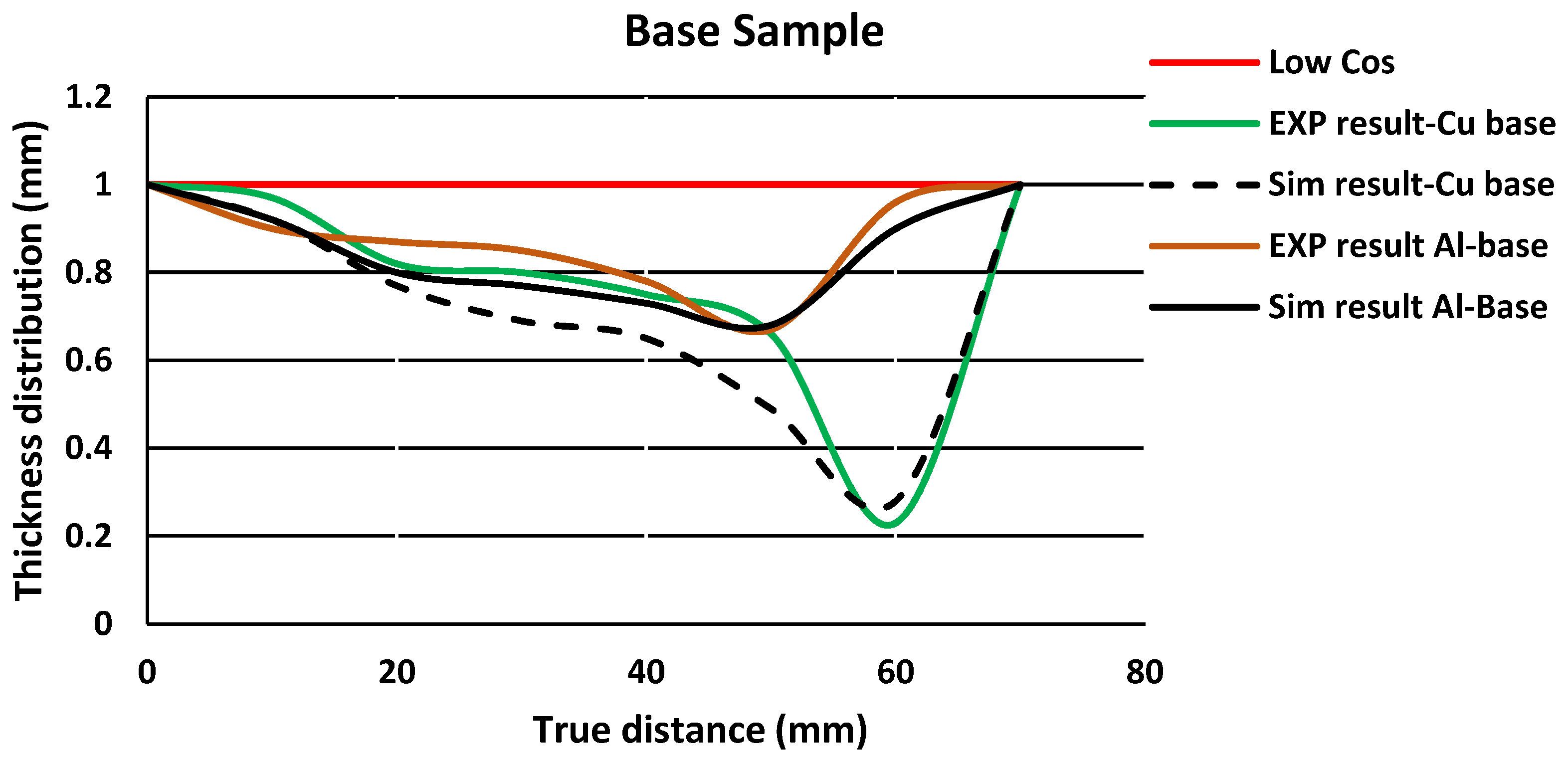
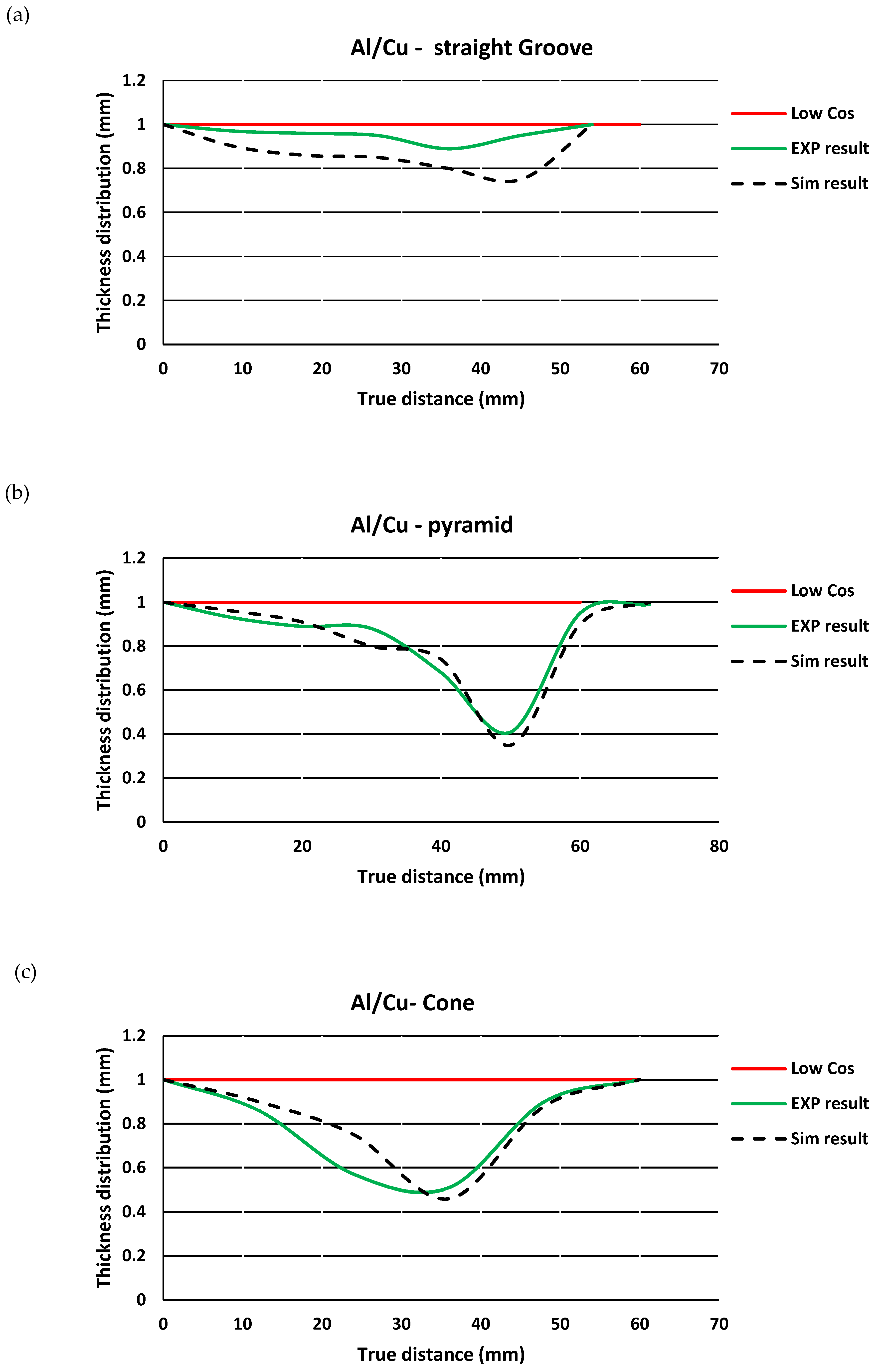
3.5.1. Thickness Distribution
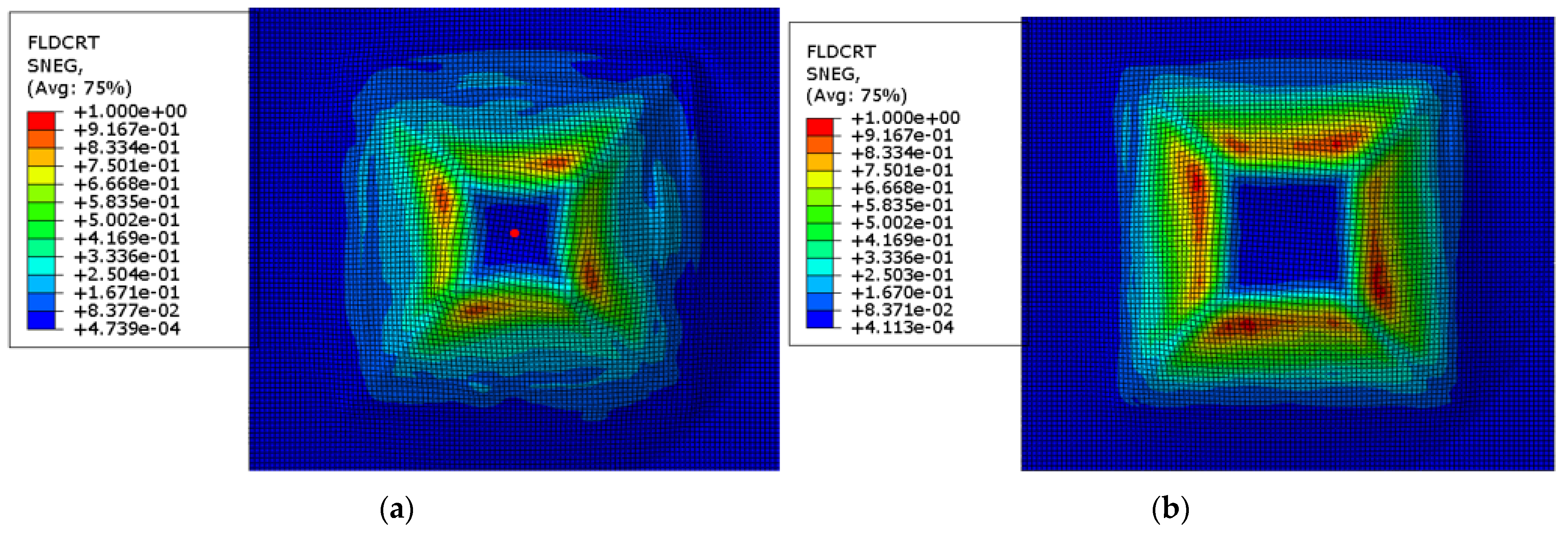
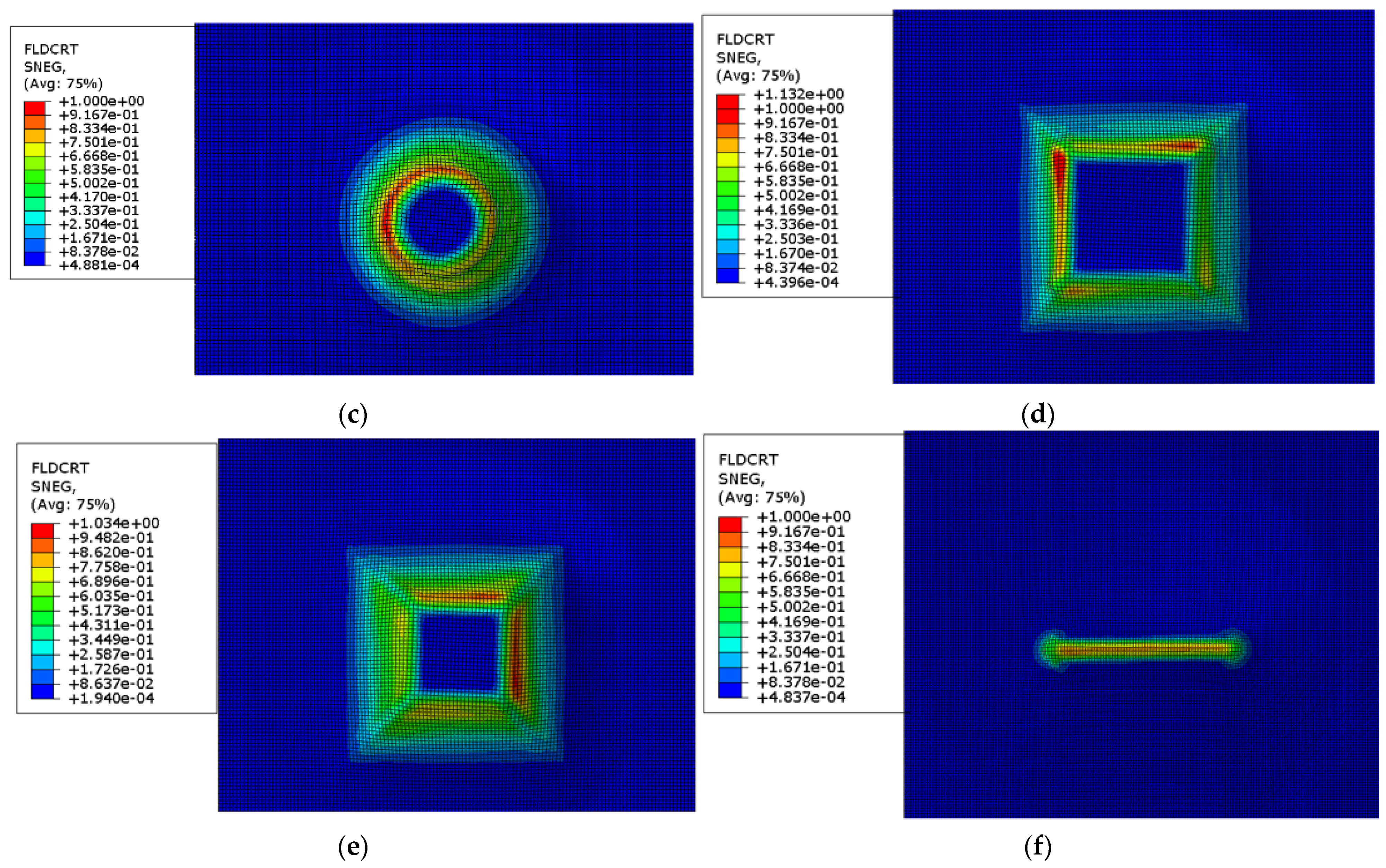
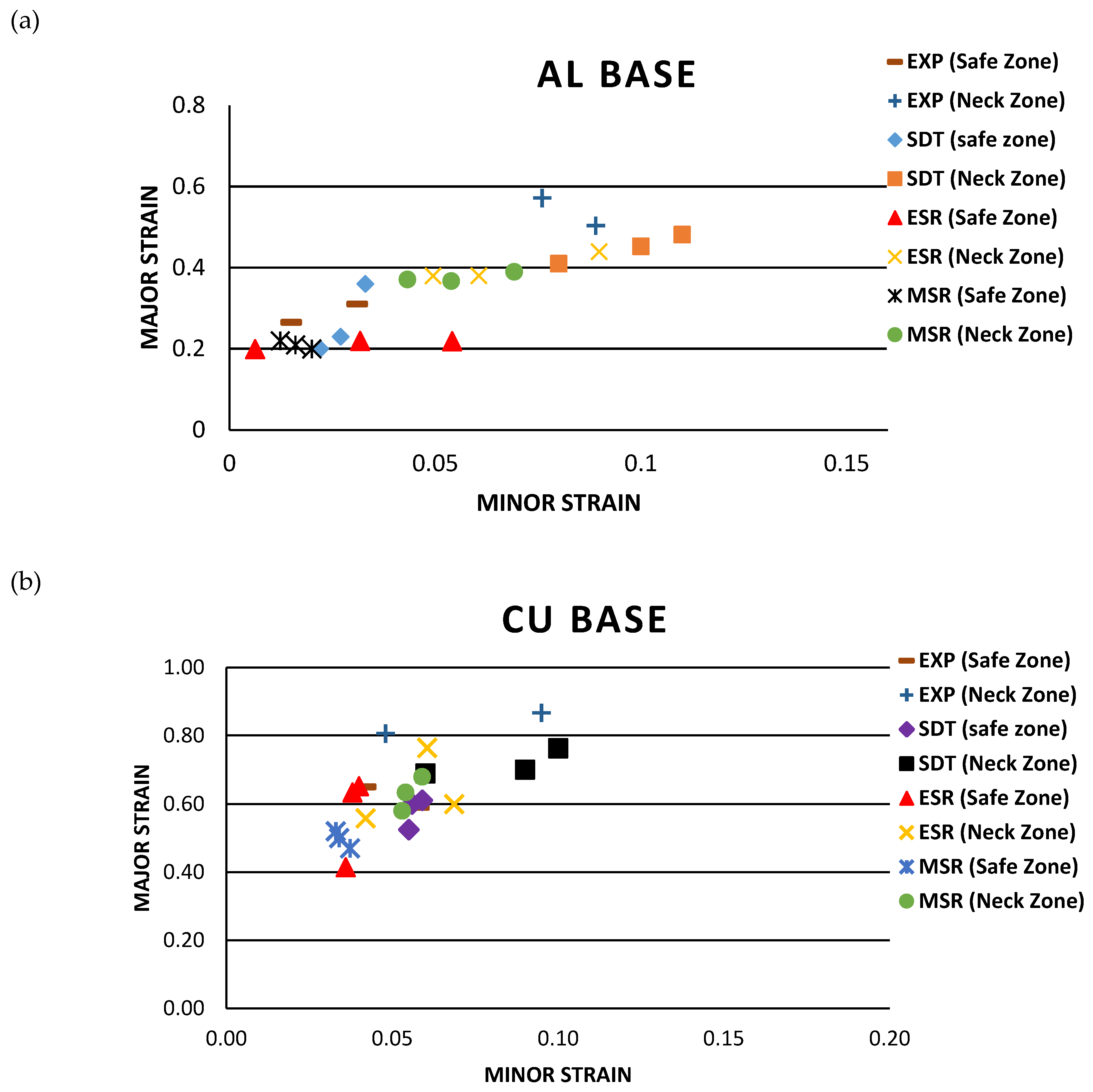
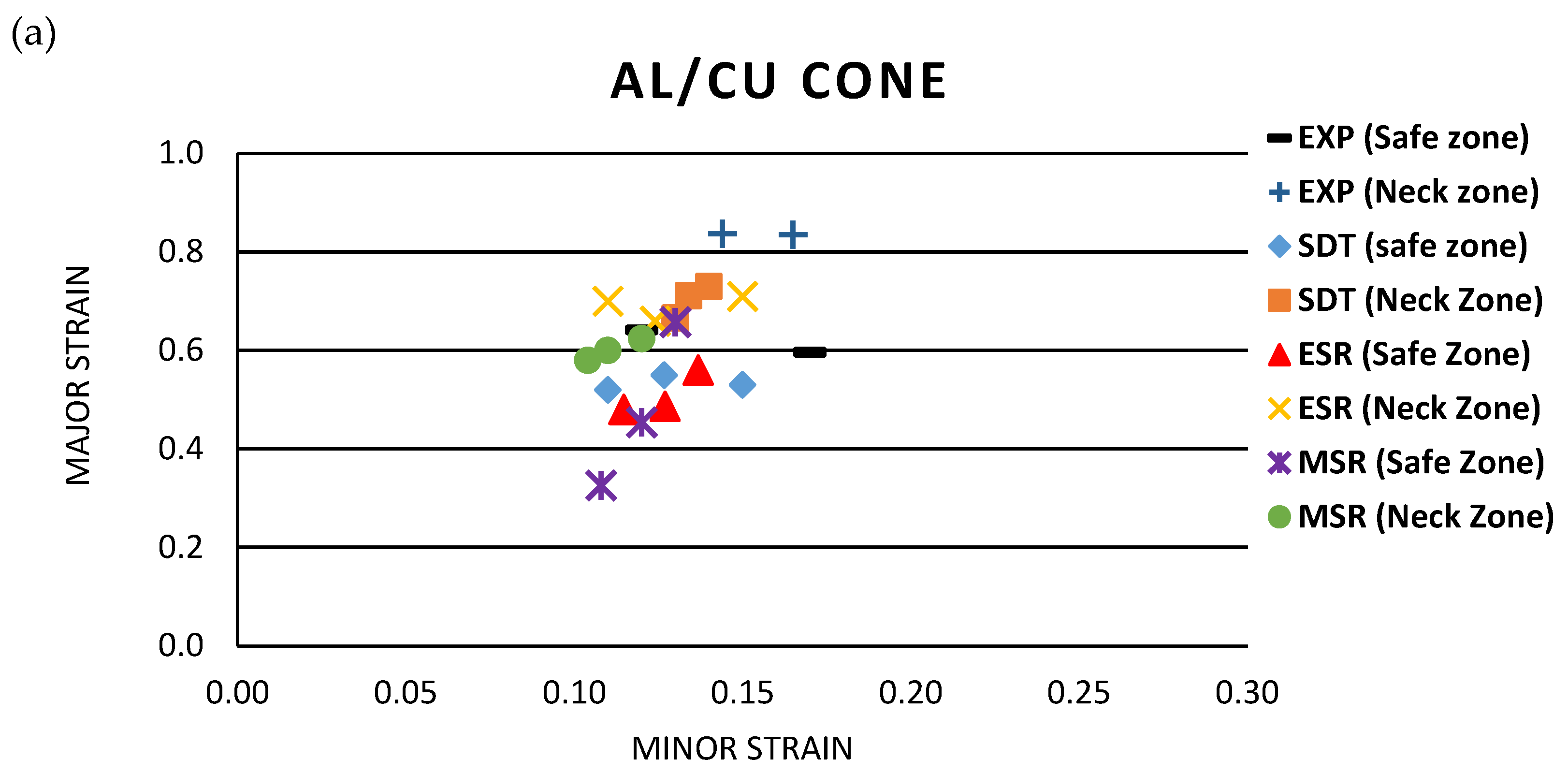
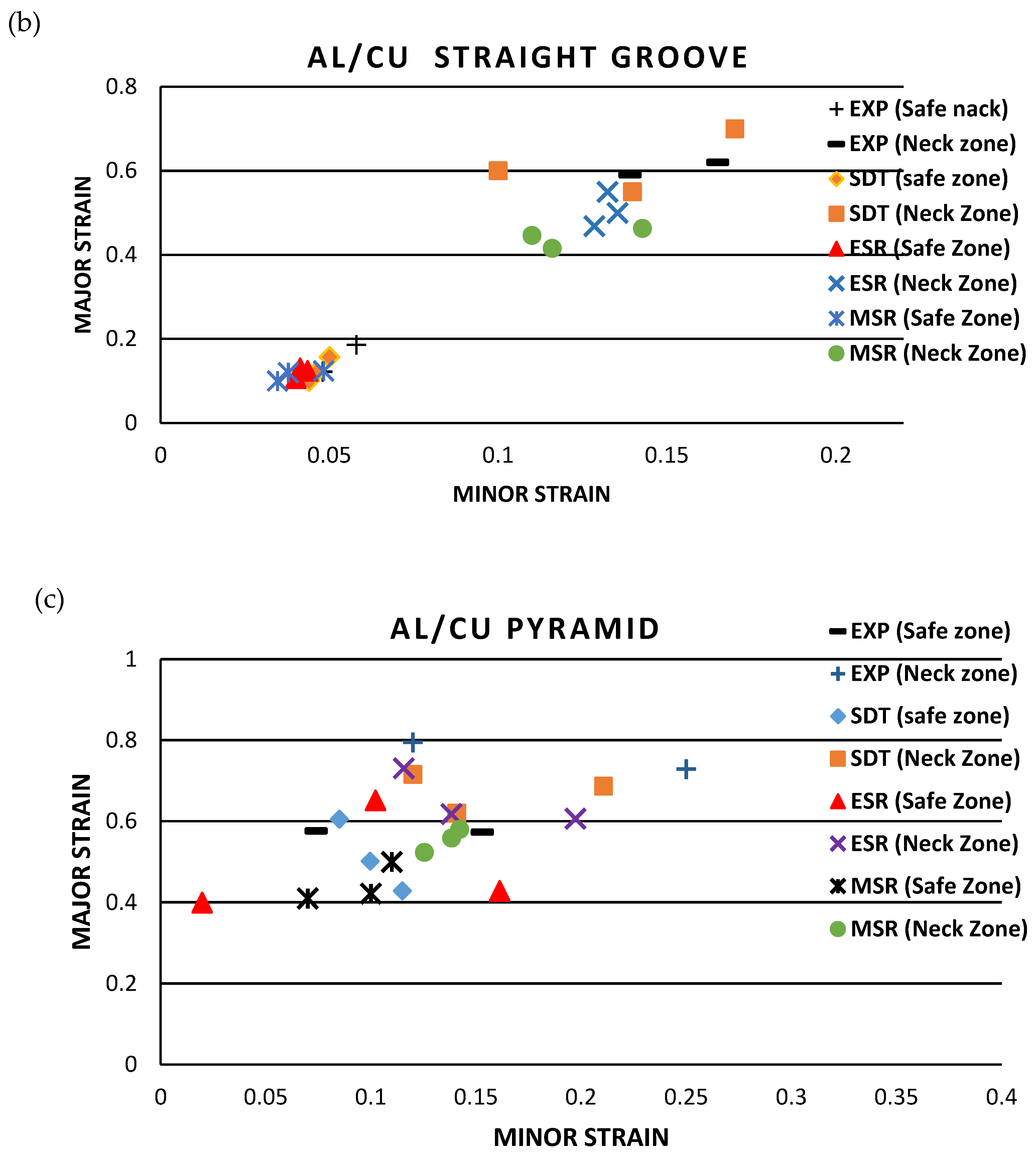
3.5.2. Study of FLD Prediction in FEM
4. Conclusions
- -
- The uniaxial tension results show that the strength of the two-layer sheet after explosive welding and rolling has increased compared to the aluminum base sheet, but it has not increased compared to the copper base sheet.
- -
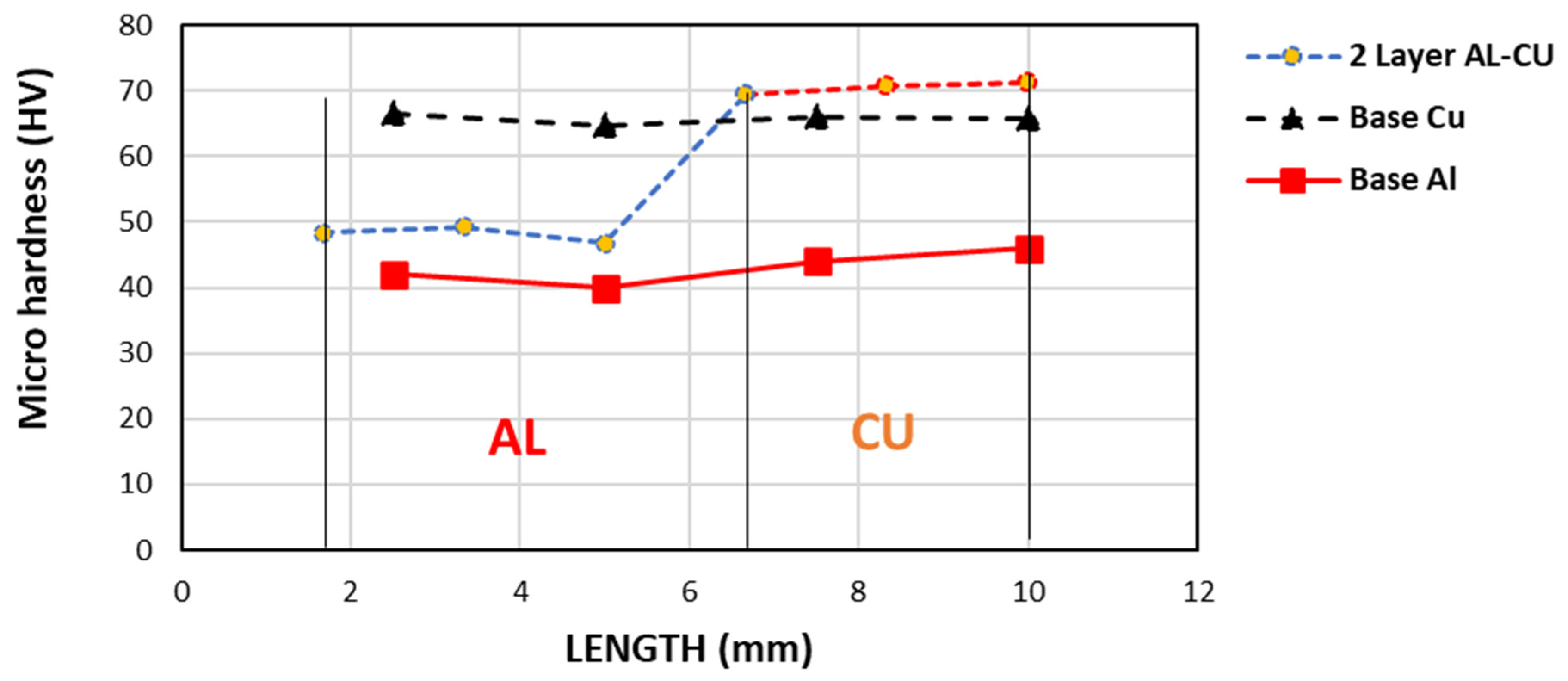
- The results of the hardness test show that the hardness of the two-layer samples has increased compared to the base sheets.
- -
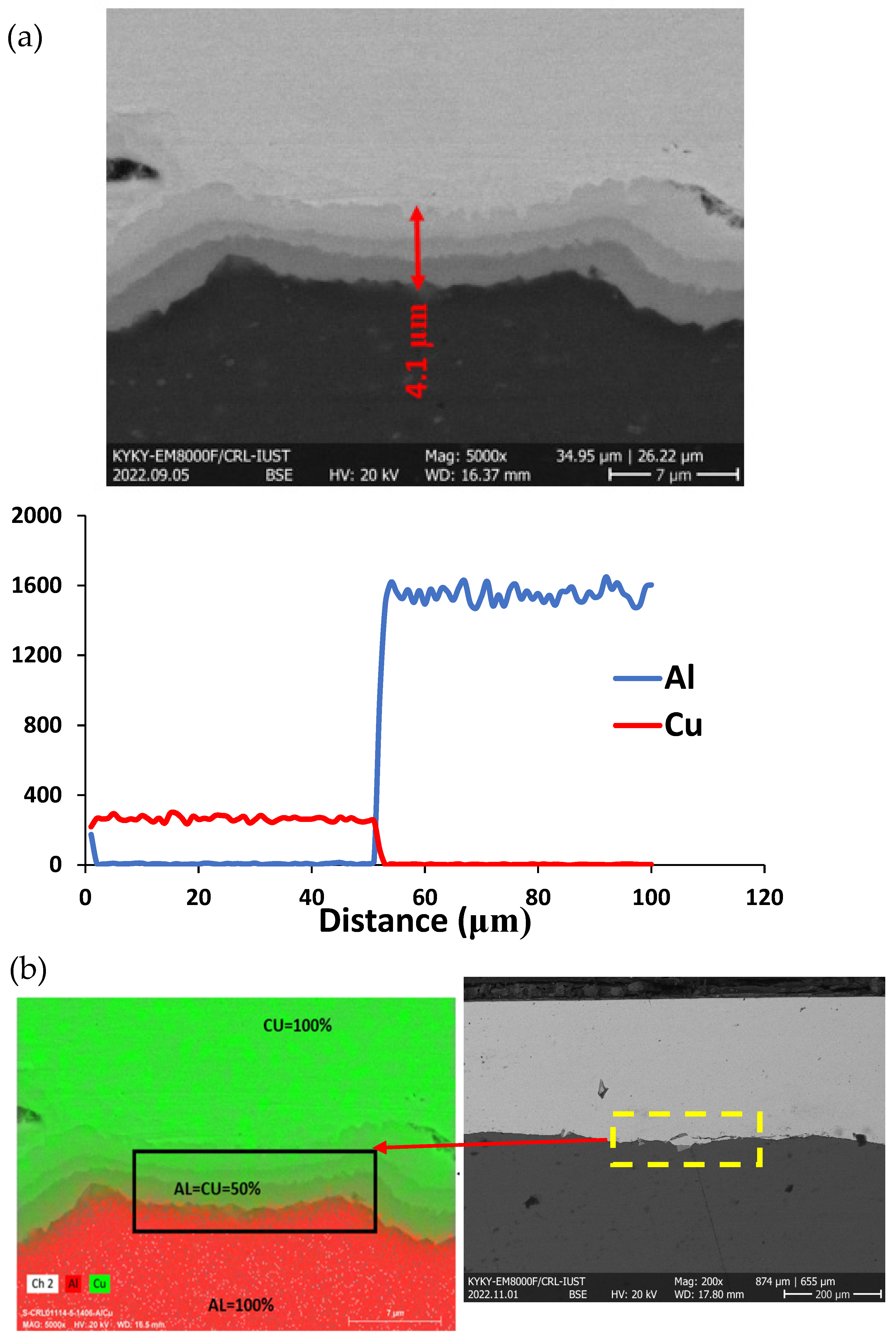
- By examining the SEM ESD-line results in the infiltration area of the two-layer sheet, it can be seen that the infiltration has been performed well, and the combination of Al and Cu in the infiltration area is homogeneous.
- -
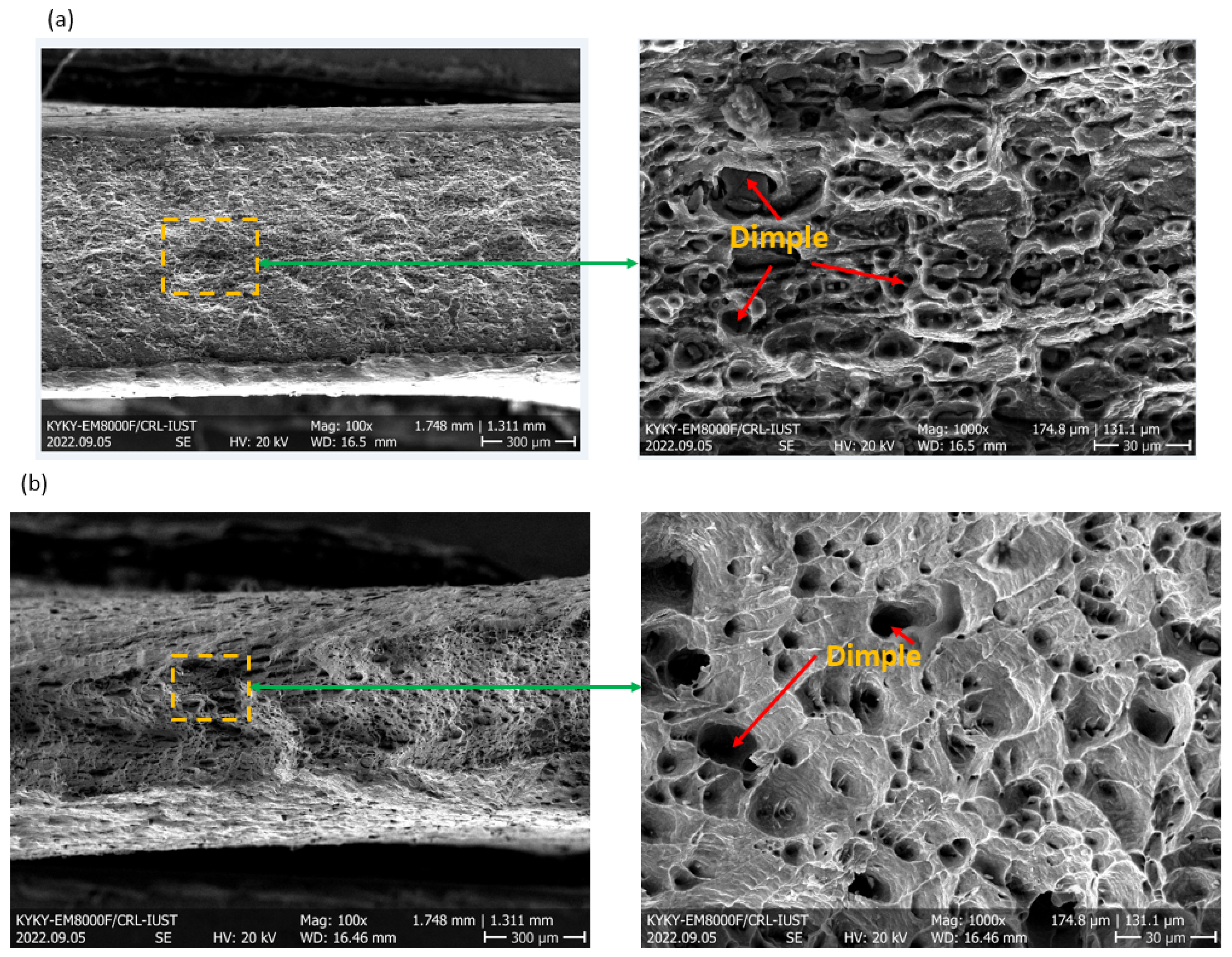
- The tension fracture surface analysis showed that the base samples’ fracture mechanism has changed from the ductile fracture mode to the brittle fracture mode compared to the two-layer sample.
- -
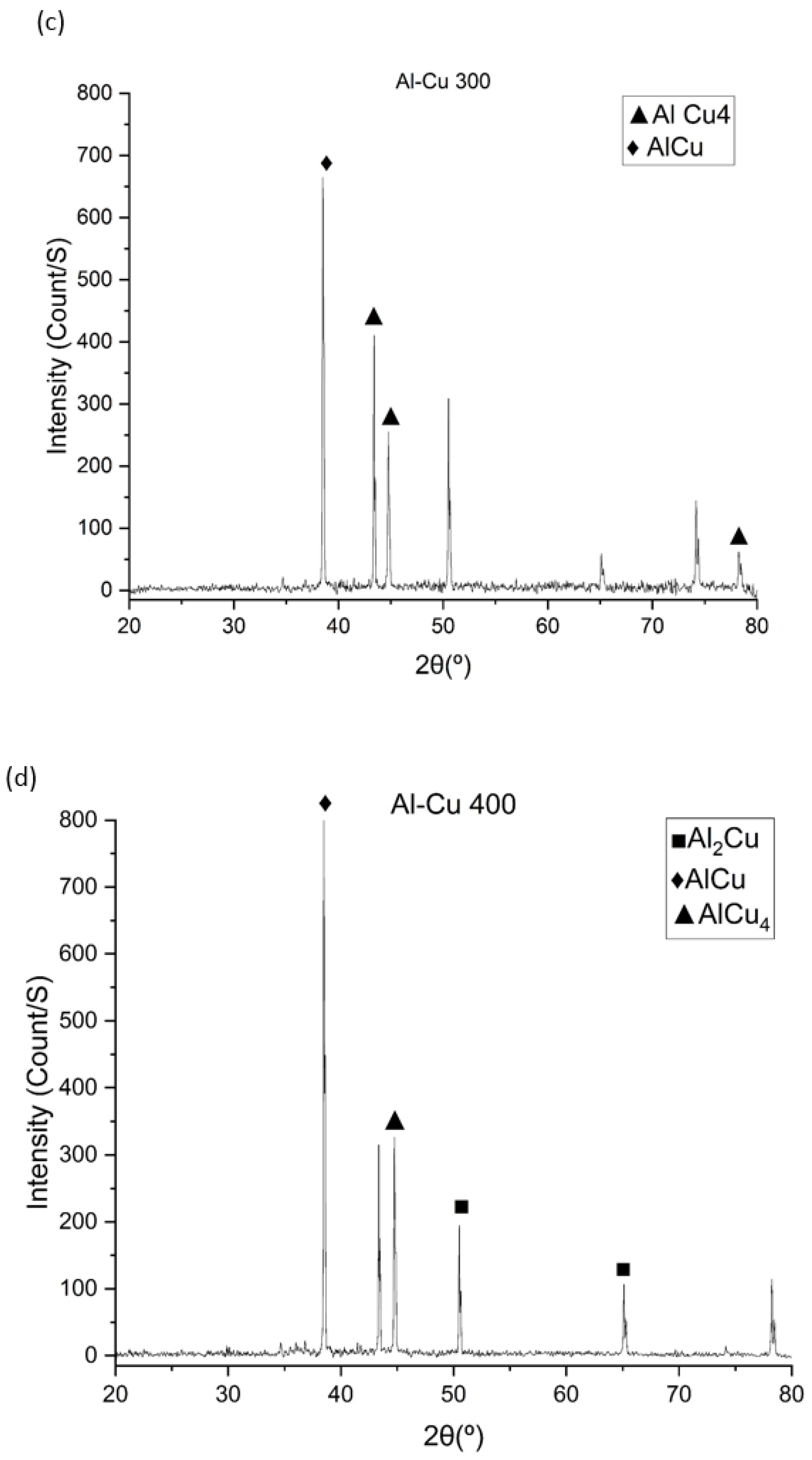
- The intermetallic phases for the two-layer sample are produced with higher density by increasing the annealing temperature. In the penetration zone, it is clear that increasing the temperature causes more intermetallic phases to be produced.
- -
- The experimental results of SPIF showed that the formability of the two-layer samples has increased compared to the base sheet samples. Also, by examining the layer arrangement effect, it was observed that the formability increases when the Cu sample is placed in the outer layer.
- -
- The experimental and numerical results of the thickness distribution for the base and two-layer sheet samples were checked and showed good agreement. The highest error value was reported as 9%.
- -
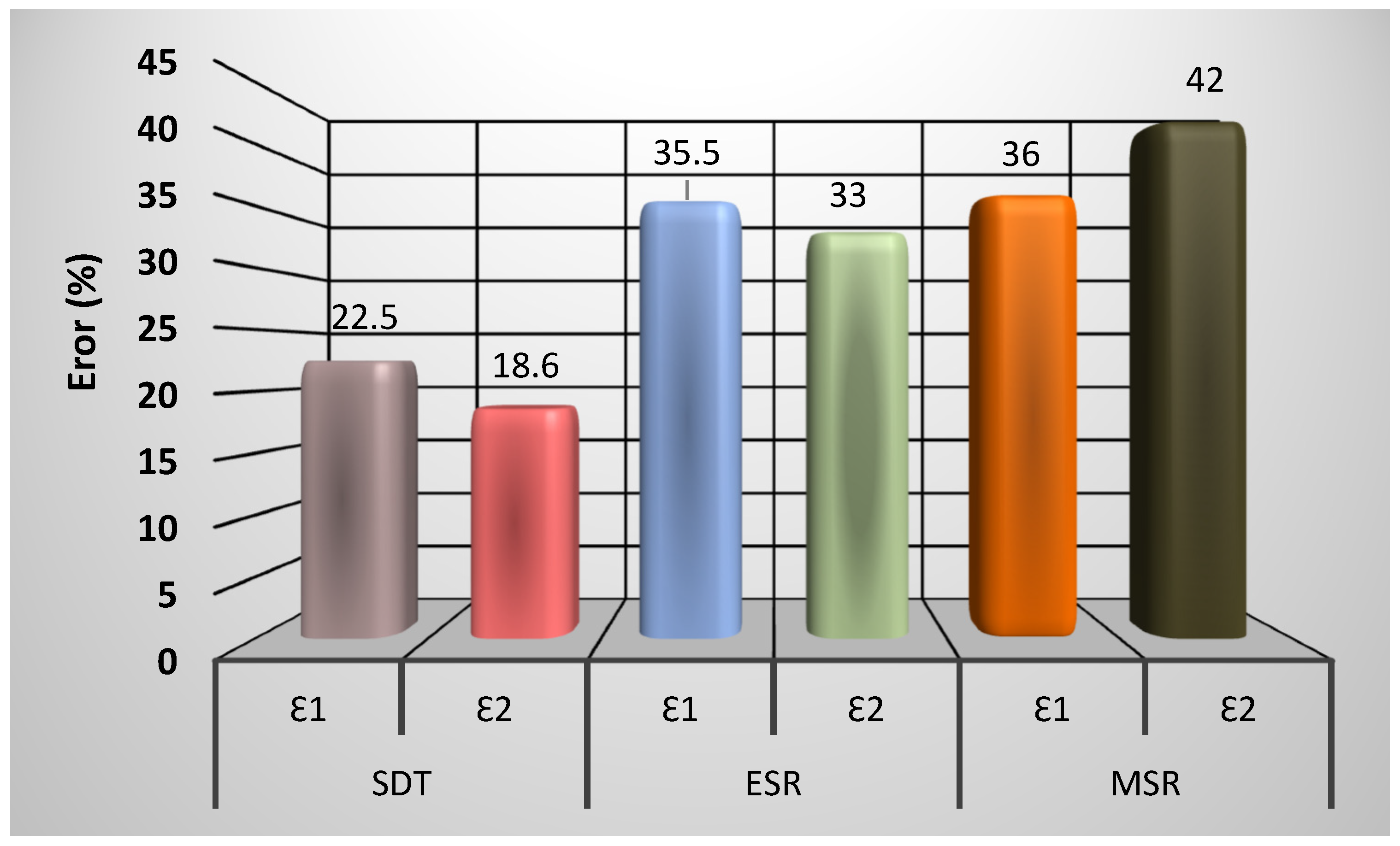
- The FLDcrt method, a numerical–experimental method, provided the most accurate time and necking area prediction compared to the three numerical methods (SDT, ESR, and MSR). However, in the numerical methods, the SDT method reported the most precise prediction of the necking test.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Korouyeh, R.S.; Naeini, H.M.; Liaghat, G. Forming limit diagram prediction of tailor-welded blank using experimental and numerical methods. J. Mater. Eng. Perform. 2012, 21, 2053–2061. [Google Scholar] [CrossRef]
- Filice, L.; Fratini, L.; Micari, F. Analysis of material formability in incremental forming. CIRP Ann.-Manuf. Technol. 2002, 51, 199–202. [Google Scholar] [CrossRef]
- Ramkumar, K.; Baskar, N.; Elangovan, K.; Narayanan, C.S.; Selvarajan, K.A.; Jesuthanam, C.P. Comparison of multi point incremental forming tool with single point incremental forming tool using FLD, Fractography and 3D-surface roughness analysis on Cr/Mn/Ni/Si based stainless steel. Silicon 2021, 13, 487–494. [Google Scholar] [CrossRef]
- Chu, X.; Leotoing, L.; Guines, D.; Ragneau, E. Temperature and strain rate influence on AA5086 Forming Limit Curves: Experimental results and disCussion on the validity of the M-K model. Int. J. Mech. Sci. 2014, 78, 27–34. [Google Scholar] [CrossRef]
- Uppaluri, R.; Venkata Reddy, N.; Dixit, P.M. An analytical approach for the prediction of forming limit Curves subjected to combined strain paths. Int. J. Mech. Sci. 2011, 53, 365–373. [Google Scholar] [CrossRef]
- Dilmec, M.; Halkaci, H.S.; Ozturk, F.; Livatyali, H.; Yigit, O. Effects of sheet thickness and anisotropy on forming limit Curves of AA2024-T4. Int. J. Adv. Manuf. Technol. 2013, 67, 2689–2700. [Google Scholar] [CrossRef]
- Honarpisheh, M.; Keimasi, M.; Alinaghian, I. Numerical and experimental study on incremental forming process of Al/Cu bimetals: Influence of process parameters on the forming force, dimensional accuracy and thickness variations. J. Mech. Mater. Struct. 2018, 13, 35–51. [Google Scholar] [CrossRef]
- Gheysarian, A.; Honarpisheh, M. An experimental study on the process parameters of incremental forming of Al-Cu Bimetal. J. Comput. Appl. Res. Mech. Eng. 2017, 7, 73–83. [Google Scholar] [CrossRef]
- Alaie, A.; Hashemi, R.; Kazemi, F. Investigation of forming limit diagram and mechanical properties of the bimetallic Al/Cu composite sheet at different temperatures which fabricated by explosive welding. Proc. Inst. Mech. Eng. Part. B J. Eng. Manuf. 2021, 235, 73–84. [Google Scholar] [CrossRef]
- Chang, D.; Wang, P.; Zhao, Y. Effects of asymmetry and annealing on interfacial microstructure and mechanical properties of Cu/Al laminated composite fabricated by asymmetrical roll bonding. J. Alloys Compd. 2020, 815, 152453. [Google Scholar] [CrossRef]
- Rezaei, H.; Honarpisheh, M. Experimental and Numerical Investigation of Forming Limit Diagram of CP-Ti/St12 Bimetal in the Incremental Forming Process. Strength Mater. 2022, 54, 681–694. [Google Scholar] [CrossRef]
- Liu, Z.; Li, G. Single point incremental forming of Cu-Al composite sheets: A comprehensive study on deformation behaviors. Arch. Civ. Mech. Eng. 2019, 19, 484–502. [Google Scholar] [CrossRef]
- Dizajyekan, A.Z.; Mirnia, M.J.; Dariani, B. Fracture investigation in single point incremental forming of the Al/Cu laminated sheets using coupled damage plasticity model. CIRP J. Manuf. Sci. Technol. 2023, 43, 242–259. [Google Scholar] [CrossRef]
- Puchlerska, S.; Kuczek, Ł.; Trzepieci, T. Effect of Step Size on the Formability of Al/Cu Bimetallic Sheets in Single Point Incremental Sheet Forming. Materials 2023, 16, 367. [Google Scholar] [CrossRef]
- Jalali, A.; Hashemi, R.; Rajabi, M.; Tayebi, P. Finite element simulations and experimental verifications for forming limit curve determination of two-layer aluminum/brass sheets considering the incremental forming process. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 236, 361–373. [Google Scholar] [CrossRef]
- Pambhar, A.C.; Valaki, J.B. Experimental studies of formability in single point incremental forming of Cu-Al bimetallic sheets. Mater. Today 2023, in press. [CrossRef]
- Standard Test Methods for Tension Testing of Metallic Materials, ASTM Standards, E8/E8M—13a. Published August 2013. Available online: https://www.astm.org/e0008_e0008m-13a.html (accessed on 1 February 2024).
- Tayebi, P.; Fazli, A.; Asadi, P.; Soltanpour, M. Formability analysis of dissimilar friction stir welded AA 6061 and AA 5083 blanks by SPIF process. CIRP J. Manuf. Sci. Technol. 2019, 25, 50–68. [Google Scholar] [CrossRef]
- Darvishi, M.; Morovvati, M.; Aghchai, A.J. Effects of equal channel angular rolling process on the mechanical properties of Al-Cu two-layer sheets: Experimental and numerical approaches. Eng. Res. Express 2023, 5, 035023. [Google Scholar] [CrossRef]
- Zahedi, A.; Dariani, B.M.; Mirnia, M.J. Using a damage plasticity model, experimental determination and numerical prediction of necking and fracture forming limit Curves of laminated Al/Cu sheets. Int. J. Mech. Sci. 2019, 153–154, 341–358. [Google Scholar] [CrossRef]
- Dietrich, D.; Nickel, D.; Krause, M.; Lampke, T.; Coleman, M.P.; Randle, V. Formation of intermetallic phases in diffusion-welded joints of aluminium and magnesium alloys. J. Mater. Sci. 2011, 46, 357–364. [Google Scholar] [CrossRef]
- Dieter, G.E. Mechanical Metallurgy; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Jafarian, M.; Rizi, M.S.; Javadinejad, R.; Ghaheri, A.; Taghi, M. Effect of thermal tempering on microstructure and mechanical properties of Mg-AZ31/Al-6061 diffusion bonding. Mater. Sci. Eng. A 2016, 666, 372–379. [Google Scholar] [CrossRef]
- Cuzacq, L.; Polido, C.; Silvain, J.; Bobet, J. Hydrogen production properties of aluminum–magnesium alloy presenting β-phase Al3Mg2. Metals 2023, 13, 1868. [Google Scholar] [CrossRef]
- Mahendran, G.; Balasubramanian, V.; Senthilvelan, T. Developing diffusion bonding windows for joining AZ31B magnesium-AA2024 aluminium alloys. Mater. Des. 2009, 30, 1240–1244. [Google Scholar] [CrossRef]
- Razin, L.V.; Rudashevskij, N.S.; Vyalsov, L.N. New natural intermetallic compounds of aluminum, copper and zinc—Khatyrkite CuAl2, Cupalite CuAl and zinc aluminides from hyperbasites of dunite-harzburgite formation. Zap. Vsesoyuznogo Mineral. Obs. 1985, 114, 90–100. [Google Scholar]
- Jandaghi, M.R.; Saboori, A.; Khalaj, G.; Shiran, M.K.G. Microstructural evolutions and its impact on the corrosion behaviour of explosively welded Al/Cu bimetal. Metals 2020, 10, 634. [Google Scholar] [CrossRef]
- Denmeade, J. Investigation of Novel Precursor Routes for Incorporation of Oxynitride Spinel Phases into Ceramic-Metallic Composites Formed via the TCON Process. Ph.D. Thesis. 2013. Available online: https://digital.maag.ysu.edu/xmlui/handle/1989/11363 (accessed on 1 February 2024).
- Pineau, A.; Benzerga, A.A.; Pardoen, T. Failure of metals III: Fracture and fatigue of nanostructured metallic materials. Acta Mater. 2016, 107, 508. [Google Scholar] [CrossRef]
- Pandivelan, C.; Jeevanantham, A.K. Formability evaluation of AA 6061 alloy sheets on single point incremental forming using CNC vertical milling machine. J. Mater. Environ. Sci. 2015, 6, 1343–1353. [Google Scholar]
- Darabi, R.; Azodi, H.D.; Bagherzadeh, S. Investigation into the effect of material properties and arrangement of each layer on the formability of bimetallic sheets. J. Manuf. Process 2017, 29, 133–148. [Google Scholar] [CrossRef]
- Darban, H.; Mohammadi, B.; Djavanroodi, F. Effect of equal channel angular pressing on fracture toughness of Al-7075. Eng. Fail. Anal. 2016, 65, 1–10. [Google Scholar] [CrossRef]
- Pepelnjak, T.; Petek, A.; Kuzman, K. Analyses of the Forming Limit Diagram in Digital Environment. Adv. Mater. Res. 2005, 6–8, 697–704. [Google Scholar] [CrossRef]
- Narasimhan, K.; Wagoner, R.H. Finite Element Modeling Simulation of In-Plane Forming Limit Diagrams of Sheets Containing Finite Defects. Metall. Trans. A 1991, 22, 2655–2665. [Google Scholar] [CrossRef]
- Tayebi, P.; Hashemi, R. Study of single point incremental forming limits of Al 1050/Mg-AZ31B two-layer sheets fabricated by roll bonding technique: Finite element simulation and experiment. J. Mater. Res. Technol. 2024, 24, 149–169. [Google Scholar] [CrossRef]
- Seong, D.Y.; Haque, M.; Kim, J.; Stoughton, T.; Yoon, J. Suppression of necking in incremental sheet forming. Int. J. Solids Struct. 2014, 51, 2840–2849. [Google Scholar] [CrossRef]
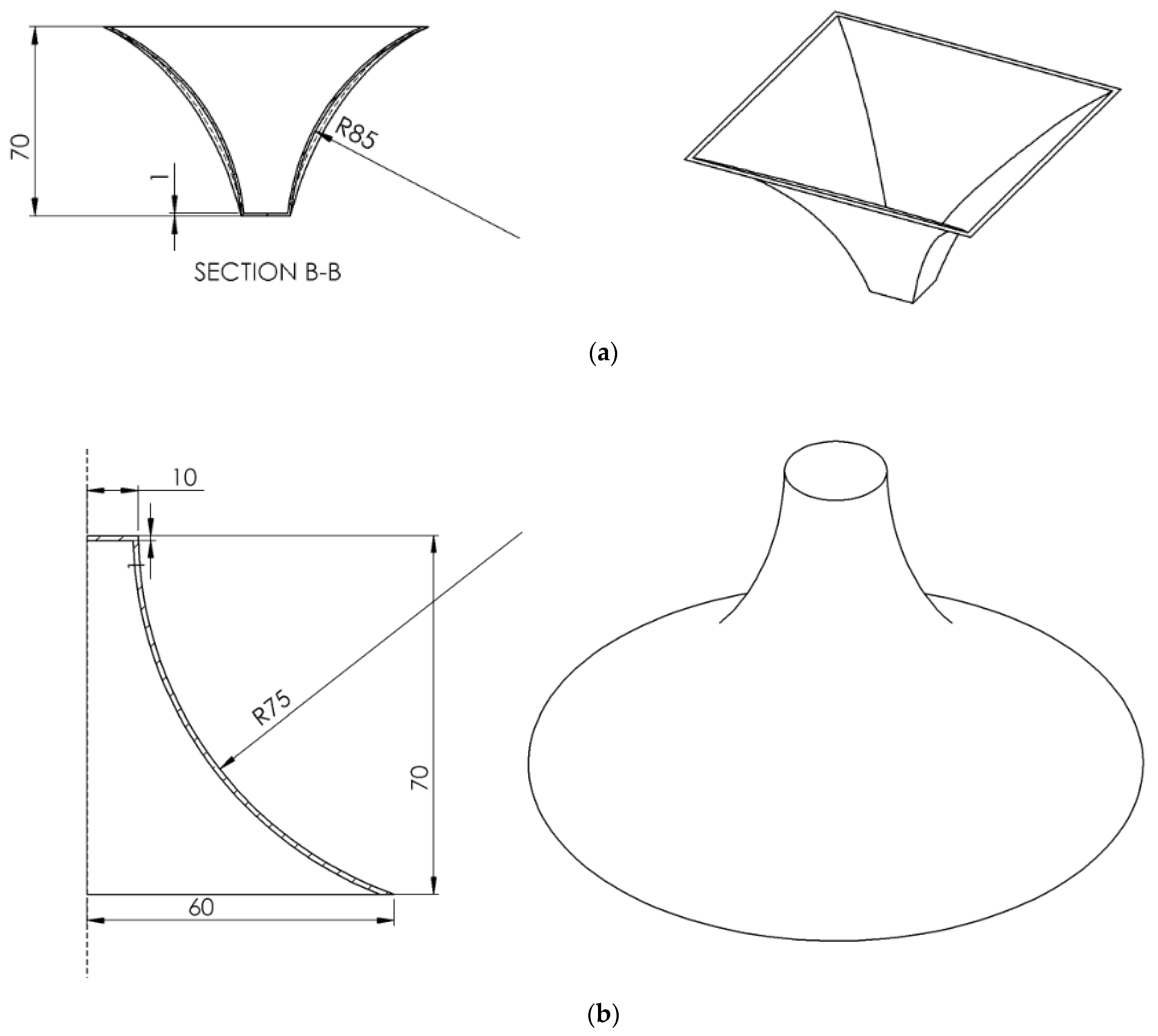
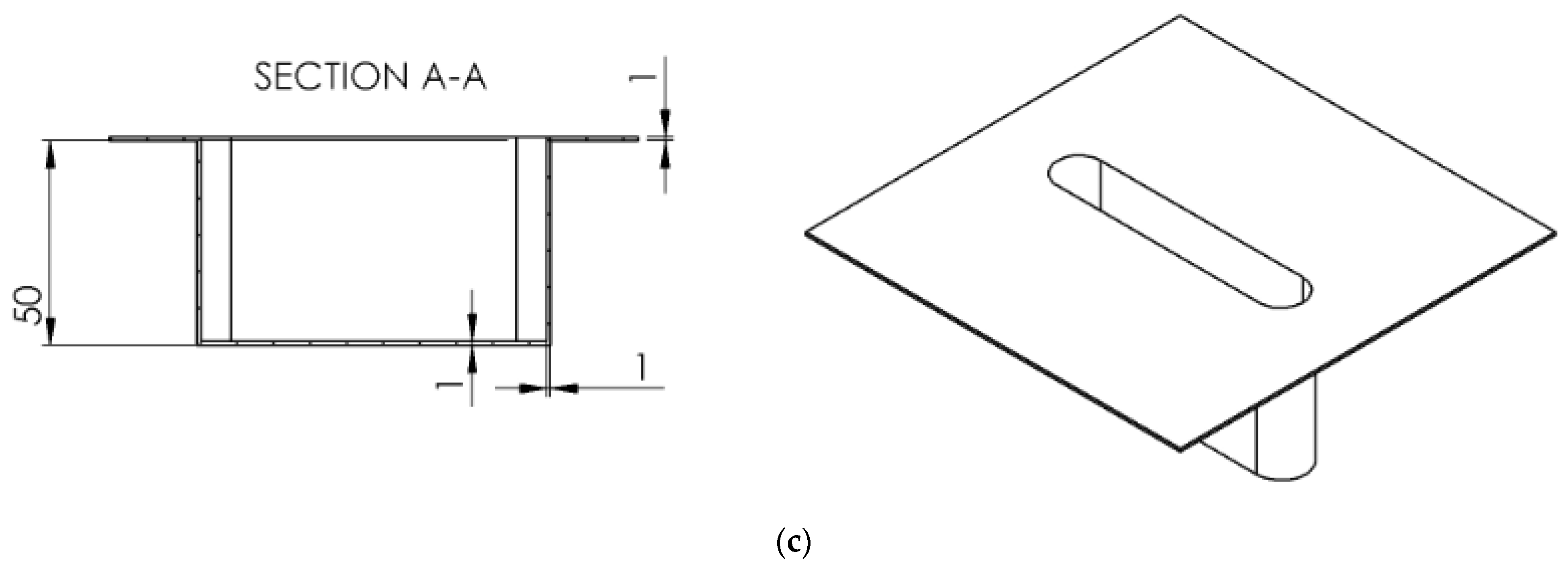


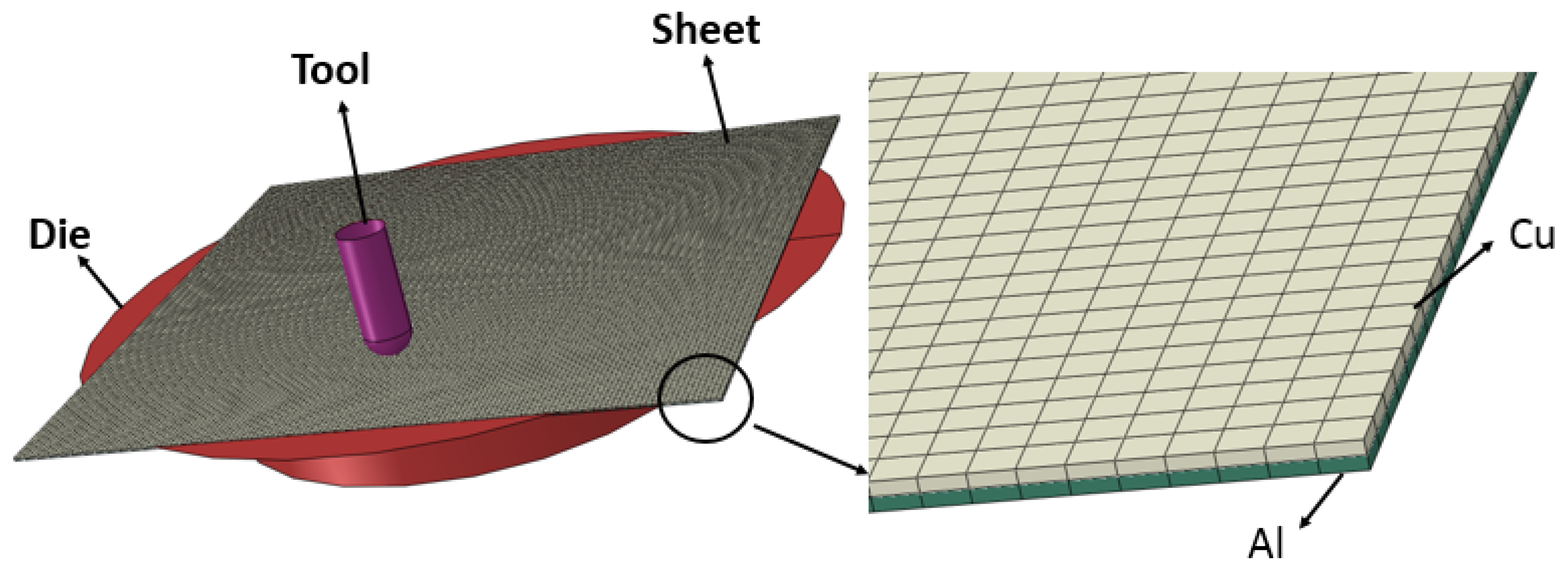







| Sample | Forming Depth (mm) | Forming Limit Angle (Degree) |
|---|---|---|
| Base Al | 17.38 | 44.5 |
| Base Cu | 35 | 59.6 |
| Pyramid Al/Cu | 37.4 | 61.5 |
| Cone Al/Cu | 47.5 | 68.8 |
| Straight groove | 13.77 | 90 |
| Pyramid Cu/Al | 28 | 53.9 |
| Sample | Forming Depth (mm) | Forming Limit Angle (Degree) |
|---|---|---|
| Base Al | 17.38 | 44.5 |
| Base Cu | 35 | 59.6 |
| Pyramid Al/Cu | 37.4 | 61.5 |
| Cone Al/Cu | 47.5 | 68.8 |
| Straight groove | 13.77 | 90 |
| Pyramid Cu/Al | 28 | 53.9 |
| Sample | Major Strain (EXP) | Major Strain (SIM) | Error % (Major Strain) | Minor Strain (EXP) | Minor Strain (SIM) | Error % (Minor Strain) |
|---|---|---|---|---|---|---|
| Al base-ESR | 0.2875 | 0.212 | 35.5% | 0.023 | 0.030 | 33% |
| Al base-MSR | 0.21 | 36% | 0.016 | 42% | ||
| Al base-SDT | 0.263 | 9.5% | 0.027 | 18.6% | ||
| Cu base-ESR | 0.620 | 0.567 | 9.5% | 0.050 | 0.038 | 31.5% |
| Cu base-MSR | 0.497 | 24% | 0.035 | 27% | ||
| Cu base-SDT | 0.579 | 7.2% | 0.057 | 13.5% |
| Sample | Major Strain (EXP) | Major Strain (SIM) | Error % (Major Strain) | Minor Strain (EXP) | Minor Strain (SIM) | Error % (Minor Strain) |
|---|---|---|---|---|---|---|
| Al/Cu-ESR (Cone) | 0.619 | 0.509 | 21.5% | 0.145 | 0.126 | 14.9% |
| Al/Cu-MSR (Cone) | 0.479 | 29% | 0.119 | 21.5% | ||
| Al/Cu-SDT (Cone) | 0.533 | 16% | 0.129 | 12.5% | ||
| Al/Cu-ESR (pyramid) | 0.575 | 0.493 | 16.5% | 0.115 | 0.094 | 20% |
| Al/Cu-MSR (pyramid) | 0.444 | 29.7% | 0.093 | 21.8% | ||
| Al/Cu-SDT (pyramid) | 0.512 | 12.7% | 0.100 | 13.6% | ||
| Al/Cu-ESR (straight groove) | 0.154 | 0.12 | 27.5% | 0.053 | 0.0416 | 27% |
| Al/Cu-MSR (straight groove) | 0.115 | 34.5% | 0.040 | 31.7% | ||
| Al/Cu-SDT (straight groove) | 0.125 | 22.5% | 0.0466 | 13.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tayebi, P.; Nasirin, A.R.; Akbari, H.; Hashemi, R. Experimental and Numerical Investigation of Forming Limit Diagrams during Single Point Incremental Forming for Al/Cu Bimetallic Sheets. Metals 2024, 14, 214. https://doi.org/10.3390/met14020214
Tayebi P, Nasirin AR, Akbari H, Hashemi R. Experimental and Numerical Investigation of Forming Limit Diagrams during Single Point Incremental Forming for Al/Cu Bimetallic Sheets. Metals. 2024; 14(2):214. https://doi.org/10.3390/met14020214
Chicago/Turabian StyleTayebi, Payam, Amir Reza Nasirin, Habibolah Akbari, and Ramin Hashemi. 2024. "Experimental and Numerical Investigation of Forming Limit Diagrams during Single Point Incremental Forming for Al/Cu Bimetallic Sheets" Metals 14, no. 2: 214. https://doi.org/10.3390/met14020214
APA StyleTayebi, P., Nasirin, A. R., Akbari, H., & Hashemi, R. (2024). Experimental and Numerical Investigation of Forming Limit Diagrams during Single Point Incremental Forming for Al/Cu Bimetallic Sheets. Metals, 14(2), 214. https://doi.org/10.3390/met14020214







