Effects of Chemical Short-Range Order and Lattice Distortion on Crack-Tip Behavior of Medium-Entropy Alloy by Atomistic Simulations
Abstract
:1. Introduction
2. Methodology
2.1. MD Simulations
2.2. Free-End Nudged Elastic Band Estimation
2.3. Crack-Tip Field Theory
2.3.1. J-Integral
2.3.2. Localized Deformation Zone
3. Results and Discussion
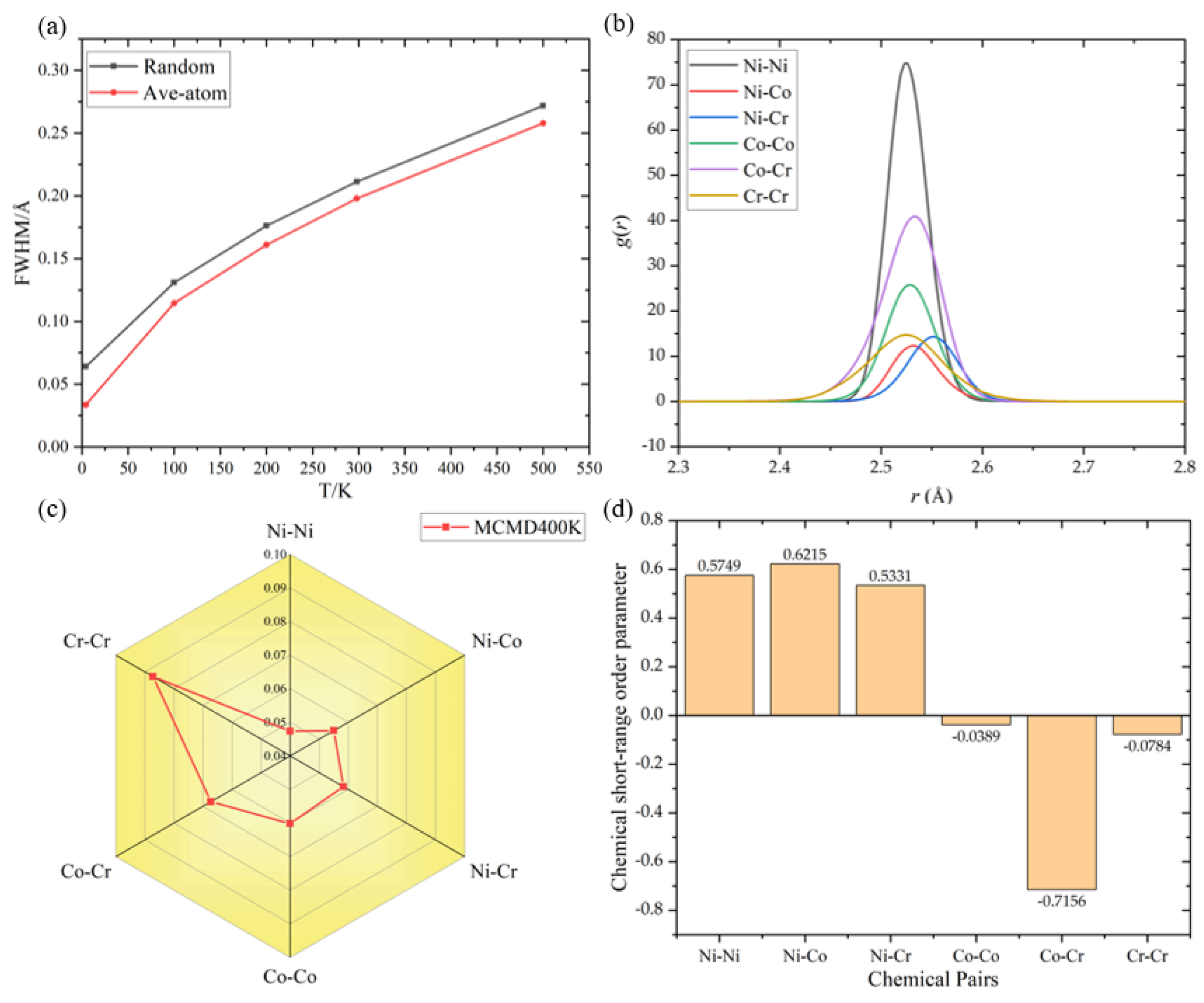
3.1. Degree of Lattice Distortion and Chemical Short Range Order
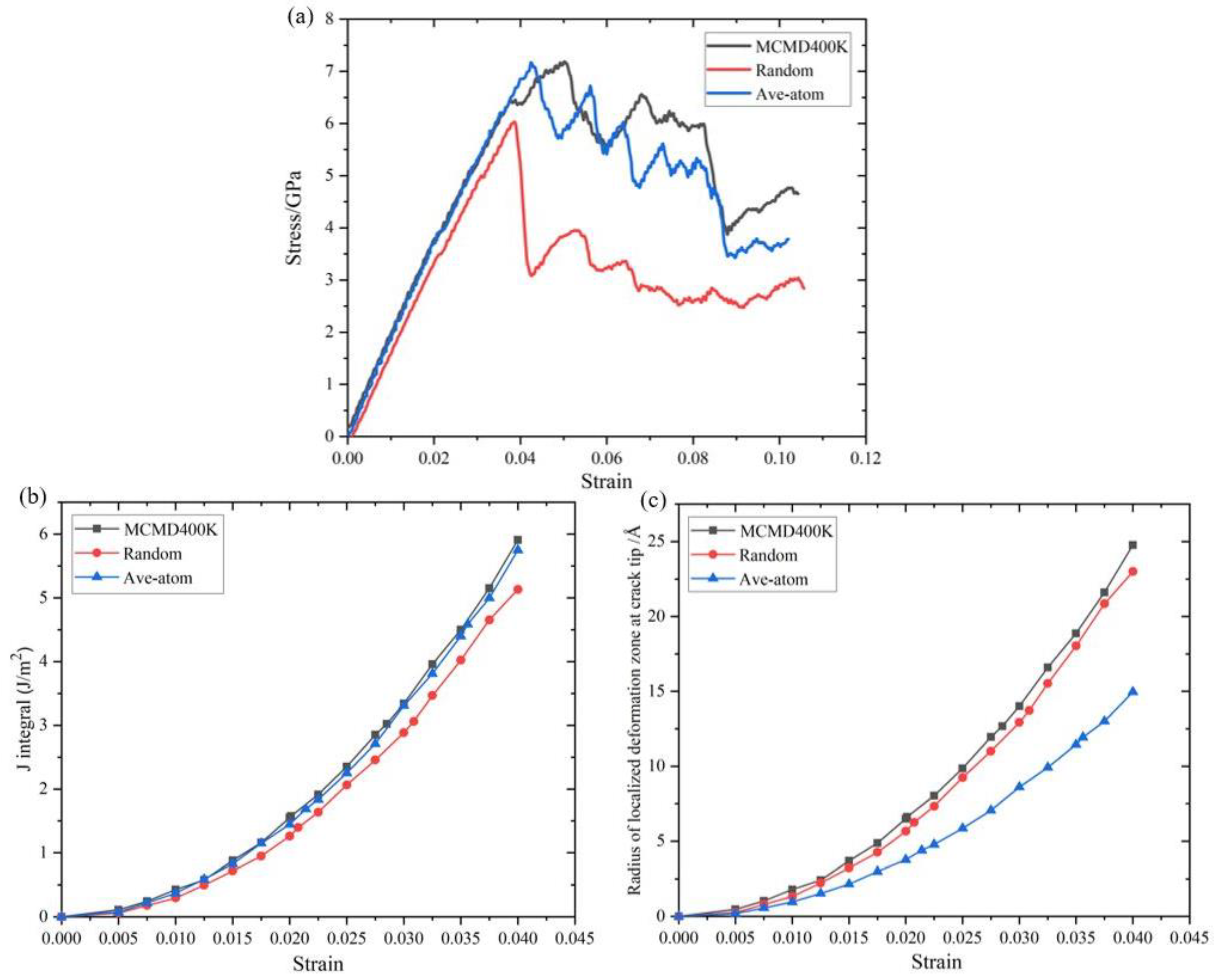
3.2. Results of the J-Integral and Localized Deformation Zone Size
3.3. Deformation Behavior and Mechanism of the Crack-Tip Field
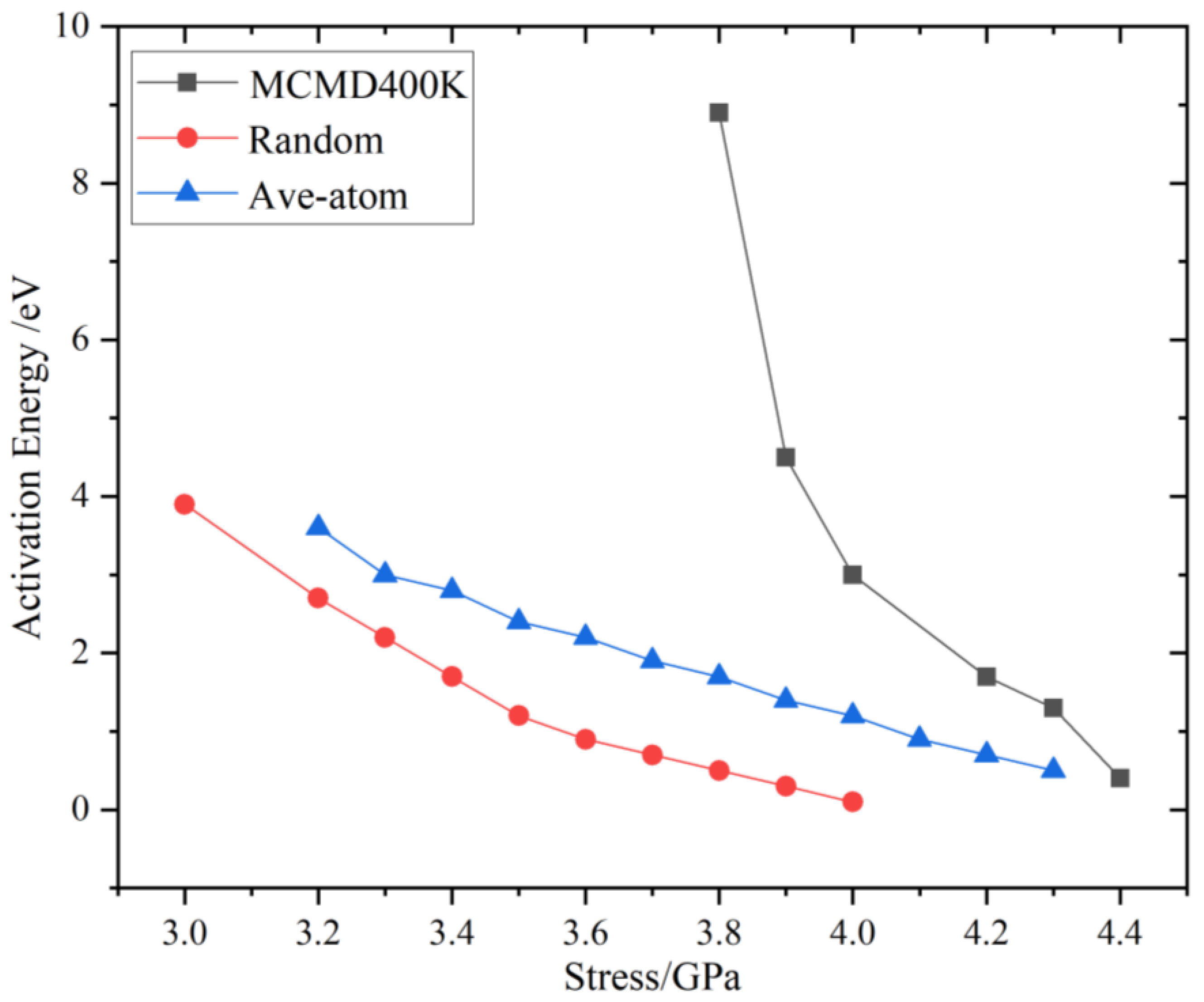
3.4. Stress-Dependent MEP of Dislocation Nucleation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- George, E.P.; Raabe, D.; Ritchie, R.O. High-entropy alloys. Nat. Rev. Mater. 2019, 4, 515–534. [Google Scholar] [CrossRef]
- Yeh, J.W. Recent progress in high-entropy alloys. Ann. Chim.-Sci. Mater. 2006, 31, 633–648. [Google Scholar] [CrossRef]
- Li, W.; Xie, D.; Li, D.; Zhang, Y.; Gao, Y.; Liaw, P.K. Mechanical behavior of high-entropy alloys. Prog. Mater. Sci. 2021, 118, 100777. [Google Scholar] [CrossRef]
- Yang, X.G.; He, L.; Li, E.R.; Yang, C.L. Microstructure and Properties of Non-Equiatomic Ni10Cr6WFe9TiAlx High-Entropy Alloys Combined with High Strength and Toughness. Metals 2023, 13, 1179. [Google Scholar] [CrossRef]
- Yi, H.L.; Bi, M.Y.; Yang, K.; Zhang, B. Significant Improvement the Mechanical Properties of CoCrNi Alloy by Tailoring a Dual FCC-Phase Structure. Materials 2020, 13, 4909. [Google Scholar] [CrossRef] [PubMed]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef] [PubMed]
- Gludovatz, B.; Hohenwarter, A.; Thurston, K.V.S.; Bei, H.B.; Wu, Z.G.; George, E.P.; Ritchie, R.O. Exceptional damage-tolerance of a medium-entropy alloy CrCoNi at cryogenic temperatures. Nat. Commun. 2016, 7, 10602. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Shi, X.H.; Zhang, M.; Qiao, J.W. Development of Refractory High Entropy Alloys with Tensile Ductility at Room Temperature. Metals 2023, 13, 329. [Google Scholar] [CrossRef]
- Qiu, X.W.; Zhang, Y.P.; He, L.; Liu, C.G. Microstructure and corrosion resistance of AlCrFeCuCo high entropy alloy. J. Alloys Compd. 2013, 549, 195–199. [Google Scholar] [CrossRef]
- Li, T.R.; Wang, D.B.; Zhang, S.D.; Wang, J.Q. Corrosion Behavior of High Entropy Alloys and Their Application in the Nuclear Industry-An Overview. Metals 2023, 13, 363. [Google Scholar] [CrossRef]
- Luo, H.; Sohn, S.S.; Lu, W.J.; Li, L.L.; Li, X.G.; Soundararajan, C.K.; Krieger, W.; Li, Z.M.; Raabe, D. A strong and ductile medium-entropy alloy resists hydrogen embrittlement and corrosion. Nat. Commun. 2020, 11, 3081. [Google Scholar] [CrossRef]
- Lu, K.; Zhu, J.; Guo, D.; Yang, M.; Sun, H.; Wang, Z.; Hui, X.; Wu, Y. Microstructures, Corrosion Resistance and Wear Resistance of High-Entropy Alloys Coatings with Various Compositions Prepared by Laser Cladding: A Review. Coatings 2022, 12, 1023. [Google Scholar] [CrossRef]
- Kołodziejczak, P.; Bober, M.; Chmielewski, T. Wear Resistance Comparison Research of High-Alloy Protective Coatings for Power Industry Prepared by Means of CMT Cladding. Appl. Sci. 2022, 12, 4568. [Google Scholar] [CrossRef]
- Liu, X.F.; Tian, Z.L.; Zhang, X.F.; Chen, H.H.; Liu, T.W.; Chen, Y.; Wang, Y.J.; Dai, L.H. “Self-sharpening” tungsten high-entropy alloy. Acta Mater. 2020, 186, 257–266. [Google Scholar] [CrossRef]
- Wu, Z.; Bei, H.; Pharr, G.M.; George, E.P. Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 2014, 81, 428–441. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Yang, T.; Tong, Y.; Wang, J.; Luan, J.H.; Jiao, Z.B.; Chen, D.; Yang, Y.; Hu, A.; Liu, C.T.; et al. Heterogeneous precipitation behavior and stacking-fault-mediated deformation in a CoCrNi-based medium-entropy alloy. Acta Mater. 2017, 138, 72–82. [Google Scholar] [CrossRef]
- Li, X.T.; Sheinerman, A.G.; Yang, H.; Zhu, Z.Y. Theoretical modeling of toughening mechanisms in the CrMnFeCoNi high-entropy alloy at room temperature. Int. J. Plast. 2022, 154, 103304. [Google Scholar] [CrossRef]
- Li, J.; Chen, H.T.; He, Q.F.; Fang, Q.H.; Liu, B.; Jiang, C.; Liu, Y.; Yang, Y.; Liaw, P.K. Unveiling the atomic-scale origins of high damage tolerance of single-crystal high entropy alloys. Phys. Rev. Mater. 2020, 4, 103612. [Google Scholar] [CrossRef]
- Singh, S.K.; Parashar, A. Atomistic simulations to study crack tip behaviour in multi-elemental alloys. Eng. Fract. Mech. 2021, 243, 107536. [Google Scholar] [CrossRef]
- Kim, S.W.; Kim, J.H. In-situ observations of deformation twins and crack propagation in a CoCrFeNiMn high-entropy alloy. Mater. Sci. Eng. A 2018, 718, 321–325. [Google Scholar] [CrossRef]
- Li, X.T.; Jiang, X.Y. Theoretical analyses of nanocrack nucleation near the main crack tip in nano and micro crystalline materials. Eng. Fract. Mech. 2019, 221, 106672. [Google Scholar] [CrossRef]
- Clement, N.; Caillard, D.; Martin, J.L. Heterogeneous deformation of concentrated Ni-Cr FCC alloys—Macroscopic and microscopic behavior. Acta Mater. 1984, 32, 961–975. [Google Scholar] [CrossRef]
- Dubiel, S.M.; Cieslak, J. Short-range order in iron-rich Fe-Cr alloys as revealed by Mossbauer spectroscopy. Phys. Rev. B 2011, 83, 180202. [Google Scholar] [CrossRef]
- Owen, L.R.; Playford, H.Y.; Stone, H.J.; Tucker, M.G. Analysis of short-range order in Cu3Au using X-ray pair distribution functions. Acta Mater. 2017, 125, 15–26. [Google Scholar] [CrossRef]
- Schonfeld, B. Local atomic arrangements in binary alloys. Prog. Mater. Sci. 1999, 44, 435–543. [Google Scholar] [CrossRef]
- Santodonato, L.J.; Zhang, Y.; Feygenson, M.; Parish, C.M.; Gao, M.C.; Weber, R.J.K.; Neuefeind, J.C.; Tang, Z.; Liaw, P.K. Deviation from high-entropy configurations in the atomic distributions of a multi-principal-element alloy. Nat. Commun. 2015, 6, 5964. [Google Scholar] [CrossRef]
- Singh, P.; Smirnov, A.V.; Johnson, D.D. Atomic short-range order and incipient long-range order in high-entropy alloys. Phys. Rev. B 2015, 91, 224204. [Google Scholar] [CrossRef]
- Tamm, A.; Aabloo, A.; Klintenberg, M.; Stocks, M.; Caro, A. Atomic-scale properties of Ni-based FCC ternary, and quaternary alloys. Acta Mater. 2015, 99, 307–312. [Google Scholar] [CrossRef]
- Chen, X.F.; Wang, Q.; Cheng, Z.Y.; Zhu, M.L.; Zhou, H.; Jiang, P.; Zhou, L.L.; Xue, Q.Q.; Yuan, F.P.; Zhu, J.; et al. Direct observation of chemical short-range order in a medium-entropy alloy. Nature 2021, 592, 712–716. [Google Scholar] [CrossRef]
- Zhou, L.L.; Wang, Q.; Wang, J.; Chen, X.F.; Jiang, P.; Zhou, H.; Yuan, F.P.; Wu, X.L.; Cheng, Z.Y.; Ma, E. Atomic-scale evidence of chemical short-range order in CrCoNi medium-entropy alloy. Acta Mater. 2022, 224, 117490. [Google Scholar] [CrossRef]
- Ding, J.; Yu, Q.; Asta, M.; Ritchie, R.O. Tunable stacking fault energies by tailoring local chemical order in CrCoNi medium-entropy alloys. Proc. Natl. Acad. Sci. USA 2018, 115, 8919–8924. [Google Scholar] [CrossRef]
- Li, Q.J.; Sheng, H.; Ma, E. Strengthening in multi-principal element alloys with local-chemical-order roughened dislocation pathways. Nat. Commun. 2019, 10, 3563. [Google Scholar] [CrossRef]
- Han, D.; Wang, Z.Y.; Yan, Y.; Shi, F.; Li, X.W. A good strength-ductility match in Cu-Mn alloys with high stacking fault energies: Determinant effect of short range ordering. Scr. Mater. 2017, 133, 59–64. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Han, D.; Li, X.W. A unique two-stage strength-ductility match in low solid-solution hardening Ni-Cr alloys: Decisive role of short range ordering. Scr. Mater. 2020, 178, 269–273. [Google Scholar] [CrossRef]
- Zhang, R.P.; Zhao, S.T.; Ding, J.; Chong, Y.; Jia, T.; Ophus, C.; Asta, M.; Ritchie, R.O.; Minor, A.M. Short-range order and its impact on the CrCoNi medium-entropy alloy. Nature 2020, 581, 283–287. [Google Scholar] [CrossRef]
- Ghosh, S.; Sotskov, V.; Shapeev, A.V.; Neugebauer, J.; Körmann, F. Short-range order and phase stability of CrCoNi explored with machine learning potentials. Phys. Rev. Mater. 2022, 6, 113804. [Google Scholar] [CrossRef]
- Lee, C.; Song, G.; Gao, M.C.; Feng, R.; Chen, P.Y.; Brechtl, J.; Chen, Y.; An, K.; Guo, W.; Poplawsky, J.D.; et al. Lattice distortion in a strong and ductile refractory high-entropy alloy. Acta Mater. 2018, 160, 158–172. [Google Scholar] [CrossRef]
- Jian, W.R.; Xie, Z.C.; Xu, S.Z.; Su, Y.Q.; Yao, X.H.; Beyerlein, I.J. Effects of lattice distortion and chemical short-range order on the mechanisms of deformation in medium entropy alloy CoCrNi. Acta Mater. 2020, 199, 352–369. [Google Scholar] [CrossRef]
- Utt, D.; Stukowski, A.; Albe, K. Grain boundary structure and mobility in high-entropy alloys: A comparative molecular dynamics study on a Sigma 11 symmetrical tilt grain boundary in face-centered cubic CuNiCoFe. Acta Mater. 2020, 186, 11–19. [Google Scholar] [CrossRef]
- Peng, W.; Yuan, W.; Jiabin, L.; Hongtao, W. Impacts of atomic scale lattice distortion on dislocation activity in high-entropy alloys. Extrem. Mech. Lett. 2017, 17, 38–42. [Google Scholar]
- Bahramyan, M.; Mousavian, R.T.; Brabazon, D. Determination of atomic-scale structure and compressive behavior of solidified AlxCrCoFeCuNi high entropy alloys. Int. J. Mech. Sci. 2020, 171, 105389. [Google Scholar] [CrossRef]
- Bahramyan, M.; Mousavian, R.T.; Brabazon, D. Study of the plastic deformation mechanism of TRIP-TWIP high entropy alloys at the atomic level. Int. J. Plast. 2020, 127, 102649. [Google Scholar] [CrossRef]
- Afkham, Y.; Bahramyan, M.; Mousavian, R.T.; Brabazon, D. Tensile properties of AlCrCoFeCuNi glassy alloys: A molecular dynamics simulation study. Mater. Sci. Eng. A 2017, 698, 143–151. [Google Scholar] [CrossRef]
- Zhou, L.; Guo, Y.F. Dislocation-Governed Plastic Deformation and Fracture Toughness of Nanotwinned Magnesium. Materials 2015, 8, 5250–5264. [Google Scholar] [CrossRef]
- Cao, F.H.; Chen, Y.; Wang, H.Y.; Dai, L.H. Chemical inhomogeneity inhibits grain boundary fracture: A comparative study in CrCoNi medium entropy alloy. J. Mater. Sci. Technol. 2023, 153, 228–241. [Google Scholar] [CrossRef]
- Rice, J.R. A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Shih, C.F. Relationships between the J-integral and the crack opening displacement for stationary and extending cracks. J. Mech. Phys. Solids 1981, 29, 305–326. [Google Scholar] [CrossRef]
- Roy, S.; Roy, A. A computational investigation of length-scale effects in the fracture behaviour of a graphene sheet using the atomistic J-integral. Eng. Fract. Mech. 2019, 207, 165–180. [Google Scholar] [CrossRef]
- Chowdhury, S.C.; Wise, E.A.; Ganesh, R.; Gillespie, J.W. Effects of surface crack on the mechanical properties of Silica: A molecular dynamics simulation study. Eng. Fract. Mech. 2019, 207, 99–108. [Google Scholar] [CrossRef]
- Ji, W.M.; Wu, M.S. Atomistic studies of ductile fracture of a single crystalline cantor alloy containing a crack at cryogenic temperatures. Eng. Fract. Mech. 2021, 258, 108120. [Google Scholar] [CrossRef]
- Cao, F.H.; Chen, Y.; Zhao, S.T.; Ma, E.; Dai, L.H. Grain boundary phase transformation in a CrCoNi complex concentrated alloy. Acta Mater. 2021, 209, 116786. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Cao, F.H.; Wang, Y.J.; Dai, L.H. Novel atomic-scale mechanism of incipient plasticity in a chemically complex CrCoNi medium-entropy alloy associated with inhomogeneity in local chemical environment. Acta Mater. 2020, 194, 283–294. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Zhang, H.W.; Ye, H.F.; Zheng, Y.G. Free-end adaptive nudged elastic band method for locating transition states in minimum energy path calculation. J. Chem. Phys. 2016, 145, 094104. [Google Scholar] [CrossRef]
- Zhu, T.; Li, J.; Samanta, A.; Kim, H.G.; Suresh, S. Interfacial plasticity governs strain rate sensitivity and ductility in nanostructured metals. Proc. Natl. Acad. Sci. USA 2007, 104, 3031–3036. [Google Scholar] [CrossRef]
- Liang, L.W.; Dai, S.C.; Chen, Y.; Wang, H.Y.; Wang, Y.J.; Dai, L.H. Emergent failure transition of pearlitic steel at extremely high strain rates. Comput. Mater. Sci. 2023, 219, 112005. [Google Scholar] [CrossRef]
- Krull, H.; Yuan, H.A. Suggestions to the cohesive traction-separation law from atomistic simulations. Eng. Fract. Mech. 2011, 78, 525–533. [Google Scholar] [CrossRef]
- Ji, W.M.; Wu, M.S. Nanoscale insights into the damage tolerance of Cantor alloys at cryogenic temperatures. Int. J. Mech. Sci. 2022, 226, 107406. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Cao, F.; Dai, L.; Chen, Y. Effects of Chemical Short-Range Order and Lattice Distortion on Crack-Tip Behavior of Medium-Entropy Alloy by Atomistic Simulations. Metals 2024, 14, 226. https://doi.org/10.3390/met14020226
Zhu X, Cao F, Dai L, Chen Y. Effects of Chemical Short-Range Order and Lattice Distortion on Crack-Tip Behavior of Medium-Entropy Alloy by Atomistic Simulations. Metals. 2024; 14(2):226. https://doi.org/10.3390/met14020226
Chicago/Turabian StyleZhu, Xiuju, Fuhua Cao, Lanhong Dai, and Yan Chen. 2024. "Effects of Chemical Short-Range Order and Lattice Distortion on Crack-Tip Behavior of Medium-Entropy Alloy by Atomistic Simulations" Metals 14, no. 2: 226. https://doi.org/10.3390/met14020226
APA StyleZhu, X., Cao, F., Dai, L., & Chen, Y. (2024). Effects of Chemical Short-Range Order and Lattice Distortion on Crack-Tip Behavior of Medium-Entropy Alloy by Atomistic Simulations. Metals, 14(2), 226. https://doi.org/10.3390/met14020226





