Next Article in Journal
Utilization of Galvanizing Flue Dust Residue: A Sustainable Approach towards Complete Material Recycling
Previous Article in Journal
Hydrogen Embrittlement of Ti-Al6-V4 Alloy Manufactured by Laser Powder Bed Fusion Induced by Electrochemical Charging
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 14
Issue 2
10.3390/met14020252
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Atomistic Simulation of the Interaction between the Σ9[110](221) Shear-Coupled Grain Boundary Motion and the Cu-rich Precipitates in α-Iron

by
Jian Yin
1,
Huaiyu Hou
2,
Jing-Tao Wang
2,
Xiangbing Liu
1,*,
Chaoliang Xu
1,
Yuanfei Li
1,
Wangjie Qian
1,
Xiao Jin
1,
Huanchun Wu
1,
Wenqing Jia
1 and
Qiwei Quan
1
1
Materials Engineering Research Center, Suzhou Nuclear Power Research Institute, Suzhou 215004, China
2
School of Materials Science and Engineering, Nanjing University of Science and Technology, Nanjing 210094, China
*
Author to whom correspondence should be addressed.
Metals 2024, 14(2), 252; https://doi.org/10.3390/met14020252
Submission received: 4 December 2023 / Revised: 27 December 2023 / Accepted: 10 January 2024 / Published: 19 February 2024
(This article belongs to the Section Computation and Simulation on Metals)
Browse Figures
Versions Notes

Abstract

:
Shear-coupled grain boundary motion (SCGBM) is an important and efficacious plasticity mechanism in the deformation of metals. In this work, a molecular dynamic (MD) simulation of the interaction between the SCGBM of Σ9[110](221) GB and Cu-rich precipitates in α-iron was carried out. The effects of the size, the temperature, and the composition of the Cu precipitates were also studied. It was found that the precipitates inhibited the GB motion significantly, and the configuration transformation from spheroid to ellipsoid was also investigated in the simulation results. The critical stress of the interaction increased with the size of the precipitates. At higher temperatures, the GB sliding event increased the critical stress of the GB motion, which was higher than that of the interaction, inducing no stress-rise stage in the stress–time curve. The critical stress of the CuNi precipitates on the SCGBM was higher than that of the pure Cu precipitates with the same size, which was one of the reasons for the outstanding strength of the high-strength low-alloy (HSLA) steels compared with the traditional Cu-containing steels.

1. Introduction

Shear-coupled grain boundary motion (SCGBM) is an important and efficacious plasticity mechanism in the deformation of metals, especially nanocrystalline metals [1]. Due to the challenge of the experimental measurement of grain boundary (GB) mobility, molecular dynamic (MD) simulation has been widely used for researching the problems of GB migration. Mostly, SCGBM behavior has been investigated in face-centered cubic (FCC) metals via both experiments [2] and simulations [3,4,5,6,7]. In the last ten years, it was found that SCGBM is also one of the important deformation mechanisms in body-centered cubic (BCC) metals [8,9,10]. The effects of many factors, such as temperature [11,12], GB style [4,5], and GB structure [10], have been studied, and it was demonstrated that SCGBM is sensitive to these factors. In addition, simulations of the influence of other defects in the matrix on SCGBM were the research focus which helped us to understand the actual behavior of the GBs. Wang [13] and Bai [14] studied the effects of carbon and chromium atoms on the SCGBM in iron, respectively. The GB structural transformation induced by the alloy atoms determined the atomic mechanism of the SCGBM. It was found from the simulation of the interaction between the cracks and the SCGBM that GB migration could heal the cracks [15]. Precipitates are usually used to strengthen materials. Theoretical models have been established for the interaction between GBs and precipitates [16,17]. Precipitates strongly inhibit the motion of GBs.
Reactor pressure vessel (RPV) steel works under extreme conditions, such as high temperature, high pressure, and high-neutron-irradiation doses, during its service time [18,19,20]. Irradiation-induced hardening and embrittlement are the major limiting factors for the lifetime of RPV steels. The obstruction of dislocation motion by irradiation-induced defects, especially Cu-rich nano-precipitates, is the principal reason for RPV steels’ embrittlement. Therefore, lots of simulations on the interaction between pure Cu precipitates and dislocations have been investigated [21,22,23,24,25,26]. However, it is well known that the formed Cu-rich precipitates also consist of other kinds of atoms, such as Ni (nickel), Mn (manganese), and Si (silicon) atoms [20,27], which have been investigated using multiscale simulations and experiments of atom-probe tomography (APT) and small-angle neutron-scattering techniques (SANS) [28,29,30,31]. Of all these kinds of elements, the influence of Ni on RPV steels’ hardness is most often discussed. It was found using simulations that added Ni atoms promote Cu precipitation [30], and Cu-Ni mixed precipitates are easier to precipitate from the matrix than pure Cu ones [32]. It has been found that mixed precipitates prefer to form as a shell–core structure, where the outer Ni shell covers the surrounding inner Cu precipitate [32,33,34,35,36]. Al-Motasem [32] and Zhu [33] confirmed this phenomenon through simulation methods such as Monte Carlo (MC), MD, and density-functional theory (DFT). This is consistent with the results of experiments of SANS and APT by Wagner [34] and Fukuya [35]. In our previous work, an MD simulation of the SCGBM of a [110] symmetric-tilt GB, Σ9[110](221), was performed in iron, and the deformation mechanism was studied well. The Cu-rich precipitates in the RPV steel were the obstacles for not only the slipping of the dislocation but also the migration of the GBs. However, the influence of Cu-rich precipitates on SCGBM is still not clear.
In this work, the interaction between the SCGBM of Σ9[110](221) GB and Cu-rich precipitates in α-Fe is investigated using MD simulation. In Section 2, the general atomistic simulation method is described. The simulation results and discussion are presented in Section 3. Finally, a summary of this work is given in Section 4.

2. Computational Model

In this paper, an MD simulation was realized by using large-scale atomic/molecular massively parallel simulator (LAMMPS) code. The ternary Fe-Cu-Ni embedded atom method (EAM) interatomic potential [37] was used to describe the interaction between different atoms. In this potential, the same species interactions, Fe-Fe, Cu-Cu, and Ni-Ni interactions, were described by the iron potential of Mendelev et al. [38], the copper potential of Mishin et al. [39], and the nickel potential from Voter and Chen [40], respectively. The atomic configurations were visualized using Ovito [41]. The common neighbor analysis (CNA) method [42] was conducted to analyze the defect evolution during the deformation, and the center symmetry parameter (CSP) [43], which was defined as flowing, was used to analyze the degree of lattice distortion for the atoms.
P = ∑ i = 1 N p | r i + r i + N p | 2
where ri and ri+Np are vectors corresponding to the four pairs of opposite nearest neighbors in the BCC structure (Np = 4 for BCC structure).
A [110] symmetric-tilt GB, Σ9[110](221), with a misorientation angle of 141.06° in α-iron was constructed [44]. Compared with our previous research of SCGBM in iron [10], the modeling box was elongated along the z direction to avoid the influence of the precipitates with each other. The simulation model with three dimensions of approximately 80 a0 × 100 a0 × 30 a0, where a0 is the lattice constant of iron, is shown in Figure 1a. The Fe atoms are colored using the CSP, where blue atoms represent the BCC-structured atoms and the other colored atoms represent the defect atoms. The GB was located in the middle along the y direction, and the distance between the precipitates’ center and the GB plane was 4 nm. The Cu-rich precipitates with a diameter of 1~4 nm were inserted into the simulation box, shown as the yellow atoms in Figure 1a. The initial precipitates were constructed by replacing the Fe atoms with Cu or Ni atoms artificially in the simulation box. A shell–core structure was applied in the Cu-Ni precipitates, and the Ni concentration was set to 20%. Periodic boundary conditions were applied along the x and z directions, and a free-surface boundary condition was applied along the y direction in the simulation. Two thin slabs of atoms (y direction) with 4–5-atom layers (the black blocks in Figure 1) were fixed.
The initial model was firstly energy-minimized using a conjugate gradient (CG) algorithm and relaxed sufficiently (40 ps) to obtain the equilibrium structure. The equilibrium structures of the Σ9[110](221) GB at 10 K are presented in Figure 1b. Then, the MD simulations were performed in an isothermal–isobaric NPT ensemble at the applied temperature (10, 300 K), while the pressures along the x and z directions were controlled to be around 0 GPa. A constant velocity (10 m/s) was applied to the top slab along the positive x direction, and the bottom slab was fixed invariably. The position of the GB plane was represented by the average coordinates of the defect atoms. Details of the model parameters are listed in Table 1.

3. Results and Discussion

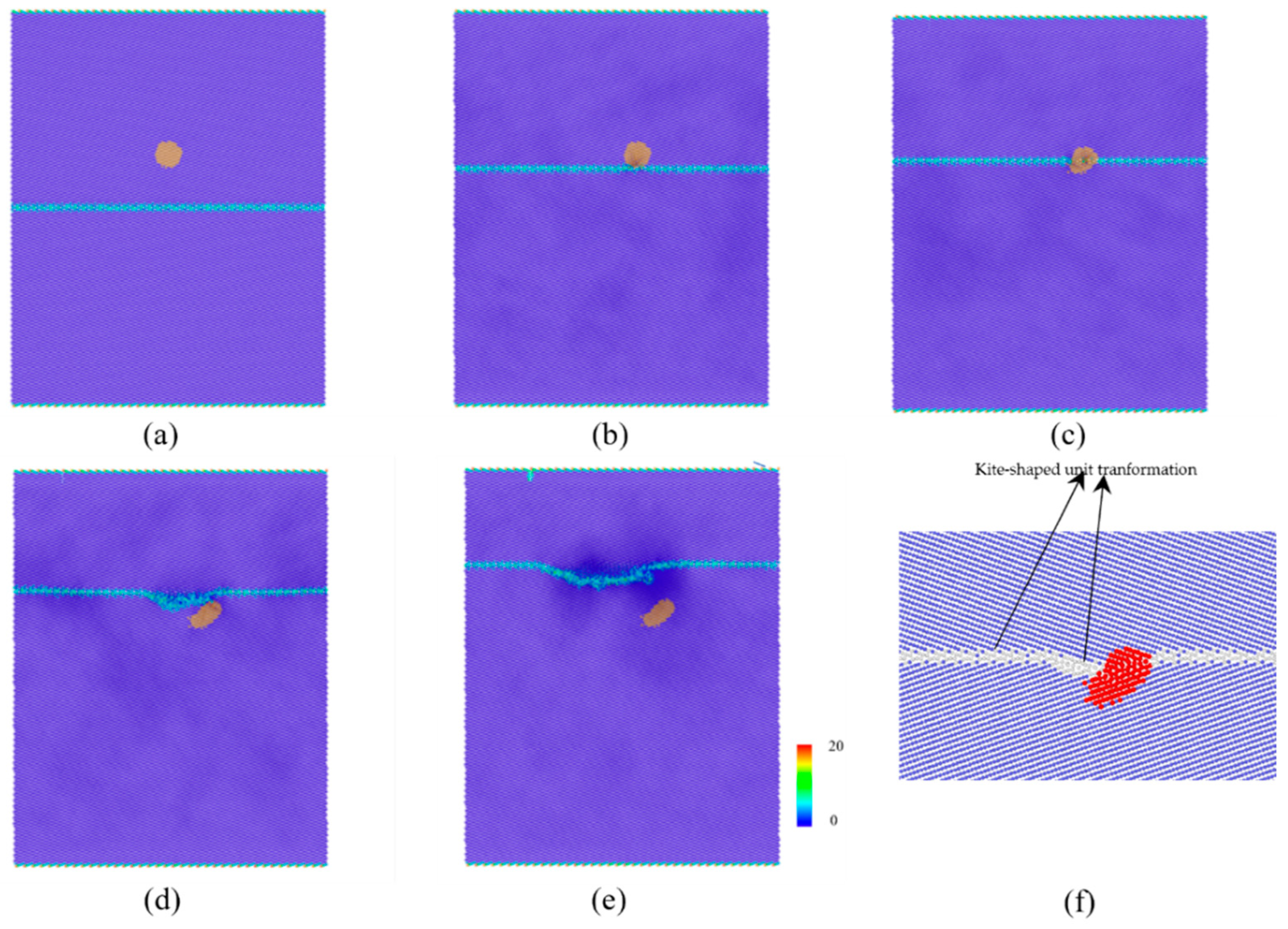
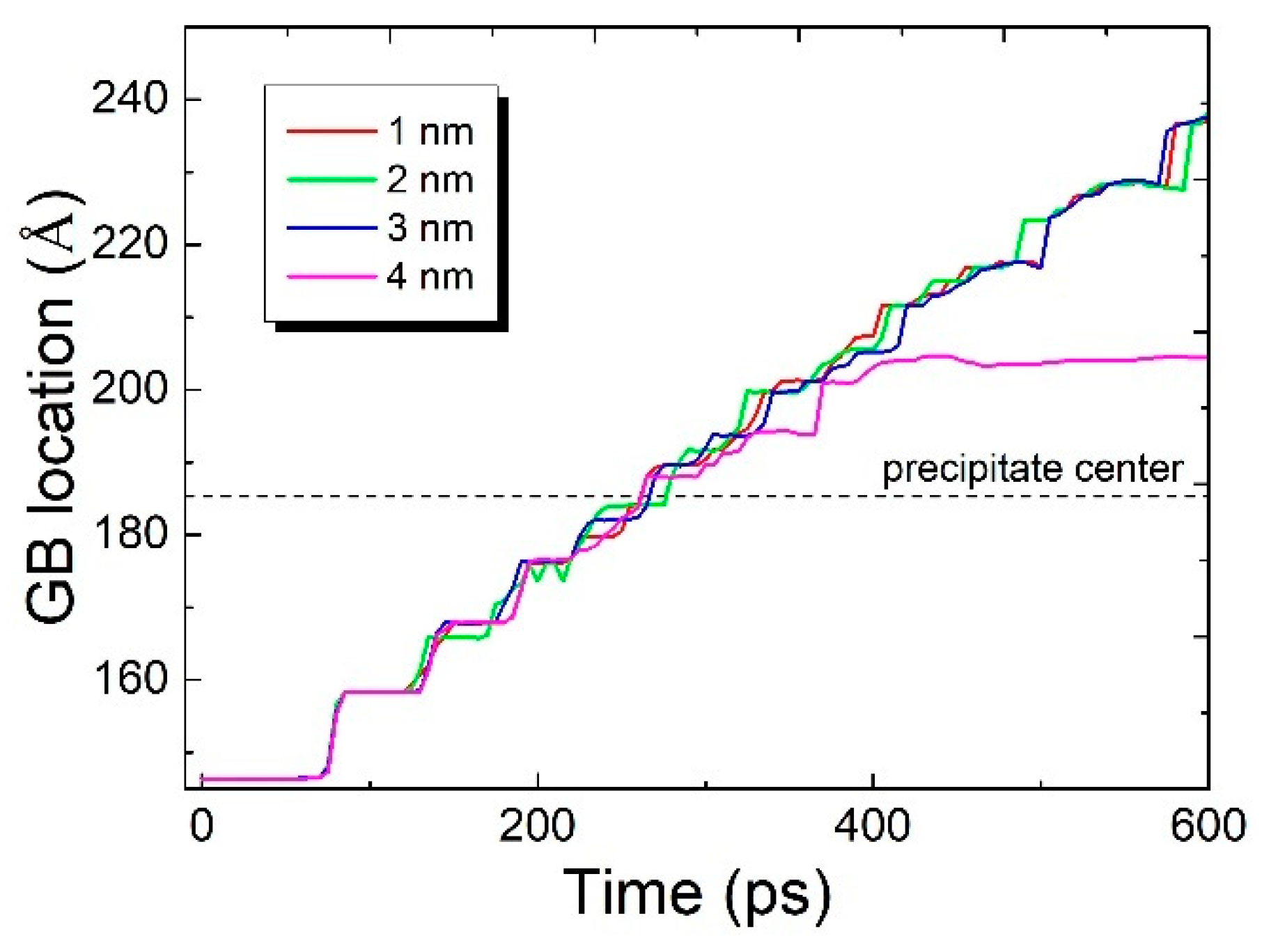
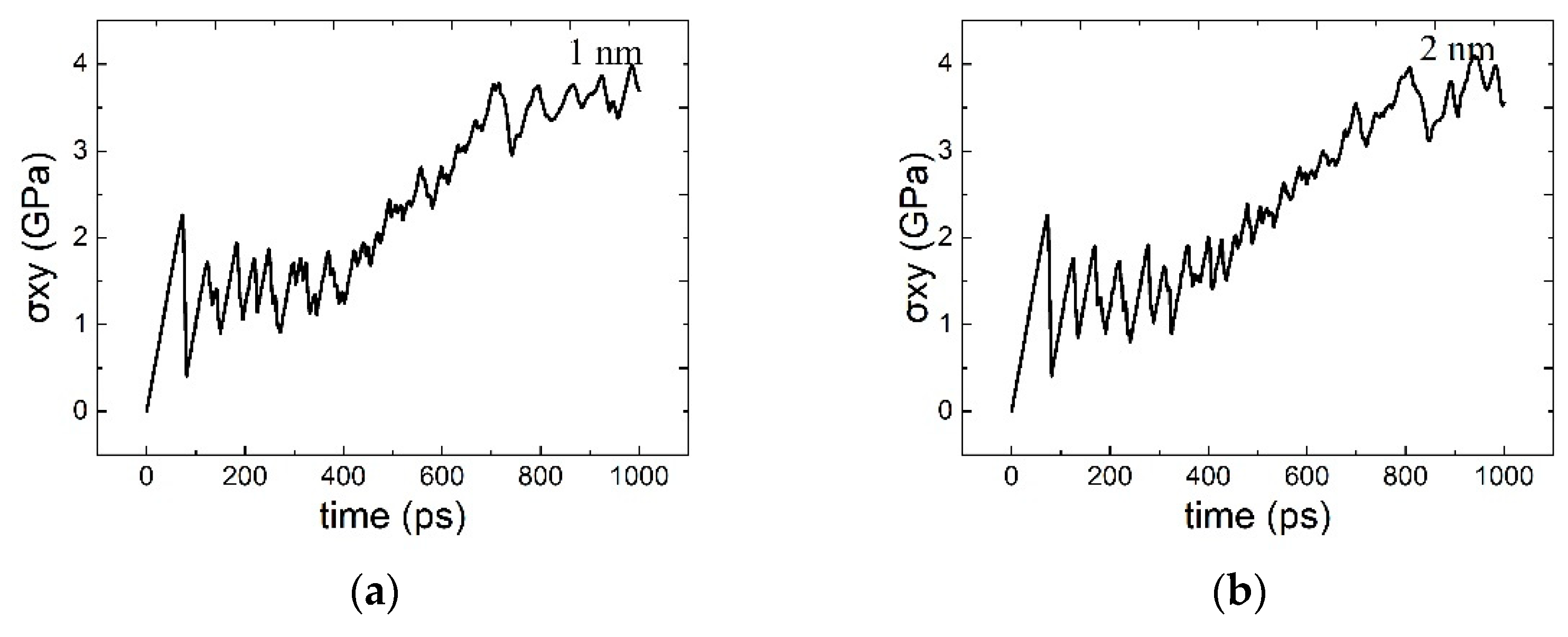
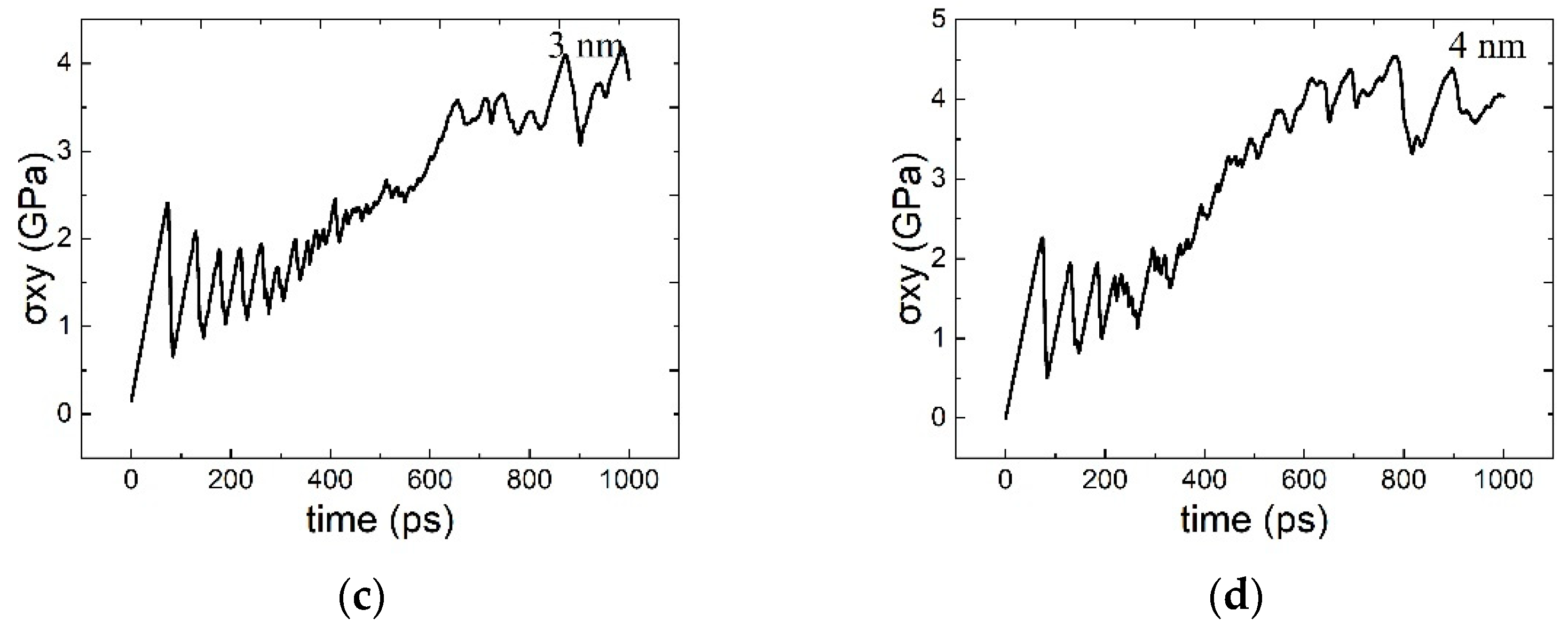
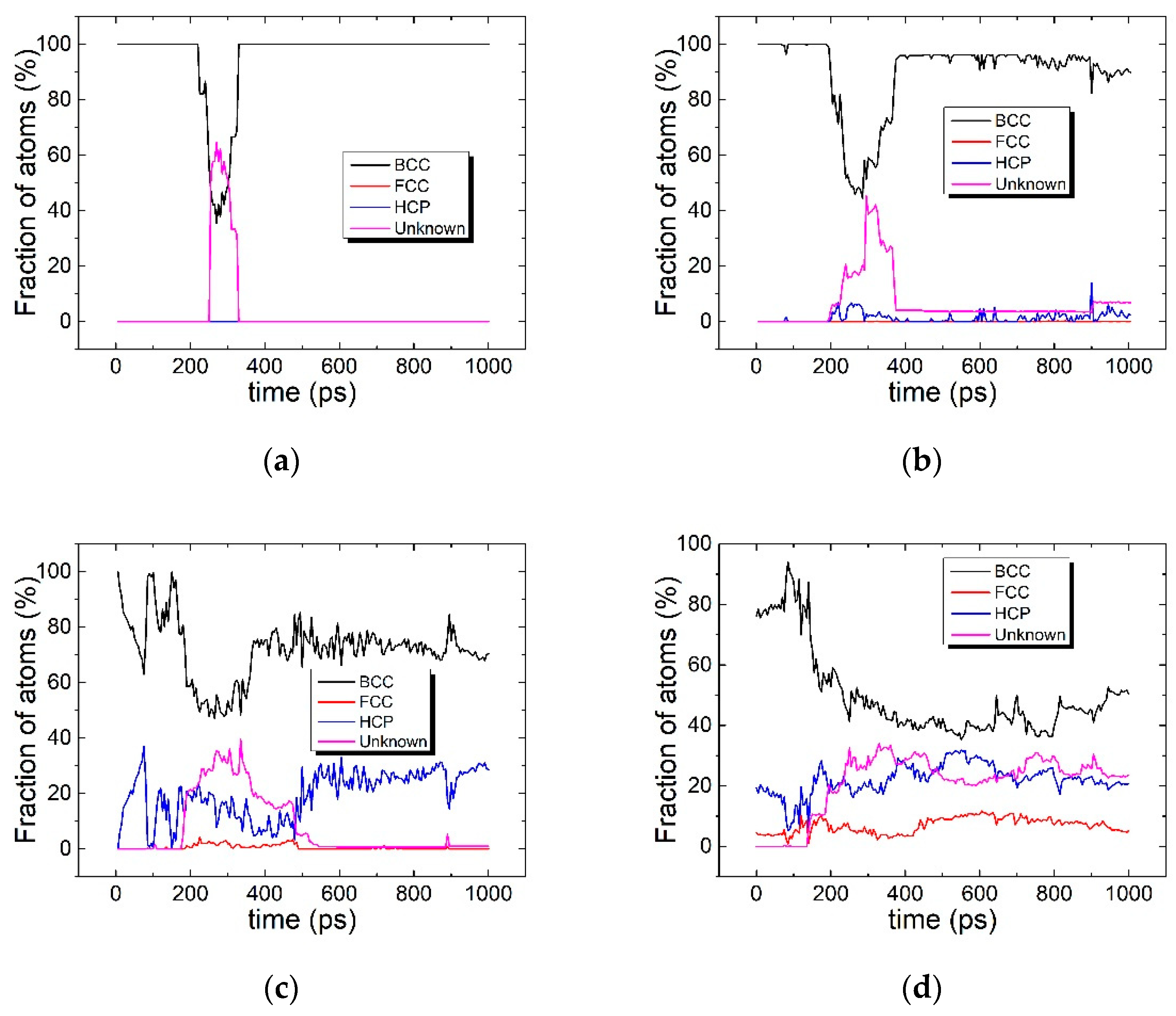
3.1. The Interaction between the SCGBM and Cu Precipitates at 10 K

The MD simulation was carried out at 10 K to avoid thermal effects. MD snapshots of the interactions between the Cu precipitates with a diameter of 2 nm and the Σ9[110](221) SCGBM are shown in Figure 2. In the figure, the iron atoms are colored using the CSP, and the blue atoms represent the atoms whose CSP equaled 0. The CSP value of the GB atoms was higher than the matrix atoms because of local lattice distortion, represented as the light blue atoms in the middle of the box shown in Figure 2a–e. To investigate the configuration transformation of the Cu precipitates, the copper atoms are colored yellow to distinguish them from the iron atoms. With the GBs passing through the precipitates, the configuration of the Cu precipitates was influenced by the SCGBM. As shown Figure 2c, the half precipitate upon the GB plane maintained its original shape, and the obvious shear deformation was investigated in the other half precipitate below the GB plane. When the GB plane departed away from the Cu precipitates, the configuration of the Cu precipitates transformed from a spheroid to an ellipsoid, which has also been investigated in experiments such as APT and SANS [45]. Due to the inhibition of the precipitates to the GB, the GB plane bowed to the Cu precipitates, as shown in Figure 2d. Until it was completely detached from the precipitates, the GB plane could not return to a flat plane like its initial configuration. The GB plane remained bent in the subsequent SCGBM, as shown in Figure 2e. The defect formation energy of the Cu/Ni atoms was calculated by replacing one iron atom with a Cu/Ni atom in the matrix for the applied ternary potential. The values of the formation energy of the Cu and Ni atoms were about 1.017 and −0.157 eV. The positive value of the formation energy means that Cu atoms were difficult to solute in the iron matrix. On the other hand, the BCC crystal lattice parameters for the iron, copper, and nickel atoms in the current work using the Fe-Cu-Ni ternary potential were 2.855 Å (Fe), 2.868 Å (Cu), and 2.812 Å (Ni), respectively. The lattice parameter of the BCC Cu was larger than that of iron. It is indicated that the Cu atoms will lead to the expansion of the lattice in the iron matrix. The space in the GB region could reduce the expansion effect. As the GB region is the source and sink of the vacancy, the space induced by the lower lattice parameter of Ni atoms will be attracted by the GB. The formation energy of the Cu/Ni atoms in the GB region will both decrease compared with that of the matrix. The atomic structure of the GB during the interaction is presented in Figure 2f. The red atoms present the Cu atoms, and the iron atoms are colored using the CNA parameter. Compared with Figure 1a, the kite-shaped GB structure unit (A) did not change in the region far away from the Cu precipitates. Another kind of kite-shaped GB structure unit (A’) with more atoms was investigated near the Cu precipitates. The A’ structure unit consisted of about 13 atoms (12 atoms around the middle atom), which had more space than the A structure unit. The structure unit transformation occurred near the Cu precipitates because the A’ structure unit could provide more space for the Cu precipitates.
The GB location–time curves for the precipitates with different sizes are shown in Figure 3. The position of the GB plane is represented by the average coordinates of the defect atoms. The xy component of the shear stress (σxy)–time curves of the interaction between the SCGBM and Cu precipitates with a diameter of 1–4 nm are presented in Figure 4. Consistent with our previous research results [10], the platform-shaped GB location–time curves were consistent with the sawtooth-shaped stress–time curves. Before the shear stress reached the peak stress of one sawtooth, the GB location remained invariable corresponding to the platform in the GB location–time curves. When the stress dropped, the GBs stepped up to a new position rapidly. The dashed line in Figure 3 represents the position of the center of the precipitates. When the GBs moved to a location near the center of the precipitates, the height of the platform step decreased, which means that the GB motion became difficult due to the obstruction of the precipitates. For the precipitates with a diameter of 4 nm, there was even a relatively long platform in the GB location–time curve after about 400 ps. In addition, the bent GB plane, as the MD snapshots show in Figure 2, influenced the calculation of the GB position. It is indicated that the precipitates hindered the movement of the GBs and had a pinning effect on the SCGBM. With the increase in the precipitates’ size, a more significant pinning effect on the GB movement was presented by the Cu precipitates.
Different from the SCGBM in previous results [10], there was an obvious stress-rise stage in the shear stress–time curves, as shown in Figure 4. We divided the curves into three stages: (1) an initial stage; (2) a stress-rise stage; and (3) a detachment stage. In the initial stage, the GBs moved from the initial position to the surface of the precipitates. The GB motion stayed consistent with the SCGBM until the end of this stage. In this simulation, the same location of the center of the precipitates was set for all precipitate sizes. Therefore, the time required for the GBs to reach the stress-rise stage was different, and the initial stage time cost of the Cu precipitates with a diameter of 4 nm was the least. Subsequently, due to the high energy barrier induced by the inhibition of the precipitates, a higher shear stress was needed for the SCGBM. Until the shear stress reached the peak value, which is the end of the stress-rise stage, the GB plane detached from the precipitates absolutely. This peak stress is the critical stress, representing the inhibition of the precipitates on the SCGBM, which serves as a base to compare the effect of the Cu precipitates in the following part of this paper. The critical stresses were 3.745, 3.959, 4.096, and 4.530 GPa for the Cu precipitates with a diameter of 1–4 nm, respectively. With the increase in the precipitates’ size, the critical stress increased, which was consistent with the interaction between the dislocation and the Cu precipitates in iron [25,26,46,47]. Then, the SCGBM with a higher stress was investigated in the detachment stage.

3.2. The Structural Transformation of Cu Precipitates

During the interaction between the SCGBM and the Cu precipitates, the local atom structure of the precipitates was influenced by the lattice distortion of the GBs. The CNA parameter was calculated for the atoms of the precipitates to evaluate the structural transformation in the simulation. The structural transformation of the Cu precipitates during the interaction between the Σ9(221) SCGBM and the pure Cu precipitates with a diameter of 1–4 nm is presented in Figure 5a–d.
The pure Cu precipitates of the initial state were mainly in a BCC structure. The precipitates with a diameter of 1 and 2 nm were basically composed of 100% Cu atoms with a BCC structure, which were completely coherent with the matrix. Some atoms in the precipitates with a diameter of 3 and 4 nm transformed into HCP or FCC structures, but BCC-structured atoms still accounted for more than 80%. As shown in Figure 5a, during the process of the precipitates passing through the GB (hereinafter referred to as the transformation stage), the precipitates atoms underwent a transition from a BCC structure to an unknown structure, but after the GB detached from the precipitates (hereinafter referred to as the recovery stage), the precipitates returned to a 100% BCC structure, which was the same as the initial atomic structure. For the precipitates with a diameter of 2 nm, atoms with an HCP structure were investigated in the transformation stage. In addition, about 5% of the atoms remained in an unknown or HCP structure in the recovery stage, as shown in Figure 5b. Different from the smaller precipitates, about 2-3% of the Cu atoms transformed into FCC structures during the transformation process for the precipitates with a 3 nm diameter. In the recovery stage, the proportion of BCC-structured atoms was about 75%, which was smaller than that of the 2 nm precipitates, while most of the remaining atoms had an HCP structure. As shown in Figure 5d, the recovery process was not observed clearly, and only about 40% of the atoms remained as a BCC structure after the interaction. The final structure of the precipitates with a diameter of 4 nm was more complicated, which may be an intermediate structure between a BCC and FCC structure, such as a 9R and 3R structure. This structural transformation is the reason of the significant increase in the critical stress for the 4 nm precipitates calculated in Section 3.1. And, it is indicated that the SCGBM also promoted the structural transformation of the precipitates like the dislocations [46].

3.3. The Interaction between the SCGBM and Cu Precipitates at 300 K

It has been demonstrated that a different deformation mechanism (GB sliding) exists at high temperature (≥300 K) for Σ9(221) SCGBM [10]. The critical temperature is less than 300 K. This is the reason why we chose two temperatures (10, 300K) to study the effect of the temperature. In this section, the MD simulation of the interaction between the Σ9(221) SCGBM and Cu precipitates with a diameter of 2 nm was carried out at 300 K to investigate the effect of the GB sliding. The MD snapshot at 900 ps is presented in Figure 6a. Compared with Figure 2, a more elongated ellipsoid Cu precipitate was observed, and it is obviously indicated that the GB sliding mechanism still existed in this simulation. In the process of SCGBM, the coupling factor β is defined as the ratio of the velocity of GB translation, v s , to GB migration, v n , which can also be calculated by the displacements of GB translation, S, and migration, H, as Equation (2) shows [1].
β = v s v n = S H
If GB sliding events occur, the shear couple factor, β, should be changed as follows [1]:
β = ( v s − v d ) v n ,
where v d is the velocity of the GB sliding. The GB sliding increased the displacement of the GB translation, S. After the interaction, the horizontal component of the displacement of the atoms in the precipitates also increased, which induced a more elongated ellipsoid shape of the precipitates. The shear stress–time curve with a sawtooth configuration is shown in Figure 6b, which confirms that SCGBM was still the main the deformation mechanism. However, different from the interaction at a relatively low temperature (<300 K), there was no obvious stress-rise stage in the stress–time curve. Consistent with our previous research results [10], a higher critical stress was needed if GB sliding events occurred, which was also higher than the critical stress of the interaction between the GB and the precipitates. Therefore, without increasing the shear stress, the SCGBM could pass through the precipitates. Moreover, the migration displacement of the SCGBM was reduced by the GB sliding. This is the reason that the time cost for the interaction was longer than that at low temperature.

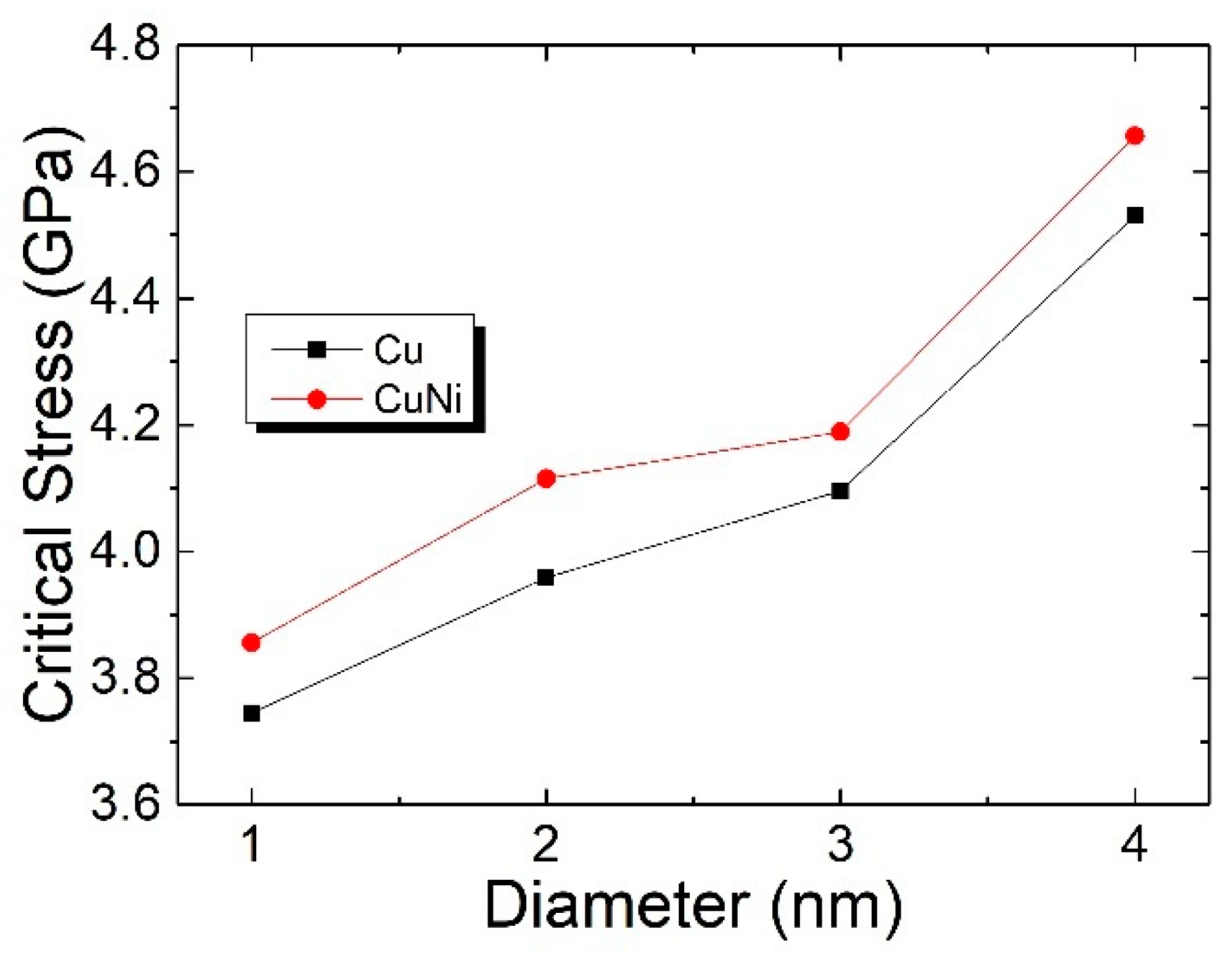
3.4. The Interaction between the SCGBM and CuNi Precipitates at 10 K

To determine the effect of the Ni shell, the MD simulation of the interaction between the SCGBM and the CuNi precipitates was performed at 10 K. In this work, the Ni concentration of the CuNi precipitates with a shell–core structure was set to 20%, and the other simulation conditions were the same as those of the pure Cu precipitates. The MD results indicated that the Ni shell had almost no influence on the deformation mechanism of the interaction, but the critical stress for the inhibition of the CuNi precipitates was determined by the Ni shell. The relationship between the critical stress and the precipitate size for Cu and CuNi precipitates is shown in Figure 7. Similar to the Cu precipitates, the critical stress of the CuNi precipitates increased with the precipitate size. And, for the same size, the critical stress of the CuNi precipitates was larger than that of the Cu precipitates. It is indicated that the Ni shell promoted the inhibition of the precipitates on the SCGBM.
For some high-strength low-alloy (HSLA) steels, the strength increment contributed by CuNi precipitates is much larger than that of Cu precipitates [48], which is mostly in terms of precipitation strengthening and grain size refinement strengthening. The addition of Ni atoms promotes the precipitation of Cu atoms and increases the number density of the precipitates. The added Ni atoms refine the precipitates by inhibiting the growth of Cu precipitates. Because of their larger critical resolved shear stress (CRSS) than Cu precipitates with the same size, CuNi precipitates enhance the precipitation strengthening. In addition, the increment in the grain size refinement strengthening is also induced by the increased number density of the CuNi precipitates. On the other hand, the critical stress of the CuNi precipitates on the SCGBM was larger than that of the Cu precipitates with the same size in our simulation. As GB migration is the one of the important processes of GB growth, the CuNi precipitates had a more significant inhibit influence on the GB migration, inducing more refined grains in the matrix. Therefore, the higher number density and the larger critical stress for the SCGBM of CuNi precipitates are the reason for the fact that HSLA steels have outstanding strength compared with traditional Cu-containing steels.
Then, what is the role that CuNi precipitates play in the SCGBM of RPV steels? As we know, the GB can be regarded as the sink and source of the point defects and dislocations. In the process of GB migration or SCGBM, the point defects and dislocations can be absorbed into the GB structure. Cracks can even be healed by SCGBM, which has been investigated in some simulations [15]. The inhibition of Cu-rich precipitates on the SCGBM means that more point defects and dislocations are left in the matrix. Then, the stress concentration resulting from the Cu-rich precipitates obstructing the dislocation motion induces the embrittlement of RPV steels.

4. Summary and Conclusions

We have presented the results of an MD simulation of the interaction between the SCGBM of Σ9[110](221) GB and Cu-rich precipitates in α-Fe. And, the influences of the size of the precipitates (1–4 nm), the temperature (10, 300 K), and the Cu precipitate composition (pure Cu and CuNi precipitates) were also studied.
The precipitates inhibited the migration of the GBs, while the configuration transformation from spheroid to ellipsoid was investigated after the interaction. The GB structure unit transformation (kite-shaped GB structure unit A–A’) occurred near the Cu precipitates because the A’ structure unit could provide more space for the Cu precipitates. The critical stress for the interaction increased with the precipitate size, which was consistent with the interaction between the dislocation and the Cu precipitates in iron. The structural transformation from a BCC to an FCC, HCP, or unknown structure was investigated during the interaction. Only for the precipitates with a diameter of 4 nm did the atomic structure not return to a BCC structure. At 300 K, the GB sliding increased the critical stress of the GB migration, which was higher than that of the interaction between the SCGBM and the precipitates, inducing no stress-rise stage in the stress–time curve.
The critical stress of the CuNi precipitates on the SCGBM was higher than that of the pure Cu precipitates with the same size, and the Ni shell promoted the inhibition of the precipitates on the SCGBM. The CuNi precipitates enhanced the precipitation strengthening. This could explain the experiment results that showed that HSLA steels have outstanding strength compared with traditional Cu-containing steels from the insight of atomic simulation. On the other hand, the inhibition of Cu-rich precipitates on the SCGBM means that more point defects and dislocations are left in RPV steels. As we know, the obstruction of dislocation motion by irradiation-induced defects, especially Cu-rich nano-precipitates, is the principal reason for the embrittlement of RPV steels. The inhibition of the Cu-rich precipitates on the SCGBM induced the embrittlement of the RPV steels indirectly. This is the reason that the Cu-rich precipitates played opposite roles for the two materials in the different service environments.

Author Contributions

Conceptualization, J.Y., H.H. and J.-T.W.; methodology, J.Y., H.H. and J.-T.W.; formal analysis, H.H., X.J., C.X., Y.L., H.W. and W.J.; investigation, W.Q., X.J., H.W. and Q.Q.; visualization, W.Q., C.X., Y.L., X.J. and H.W.; writing—original draft preparation, J.Y., H.H., X.J., C.X., Y.L., H.W. and J.-T.W.; writing—review and editing, J.-T.W., X.L., W.Q., W.J. and Q.Q.; project administration, X.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Guangdong Major Project of Basic and Applied Basic Research (No. 2019B030302011), the National Key Research and Development Program of China (grant No. 2021YFA1600903), and the Natural Science Foundation of China under grant Nos. 12275200, 12075274, and U23B2072.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Cahn, J.W.; Mishin, Y.; Suzuki, A. Coupling grain boundary motion to shear deformation. Acta Mater. 2006, 54, 4953–4975. [Google Scholar] [CrossRef]
  2. Li, C.H.; Edwards, E.H.; Washburn, J.; Parker, E.R. Stress-induced movement of crystal boundaries. Acta Metall. 1953, 1, 223–229. [Google Scholar] [CrossRef]
  3. Wan, L.; Wang, S. Shear response of the Σ9⟨110⟩{221} symmetric tilt grain boundary in fcc metals studied by atomistic simulation methods. Phys. Rev. B 2010, 82, 214112. [Google Scholar] [CrossRef]
  4. Trautt, Z.T.; Adland, A.; Karma, A.; Mishin, Y. Coupled motion of asymmetrical tilt grain boundaries: Molecular dynamics and phase field crystal simulations. Acta Mater. 2012, 60, 6528–6546. [Google Scholar] [CrossRef]
  5. Zhang, L.; Lu, C.; Tieu, K.; Zhao, X.; Pei, L. The shear response of copper bicrystals with Sigma11 symmetric and asymmetric tilt grain boundaries by molecular dynamics simulation. Nanoscale 2015, 7, 7224–7233. [Google Scholar] [CrossRef]
  6. Hoyt, J.J. Atomistic simulations of grain and interphase boundary mobility. Model. Simul. Mater. Sci. Eng. 2014, 22, 033001. [Google Scholar] [CrossRef]
  7. Fensin, S.J.; Asta, M.; Hoagland, R.G. Temperature dependence of the structure and shear response of a Σ11 asymmetric tilt grain boundary in copper from molecular-dynamics. Philos. Mag. 2012, 92, 4320–4333. [Google Scholar] [CrossRef]
  8. Niu, L.L.; Zhang, Y.; Shu, X.; Gao, F.; Jin, S.; Zhou, H.B.; Lu, G.H. Shear-coupled grain boundary migration assisted by unusual atomic shuffling. Sci. Rep. 2016, 6, 23602. [Google Scholar] [CrossRef]
  9. Niu, L.; Shu, X.; Zhang, Y.; Gao, F.; Jin, S.; Zhou, H.; Lu, G. Atomistic insights into shear-coupled grain boundary migration in bcc tungsten. Mater. Sci. Eng. A 2016, 677, 20–28. [Google Scholar] [CrossRef]
  10. Yin, J.; Wang, Y.; Yan, X.; Hou, H.; Wang, J.T. Atomistic simulation of shear-coupled motion of [1 1 0] symmetric tilt grain boundary in α-iron. Comput. Mater. Sci. 2018, 148, 141–148. [Google Scholar] [CrossRef]
  11. Frolov, T. Effect of interfacial structural phase transitions on the coupled motion of grain boundaries: A molecular dynamics study. Appl. Phys. Lett. 2014, 104, 211905. [Google Scholar] [CrossRef]
  12. Zhang, L.; Lu, C.; Michal, G.; Tieu, K.; Zhao, X.; Deng, G. Influence of temperature and local structure on the shear-coupled grain boundary migration. Phys. Status Solidi (B) 2016, 254, 1600477. [Google Scholar] [CrossRef]
  13. Wang, C.; Wang, Y.; Yu, Z.; Yin, J.; Lai, W. Revealing the influence of carbon on shear-coupled grain boundary migrationin alpha-iron via molecular dynamics simulations. Model. Simul. Mater. Sci. Eng. 2022, 30, 085001. [Google Scholar] [CrossRef]
  14. Bai, Z.; Yan, X.; Yin, J.; Hou, H. Influence of Chromium Atoms on the Shear-Coupled Motion of [110] Symmetric Tilt Grain Boundary in α-Iron: Atomic Simulation. Metals 2022, 12, 1451. [Google Scholar] [CrossRef]
  15. Aramfard, M.; Deng, C. Interaction of shear-coupled grain boundary motion with crack: Crack healing, grain boundary decohesion, and sub-grain formation. J. Appl. Phys. 2016, 119, 085308. [Google Scholar] [CrossRef]
  16. Xu, Y.; Geslin, P.A.; Karma, A. Elastically-mediated interactions between grain boundaries and precipitates in two-phase coherent solids. Phys. Rev. B 2016, 94, 144106. [Google Scholar] [CrossRef]
  17. Tan, F.; Fang, Q.; Li, J.; Wu, H. Interaction of precipitate with shear–coupled grain boundary migration. Acta Mech. 2020, 231, 237–250. [Google Scholar] [CrossRef]
  18. Phythian, W.J.; English, C.A. Microstrustural evolution in reactor pressure vessel steels. J. Nucl. Mater. 1993, 205, 162–177. [Google Scholar] [CrossRef]
  19. Odette, G.R.; Lucas, G.E. Recent progress in understanding reactor pressure vessel steel embrittlement. Radiat. Eff. Defects Solids 1998, 144, 189–231. [Google Scholar] [CrossRef]
  20. Bonny, G.; Terentyev, D.; Bakaev, A.; Zhurkin, E.E.; Hou, M.; Van Neck, D.; Malerba, L. On the thermal stability of late blooming phases in reactor pressure vessel steels: An atomistic study. J. Nucl. Mater. 2013, 442, 282–291. [Google Scholar] [CrossRef]
  21. Hu, S.Y.; Schmauder, S.; Chen, L.Q. Atomistic simulations of interactions between Cu precipitates and an edge dislocation in a b.c.c. Fe single crystal. Phys. Status Solidi B 2000, 220, 845–856. [Google Scholar] [CrossRef]
  22. Hu, S.Y.; Li, Y.L.; Watanabe, K. Calculation of internal stresses around Cu precipitates in the bcc Fe matrix by atomic simulation. Model. Simul. Mater. Sci. Eng. 1999, 7, 641–655. [Google Scholar] [CrossRef]
  23. Nedelcu, S.; Kizler, P.; Schmauder, S.; Moldovan, N. Atomic scale modelling of edge dislocation movement in the-Fe–Cu system. Model. Simul. Mater. Sci. Eng. 2000, 8, 181–191. [Google Scholar] [CrossRef]
  24. Shim, J.H.; Cho, Y.W.; Kwon, S.C.; Kim, W.W.; Wirth, B.D. Screw dislocation assisted martensitic transformation of a bcc Cu precipitate in bcc Fe. Appl. Phys. Lett. 2007, 90, 021906. [Google Scholar] [CrossRef]
  25. Harry, T.; Bacon, D.J. Computer simulation of the core structure of the <111> screw dislocation in α-iron containing copper precipitates II. Dislocation–precipitate interaction and the strengthening effect. Acta Mater. 2002, 50, 209–222. [Google Scholar]
  26. Harry, T.; Bacon, D.J. Computer simulation of the core structure of the <111> screw dislocation in α-iron containing copper precipitates I. Structure in the matrix and a precipitate. Acta Mater. 2002, 50, 195–208. [Google Scholar]
  27. Odette, G.R.; Wirth, B.D. A computational microscopy study of nanostructural evolution in irradiated pressure vessel steels. J. Nucl. Mater. 1997, 251, 157–171. [Google Scholar] [CrossRef]
  28. Fine, M.E.; Liu, J.Z.; Asta, M.D. An unsolved mystery: The composition of bcc Cu alloy precipitates in bcc Fe and steels. Mater. Sci. Eng. A 2007, 463, 271–274. [Google Scholar] [CrossRef]
  29. Schober, M.; Eidenberger, E.; Leitner, H.; Staron, P.; Reith, D.; Podloucky, R. A critical consideration of magnetism and composition of (bcc) Cu precipitates in (bcc) Fe. Appl. Phys. A 2010, 99, 697–704. [Google Scholar] [CrossRef]
  30. Zhang, C.; Enomoto, M. Study of the influence of alloying elements on Cu precipitation in steel by non-classical nucleation theory. Acta Mater. 2006, 54, 4183–4191. [Google Scholar] [CrossRef]
  31. Toyama, T.; Nagai, Y.; Tang, Z.; Hasegawa, M.; Almazouzi, A.; van Walle, E.; Gerard, R. Nanostructural evolution in surveillance test specimens of a commercial nuclear reactor pressure vessel studied by three-dimensional atom probe and positron annihilation. Acta Mater. 2007, 55, 6852–6860. [Google Scholar] [CrossRef]
  32. Al-Motasem, A.T.; Posselt, M.; Bergner, F. Nanoclusters in bcc-Fe containing vacancies, copper and nickel: Structure and energetics. J. Nucl. Mater. 2011, 418, 215–222. [Google Scholar] [CrossRef]
  33. Zhu, L.S.; Zhao, S.J. Influence of Ni on Cu precipitation in Fe–Cu–Ni ternary alloy by an atomic study. Chin. Phys. B 2014, 23, 063601. [Google Scholar] [CrossRef]
  34. Wagner, A.; Ulbricht, A.; Bergner, F.; Altstadt, E. Influence of the copper impurity level on the irradiation response of reactor pressure vessel steels investigated by SANS. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2012, 280, 98–102. [Google Scholar] [CrossRef]
  35. Fukuya, K.; Ohno, K.; Nakata, H.; Dumbill, S.; Hyde, J.M. Microstructural evolution in medium copper low alloy steels irradiated in a pressurized water reactor and a material test reactor. J. Nucl. Mater. 2003, 312, 163–173. [Google Scholar] [CrossRef]
  36. Lv, G.; Zhang, H.; He, X.; Yang, W.; Su, Y. Atomistic simulation of Cu–Ni precipitates hardening in α-iron. J. Phys. D Appl. Phys. 2015, 48, 115302. [Google Scholar] [CrossRef]
  37. Bonny, G.; Pasianot, R.C.; Castin, N.; Malerba, L. Ternary Fe-Cu-Ni many-body potential to model reactor pressure vessel steels: First validation by simulated thermal annealing. Philos. Mag. 2009, 89, 3531–3546. [Google Scholar] [CrossRef]
  38. Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
  39. Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A.; Voter, A.F.; Kress, J.D. Structural stability and lattice defects in copper:Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63, 224106. [Google Scholar] [CrossRef]
  40. Voter, A.F.; Chen, S.P. Accurate Interatomic Potentials for Ni, Al and Ni3Al. Mater. Res. Soc. Symp. Proc. 1987, 82, 175. [Google Scholar] [CrossRef]
  41. Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
  42. Tsuzuki, H.; Branicio, P.S.; Rino, J.P. Structural characterization of deformed crystals by analysis of common atomic neighborhood. Comput. Phys. Commun. 2007, 177, 518–523. [Google Scholar] [CrossRef]
  43. Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085–11088. [Google Scholar] [CrossRef]
  44. Tschopp, M.A.; Coleman, S.P.; McDowell, D.L. Symmetric and asymmetric tilt grain boundary structure and energy in Cu and Al (and transferability to other fcc metals). Integr. Mater. Manuf. Innov. 2015, 4, 176–189. [Google Scholar] [CrossRef]
  45. Ahlawat, S.; Sarkar, S.K.; Sen, D.; Biswas, A. Revisiting temporal evolution of Cu-rich precipitates in Fe–Cu alloy: Correlative small angle neutron scattering and atom-probe tomography studies. Microsc. Microanal. 2019, 25, 840–848. [Google Scholar] [CrossRef]
  46. Yin, J.; Wang, Y.; Hou, H.; Wang, J.T.; Liu, X.; Xue, F. Atomistic simulation of interactions between an edge dislocation and Cu precipitates with different chemical compositions in α-Fe. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2019, 458, 39–43. [Google Scholar] [CrossRef]
  47. Osetsky, Y.N.; Bacon, D.; Mohles, V. Atomic modelling of strengthening mechanisms due to voids and copper precipitates in α-iron. Philos. Mag. 2003, 83, 3623–3641. [Google Scholar] [CrossRef]
  48. Jiao, Z.B.; Luan, J.H.; Zhang, Z.W.; Miller, M.K.; Ma, W.B.; Liu, C.T. Synergistic effects of Cu and Ni on nanoscale precipitation and mechanical properties of high-strength steels. Acta Mater. 2013, 61, 5996–6005. [Google Scholar] [CrossRef]
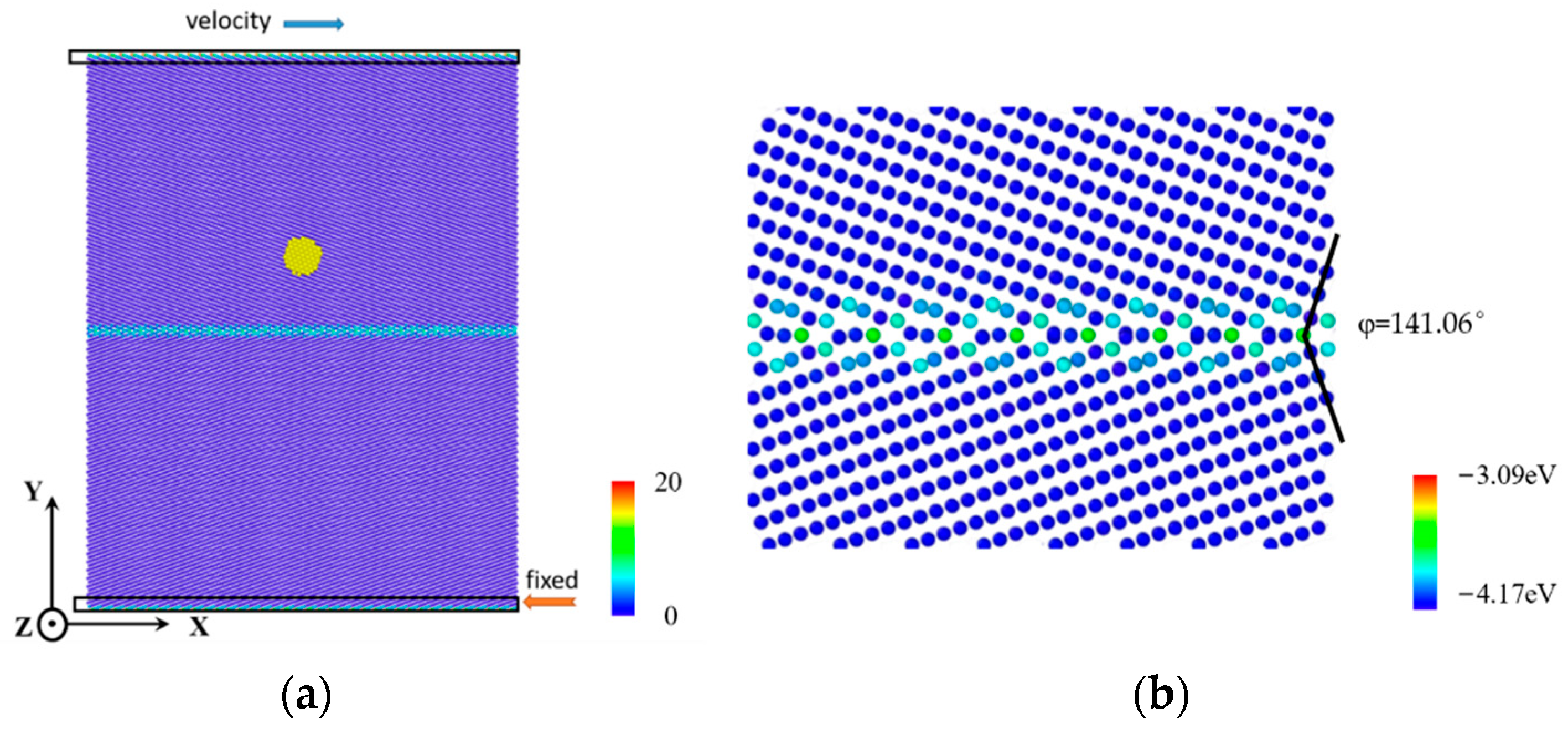
Metals 14 00252 g001
Figure 1. (a) The equilibrium structures of the Σ9[110](221) GB at 10 K and (b) the MD model of interaction between shear-coupled grain boundary motion and copper precipitates.
Figure 1. (a) The equilibrium structures of the Σ9[110](221) GB at 10 K and (b) the MD model of interaction between shear-coupled grain boundary motion and copper precipitates.
Metals 14 00252 g001
Metals 14 00252 g002
Figure 2. The progress of the interaction between Σ9(221) SCGBM and copper precipitate with diameter of 2 nm. (a–e) The MD snapshots of 0, 200, 275, 365, and 485 ps in the MD simulation (yellow atoms present the Cu atoms, and the iron atoms are colored using the CSP), and (f) the atomic structure of GB during the interaction (red atoms present the Cu atoms, and iron atoms are colored using CNA parameter).
Figure 2. The progress of the interaction between Σ9(221) SCGBM and copper precipitate with diameter of 2 nm. (a–e) The MD snapshots of 0, 200, 275, 365, and 485 ps in the MD simulation (yellow atoms present the Cu atoms, and the iron atoms are colored using the CSP), and (f) the atomic structure of GB during the interaction (red atoms present the Cu atoms, and iron atoms are colored using CNA parameter).
Metals 14 00252 g002
Metals 14 00252 g003
Figure 3. The GB location–time curves for the precipitates with different sizes.
Figure 3. The GB location–time curves for the precipitates with different sizes.
Metals 14 00252 g003
Metals 14 00252 g004aMetals 14 00252 g004b
Figure 4. Shear stress (σxy)–time curves of the interaction between SCGBM and Cu precipitates for (a–d) Cu precipitates with diameter of 1–4 nm.
Figure 4. Shear stress (σxy)–time curves of the interaction between SCGBM and Cu precipitates for (a–d) Cu precipitates with diameter of 1–4 nm.
Metals 14 00252 g004aMetals 14 00252 g004b
Metals 14 00252 g005
Figure 5. The structural transformation of Cu precipitates during the interaction between Σ9(221) SCGBM and pure Cu precipitates for (a–d): Cu precipitates with diameter of 1–4 nm.
Figure 5. The structural transformation of Cu precipitates during the interaction between Σ9(221) SCGBM and pure Cu precipitates for (a–d): Cu precipitates with diameter of 1–4 nm.
Metals 14 00252 g005
Metals 14 00252 g006
Figure 6. The interaction between SCGBM of Σ9(221) grain boundary and pure copper precipitate with diameter of 2 nm at 300 K. (a) The MD snapshot at 900 ps (yellow atoms represent the Cu atoms, and the iron atoms are colored using the CSP) and (b) the shear stress–time curve.
Figure 6. The interaction between SCGBM of Σ9(221) grain boundary and pure copper precipitate with diameter of 2 nm at 300 K. (a) The MD snapshot at 900 ps (yellow atoms represent the Cu atoms, and the iron atoms are colored using the CSP) and (b) the shear stress–time curve.
Metals 14 00252 g006
Metals 14 00252 g007
Figure 7. The relationship between critical stress and precipitate size for pure Cu and CuNi precipitates.
Figure 7. The relationship between critical stress and precipitate size for pure Cu and CuNi precipitates.
Metals 14 00252 g007
Table 1. Parameters of the simulation model.
Table 1. Parameters of the simulation model.
ParametersValueParametersValue
LX (length in x direction) 233.497 ÅT (temperature) 10, 300 K
LY (length in y direction) 291.021 Åv (velocity) 10 m/s
LZ (length in z direction) 120.739 Åc (Ni concentration) 20%
D (precipitate diameter)1~4 nm
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Yin, J.; Hou, H.; Wang, J.-T.; Liu, X.; Xu, C.; Li, Y.; Qian, W.; Jin, X.; Wu, H.; Jia, W.; et al. Atomistic Simulation of the Interaction between the Σ9[110](221) Shear-Coupled Grain Boundary Motion and the Cu-rich Precipitates in α-Iron. Metals 2024, 14, 252. https://doi.org/10.3390/met14020252

AMA Style

Yin J, Hou H, Wang J-T, Liu X, Xu C, Li Y, Qian W, Jin X, Wu H, Jia W, et al. Atomistic Simulation of the Interaction between the Σ9[110](221) Shear-Coupled Grain Boundary Motion and the Cu-rich Precipitates in α-Iron. Metals. 2024; 14(2):252. https://doi.org/10.3390/met14020252

Chicago/Turabian Style

Yin, Jian, Huaiyu Hou, Jing-Tao Wang, Xiangbing Liu, Chaoliang Xu, Yuanfei Li, Wangjie Qian, Xiao Jin, Huanchun Wu, Wenqing Jia, and et al. 2024. "Atomistic Simulation of the Interaction between the Σ9[110](221) Shear-Coupled Grain Boundary Motion and the Cu-rich Precipitates in α-Iron" Metals 14, no. 2: 252. https://doi.org/10.3390/met14020252

APA Style

Yin, J., Hou, H., Wang, J. -T., Liu, X., Xu, C., Li, Y., Qian, W., Jin, X., Wu, H., Jia, W., & Quan, Q. (2024). Atomistic Simulation of the Interaction between the Σ9[110](221) Shear-Coupled Grain Boundary Motion and the Cu-rich Precipitates in α-Iron. Metals, 14(2), 252. https://doi.org/10.3390/met14020252

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop