Buckling Defect Optimization of Constrained Ring Rolling of Thin-Walled Conical Rings with Inner High Ribs Combining Response Surface Method with FEM
Abstract
:1. Introduction
2. Optimization Method
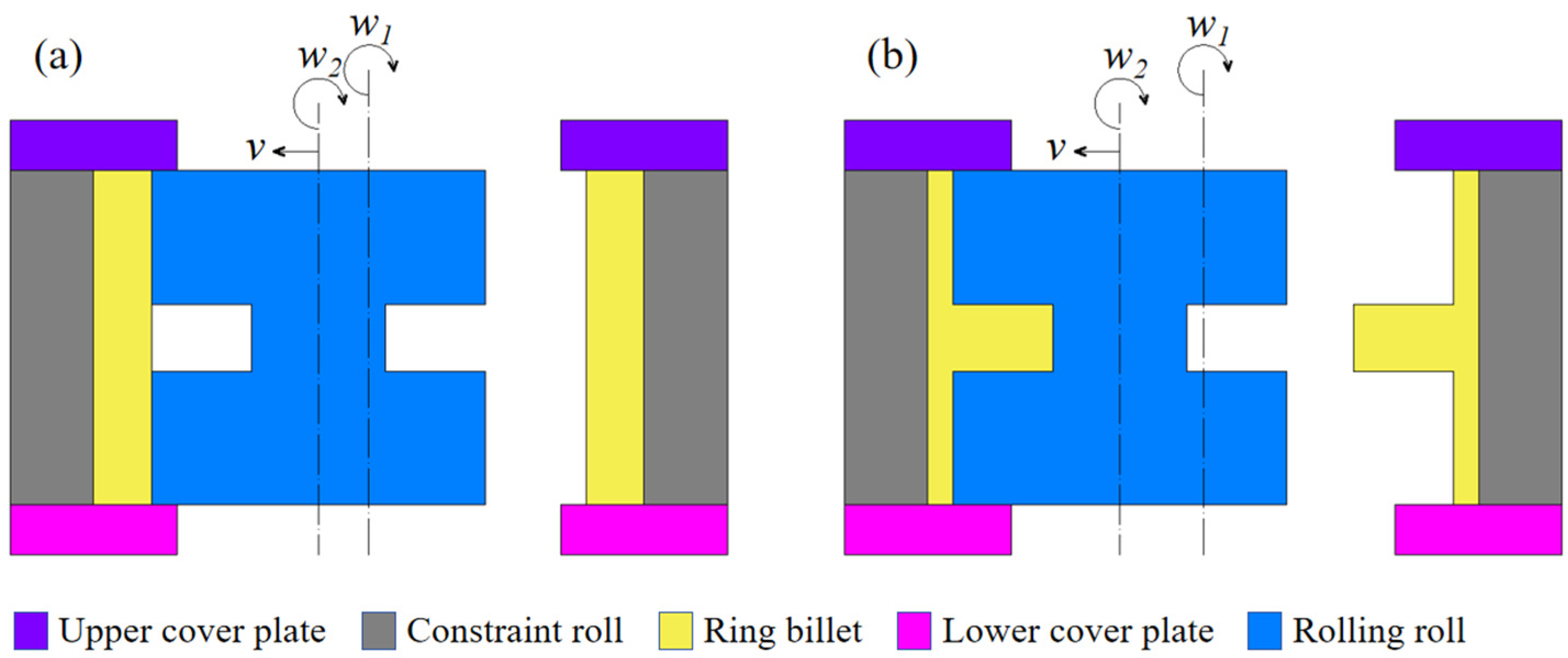
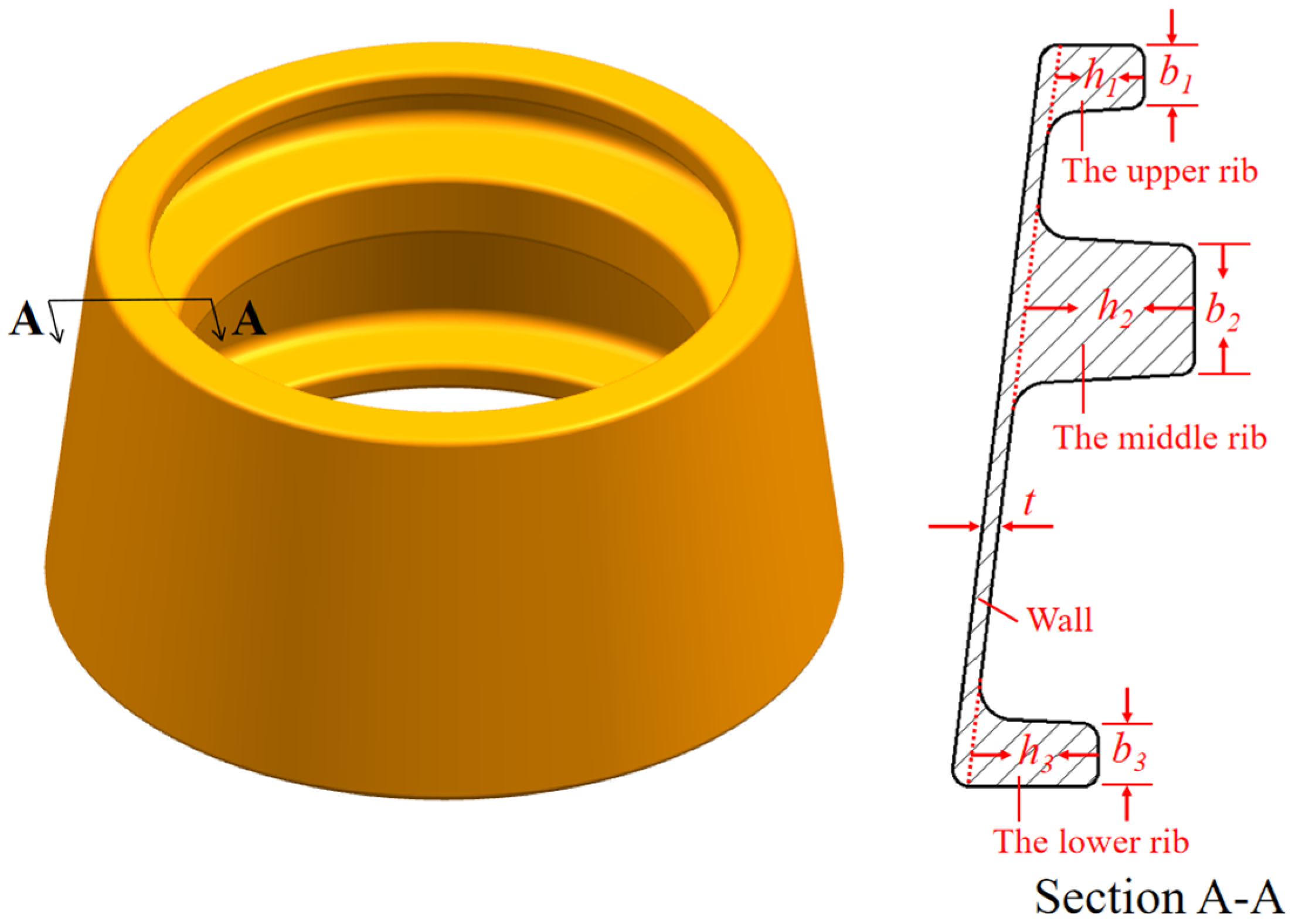
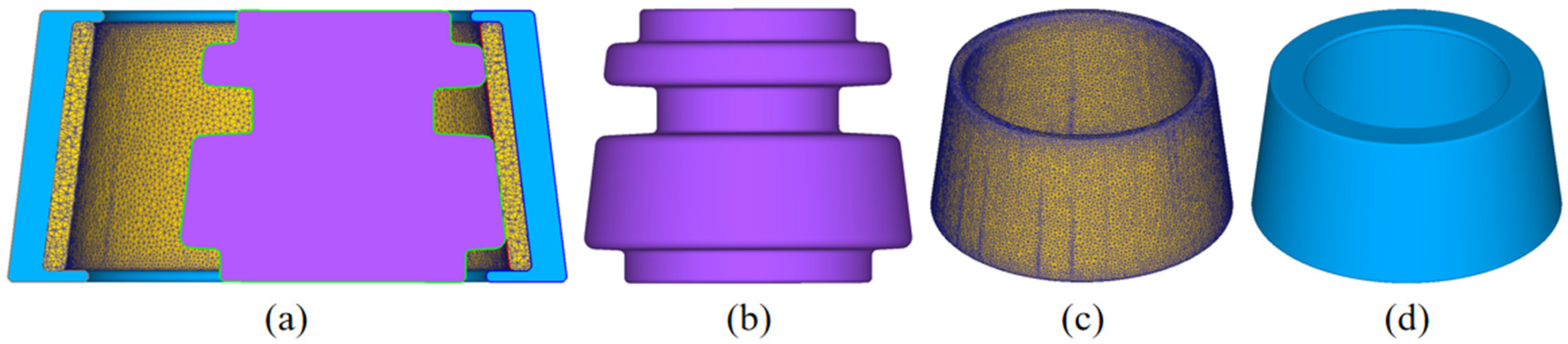
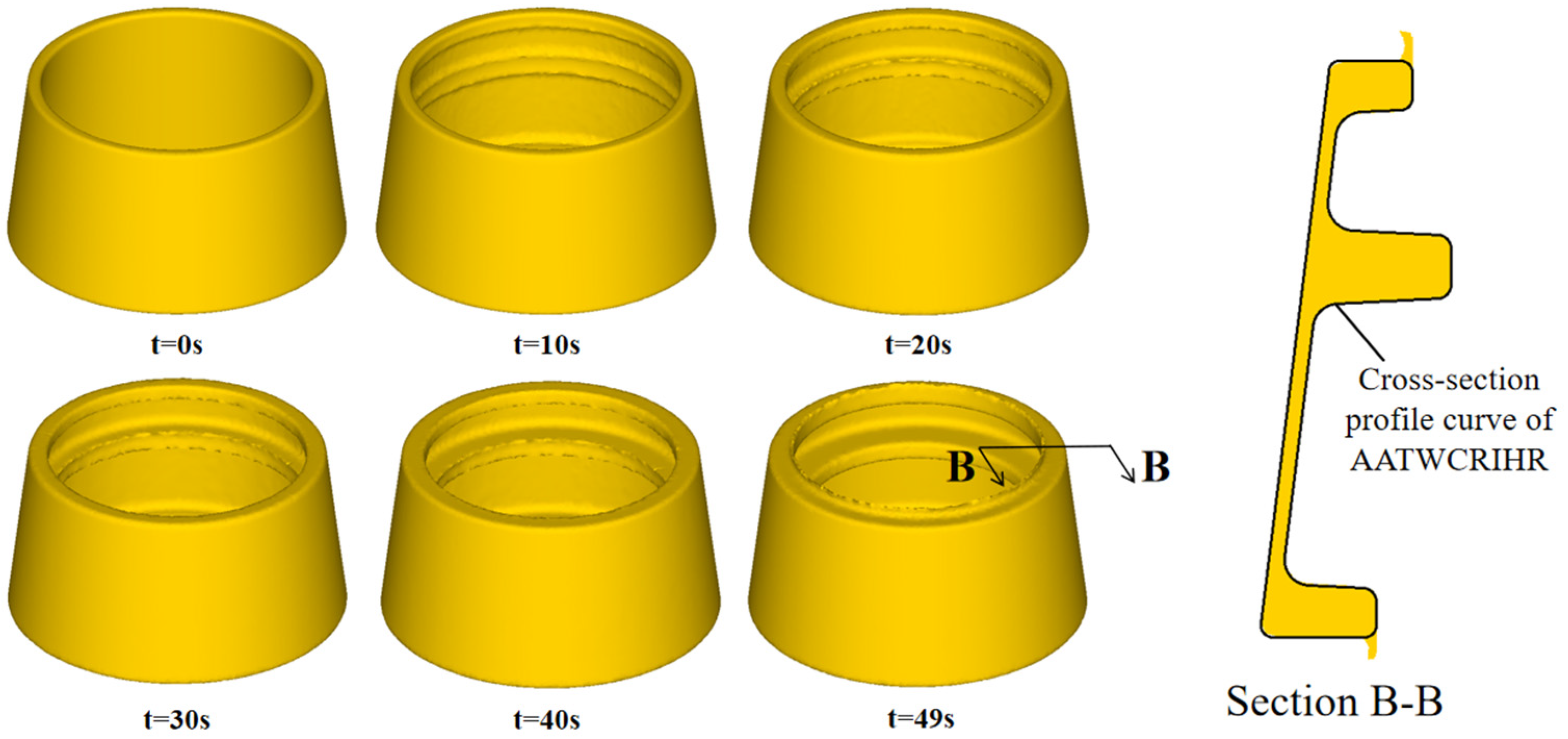
2.1. Establishment of Finite Element Model of Constrained Ring Rolling of AATWCRIHR
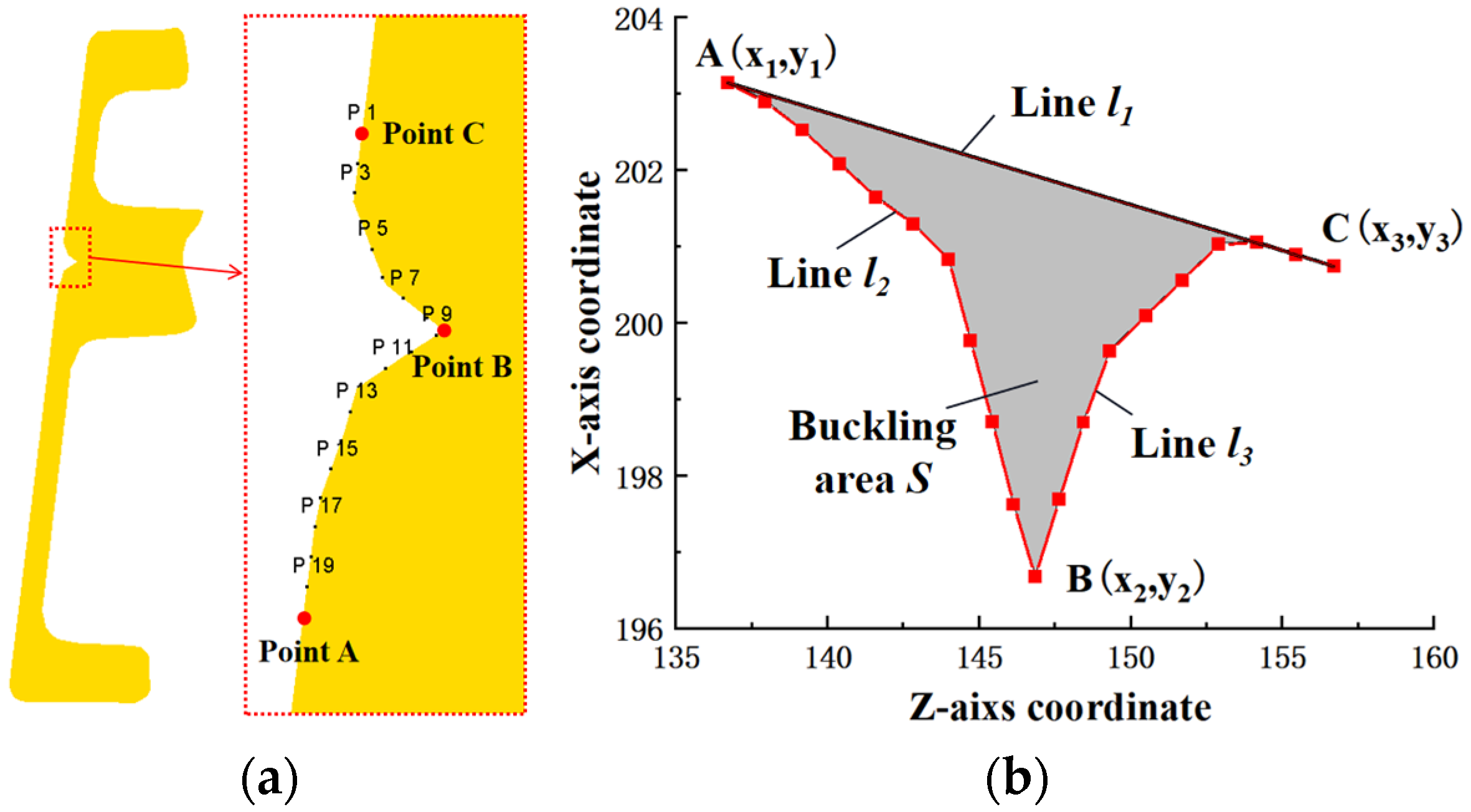
2.2. Evaluation Criteria of Buckling Defect
2.3. Determination of Experimental Scheme
3. Results and Analysis
3.1. Orthogonal Experimental Analysis
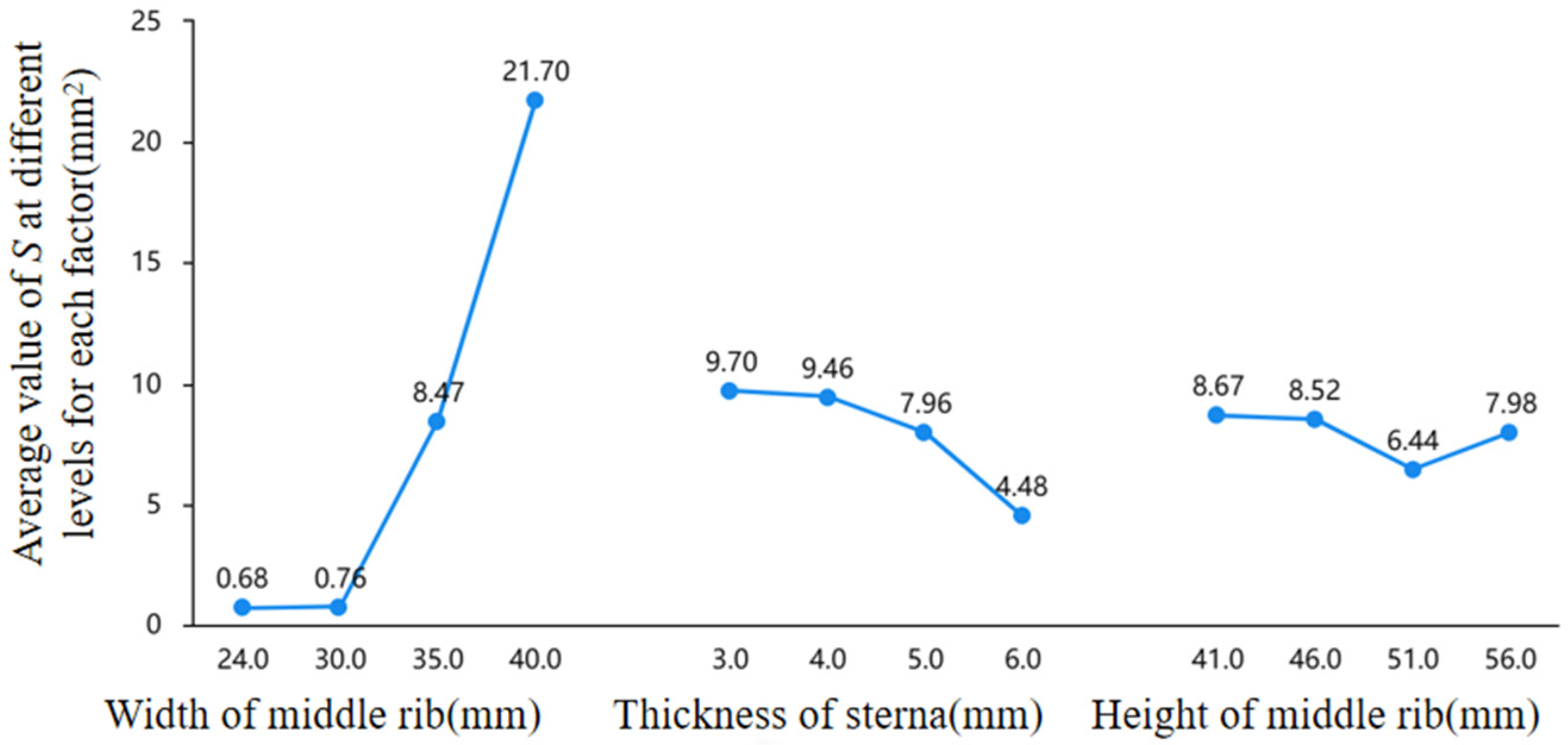
3.2. Orthogonal Experimental Level Analysis
3.3. Establishment of Response Surface Model
0.0035 × A × C + 0.0019 × B × C + 0.1262 × A2 − 0.9025 × B2 + 0.0185 × C2
3.4. Analysis of Variance (ANOVA)
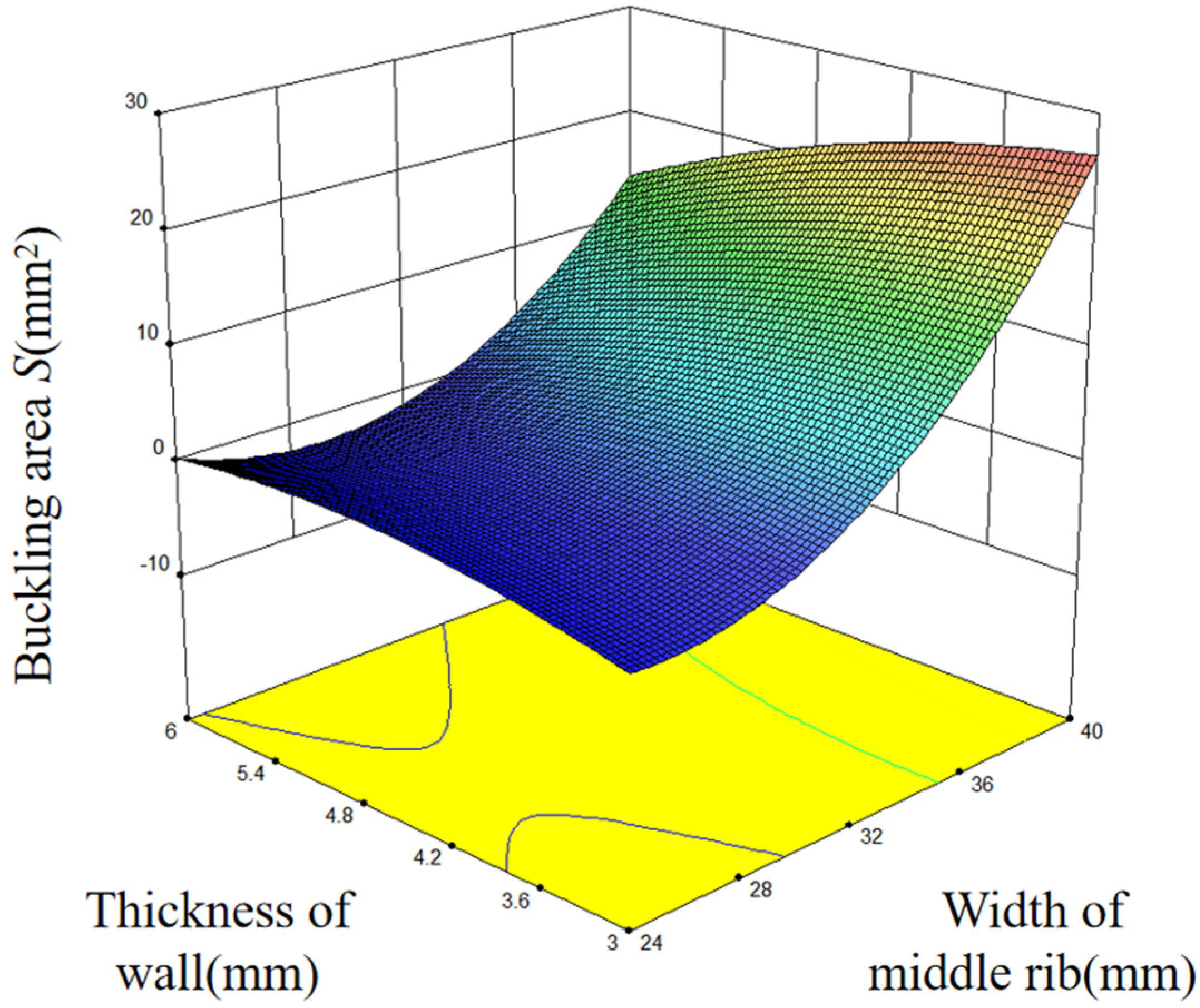
3.5. RSM Analysis
4. Verification Model
5. Conclusions
- The degree of influence on the buckling defect is the width of the middle rib, the wall thickness, and the height of the middle rib, in that order.
- The buckling area is the smallest and the degree of the buckling defect on the back of the middle rib is the lowest when the width of the middle rib is 24 mm, the wall thickness is 6 mm, and the height of the middle rib is 51 mm.
- When the width of the middle rib is larger, the degree of the buckling defect becomes more significant with the decrease in wall thickness. When the width of the middle rib is smaller, the thickness of the wall has little influence on the buckling defect, and the degree of the buckling defect is light.
- The quantitative representation of the buckling defect proposed using the buckling profile S is feasible, and the response surface model can predict the degree of the buckling defect at a given geometry dimension of the middle rib and the wall thickness of the conical ring billet by verification.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qian, D.; Li, G.; Deng, J.; Wang, F. Effect of die structure on extrusion forming of thin-walled component with I-type longitudinal ribs. Int. J. Adv. Manuf. Technol. 2020, 108, 1959–1971. [Google Scholar] [CrossRef]
- Zeng, X.; Fan, X.; Li, H.; Li, S. Flow forming process of thin-walled tubular parts with cross inner ribs. Procedia Manuf. 2018, 15, 1239–1246. [Google Scholar] [CrossRef]
- Lei, Y.; Zhan, M.; Fan, X.; Zhang, A.; Niu, H.; Bai, D.; Gao, P.; Zheng, Z. A review on manufacturing technologies of thin-walled components with ribs. J. Northwestern Polytech. Univ. 2022, 40, 1–17. [Google Scholar] [CrossRef]
- Hua, L.; Pan, L.B.; Lan, J. Researches on the ring stiffness condition in radial–axial ring rolling. J. Mater. Process. Technol. 2009, 209, 2570–2575. [Google Scholar] [CrossRef]
- Kopp, R.; Böhlke, P. A New Rolling Process for Strips with a Defined Cross Section. CIRP Ann. 2003, 52, 197–200. [Google Scholar] [CrossRef]
- Cleaver, C.J.; Lohmar, J.; Tamimi, S. Limits to making L-shape ring profiles without ring growth. J. Mater. Process. Technol. 2021, 292, 117062. [Google Scholar] [CrossRef]
- Lohmar, J.; Cleaver, C.J.; Allwood, J.M. The influence of constraint rolls on temperature evolution and distribution in radial ring rolling. J. Mater. Process. Technol. 2020, 282, 116663. [Google Scholar] [CrossRef]
- Li, X.; Guo, L.; Wang, F. On a plastic instability criterion for ultra-large radial-axial ring rolling process with four guide rolls. Chin. J. Aeronaut. 2021, 35, 391–406. [Google Scholar] [CrossRef]
- Yeom, J.-T.; Kim, J.H.; Park, N.K.; Choi, S.-S.; Lee, C.S. Ring-rolling design for a large-scale ring product of Ti-6Al-4V alloy. J. Mater. Process. Technol. 2007, 187, 747–751. [Google Scholar] [CrossRef]
- Liang, L.; Guo, L.; Liu, Z.H.; Wang, P.-P.; Zhang, H. On a precision forming criterion for groove-section profiled ring rolling process. J. Mater. Process. Technol. 2021, 296, 117207. [Google Scholar] [CrossRef]
- Han, X.; Hua, L.; Lu, P.; Wei, F. An innovative radial envelope forming method for manufacturing thin-walled cylindrical ring with inner web ribs. J. Mater. Process. Technol. 2020, 286, 116836. [Google Scholar] [CrossRef]
- Tian, D.; Han, X.; Hua, L.; Wang, X.; Chen, F. Constraining ring rolling of thin-walled conical rings with transverse ribs. Int. J. Mech. Sci. 2022, 226, 107394. [Google Scholar] [CrossRef]
- Hua, L.; Deng, J.; Qian, D.; Lan, J.; Long, H. Modeling and application of ring stiffness condition for radial-axial ring rolling. Int. J. Mach. Tools Manuf. 2016, 110, 66–79. [Google Scholar] [CrossRef]
- Tian, D.; Han, X.; Hua, L.; Hu, X. An innovative constraining ring rolling process for manufacturing conical rings with thin sterna and high ribs. Chin. J. Aeronaut. 2022, 35, 324–339. [Google Scholar] [CrossRef]
- Zheng, Y. Multi-objective Optimization of Process Parameters of Aluminium Alloy Rib-web Forgings Based on Orthogonal Experiment. Hot Work. Technol. 2015, 44, 168–172. [Google Scholar]
- Zhao, G.; Wright, E.D.; Grandhi, R.V. Preform Die Shape Design in Metal Forming Using an Optimization Method. Int. J. Numer. Methods Eng. 1997, 40, 1213–1230. [Google Scholar] [CrossRef]
- Fourment, L.; Chenot, J.L. Optimal Design for Non-Steady-State Metal Forming Processes—I. Shape Optimization Method. Int. J. Numer. Methods Eng. 1996, 39, 33–50. [Google Scholar] [CrossRef]
- Kusiak, J. A technique of tool-shape optimization in large scale problems of metal forming. J. Mater. Process. Technol. 1996, 57, 79–84. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Gheysarian, A.; Honarpisheh, M. Process Parameters Optimization of the Explosive-Welded Al/Cu Bimetal in the Incremental Sheet Metal Forming Process. Iran. J. Sci. Technol. Trans. Mech. Eng. 2018, 43, 945–956. [Google Scholar] [CrossRef]
- Gulati, V.; Aryal, A.; Katyal, P.; Goswami, A. Process Parameters Optimization in Single Point Incremental Forming. J. Inst. Eng. (India) Ser. C 2015, 97, 185–193. [Google Scholar] [CrossRef]
- Pan, Y.; Cai, G. Optimization of Processing Parameters of Aluminum Alloy Cylindrical Parts Based on Response Surface Method during Hydromechanical Deep Drawing. Metals 2023, 13, 1406. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Z.; Jia, H.; Ren, M. The Optimization of Welding Spots’ Arrangement in A-Pillar Patchwork Blank Hot Stamping. Metals 2023, 13, 1409. [Google Scholar] [CrossRef]
- Hu, J.; Wen, T.; Zhang, M.; Zhang, Z. Optimization on rolling process parameters for rib stiffened plates based on respond surface method. Forg. Stamp. Technol. 2019, 44, 35–40. [Google Scholar]
- Hu, Z.; Wei, Z.; Sun, H.; Yang, J.; Wei, L. Optimization of Metal Rolling Control Using Soft Computing Approaches: A Review. Arch. Comput. Methods Eng. 2019, 28, 405–421. [Google Scholar] [CrossRef]
- Feng, W.; Hua, L. Multi-objective optimization of process parameters for the helical gear precision forging by using Taguchi method. J. Mech. Sci. Technol. 2011, 25, 1519–1527. [Google Scholar]
- Feng, W.; Hua, L. Process Parameters Optimisation for Helical Gears Precision Forging with Damage Minimization. In Proceedings of the 2010 International Conference on Digital Manufacturing & Automation, Changsha, China, 18–20 December 2010; pp. 117–120. [Google Scholar]
- Anupama Francy, K.; Sai Sudheer, S.V.; Naga Krishna, N.; Gopalakrishnaih, P. Optimization of input process parameters for Al 2024 alloy in cold extrusion process. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Li, H.; Chang, C.; Huang, Y.; Fu, R.; Shao, H. Optimization of numerical parameters and microstructure evolution on 2195 Al–Li alloy extrusion process. J. Mater. Res. Technol. 2023, 26, 7694–7706. [Google Scholar] [CrossRef]
- Luo, W.; Tang, L.; Guo, F. Mold design and forming process parameters optimization for passenger vehicle front wing plate. J. Mech. Sci. Technol. 2022, 36, 187–196. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Sedighi, M.; Mosayebnezhad, J. Numerical and experimental investigation of central cavity formation in aluminum during forward extrusion process. J. Mech. Sci. Technol. 2016, 30, 1951–1956. [Google Scholar] [CrossRef]


| Parameter | Tensile Strength (MPa) | Yield Strength (MPa) | Elastic Modulus (GPa) | Poisson’s Ratio | Thermal Conductivity (W × m−1 × K−1) | Specific Heat Capacity (J × Kg−1 K−1) |
|---|---|---|---|---|---|---|
| Value | 175 | 75 | 73 | 0.33 | 180.2 | 901 |
| Symbol | Factors | Level 1 | Level 2 | Level 3 | Level 4 |
|---|---|---|---|---|---|
| A | Width of rib/b2 (mm) | 24 | 30 | 35 | 40 |
| B | Thickness of wall/t (mm) | 3 | 4 | 5 | 6 |
| C | Height of rib/h2 (mm) | 41 | 46 | 51 | 56 |
| Experiment NO. | A (mm) | B (mm) | C (mm) | S (mm2) |
|---|---|---|---|---|
| 1 | 24 | 3 | 41 | 0.58 |
| 2 | 24 | 4 | 56 | 0.85 |
| 3 | 24 | 5 | 51 | 0.87 |
| 4 | 24 | 6 | 46 | 0.44 |
| 5 | 30 | 3 | 46 | 0.57 |
| 6 | 30 | 4 | 56 | 0.83 |
| 7 | 30 | 5 | 51 | 0.82 |
| 8 | 30 | 6 | 41 | 0.83 |
| 9 | 35 | 3 | 51 | 11.35 |
| 10 | 35 | 4 | 41 | 10.85 |
| 11 | 35 | 5 | 46 | 7.75 |
| 12 | 35 | 6 | 56 | 3.92 |
| 13 | 40 | 3 | 56 | 26.30 |
| 14 | 40 | 4 | 46 | 25.32 |
| 15 | 40 | 5 | 41 | 22.42 |
| 16 | 40 | 6 | 51 | 12.75 |
| K1 | 0.68 | 9.70 | 8.67 | |
| K2 | 0.76 | 9.46 | 8.52 | |
| K3 | 8.47 | 7.69 | 6.44 | |
| K4 | 21.70 | 4.48 | 7.98 | |
| Range Rs | −21.01 | −5.21 | −2.23 |
| Source | Sum of Squares | DOF | Mean Square | F-Value | p-Value | Degree of Significance |
|---|---|---|---|---|---|---|
| Model | 1316.65 | 9 | 146.29 | 104.82 | <0.0001 | significant |
| A | 926.77 | 1 | 926.77 | 664.04 | <0.0001 | |
| B | 47.21 | 1 | 47.21 | 33.83 | 0.0011 | |
| C | 10.96 | 1 | 10.96 | 7.85 | 0.0311 | |
| AB | 38.32 | 1 | 38.32 | 27.46 | 0.0019 | |
| AC | 0.073 | 1 | 0.073 | 0.052 | 0.8269 | |
| BC | 1.206 × 10−3 | 1 | 1.206 × 10−3 | 8.640 × 10−4 | 0.9775 | |
| A2 | 211.28 | 1 | 211.28 | 151.38 | <0.0001 | |
| B2 | 4.57 | 1 | 4.57 | 3.27 | 0.1205 | |
| C2 | 3.40 | 1 | 3.40 | 2.44 | 0.1695 | |
| Residual error | 8.37 | 6 | 1.40 | |||
| Correlation coefficient R2 | Modified coefficient of determination Radj2 | Model prediction coefficient Rpred2 | S/N Ratio | |||
| 0.9937 | 0.9842 | 0.9355 | 28.303 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, W.; Zhao, P. Buckling Defect Optimization of Constrained Ring Rolling of Thin-Walled Conical Rings with Inner High Ribs Combining Response Surface Method with FEM. Metals 2024, 14, 378. https://doi.org/10.3390/met14040378
Feng W, Zhao P. Buckling Defect Optimization of Constrained Ring Rolling of Thin-Walled Conical Rings with Inner High Ribs Combining Response Surface Method with FEM. Metals. 2024; 14(4):378. https://doi.org/10.3390/met14040378
Chicago/Turabian StyleFeng, Wei, and Peng Zhao. 2024. "Buckling Defect Optimization of Constrained Ring Rolling of Thin-Walled Conical Rings with Inner High Ribs Combining Response Surface Method with FEM" Metals 14, no. 4: 378. https://doi.org/10.3390/met14040378
APA StyleFeng, W., & Zhao, P. (2024). Buckling Defect Optimization of Constrained Ring Rolling of Thin-Walled Conical Rings with Inner High Ribs Combining Response Surface Method with FEM. Metals, 14(4), 378. https://doi.org/10.3390/met14040378






