Optimization of Welded Joints under Fatigue Loadings
Abstract
1. Introduction
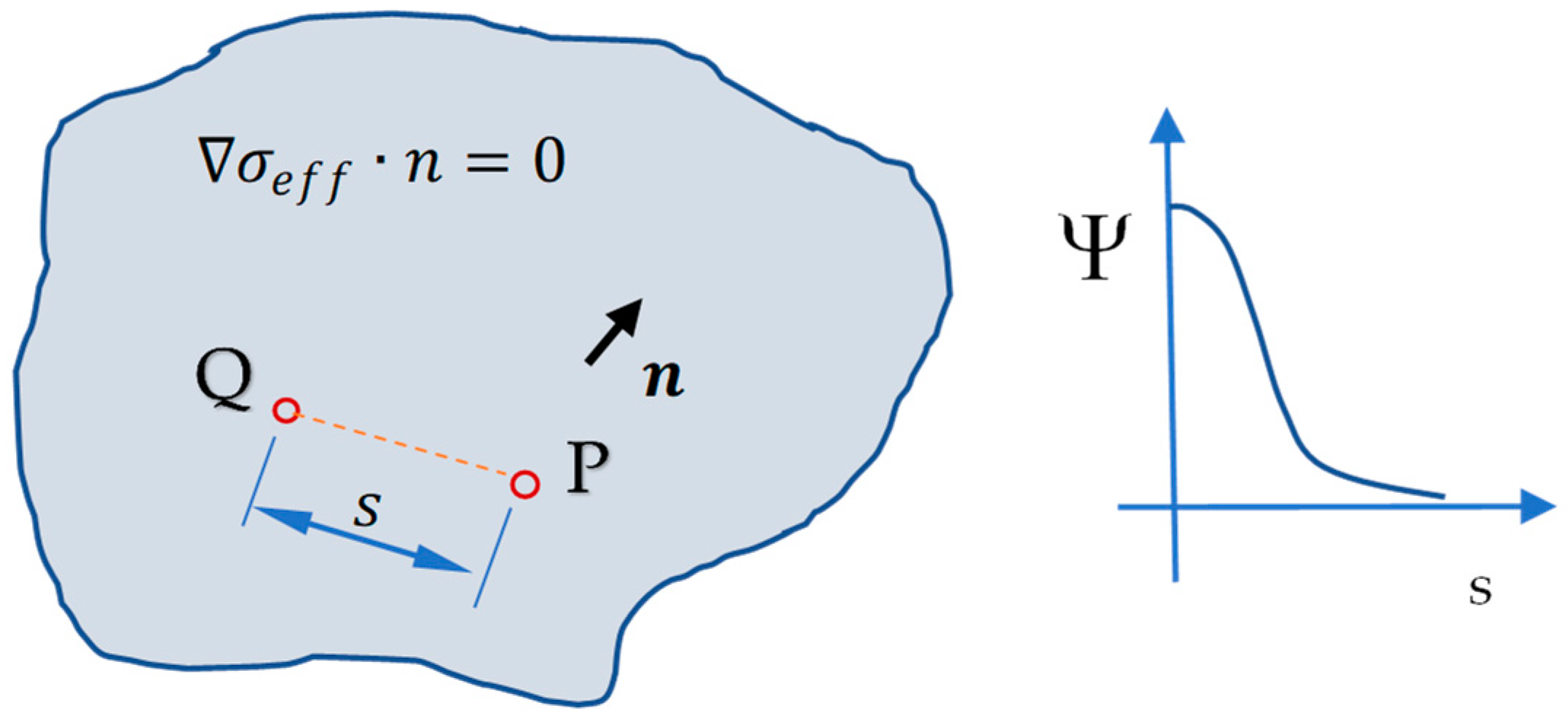
2. The Fatigue Strength Curve for Welds with the Implicit Gradient Method
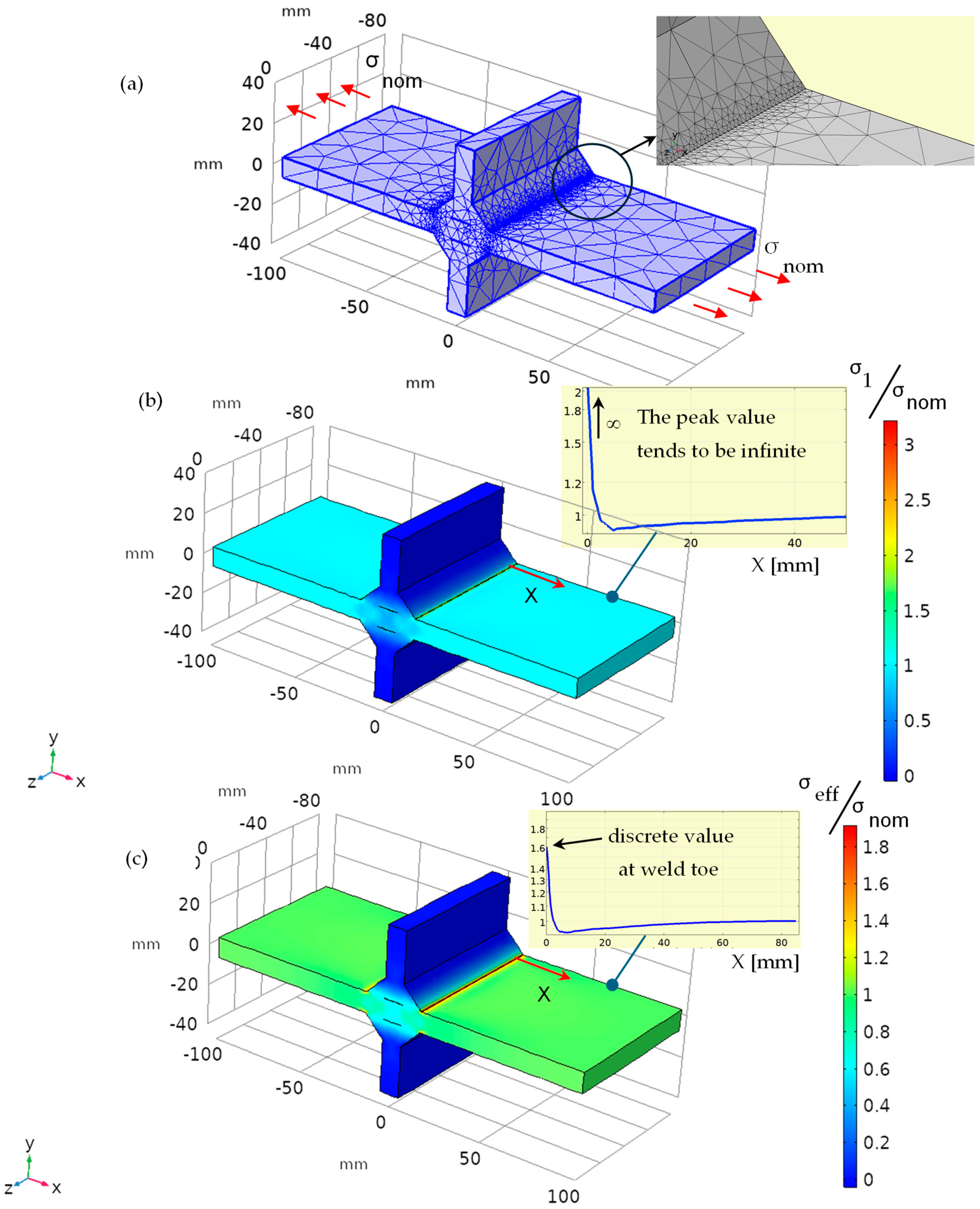
3. Optimisation of the Weld Bead Shape in Load-Carrying Cruciform Joints
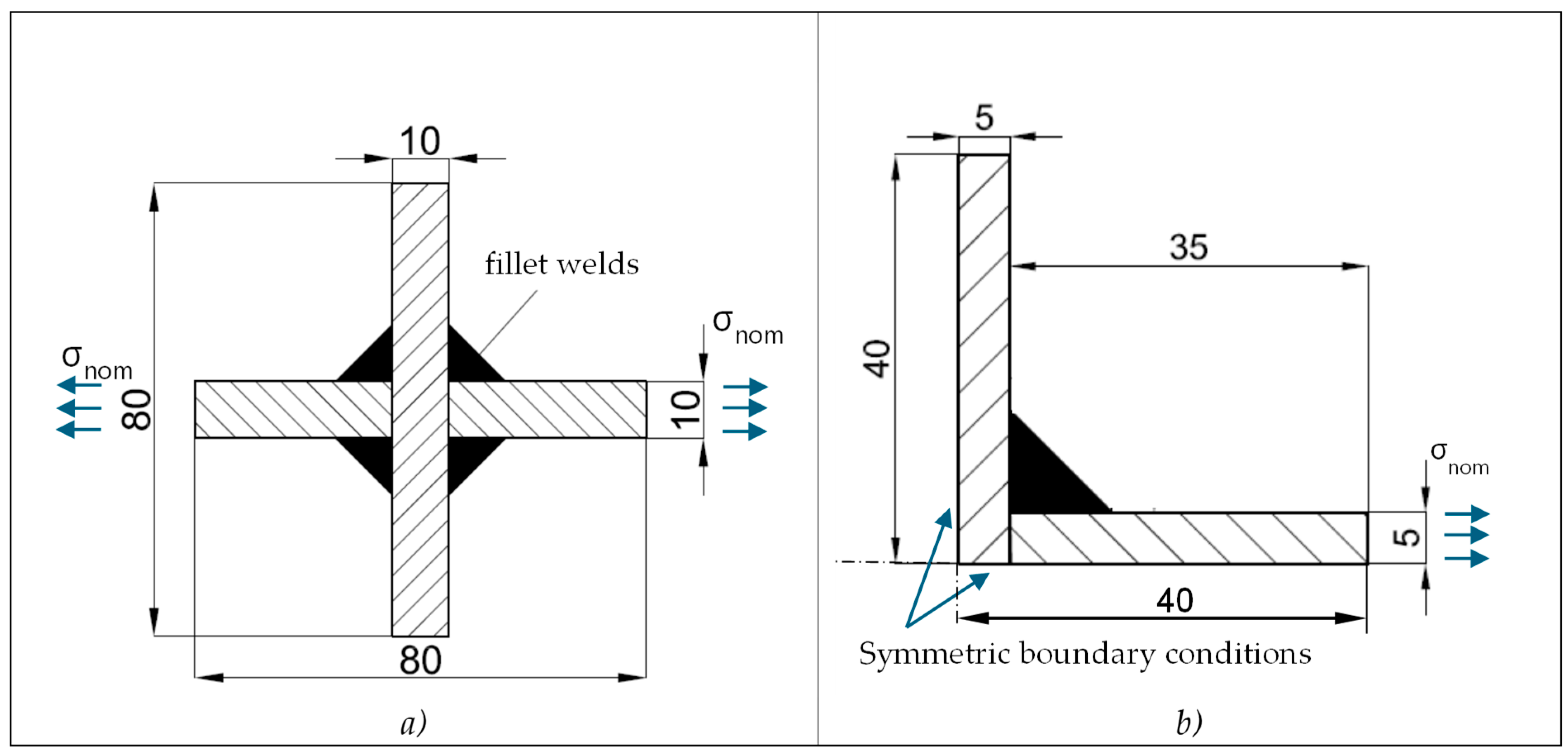
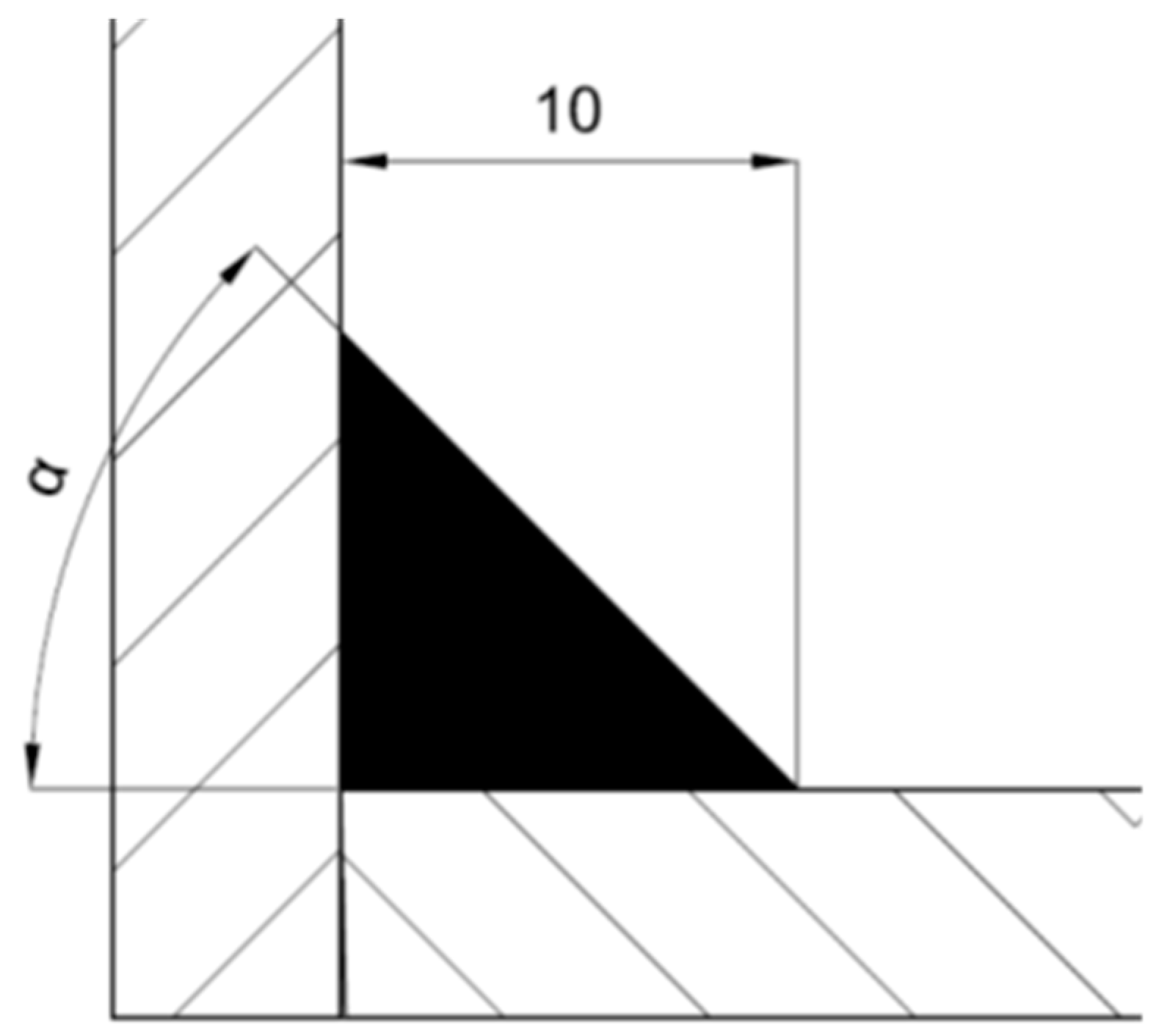
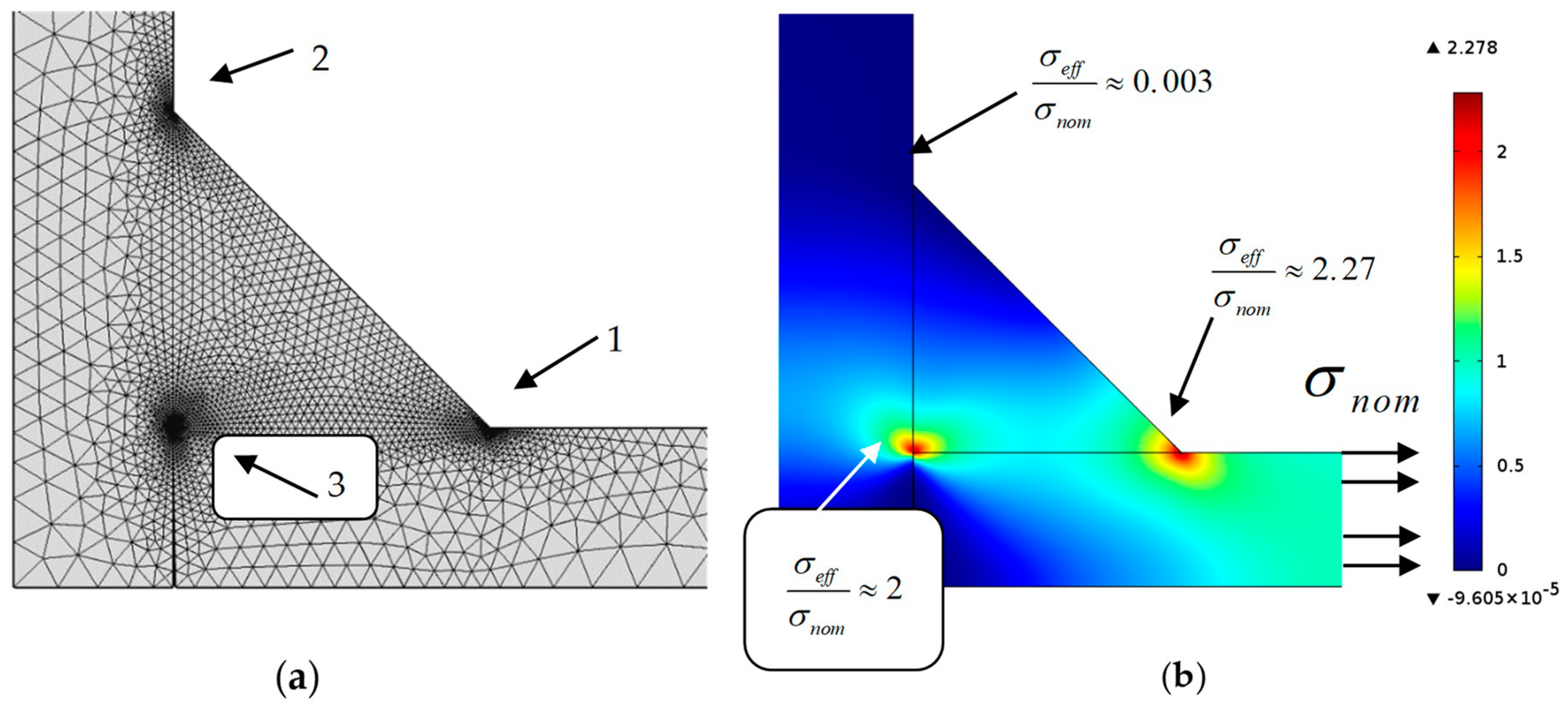
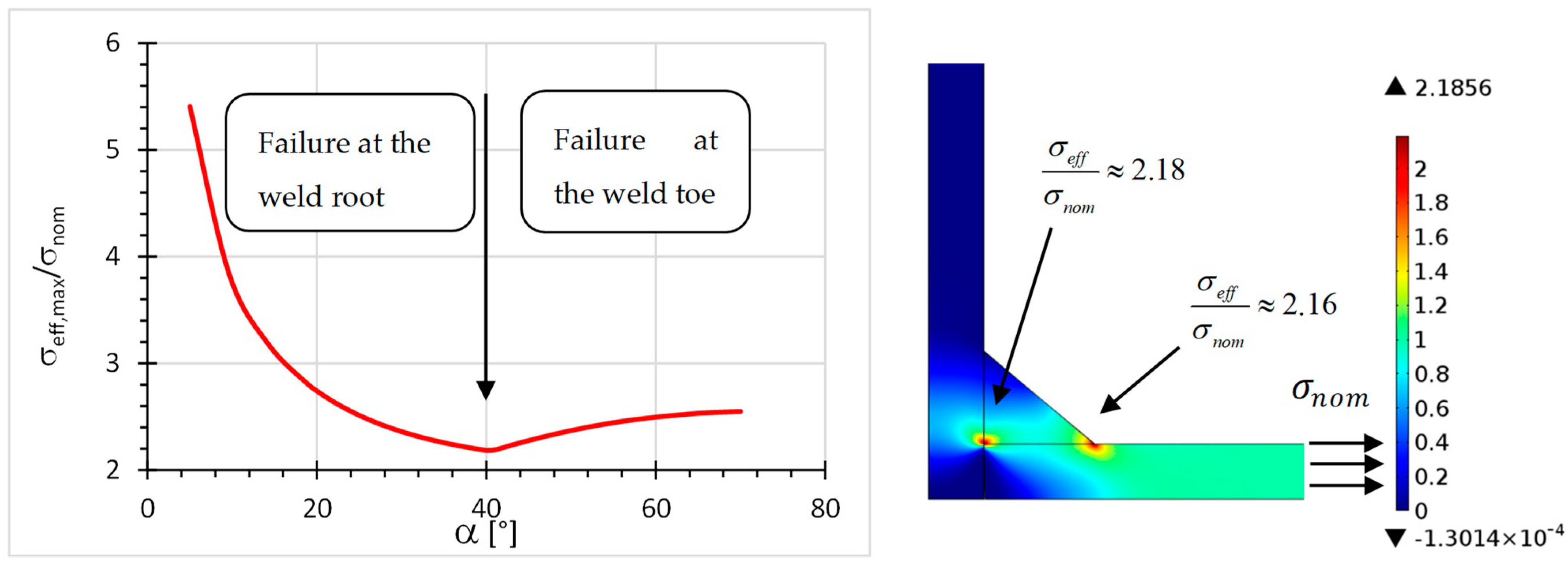
3.1. Weld Bead Optimisation in a Load-Carrying Cruciform Joint with Constant Weld Leg Length under Tensile Loading
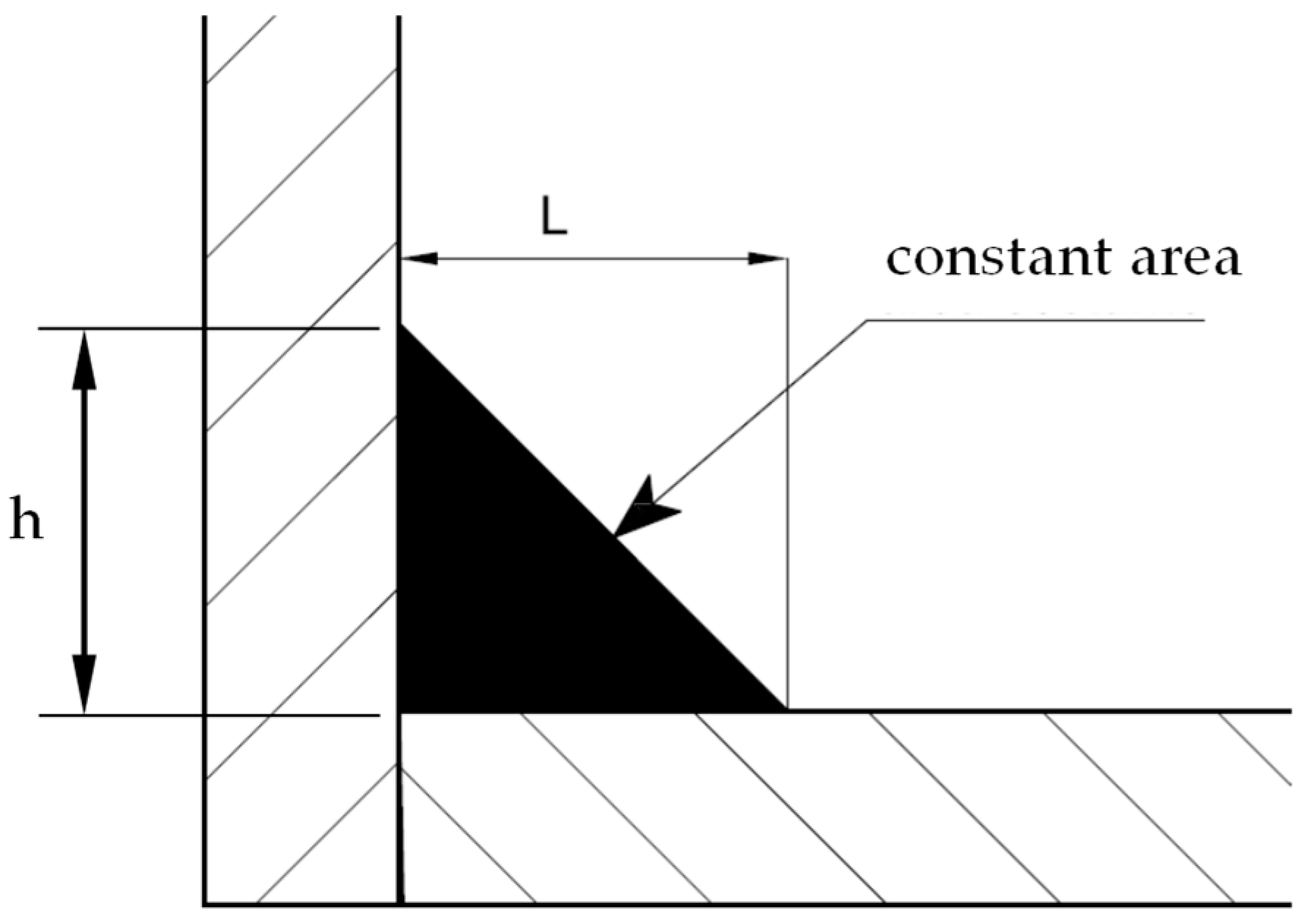
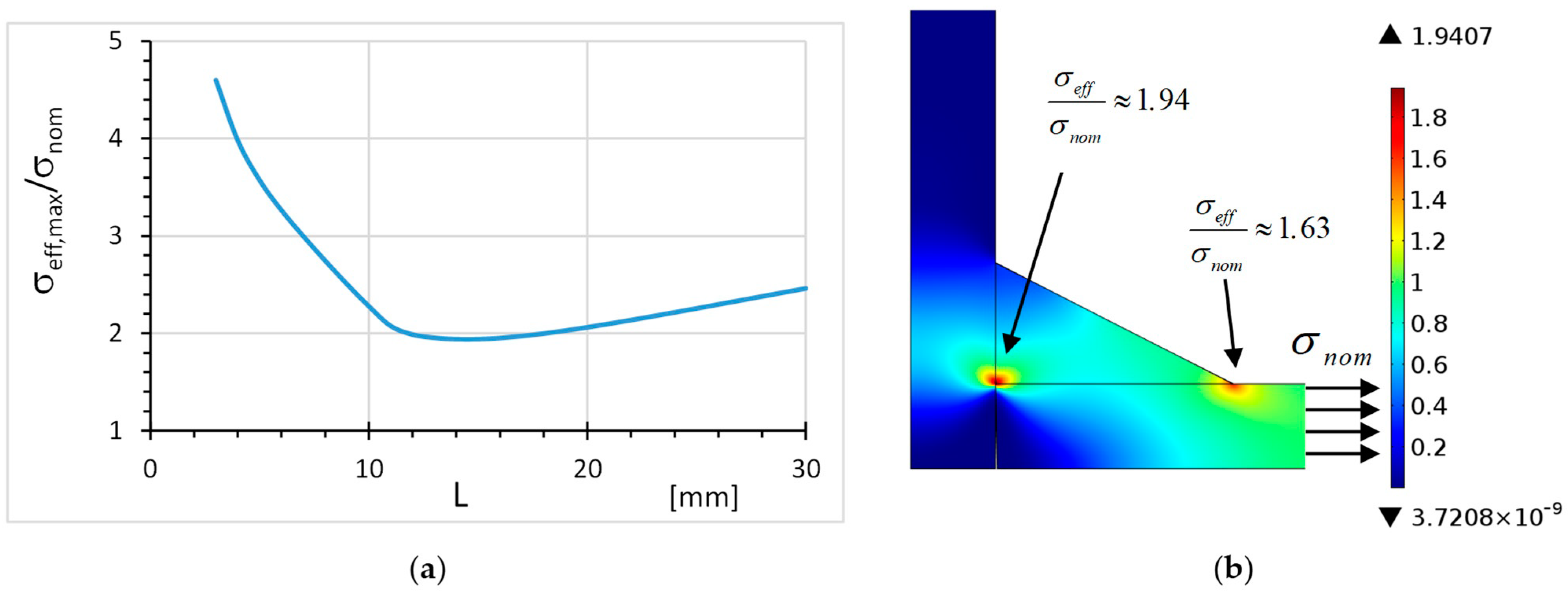
3.2. Weld Bead Optimisation in a Load-Carrying Cruciform Joint with a Constant Area of the Weld under Tensile Loading
4. Optimisation of Spot-Welded Joints
4.1. Lap Joint with a Single Weld Point
4.2. Lap Joint with Two Spot-Welded Points
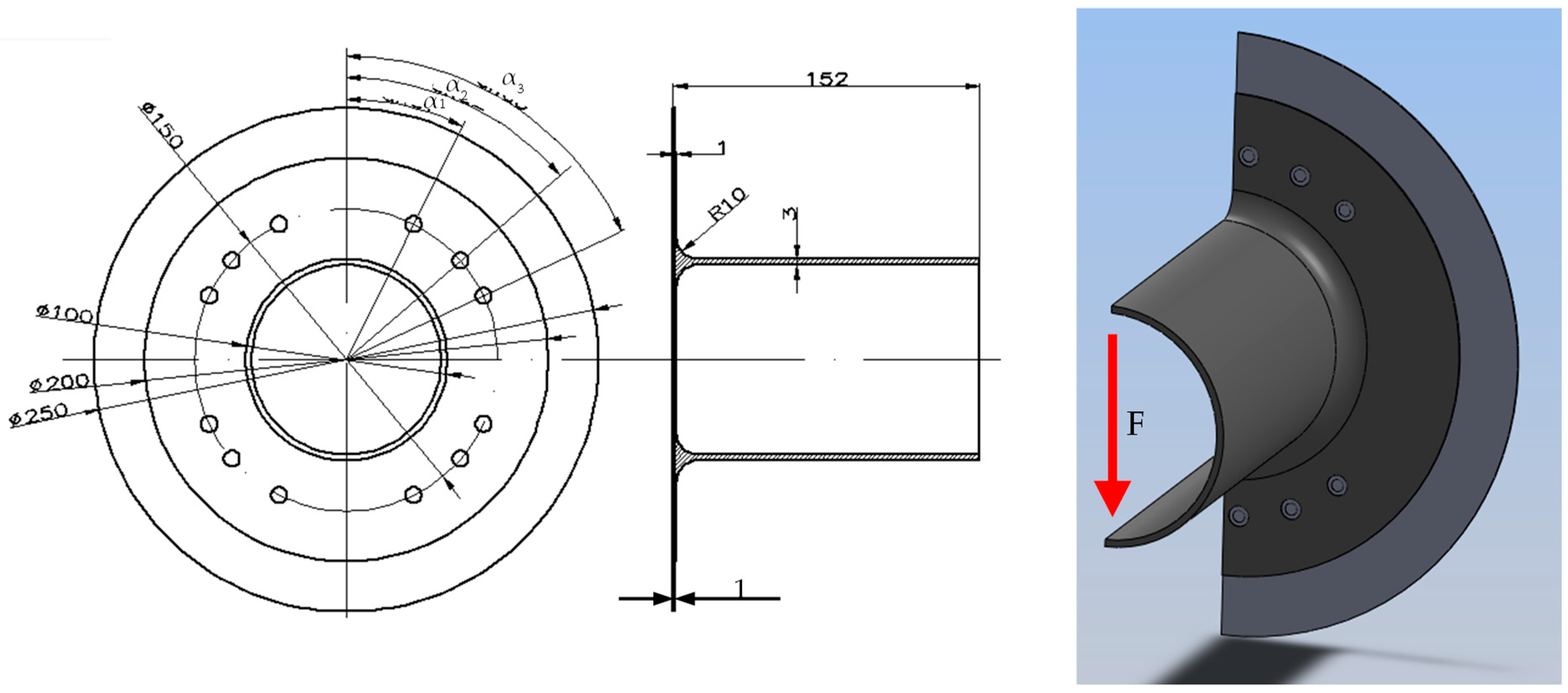
4.3. Tubular T Joints under Bending
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eurocode 3; Design of Steel Structures; General Rules; CEN: Brussels, Belgium, 1993.
- Radaj, D.; Sonsino, C.M.; Fricke, W. Fatigue Assessment of Welded Joints by Local Approaches, 2nd ed.; Woodhead Publishing: Cambridge, UK; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Hobbacher, A. Recommendations for Fatigue Design of Welded Joints and Components; Document XIII-1823e07/XV-1254-07; IIW International Institute of Welding: Paris, France, 2007. [Google Scholar]
- Niemi, E. Recommendations Concerning Stress Determination for Fatigue Analysis of Welded Components; IIW Doc. XIII-1458-92/XV-797-92; IIW International Institute of Welding: Paris, France, 1992. [Google Scholar]
- Karabulut, B.; Rossi, B. On the applicability of the hot spot stress method to high strength duplex and carbon steel welded details. Eng. Fail. Anal. 2021, 128, 105629. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, Y.; Wang, W.; Xie, W.; Ying, T.; Yue, G. Investigation of hot spot stress for welded tubular K-joints with stiffeners. J. Constr. Steel Res. 2002, 197, 107452. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, Y.; Jiang, W.; Pei, X.; Wang, P.; Dong, P.; Wang, B.; Xie, X. Notch structural stress theory: Part II predicting total fatigue lives of notched structures. Int. J. Fatigue 2024, 182, 108201. [Google Scholar] [CrossRef]
- Radaj, D. Design and Analysis of Fatigue Resistant Welded Structures; Abbington Publishing: Cambridge, UK, 1990. [Google Scholar]
- Sonsino, C.M.; Baumgartner, J.; Breitenberger, M. Equivalent stress concepts for transforming of variable amplitude into constant amplitude loading and consequences for design and durability approval. Int. J. Fatigue 2022, 162, 106949. [Google Scholar] [CrossRef]
- Ng, C.T.; Sonsino, C.M.; Susmel, L. Multiaxial fatigue assessment of welded joints: A review of Eurocode 3 and International Institute of Welding criteria with different stress analysis approaches. Fatigue Fract. Eng. Mater. Struct. 2024, 1–34. [Google Scholar] [CrossRef]
- Karakaş, Ö.; Baumgartner, J.; Susmel, L. On the use of a fictitious notch radius equal to 0.3 mm to design against fatigue welded joints made of wrought magnesium alloy AZ31. Int. J. Fatigue 2020, 139, 105747. [Google Scholar] [CrossRef]
- Glienke, R.; Kalkowsky, F.; Hobbacher, A.F.; Holch, A.; Thiele, M.; Marten, F.; Kersten, R.; Henkel, K.-M. Evaluation of the Fatigue Resistance of Butt-Welded Joints in Towers of Wind Turbines—A Comparison of Experimental Studies with Small Scale and Component Tests as Well as Numerical Based Approaches with Local Concepts. Weld. World 2024, 68, 1143–1168. [Google Scholar] [CrossRef]
- Lazzarin, P.; Zambardi, R. A finite-volume-energy based approach to predict the static and fatigue behavior of components with sharp V-shaped notches. Int. J. Fract. 2001, 112, 275–298. [Google Scholar] [CrossRef]
- Livieri, P.; Lazzarin, P. Fatigue strength of steel and aluminium welded joints based on generalised stress intensity factors and local strain energy values. Int. J. Fract. 2005, 133, 247–276. [Google Scholar] [CrossRef]
- Schuscha, M.; Leitner, M.; Stoschka, M.; Meneghetti, G. Local strain energy density approach to assess the fatigue strength of sharp and blunt V-notches in cast steel. Int. J. Fatigue 2020, 132, 105334. [Google Scholar] [CrossRef]
- Shoda, K.; Arai, K.; Nakamura, S.; Okada, H. Application of redefined J-integral range ΔJ for ultra-low cycle fatigue problems with large magnitude of elastic-plastic deformation. Theor. Appl. Fract. Mech. 2023, 126, 103938. [Google Scholar] [CrossRef]
- Meneghetti, G.; Campagnolo, A. State-of-the-art review of peak stress method for fatigue strength assessment of welded joints. Int. J. Fatigue 2020, 139, 105705. [Google Scholar] [CrossRef]
- Visentin, A.; Campagnolo, A.; Meneghetti, G. Analytical expressions to estimate rapidly the notch stress intensity factors at V-notch tips using the Peak Stress Method. Fatigue Fract. Eng. Mater. Struct. 2022, 46, 1572–1595. [Google Scholar] [CrossRef]
- Tovo, R.; Livieri, P. An implicit gradient application to fatigue of sharp notches and weldments. Eng. Fract. Mech. 2007, 74, 515–526. [Google Scholar] [CrossRef]
- Livieri, P.; Tovo, R. Overview of the geometrical influence on the fatigue strength of steel butt welds by a nonlocal approach. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 502–514. [Google Scholar] [CrossRef]
- Livieri, P.; Tovo, R. Fatigue strength of aluminium welded joints by a non-local approach. Int. J. Fatigue 2021, 143, 106000. [Google Scholar] [CrossRef]
- Tovo, R.; Livieri, P. A numerical approach to fatigue assessment of spot weld joints. Fatigue Fract. Eng. Mater. Struct. 2011, 34, 32–45. [Google Scholar] [CrossRef]
- Allaire, G.; Craig, A. Numerical Analysis and Optimization: An Introduction to Mathematical Modelling and Numerical Simulation; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Amiri, N.; Farrahi, G.H.; Kashyzadeh, K.R.; Chizari, M. Applications of ultrasonic testing and machine learning methods to predict the static & fatigue behavior of spot-welded joints. J. Alloys Compd. 2020, 980, 173664. [Google Scholar]
- Yu, Z.; Ma, N.; Murakawa, H.; Watanabe, G.; Liu, M.; Ma, Y. Prediction of the fatigue curve of high—Strength steel resistance spot welding joints by finite element analysis and machine learning. Int. J. Adv. Manuf. Tech. 2023, 128, 63–2779. [Google Scholar] [CrossRef]
- Pijaudier-Cabot, G.; Bažant, Z.P. Nonlocal Damage Theory. J. Eng. Mech. 1987, 10, 1512–1533. [Google Scholar] [CrossRef]
- Bažant, Z.P. Imbrigate continuum and its variational derivation. J. Eng. Mech. Div. ASCE 1984, 110, 1693–1712. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; de Borst, R.; Brekelmans, W.A.M.; de Vree, J.H.P. Gradient enhanced damage for quasi-brittle material. Int. J. Numer. Methods Eng. 1996, 39, 3391–3403. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; Geers, M.G.D.; de Borst, R.; Brekelmans, W.A.M. A critical comparison of nonlocal and gradient-enhanced softening continua. Int. J. Solids Struct. 2001, 38, 7723–7746. [Google Scholar] [CrossRef]
- Aifantis, E.C. Update on a class of gradient theories. Mech. Mater. 2003, 35, 259–280. [Google Scholar] [CrossRef]
- Williams, M.L. Stress singularities resulting from various boundary conditions in angular corners of plates in extension. J. Appl. Mech. 1952, 19, 526–528. [Google Scholar] [CrossRef]
- Tovo, R.; Livieri, P. An implicit gradient application to fatigue of complex structures. Eng. Fract. Mech. 2008, 75, 1804–1814. [Google Scholar] [CrossRef]
- Haibach, E. Service Fatigue-Strength—Methods and Data for Structural Analysis; VDI-Verlag: Dusseldorf, Germany, 1989. [Google Scholar]
- Sakaguchi, M.; Kurokawa, Y.; Nakamura, F.; Hashimura, T. Fatigue strength of steel–aluminum alloy dissimilar lap joints fabricated by dimple spot welding for automotive application. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 939–951. [Google Scholar] [CrossRef]
- Yang, L.; Yang, B.; Yang, G.; Xiao, S.; Zhu, T.; Wang, F. A comparative study of fatigue estimation methods for single-spot and multispot welds. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1142–1158. [Google Scholar] [CrossRef]
- Tanegashima, R.; Ohara, I.; Akebono, H.; Kato, M.; Sugeta, A. Cumulative fatigue damage evaluations on spot-welded joints using 590 MPa-class automobile steel. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 870–879. [Google Scholar] [CrossRef]
- Pan, N.; Sheppard, S. Spot welds fatigue life prediction with cyclic strain range. Int. J. Fatigue 2002, 24, 519–528. [Google Scholar] [CrossRef]
- Long, X.; Khanna, S.K. Fatigue properties and failure characterization of spot welded high strength steel sheet. Int. J. Fatigue 2007, 29, 879–886. [Google Scholar] [CrossRef]
- Lin, S.-H.; Pan, J.; Wung, P.; Chiang, J. A fatigue crack growth model for spot welds under cyclic loading conditions. Int. J. Fatigue 2006, 28, 792–803. [Google Scholar] [CrossRef]
- Gao, Y.; Chucas, D.; Lewis, C.; McGregor, I.J. Rewiew of CAE fatigue analysis techniques for spot-welded high strength steel automotive structures. In SAE 2001 World Congress; 2001-01-0835; SAE Transactions: Warrendale, PA, USA, 2001. [Google Scholar]

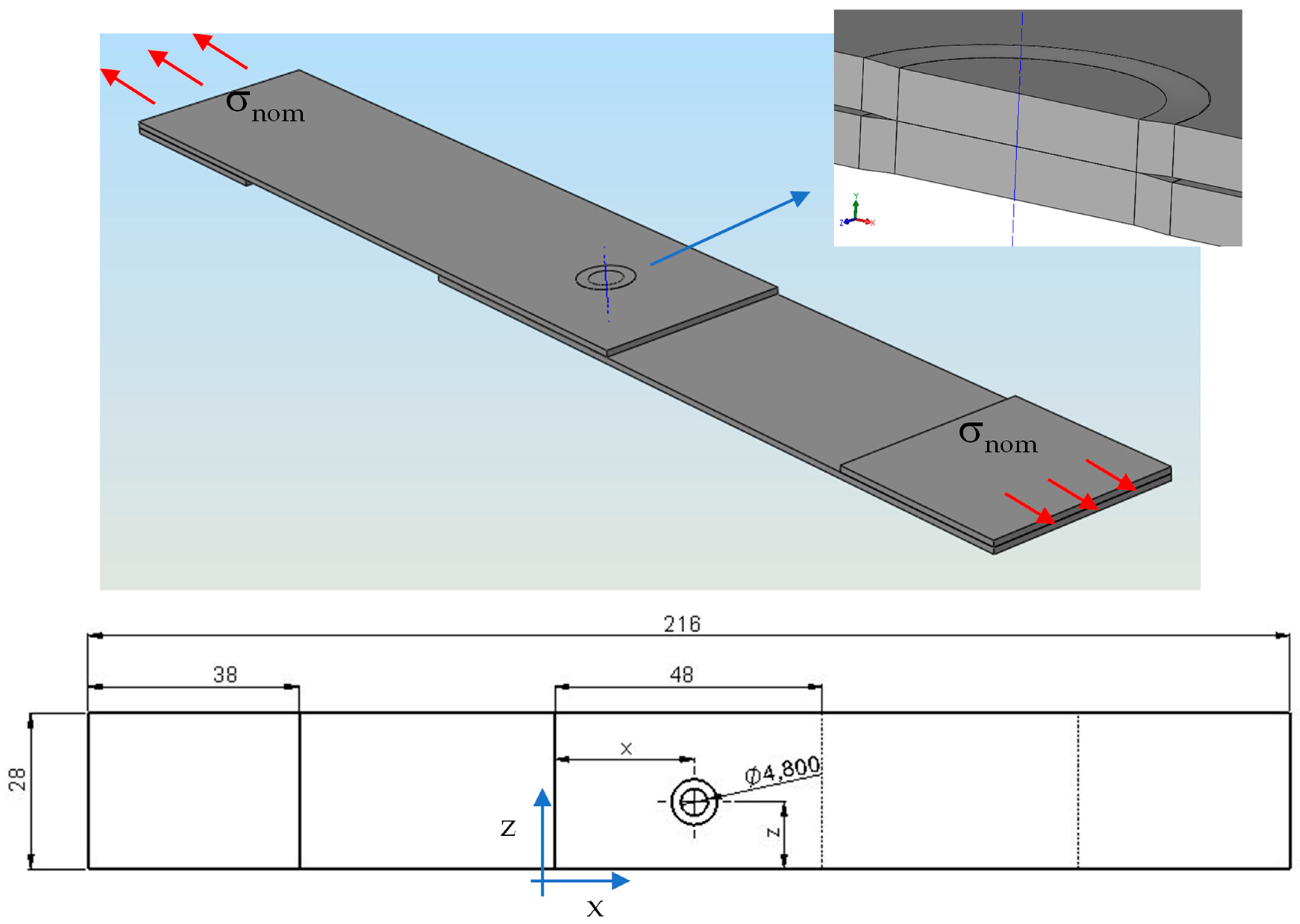

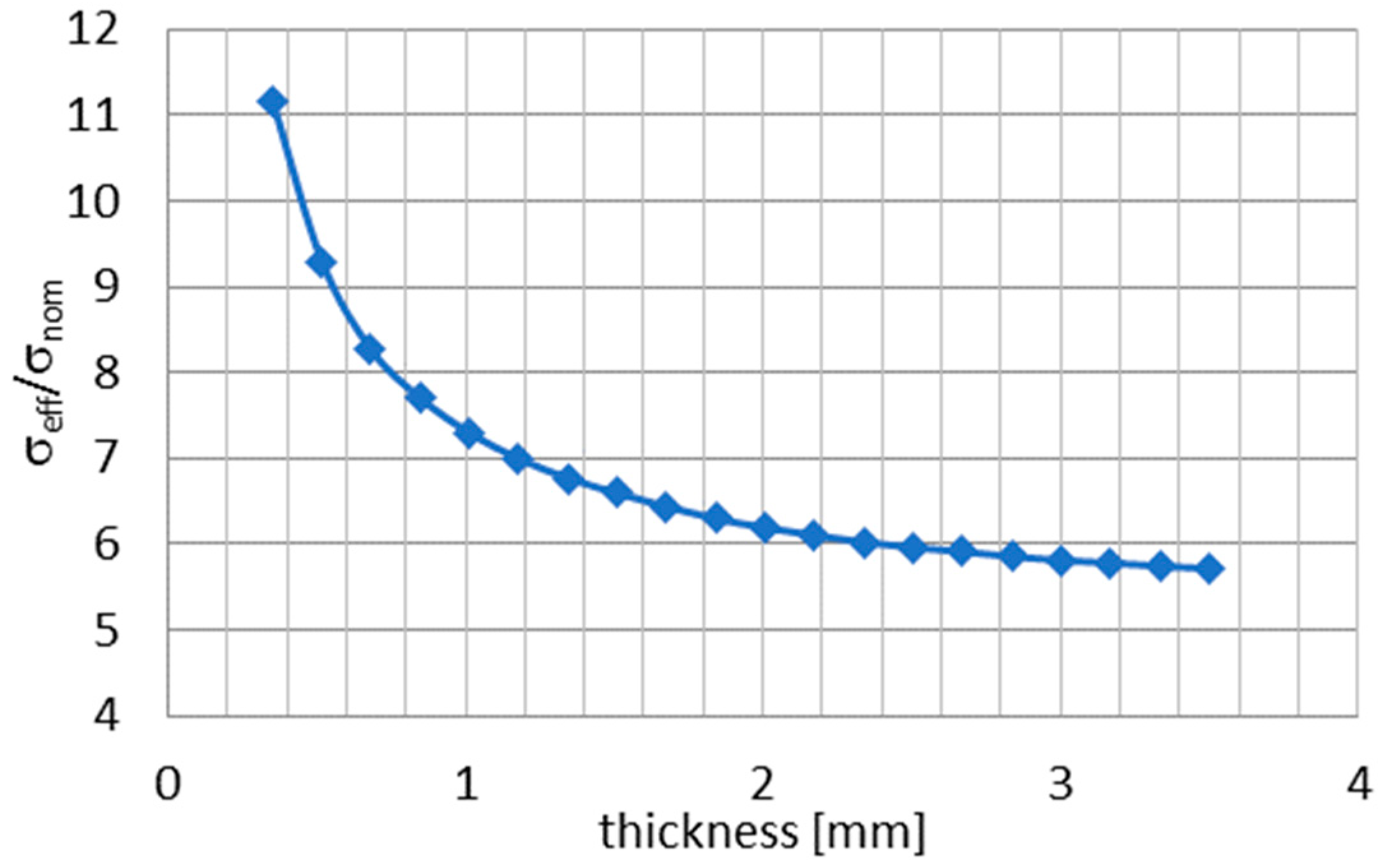
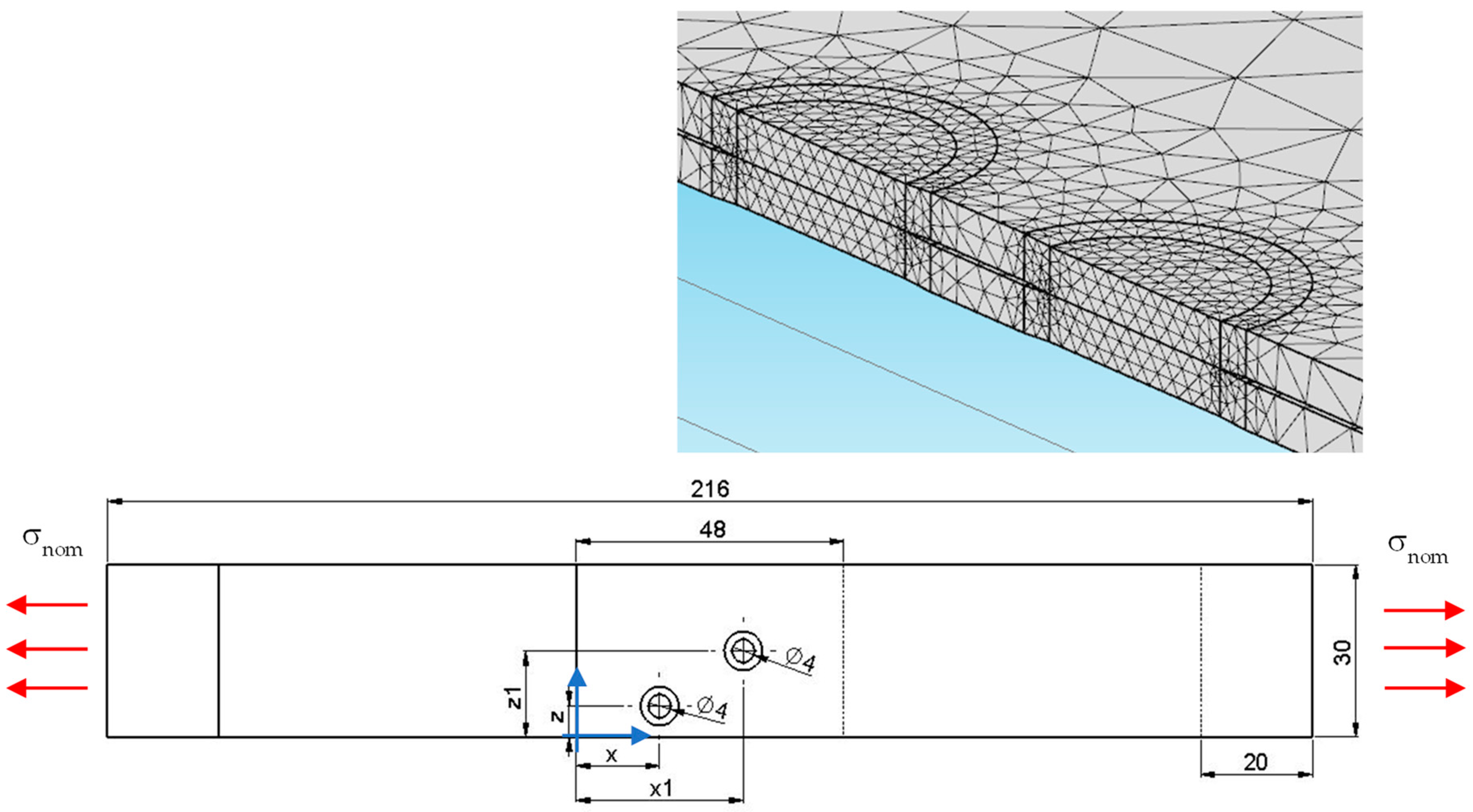



| Position | ||
|---|---|---|
| x [mm] | 7 | 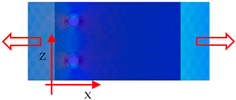 |
| z [mm] | 7.2 | |
| x1 [mm] | 7 | |
| z1 [mm] | 22.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Livieri, P.; Tovo, R. Optimization of Welded Joints under Fatigue Loadings. Metals 2024, 14, 613. https://doi.org/10.3390/met14060613
Livieri P, Tovo R. Optimization of Welded Joints under Fatigue Loadings. Metals. 2024; 14(6):613. https://doi.org/10.3390/met14060613
Chicago/Turabian StyleLivieri, Paolo, and Roberto Tovo. 2024. "Optimization of Welded Joints under Fatigue Loadings" Metals 14, no. 6: 613. https://doi.org/10.3390/met14060613
APA StyleLivieri, P., & Tovo, R. (2024). Optimization of Welded Joints under Fatigue Loadings. Metals, 14(6), 613. https://doi.org/10.3390/met14060613






