Plastic Shakedown Behavior and Deformation Mechanisms of Ti17 Alloy under Long Term Creep–Fatigue Loading
Abstract
1. Introduction
2. Materials and Experiments
2.1. As-Received Material
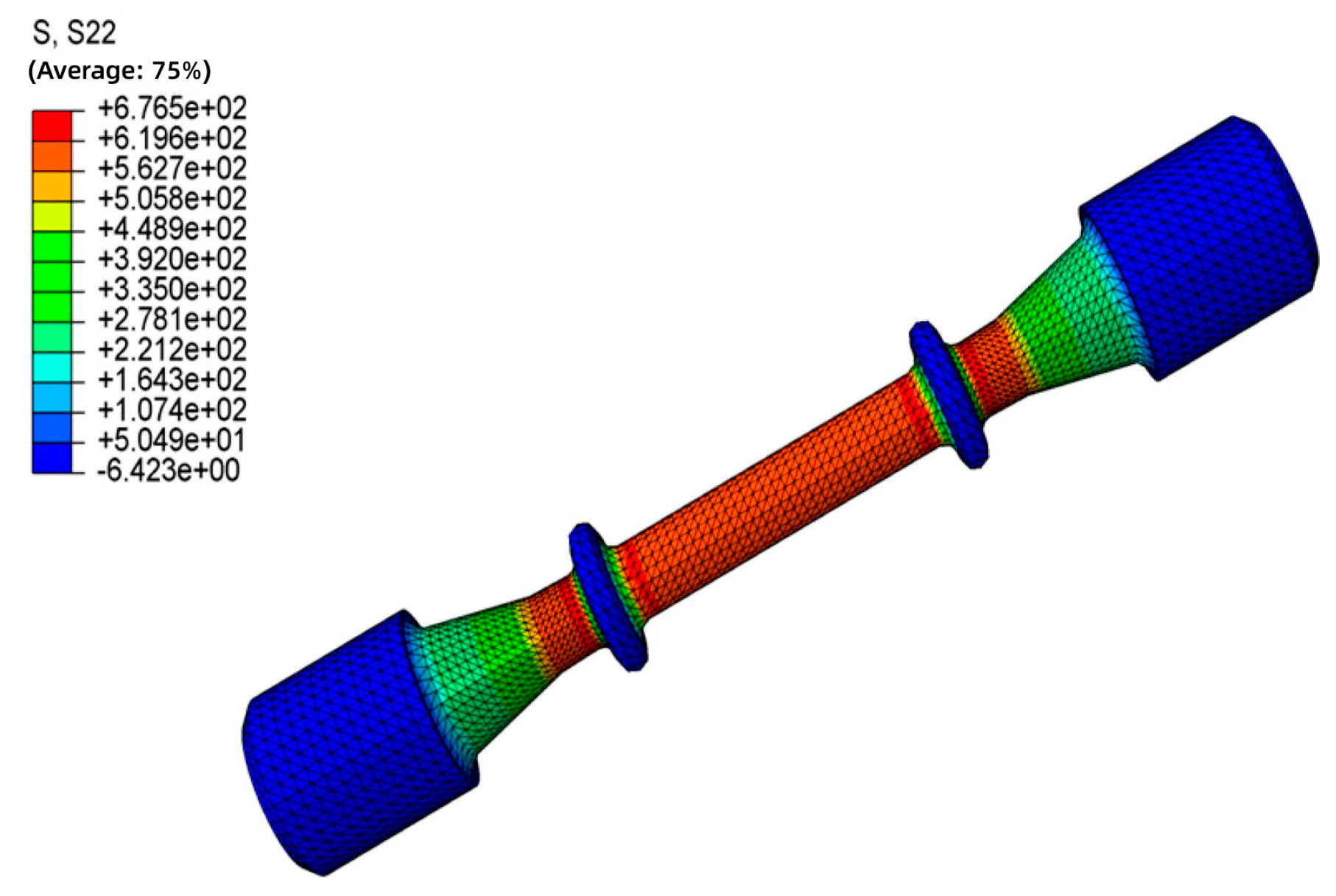
2.2. Mechanical Tests
2.3. Microstructure Characterization
3. Shakedown Theory Model
3.1. Main Equations
3.2. Ohno–Abdel–Karim Nonlinear Kinematic Hardening
3.3. Determination of Material Parameters
4. Results and Discussion
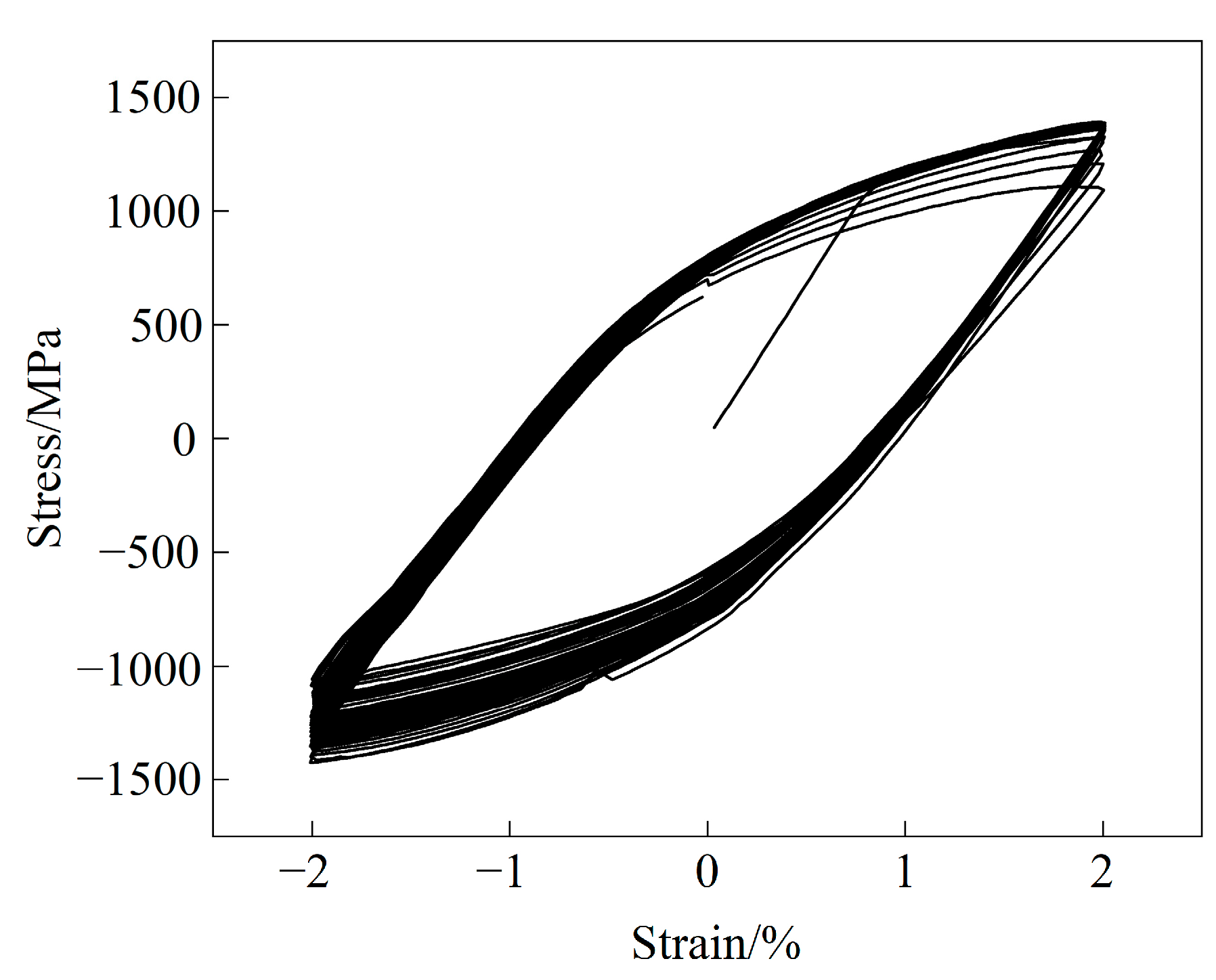
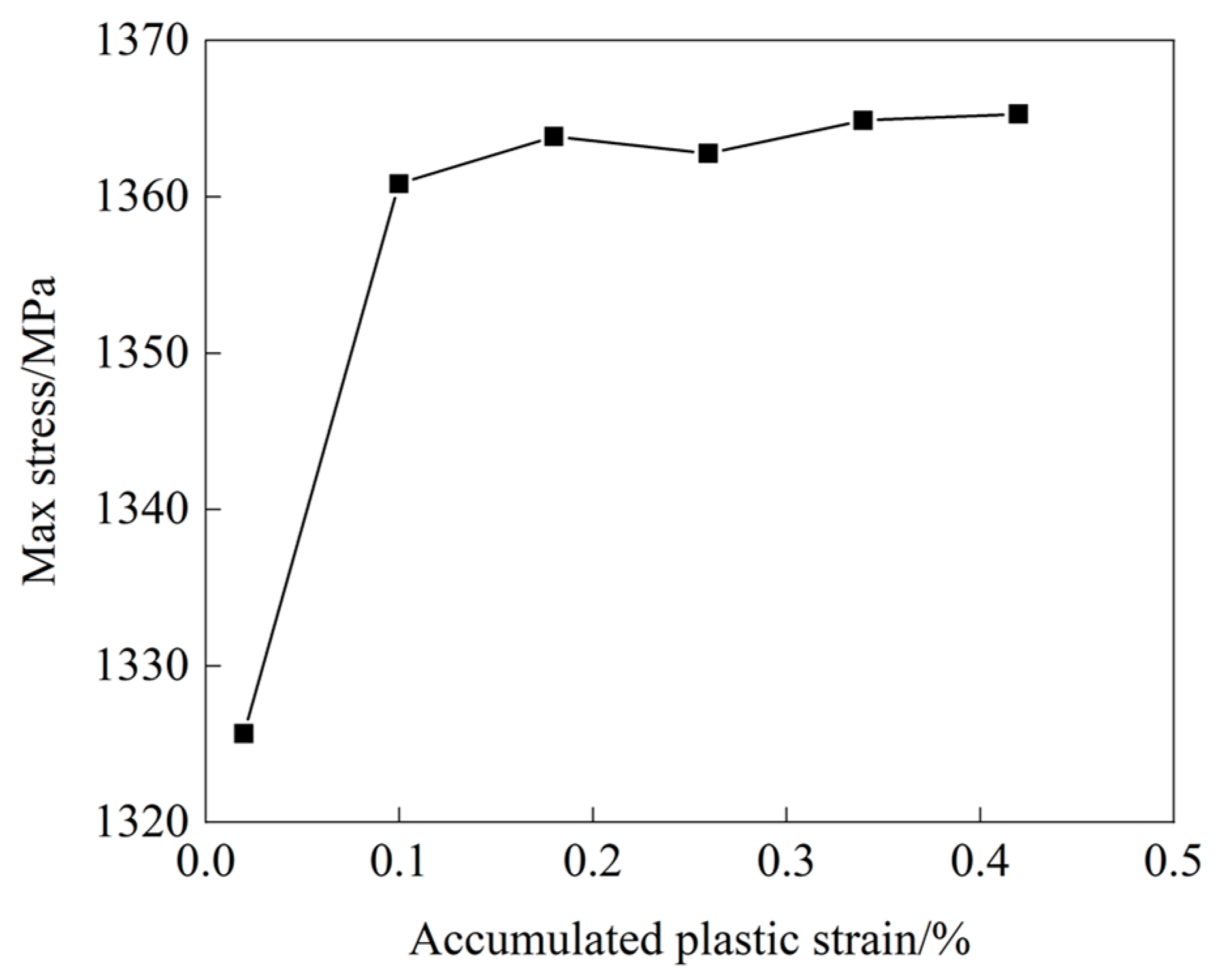
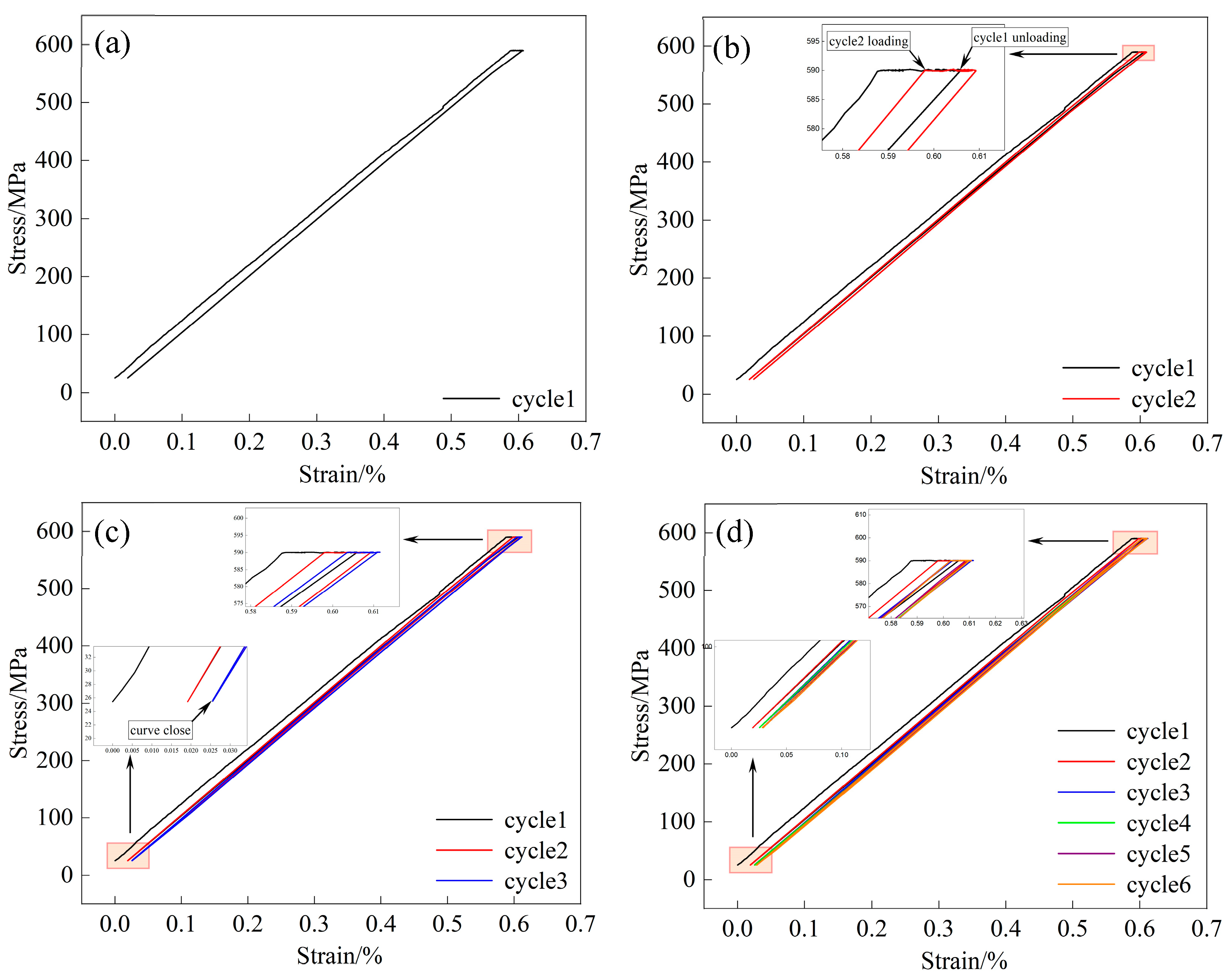
4.1. Stress–Strain Curves
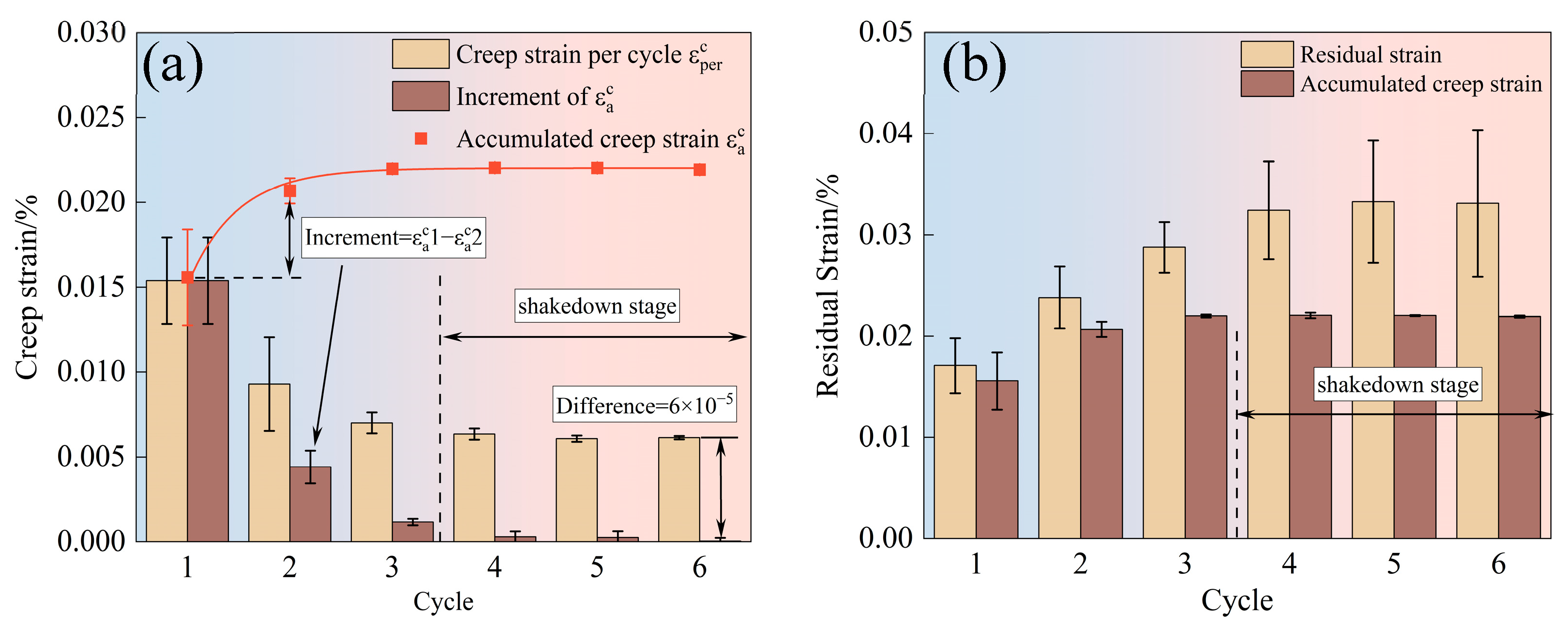
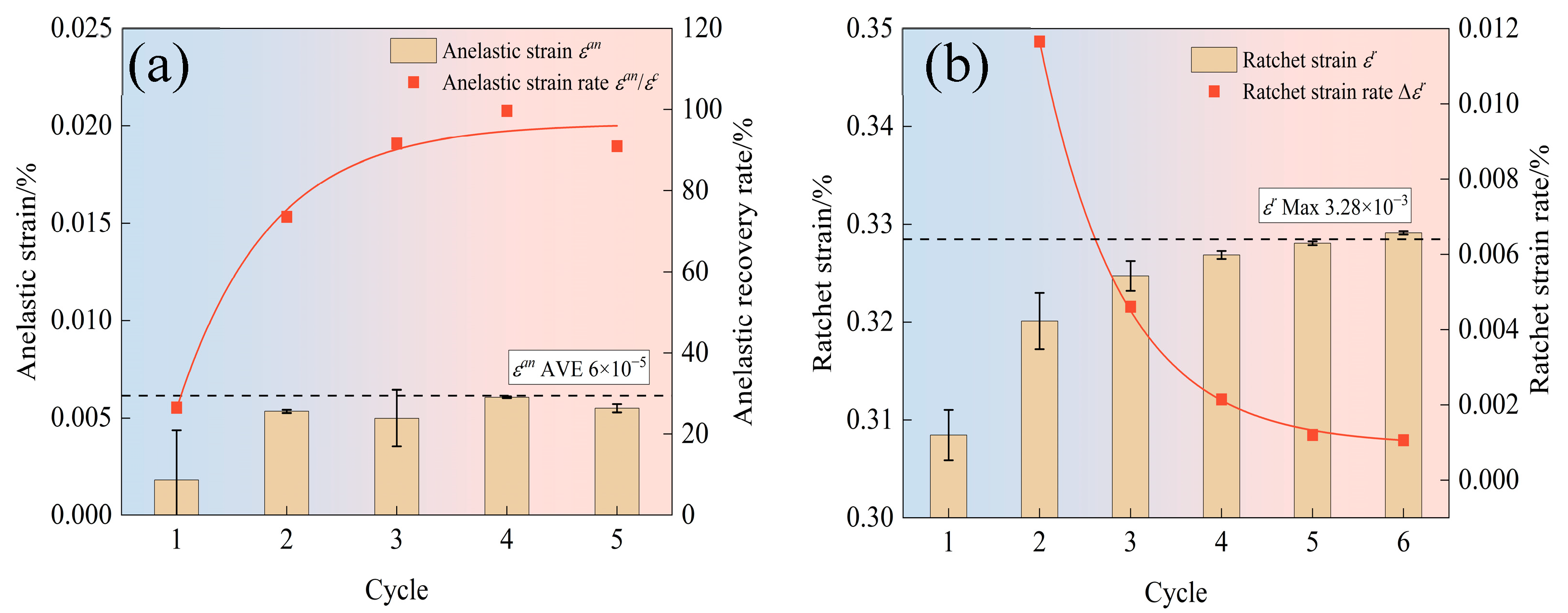
4.2. The Evolution of Strain Components
4.3. Validation of Shakedown Theory Model
4.4. Microscopic Mechanisms of Plastic Shakedown
5. Conclusions
- (1)
- Ti17 alloy specimens experience CF tests at 300 °C. During the initial stage, significant strain is observed, with the creep strain per cycle rapidly decreasing, while residual strain εre and ratchet strain εr increase rapidly. After three cycles, the specimens reach a plastic shakedown state, with the strain components tending to stabilize. The anelastic recovery rate increases to 100%, and the ratchet strain rate decreases to 0%.
- (2)
- Based on the plasticity–creep superposition model, a theory model for the CF shakedown behavior of Ti17 alloy is established. This model can accurately describe the shakedown behavior of Ti17 alloy at 300 °C, and the relative error between the simulation and experimental results can be controlled within 4%.
- (3)
- TEM observations reveal that the multiplication and pile-up of dislocations during cyclic loading, as well as the non-uniformity of deformation, result in strong back stress cyclic hardening. The increased resistance to dislocation slip leads to the elastic bending of dislocation segments during the stress-holding stage and their subsequent re-straightening upon unloading, giving rise to anelastic recovery. Back stress cyclic hardening and anelastic recovery are the main mechanisms for the plastic shakedown behavior of the Ti17 alloy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, D.G.; Xu, X.Y.; Wu, Y.; Qi, Y.C. Factors influencing and research progress on dwell fatigue of titanium alloys. Chin. J. Mater. Res. 2019, 38, 722–728. [Google Scholar]
- Sui, J.C.; Guo, T.; Meng, Z.W.; Tian, X.L. Process research on integrated three-level disc shaft. China New Technol. Prod. 2015, 22, 56–57. [Google Scholar]
- Bache, M.R. A review of dwell sensitive fatigue in titanium alloys: The role of microstructure, texture and operating conditions. Int. J. Fatigue 2003, 25, 1079–1087. [Google Scholar] [CrossRef]
- Chen, K.M.; Tian, R.Z.; Guo, S.J.; Wang, R.Z.; Zhang, C.C.; Chen, H.F.; Zhang, X.C.; Tu, S.D. Prediction of creep-fatigue life of aviation turbine discs under cyclic thermal-mechanical loading. Acta Aeronaut. Astronaut. Sin. 2022, 43, 336–346. [Google Scholar]
- Xuan, F.Z.; Zheng, X.T. Stability Analysis and Design of Pressure Equipment; Science Press: Beijing, China, 2020; pp. 1–4. [Google Scholar]
- Boiler, A. ASME Boiler and Pressure Vessel Code: An International Code; American Society of Mechanical Engineers: New York, NY, USA, 1998; pp. 28–29. [Google Scholar]
- Ota, Y.; Kubushiro, K.; Yamazaki, Y. The life evaluation by linear cumulative damage rule for cold dwell fatigue of Ti-6Al-4V alloy. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 259–269. [Google Scholar] [CrossRef]
- Zhang, M.D.; Cao, J.X.; Zhai, Z.J.; Yang, Z.N.; Zhang, B.; Sui, N.; Huang, X. Influence of dwell time and stress ratio on stress-strain response of Ti6242 alloy. Chin. J. Nonferrous Met. 2022, 32, 1685–1692. [Google Scholar]
- Kumar, J.; Rao, A.V.; Raman, S.G.S.; Kumar, V. Creep-fatigue damage simulation at multiple length scales for an aeroengine titanium alloy. Int. J. Fatigue 2018, 116, 505–512. [Google Scholar] [CrossRef]
- Zeng, L.R.; Lei, L.M.; Luo, X.M.; Zhang, G.P. Toward an understanding of dwell fatigue damage mechanism of bimodal Ti-6Al-4V alloys. J. Mater. Sci. Technol. 2022, 108, 244–255. [Google Scholar] [CrossRef]
- Han, Y.; Zhao, F.; Liu, Y.; Huang, C.W. Quantitative relationships between mechanical properties and microstructure of Ti17 alloy after thermomechanical treatment. Metals 2020, 10, 67–83. [Google Scholar] [CrossRef]
- Sun, J.Z.; Li, M.Q.; Li, H. Deformation behavior of TC17 titanium alloy with basket-weave microstructure during isothermal compression. J. Alloys Compd. 2018, 730, 533–543. [Google Scholar] [CrossRef]
- Guo, P.; Pan, H.; Jia, G.Y.; Hou, H.M. Conventional low-cycle fatigue and dwell fatigue damage behavior of TC17 titanium alloy under high load conditions. Rare Met. Mater. Eng. 2022, 51, 301–305. [Google Scholar]
- Kang, G.Z.; Kan, Q.H. Constitutive modeling for uniaxial time-dependent ratcheting of SS304 stainless steel. Mech. Mater. 2007, 39, 488–499. [Google Scholar] [CrossRef]
- Kan, Q.H.; Kang, G.Z.; Zhang, J. Constitutive description of correlated ratcheting behavior of SS304 stainless steel under uniaxial tension. Nucl. Power Eng. 2007, 28, 66–71. [Google Scholar]
- Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part II: Application to experiments of ratchetting behavior. Int. J. Plast. 1993, 9, 391–403. [Google Scholar] [CrossRef]
- Cao, Y.; Cui, X.; Ji, D.M. Creep-fatigue damage behavior of P92 steel and the development of damage constitutive model. Mech. Eng. Mater. 2021, 45, 50–65. [Google Scholar]
- Kang, G.Z.; Gao, Q.; Yang, X.J. A visco–plastic constitutive model incorporated with cyclic hardening for uniaxial/multiaxial ratcheting of SS304 stainless steel at room temperature. Mech. Mater. 2022, 34, 521–531. [Google Scholar] [CrossRef]
- Fang, T. Experimental and Theoretical Models on Ratcheting-Fatigue Interaction of Wheel and Rail Steels. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2014; pp. 28–30. [Google Scholar]
- Abdel-Karim, M.; Ohno, N. Kinematic hardening model suitable for ratchetting with steady-state. Int. J. Plast. 2000, 16, 225–240. [Google Scholar] [CrossRef]
- Wang, Y.J.; Wang, X.H.; Yang, Y.F.; Lan, X.; Zhang, Z.; Li, H. Study on creep-fatigue mechanical behavior and life prediction of Ti2AlNb-based alloy. Materials 2022, 15, 6238. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.L. Study on plastic shakedown state of metallic materials. Mech. Eng. Autom. 2005, 1, 47–50. [Google Scholar]
- Shi, J.Y.; Zhang, M.; Cheng, Y.D.; Wang, B.K.; Liu, F.L. A study on the shakedown mechanism of mining ring chain steel 23MnNiCrMo54. J. Heat Treat. Mater. 2005, 26, 90–92. [Google Scholar]
- Kang, G.Z.; Sun, Y.F.; Zhang, J.; Kan, Q.H. Time-dependent ratcheting behavior of SS304 stainless steel under cyclic loading at room temperature. Acta Metall. Sin. 2005, 41, 277–281. [Google Scholar]
- Yu, L.; Song, X.P.; You, L.; Jiao, Z.H.; Yu, H.C. Effect of dwell time on creep-fatigue life of a High-Nb TiAl alloy at 750 °C. Scr. Mater. 2015, 109, 61–63. [Google Scholar] [CrossRef]
- Alsmadi, Z.Y.; Abouelella, H.; Alomari, A.S.; Murty, K.L. Stress-controlled creep–fatigue of an advanced austenitic stainless steel at elevated temperatures. Materials 2022, 15, 3984. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.T. Shakedown Analysis and Evaluation Approaches to Structures under Complicated Conditions. Ph.D. Thesis, East China University of Science and Technology, Shanghai, China, 2012; pp. 69–74. [Google Scholar]
- Es-Souni, M. Primary, secondary and anelastic creep of a high temperature near α-Ti alloy Ti6242Si. Maretials Charact. 2000, 45, 153–164. [Google Scholar] [CrossRef]
- Głuchowski, A.; Sas, W. Long-term cyclic loading impact on the creep deformation mechanism in cohesive materials. Materials 2020, 13, 3907. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.L.; Xuan, F.Z.; Guo, S.J.; Zhao, P. The role of anelastic recovery in the creep-fatigue interaction of 9–12% Cr steel at high temperature. Int. J. Mech. Sci. 2017, 122, 95–103. [Google Scholar] [CrossRef]
- Chen, G.X.; Peng, Y.; Liu, C.Y. Periodic plastic deformation behavior of Ti-6Al-4V titanium alloy based on strain controlling mode. J. Fail. Anal. Prev. 2020, 20, 597–604. [Google Scholar] [CrossRef]
- Zhou, Y.; Pang, Y.H.; Zhou, Y.G. Deformation characteristics and dislocation structures of TC11 titanium alloy under creep-fatigue interaction. Acta Aeronaut. Astronaut. Sin. 1994, 15, 691–695. [Google Scholar]
- Sun, F.C. Possible dislocations in alpha titanium alloys. Rare Met. Mater. Eng. 1985, 1, 3–6. [Google Scholar]
- Huang, J.; Wang, Z.; Xue, K. Cyclic deformation response and micro-mechanisms of Ti Alloy Ti–5Al–5V–5Mo–3Cr–0.5Fe. Mater. Sci. Eng. A 2011, 528, 8723–8732. [Google Scholar] [CrossRef]
- Paton, N.E.; Backofen, W.A. Plastic deformation of titanium at elevated temperatures. Mech. Behav. 1970, 1, 2839–2847. [Google Scholar] [CrossRef]
- Zhao, J.W.; Qiu, F.; Xu, C.G. Review of creep-thermomechanical fatigue behavior of austenitic stainless steel. Crystals 2023, 13, 70. [Google Scholar] [CrossRef]
- Li, X.X.; Xia, C.Q.; Qi, Y.L.; Wang, Z.H.; Niu, G.S.; Sun, W. Study on high-temperature tensile creep behavior of TC6 titanium alloy. Rare Met. Mater. Eng. 2013, 42, 1901–1904. [Google Scholar]
- Xu, H.F. Study on Low-Cycle Fatigue Mechanical Behavior and Life Prediction Energy Model of Ti-6Al-4V Alloy Based on Internal Stress. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2018; pp. 281–282. [Google Scholar]
- Lu, C.Y.; Wang, P.; Luo, S.Y.; Li, Y.F.; Wang, R.Z.; He, Y.M.; Gao, Z.L.; Tu, S.T. Influence of anelastic recovery on the cyclic creep behavior of AlCoCrFeNi2.1 eutectic high-entropy alloy. Int. J. Fatigue 2024, 180, 10811. [Google Scholar] [CrossRef]
- Ying, C.H.; Chen, L.J.; Liu, T.L.; Guo, L.Q. Influence of hold time on cyclic creep behavior of 409 ferritic stainless steel. J. Shenyang Univ. Technol. 2016, 38, 634–638. [Google Scholar]
- Rao, A.; Bouchard, R.J.; Northover, S.M.; Fitzpatrick, M.E. Anelasticity in austenitic stainless steel. Acta Mater. 2012, 60, 6851–6861. [Google Scholar] [CrossRef]
- Nardone, V.C.; Matejczyk, D.E.; Tien, J.K. A model for anelastic relaxation controlled cyclic creep. Metall. Trans. A 1985, 16, 1117–1122. [Google Scholar] [CrossRef]

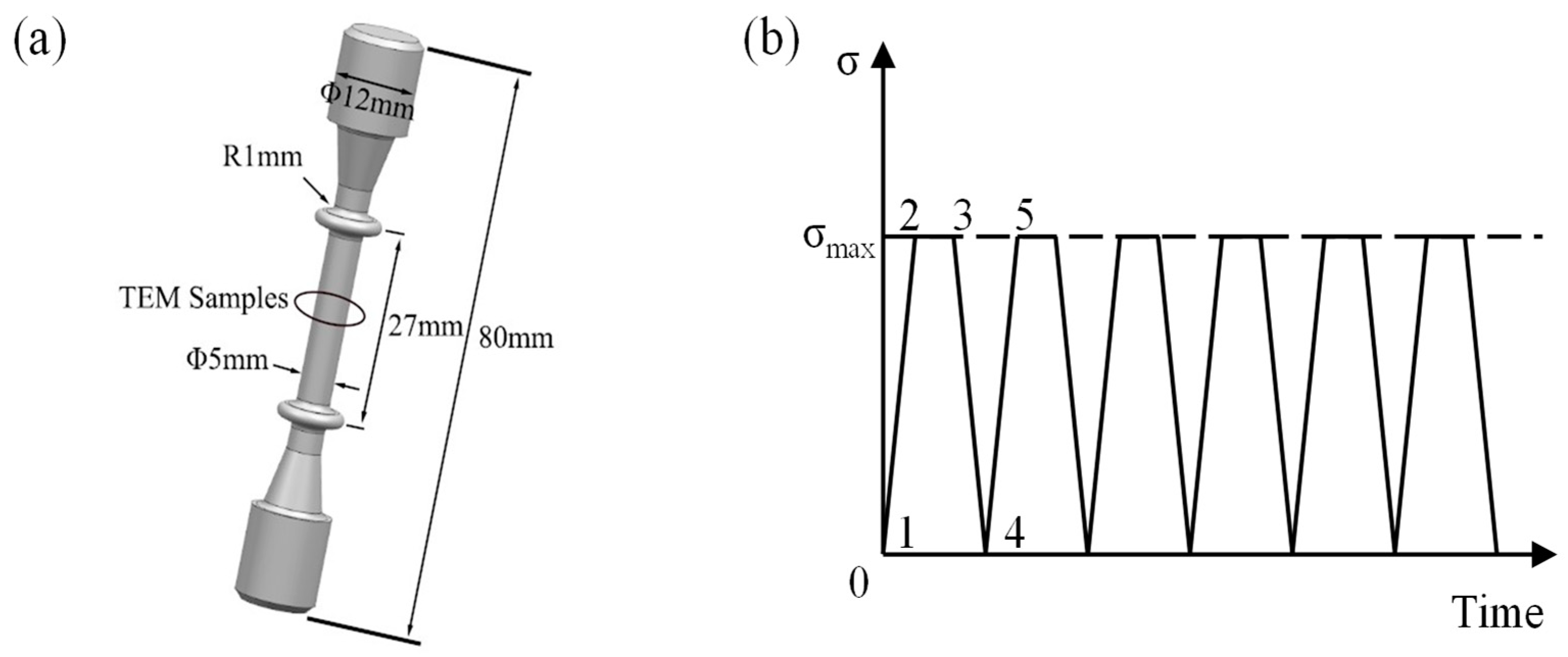







| Element | Al | Sn | Zr | Mo | Cr | Fe | C | N | H | O | Ti |
|---|---|---|---|---|---|---|---|---|---|---|---|
| wt./% | 5.0 | 2.1 | 1.9 | 3.9 | 4.0 | 0.30 | 0.05 | 0.05 | 0.0125 | 0.08 | Bal. |
| Temperature | Material Parameters |
|---|---|
| 300 °C | E = 102 GPa, ν = 0.30, Q0 = 580 Mpa, Qsa = 104 MPa, K = 665 MPa, n = 150, γ = 29.8, μ = 0.05, x(k) = 2.9 × 10−9, m(k) = 3.5, M = 8; ζ(1) = 522.2, ζ(2) = 309.7, ζ(3) = 257.1, ζ(4) = 176.9, ζ(5) = 118.3, ζ(6) = 75.4, ζ(7) = 43.6, ζ(8) = 26.6; r(1) = 6.61, r(2) = 5.28, r(3) = 18.31, r(4) = 37.93, r(5) = 20.93, r(6) = 21.79, r(7) = 30.41, r(8) = 41.26 |
| Cycle | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Error value/% | 0.020 | 0.021 | 0.018 | 0.014 | 0.008 | 0.006 |
| Percentage/% | 3.26 | 3.41 | 2.96 | 2.20 | 1.28 | 0.99 |
| g | <a> | <c> | <a + c> |
|---|---|---|---|
| 1/3<11−20> | [0001] | 1/3<11−23> | |
| 0002 | None | All | All |
| 01−10 | All | None | All |
| −2110 | All | None | All |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Man, T.; Liu, D.; Zhang, Z.; Zhang, C.; Sun, Y. Plastic Shakedown Behavior and Deformation Mechanisms of Ti17 Alloy under Long Term Creep–Fatigue Loading. Metals 2024, 14, 743. https://doi.org/10.3390/met14070743
Wang J, Man T, Liu D, Zhang Z, Zhang C, Sun Y. Plastic Shakedown Behavior and Deformation Mechanisms of Ti17 Alloy under Long Term Creep–Fatigue Loading. Metals. 2024; 14(7):743. https://doi.org/10.3390/met14070743
Chicago/Turabian StyleWang, Jianguo, Tongchi Man, Dong Liu, Zhihong Zhang, Chi Zhang, and Yuxiang Sun. 2024. "Plastic Shakedown Behavior and Deformation Mechanisms of Ti17 Alloy under Long Term Creep–Fatigue Loading" Metals 14, no. 7: 743. https://doi.org/10.3390/met14070743
APA StyleWang, J., Man, T., Liu, D., Zhang, Z., Zhang, C., & Sun, Y. (2024). Plastic Shakedown Behavior and Deformation Mechanisms of Ti17 Alloy under Long Term Creep–Fatigue Loading. Metals, 14(7), 743. https://doi.org/10.3390/met14070743






