A New Critical Plane Multiaxial Fatigue Criterion with an Exponent to Account for High Mean Stress Effect
Abstract
:1. Introduction
2. Materials and Methods
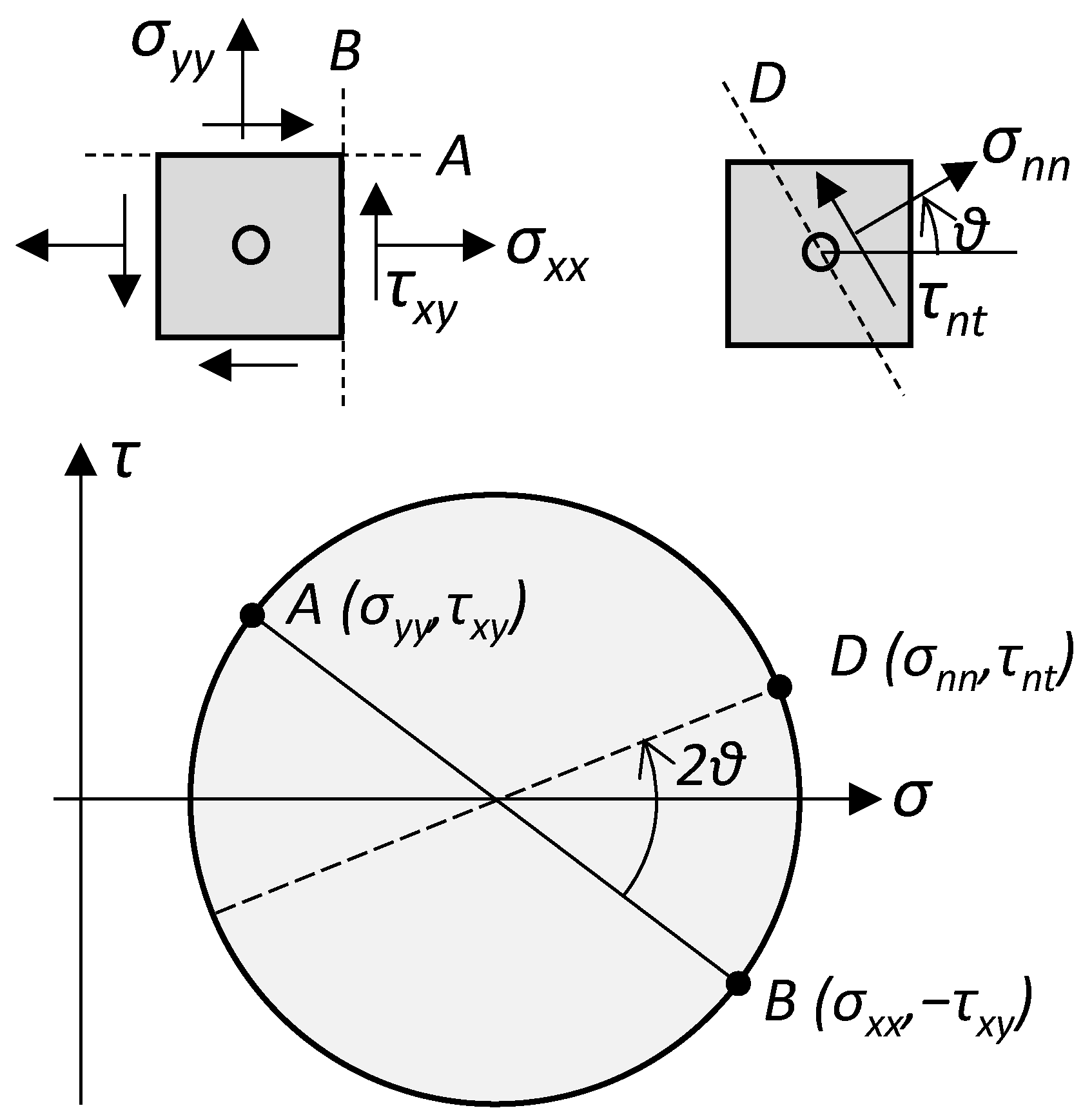
2.1. Critical Plane Methods
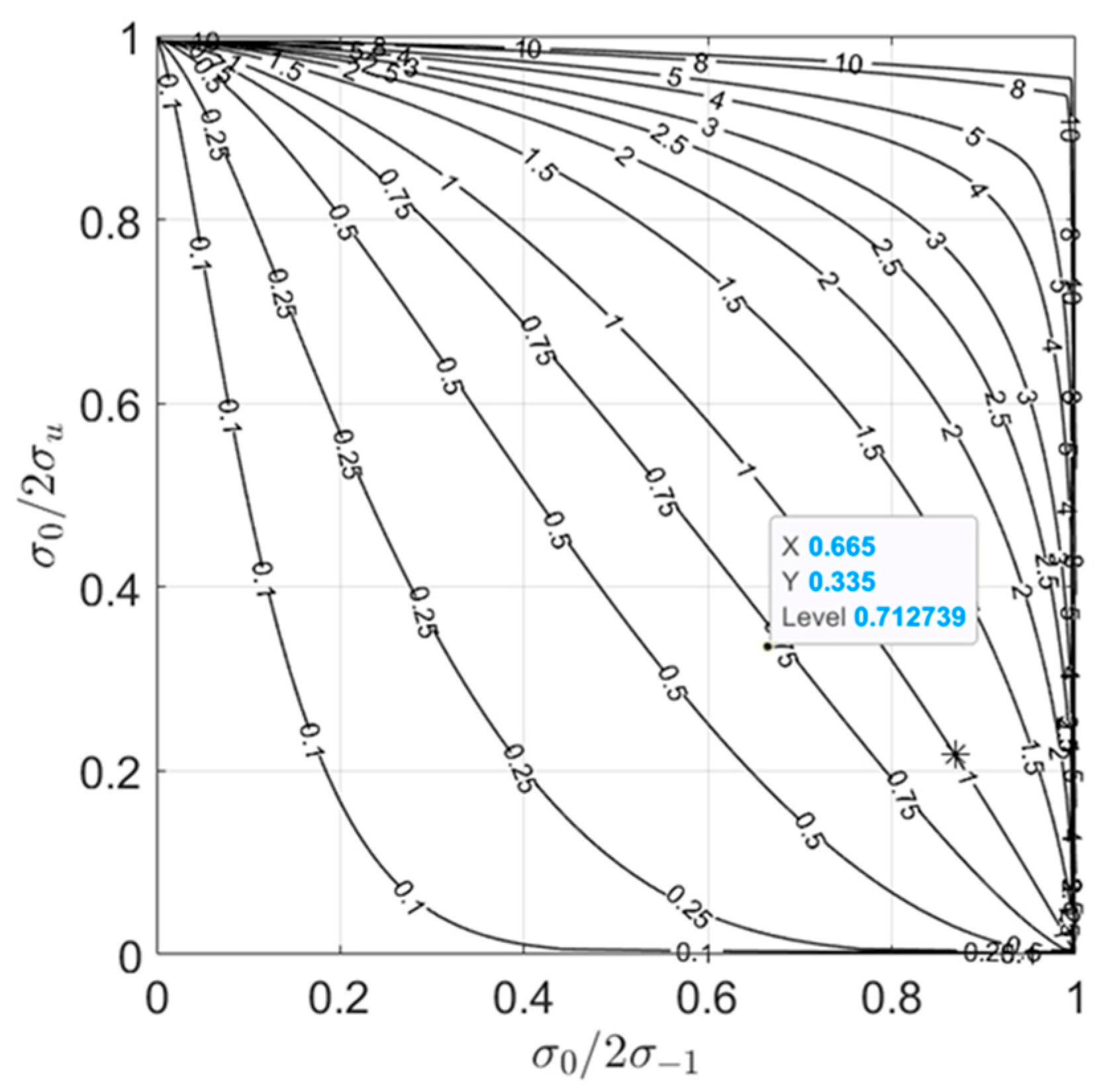
2.2. New Critical Plane Method
2.3. Experimental Database and Numerical Implementation
| Reference | Number of Data Items | Material | Reason for the Selection |
|---|---|---|---|
| Papuga [3] | 15 | Various | Mean compressive loads applied |
| Sauer [23] | 8 | 14S-T aluminium | Static bending or static torsion stresses |
| O’Connor [41], Chodorowski [42] | 10 | NiCrMo steel | High values of mean axial tension and compressive loads |
| Ukrainetz [43] | 6 | 0.1 C steel | Mean axial tension loads. Static shear stresses on torsional fatigue loading |
| Grün et al. [44] | 5 | 25CrMo4 steel | High values of mean axial tension and compression loads |
| Lüpfert et al. [45] | 8 | 20MnCr steel | High values of static compressive loads. Only biaxial loadings considered. |
| Rausch [46] | 14 | EN-GJV-450 cast iron | High values of mean axial tension and compression loads. Static shear stresses on torsional fatigue loading |
| Tovo [47] | 6 | EN-GJS-400-18 ductile cast iron | Mean axial tensile and compressive loads. Static shear stresses on torsional fatigue loading |
| Pallarés-Santasmartas [48,49] | 6 | 34CrMo6 steel | Mean axial tensile and compressive loads. Static shear stresses on torsional fatigue loading |
3. Results and Discussion
3.1. General Results for the Complete Database
3.2. Results for Uniaxial Load Cases
3.3. Results for Load Cases with No Mean Stress
3.4. Results for Load Cases with Mean Stress
3.5. Results for Torsional Load Cases
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a, b, c, d | parameters of the critical plane criteria |
| κ | fatigue limit ratio κ = σ−1/τ−1 |
| σ0 | fatigue limit in repeated axial loading |
| σ−1 | fully reversed axial fatigue limit |
| σu | ultimate tensile strength |
| σnn,a | normal stress amplitude on the critical plane |
| σnn,m | mean normal stress on the critical plane |
| σeq | equivalent normal stress amplitude |
| τ−1 | fully reversed torsional fatigue limit |
| τnt,a | alternating shear stress on the critical plane |
| R | load ratio |
Appendix A
Appendix A.1. Static Tensile Test
Appendix A.2. Repeated Axial Loading Fatigue Test

References
- Papuga, J.; Nesládek, M.; Hasse, A.; Cízová, E.; Suchý, L. Benchmarking Newer Multiaxial Fatigue Strength Criteria on Data Sets of Various Sizes. Metals 2022, 12, 289. [Google Scholar] [CrossRef]
- Papadopoulos, I.V.; Davoli, P.; Gorla, C.; Filippini, M.; Bernasconi, A. A comparative study of multiaxial high-cycle fatigue for metals. Int. J. Fatigue 1997, 19, 219–235. [Google Scholar] [CrossRef]
- Papuga, J. A survey on evaluating the fatigue limit under multiaxial loading. Int. J. Fatigue 2011, 33, 153–165. [Google Scholar] [CrossRef]
- Gough, H.J.; Pollard, H.V. The strength of metals under combined alternating stresses. Proc. Inst. Mech. Eng. 1935, 131, 3–103. [Google Scholar] [CrossRef]
- Smith, J.O. The Effect of Range of Stress on the Fatigue Strength of Metals; University of Illinois Engineering Experiment Station, Bulletin Series No. 334; University of Illinois: Urbana, IL, USA, 1942. [Google Scholar]
- Marin, J. Interpretation of fatigue strengths for combined stresses. In Proceedings of the International Conference on Fatigue of Metals, New York, NY, USA, 28–30 November 1956; Institution of Mechanical Engineers: London, UK, 1956; pp. 184–195. [Google Scholar]
- Crossland, B. Effect of large hydrostatic pressure on the torsional fatigue strength of an alloy steel. In Proceedings of the International Conference on Fatigue of Metals, New York, NY, USA, 28–30 November 1956; Institution of Mechanical Engineers: London, UK, 1956; pp. 138–149. [Google Scholar]
- Findley, W.N.; Coleman, J.J.; Hanley, B.C. Theory for combined bending and torsion fatigue with data for SAE 4340 steel. In Proceedings of the International Conference on Fatigue of Metals, New York, NY, USA, 28–30 November 1956; Institution of Mechanical Engineers: London, UK, 1956; pp. 150–157. [Google Scholar]
- Findley, W.N. A theory for the effect of mean stress on fatigue of metals under combined torsion and axial load or bending. J. Eng. Ind. Trans ASME 1959, 81, 301–306. [Google Scholar] [CrossRef]
- Baier, F. Time and Fatigue Strength with Superimposed Static and Oscillating Tensile Compression and Torsion Loading. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 1970. [Google Scholar]
- Simbürger, A. Festigkeitsverhalten zäher Werkstoffe bei einer Mehrachsigen Phaseverschobenen Schwingbeanspruchungmit Körperfesten und Veränderlichen Hauptspannungsrichtungen; TH Darmstadt: Darmstadt, The Netherlands, 1975. [Google Scholar]
- Troost, A.; Akin, O.; Klubberg, F. Dauerfestigkeitsverhalten metallischer Werkstoffe bei zweiachsiger Beanspruchung durch drei phasenverschoben schwingende Lastspannungen. Konstruktion 1987, 39, 479–488. [Google Scholar]
- Froustey, C.; Lasserre, S. Multiaxial fatigue endurance of 30NCD16 steel. Int. J. Fatigue 1989, 11, 169–175. [Google Scholar] [CrossRef]
- Zenner, H.; Simbürger, A.; Liu, J. On the fatigue limit of ductile metals under complex multiaxial loading. Int. J. Fatigue 2000, 22, 137–145. [Google Scholar] [CrossRef]
- Grubisic, V.; Simbiirger, A. Fatigue under Combined out of Phase Multiaxial Stresses. In Proceedings of the International Conference Fatigue Testing and Design, London, UK, 5–9 April 1976; Society of Environmental Engineers: London, UK, 1976; pp. 27.1–27.8. [Google Scholar]
- Froustey, C.; Lasserre, S.; Dubar, L. Multiaxial and block fatigue tests validation of a criterion for metallic materials. In Proceedings of the MAT-TEC 1992, Grenoble, France, 14–16 October 1992. [Google Scholar]
- Robert, J.L. Contribution à L’étude de la Fatigue Multiaxiale sous Sollicitations Périodiques ou Aléatoires. Ph.D. Thesis, Institut National des Sciences Appliquées de Lyon, Lyon, France, 1992. [Google Scholar]
- Susmel, L.; Tovo, R.; Lazzarin, P. The mean stress effect on the high-cycle fatigue strength from a multiaxial fatigue point of view. Int. J. Fatigue 2005, 27, 928–943. [Google Scholar] [CrossRef]
- Koutiri, I.; Bellett, D.; Morel, F. The effect of mean stress and stress biaxiality in high-cycle fatigue. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 440–455. [Google Scholar] [CrossRef]
- Ince, A. A mean stress correction model for tensile and compressive mean stress fatigue loadings. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 939–948. [Google Scholar] [CrossRef]
- Gough, H.J.; Pollard, H.V.; Clenshaw, W.J. Some Experiments on the Resistance of Metals to Fatigue under Combined Stresses; Aeronautical Research Council Reports and Memoranda; His Majesty’s Stationery Office: London, UK, 1951. [Google Scholar]
- Hanley, B.C.; Dolan, T.J. The Effects of Range of Stress and State of Stress on the Fatigue Strength of SAE 4340 Steel; Report No. 22, Project NR-031-005; University of Illinois: Urbana, IL, USA, 1951. [Google Scholar]
- Sauer, J.A. A study of fatigue phenomena under combined stress. In Proceedings of the Seventh International Congress for Applied Mechanics, London, UK, 5–11 September 1948; pp. 150–164. [Google Scholar]
- Findley, W.N. Combined-Stress Fatigue Strength of 76S-T61 Aluminum Alloy with Superimposed Mean Stresses and Corrections for Yielding; NACA-TN-2924; NACA: Washington, DC, USA, 1953. [Google Scholar]
- Findley, W.N. Theories relating to fatigue of materials under combinations of stress. In Colloquium on Fatigue/Colloque de Fatigue/ Kolloquiumüber Ermüdungsfestigkeit; Weibull, W., Odqvist, F.K.G., Eds.; Springer-Verlag OHG.: Berlin/Gottingen/Heidelberg, Germany, 1956. [Google Scholar]
- Stulen, F.B.; Cummings, H.N. A Failure Criterion for Multi-Axial Fatigue Stresses. Proc. ASTM 1954, 54, 822–835. [Google Scholar]
- Findley, W.N. Comments on the sessions. Session 2. In Proceedings of the International Conference on Fatigue of Metals, New York, NY, USA, 28–30 November 1956; Institution of Mechanical Engineers: London, UK, 1956. [Google Scholar]
- Papuga, J.; Ruzicka, M. Two new multiaxial criteria for high cycle fatigue computation. Int. J. Fatigue 2008, 30, 58–66. [Google Scholar] [CrossRef]
- Bomas, H.; Bacher-Hoechst, M.; Kienzler, R.; Kunow, S.; Loewisch, G.; Muehleder, F.; Schroeder, R. Crack initiation and endurance limit of a hard steel under multiaxial cyclic loads. Fatigue Fract. Eng. Mater. Struct. 2009, 33, 126–139. [Google Scholar] [CrossRef]
- Papuga, J. Improvements of two criteria for multiaxial fatigue limit evaluation. Bull. Appl. Mech. 2009, 5, 80–86. [Google Scholar]
- Papuga, J. Mapping of Fatigue Damages—Program Shell of FE Calculation. Ph.D. Thesis, Czech Technical University in Prague, Prague, Czech Republic, 2005. [Google Scholar]
- Charkaluk, E.; Constantinescu, A.; Maïtournam, H.; Dang Van, K. Revisiting the Dang Van criterion. Procedia Eng. 2009, 1, 143–146. [Google Scholar] [CrossRef]
- Vantadori, S.; Carpinteri, A.; Luciano, R.; Ronchei, C.; Scorza, D.; Zanichelli, A. Mean stress effect on fatigue life estimation for Inconel 718 alloy. Int. J. Fatigue 2020, 133, 105391. [Google Scholar] [CrossRef]
- Vantadori, S.; Vazquez, J.; Zanichelli, A.; Carpinteri, A.; Luciano, R. Structural integrity of shot peened Ti6Al4V specimens under fretting fatigue. Int. J. Fract. 2021, 234, 45–55. [Google Scholar] [CrossRef]
- Bernasconi, A.; Foletti, S.; Papadopoulos, I.V. A study on combined torsion and axial load fatigue limit tests with stresses of different frequencies. Int. J. Fatigue 2008, 30, 1430–1440. [Google Scholar] [CrossRef]
- Papadopoulos, I.V. Critical plane approaches in high-cycle fatigue: On the definition of the amplitude and mean value of the shear stress acting on the critical plane. Fatigue Fract. Eng. Mater. Struct. 2002, 21, 269–285. [Google Scholar] [CrossRef]
- Dowling, N.E. Mean Stress Effects in Stress-Life and Strain-Life Fatigue. SAE Int. J. Adv. Curr. Pract. Mobil. 2004, 32, 1004–1019. [Google Scholar] [CrossRef]
- Pallarés-Santasmartas, L. Development of Two Multiaxial Fatigue Methods for Ductile Metals Based on Energy Considerations. Ph.D. Thesis, University of the Basque Country, Leioa, Spain, 2021. [Google Scholar]
- Dowling, N.E.; Calhoun, C.A.; Arcari, A. Mean stress effects in stress-life fatigue and the Walker equation. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 163–179. [Google Scholar] [CrossRef]
- Li, B.; Reis, L.; de Freitas, M. Comparative study of multiaxial fatigue damage models for ductile structural steels and brittle materials. Int. J. Fatigue 2009, 31, 1895–1906. [Google Scholar] [CrossRef]
- O’Connor, H.C.; Morrison, J.L.M. The Effect of Mean Stress on the Push-Pull Fatigue Properties of an Alloy Steel. In Proceedings of the International Conference on Fatigue of Metals, New York, NY, USA, 28–30 November 1956; Institution of Mechanical Engineers: London, UK, 1956; pp. 102–109. [Google Scholar]
- Chodorowski, W.T. Fatigue strength in shear of an alloy steel, with particular reference to the effect of mean stress and directional properties. In Proceedings of the International Conference on Fatigue of Metals, New York, NY, USA, 28–30 November 1956; pp. 122–131. [Google Scholar]
- Ukrainetz, P.R. The Effect of the Mean Stress on the Endurance Limit. M.Sc. Thesis, The University of Columbia, New York, NY, USA, 1960. [Google Scholar]
- Grün, P.; Troost, A.; Akin, O.; Klubberg, F. Langzeitund Dauerschwingfestigkeit des Vergütungsstahls 25CrMo4 bei mehrachsiger Beanspruchung durch dreischwingende Lastspannungen. Mater. Werkst. 1991, 22, 73–80. [Google Scholar] [CrossRef]
- Lüpfert, H.P.; Spies, H.J. Fatigue strength of heat-treated steel under static multiaxial compression stress. Adv. Eng. Mater. 2004, 6, 544–550. [Google Scholar] [CrossRef]
- Rausch, T. Zum Schwingfestigkeitsverhalten von Gusseisenwerkstoffen unter Einachsiger und Mehrachsiger Beanspruchung am Beispiel von EN-GJV-450. Ph.D. Thesis, Aachen University, Aachen, Germany, 2011. [Google Scholar]
- Tovo, R.; Lazzarin, P.; Berto, F.; Cova, M.; Maggiolini, E. Experimental investigation of the multiaxial fatigue strength of ductile cast iron. Theor. Appl. Fract. Mech. 2014, 73, 60–67. [Google Scholar] [CrossRef]
- Pallarés-Santasmartas, L.; Albizuri, J.; Avilés, A.; Avilés, R. Mean Stress Effect on the Axial Fatigue Strength of DIN 34CrNiMo6 Quenched and Tempered Steel. Metals 2018, 8, 213. [Google Scholar] [CrossRef]
- Pallarés-Santasmartas, L.; Albizuri, J.; Avilés, A.; Saintier, N.; Merzeau, J. Influence of mean shear stress on the torsional fatigue behaviour of 34CrNiMo6 steel. Int. J. Fatigue 2018, 113, 54–68. [Google Scholar] [CrossRef]
- Weber, B. Fatigue Multiaxiale des Structures Industrielles sous Chargement Quelconque. Ph.D. Thesis, INSA Lyon, Villeurbanne, France, 1999. [Google Scholar]
- Gyekenyesi, J.Z.; Murthy, P.L.N.; Mital, S.K. NASALIFE—Component Fatigue and Creep Life Prediction Program; NASA/TM—2005-213886; NASA Center for Aerospace Information: Hanover, MD, USA, 2005. [Google Scholar]
- Davoli, P.; Bernasconi, A.; Filippini, M.; Foletti, S.; Papadopoulos, I. Independence of the torsional fatigue limit upon a mean shear stress. Int. J. Fatigue 2003, 25, 471–480. [Google Scholar] [CrossRef]
- Pinho de Castro, J.T.; Meggiolaro, M.A. Fatigue Design Techniques under Real Service Loads: Volume II—Low Cycle Fatigue and Multiaxial Fatigue; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2016; pp. 613–620. [Google Scholar]
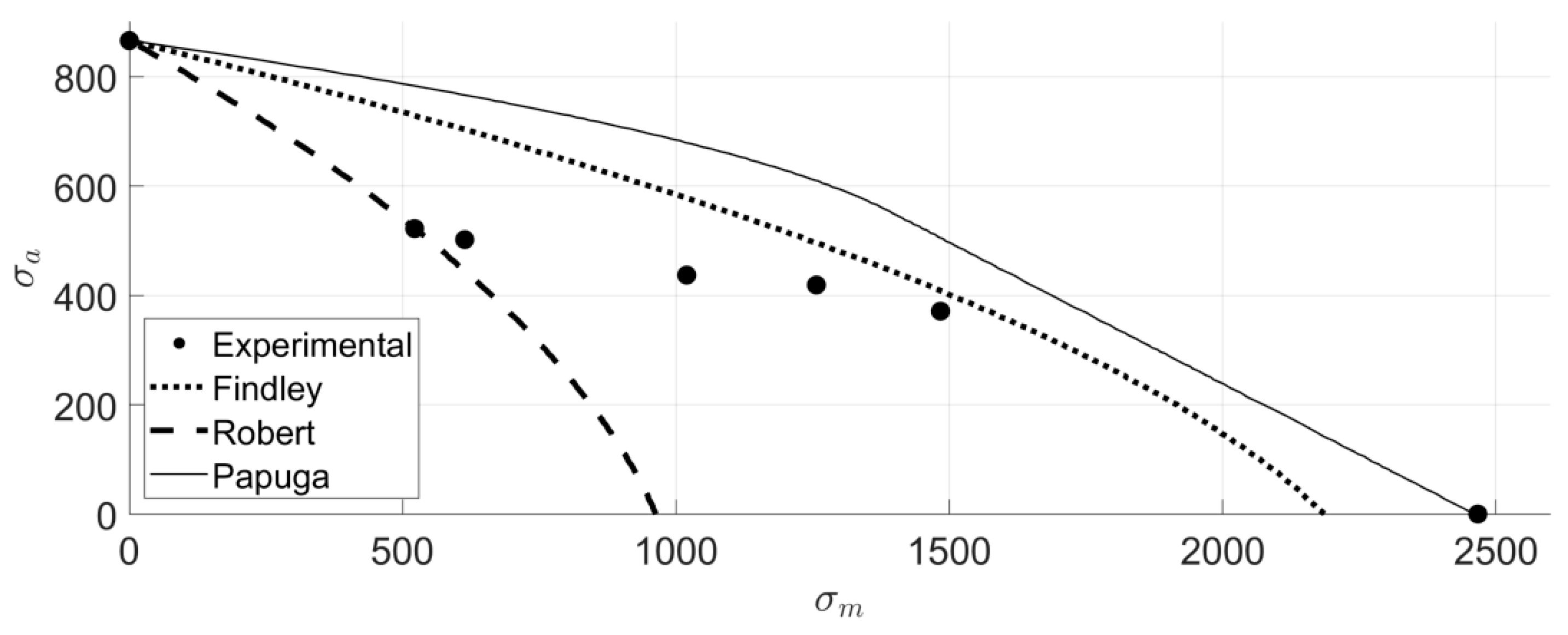

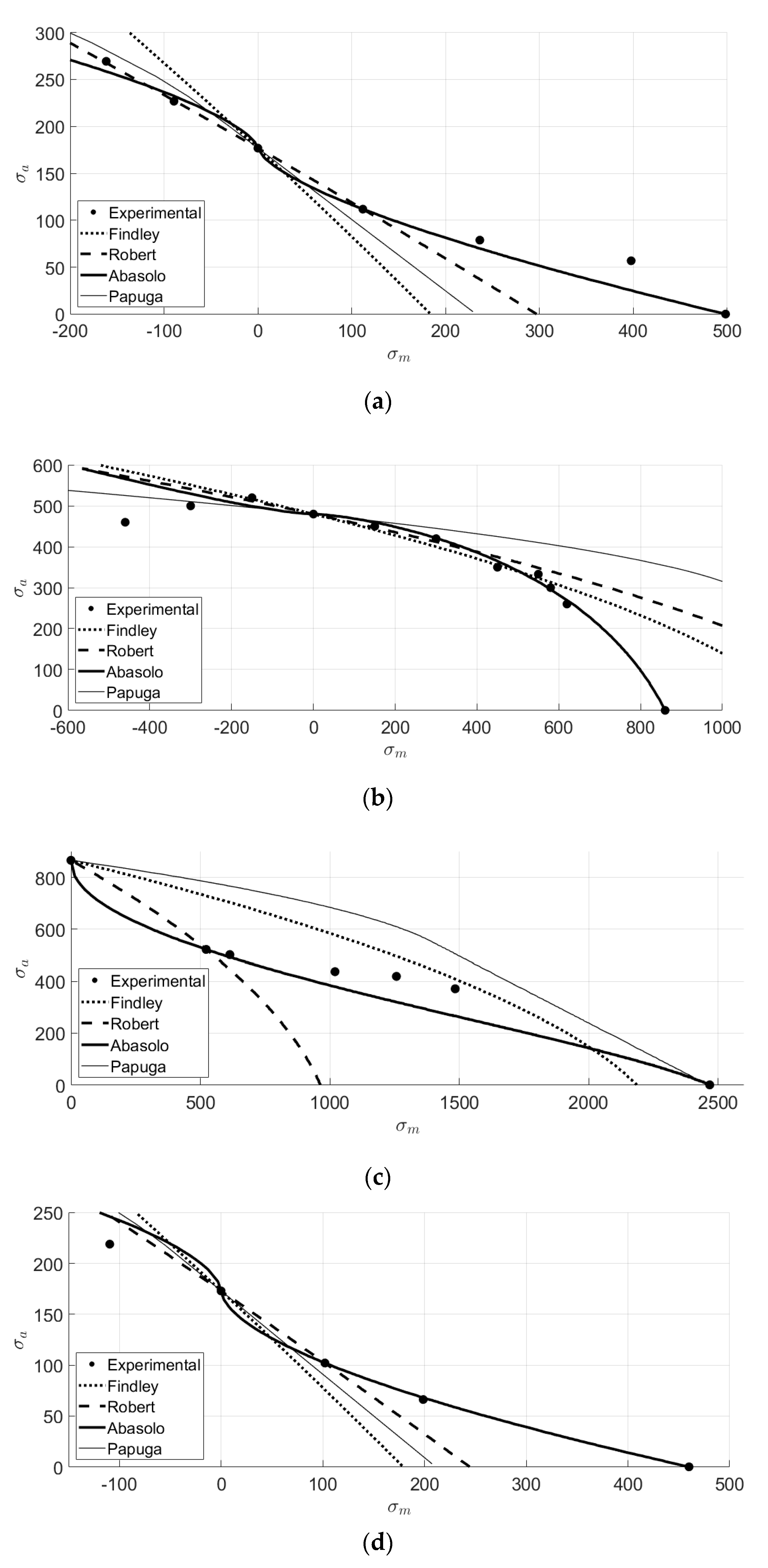
| Criterion | Equation (No Failure Condition) | Parameter Values |
|---|---|---|
| Findley (F) [9] | ||
| Robert (R) [17] | ||
| Papuga (P) [28] | ||
| Abasolo (A) * | ||
| for | ||
| Complete Database: 485 Experiments | Findley | Robert | Abasolo | Papuga |
|---|---|---|---|---|
| Mean value of the error | 8.4 | 3.5 | 3.9 | −0.6 |
| Standard deviation | 17.6 | 10.3 | 9.7 | 7.4 |
| Maximum value of the error | 147.0 | 77.3 | 43.9 | 42.6 |
| Minimum value of the error | −38.7 | −36.4 | −32.1 | −36.4 |
| Range of the error | 185.7 | 113.7 | 76.0 | 78.9 |
| Mean absolute value of the error | 12.4 | 7.0 | 7.2 | 5.2 |
| “Accurate” results (error range ± 5%) | 40.5 | 49.6 | 49.6 | 63.4 |
| “Acceptable” results (error range ± 15%) | 70.0 | 87.4 | 86.0 | 94.4 |
| Conservative results (error range + 5% + 40%) | 41.6 | 36.0 | 36.8 | 17.1 |
| Non-conservative results (error range − 5% − 40%) | 12.6 | 13.8 | 13.4 | 19.3 |
| Pure Axial Cases: 76 Experiments | Goodman | Gerber | Marin | Findley | Robert | Abasolo | Papuga |
|---|---|---|---|---|---|---|---|
| Mean value of the error | 50.3 | 9.5 | −8.4 | 8.3 | 4.1 | 2.6 | −2.6 |
| Standard deviation | 109.4 | 52.0 | 23.2 | 28.0 | 16.6 | 10.4 | 10.7 |
| Maximum value of the error | 596.0 | 268.4 | 68.3 | 147.0 | 77.3 | 38.9 | 42.6 |
| Minimum value of the error | −39.1 | −52.9 | −57.5 | −38.7 | −27.4 | −25.9 | −36.4 |
| Range of the error | 635.2 | 321.3 | 125.9 | 185.7 | 104.6 | 64.7 | 78.9 |
| Mean absolute value of the error | 58.9 | 25.5 | 17.6 | 19.0 | 8.8 | 6.6 | 7.7 |
| “Accurate” results (error range ± 5%) | 5.3 | 26.3 | 21.1 | 30.3 | 61.8 | 56.6 | 46.1 |
| “Acceptable” results (error range ± 15%) | 26.3 | 59.2 | 67.1 | 50.0 | 84.2 | 86.8 | 89.5 |
| Conservative results (error range + 5% + 40%) | 42.1 | 28.9 | 13.2 | 31.6 | 22.4 | 31.6 | 17.1 |
| Non-conservative results (error range − 5% − 40%) | 21.1 | 34.2 | 50.0 | 26.3 | 11.8 | 11.8 | 35.5 |
| Pure Axial Cases with High Mean Stress (0.05 ≤ R < 1): 35 Experiments | Goodman | Gerber | Marin | Findley | Robert | Abasolo | Papuga |
|---|---|---|---|---|---|---|---|
| Mean value of the error | 94.8 | 18.2 | −14.9 | 18.4 | 10.8 | 8.0 | −2.0 |
| Standard deviation | 147.6 | 73.5 | 27.7 | 35.3 | 21.4 | 11.2 | 14.5 |
| Maximum value of the error | 596.0 | 268.4 | 68.3 | 147.0 | 77.3 | 38.9 | 42.6 |
| Minimum value of the error | −32.6 | −52.9 | −57.5 | −38.7 | −14.9 | −9.7 | −36.4 |
| Range of the error | 628.6 | 321.3 | 125.9 | 185.7 | 92.1 | 48.6 | 78.9 |
| Mean absolute value of the error | 100.4 | 41.2 | 24.9 | 27.3 | 14.0 | 9.4 | 10.8 |
| “Accurate” results (error range ± 5%) | 2.9 | 11.4 | 11.4 | 25.7 | 45.7 | 37.1 | 25.7 |
| “Acceptable” results (error range ± 15%) | 20.0 | 40.0 | 48.6 | 34.3 | 74.3 | 80.0 | 80.0 |
| Conservative results (error range + 5% + 40%) | 22.9 | 31.4 | 5.7 | 28.6 | 37.1 | 57.1 | 25.7 |
| Non-conservative results (error range − 5% − 40%) | 14.3 | 37.1 | 51.4 | 20.0 | 8.6 | 5.7 | 45.7 |
| No Mean Stress Cases: 172 Experiments | Findley | Robert | Abasolo | Papuga |
|---|---|---|---|---|
| Mean value of the error | 1.6 | 1.6 | 1.6 | 1.1 |
| Standard deviation | 5.0 | 5.0 | 5.0 | 3.7 |
| Maximum value of the error | 16.1 | 16.1 | 16.1 | 12.4 |
| Minimum value of the error | −12.4 | −12.4 | −12.4 | −9.7 |
| Range of the error | 28.4 | 28.4 | 28.4 | 22.1 |
| Mean absolute value of the error | 4.1 | 4.1 | 4.1 | 3.1 |
| “Accurate” results (error range ± 5%) | 70.5 | 70.5 | 70.5 | 81.5 |
| “Acceptable” results (error range ± 15%) | 98.8 | 98.8 | 98.8 | 100.0 |
| Conservative results (error range + 5% + 40%) | 21.4 | 21.4 | 21.4 | 13.9 |
| Non-conservative results (error range − 5% − 40%) | 8.1 | 8.1 | 8.1 | 4.6 |
| Mean Stress Cases: 313 Experiments | Findley | Robert | Abasolo | Papuga |
|---|---|---|---|---|
| Mean value of the error | 12.1 | 4.6 | 5.1 | −1.5 |
| Standard deviation | 20.7 | 12.1 | 11.4 | 8.7 |
| Maximum value of the error | 147.0 | 77.3 | 43.9 | 42.6 |
| Minimum value of the error | −38.7 | −36.4 | −32.1 | −36.4 |
| Range of the error | 185.7 | 113.7 | 76.0 | 78.9 |
| Mean absolute value of the error | 17.3 | 9.0 | 9.3 | 6.5 |
| “Accurate” results (error range ± 5%) | 24.0 | 38.0 | 38.0 | 53.4 |
| “Acceptable” results (error range ± 15%) | 54.0 | 81.2 | 78.9 | 91.4 |
| Conservative results (error range + 5% + 40%) | 52.7 | 44.1 | 45.4 | 18.8 |
| Non-conservative results (error range − 5% − 40%) | 15.0 | 16.9 | 16.3 | 27.5 |
| High Mean Stress Cases (0.05 ≤ RvM < 1): 110 EXPERIMENTS | Findley | Robert | Abasolo | Papuga |
|---|---|---|---|---|
| Mean value of the error | 19.5 | 6.5 | 8.2 | −2.3 |
| Standard deviation | 27.9 | 15.7 | 13.2 | 11.7 |
| Maximum value of the error | 147.0 | 77.3 | 43.9 | 42.6 |
| Minimum value of the error | −38.7 | −18.0 | −16.6 | −36.4 |
| Range of the error | 185.7 | 95.2 | 60.5 | 78.9 |
| Mean absolute value of the error | 25.8 | 11.7 | 12.1 | 9.0 |
| “Accurate” results (error range ± 5%) | 17.3 | 28.2 | 27.3 | 37.3 |
| “Acceptable” results (error range ± 15%) | 35.5 | 74.5 | 69.1 | 82.7 |
| Conservative results (error range + 5% + 40%) | 43.6 | 47.3 | 55.5 | 24.5 |
| Non-conservative results (error range − 5% − 40%) | 17.3 | 21.8 | 16.4 | 37.3 |
| Mean Stress Cases, Pure Torsion: 33 Experiments | Findley | Robert | Abasolo | Papuga |
|---|---|---|---|---|
| Mean value of the error | −0.7 | −4.7 | −5.4 | −7.5 |
| Standard deviation | 11.0 | 6.3 | 5.6 | 8.3 |
| Maximum value of the error | 29.1 | 5.8 | 5.4 | 7.7 |
| Minimum value of the error | −31.0 | −18.0 | −16.6 | −31.3 |
| Range of the error | 60.1 | 23.7 | 22.0 | 39.0 |
| Mean absolute value of the error | 7.4 | 5.9 | 5.9 | 8.1 |
| “Accurate” results (error range ± 5%) | 54.5 | 51.5 | 45.5 | 45.5 |
| “Acceptable” results (error range ± 15%) | 87.9 | 90.9 | 93.9 | 84.8 |
| Conservative results (error range + 5% + 40%) | 24.2 | 3.0 | 3.0 | 3.0 |
| Non-conservative results (error range − 5% − 40%) | 21.2 | 45.5 | 51.5 | 51.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abasolo, M.; Pallares-Santasmartas, L.; Eizmendi, M. A New Critical Plane Multiaxial Fatigue Criterion with an Exponent to Account for High Mean Stress Effect. Metals 2024, 14, 964. https://doi.org/10.3390/met14090964
Abasolo M, Pallares-Santasmartas L, Eizmendi M. A New Critical Plane Multiaxial Fatigue Criterion with an Exponent to Account for High Mean Stress Effect. Metals. 2024; 14(9):964. https://doi.org/10.3390/met14090964
Chicago/Turabian StyleAbasolo, Mikel, Luis Pallares-Santasmartas, and Martin Eizmendi. 2024. "A New Critical Plane Multiaxial Fatigue Criterion with an Exponent to Account for High Mean Stress Effect" Metals 14, no. 9: 964. https://doi.org/10.3390/met14090964





