Study on Near-Net Shape Forging of Large Marine Crank Throws
Abstract
1. Introduction
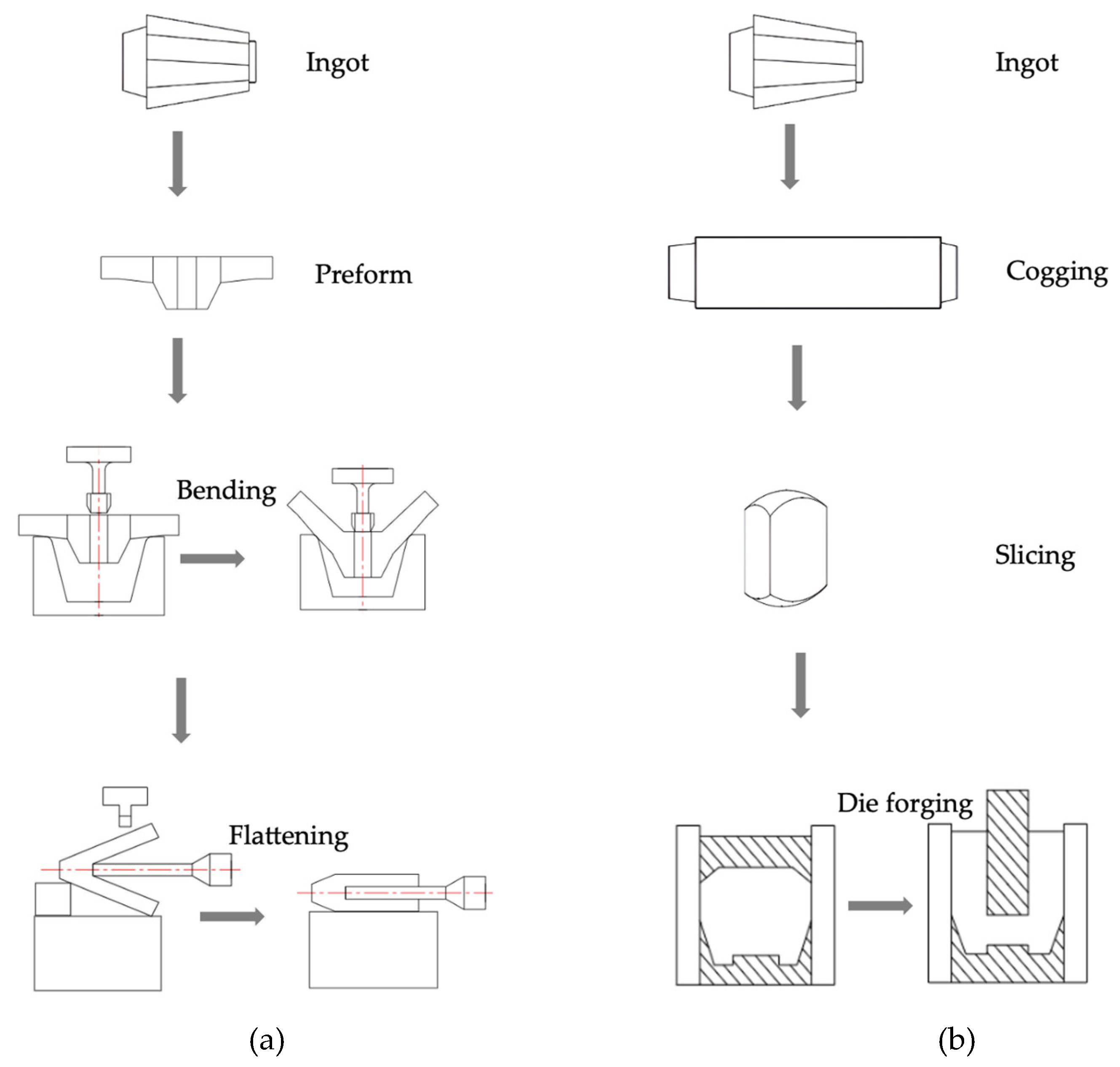
2. Objective of the NNS Forging of a Large Marine Crank Throw
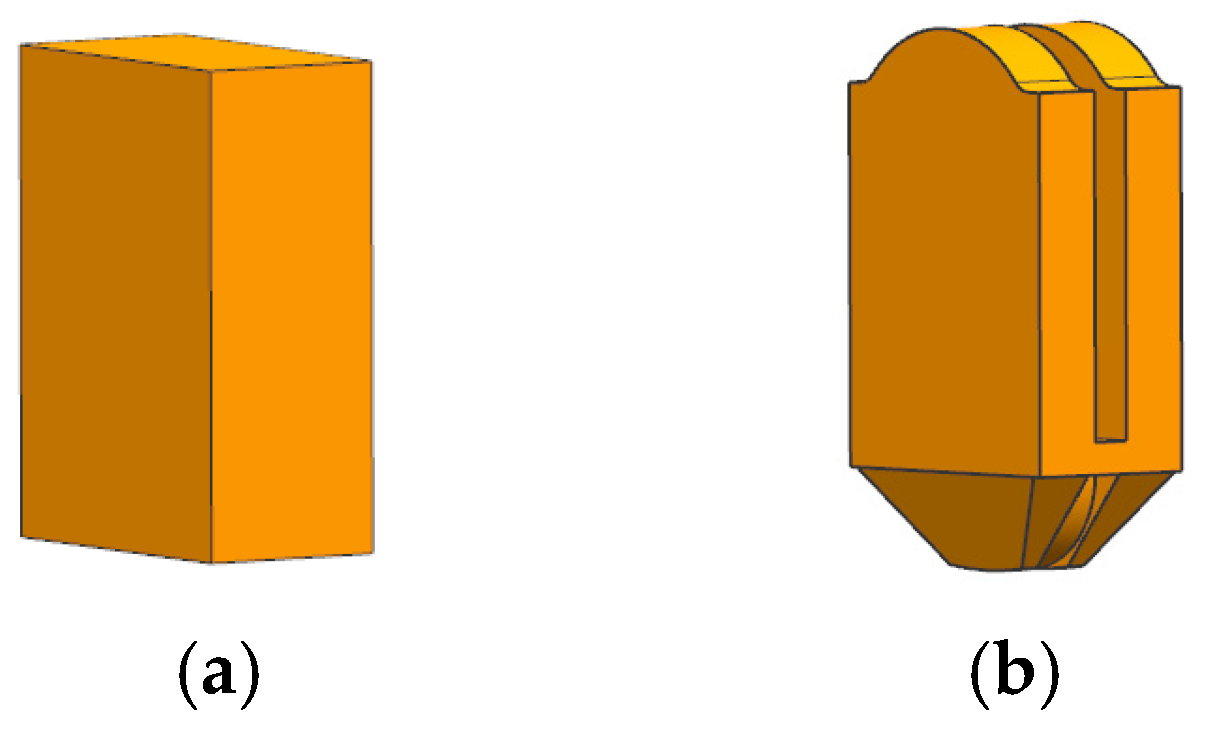
3. Analysis of NNS Forging Methods of Crank Throw
3.1. One-Step Extrusion (OSE)
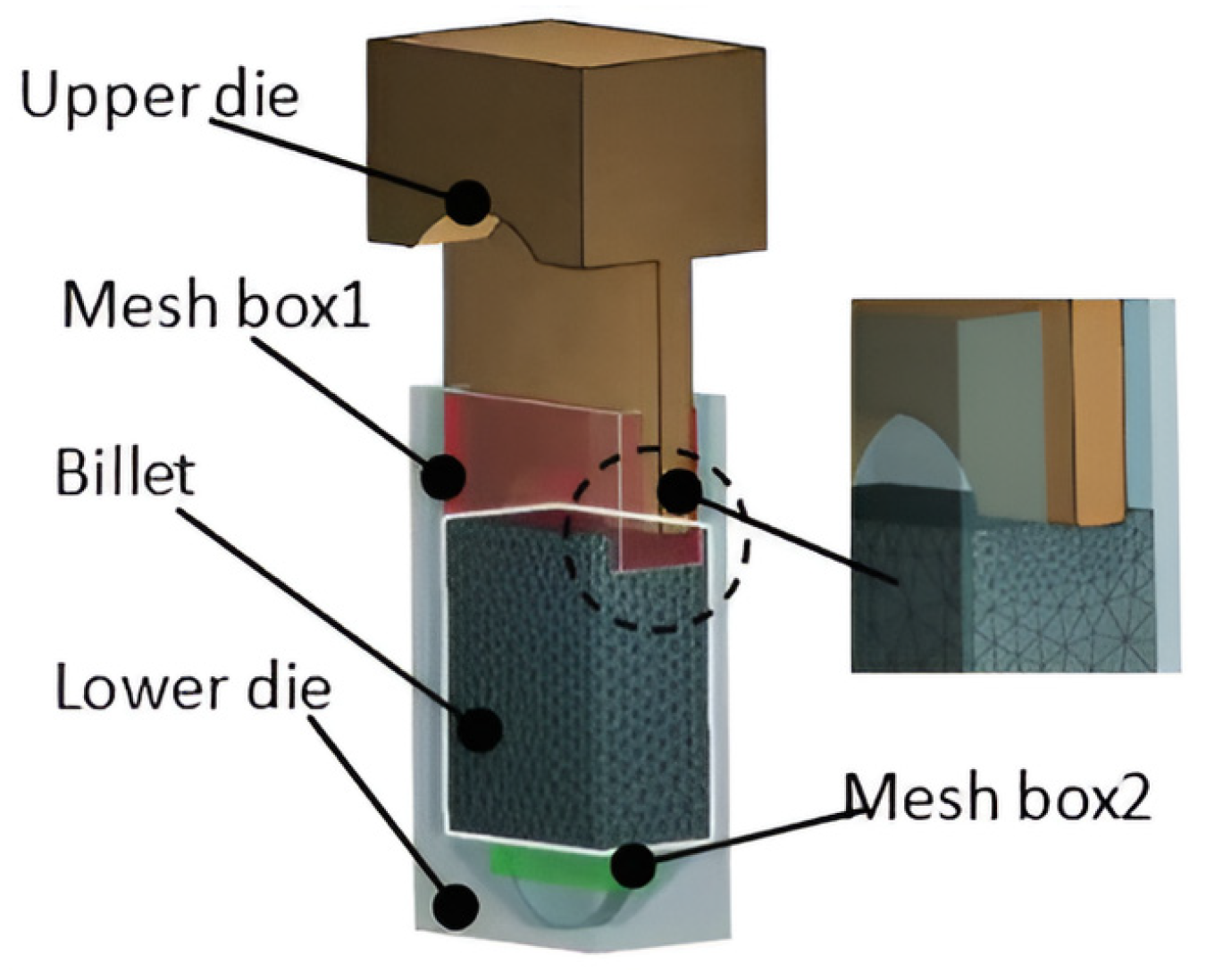
3.1.1. Numerical Simulation and Analysis of OSE
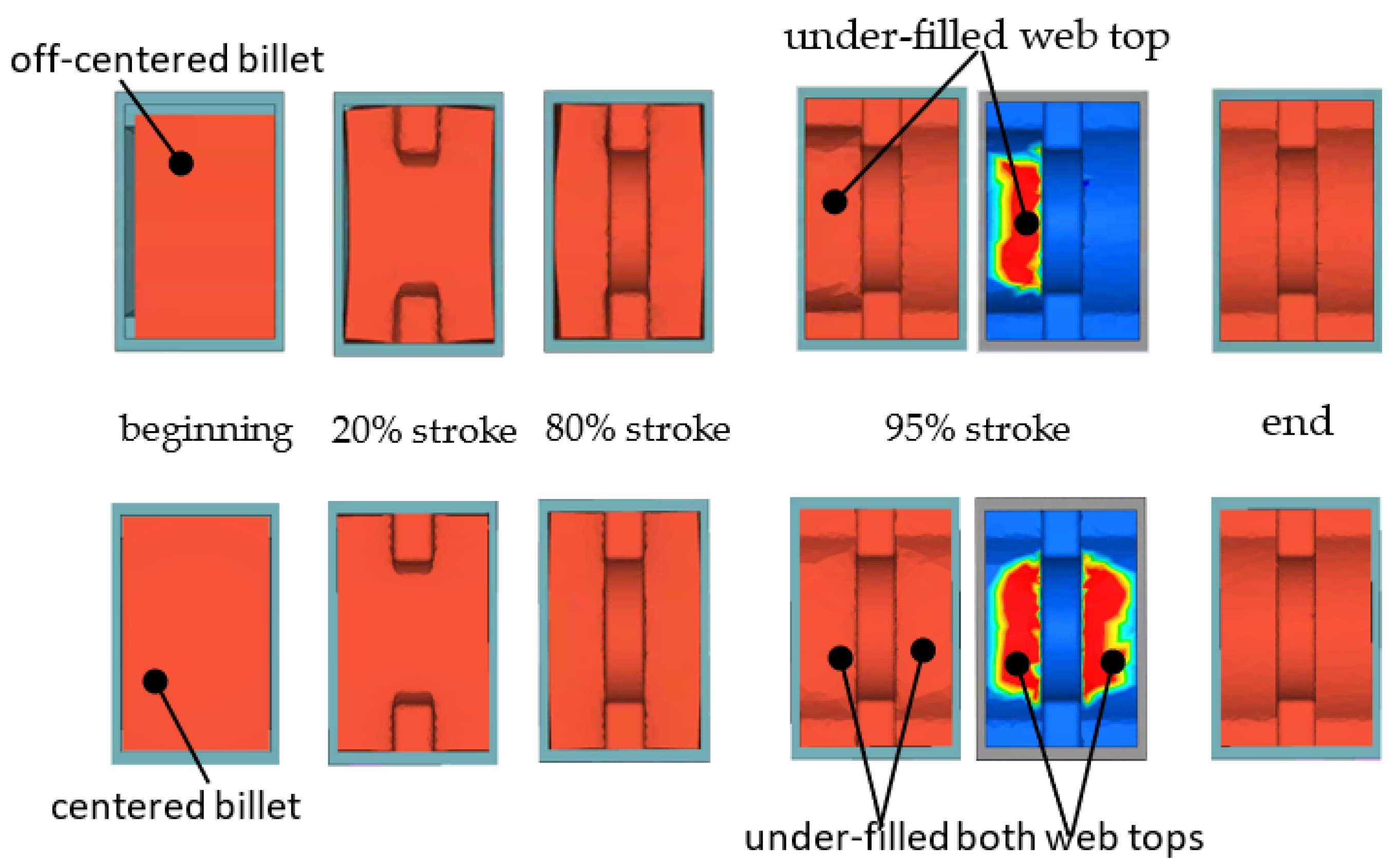
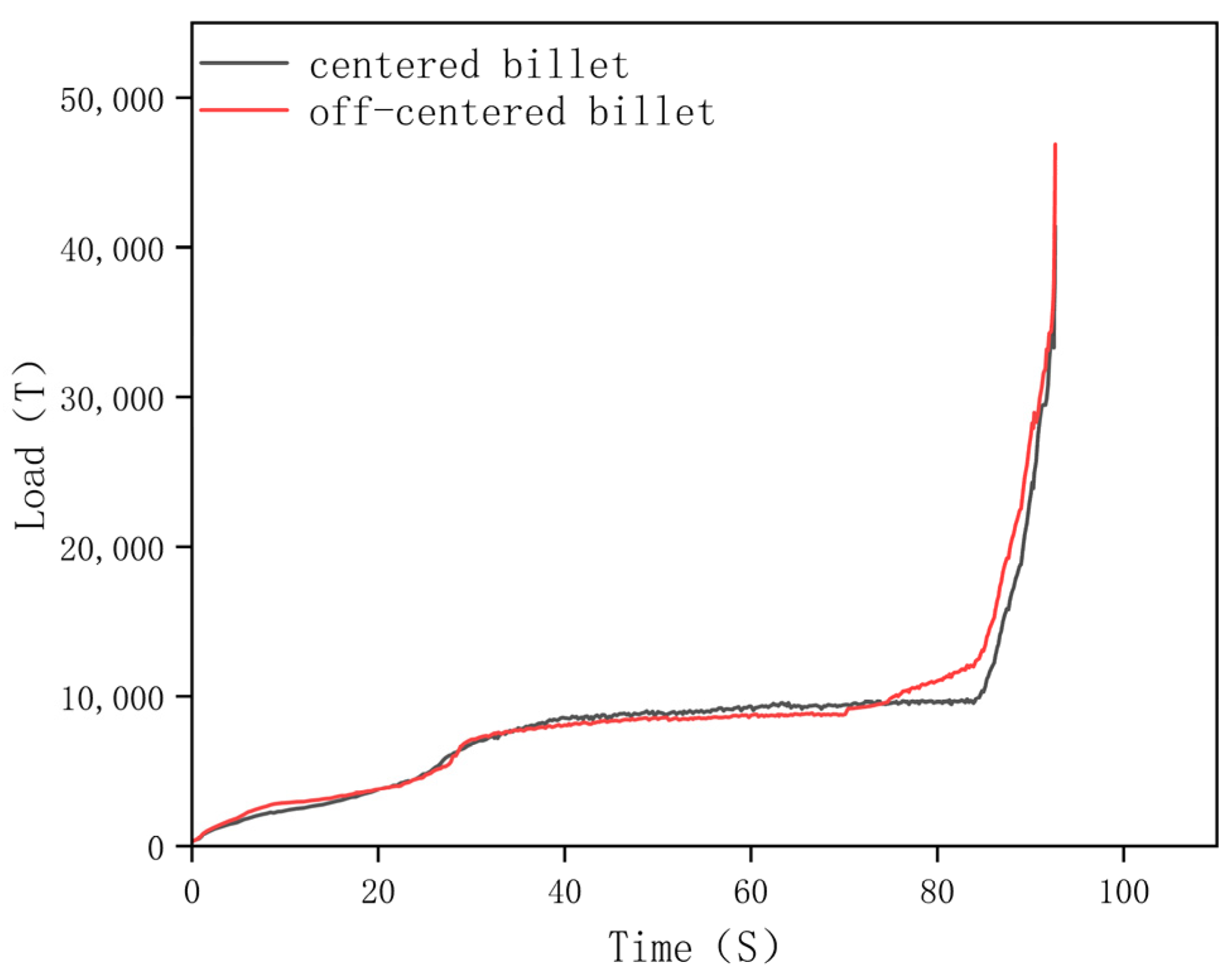
3.1.2. Influence of Asymmetrically-Placed Billets
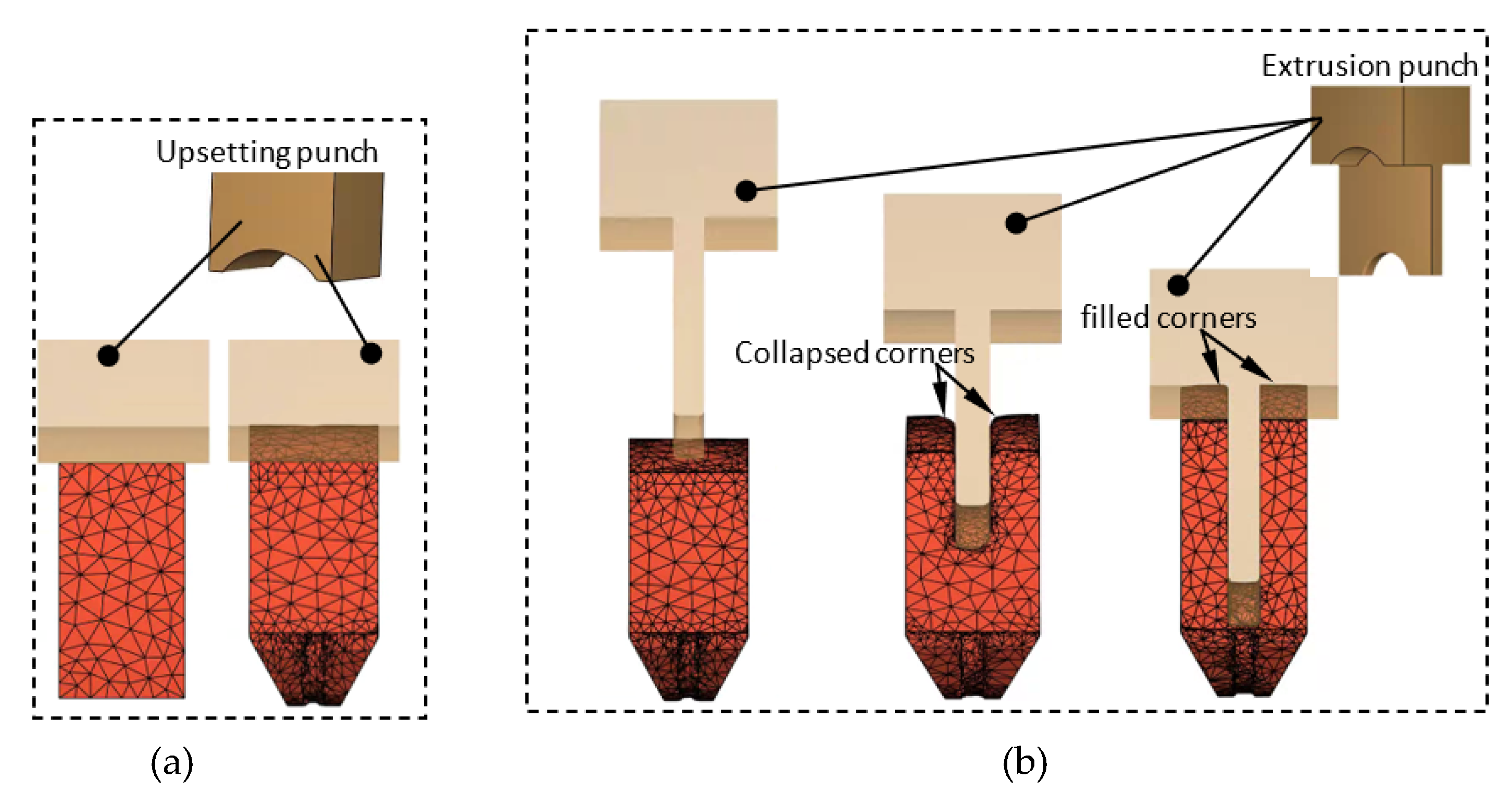
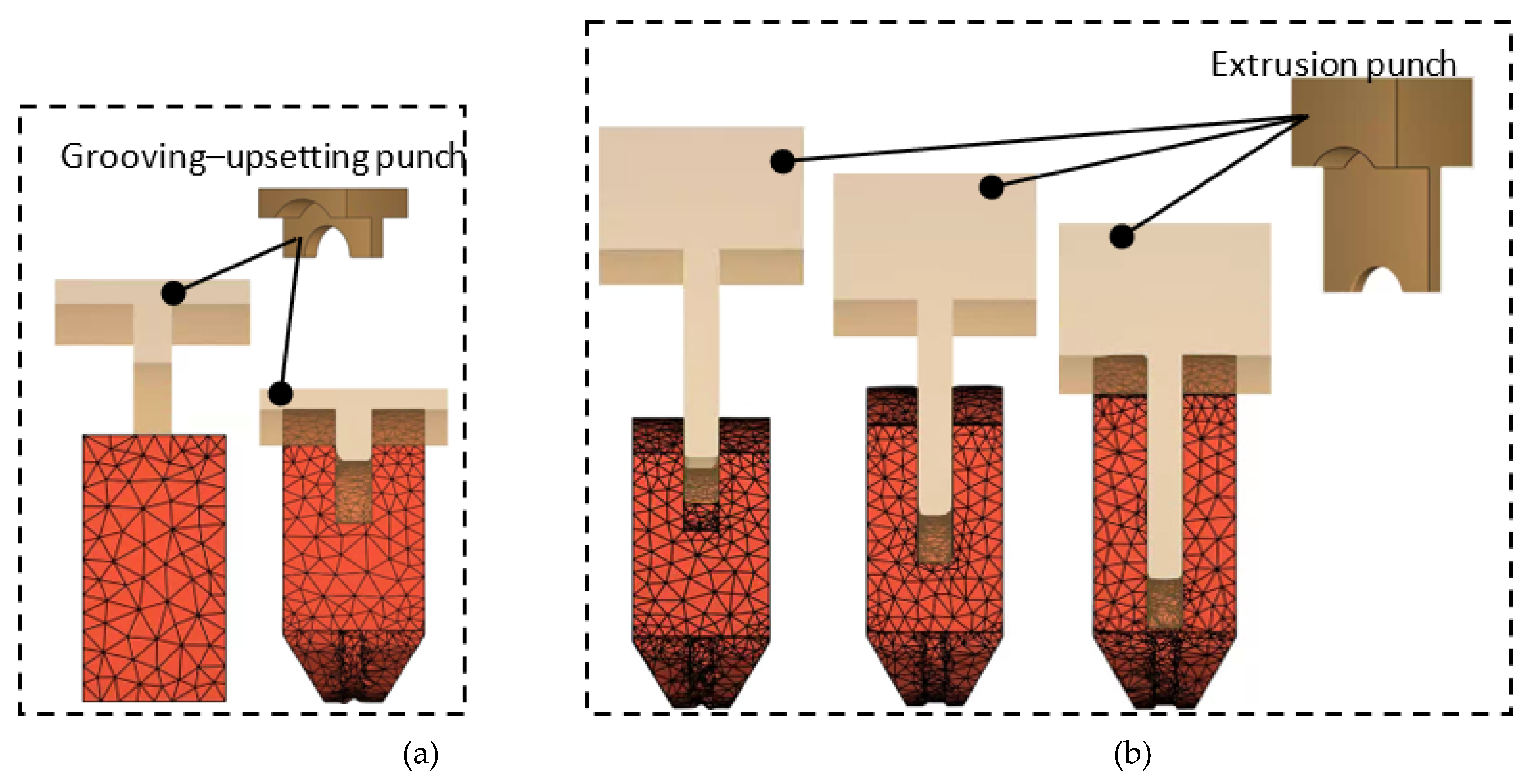
3.2. Upsetting/Backward Extrusion (U/BE)
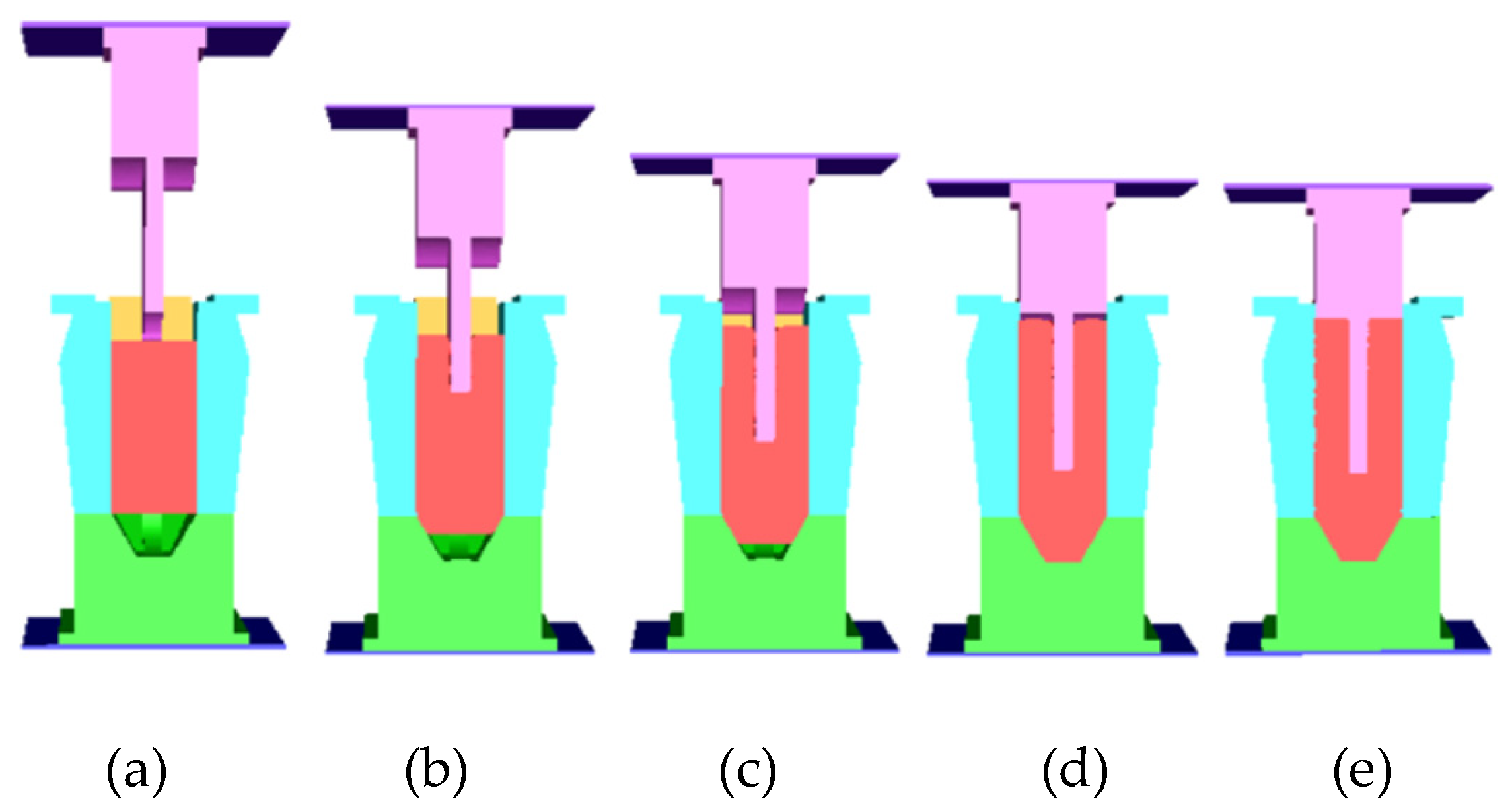
3.3. Grooving–Upsetting/Backward Extrusion (G–U/BE)
3.4. Determination of the Optimal Method
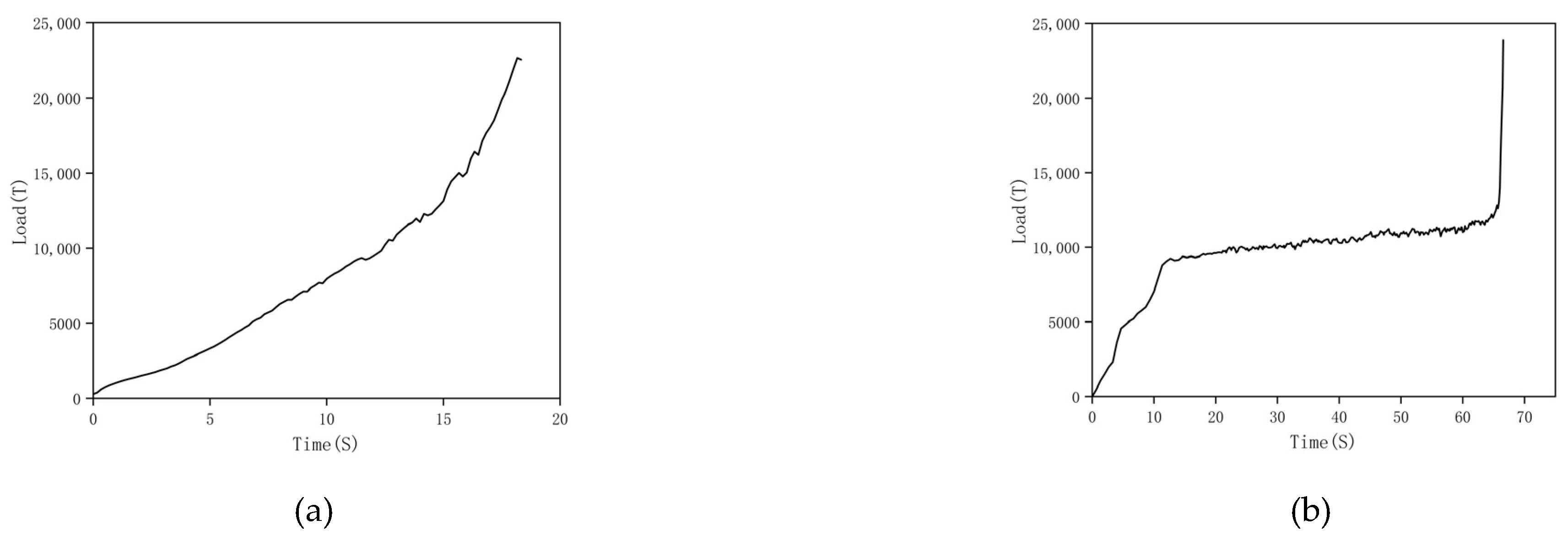
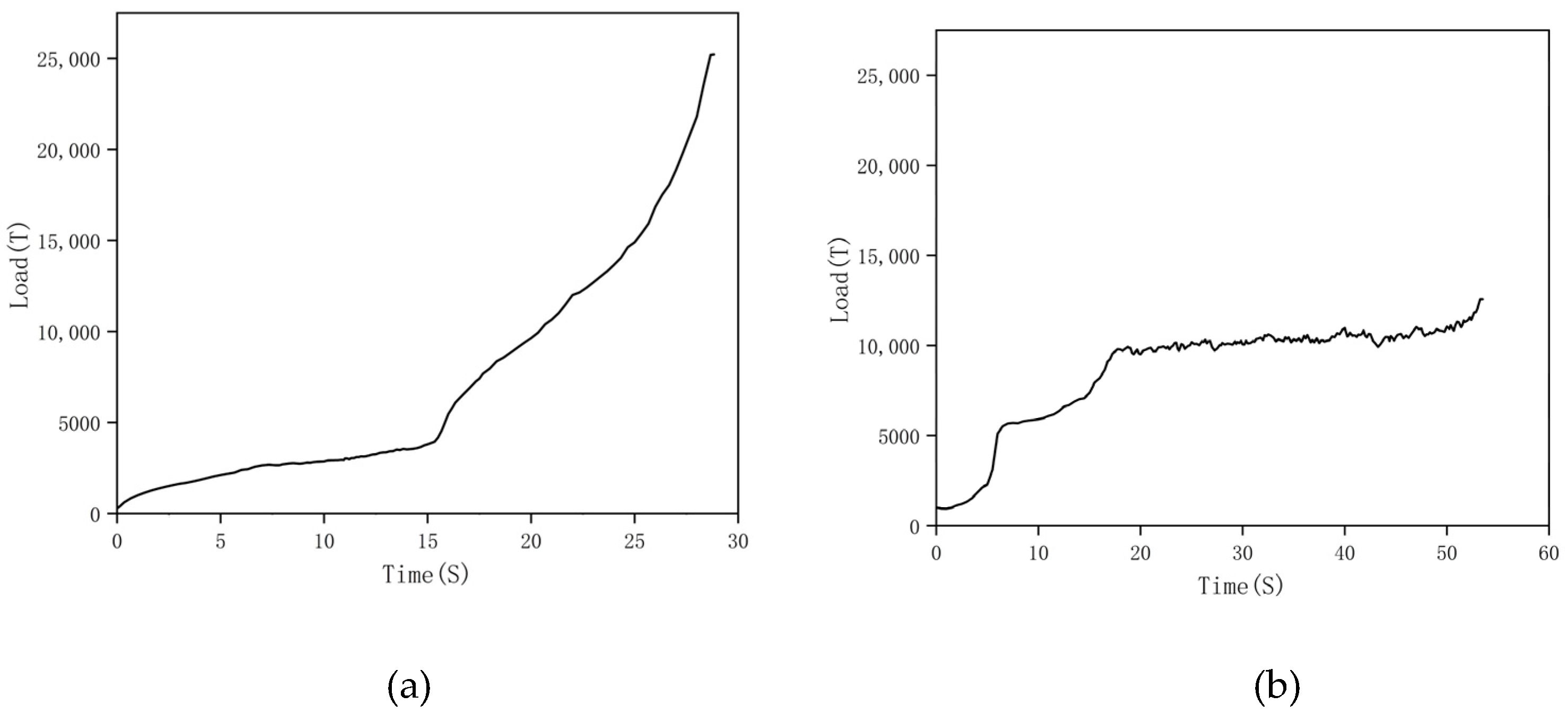
3.4.1. Forging Load
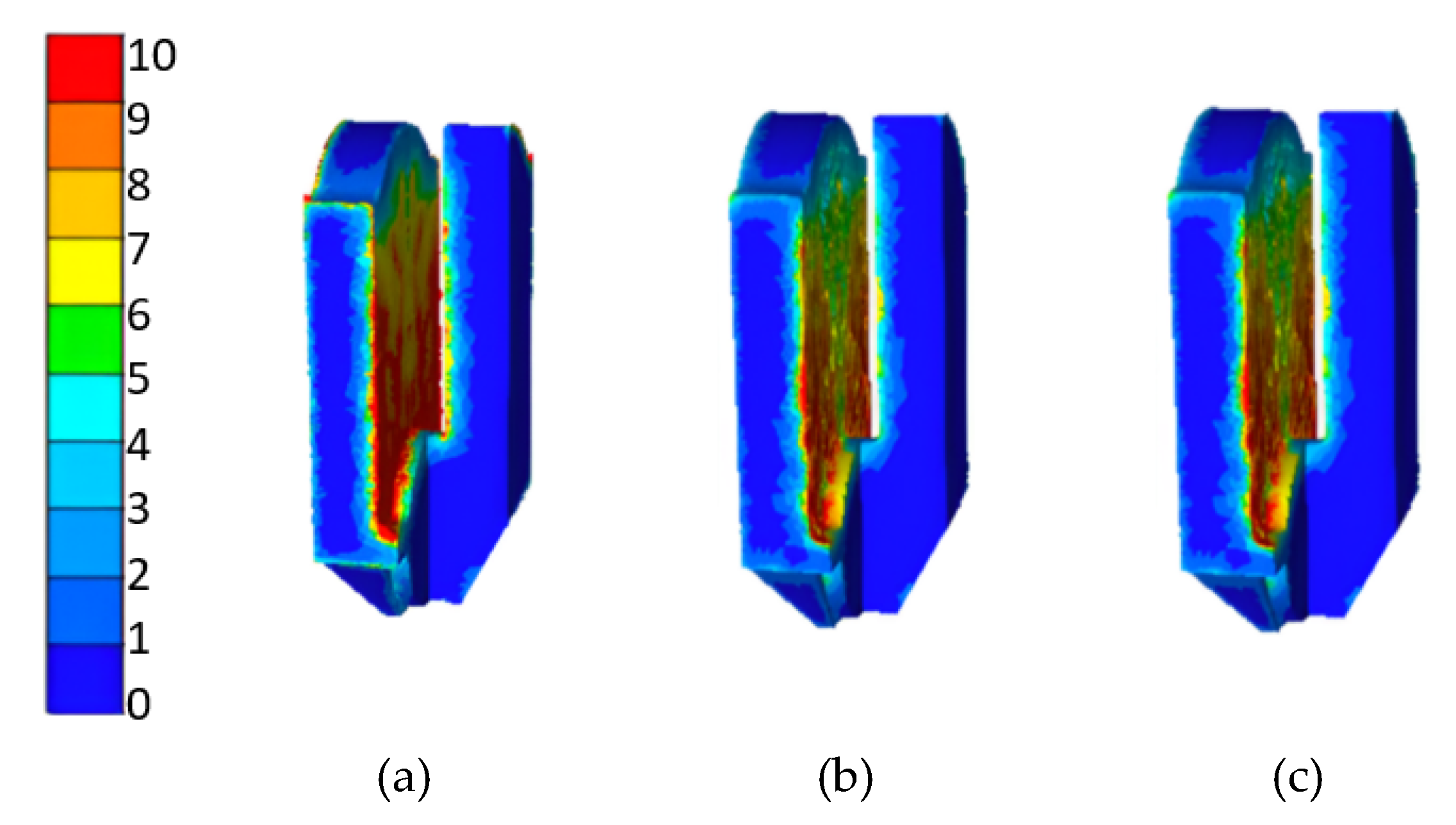
3.4.2. Comparison of Forging Forming Quality
3.4.3. Comparison of the Temperature Rise of the Lower Die
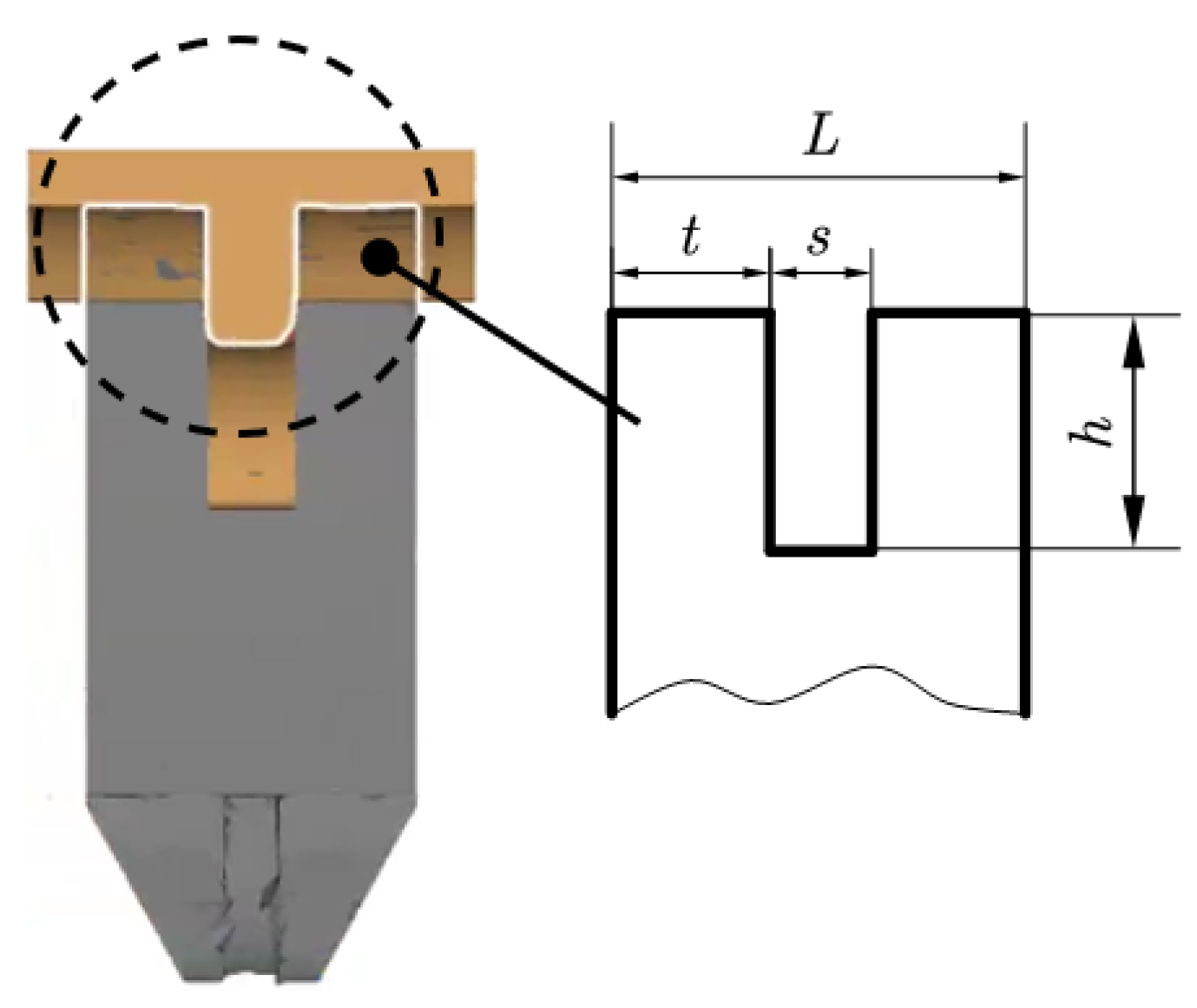
4. Study on the Optimal Groove Shape
4.1. Selection of the Optimal Groove Shape
4.2. Influence of the Groove Depth (h) on the Shape of the Journal End
5. Experiment
5.1. Near-Net Forged Crank Throw Experiment
5.2. Microstructure and Performance Testing
6. Conclusions
- Finite element (FE) software was used to simulate three near-net-shape (NNS) forming methods: OSE, U/BE, and G–U/BE. The results indicate that G–U/BE requires the lowest load.
- The journal end web shapes formed at the end of the grooving–upsetting step in the G–U/BE process create a rigid zone that remains intact during the subsequent backward extrusion. The relative groove depth (χ) significantly influences the final forging. Deeper grooves are more favorable for the final crank throw formation but require a higher load at the grooving–upsetting stage.
- When χ is greater than or equal to 1.5, the web’s journal end shape is optimal. However, if the groove depth exceeds this value, the required load increases to levels comparable to one-step extrusion, rendering the grooving–upsetting step ineffective. Therefore, the optimal value of χ is 1.5.
- Scaled-down experiment results confirm that G–U/BE is a practical and feasible NNS forming method for producing large marine crank throw forgings, achieving both the desired shape and microstructure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gomes, J.; Gaivota, N.; Martins, R.F.; Silva, P.P. Failure analysis of crankshafts used in maritime V12 diesel engines. Eng. Fail. Anal. 2018, 92, 466–479. [Google Scholar] [CrossRef]
- Meier-Peter, H.; Bernhard, F. Compendium Marine Engineering; Seehafen Verlag: Hamburg, Germany, 2009. [Google Scholar]
- Kubo, H.; Mori, H. Trends in Manufacturing and Technological Development of Crankshaft Material. Mar. Eng. 2006, 41, 672–676. [Google Scholar] [CrossRef] [PubMed]
- Hanawa, Y.; Kajihara, S.; Kagawa, Y.; Mori, H.; Hamada, T. Development of High Strength Cast Steel for Semi-built up Type Crankshaft of Low Speed Diesel Engine, and Stress Measurement and Evaluation of Crankshaft. Mar. Eng. 2005, 40, 254–259. [Google Scholar] [CrossRef] [PubMed]
- Fonte, M.; Duarte, P.; Anes, V.; Freitas, M.; Reis, L. On the assessment of fatigue life of marine diesel engine crankshafts. Eng. Fail. Anal. 2015, 56, 51–57. [Google Scholar] [CrossRef]
- Instructions on the Group Standard of General Technical Specifications for Die Forging Marine Crankshaft Forgings. 2022, Confederation of Chinese Metalforming Industry. Available online: https://max.book118.com/html/2023/1222/5032211321011030.shtm (accessed on 25 December 2024). (In Chinese).
- Liu, K. Study on Die Forging Process of Large-Sized Crankthrow by Simulation; Yanshan University: Qinhuangdao, China, 2012. [Google Scholar]
- Song, M.C.; Lee, Y.U.; VanTyne, C.; Moon, Y.H. Symmetric bending technology using a floating die to forge crank throws for marine engines. J. Mater. Process. Technol. 2016, 237, 197–207. [Google Scholar] [CrossRef]
- Fujitsuna, N. Development of Steel Castings and Forgings for Vessels. Kobelco Technol. Rev. 2017, 35, 1–6. [Google Scholar]
- Altan, T.; Fiorentino, R.J. Prediction of Loads and Stresses in Closed-Die Forging. J. Eng. Ind. 1971, 93, 477–484. [Google Scholar] [CrossRef]
- Tanishq Jaiswal, V.I.; Kakde, A. A Review on closed die forging. Int. J. Adv. Eng. Manag. 2022, 4, 5. [Google Scholar]
- Sheth, D.; Das, S.; Chatterjee, A.; Bhattacharya, A. Modeling of Closed-Die Forging for Estimating Forging Load. J. Inst. Eng. Ser. C 2017, 98, 53–61. [Google Scholar] [CrossRef]
- Li, C.; Li, M.V.; Li, S.; Li, D.; Peng, X. Effect of stresses on martensite transformation kinetics and transformation plasticity of S34MnV steel. Mater. Res. Express 2019, 6, 076531. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Zhou, Y.; Guo, W.; Jiang, R.; Zhu, Y. Research on Thermal Deformation Behavior of Marine Crankshaft S34MnV Steel. Steel Res. Int. 2021, 92, 2100140. [Google Scholar] [CrossRef]
- Yan, Y.; Li, M.V.; Bu, H.; Zheng, S. Continuous Cooling Transformation Behavior and Transformation Kinetics of S34MnV Steel. Cailiao Daobao/Mater. Rep. 2021, 35, 20129–20136. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, K.; Yang, Y. A comparative study on the activation energy for hot deformation of 5CrNiMoV and S34MnV steel. Curr. Mater. Sci. 2021, 14, 70–79. [Google Scholar] [CrossRef]
- Chen, Z.; Nash, P. Hot Deformation Behavior and Processing Maps for a Large Marine Crankshaft S34MnV Steel. Steel Res. Int. 2018, 89, 1700321. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, K.; Yang, Y. Modelling and simulation of a bending process for S34MnV steel. Int. J. Microstruct. Mater. Prop. 2019, 14, 432–447. [Google Scholar] [CrossRef]
- Chen, Z.; Nash, P.; Zhang, Y. Correlation of Cooling Rate, Microstructure and Hardness of S34MnV Steel. Metall. Mater. Trans. B 2019, 50, 1718–1728. [Google Scholar] [CrossRef]
- Jayanthi, A.; Anilkumar, M.; Ravisankar, B. Selection of forging process for compressor disc for aero engine using finite element analysis. Mater. Today Proc. 2022, 60, 2111–2116. [Google Scholar] [CrossRef]
- Raja, N.; Daniel, B.S.S. Microstructural and mechanical characteristics of hot worked homogenized AA7068 using 3D processing map and DEFORM-3D. Mater. Today Commun. 2023, 36, 106574. [Google Scholar] [CrossRef]
- Zeng, Y.; Ji, H.; Song, C.; Wang, M.; Li, J. Numerical simulation and experiment on hot forging of high-Mn steel turnout core. Mater. Today Commun. 2024, 40, 109588. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, R.; Tang, J.; Jiang, F.; Fu, D.; Zhang, H.; Teng, J. Microstructural Evolution and Mechanical Properties of a Continuously Cast Al–Mg–Si–Cu Alloy Processed by Repetitive Continuous Extrusion Forming. Met. Mater. Int. 2023, 29, 2028–2039. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, S.; Gao, L.; Qiao, X.; Cui, Y. Fatigue life analysis model of crankshaft under uncertain working conditions based on physical-data collaboration. J. Eng. Res. 2023, in press. [Google Scholar] [CrossRef]
- Derazkola, H.A.; Garcia, E.; Murillo-Marrodán, A.; Hardell, J. The effect of temperature and strain rate on the mechanical properties and microstructure of super Cr13 martensitic stainless steel. J. Mater. Res. Technol. 2023, 24, 3464–3476. [Google Scholar] [CrossRef]
- Derazkola, H.A.; García Gil, E.; Murillo-Marrodán, A.; Méresse, D. Review on dynamic recrystallization of martensitic stainless steels during hot deformation: Part I—Experimental Study. Metals 2021, 11, 572. [Google Scholar] [CrossRef]
- Momeni, A.; Dehghani, K. Prediction of dynamic recrystallization kinetics and grain size for 410 martensitic stainless steel during hot deformation. Met. Mater. Int. 2010, 16, 843–849. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Chen, Z. Study on Numerical Simulation of Metal Flow and Microstructure Evolution of a Crankshaft Forging Process. 2013. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=af5310c3647d0b4a20fb10c916c9fce2&site=xueshu_se (accessed on 25 December 2024).
- Taylor, D.A. Introduction to Marine Engineering; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Society, C. Section 4 Forgings for Crankshafts. Available online: https://www.imorules.com/LRMAT_CH5_4.html (accessed on 28 November 2024).
- ASTM E112-13; Standard Test Methods for Determining Average Grain Size. ASTM International: West Conshohocken, PA, USA, 2021.




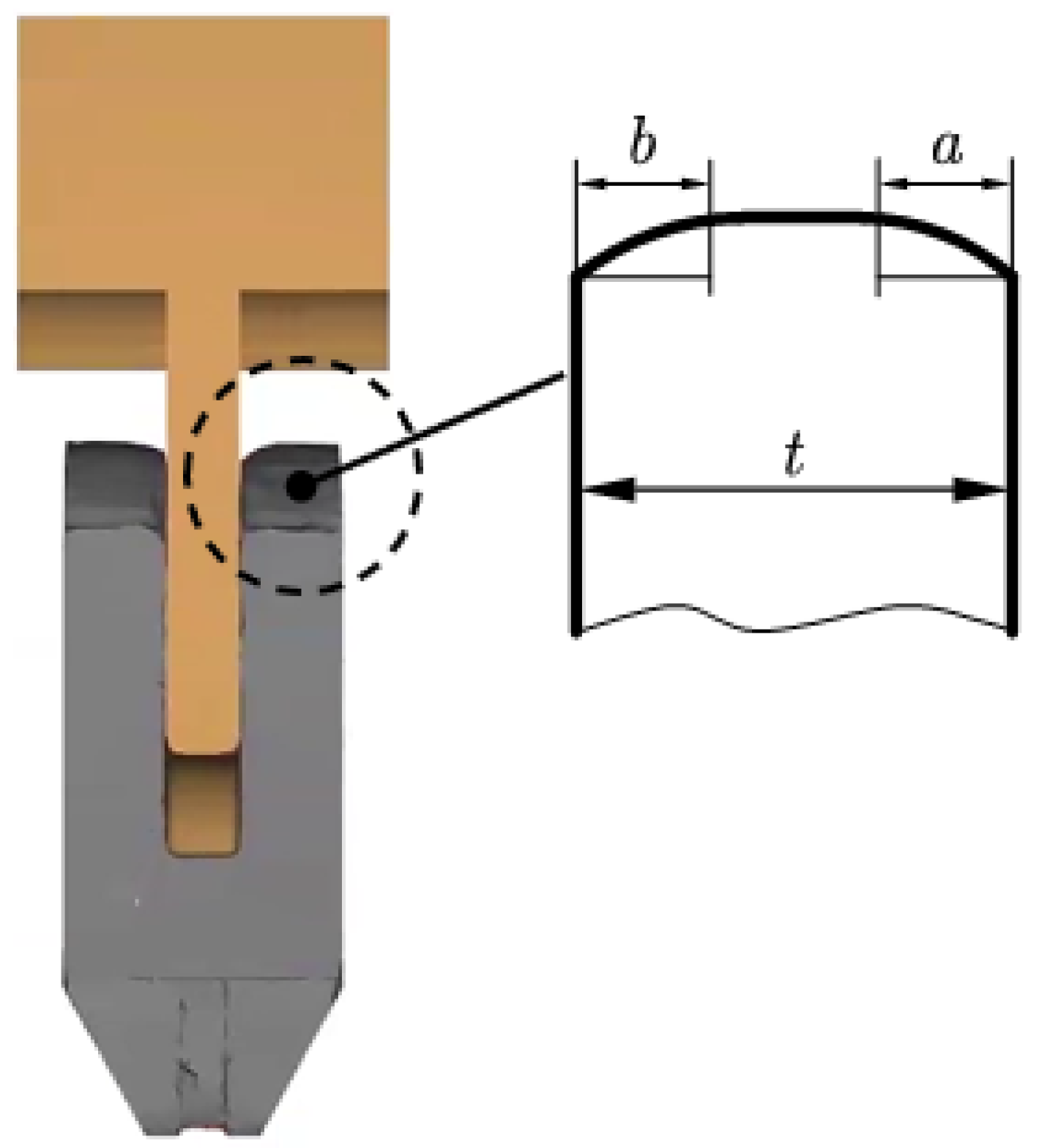
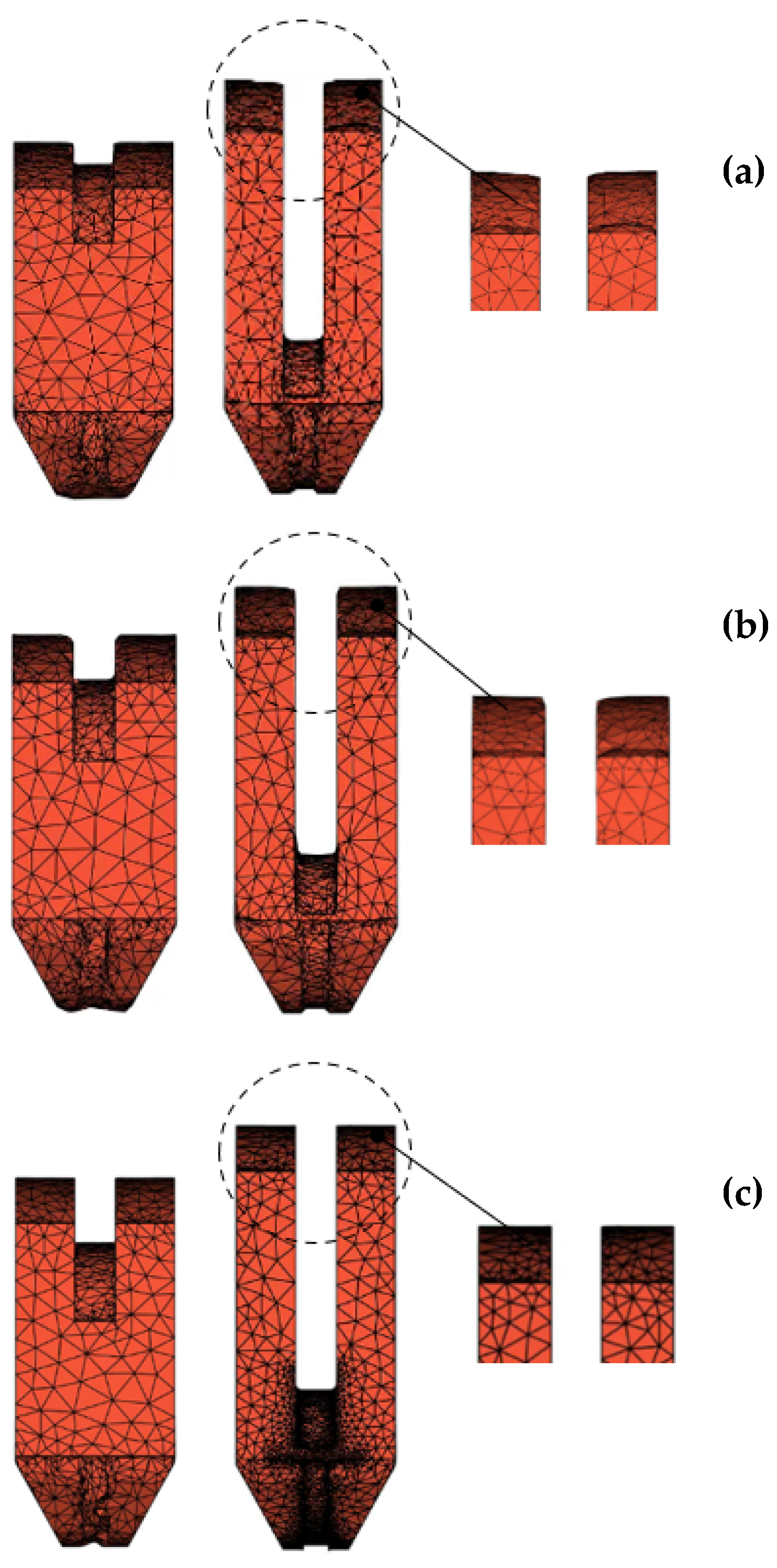





| Item Tested | Temp. °C | Min. Tensile Strength (MPa) | Min. Yield Strength (MPa) | Min. Elongation (%) | Reduction of Area (%) | Charpy V-Notch (J) | Hardness (HB) | |
|---|---|---|---|---|---|---|---|---|
| Longitudinal | Longitudinal | Longitudinal | Min. | Max. | ||||
| Specifications | 20 | 610 | 350 | 18 | 40 | 18 | 180 | 220 |
| Component | C | Si | Mn | P | S | Cr | Ni | Mo | V |
|---|---|---|---|---|---|---|---|---|---|
| Measured | 0.35 | 0.02 | 1.13 | 0.006 | 0.002 | 0.27 | 0.26 | 0.11 | 0.10 |
| Parameters | Value |
|---|---|
| Billet’s initial temperature | 1200 °C |
| Die’s initial temperature | 50 °C |
| Friction coefficient between billet and dies | 0.15 (water + graphite) |
| Heat transfer coefficient between billet and dies | 2000 W/m2·K |
| Heat transfer coefficient between billet and air | 10 W/m2·K |
| Upper die speed | 60 mm/s |
| Method | Load (tons) | ||
|---|---|---|---|
| Upsetting | Grooving–Upsetting | Backward Extrusion | |
| OSE | - | - | 49,000 |
| U/BE | 22,500 | - | 25,000 |
| G–U/BE | - | 24,700 | 12,500 |
| Method | OSE | U/BE | G–U/BE |
|---|---|---|---|
| Temperature (°C) | 408 | 280 | 246 |
| 0.5 | 0.65 | 0.8 | |||||
|---|---|---|---|---|---|---|---|
| 0 | 0.37 | 0.29 | 0.25 | ||||
| 0.35 | 0.31 | 0.29 | |||||
| 0.5 | 0.097 | 0.089 | 0.083 | ||||
| 0.084 | 0.081 | 0.077 | |||||
| 1.0 | 0.029 | 0.021 | 0.018 | ||||
| 0.026 | 0.019 | 0.016 | |||||
| 1.5 | 0.006 | 0.005 | 0.003 | ||||
| 0.005 | 0.003 | 0.002 | |||||
| 2.0 | 0.004 | 0.003 | 0.002 | ||||
| 0.005 | 0.003 | 0.002 | |||||
| k | 0.5 | 0.65 | 0.8 | ||
|---|---|---|---|---|---|
| z | |||||
| 0.0 | 1.00 | 1.00 | 1.00 | ||
| 0.5 | 1.03 | 1.02 | 1.02 | ||
| 1.0 | 1.06 | 1.04 | 1.03 | ||
| 1.5 | 1.08 | 1.05 | 1.04 | ||
| Item | |||||
|---|---|---|---|---|---|
| Required | 610 | 350 | 18 | 40 | 18 |
| Measured | 658 | 390 | 23.7 | 52.3 | 29 |
| Specimen No. | Grain Size Number (G) | Microstructure |
|---|---|---|
| 1 | 6.5 | Ferrite + Pearlite |
| 2 | 7.5 | Ferrite + Pearlite |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, L.; Zhang, Q.; Zhang, Y.; Wang, J.; Luo, W.; Liu, D.; Ma, T.; Velay, X. Study on Near-Net Shape Forging of Large Marine Crank Throws. Metals 2025, 15, 14. https://doi.org/10.3390/met15010014
Niu L, Zhang Q, Zhang Y, Wang J, Luo W, Liu D, Ma T, Velay X. Study on Near-Net Shape Forging of Large Marine Crank Throws. Metals. 2025; 15(1):14. https://doi.org/10.3390/met15010014
Chicago/Turabian StyleNiu, Longjiang, Qingliang Zhang, Yongwan Zhang, Jingyu Wang, Weiping Luo, Donghang Liu, Tengfei Ma, and Xavier Velay. 2025. "Study on Near-Net Shape Forging of Large Marine Crank Throws" Metals 15, no. 1: 14. https://doi.org/10.3390/met15010014
APA StyleNiu, L., Zhang, Q., Zhang, Y., Wang, J., Luo, W., Liu, D., Ma, T., & Velay, X. (2025). Study on Near-Net Shape Forging of Large Marine Crank Throws. Metals, 15(1), 14. https://doi.org/10.3390/met15010014






