Thermodynamic Guidelines for Minimizing Chromium Losses in Electric Arc Furnace Steelmaking
Abstract
1. Introduction
2. Thermodynamic Characteristics of Chromium and Carbon Oxidation
3. Conclusions
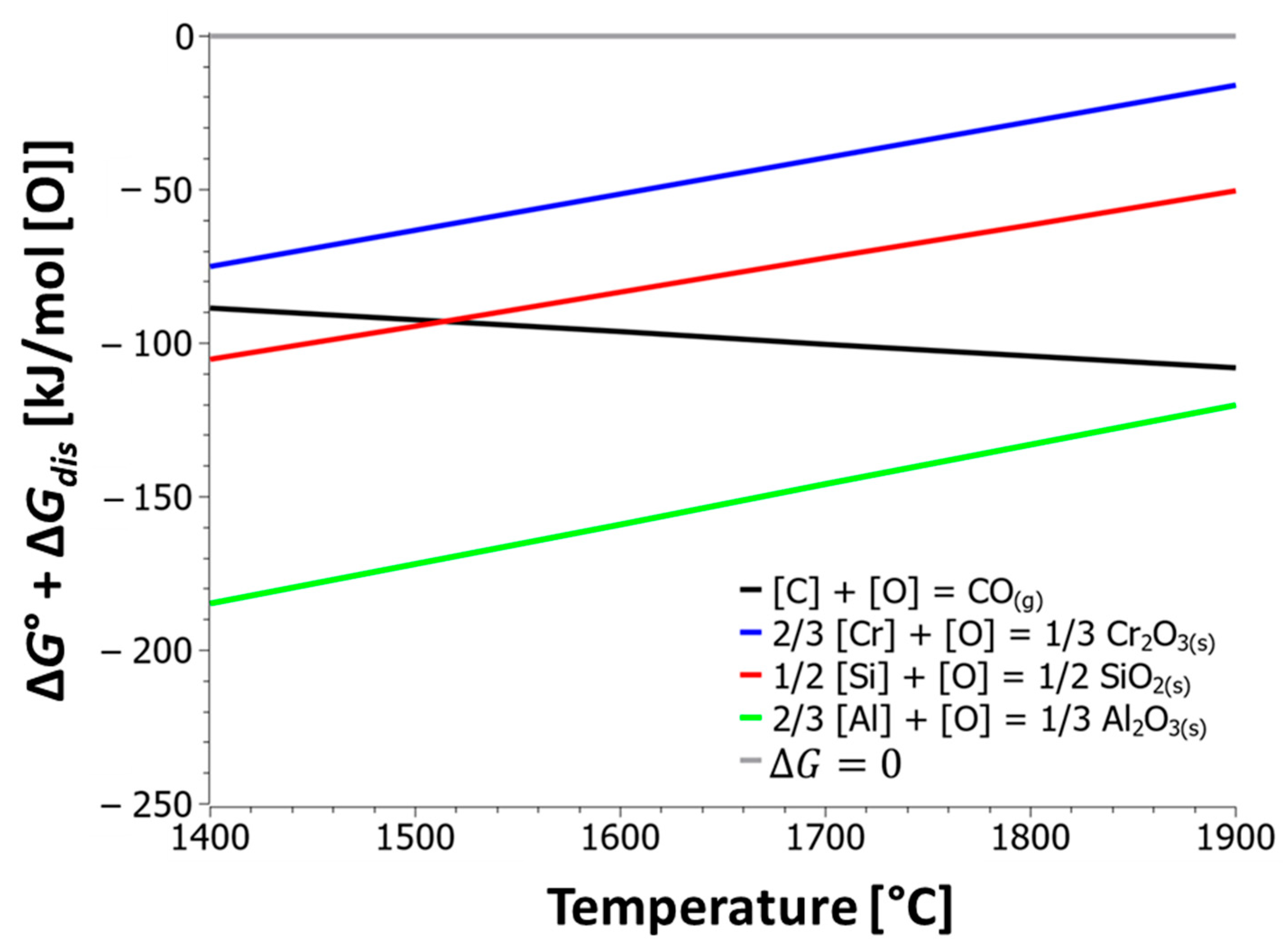
- The literature review revealed significant inconsistencies in reported Gibbs free energies (ΔG°) and interaction parameters, which result in highly varied predictions of Cr-C equilibrium solubility. By selecting a mean baseline using the HSC 8.0 database and Sigworth et al. [22] interaction parameters, a robust thermodynamic framework was established for subsequent process modeling.
- The thermodynamic calculations demonstrate that temperature is the most powerful variable for selective decarburization. Increasing the melt temperature drastically reduces the equilibrium carbon content, thereby limiting chromium oxidation. Specifically, at 15 wt.% Cr, increasing the temperature from 1550 °C to 1800 °C lowers the equilibrium carbon concentration from 1.21 wt.% C to 0.28 wt.% C. This confirms that decarburization in the EAF should be conducted at temperatures above 1650 °C.
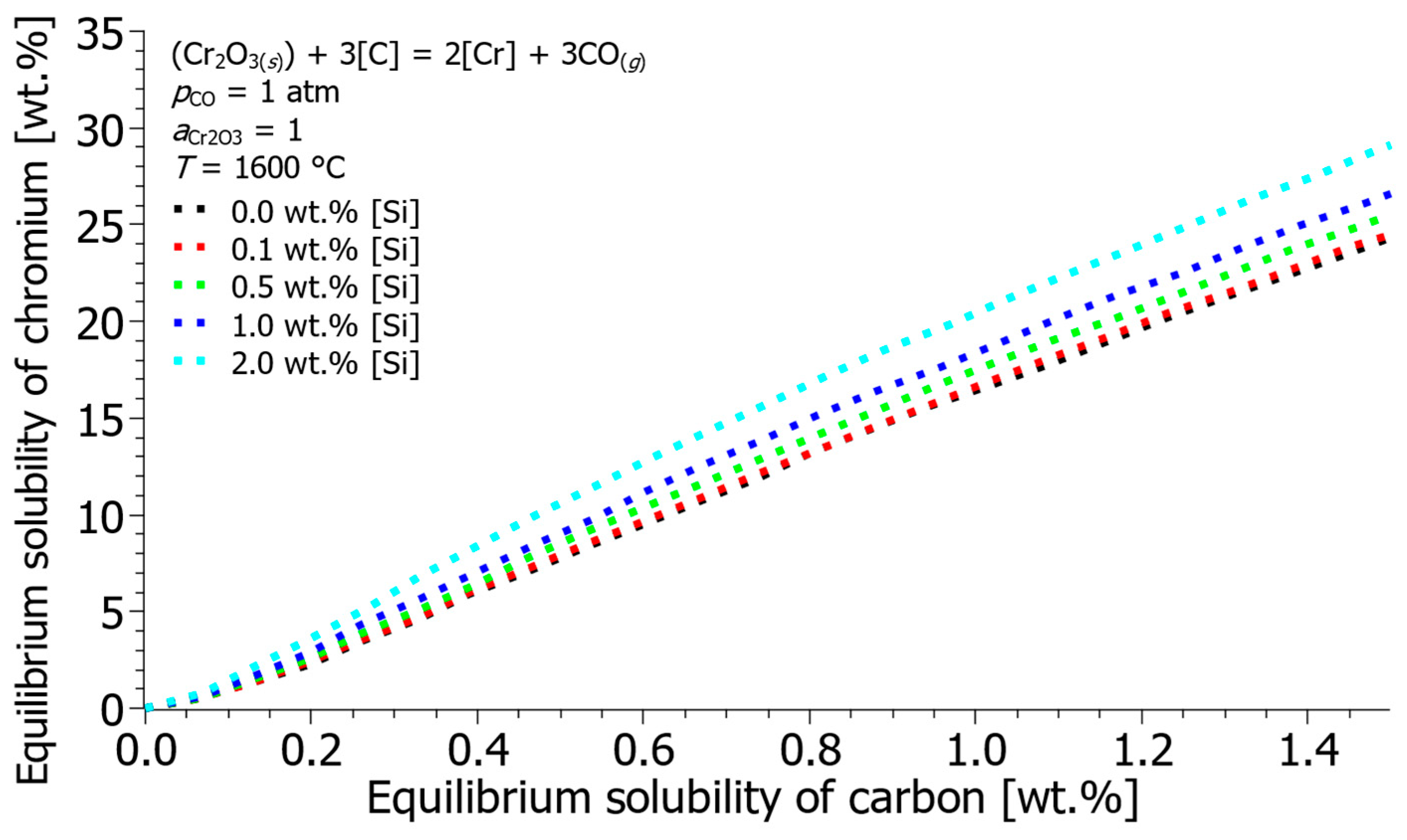
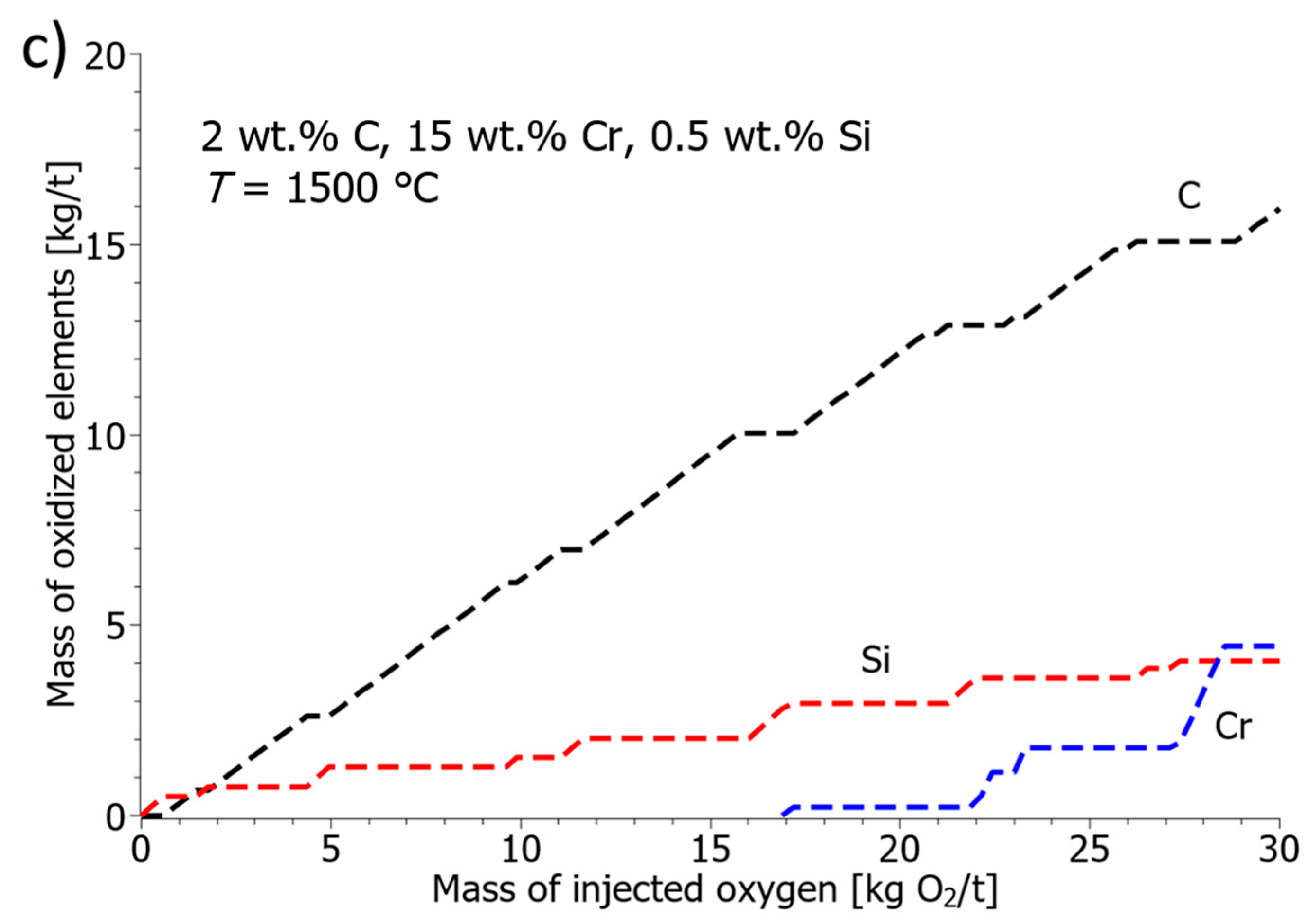
- The oxidation model confirmed the protective role of silicon, especially at low temperatures. In a melt at 1500 °C and 20 kg of injected oxygen per ton of steel, the presence of 0.5 wt.% Si reduced the oxidized chromium from 7 kg/t to 0.3 kg/t. Silicon preferentially oxidizes first, protecting chromium and allowing carbon combustion to dominate the second phase.
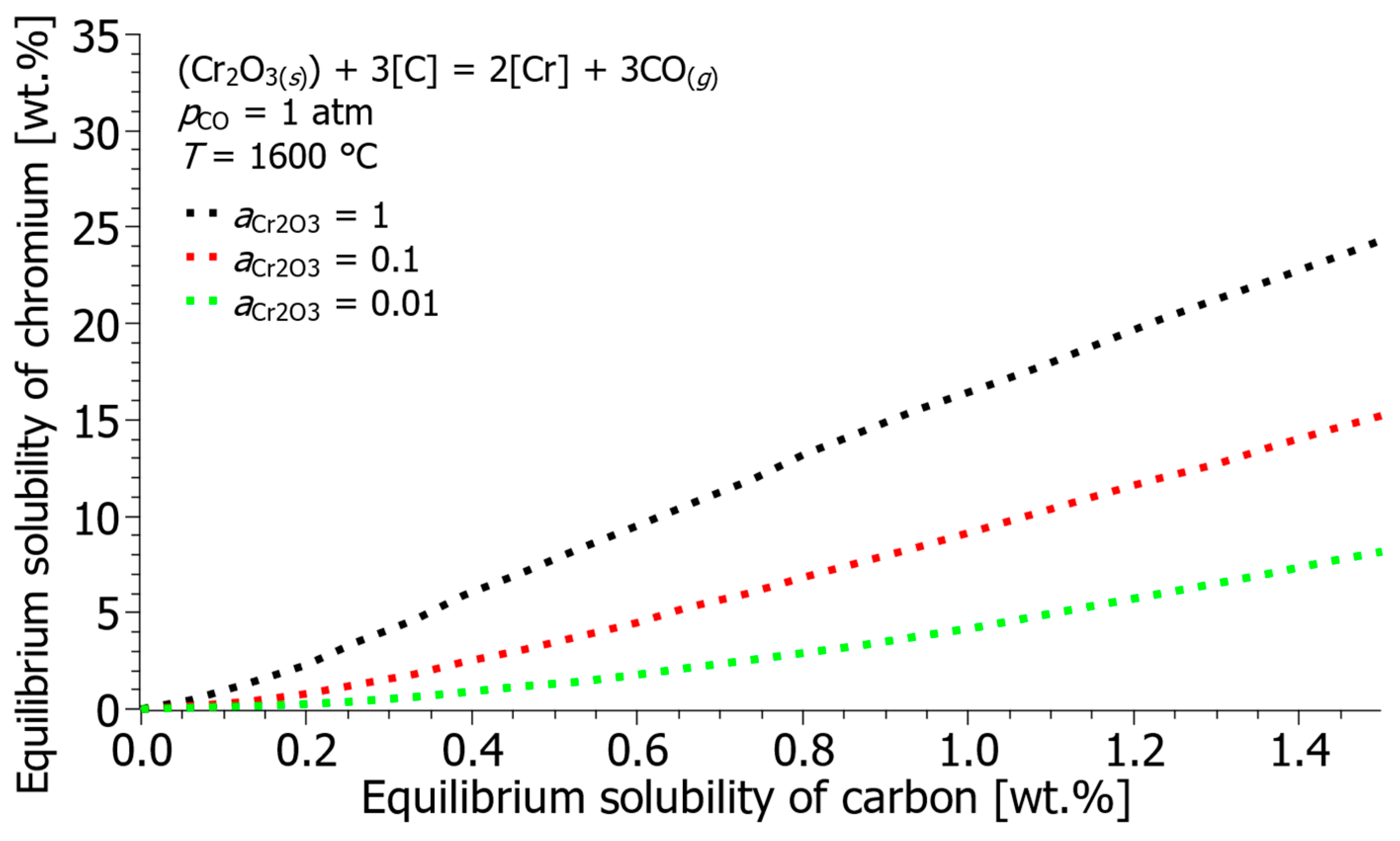
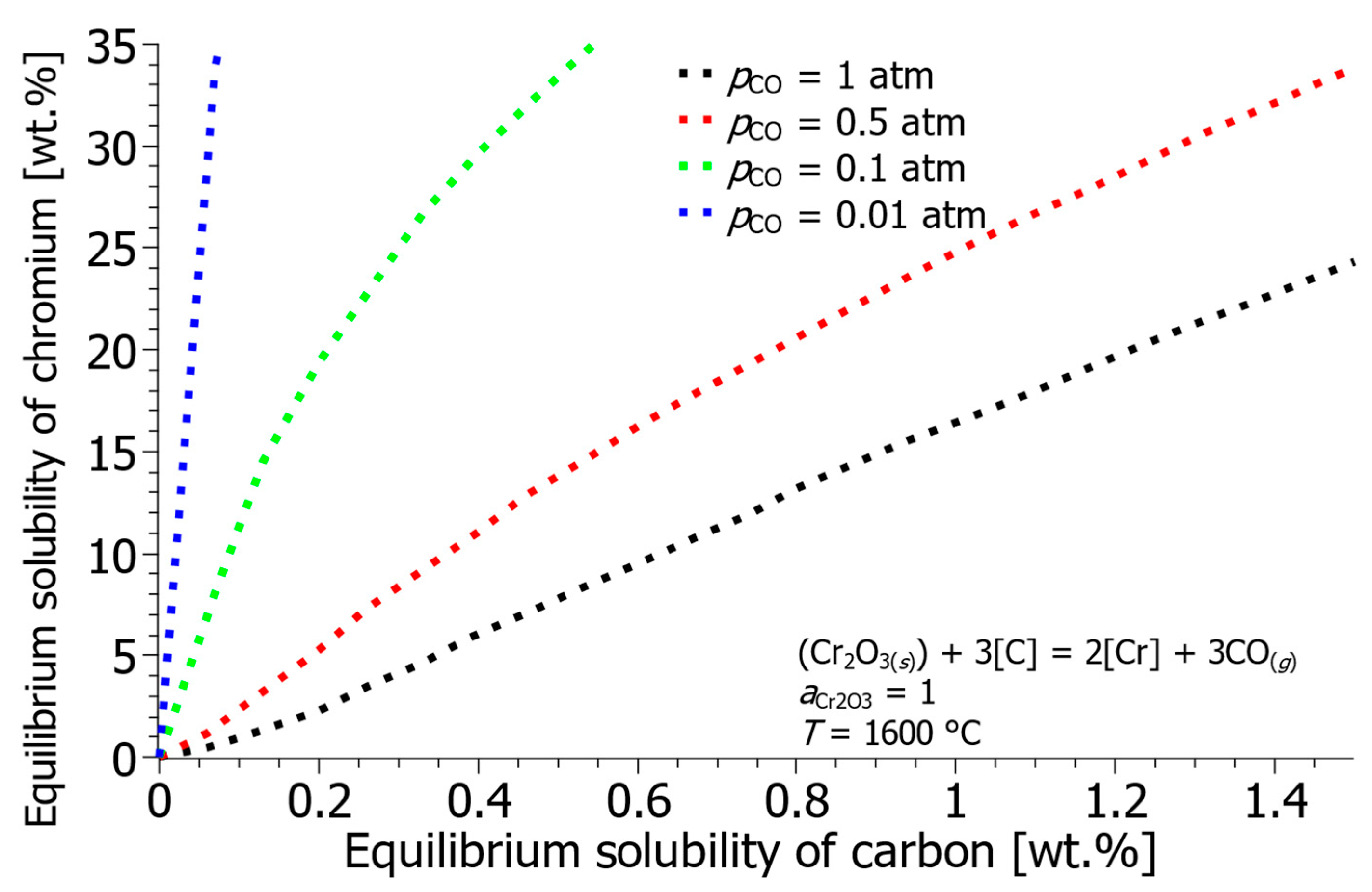
- The equilibrium calculations show that reducing the partial pressure of CO in subsequent processes (like VOD) is essential, as the Cr solubility increases drastically with decreasing pCO. That means that oxidation in the EAF should be limited.
- Furthermore, while the 1 wt.% standard state is practical, calculations using the modified Henrian standard state (taking the solvent activity coefficient into account) predict a slightly higher equilibrium chromium solubility at increased carbon concentrations, providing a more accurate theoretical benchmark for non-dilute solutions.
- Chromium losses during the initial low-temperature stages of the EAF phase must be minimized by limiting oxygen blowing during heating and adding sufficient Si. Conversely, the high-temperature EAF decarburization phase must be stopped when kinetics indicate a sharp drop in CO2 in off-gases, signifying the onset of intense chromium oxidation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ΔG° | Standard Gibbs free energy |
| ΔH° | Standard enthalpy |
| ΔS° | Standard entropy |
| ΔG | Gibbs free energy of reaction |
| ΔGdis | Gibbs free energy of dissolution of elements |
| ΔHdis | Enthalpy of dissolution |
| ΔSdis | Entropy of dissolution |
| T | Temperature |
| R | Gas constant |
| K | Equilibrium constant |
| pCO | Partial pressure of carbon monoxide |
| ai | Activity of element i |
| ai% | Activity of element i, using 1 wt.% standard state |
| aiH | Activity of element i, using Henrian standard state |
| fi | Activity coefficient of element i, using 1 wt.% standard state |
| γi | Activity coefficient of element i, using Henrian standard state |
| γi° | Zero-order activity coefficient |
| γsol | Solvent activity coefficient |
| wt.% i, wt.% j | Weight percentages of dissolved elements i and j |
| X | Mole fraction |
| Mj | Molar mass of element j |
| M1 | Molar mass of the solvent element |
| eii | First-order self-interaction parameter (effect of element i on its own activity, 1 wt.% standard state) |
| eij | First-order cross-interaction parameter (effect of alloying element j on element i, 1 wt.% standard state) |
| εij | Interaction parameter (effect of element j on element i, Henrian standard state) |
References
- Wang, H. Investigations on the Oxidation of Iron-Chromium and Iron-Vanadium Molten Alloys. Ph.D. Thesis, Royal Institute of Technology—KTH, Stockholm, Sweden, 31 May 2010. [Google Scholar]
- Heikkinen, E.-P.; Fabritius, T. Modelling of the Refining Processes in the Production of Ferrochrome and Stainless Steel. In Recent Researches in Metallurgical Engineering—From Extraction to Forming; InTech: London, UK, 2012; pp. 65–88. [Google Scholar]
- Kirschen, M.; Jung, I.H.; Hackl, G. Phase Equilibrium Diagram for Electric Arc Furnace Slag Optimization in High Alloyed Chromium Stainless Steelmaking. Metals 2020, 10, 826. [Google Scholar] [CrossRef]
- Kho, T.S.; Swinbourne, D.R.; Blanpain, B.; Arnout, S.; Langberg, D. Understanding Stainless Steelmaking through Computational Thermodynamics Part 1: Electric Arc Furnace Melting. Trans. Inst. Min. Metall. Sect. C Miner. Process. Extr. Metall. 2010, 119, 1–8. [Google Scholar] [CrossRef]
- Ghosh, A.; Chatterjee, A. Ironmaking and Steelmaking: Theory and Practice; PHI Learning Private Limited: New Delhi, India, 2008; ISBN 9788120332898. [Google Scholar]
- Arh, B.; Tehovnik, F. The Oxidation and Reduction of Chromium of Stainless Steels in an Electric Arc Furnace. Mater. Tehnol. 2007, 41, 203–211. [Google Scholar]
- Swinbourne, D.R.; Kho, T.S.; Langberg, D.; Blanpain, B.; Arnout, S. Understanding Stainless Steelmaking through Computational Thermodynamics Part 2—VOD Converting. Trans. Inst. Min. Metall. Sect. C Miner. Process. Extr. Metall. 2010, 119, 107–115. [Google Scholar] [CrossRef]
- Swinbourne, D.R.; Kho, T.S.; Blanpain, B.; Arnout, S.; Langberg, D.E. Understanding Stainless Steelmaking through Computational Thermodynamics: Part 3—AOD Converting. Trans. Inst. Min. Metall. Sect. C Miner. Process. Extr. Metall. 2012, 121, 23–31. [Google Scholar] [CrossRef]
- Sano, N. Reduction of Chromium Oxide in Stainless Steel Slags. In Proceedings of the 10th International Ferroalloys Congress, Cape Town, South Africa, 1–4 February 2004; pp. 670–677. [Google Scholar]
- Guo, M.; Durinck, D.; Jones, P.T.; Heylen, G.; Hendrickx, R.; Baeten, R.; Blanpain, B.; Wollants, P. EAF Stainless Steel Refining—Part I: Observational Study on Chromium Recovery in an Eccentric Bottom Tapping Furnace and a Spout Tapping Furnace. Steel Res. Int. 2007, 78, 117–124. [Google Scholar] [CrossRef]
- Burja, J.; Tehovnik, F.; Vode, F.; Arh, B. Microstructural Characterisation of Chromium Slags. Metalurgija 2015, 54, 379–382. [Google Scholar]
- Björkvall, J.; Ångström, S.; Kallin, L. Reduction of Chromium Oxide Containing Slags Using CaC2. In Proceedings of the VII International Conference on Molten Slags Fluxes and Salts, Cape Town, South Africa, 25–28 January 2004; pp. 663–670. [Google Scholar]
- Shibata, E.; Egawa, S.; Nakamura, T. Reduction Behavior of Chromium Oxide in Molten Slag Using Aluminum, Ferrosilicon and Graphite. ISIJ Int. 2002, 42, 609–613. [Google Scholar] [CrossRef]
- Heikkinen, E.-P.; Ikäheimonen, T.; Mattila, O.; Fabritius, T. A Thermodynamic Study on the Oxidation of Silicon, Carbon and Chromium in the Ferrochrome Converter. In Proceedings of the 12th International Ferroalloys Congress: Sustainable Future, Helsinki, Finland, 6–9 June 2010; pp. 229–237. [Google Scholar]
- Wang, H.; Nzott, M.M.; Teng, L.; Seetharaman, S. Decarburization of Ferrochrome and High Alloy Steels with Optimized Gas and Slag Phases towards Improved Cr Retention. J. Min. Metall. Sect. B Metall. 2013, 49, 175–181. [Google Scholar] [CrossRef]
- Carboni, M.C.; Espinosa, D.C.R.; Tenório, J.A.S. Reduction of Chromium from Al2O3-CaO-SiO2-CrOx Slags by Carbon Dissolved in Liquid Iron. ISIJ Int. 2011, 51, 523–529. [Google Scholar] [CrossRef]
- Ma, Z.; Janke, D. Thermodynamic Assessment to Chromium Oxidation in the Production of Stainless Steel. Steel Res. 2003, 74, 99–103. [Google Scholar] [CrossRef]
- Pretorius, E.B.; Nunnington, R.C. Stainless Steel Slag Fundamentals—From Furnace to Tundish. Ironmak. Steelmak. 2002, 29, 133–139. [Google Scholar] [CrossRef]
- Seetharaman, S. Treatise on Process Metallurgy, Volume 1: Process Fundamentals, 1st ed.; Seetharaman, S., McLean, A., Guthrie, R., Sridhar, S., Eds.; Elsevier: Oxford, UK, 2013; ISBN 9780080969862. [Google Scholar]
- Barin, I. Therrnochernical Data of Pure Substances, 3rd ed.; Wiley: Weinheim, Germany, 1995; ISBN 3527287450. [Google Scholar]
- Mihara, R.; Gao, X.; Kaneko, S.; Kim, S.; Ueda, S.; Shibata, H.; Seok, M.O.; Kitamura, S.y. Observation of Oxide Formation for Molten Fe-Cr-C Alloy at a High Carbon Region by Oxygen Top Blowing. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2016, 47, 1035–1051. [Google Scholar] [CrossRef]
- Sigworth, G.K.; Elliott, J.F. The Thermodynamics of Liquid Dilute Iron Alloys. Metal Sci. 1974, 8, 298–310. [Google Scholar] [CrossRef]
- Wagner, C. Thermodynamics of Alloys; Addison-Wesley Press: Boston, MA, USA, 1962. [Google Scholar]
- Lupis, C.H.P. Generalized Interaction Coefficients. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1965. [Google Scholar]
- Steelmaking Data Sourcebook. The Japan Society for the Promotion of Science. In The 19th Committee on Steelmaking Steelmaking Data Sourcebook; Gordon and Breach Science Publisher: New York, NY, USA, 1988. [Google Scholar]
- Materia, T. Production of Stainless Steel: Part One. Available online: https://www.totalmateria.com/page.aspx?ID=CheckArticle&site=kts&NM=215 (accessed on 21 November 2022).
- Lupis, C.H.P.; Elliott, J.F. Generalized Interaction Coefficients. Part I: Definitions. Acta. Metall. 1966, 14, 529–538. [Google Scholar] [CrossRef]
- Bale, C.W.; Pelton, A.D. The Unified Interaction Parameter Formalism Thermodynamic Consistency and Applications. Metall. Trans. A 1990, 21, 1997–2002. [Google Scholar] [CrossRef]
- Pelton, A.D.; Bale, C.W. A Modified Interaction Parameter Formalism for Non-Dilute Solutions. Metall. Trans. A 1986, 17, 1211–1215. [Google Scholar] [CrossRef]
- Echterhof, T.; Risonarta, V.Y.; Beiler, C.; Lenz, S.; Jung, H.P.; Pfeifer, H. Decarburization Control during Stainless Steel Making in an EAF. In Proceedings of the SteelSim 2011, 4th International Conference on Modelling and Simulation of Metallurgical Processes in Steelmaking, Düsseldorf, Germany, 27th June 2011; pp. 1–8. [Google Scholar]
- Bajželj, A.; Burja, J. Optimization of partial stainless steel melt oxidation in the EAF. In Proceedings of the METAL 2024, 33rd International Conference on Metallurgy and Materials, Brno, Czech Republic, 22–24 May 2024; pp. 19–24. [Google Scholar] [CrossRef]
- Ito, K.; Fruehan, R.J. Slag Foaming in Electric Furnace Steelmaking. Trans. ISS Iron Steelmak. 1989, 16, 55–60. [Google Scholar]
- Corbari, R.; Matsuura, H.; Halder, S.; Walker, M.; Fruehan, R.J. Foaming and the Rate of the Carbon-Iron Oxide Reaction in Slag. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2009, 40, 940–948. [Google Scholar] [CrossRef]
- Vidacak, B.; Arvanitidis, I.; Jönsson, P.G.; Sjöberg, P. Observation on Foaming of EAF Slags in the Production of Stainless Steel. Scand. J. Metall. 2002, 31, 321–327. [Google Scholar] [CrossRef]
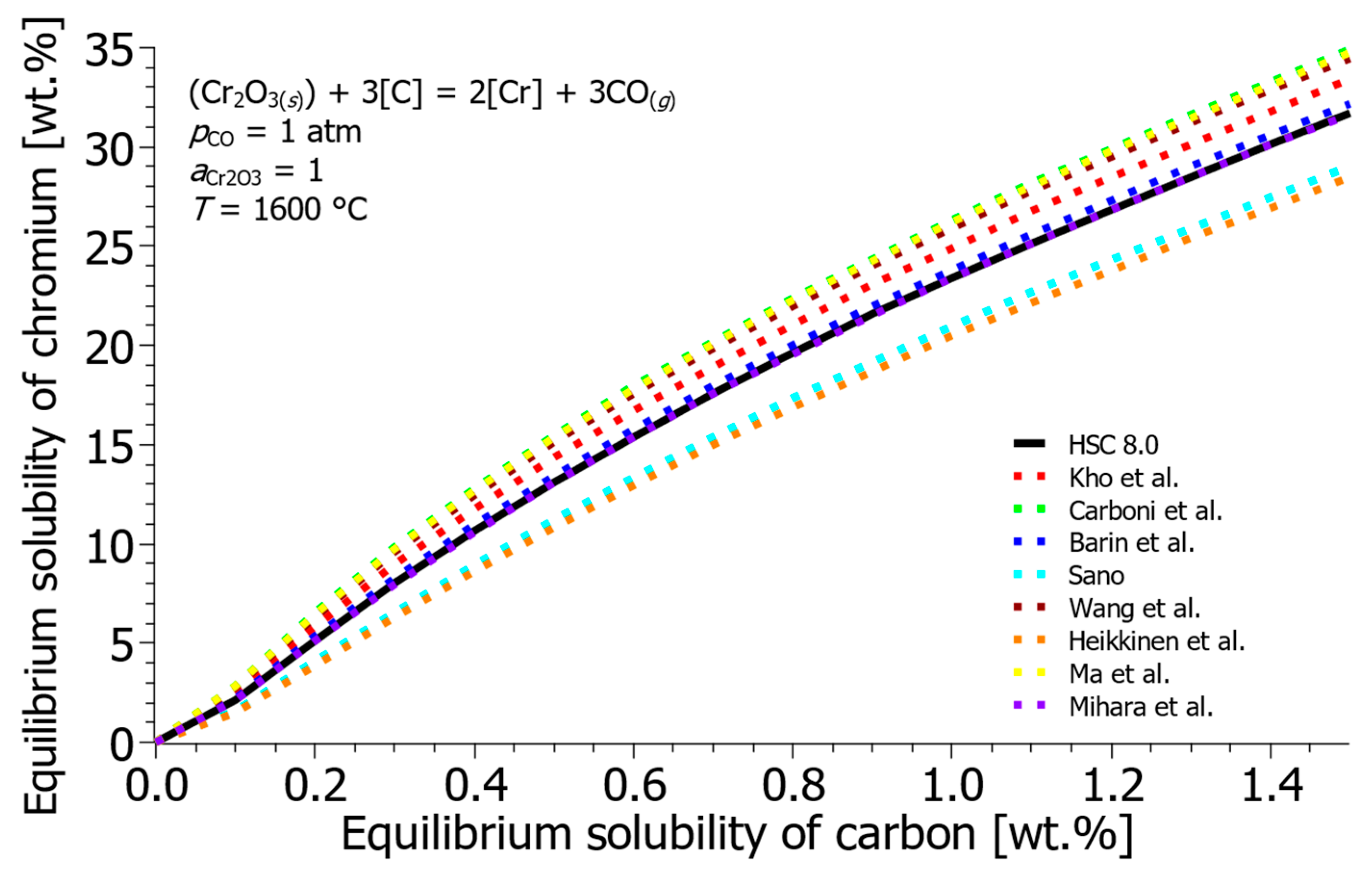
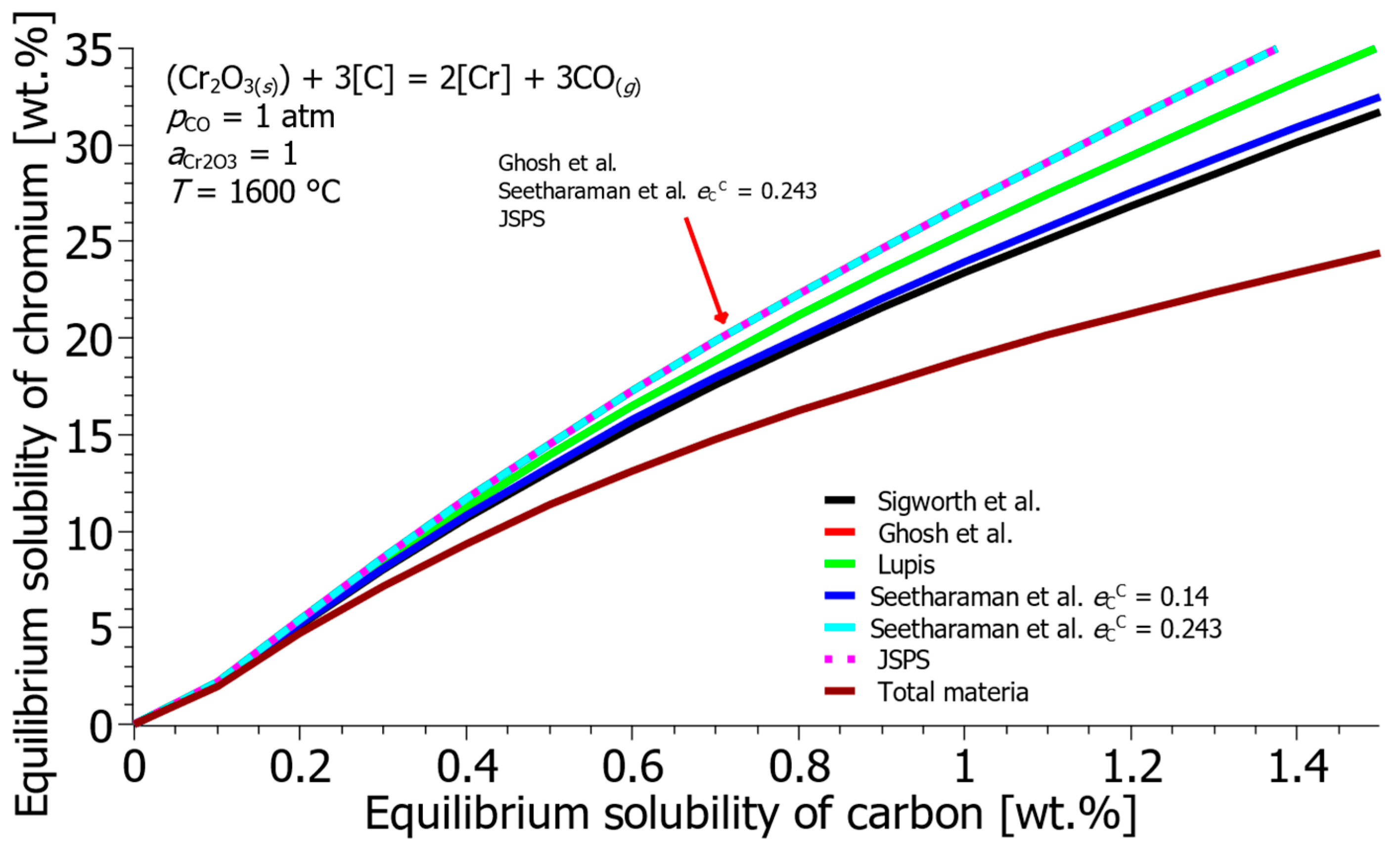
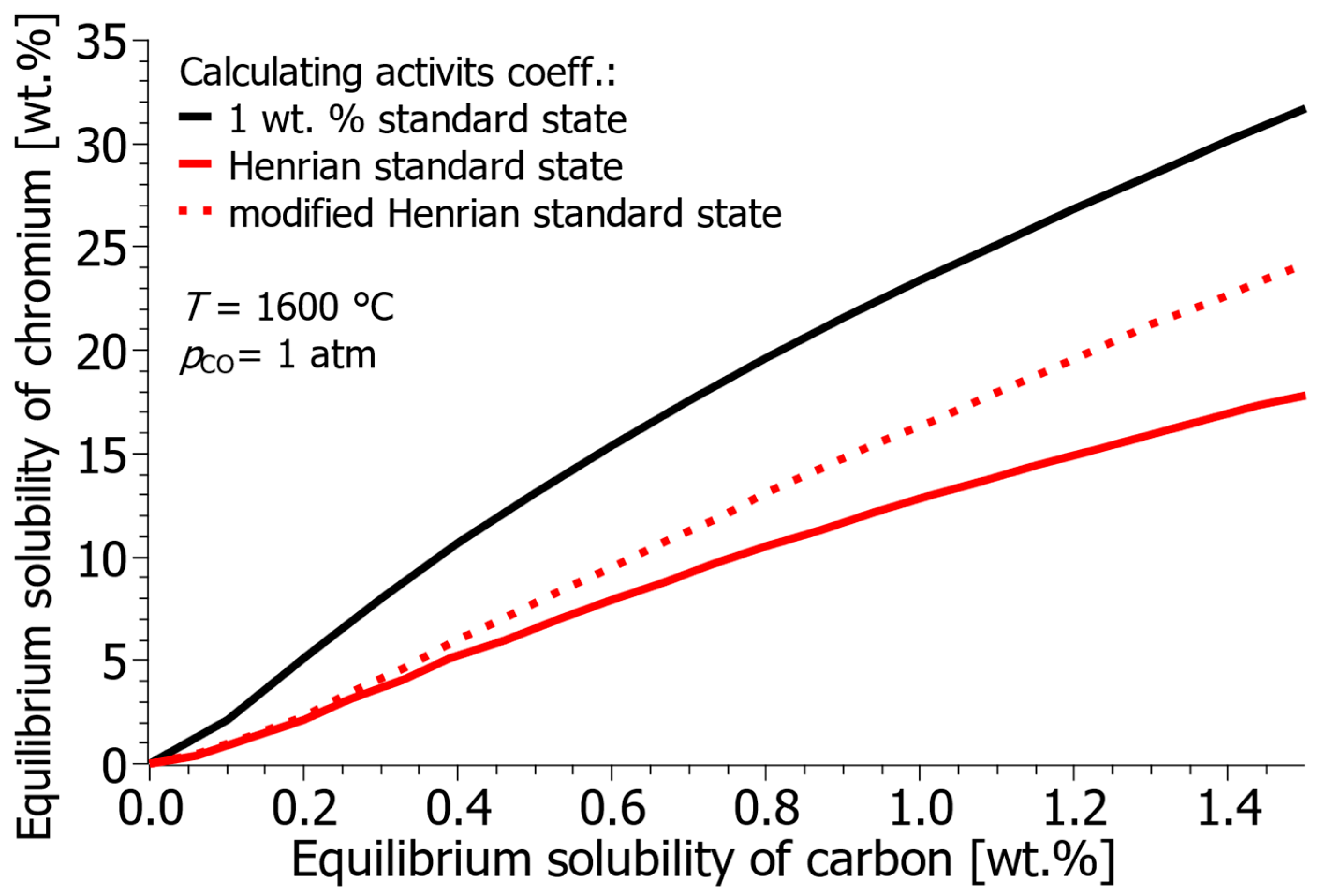

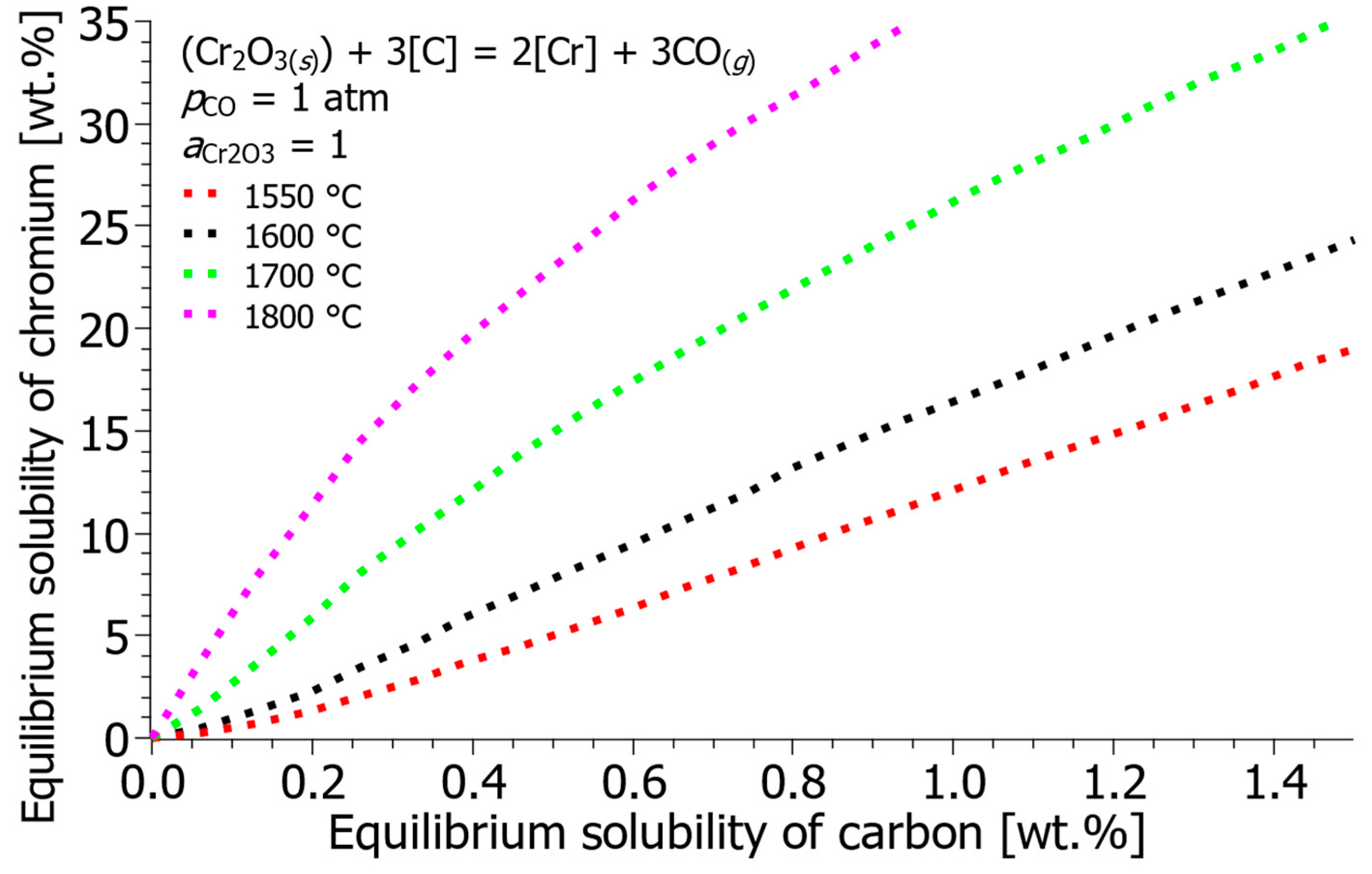


| Reference | ΔH° [J] | ΔS° [J/K] | ΔG° [J] |
|---|---|---|---|
| Kho et al. [4] (publ. 2010) | 77,000 | 133.48 1 | −173,000 |
| Carboni et al. [16] (publ. 2011) | 766,969 | 504.63 | −178,203 1 |
| Barin et al. [20] (publ. 1995) | 776,234 | 504.53 | −168,751 1 |
| HSC 8.0 | 773,918 | 502.40 | −167,077 1 |
| Sano [9] (publ. 2004) | 402,600 | 299.00 | −157,427 1 |
| Wang et al. [15] (publ. 2013) | 748,740 2 | 476.68 2 | −144,081 1,2 |
| Ma et al. [17] (publ. 2003) | 734,782 2 | 469.95 2 | −145,434 1,2 |
| Mihara et al. [21] (publ. 2016) | 776,468 1,2 | 486,25 1,2 | −134,278 1,2 |
| Heikkinen et al. [14] (publ. 2010) | 248,948 1,3 | 201.88 1,3 | −129,173 1,3 |
| ThermoCalc SSUB3 | 776,631 | 505.10 | −169,417 |
| Reaction | ΔHdis [J] | ΔSdis [J/K] | ΔGdis [J] |
|---|---|---|---|
| 22,594 | 42.26 | −56,559 1 | |
| 19,246 | 46.86 | −68,523 1 | |
| 0 | 37.70 | −70,612 1 | |
| 22,594 | 16.74 | −8760 1 | |
| 19,246 | 9.16 | 2089 1 | |
| 0 | 0 | 0 1 |
| Sigworth et al. [22] | Ghosh et al. [5] | Lupis [24] | Seetharaman et al. [19] | JSPS [25] | Total Materia [26] | |
|---|---|---|---|---|---|---|
| 0.14 | 0.243 | 0.22 | 0.243/0.14 | 0.243 | 0.14 | |
| −0.024 | −0.023 | −0.024 | −0.023 | −0.023 | −0.024 | |
| −0.0003 | −0.0003 | / | −0.0003 | −0.0003 | 0.0003 | |
| −0.12 | −0.114 | −0.118 | −0.114 | −0.114 | 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bajželj, A.; Burja, J. Thermodynamic Guidelines for Minimizing Chromium Losses in Electric Arc Furnace Steelmaking. Metals 2025, 15, 1129. https://doi.org/10.3390/met15101129
Bajželj A, Burja J. Thermodynamic Guidelines for Minimizing Chromium Losses in Electric Arc Furnace Steelmaking. Metals. 2025; 15(10):1129. https://doi.org/10.3390/met15101129
Chicago/Turabian StyleBajželj, Anže, and Jaka Burja. 2025. "Thermodynamic Guidelines for Minimizing Chromium Losses in Electric Arc Furnace Steelmaking" Metals 15, no. 10: 1129. https://doi.org/10.3390/met15101129
APA StyleBajželj, A., & Burja, J. (2025). Thermodynamic Guidelines for Minimizing Chromium Losses in Electric Arc Furnace Steelmaking. Metals, 15(10), 1129. https://doi.org/10.3390/met15101129







