Columnar-to-Equiaxed Transition on Laser Powder Bed Fusion Ultra-Precision Additive Manufacturing Accuracy and Surface Roughness for Solidified 316L Micro-Lattice Structure
Abstract
:1. Introduction
2. Modeling Methods and Experiments
2.1. Modeling of Rapid Solidification
2.2. Material and Experimental Procedures
3. Results and Discussions
3.1. CET Transition Conditions During Melt Solidification of 316L Powder
3.2. Influence of Laser Parameters on Lattice Structure Fabrication Accuracy
3.3. Microgranular Histograms of Experimental Specimen Under Overlap Variation
4. Conclusions
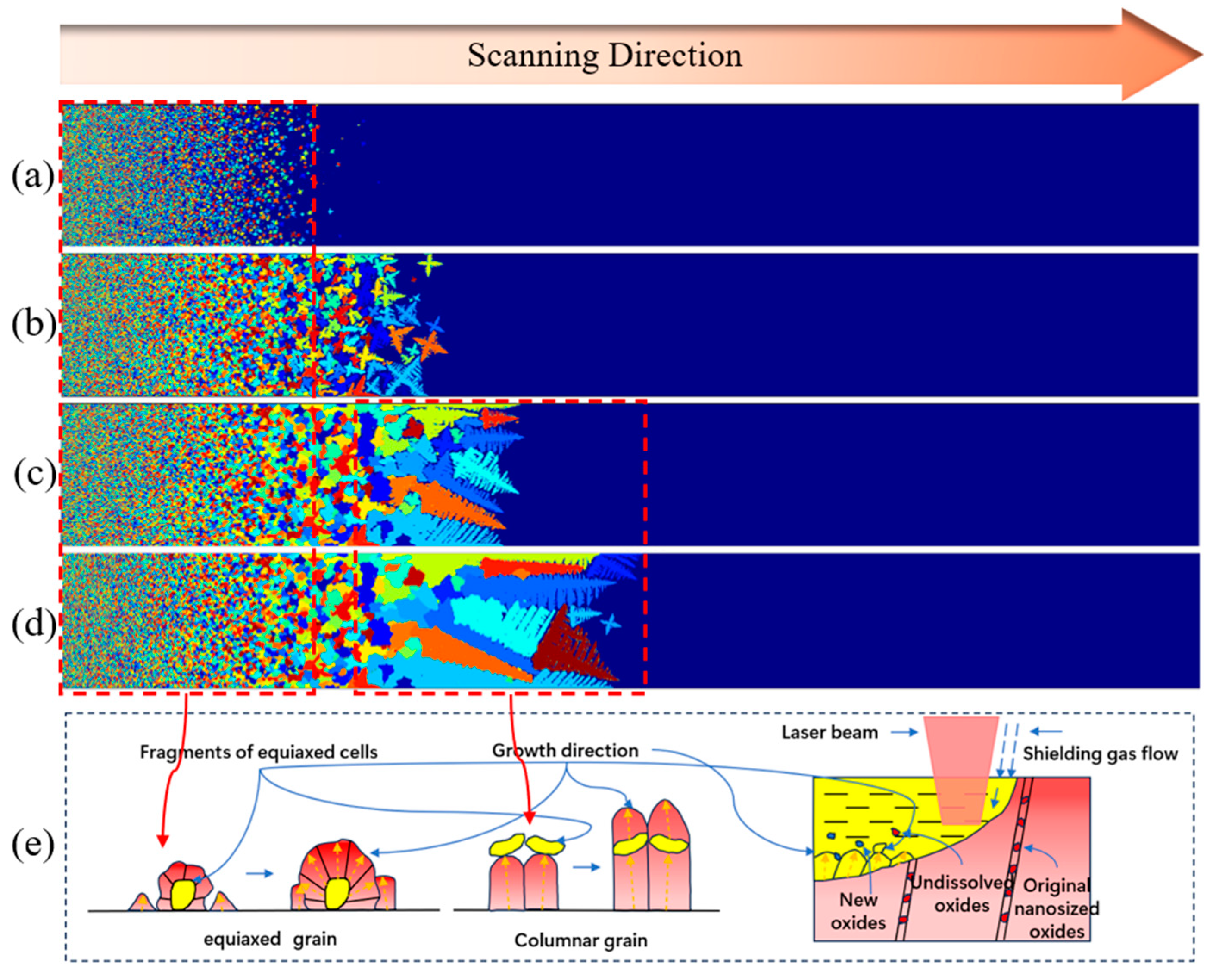
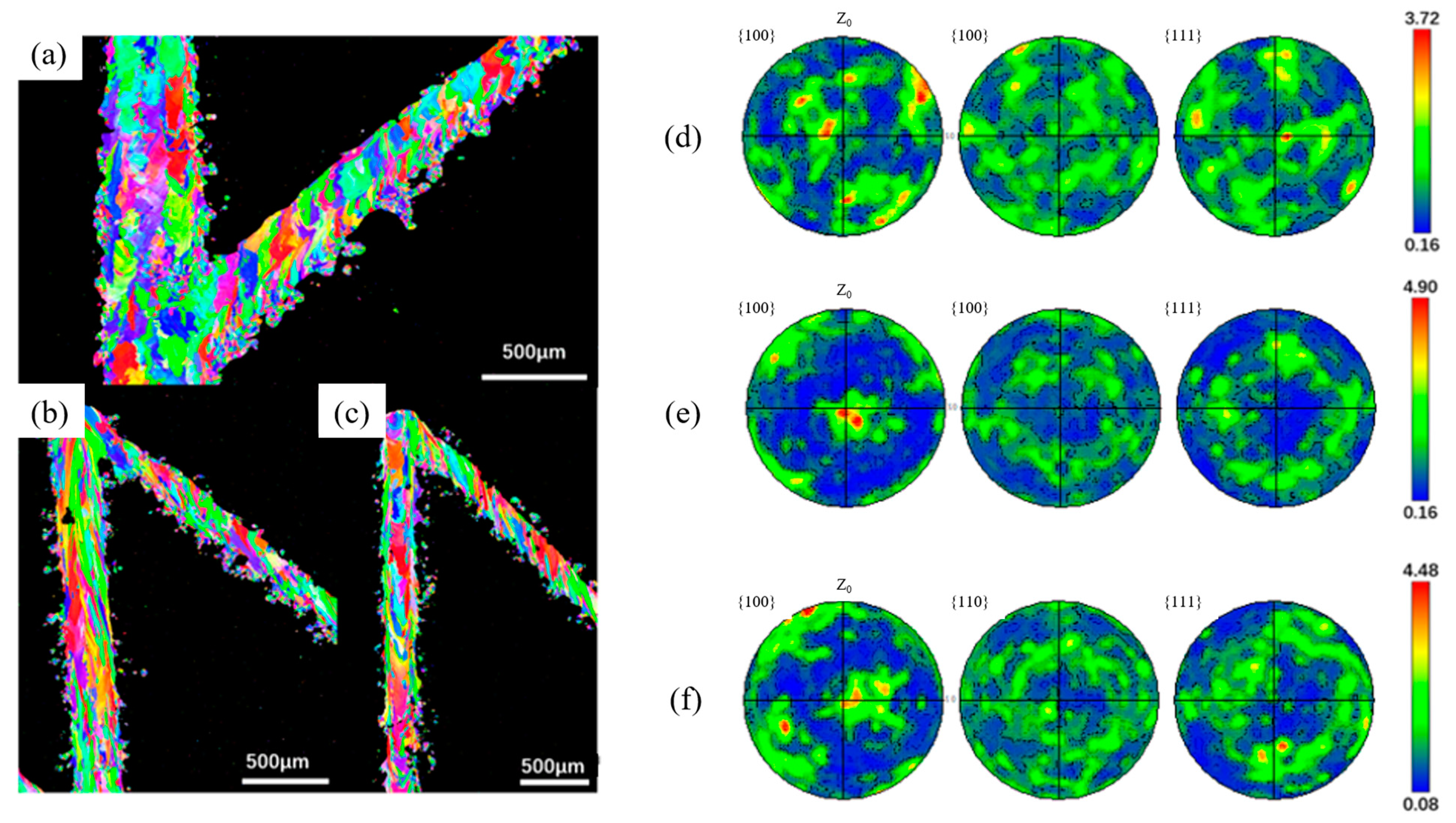
- In additive manufacturing (AM), where grain growth in a single track shows a consistent pattern: columnar grains grow perpendicular to the melt pool boundary towards the center, while grains in inclined regions grow along the laser movement direction. This pattern has been supported by both experimental and numerical studies and provides a comprehensive explanation for the distribution of partially melted powder in AM, as it correlates with heat dissipation from grain growth. The combination of gravity and splashing causes part of the incompletely melted powder to come to the lower and middle parts of the fabrication layer, resulting in a lower solidification rate in the lower and middle parts of the layer, coupled with a sharp decrease in the energy density at the forming edges, which is conducive to the heterogeneous nucleation of the constitutionally undercooled zone and limits the growth of columnar grains. The formation of equiaxed grains is accompanied by the diffusion of heat along the dendrite axis, that is, a large amount of latent heat release, which will cause more adhesion of the surrounding unmolten powder, thus increasing the surface roughness of the component, reducing the surface quality of the component, and manufacturing accuracy.
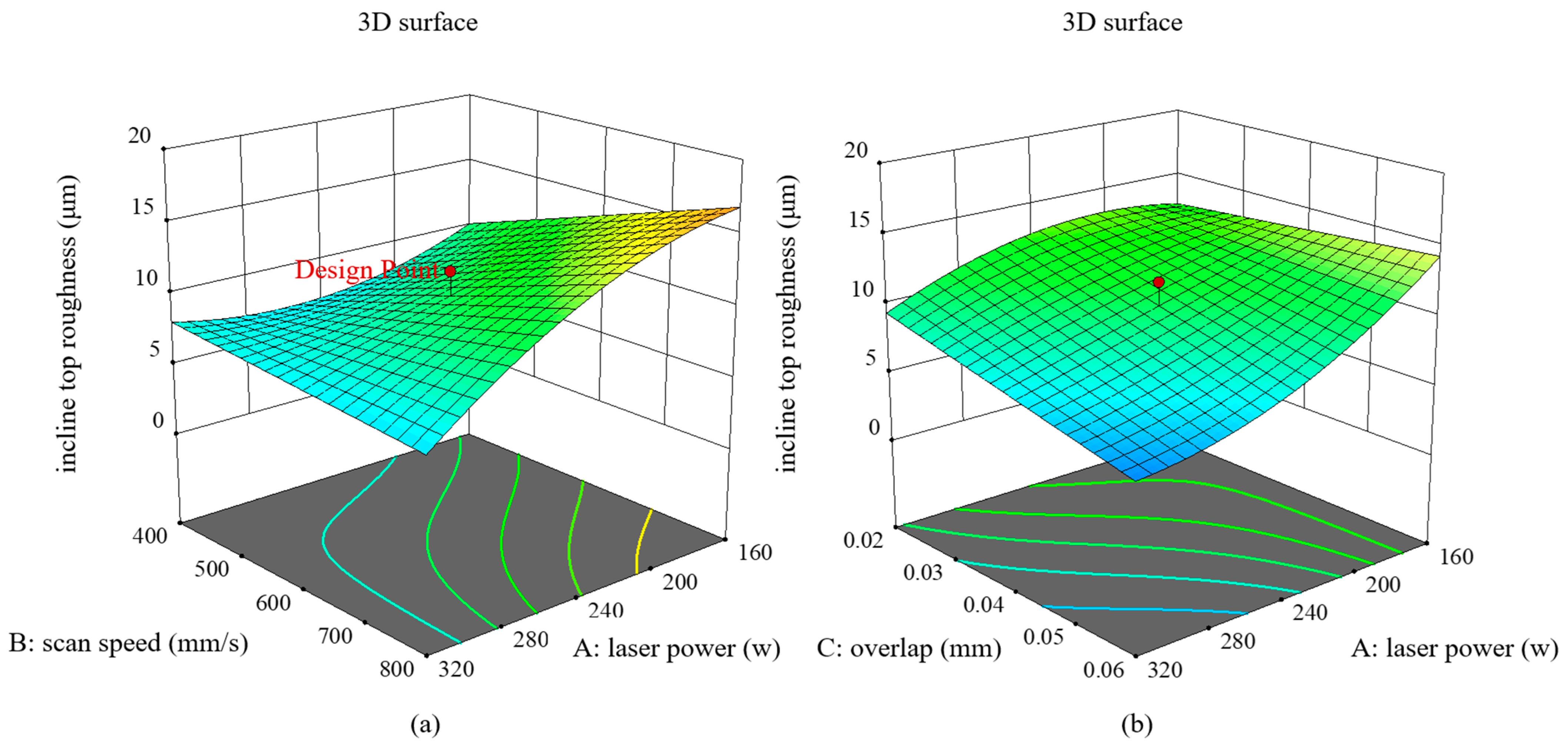
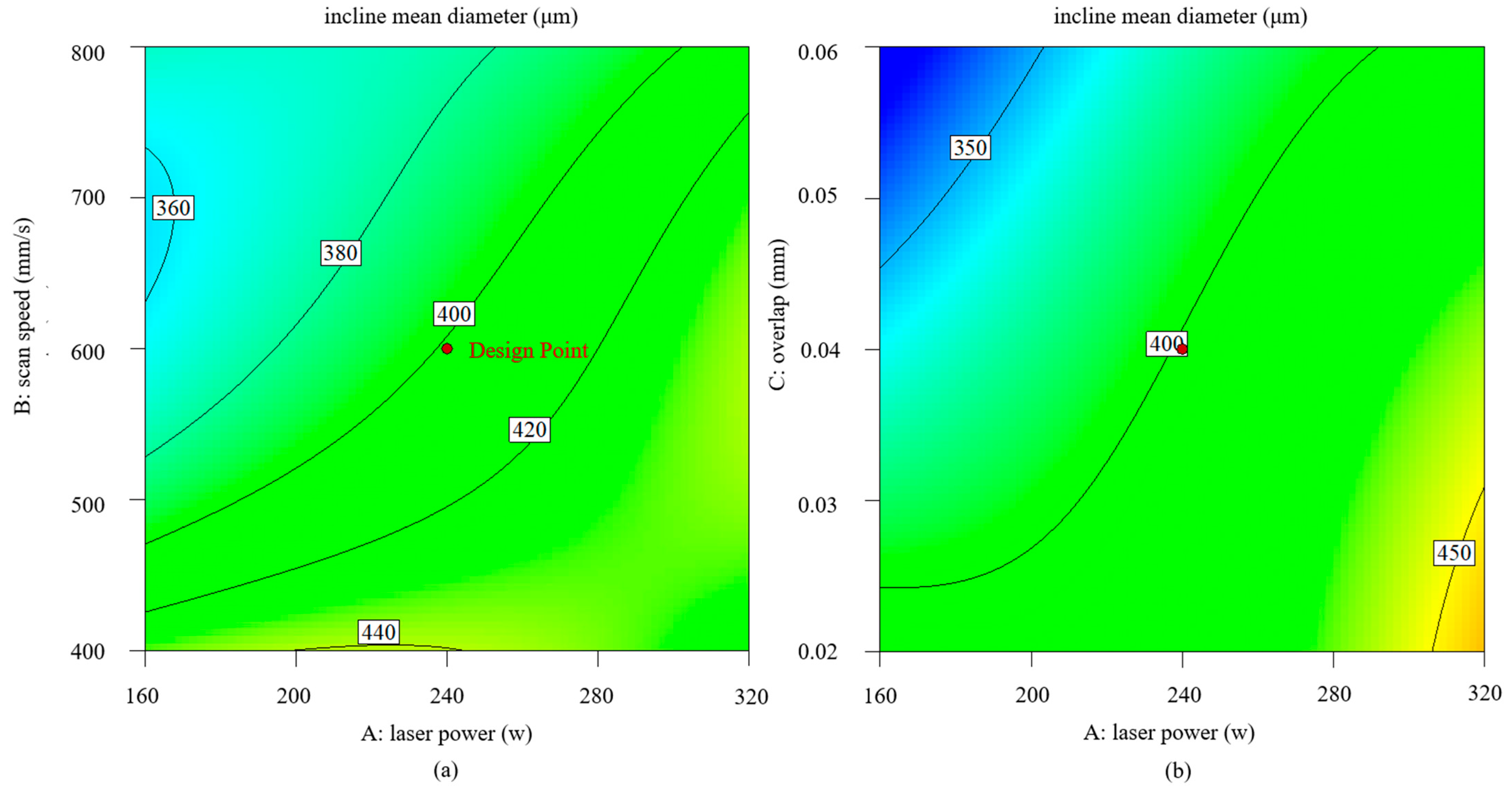
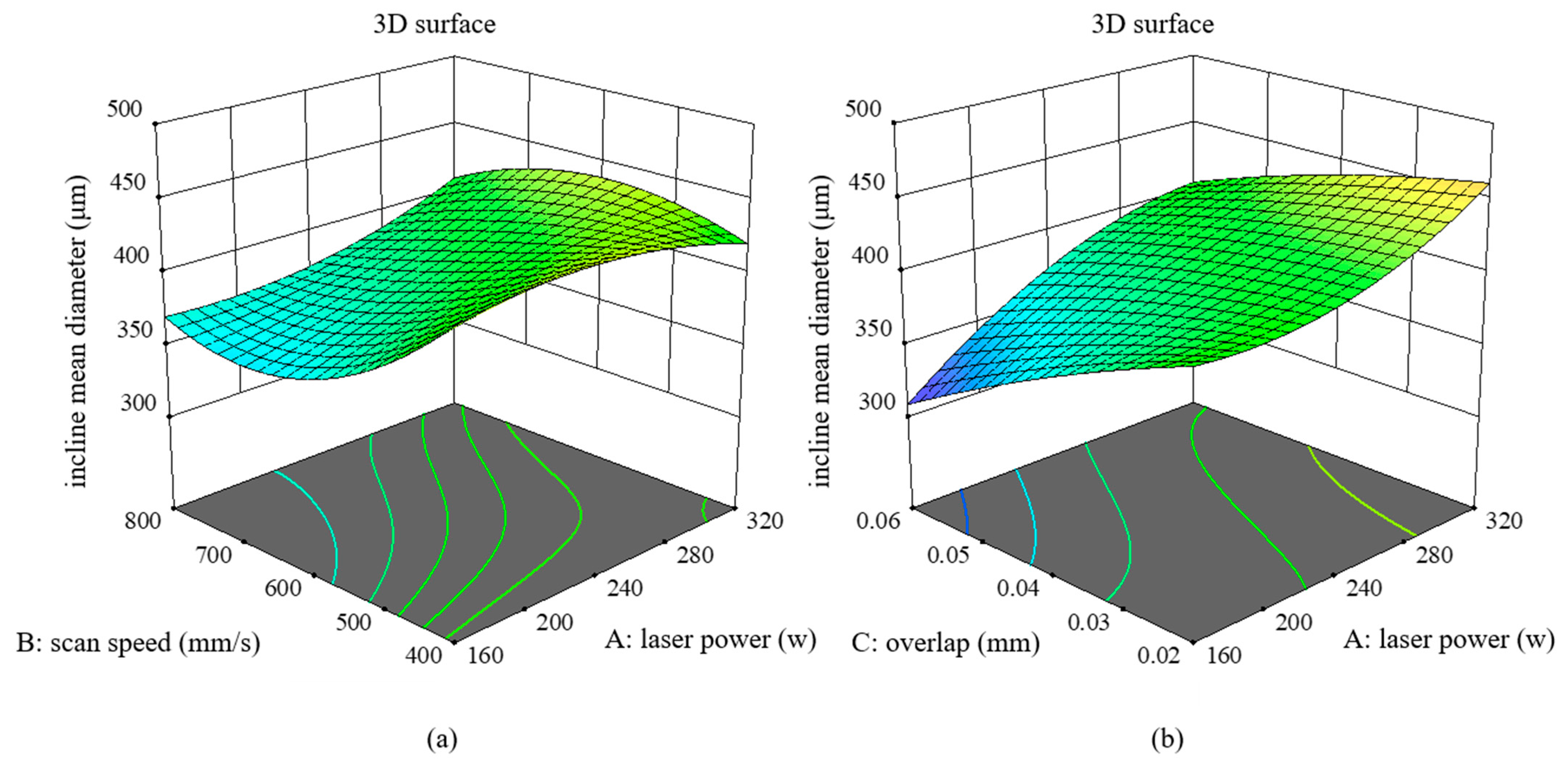
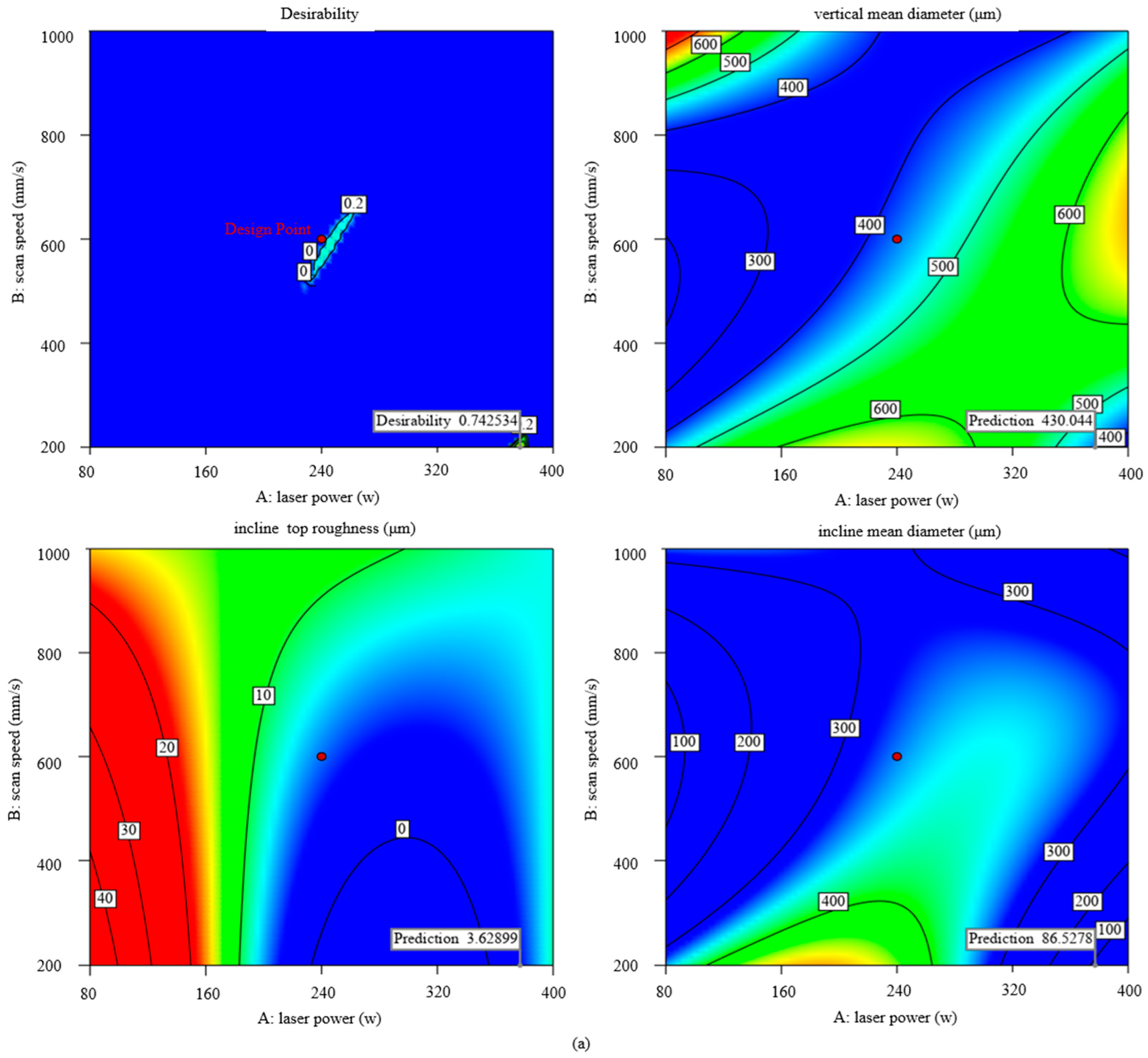
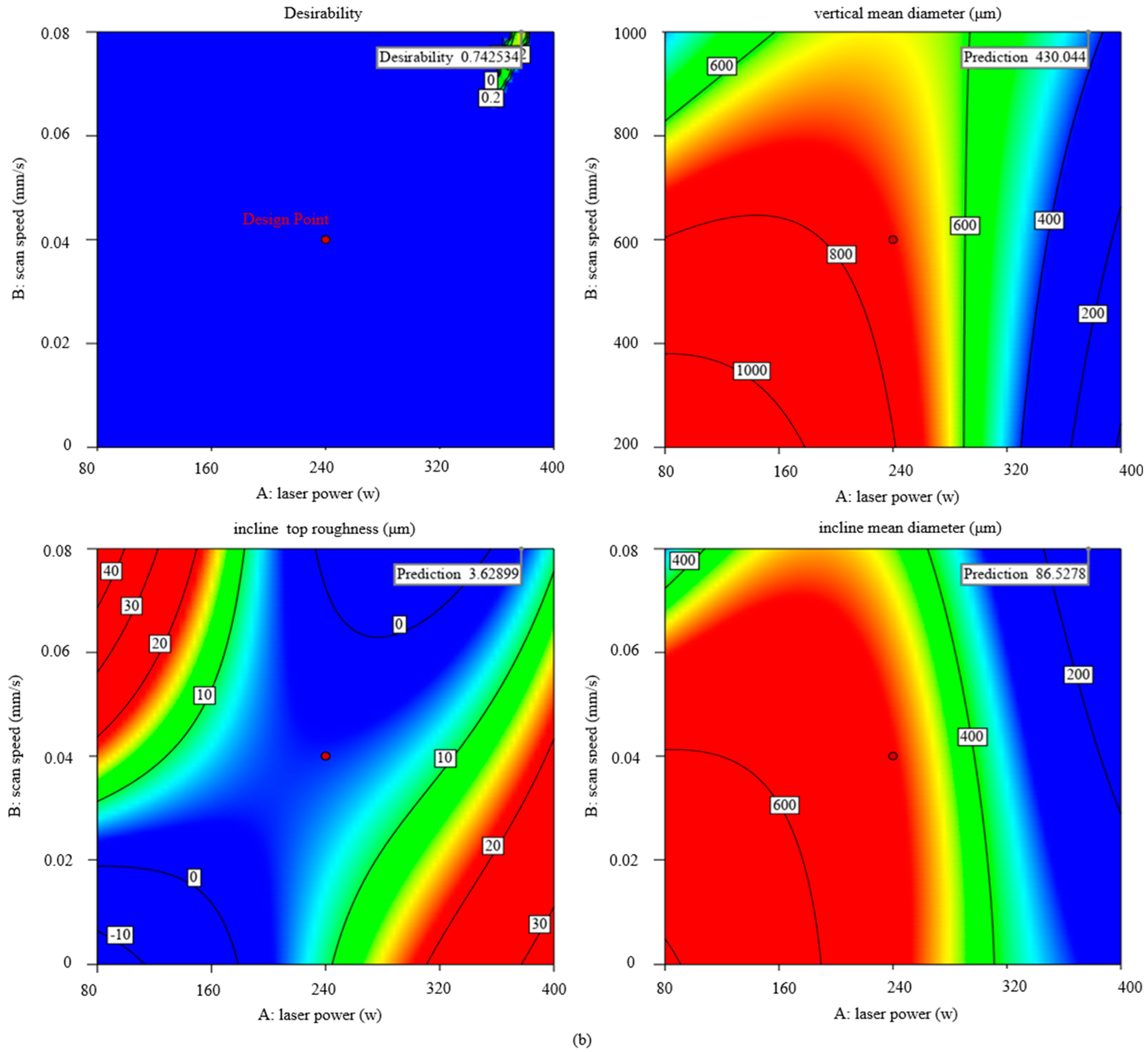
- Response surface analysis results have illustrated that the laser parameters produce significant effects on three responses: vertical mean diameter, incline top roughness, and incline mean diameter. Linear energy density and linear energy focusing F = Pd have a quantitative effect on each of these three responses: The increase of E is conducive to the reduction of surface roughness but is not conducive to the reduction of manufacturing errors; the increase of F can be beneficial to the simultaneous optimization of the two, so from a comprehensive point of view, the choice of a larger overlap is the best manufacturing optimization strategy.
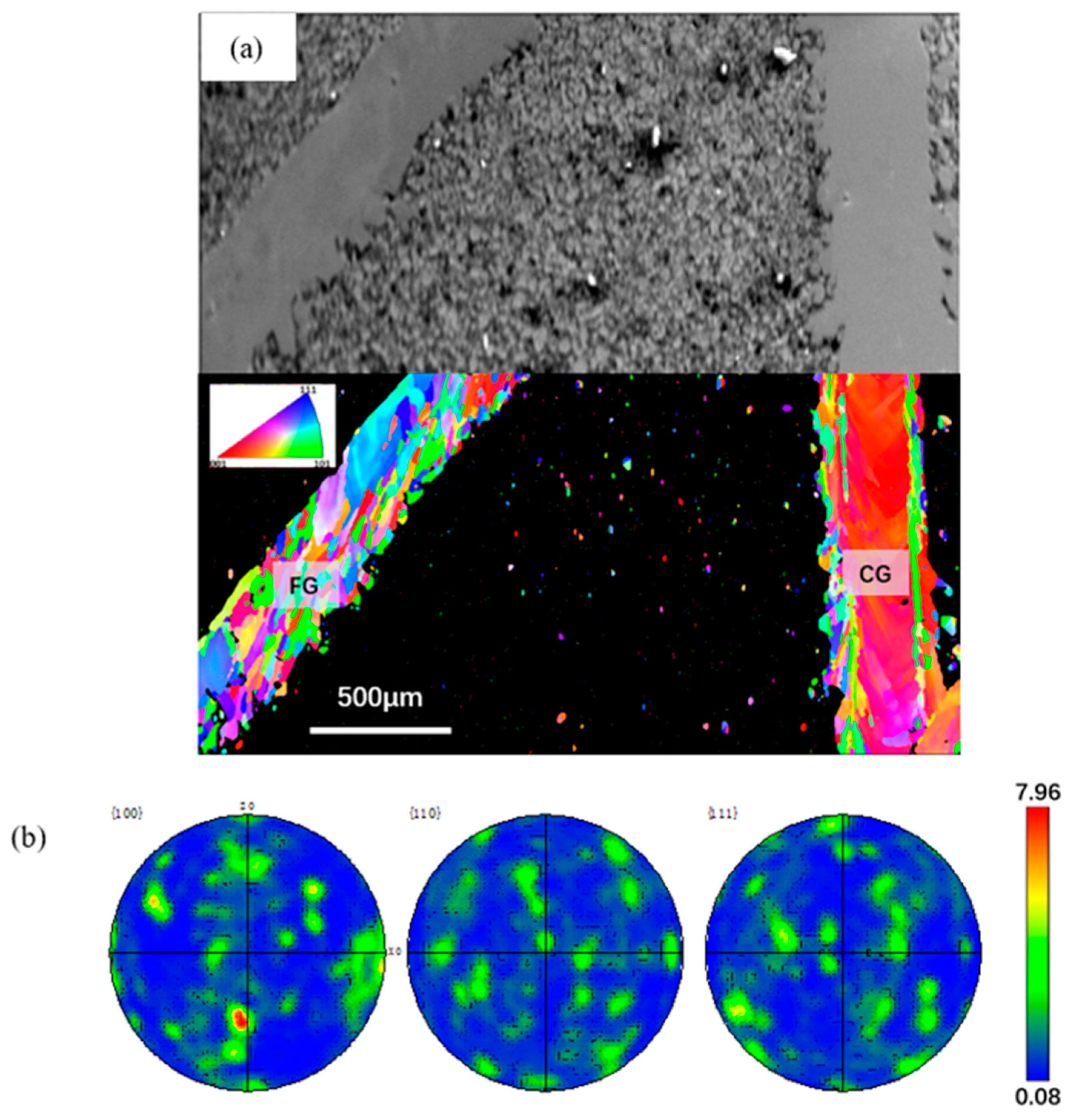
- The surface morphology with the overlap strategy presents a significant scale effect. The surface roughness Ra (SP) rapidly decreases by 68.6% from 14.53 μm to 4.26 μm, accompanied by the evident improvement in surface fluctuation. The mean diameters decrease by 18.7%. It is observed that the maximal texture index is steadily raised, and the grain weave orientation tends to be more in the direction of {100}, both of which show a clear improvement in interlayer remelting. Furthermore, for low energy density input, it is evident that the splashing of the melt pool and the powder’s own gravity cause heterogeneous nucleation at the area near the melt pool’s border in the constitutionally undercooled zone, which prevents the columnar grain from growing.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Balachandramurthi, A.R.; Moverare, J.; Dixit, N.; Pederson, R. Influence of defects and as-built surface roughness on fatigue properties of additively manufactured Alloy 718. Mater. Sci. Eng. A 2018, 735, 463–474. [Google Scholar] [CrossRef]
- Li, R.; Liu, J.; Shi, Y.; Wang, L.; Jiang, W. Balling behavior of stainless steel and nickel powder during selective laser melting process. Int. J. Adv. Manuf. Technol. 2012, 59, 1025–1035. [Google Scholar] [CrossRef]
- Beaucamp, A.T.; Namba, Y.; Charlton, P.; Jain, S.; Graziano, A.A. Finishing of additively manufactured titanium alloy by shape adaptive grinding (SAG). Surf. Topogr. Metrol. Prop. 2015, 3, 024001. [Google Scholar] [CrossRef]
- Tang, Y. A Multiscale and Multifunctional Design Method for Mesoscale Lattice Structures Fabricated by Additive Manufacturing Processes; McGill University: Montréal, QC, Canada, 2018. [Google Scholar]
- Urlea, V.; Brailovski, V. Electropolishing and electropolishing-related allowances for powder bed selectively laser-melted Ti-6Al-4V alloy components. J. Mater. Process. Technol. 2017, 242, 1–11. [Google Scholar] [CrossRef]
- Shen, M.; Fang, F. Advances in polishing of internal structures on parts made by laser-based powder bed fusion. Front. Mech. Eng. 2023, 18, 8. [Google Scholar] [CrossRef]
- Kruth, J.P.; Froyen, L.; Van Vaerenbergh, J.; Mercelis, P.; Rombouts, M.; Lauwers, B. Selective laser melting of iron-based powder. J. Mater. Process. Technol. 2004, 149, 616–622. [Google Scholar] [CrossRef]
- Spittle, J.A. Columnar to equiaxed grain transition in as solidified alloys. Int. Mater. Rev. 2006, 51, 247–269. [Google Scholar] [CrossRef]
- Lin, K.; Qiao, J.; Gu, D.; Wang, H.; Shi, B.; Zhang, W.; Shan, J.; Xu, Y.; Tian, L. Active Screen Plasma Nitriding of Laser Powder Bed Fusion Processed 316L Stainless Steel for the Application of Fuel Cell Bipolar Plates. Virtual Phys. Prototyp. 2023, 18, e2225490. [Google Scholar] [CrossRef]
- Spittle, J.A.; Brown, S.G.R. Numerical modelling of permeability variation with composition in aluminium alloy systems and its relationship to hot tearing susceptibility. Mater. Sci. Technol. 2005, 21, 1071–1077. [Google Scholar] [CrossRef]
- Liu, X.W.; Yao, J.Q.; Ma, X.N.; Wang, Y.S.; Gao, N.; Shi, Y.; Fan, Z.T.; Du, H. Columnar-to-equiaxed transition and grain refinement by solute interaction effects. Mater. Charact. 2023, 205, 113288. [Google Scholar] [CrossRef]
- Li, H.; Huang, Y.; Jiang, S.; Lu, Y.; Gao, X.; Lu, X.; Ning, Z.; Sun, J. Columnar to equiaxed transition in additively manufactured CoCrFeMnNi high entropy alloy. Mater. Des. 2021, 197, 109262. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, C.; Xing, L.; Li, K.; Chen, J.; Liu, W.; Ma, J.; Shen, Z. Grain structure and texture of the SLM single track. J. Mater. Process. Technol. 2020, 281, 116591. [Google Scholar] [CrossRef]
- Gu, Y.; Yuan, J.; Chen, L. Switching of control mechanisms during the rapid solidification of a melt pool. Phys. Rev. Mater. 2023, 7, 103401. [Google Scholar] [CrossRef]
- Ren, N.; Li, J.; Zhang, R.; Panwisawas, C.; Xia, M.; Dong, H.; Li, J. Solute trapping and non-equilibrium microstructure during rapid solidification of additive manufacturing. Nat. Commun. 2023, 14, 7990. [Google Scholar] [CrossRef]
- Ben Youssef, B. Cellular Automata-Based Modeling of Three Dimensional Multicellular Tissue Growth. In Emerging Trends in Applications and Infrastructures for Computational Biology, Bioinformatics, and Systems Biology: Systems and Applications; Elsevier Inc.: Amsterdam, The Netherlands, 2016; pp. 287–303. [Google Scholar]
- Jaafar, M.A.; Rousse, D.R.; Gibout, S.; Bédécarrats, J.P. A review of dendritic growth during solidification: Mathematical modeling and numerical simulations. Renew. Sustain. Energy Rev. 2017, 74, 1064–1079. [Google Scholar] [CrossRef]
- Quasthoff, U. Nested cellular automata: Continuous aspects of discrete systems. In Fractals in Physics; Elsevier: Amsterdam, The Netherlands, 1986; pp. 465–468. [Google Scholar]
- Zeneli, M.; Nikolopoulos, A.; Karellas, S.; Nikolopoulos, N. Numerical methods for solid-liquid phase-change problems. In Ultra-High Temperature Thermal Energy Storage, Transfer and Conversion; Woodhead Publishing: Cambridge, UK, 2021; pp. 165–199. [Google Scholar]
- Dong, H.B.; Lee, P.D. Simulation of the columnar-to-equiaxed transition in directionally solidified Al–Cu alloys. Acta Mater. 2005, 53, 659–668. [Google Scholar] [CrossRef]
- Thevoz, P.; Desbiolles, J.L.; Rappaz, M. Modeling of equiaxed microstructure formation in casting. Metall. Trans. A 1989, 20, 311–322. [Google Scholar] [CrossRef]
- Beltran-Sanchez, L.; Stefanescu, D.M. A quantitative dendrite growth model and analysis of stability concepts. Metall. Mater. Trans. A 2004, 35, 2471–2485. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta Metall. 1986, 34, 823–830. [Google Scholar] [CrossRef]
- Roehling, T.T.; Wu, S.S.; Khairallah, S.A.; Roehling, J.D.; Soezeri, S.S.; Crumb, M.F.; Matthews, M.J. Modulating laser intensity profile ellipticity for microstructural control during metal additive manufacturing. Acta Mater. 2017, 128, 197–206. [Google Scholar] [CrossRef]
- Tang, C.; Tan, J.L.; Wong, C.H. A numerical investigation on the physical mechanisms of single track defects in selective laser melting. Int. J. Heat Mass Transf. 2018, 126, 957–968. [Google Scholar] [CrossRef]
- Cho, J.-H.; Farson, D.F.; Milewski, J.O.; Hollis, K.J. Weld pool flows during initial stages of keyhole formation in laser welding. J. Phys. D Appl. Phys. 2009, 42, 175502. [Google Scholar] [CrossRef]
- Panwisawas, C.; Qiu, C.; Anderson, M.J.; Sovani, Y.; Turner, R.P.; Attallah, M.M.; Brooks, J.W.; Basoalto, H.C. Mesoscale modelling of selective laser melting: Thermal fluid dynamics and microstructural evolution. Comput. Mater. Sci. 2017, 126, 479–490. [Google Scholar] [CrossRef]
- Andreau, O.; Koutiri, I.; Peyre, P.; Penot, J.D.; Saintier, N.; Pessard, E.; De Terris, T.; Dupuy, C.; Baudin, T. Texture control of 316L parts by modulation of the melt pool morphology in selective laser melting. J. Mater. Process. Technol. 2019, 264, 21–31. [Google Scholar] [CrossRef]
- Montero-Sistiaga, M.L.; Godino-Martinez, M.; Boschmans, K.; Kruth, J.P.; Van Humbeeck, J.; Vanmeensel, K. Microstructure evolution of 316L produced by HP-SLM (high power selective laser melting). Addit. Manuf. 2018, 23, 402–410. [Google Scholar] [CrossRef]
- Nagarajan, B.; Hu, Z.; Gao, S.; Song, X.; Huang, R.; Seita, M.; Wei, J. Effect of in-situ laser remelting on the microstructure of SS316L fabricated by micro selective laser melting. In Advanced Surface Enhancement: Proceedings of the 1st International Conference on Advanced Surface Enhancement (INCASE 2019)—Research Towards Industrialisation, Singapore, 10–12 September 2019; Springer: Singapore, 2020; pp. 330–336. [Google Scholar]
- Rappaz, M.; Gandin, C.-A. Probabilistic modelling of microstructure formation in solidification processes. Acta Metall. Et Mater. 1993, 41, 345–360. [Google Scholar] [CrossRef]
- Zinovieva, O.; Zinoviev, A.; Romanova, V.; Balokhonov, R. Three-dimensional analysis of grain structure and texture of additively manufactured 316L austenitic stainless steel. Addit. Manuf. 2020, 36, 101521. [Google Scholar] [CrossRef]
- William, T.A. Preferred growth direction of metals. JoM 1957, 9, 847–855. [Google Scholar]
- Chattopadhyay, C.; Sangal, S.; Mondal, K. A relook at the preferred growth direction of the solid–liquid interface during solidification of pure metals. Acta Mater. 2010, 58, 5342–5353. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Krakhmalev, P.; Yadroitsava, I.; Johansson, S.; Smurov, I. Energy input effect on morphology and microstructure of selective laser melting single track from metallic powder. J. Mater. Process. Technol. 2013, 213, 606–613. [Google Scholar] [CrossRef]
- Li, X.; Tan, W. Numerical investigation of effects of nucleation mechanisms on grain structure in metal additive manufacturing. Comput. Mater. Sci. 2018, 153, 159–169. [Google Scholar] [CrossRef]
- Olorundaisi, E.; Jamiru, T.; Adegbola, T.A.; Ogunbiyi, O.F. Modeling and optimization of operating parameters using RSM for mechanical behaviour of dual phase steels. Mater. Res. Express 2019, 6, 105628. [Google Scholar] [CrossRef]
- Fatemi, S.A.; Ashany, J.Z.; Aghchai, A.J.; Abolghasemi, A. Experimental investigation of process parameters on layer thickness and density in direct metal laser sintering: A response surface methodology approach. Virtual Phys. Prototyp. 2017, 12, 133–140. [Google Scholar] [CrossRef]
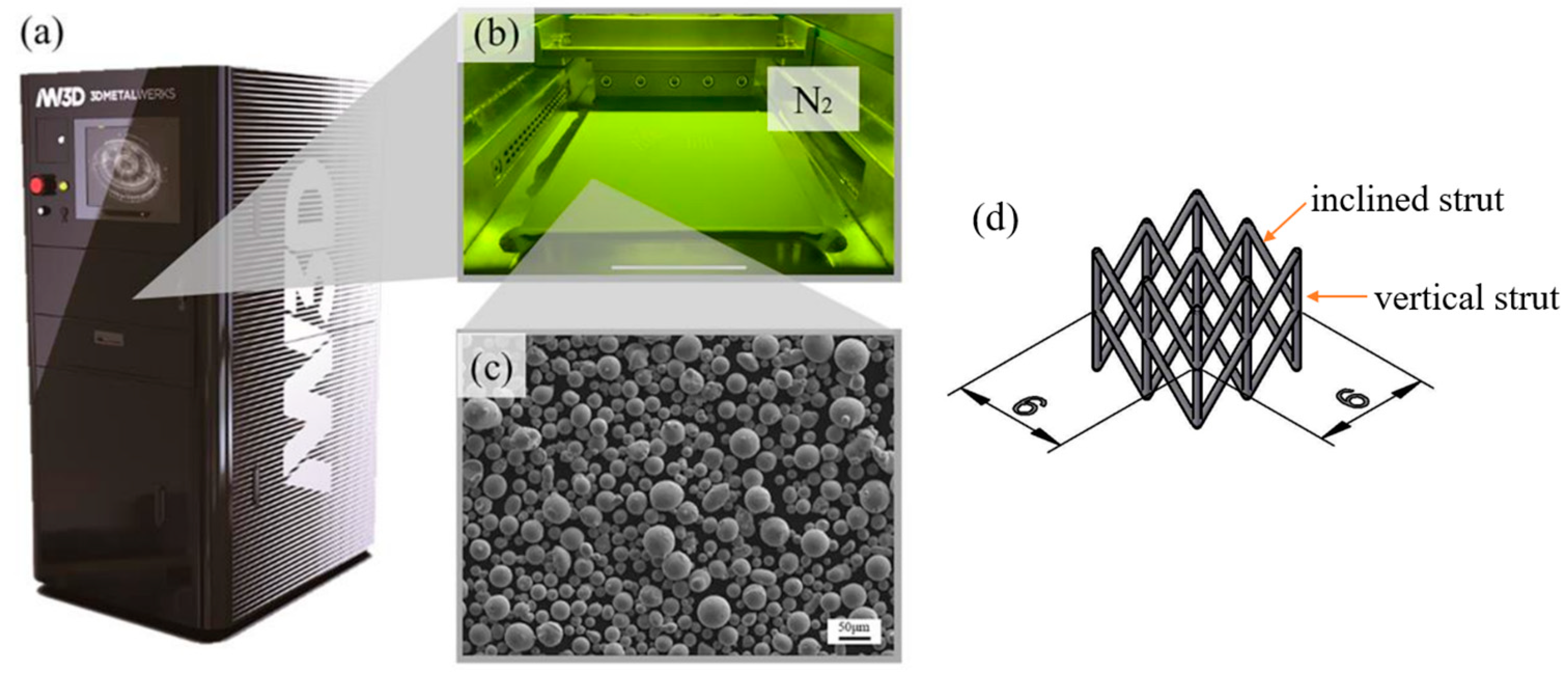



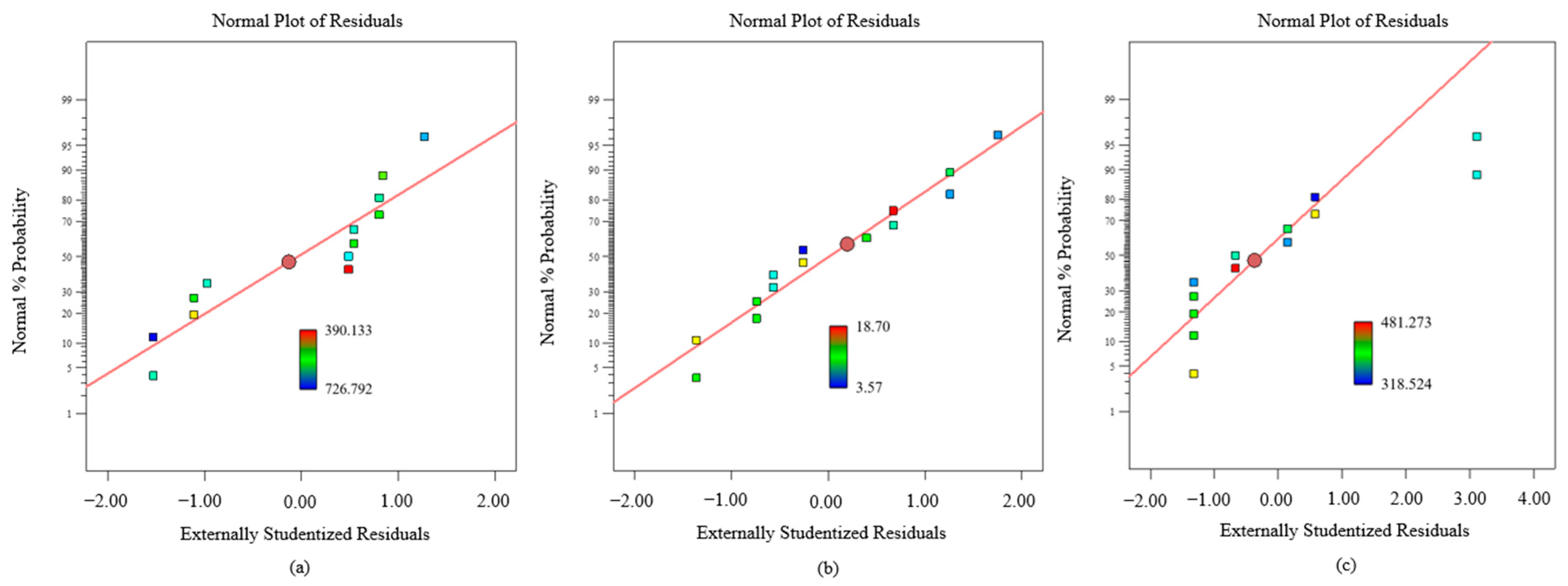

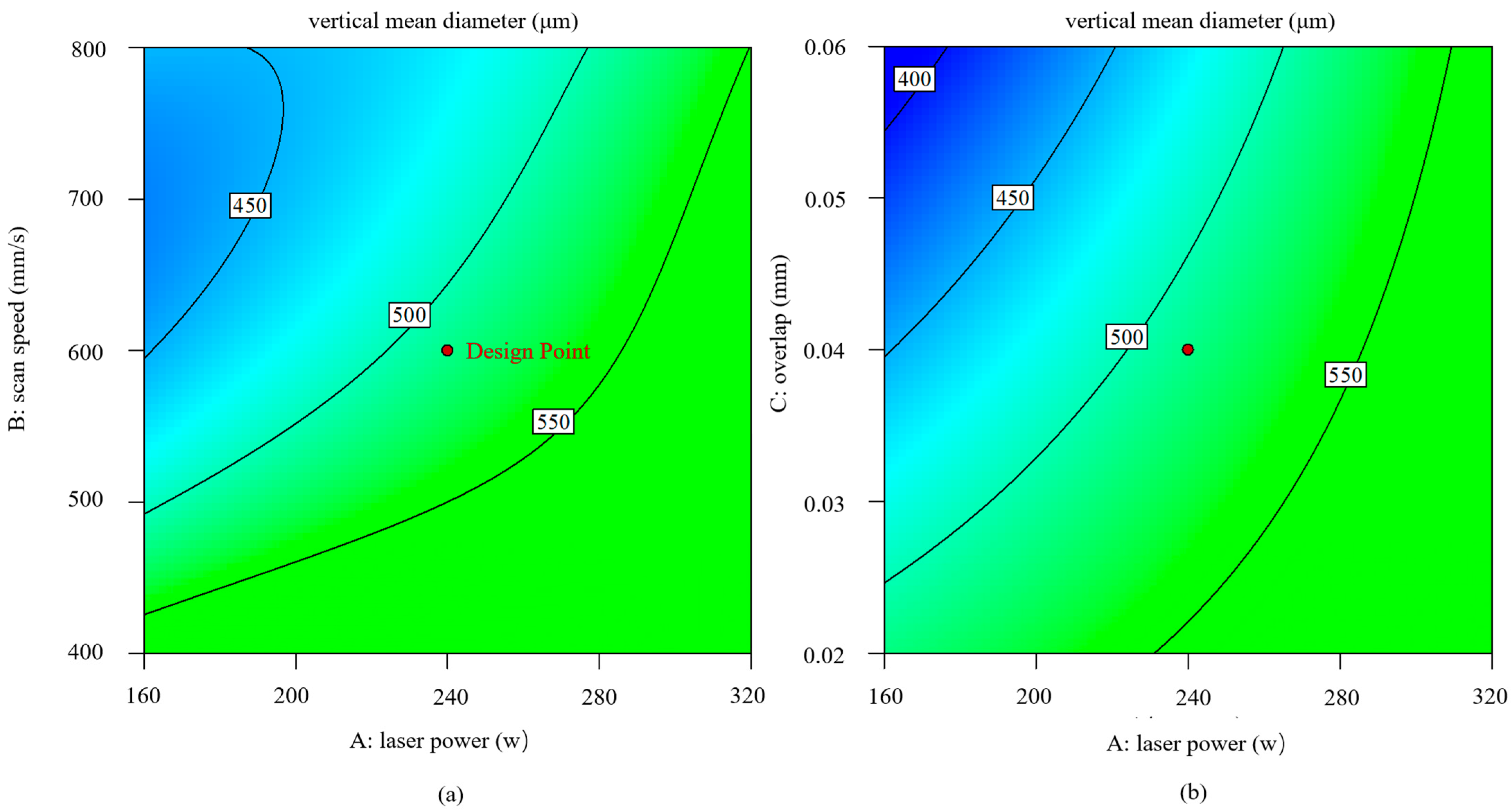
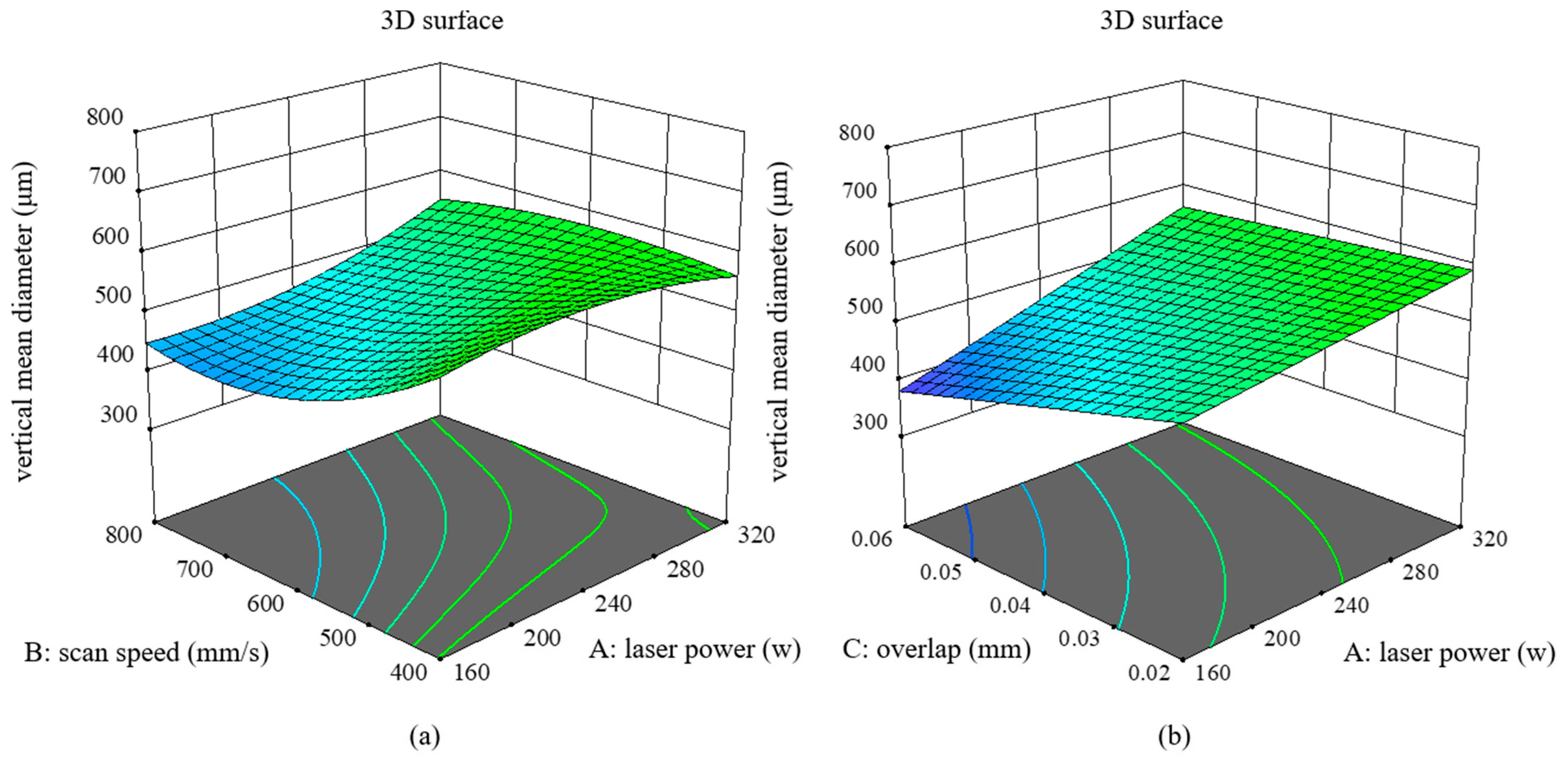
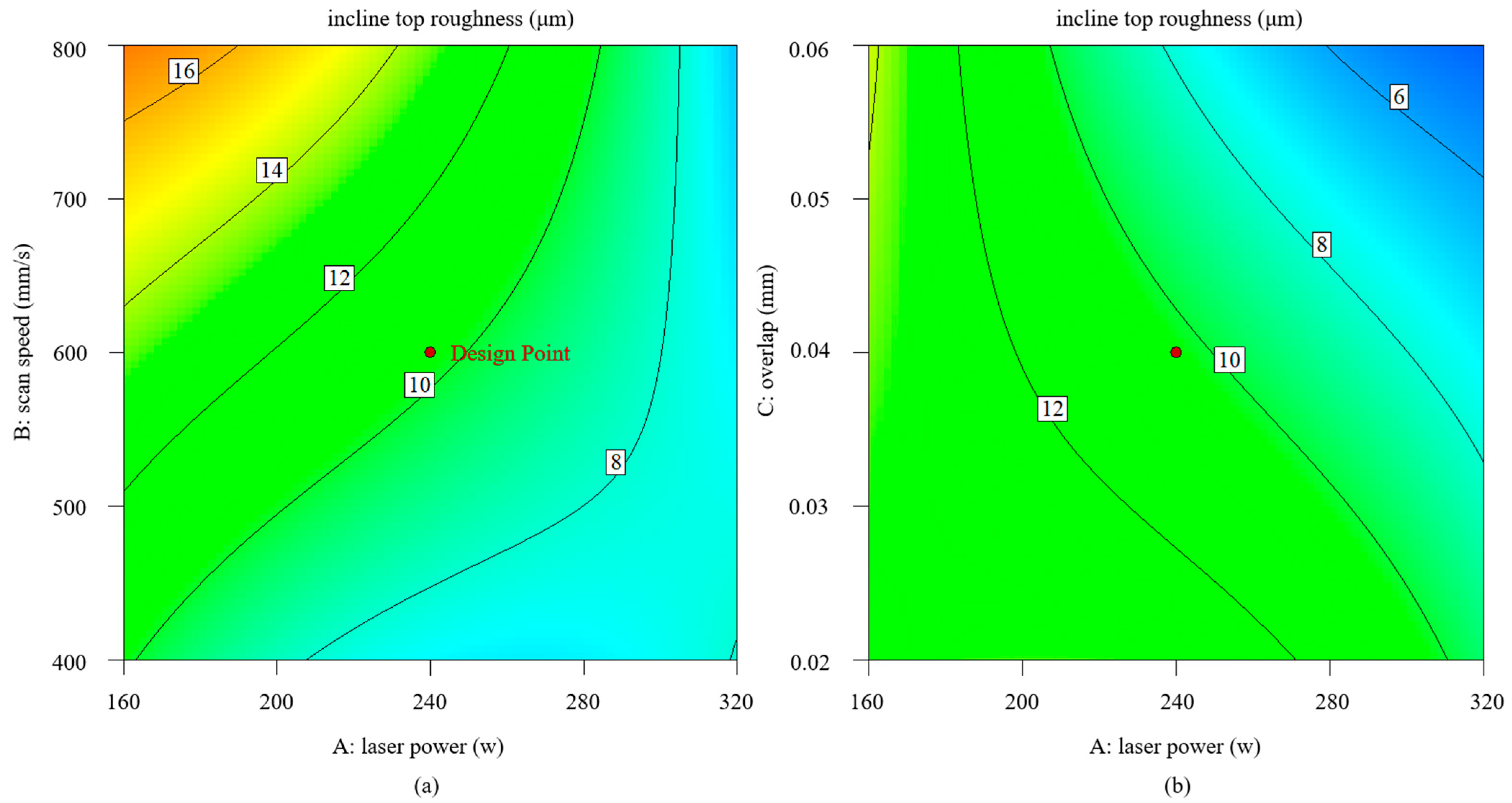

| Element | Ni | Cr | Mo | Si | Mn | C | O | S | P | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| Wt. (%) | 12.3 | 17.52 | 2.26 | 0.77 | 1.66 | 0.014 | 0.0654 | 0.003 | 0.011 | Bal. |
| No. | Laser Power (w) | Scan Speed (mm/s) | Overlap (mm) |
|---|---|---|---|
| 1 | 160 | 400 | 0.02 |
| 2 | 320 | 400 | 0.02 |
| 3 | 160 | 800 | 0.02 |
| 4 | 320 | 800 | 0.02 |
| 5 | 160 | 400 | 0.06 |
| 6 | 320 | 400 | 0.06 |
| 7 | 160 | 800 | 0.06 |
| 8 | 320 | 800 | 0.06 |
| 9 | 80 | 600 | 0.04 |
| 10 | 400 | 600 | 0.04 |
| 11 | 240 | 200 | 0.04 |
| 12 | 240 | 1000 | 0.04 |
| 13 | 240 | 600 | 0 |
| 14 | 240 | 600 | 0.08 |
| 15 | 240 | 600 | 0.04 |
| Std | Run | Factor 1 A: Laser Power w | Factor 2 B: Scan Speed mm/s | Factor 3 C: Overlap mm | Response 1 Vertical Mean Diameter μm | Response 4 Incline Top Roughness μm | Response 5 Incline Mean Diameter μm |
|---|---|---|---|---|---|---|---|
| 1 | 15 | 160 | 400 | 0.02 | 650.532 | 7.22 | 481.273 |
| 2 | 9 | 320 | 400 | 0.02 | 545.908 | 11.91 | 450.583 |
| 3 | 11 | 160 | 800 | 0.02 | 504.091 | 18.70 | 416.173 |
| 4 | 12 | 320 | 800 | 0.02 | 596.127 | 6.92 | 427.798 |
| 5 | 7 | 160 | 400 | 0.06 | 490.573 | 13.63 | 378.508 |
| 6 | 10 | 320 | 400 | 0.06 | 574.738 | 4.26 | 383.623 |
| 7 | 1 | 160 | 800 | 0.06 | 390.133 | 15.39 | 318.524 |
| 8 | 5 | 320 | 800 | 0.06 | 500.338 | 5.93 | 385.483 |
| 9 | 6 | 80 | 600 | 0.04 | |||
| 10 | 13 | 400 | 600 | 0.04 | 642.162 | 4.50 | 476.158 |
| 11 | 4 | 240 | 200 | 0.04 | 726.792 | 3.57 | 491.503 |
| 12 | 2 | 240 | 1000 | 0.04 | 472.438 | 15.96 | 363.628 |
| 13 | 3 | 240 | 600 | 0 | 610.077 | 14.53 | 416.173 |
| 14 | 8 | 240 | 600 | 0.08 | 449.653 | 4.26 | 338.519 |
| 15 | 14 | 240 | 600 | 0.04 | 493.828 | 12.04 | 392.458 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Significant or Not |
|---|---|---|---|---|---|---|
| Model | 1.071 × 105 | 9 | 11,903.56 | 26.52 | 0.0032 | Significant |
| A-laser power | 14,498.50 | 1 | 14,498.50 | 32.30 | 0.0047 | |
| B-scan speed | 32,347.94 | 1 | 32,347.94 | 72.06 | 0.0011 | |
| C-overlap | 27,367.54 | 1 | 27,367.54 | 60.97 | 0.00115 | |
| Residual | 1795.55 | 4 | 448.89 | |||
| Cor Total | 1.089 × 105 | 13 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Significant or Not |
|---|---|---|---|---|---|---|
| Model | 345.99 | 8 | 43.25 | 31.02 | 0.0008 | Significant |
| A-laser power | 115.28 | 1 | 115.28 | 82.69 | 0.0003 | |
| B-scan speed | 76.73 | 1 | 76.73 | 55.04 | 0.0007 | |
| C-overlap | 52.75 | 1 | 52.75 | 37.84 | 0.0017 | |
| Residual | 6.97 | 5 | 1.39 | |||
| Cor Total | 352.96 | 13 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Significant or Not |
|---|---|---|---|---|---|---|
| Model | 36,039.01 | 10 | 3603.90 | 36.40 | 0.0065 | Significant |
| A-laser power | 3916.35 | 1 | 3916.35 | 39.55 | 0.0081 | |
| B-scan speed | 8175.94 | 1 | 8175.94 | 82.57 | 0.0028 | |
| C-overlap | 3015.12 | 1 | 3015.12 | 30.45 | 0.0117 | |
| Residual | 297.05 | 3 | 99.02 | |||
| Cor Total | 36,336.06 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Liu, Z.; Liang, X.; Zhao, J.; Cai, Y.; Wang, B. Columnar-to-Equiaxed Transition on Laser Powder Bed Fusion Ultra-Precision Additive Manufacturing Accuracy and Surface Roughness for Solidified 316L Micro-Lattice Structure. Metals 2025, 15, 267. https://doi.org/10.3390/met15030267
Li C, Liu Z, Liang X, Zhao J, Cai Y, Wang B. Columnar-to-Equiaxed Transition on Laser Powder Bed Fusion Ultra-Precision Additive Manufacturing Accuracy and Surface Roughness for Solidified 316L Micro-Lattice Structure. Metals. 2025; 15(3):267. https://doi.org/10.3390/met15030267
Chicago/Turabian StyleLi, Chenxu, Zhanqiang Liu, Xiaoliang Liang, Jinfu Zhao, Yukui Cai, and Bing Wang. 2025. "Columnar-to-Equiaxed Transition on Laser Powder Bed Fusion Ultra-Precision Additive Manufacturing Accuracy and Surface Roughness for Solidified 316L Micro-Lattice Structure" Metals 15, no. 3: 267. https://doi.org/10.3390/met15030267
APA StyleLi, C., Liu, Z., Liang, X., Zhao, J., Cai, Y., & Wang, B. (2025). Columnar-to-Equiaxed Transition on Laser Powder Bed Fusion Ultra-Precision Additive Manufacturing Accuracy and Surface Roughness for Solidified 316L Micro-Lattice Structure. Metals, 15(3), 267. https://doi.org/10.3390/met15030267











