Simulation Study on Directional Solidification of Titanium–Aluminum Alloy Based on Liquid Metal Cooling Method
Abstract
1. Introduction
2. Materials and Methods
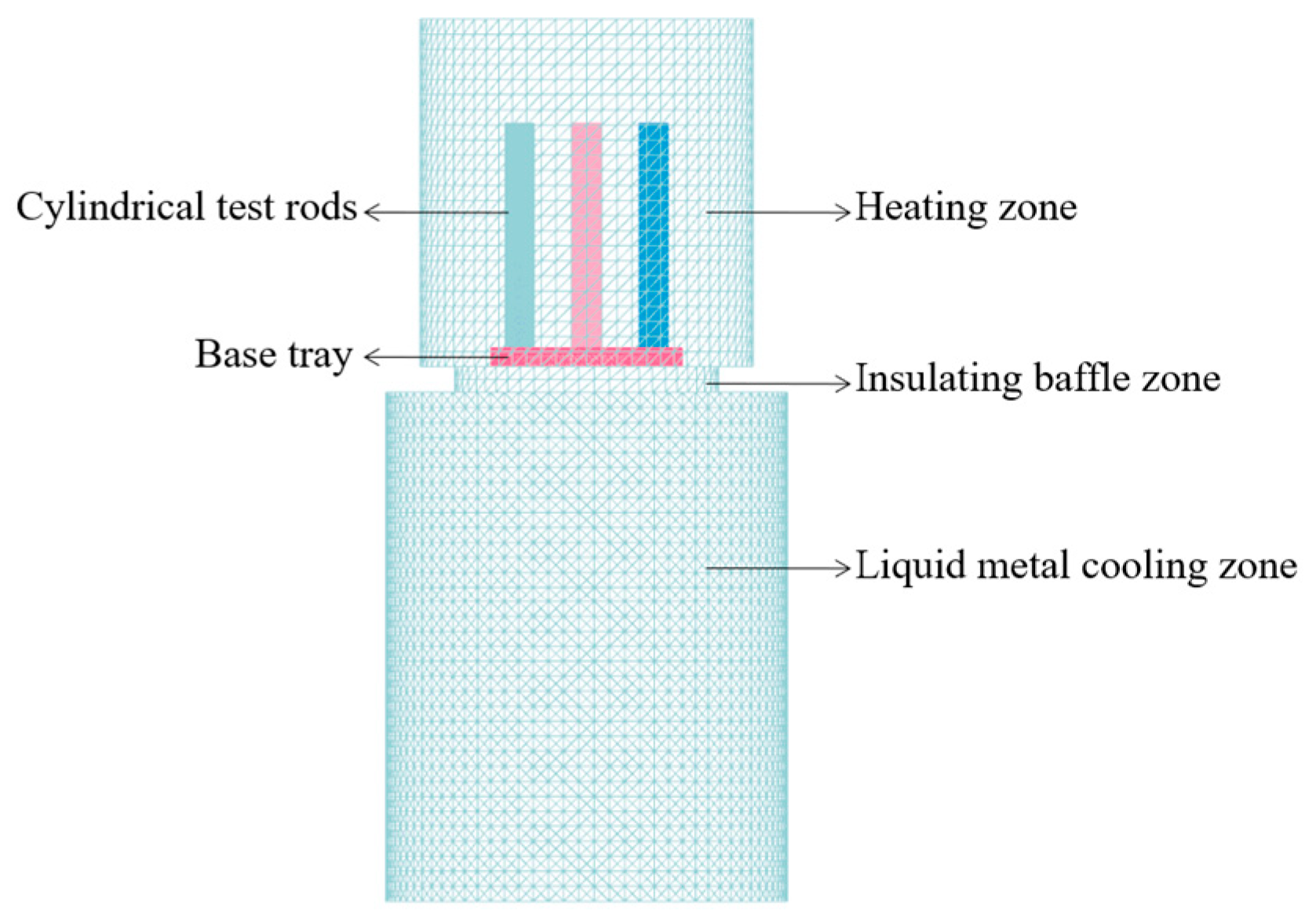
2.1. Three-Dimensional Model
2.2. Microstructure Mathematical Model
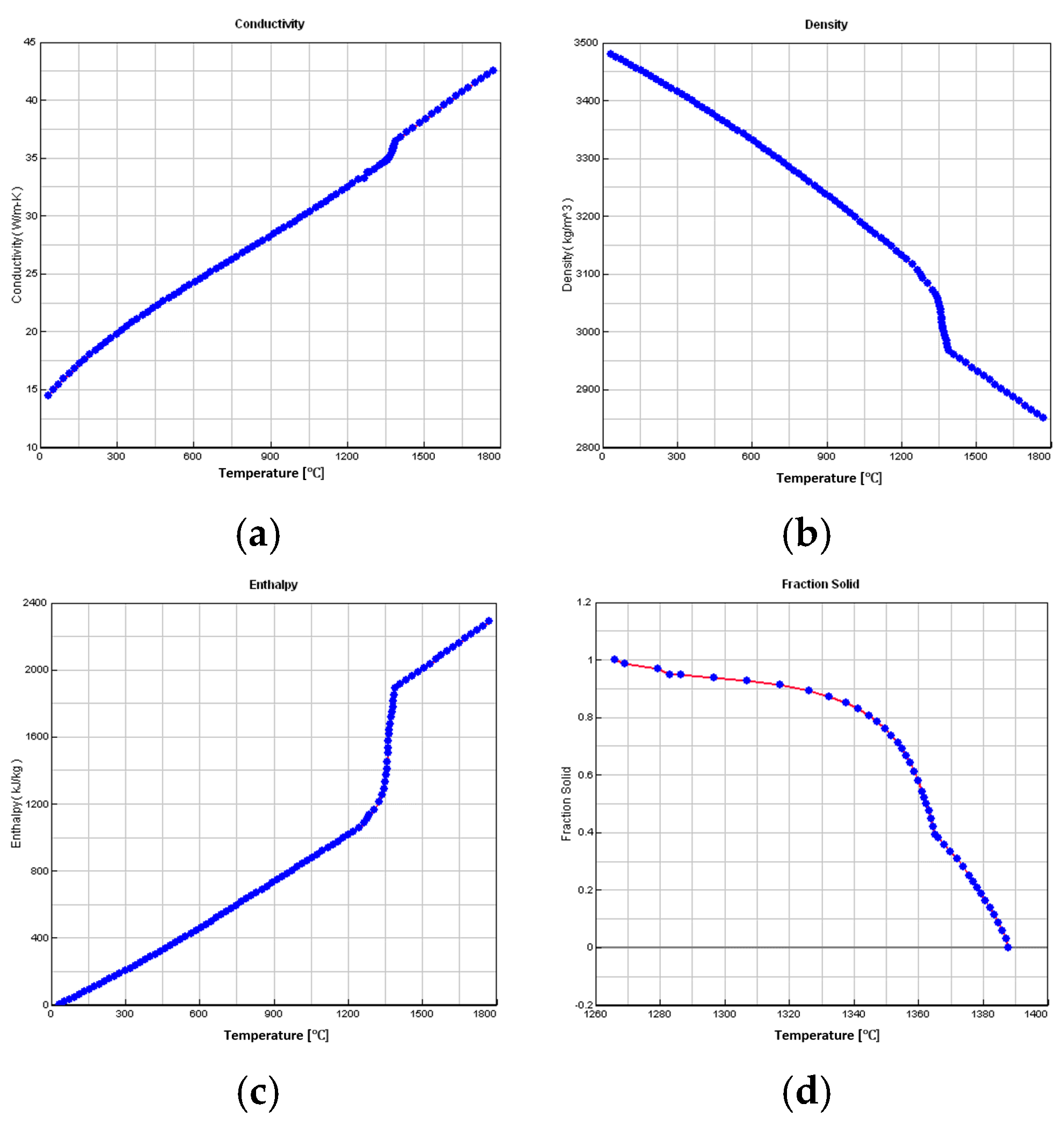
2.3. Material Parameters and Thermal Properties
2.4. Boundary Conditions
3. Results
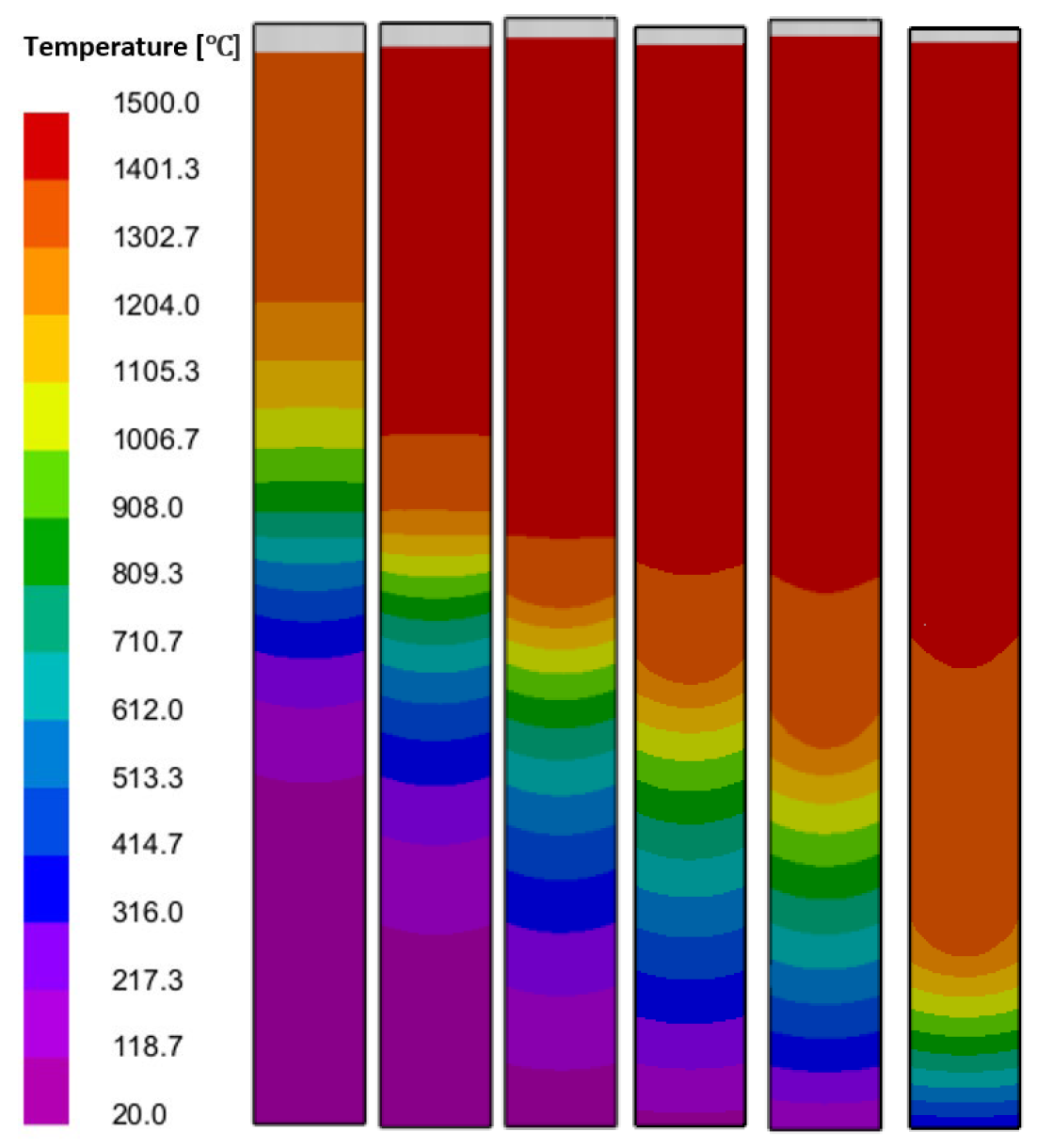
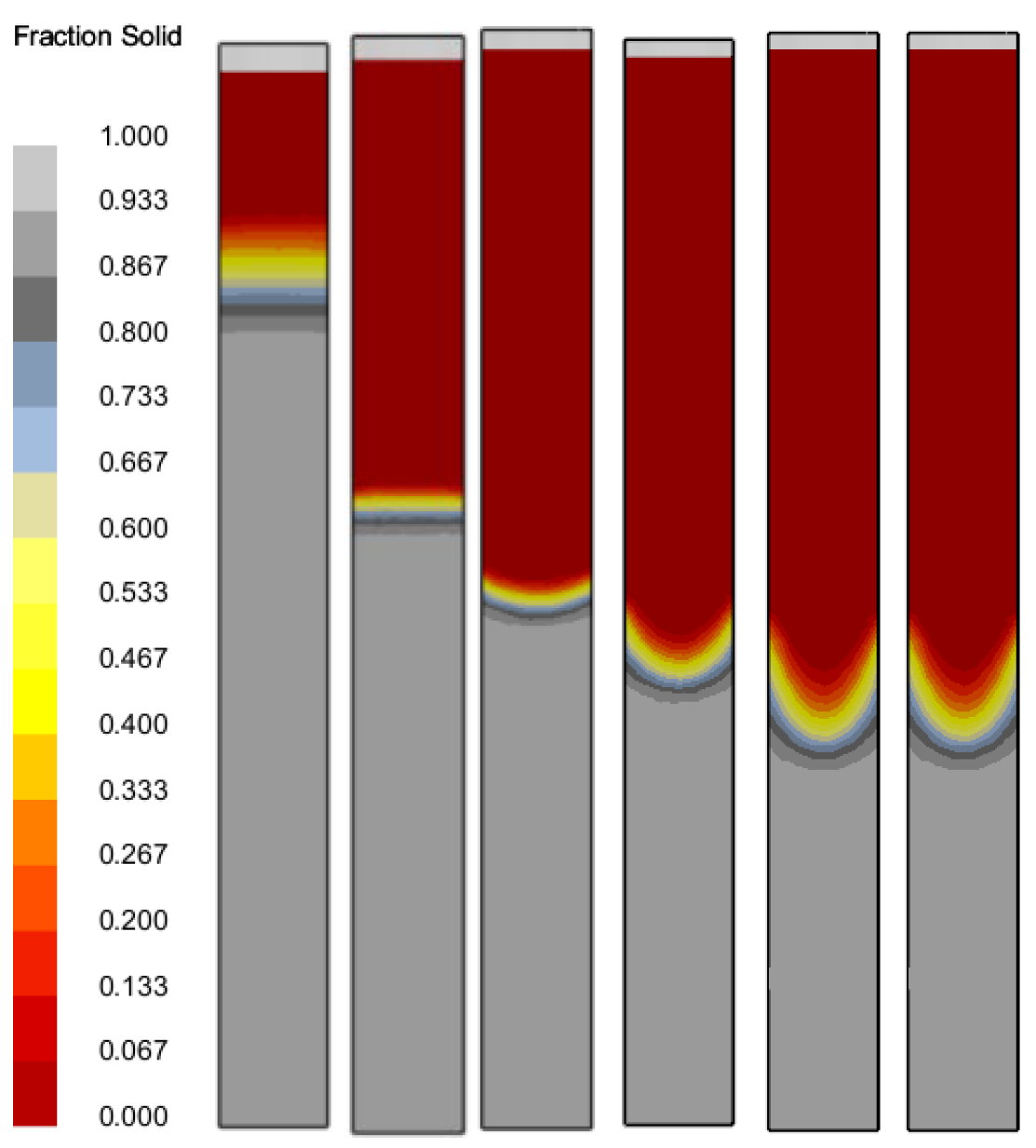
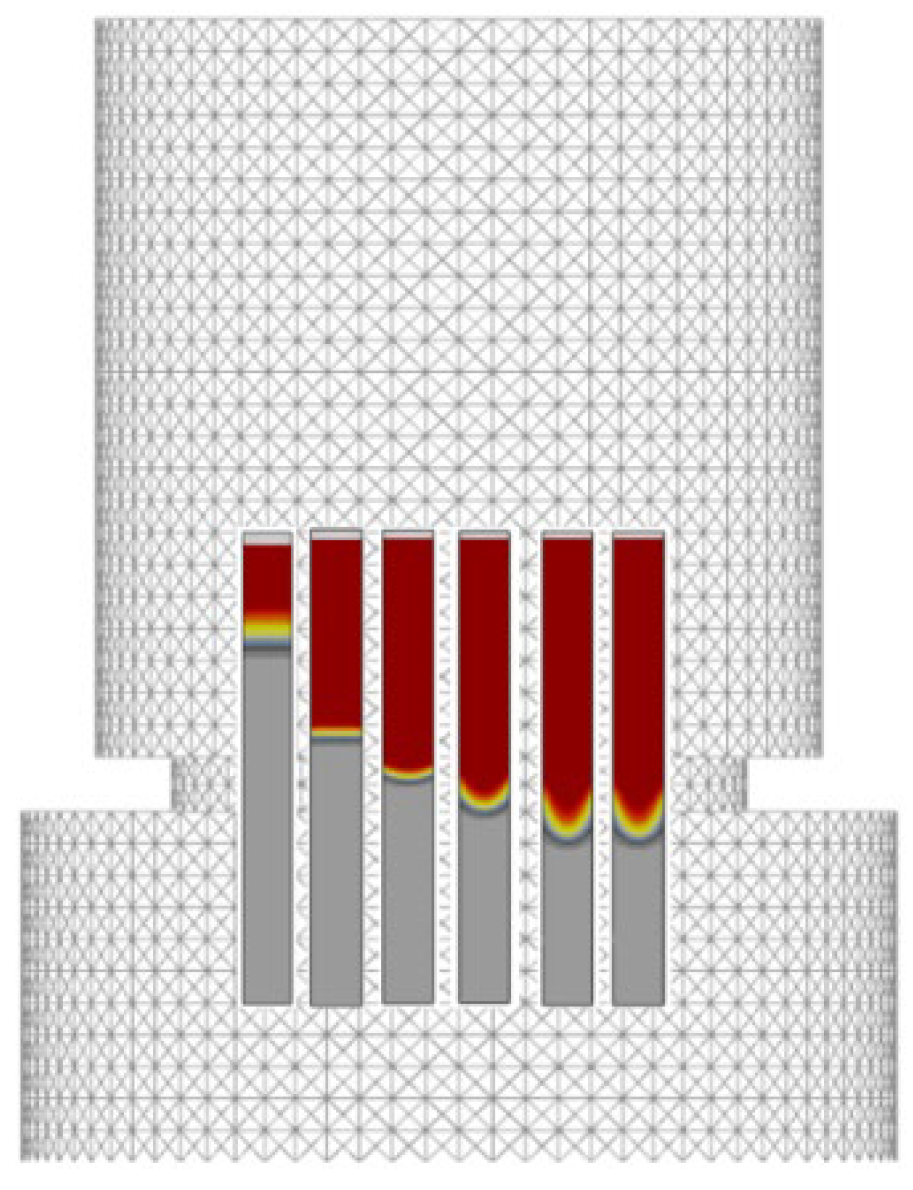
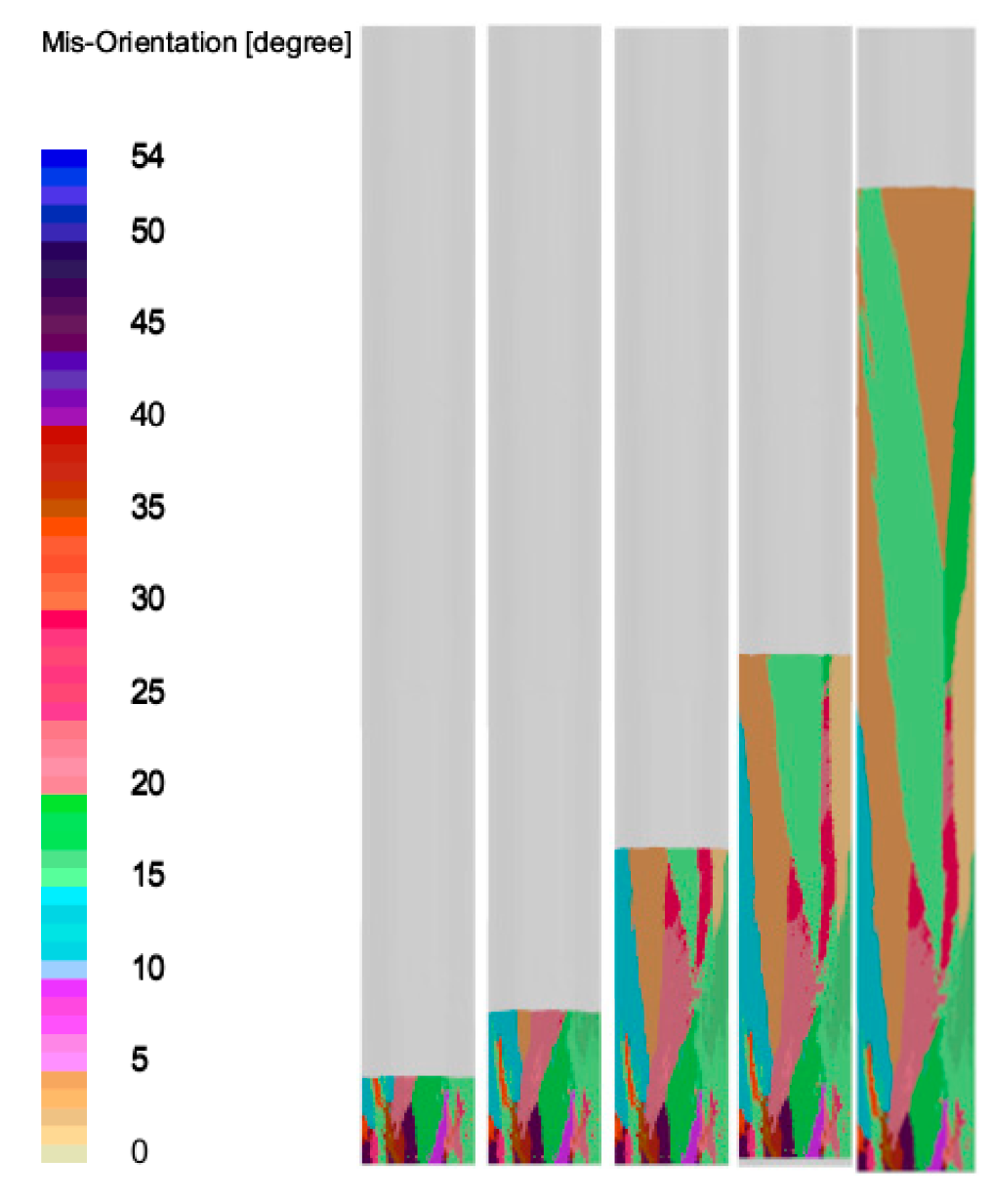
3.1. The Influence of Drawing Speed on the Temperature Field and Solidification Field of the Test Rods
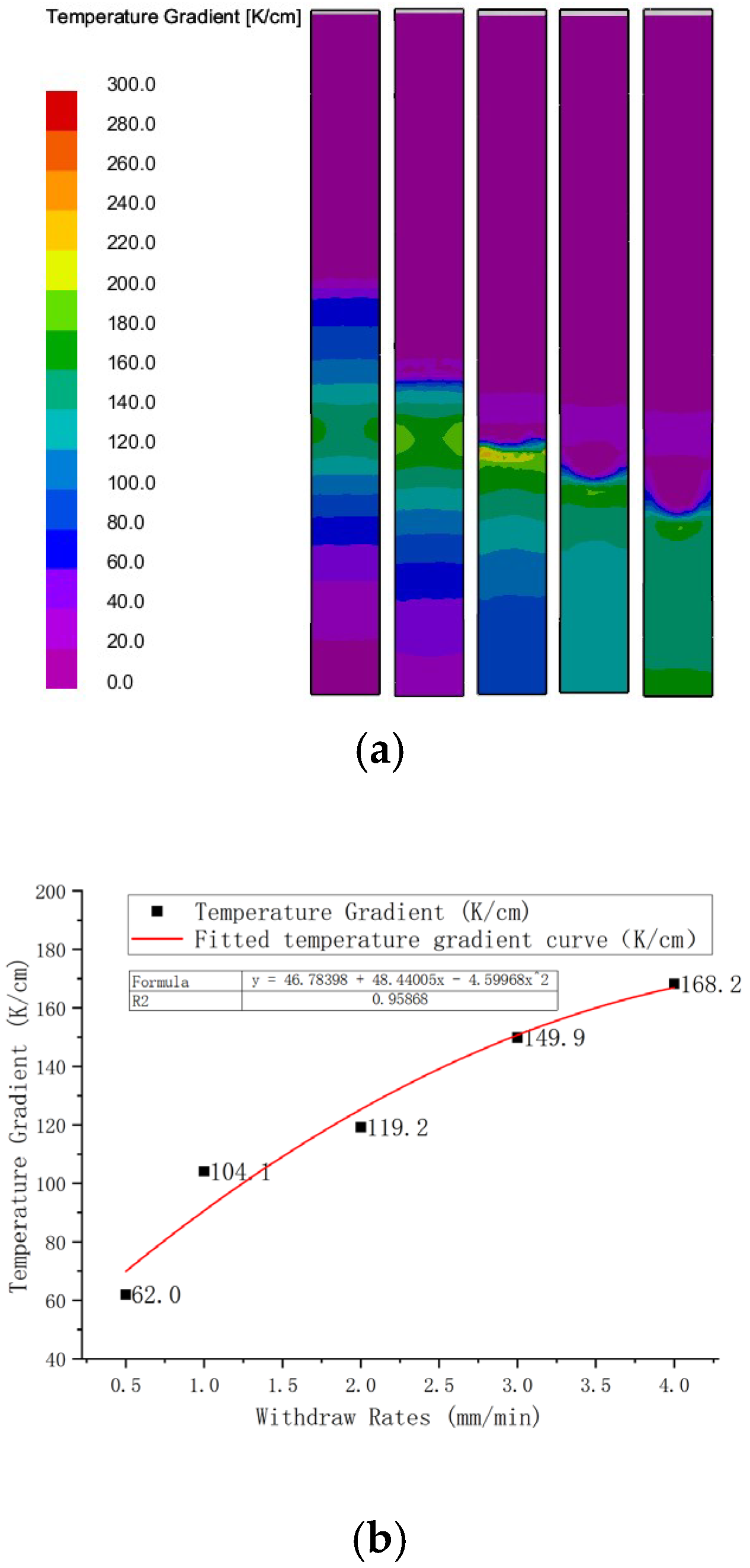
3.2. The Influence of Drawing Speed on the Temperature Gradient at the Solid–Liquid Interface of the Test Rods
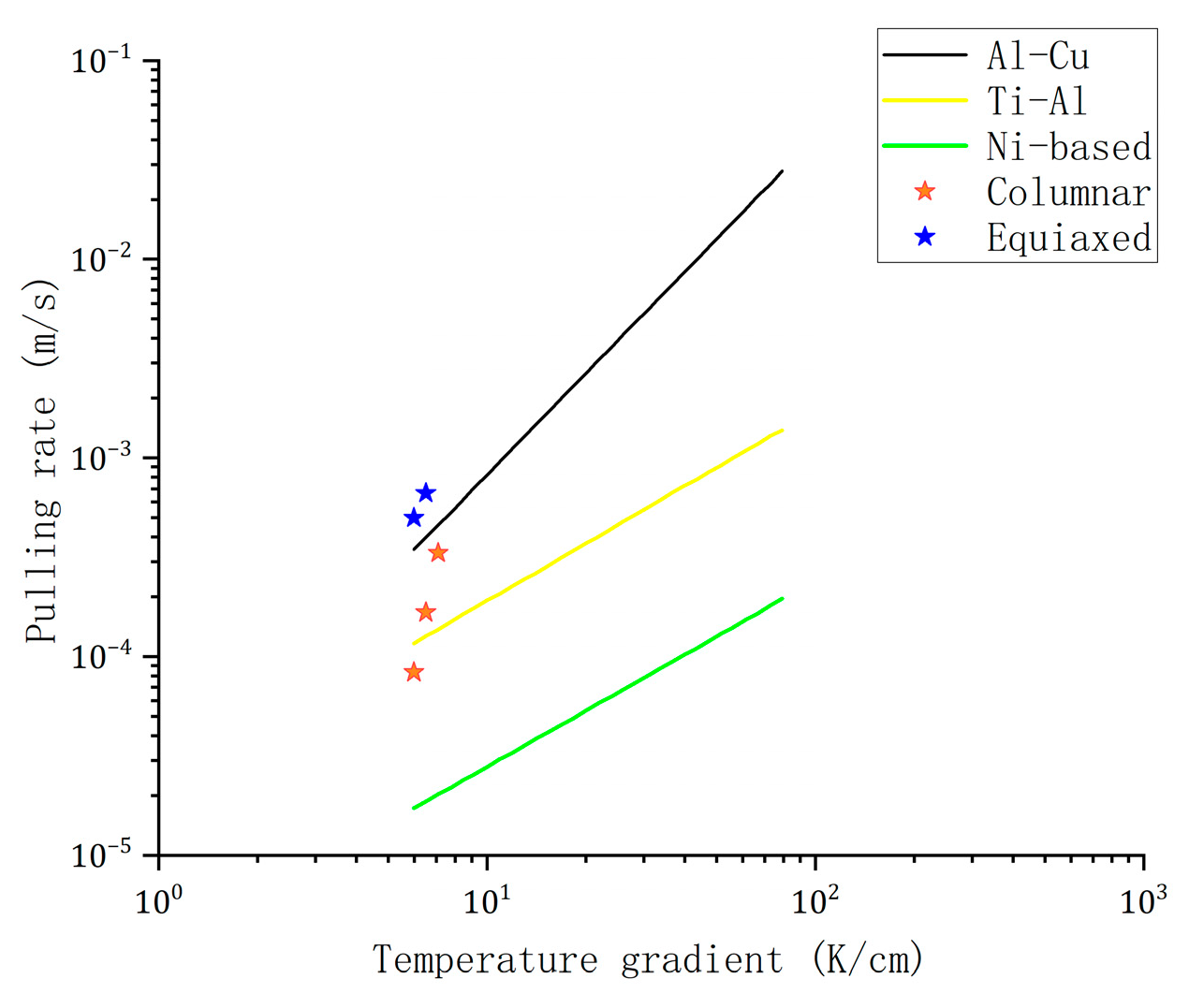
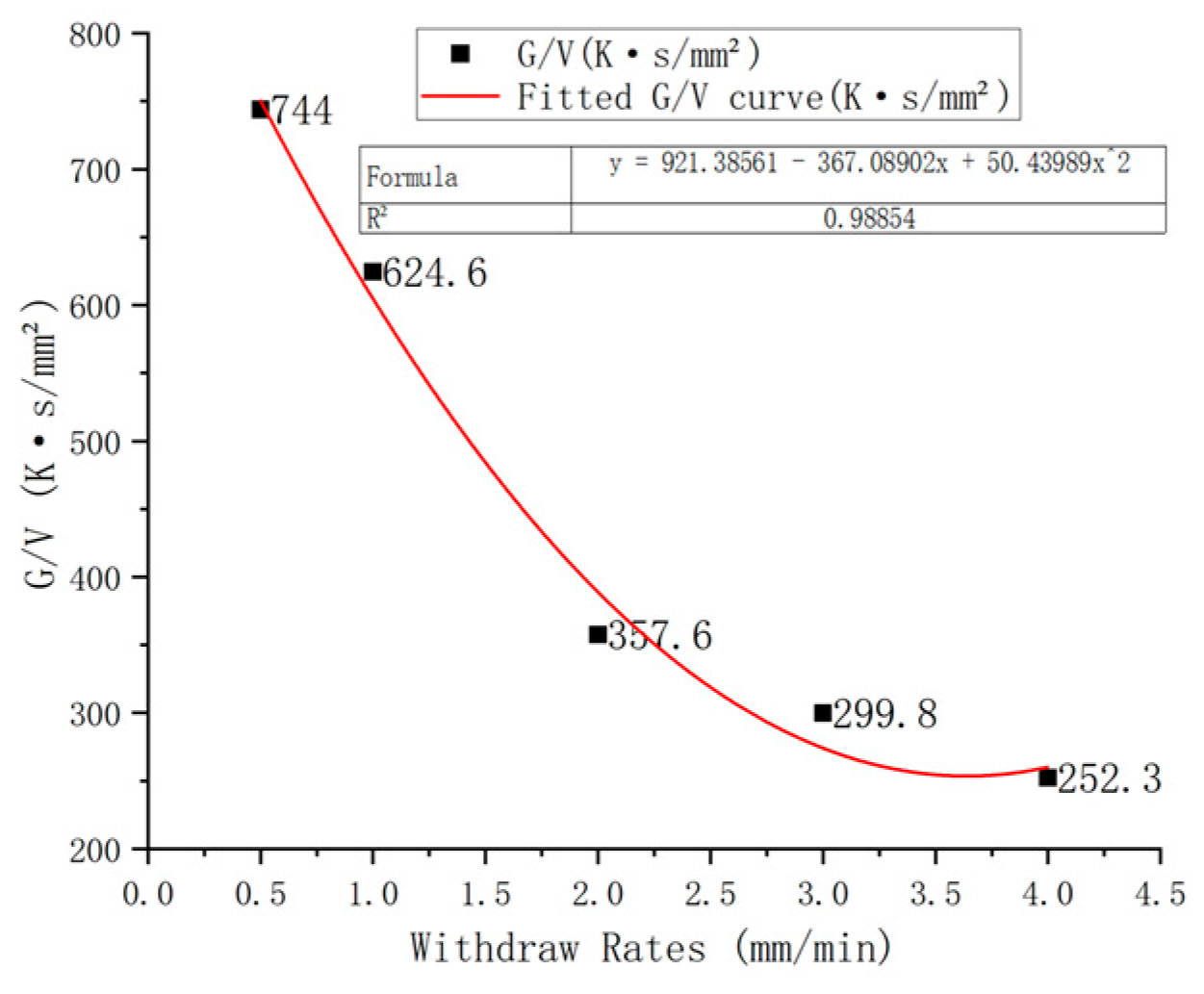
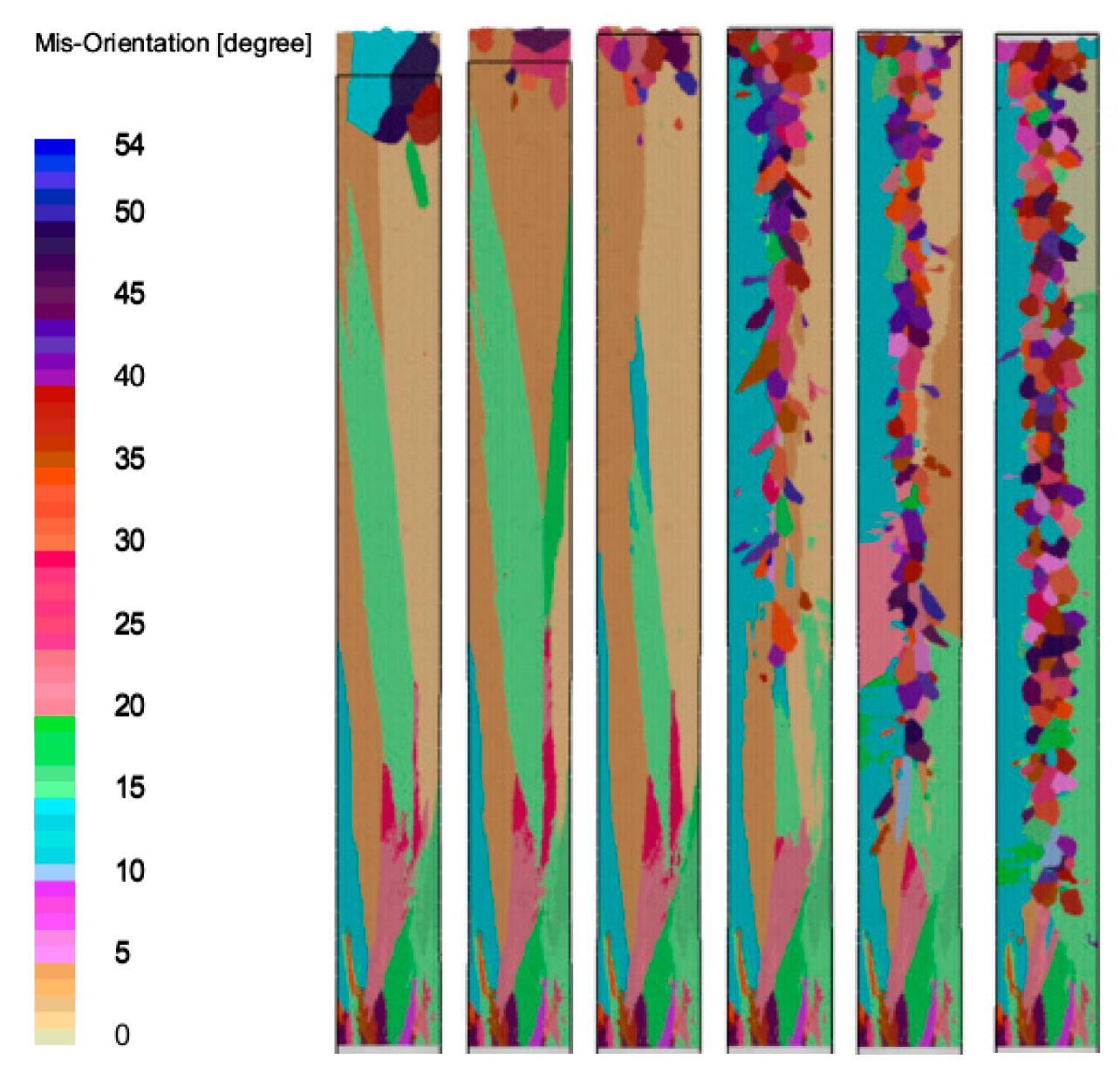
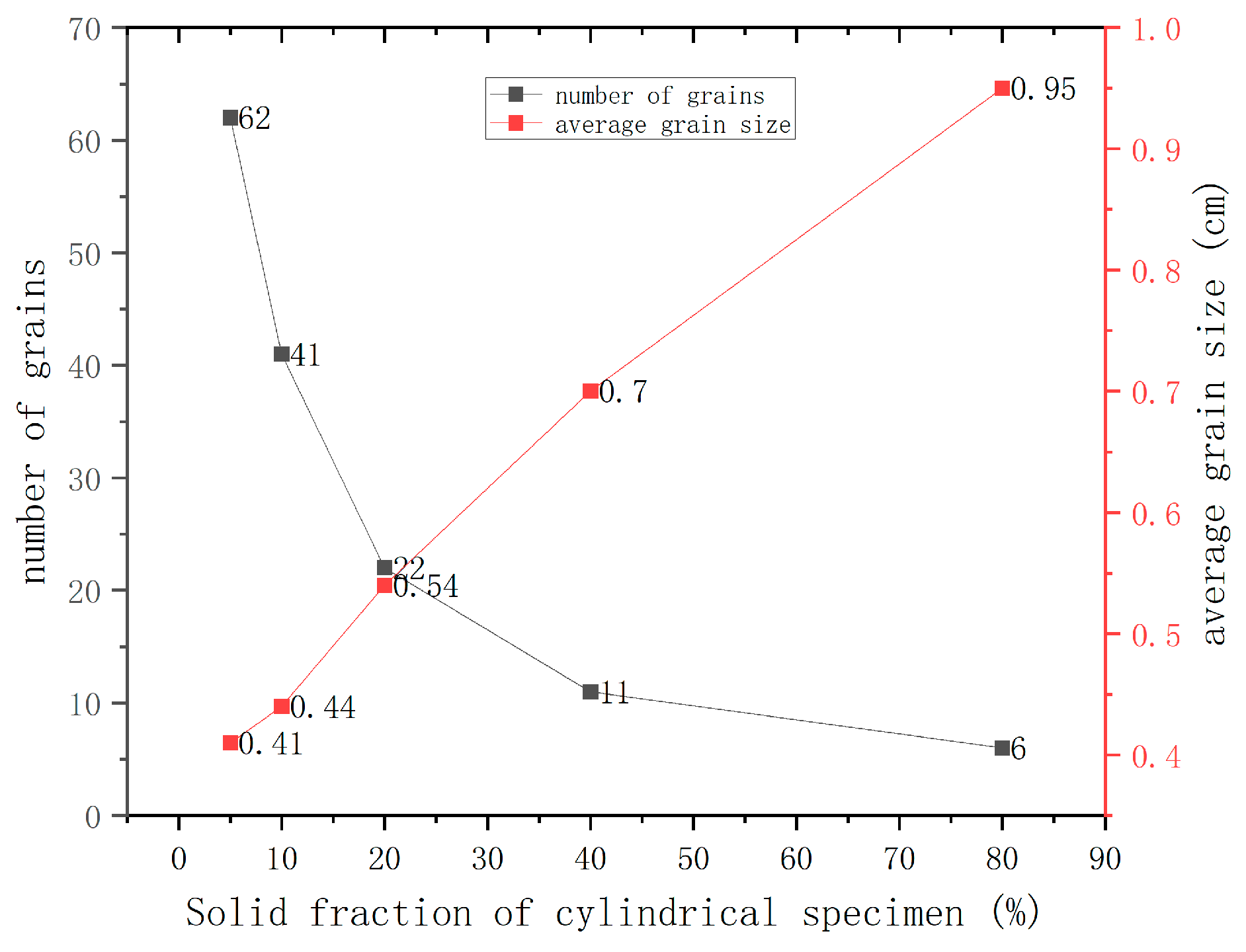
3.3. Influence of Drawing Speed on Grain Formation
3.4. Analysis of Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, R. Progress and challenges of titanium and aluminum intermetallics. J. Metals 2015, 51, 129–147. [Google Scholar]
- Bewlay, B.P.; Nag, S.; Suzuki, A.; Weimer, M.J. TiAl alloys in commercial aircraft engines. Mater. High Temp. 2016, 33, 549–559. [Google Scholar]
- Zhang, L.Q.; Ge, G.W.; Lin, J.P. Progress in hot working of TiAl alloys. Precis. Forg. 2022, 14, 1–9. [Google Scholar]
- Zhong, H.; Li, S.; Kou, H.; Li, J. The solidification path related columnar-to-equiaxed transition in Ti–Al alloys. Intermetallics 2015, 59, 81–86. [Google Scholar]
- Hunt, J.D. Steady state columnar and equiaxed growth of dendrites and eutectic. Mater. Sci. Eng. 1984, 65, 75–83. [Google Scholar]
- Wang, K.F.; Guo, J.J.; Mi, G.F.; Li, C.Y.; Fu, H.Z. Numerical simulation of columnar to equiaxed transition for directionally solidified Ti-44Al alloy. Acta Metall. Sin. (Engl. Lett.) 2008, 21, 146–156. [Google Scholar]
- Lapin, J.; Gabalcová, Z. Solidification behaviour of TiAl-based alloys studied by directional solidification technique. Intermetallics 2011, 19, 797–804. [Google Scholar]
- Wang, Q.; Ding, H.; Zhang, H.; Liu, S.; Chen, R.; Guo, J.; Fu, H. Growth rates dependence of macro/microstructures and mechanical properties of Ti-47Al-2Nb-2Cr-0.2 Er alloy directionally solidified by cold crucible. Mater. Des. 2017, 125, 146–157. [Google Scholar] [CrossRef]
- Lenart, R.; Eshraghi, M. Modeling columnar to equiaxed transition in directional solidification of Inconel 718 alloy. Comput. Mater. Sci. 2020, 172, 109374. [Google Scholar]
- Xu, X.; Ding, H.; Huang, H.; Liang, H.; Chen, R.; Guo, J.; Fu, H. Microstructure formation and columnar to equiaxed transition during cold crucible directional solidification of a high-Nb TiAl alloy. J. Mater. Res. Technol. 2021, 11, 2221–2234. [Google Scholar]
- Qu, L.; Wang, Y.; Ding, H.; Chen, R.; Guo, J.; Li, W. Equiaxed to Columnar Transition of Ti46Al8Nb0. 5B Intermetallics during Directional Solidification. Mater. Trans. 2024, 65, 616–620. [Google Scholar]
- Wang, Y.; Cui, C.J.; Zhang, K.; Deng, L.; Liu, W.; Liu, Y.; Zhao, Y.N.; Wu, C.Y. Research progress on directional solidification of intermetallic compounds. Mater. Guide 2022, 36, 135–142. [Google Scholar]
- Zhou, Y.H.; Hu, Z.Q.; Jie, W.Q. Solidification Technology; Mechanical Industry Press: Beijing, China, 1998. [Google Scholar]
- Xiong, W. Numerical Simulation of Directional Solidification Deformation of Nickel-Based Single Crystal Superalloys and Experimental Study of Recrystallization. Ph.D. Thesis, Central South University, Changsha, China, 2022. [Google Scholar]
- Ren, N.; Yang, L.W.; Li, J.; Zeng, L.; Xia, M.; Li, J. Research progress on numerical simulation of directional solidification of high-temperature alloys. Spec. Cast. Nonferrous Alloys 2023, 43, 1336–1350. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Huang, Q.M.; Lin, R.C. Numerical simulation of directional solidification process of single crystal superalloy blades. Spec. Cast. Nonferrous Alloys 2021, 41, 1361–1365. [Google Scholar] [CrossRef]
- Zhang, H.H.; Zhang, H.; Zhang, L.; Liu, Y. Influence of drawing speed on directional solidification process of single crystal blades. Foundry 2023, 72, 130–134. [Google Scholar]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta Metall. 1986, 34, 823–830. [Google Scholar]
- Yan, X.; Xu, Q.; Tian, G.; Liu, Q.; Hou, J.; Liu, B. Multi-scale modeling of liquid-metal cooling directional solidification and solidification behavior of nickel-based superalloy casting. J. Mater. Sci. Technol. 2021, 67, 36. [Google Scholar]
- Thevoz, P.; Desbiolles, J.L.; Rappaz, M. Modeling of equiaxed microstructure formation in casting. Metall. Trans. A 1989, 20, 311–322. [Google Scholar]
- Liu, Z.; Sun, H.; Xu, F.; Ma, D. Parameters determination of grain microstructure prediction for a single crystal casting simulation and its experimental validation. Int. J. Met. 2018, 12, 861–869. [Google Scholar]
- Quested, P.N.; McLean, M. Solidification morphologies in directionally solidified superalloys. Mater. Sci. Eng. 1984, 65, 171–180. [Google Scholar]
- Mullins, W.W.; Sekerka, R.F. Stability of a planar interface during solidification of a dilute binary alloy. J. Appl. Phys. 1964, 35, 444–451. [Google Scholar]
- Plevachuk, Y.; Sklyarchuk, V.; Eckert, S.; Gerbeth, G.; Novakovic, R. Thermophysical properties of the liquid Ga–In–Sn eutectic alloy. J. Chem. Eng. Data 2014, 59, 757–763. [Google Scholar]
- Hellawell, A.; Liu, S.; Lu, S.Z. Dendrite fragmentation and the effects of fluid flow in castings. Jom 1997, 49, 18–20. [Google Scholar]
- Hutt, J.; StJohn, D. The origins of the equiaxed zone—Review of theoretical and experimental work. Int. J. Cast Met. Res. 1998, 11, 13–22. [Google Scholar]
- Mullis, A.M.; Walker, D.J.; Battersby, S.E.; Cochrane, R.F. Deformation of dendrites by fluid flow during rapid solidification. Mater. Sci. Eng. A 2001, 304, 245–249. [Google Scholar]
- Neumann-Heyme, H.; Eckert, K.; Beckermann, C. Dendrite fragmentation in alloy solidification due to sidearm pinch-off. Phys. Rev. E 2015, 92, 060401. [Google Scholar]
- Ruvalcaba, D.; Mathiesen, R.; Eskin, D.; Arnberg, L.; Katgerman, L. In situ observations of dendritic fragmentation due to local solute-enrichment during directional solidification of an aluminum alloy. Acta Mater. 2007, 55, 4287–4292. [Google Scholar]





| Ti | Al | Cr | Nb |
|---|---|---|---|
| 48 | 48 | 2 | 2 |
| Drawing Rate (mm/min) | Number of Grains | Average Grain Size (mm) | Max Surface of Grain (cm2) |
|---|---|---|---|
| 0.5 | 56 | 16 | 24 |
| 1 | 58 | 15.9 | 31.6 |
| 2 | 70 | 11.8 | 27.9 |
| 3 | 142 | 10 | 17.8 |
| 4 | 187 | 7 | 16.8 |
| 8 | 262 | 5 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Huang, H.; Zong, X.; Wang, K.; Liu, H.; Liu, X.; Ding, X. Simulation Study on Directional Solidification of Titanium–Aluminum Alloy Based on Liquid Metal Cooling Method. Metals 2025, 15, 366. https://doi.org/10.3390/met15040366
Li F, Huang H, Zong X, Wang K, Liu H, Liu X, Ding X. Simulation Study on Directional Solidification of Titanium–Aluminum Alloy Based on Liquid Metal Cooling Method. Metals. 2025; 15(4):366. https://doi.org/10.3390/met15040366
Chicago/Turabian StyleLi, Feng, Hong Huang, Xiao Zong, Kehan Wang, Han Liu, Xuejun Liu, and Xianfei Ding. 2025. "Simulation Study on Directional Solidification of Titanium–Aluminum Alloy Based on Liquid Metal Cooling Method" Metals 15, no. 4: 366. https://doi.org/10.3390/met15040366
APA StyleLi, F., Huang, H., Zong, X., Wang, K., Liu, H., Liu, X., & Ding, X. (2025). Simulation Study on Directional Solidification of Titanium–Aluminum Alloy Based on Liquid Metal Cooling Method. Metals, 15(4), 366. https://doi.org/10.3390/met15040366





