Two-Fold Enhancement of Curie Temperature in Monolayer CrI3 by High Pressure
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.S.; Zhou, J.; Li, H.; Shen, L.; Feng, Y.P. Recent progress and challenges in magnetic tunnel junctions with 2D materials for spintronic applications. Appl. Phys. Rev. 2021, 8, 021308. [Google Scholar] [CrossRef]
- Ahn, Y.J.; Guo, X.Y.; Son, S.H.; Sun, Z.L.; Zhao, L.Y. Progress and prospects in two-dimensional magnetism of van der Waals materials. Prog. Quantum. Electron. 2024, 93, 100498. [Google Scholar] [CrossRef]
- Qu, Y.Q.; Liao, Y.; He, J.J.; Chen, Y.; Yao, G. High-Temperature Intrinsic Two-Dimensional-XY Ferromagnetism and Strong Magnetoelastic Coupling in Tetragonal Monolayer MnGe. J. Phys. Chem. C 2024, 128, 4631–4638. [Google Scholar] [CrossRef]
- Papavasileiou, A.V.; Menelaou, M.; Sarkar, K.J.; Sofer, Z.; Polavarapu, L.; Mourdikoudis, S. Ferromagnetic Elements in Two-Dimensional Materials: 2D Magnets and Beyond. Adv. Funct. Mater. 2024, 34, 2309046. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Xiang, G. Recent advances in two-dimensional intrinsic ferromagnetic materials Fe3X (X = Ge and Ga) Te2 and their heterostructures for spintronics. Nanoscale 2024, 16, 527–554. [Google Scholar] [CrossRef]
- Gao, H.G.; Qian, Y.; Ye, S.; Kong, K.P. First-principles study on the electric control of ferromagnetic behaviour of two-dimensional BaTiO3 (0 0 1) ultrathin film doped with Cr. Appl. Surf. Sci. 2022, 601, 154240. [Google Scholar] [CrossRef]
- Rodriguez-Vega, M.; Lin, Z.X.; Leonardo, A.; Ernst, A.; Chaudhary, G.; Vergniory, M.G.; Fiete, G.A. Phonon-mediated dimensional crossover in bilayer CrI3. Phys. Rev. B 2020, 102, 081117. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, R.; Yang, K.; Dou, J.R.; Gou, J.Z.; Zhou, G.W.; Xu, X.H. Anomalous magnetic property and broadband photodetection in ultrathin non-layered manganese selenide semiconductor. Nano Res. 2024, 17, 8578–8584. [Google Scholar] [CrossRef]
- Chen, J.M.; Cheng, Z.X.; Chen, J.H.; Li, M.L.; Jia, X.H.; Ran, Y.Q.; Zhang, Y.; Li, Y.P.; Yu, T.J.; Dai, L. Spin-Enhanced Self-Powered Light Helicity Detecting Based on Vertical WSe2-CrI3 p-n Heterojunction. ACS Nano 2024, 18, 26261–26270. [Google Scholar] [CrossRef]
- Siudzinska, A.; Gorantla, S.M.; Serafinczuk, J.; Kudrawiec, R.; Hommel, D.; Bachmatiuk, A. Electron Beam-Induced Reduction of Cuprite. Metals 2022, 12, 2151. [Google Scholar] [CrossRef]
- Gong, C.; Li, L.; Li, Z.L.; Ji, H.W.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.Z.; Wang, Y.; et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.J.; Yu, Y.J.; Song, Y.C.; Zhang, J.Z.; Wang, N.Z.; Sun, Z.Y.; Yi, Y.F.; Wu, Y.Z.; Wu, S.W.; Zhu, J.Y.; et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 2018, 563, 94–99. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.J.; Sun, Z.Y.; Wang, Z.J.; Gu, L.H.; Xu, X.D.; Wu, S.W.; Gao, C.L. Direct observation of van der Waals stacking-dependent interlayer magnetism. Science 2019, 366, 983–987. [Google Scholar] [CrossRef]
- Hu, J.K.; Fan, Z.Q.; Yang, J.B. Modulating the electronic and optical properties of CrI3/In2Se3 van der Waals heterostructures by external fields. Mater. Today Commun. 2024, 39, 108891. [Google Scholar] [CrossRef]
- Hu, X.H.; Zhao, Y.H.; Shen, X.D.; Krasheninnikov, A.V.; Chen, Z.F.; Sun, L.T. Enhanced Ferromagnetism and Tunable Magnetism in Fe3GeTe2 Monolayer by Strain Engineering. ACS Appl. Mater. Interfaces 2020, 12, 26367–26373. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, C.; Yang, M.Y.; Hu, T.; Meng, Y.; Lei, J.; Zhang, M.J. Magnetism and electronic structures of bismuth (stannum) films at the CrI3 (CrBr3) interface. Phys. Chem. Chem. Phys. 2021, 23, 4255–4261. [Google Scholar] [CrossRef]
- Liu, L.; Yang, K.; Wang, G.Y.; Wu, H. Two-dimensional ferromagnetic semiconductor VBr3 with tunable anisotropy. J. Mater. Chem. C 2020, 8, 14782–14788. [Google Scholar] [CrossRef]
- Tian, S.J.; Zhang, J.F.; Li, C.H.; Ying, T.P.; Li, S.Y.; Zhang, X.; Liu, K.; Lei, H.C. Ferromagnetic van der Waals Crystal VI3. J. Am. Chem. Soc. 2019, 141, 5326–5333. [Google Scholar] [CrossRef]
- Sun, J.X.; Zhong, X.; Cui, W.W.; Shi, J.M.; Hao, J.; Xu, M.L.; Li, Y.W. The intrinsic magnetism, quantum anomalous Hall effect and Curie temperature in 2D transition metal trihalides. Phys. Chem. Chem. Phys. 2020, 22, 2429–2436. [Google Scholar] [CrossRef]
- Kim, K.; Lee, J.U.; Cheong, H. Raman spectroscopy of two-dimensional magnetic van der Waals materials. Nanotechnology 2019, 30, 452001. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Li, J.; Herng, T.S.; Wang, Z.S.; Zhao, X.X.; Chi, X.; Fu, W.; Abdelwahab, I.; Zhou, J.; Dan, J.D.; et al. Chemically Exfoliated VSe2 Monolayers with Room-Temperature Ferromagnetism. Adv. Mater. 2019, 31, 1903779. [Google Scholar] [CrossRef]
- Torelli, D.; Thygesen, K.S.; Olsen, T. High throughput computational screening for 2D ferromagnetic materials: The critical role of anisotropy and local correlations. 2D Mater. 2019, 6, 045018. [Google Scholar] [CrossRef]
- McGuire, M.A. Crystal and Magnetic Structures in Layered, Transition Metal Dihalides and Trihalides. Crystals 2017, 7, 121. [Google Scholar] [CrossRef]
- Lu, S.H.; Zhou, Q.H.; Guo, Y.L.; Zhang, Y.H.; Wu, Y.L.; Wang, J.L. Coupling a Crystal Graph Multilayer Descriptor to Active Learning for Rapid Discovery of 2D Ferromagnetic Semiconductors/Half-Metals/Metals. Adv. Mater. 2020, 32, 2002658. [Google Scholar] [CrossRef]
- Mounet, N.; Gibertini, M.; Schwaller, P.; Campi, D.; Merkys, A.; Marrazzo, A.; Sohier, T.; Castelli, I.E.; Cepellotti, A.; Pizzi, G.; et al. Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds. Nat. Nanotech. 2018, 13, 246–252. [Google Scholar] [CrossRef]
- Liu, H.; Sun, J.T.; Liu, M.; Meng, S. Screening Magnetic Two-Dimensional Atomic Crystals with Nontrivial Electronic Topology. J. Phys. Chem. Lett. 2018, 9, 6709–6715. [Google Scholar] [CrossRef]
- Zhu, Y.; Kong, X.H.; Rhone, T.D.; Guo, H. Systematic search for two-dimensional ferromagnetic materials. Phys. Rev. Mater. 2018, 2, 081001. [Google Scholar] [CrossRef]
- Webster, L.; Liang, L.; Yan, J.A. Distinct spin-lattice and spin-phonon interactions in monolayer magnetic CrI3. Phys. Chem. Chem. Phys. 2018, 20, 23546–23555. [Google Scholar] [CrossRef]
- Jiang, P.H.; Li, L.; Liao, Z.L.; Zhao, Y.X.; Zhong, Z.C. Spin Direction-Controlled Electronic Band Structure in Two-Dimensional Ferromagnetic CrI3. Nano Lett. 2018, 18, 3844–3849. [Google Scholar] [CrossRef]
- Ye, H.S.; Wang, X.; Bai, D.M.; Zhang, J.T.; Wu, X.S.; Zhang, G.P.; Wang, J.L. Significant enhancement of magnetic anisotropy and conductivity in GaN/CrI3 van der Waals heterostructures via electrostatic doping. Phys. Rev. B 2021, 104, 075433. [Google Scholar] [CrossRef]
- Han, J.N.; Ding, Z.X.; Li, Z.H.; Cao, S.G.; Zhang, Z.H.; Deng, X.Q. CrI3/Arsenene vdW heterstructure: Outstanding physical properties and substantially enhanced magnetic stability. Appl. Surf. Sci. 2024, 669, 160443. [Google Scholar] [CrossRef]
- Zheng, Z.J.; Ren, K.; Huang, Z.M.; Zhu, Z.Y.; Wang, K.; Shen, Z.L.; Yu, J. Remarkably improved Curie temperature for two-dimensional CrI3 by gas molecular adsorption: A DFT study. Semicond. Sci. Technol. 2021, 36, 075015. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, L.; Du, A.J. Tunable magnetic anisotropy in 2D magnets via molecular adsorption. J. Mater. Chem. C 2020, 8, 14948–14953. [Google Scholar] [CrossRef]
- Mo, Y.Y.; Huang, X.K.; Xu, J.L.; Jiang, X.A.; Chen, C.; Jiang, X.P.; Liu, J.M. Interfacial engineering of orbital orientation for perpendicular magnetic anisotropy in Co-implanted CrI3 monolayer. J. Appl. Phys. 2024, 136, 084305. [Google Scholar] [CrossRef]
- Yang, Q.; Hu, X.H.; Shen, X.D.; Krasheninnikow, A.V.; Chen, Z.F.; Sun, L.T. Enhancing Ferromagnetism and Tuning Electronic Properties of CrI3 Monolayers by Adsorption of Transition-Metal Atoms. ACS Appl. Mater. Interfaces 2021, 13, 21593–21601. [Google Scholar] [CrossRef]
- Chen, G.X.; Li, B.B.; Li, X.F.; Wang, D.D.; Liu, S.; Zhang, J.M. Electronic structure and magnetic properties of CrI3 monolayer doped by rare earth metal atoms. J. Phys. Chem. Solids 2024, 187, 111838. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Lin, L.F.; Zhou, Q.H.; Li, Y.H.; Yuan, S.J.; Chen, Q.; Dong, S.; Wang, J.L. Surface Vacancy-Induced Switchable Electric Polarization and Enhanced Ferromagnetism in Monolayer Metal Trihalides. Nano Lett. 2018, 18, 2943–2949. [Google Scholar] [CrossRef]
- Bozorth, R.M.; Ferromagnetism, D. Ferromagnetism (Chapter XII); Van Nostrand Company. Inc.: New York, NY, USA, 1951; p. 867. [Google Scholar]
- Anderson, P.W. Antiferromagnetism. Theory of Superexchange Interaction. Phys. Rev. 1950, 79, 350. [Google Scholar] [CrossRef]
- Su, W.X.; Zhang, Z.M.; Cao, Q.Q.; Wang, D.H.; Lu, H.M.; Mi, W.B.; Du, Y.W. Enhancing the Curie temperature of two-dimensional monolayer CrI3 by introducing I-vacancies and interstitial H-atoms. Phys. Chem. Chem. Phys. 2021, 23, 22103–22109. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Liechtenstein, A.I.; Anisimov, V.I.; Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, 5467. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.Y.; Zhao, B.; Zhou, T.; Xue, Y.; Ma, C.L.; Yang, Z.Q. Strong magnetization and Chern insulators in compressed graphene/CrI3 van der Waals heterostructures. Phys. Rev. B 2018, 97, 085401. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Nayak, A.P.; Pandey, T.; Voiry, D.; Liu, J.; Moran, S.T.; Sharma, A.; Tan, C.; Chen, C.H.; Li, L.J.; Chhowalla, M.; et al. Pressure-Dependent Optical and Vibrational Properties of Monolayer Molybdenum Disulfide. Nano Lett. 2015, 15, 346–353. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Liang, L.; Zhang, X. Available online: https://github.com/golddoushi/mcsolver (accessed on 5 June 2024).
- Dillon, J.F.; Olson, C.E. Magnetization, Resonance, and Optical Properties of the Ferromagnet CrI3. J. Appl. Phys. 1965, 36, 1259–1260. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Webster, L.; Yan, J.A. Strain-tunable magnetic anisotropy in monolayer CrCl3, CrBr3, and CrI3. Phys. Rev. B 2018, 98, 144411. [Google Scholar] [CrossRef]
- Zhang, W.B.; Qu, Q.; Zhu, P.; Lam, C.H. Robust intrinsic ferromagnetism and half semiconductivity in stable two-dimensional single-layer chromium trihalides. J. Mater. Chem. C 2015, 3, 12457–12468. [Google Scholar] [CrossRef]
- Liu, L.; Lin, Z.Z.; Hu, J.F.; Zhang, X. Full quantum search for high TC two-dimensional van der Waals ferromagnetic semiconductors. Nanoscale 2021, 13, 8137–8145. [Google Scholar] [CrossRef]
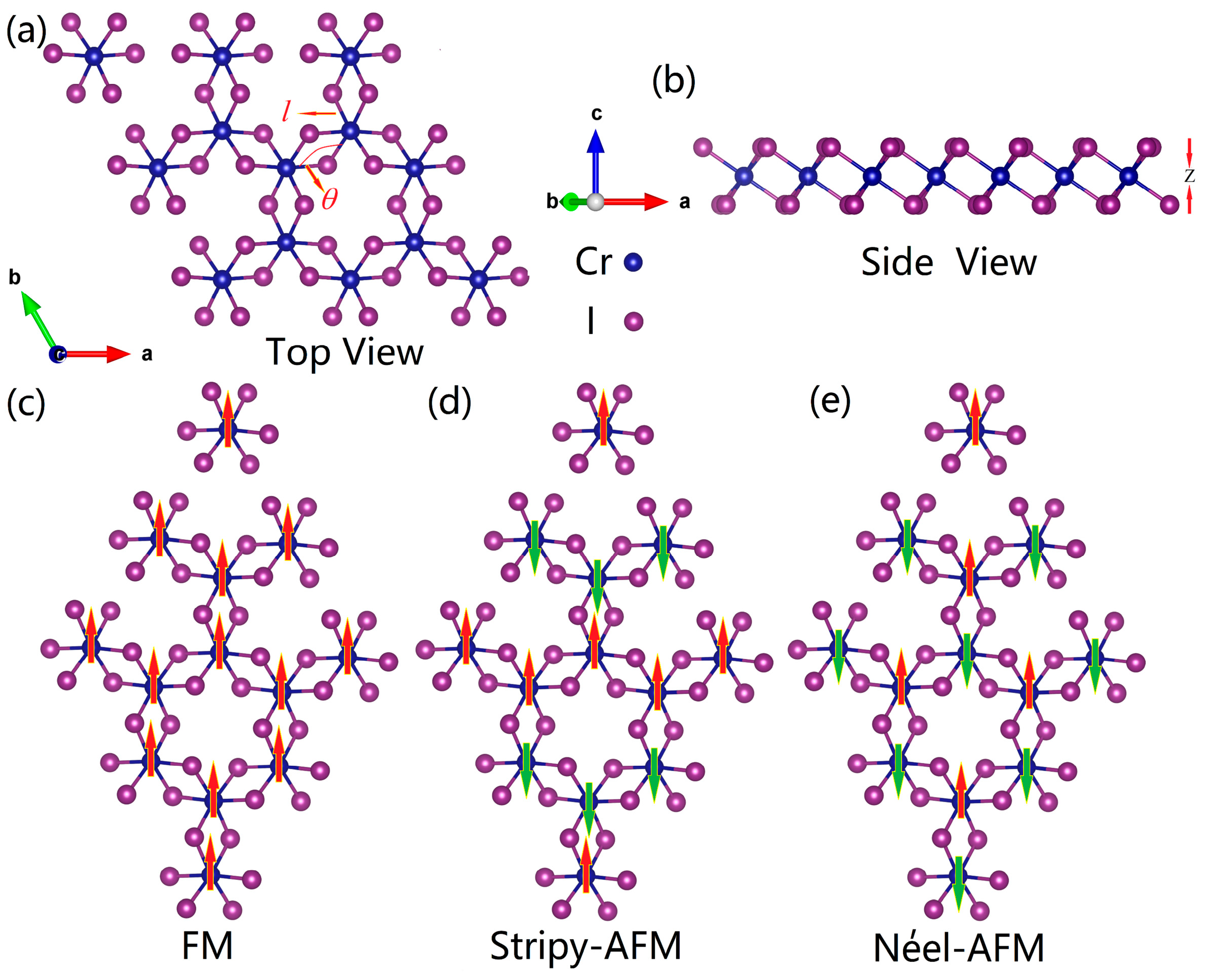
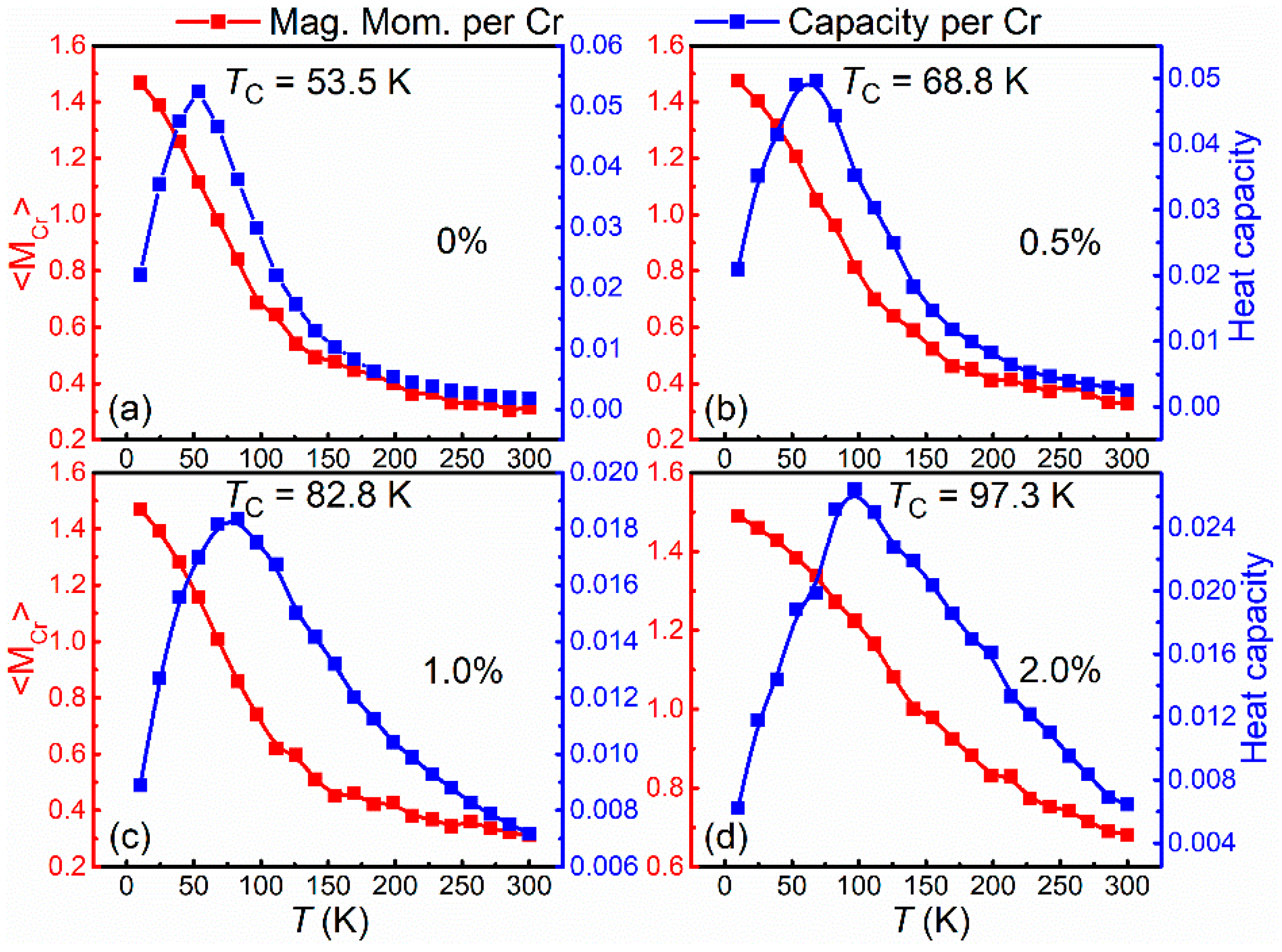

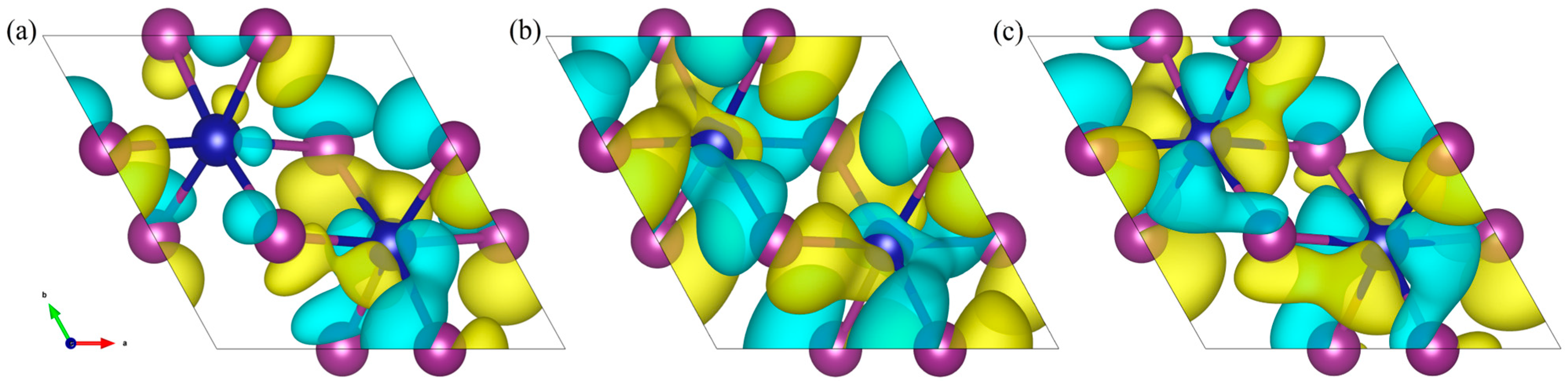
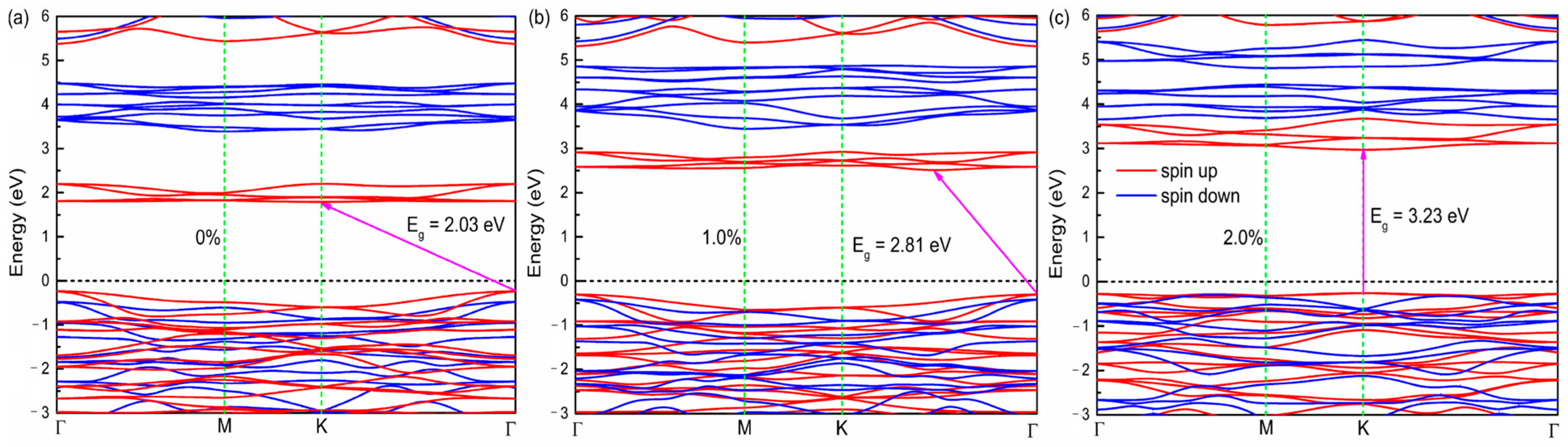
| ɛ | l (Å) | θ (deg) | J1 (meV) | J2 (meV) | TC (K) | EMA | MAE (μeV/Cr) |
|---|---|---|---|---|---|---|---|
| 0% | 2.75 | 95.2 | −1.89 | −0.31 | 53.5 | z | 778 |
| 0.5% | 2.73 | 96.0 | −2.16 | −0.27 | 68.8 | z | 437 |
| 1.0% | 2.70 | 97.0 | −2.47 | −0.23 | 82.8 | z | 124 |
| 1.2% | 2.69 | 97.3 | −2.60 | −0.19 | 83.1 | x | −9.2 |
| 1.5% | 2.68 | 97.8 | −2.85 | −0.16 | 90.6 | x | −234 |
| 2.0% | 2.66 | 98.7 | −3.23 | −0.12 | 97.3 | x | −592 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, W.; Wang, D.; Wei, D.; Dai, Z. Two-Fold Enhancement of Curie Temperature in Monolayer CrI3 by High Pressure. Metals 2025, 15, 398. https://doi.org/10.3390/met15040398
Su W, Wang D, Wei D, Dai Z. Two-Fold Enhancement of Curie Temperature in Monolayer CrI3 by High Pressure. Metals. 2025; 15(4):398. https://doi.org/10.3390/met15040398
Chicago/Turabian StyleSu, Wenxia, Dunhui Wang, Dong Wei, and Zhenhong Dai. 2025. "Two-Fold Enhancement of Curie Temperature in Monolayer CrI3 by High Pressure" Metals 15, no. 4: 398. https://doi.org/10.3390/met15040398
APA StyleSu, W., Wang, D., Wei, D., & Dai, Z. (2025). Two-Fold Enhancement of Curie Temperature in Monolayer CrI3 by High Pressure. Metals, 15(4), 398. https://doi.org/10.3390/met15040398






