Influence of Hot Deformation Temperature on Grain Size and γ′ Phase in U720Li Alloy After Sub-Solvus Heat Treatment
Abstract
1. Introduction
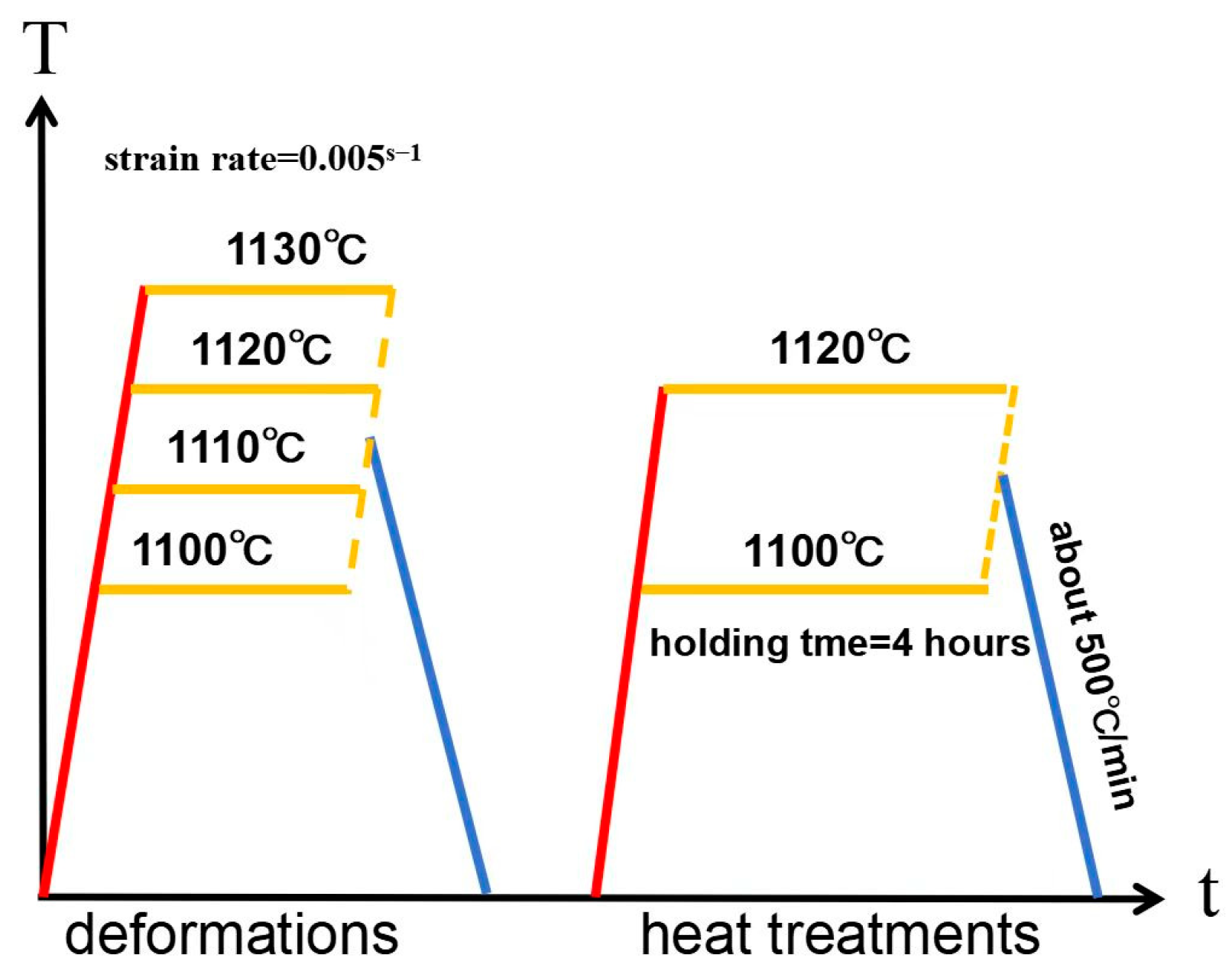
2. Materials and Experiment
3. Results and Discussion
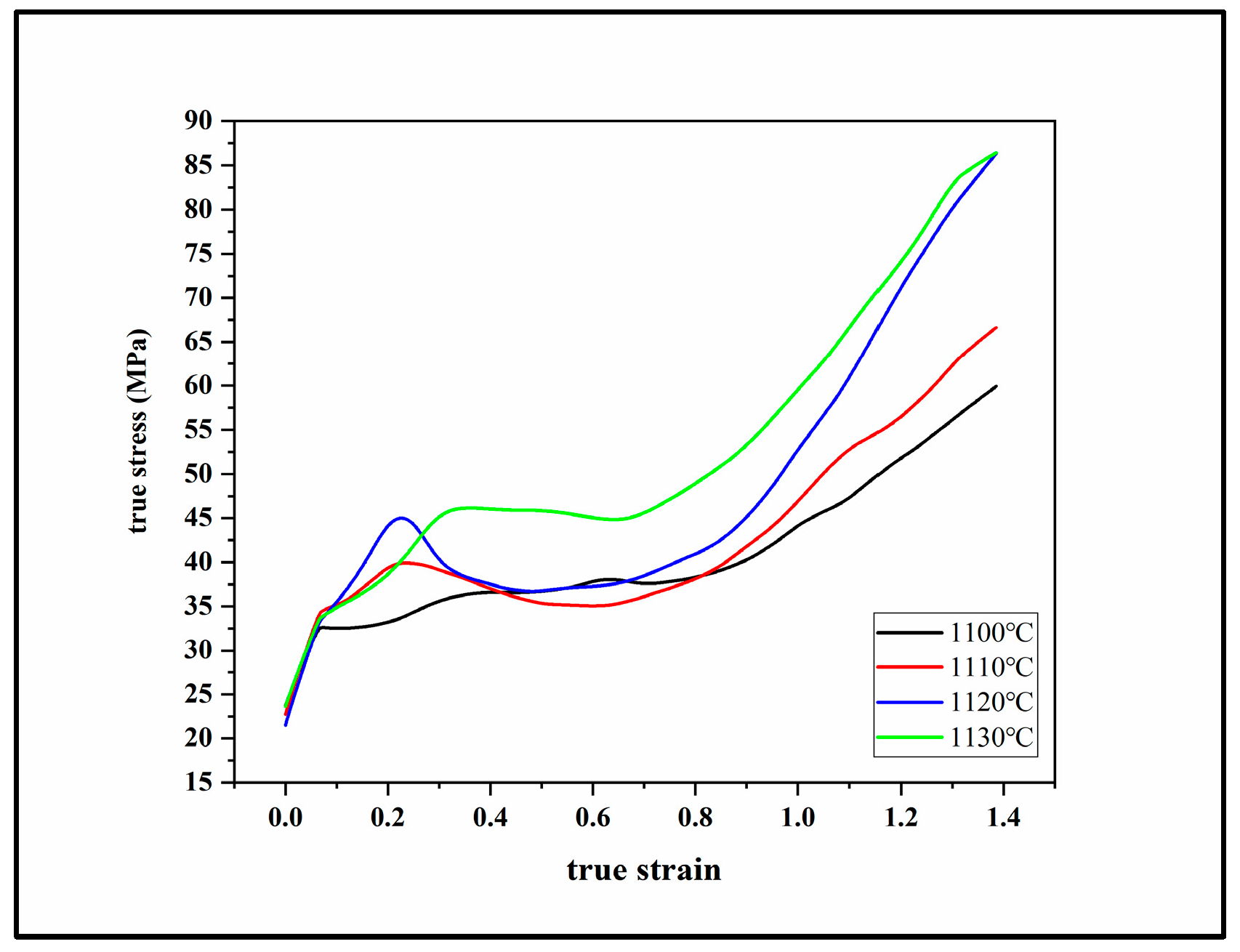
3.1. Hot Deformation Characteristics
3.2. Adiabatic Heating
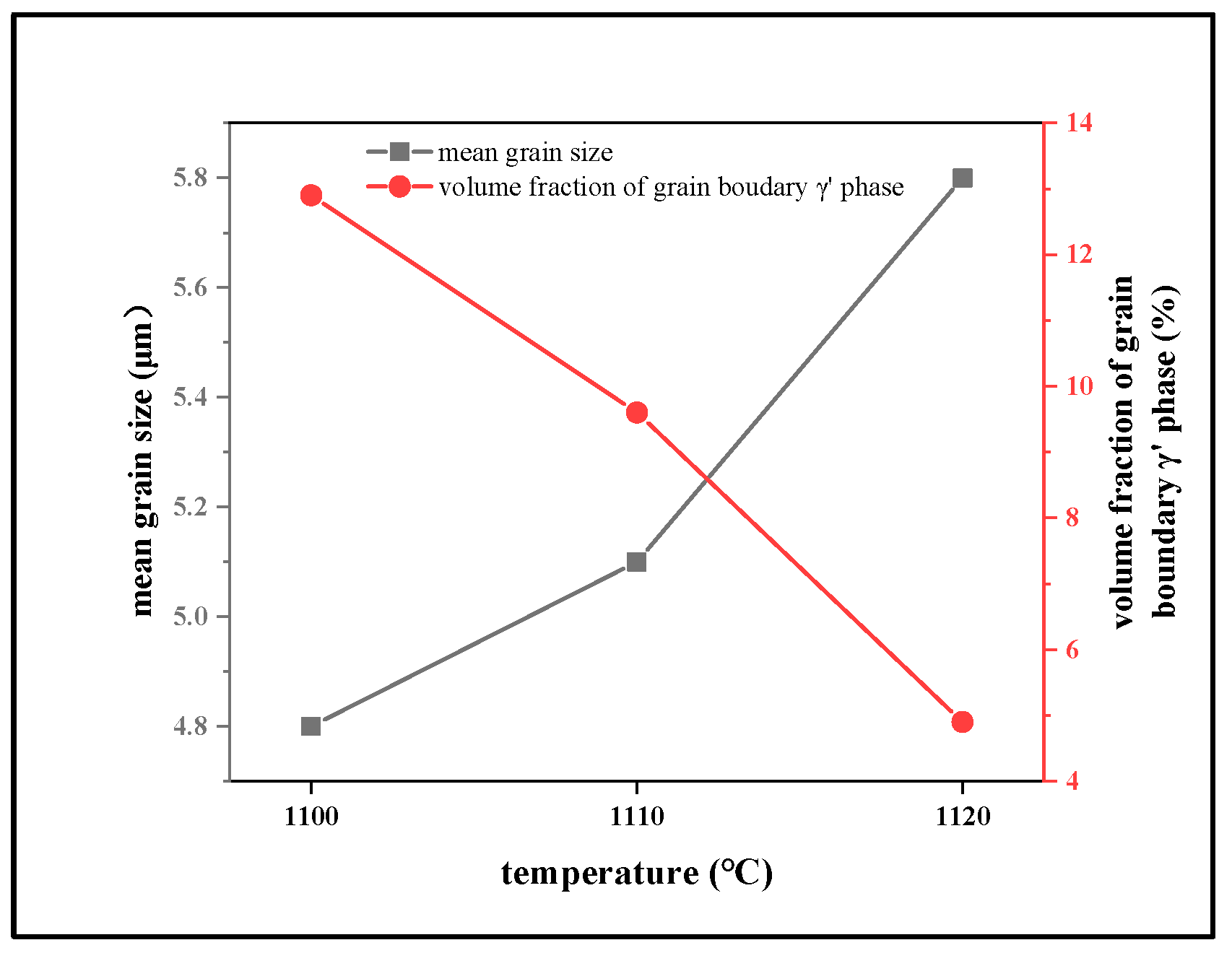
3.3. Microstructure Evolution After Deformation
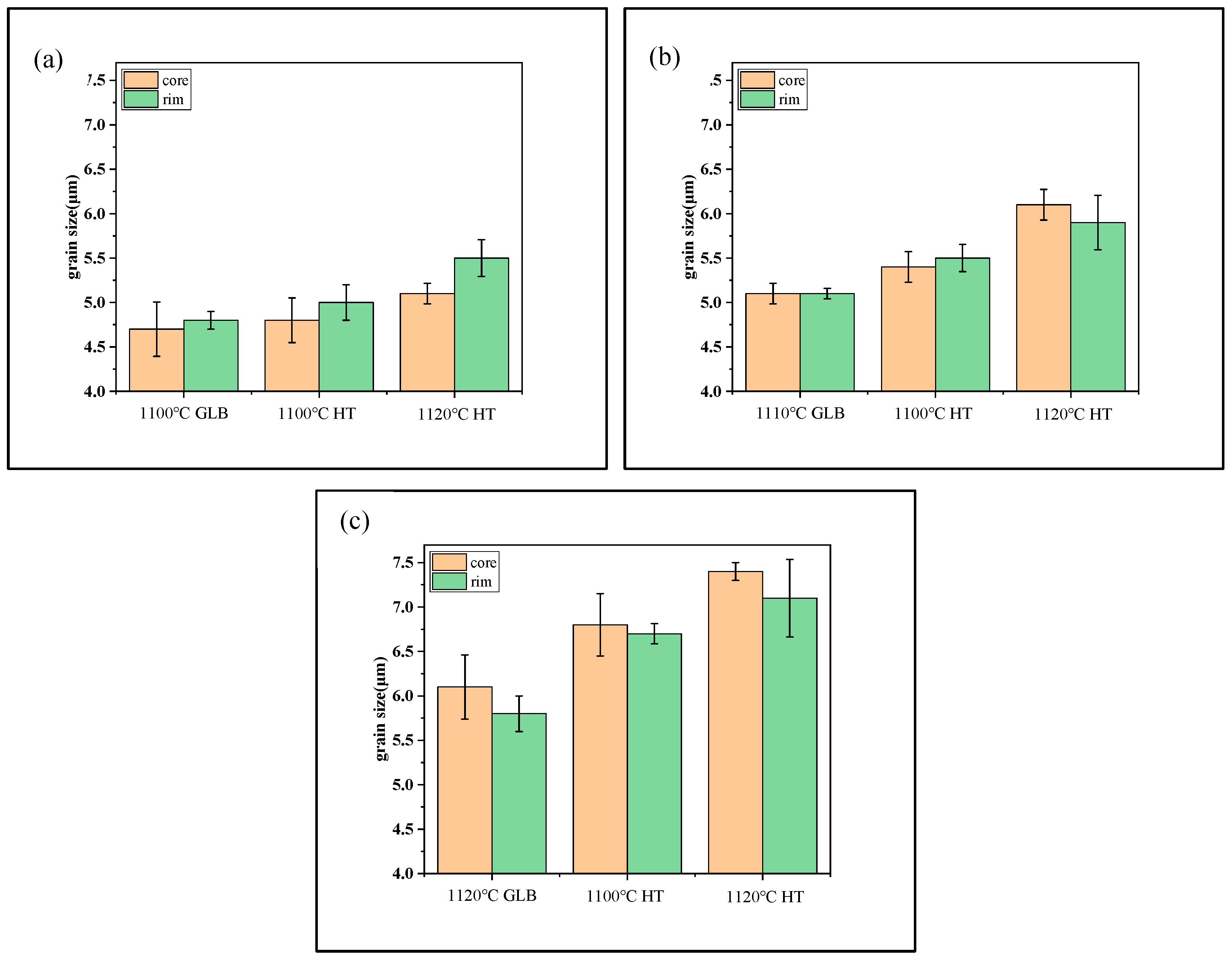
3.4. Microstructure Evolution After Heat Treatment
3.5. Effect on Mechanical Performance
4. Conclusions
- Cylindrical U720Li alloy specimens (Φ 8 × 12.8 mm), fabricated via hot isostatic pressing (HIP) and hot extrusion (HEX), were subjected to hot compression tests performed at 1100–1130 °C with a strain rate of 0.005 s−1, achieving a 75% height reduction. At a true strain of ~0.7, the alloy exhibited continuous strain hardening behavior, characterized by a steady increase in deformation resistance. Numerical simulations indicated a temperature rise of ~10 °C in the specimen core during compression.
- Increasing the deformation temperature from 1100 °C to 1120 °C resulted in larger mean grain sizes and a reduction in the γ′ phase volume fraction at grain boundaries from ~13% to ~5%. This diminished γ′ phase content weakened the pinning effect on grain boundaries. Notably, while dynamic recrystallization (DRX) fractions were comparable between samples deformed at 1100 °C and 1130 °C, the latter displayed pronounced grain growth and marginally higher grain boundary energy. Additionally, the sample deformed at 1100 °C retained higher stored deformation energy, enhancing its propensity for static recrystallization. These combined effects led to coarser grains in samples deformed at higher temperatures under identical solution heat treatment conditions.
- Hot-compressed samples were solution-treated at 1100 °C and 1120 °C for 4 h to analyze temperature-dependent microstructural changes. When the heat treatment temperature was below the deformation temperature (e.g., 1100 °C), isothermal holding induced classical Ostwald ripening, where smaller γ′ particles dissolved to coarsen larger ones. Subsequent rapid cooling produced a microstructure with a high density of medium- and small-sized γ′ precipitates. Conversely, when the heat treatment temperature exceeded the deformation temperature (e.g., 1120 °C), substantial dissolution of the γ′ phase occurred during isothermal holding. This yielded a microstructure dominated by finely dispersed small γ′ precipitates after rapid cooling, with a marked reduction or absence of medium-sized γ′ phases. These contrasting outcomes underscore the critical influence of the heat treatment temperature relative to the prior deformation temperature on γ′ phase evolution and final microstructural features.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pollock, T.M. Nickel-Based Superalloys for Advanced Turbine Engines: Chemistry, Microstructure, and Properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Rui, Z.; Peng, L.; Chuangyong, C.; Jinlong, Q.; Beijiang, Z.; Jinhui, D.; Yizhou, Z.; Xiaofeng, S. Present Research Situation and Prospect of Hot Working of Cast & Wrought Superalloys for Aero-Engine Turbine Disk in China. Acta Metall. Sin. 2021, 57, 1215–1228. [Google Scholar]
- Gudivada, G.; Pandey, A.K. Recent developments in nickel-based superalloys for gas turbine applications: Review. J. Alloys Compd. 2023, 963, 171128. [Google Scholar]
- Semiatin, S.L.; Levkulich, N.C.; Larsen, R.; Tiley, J.S.; Wertz, K.N.; Zhang, F.; Smith, T.M.; Zhang, R.Y.; Dong, H.B.; Gadaud, P.; et al. The Application of Differential Scanning Calorimetry to Investigate Precipitation Behavior in Nickel-Base Superalloys Under Continuous Cooling and Heating Conditions. Metall. Mater. Trans. A 2021, 52, 3706–3726. [Google Scholar]
- Feng, Q.; Wu, Y.; Li, J.; Cai, Y.; Zhang, Y.; Liu, J.; Liu, T. Effects of intermediate temperature on the grain boundary and γ′ precipitates of nickel-based powder superalloy under interrupted cooling. J. Alloys Compd. 2022, 922, 166310. [Google Scholar]
- Ye, X.; Yang, B.; Liu, J.; Li, Y. Correlation between Microstructure and Mechanical Properties of Heat-Treated Novel Powder Metallurgy Superalloy. Materials 2022, 15, 4524. [Google Scholar] [CrossRef]
- Kong, Y.S.; Cheepu, M.; Kim, D.G. Effects of Heat Treatment on the Mechanical Behavior of Udimet 720 Nickel-Based Superalloy. J. Mater. Eng. Perform. 2022, 31, 8327–8333. [Google Scholar] [CrossRef]
- Gabb, T.P.; Bonacuse, P.J.; Ghosn, L.J.; Sweeney, J.S.; Chatterjee, A.; Green, K.A. Assessments of Low Cycle Fatigue Behavior of Powder Metallurgy Alloy U720; NASA/TM-2000-209418; Glenn Research Center: Cleveland, OH, USA, 2000. [Google Scholar]
- Furrer, D.; Fecht, H. Ni-Based Superalloys for Turbine Discs. JOM 1999, 51, 14–17. [Google Scholar]
- Furrer, D.; Fecht, H. γ′ formation in superalloy U720Li. Scr. Mater. 1999, 40, 1215–1220. [Google Scholar] [CrossRef]
- Ortiz-de-Zarate, G.; Tiba, I.; Madariaga, A.; Linaza, A.; Garay, A.; Germain, G.; Arrazola, P.J. Udimet 720Li as a potential alternative for optimized aeroengine turbines: Thermophysical and thermomechanical characterization under wide-ranging testing conditions. Mater. Des. 2025, 252, 113700. [Google Scholar]
- Wei, Z.; Jinnan, L.; Ruifeng, D.; Zishuang, C.; Jian, L.; Xing, Z.; Qingzeng, W.; Jinlong, Q. Effect of heat treatment process parameters on the microstructure and properties of GH4720Li superalloy. Mater. Res. Express 2023, 10, 016514. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H.; Zhang, Y.; Zhang, H.; Yang, Q.; Ye, L. Investigation on Mechanical Properties of GH4720Li at High Strain Rates at Wider Temperature Range. Int. J. Photoenergy 2021, 2021, 8839411. [Google Scholar] [CrossRef]
- Rao, G.A.; Satyanarayana, D.V.V. Influence of HIP processing on microstructure and mechanical properties of superalloy Udimet 720LI. Mater. Sci. Technol. 2011, 27, 478–486. [Google Scholar]
- Jackson, M.P.; Reed, R.C. Heat treatment of UDIMET 720Li: The effect of microstructure on properties. Mater. Sci. Eng. A 1999, 259, 85–97. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Q.; Tang, Y.; Dan, W.; Ruyue, Y.; Zhihao, Y.; Yihong, H.; Yongming, Z.; Xuqing, W.; Wei, L. Microstructure and Property Stability of Powder Metallurgy Nickel-based U720Li Superalloy During Long-Term Aging. Rare Met. Mater. Eng. 2022, 51, 2356–2360. [Google Scholar]
- Liu, F.; Chen, J.; Dong, J.; Zhang, M.; Yao, Z. The hot deformation behaviors of coarse, fine and mixed grain for Udimet 720Li superalloy. Mater. Sci. Eng. A 2016, 651, 102–115. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Z.; Zhang, M. Hot Deformation Behavior of AA-FGH720Li Superalloy. Mater. Sci. Forum 2017, 898, 528–533. [Google Scholar] [CrossRef]
- Higashi, M.; Kanno, N. Effect of initial powder particles size on the hot workability of powder metallurgy Ni-based superalloys. Mater. Des. 2020, 194, 108926. [Google Scholar] [CrossRef]
- Wan, Z.; Hu, L.; Sun, Y.; Wang, T.; Li, Z. Microstructure evolution and dynamic softening mechanisms during high-temperature deformation of a precipitate hardening Ni-based superalloy. Vacuum 2018, 155, 585–593. [Google Scholar] [CrossRef]
- Monajati, H.; Jahazi, M.; Yue, S.; Taheri, A.K. Deformation characteristics of isothermally forged UDIMET720 Nickel-Base Superalloy. Metall. Mater. Trans. A 2005, 36, 895–905. [Google Scholar] [CrossRef]
- Stolz, D.S. Effect of a Supersolvus Heat Treatment on the Microstructure and Mechanical Properties of a Powder Metallurgy Processed Nickel-Base Superalloy. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2004. [Google Scholar]
- ASTM E112-13; Standard Test Methods for Determining Average Grain Size. ASTM International: West Conshohocken, PA, USA, 2021.
- ASTM E2627-13; Standard Practice for Determining Average Grain Size Using Electron Backscatter Diffraction (EBSD) in Fully Recrystallized Materials. ASTM International: West Conshohocken, PA, USA, 2019.
- Zang, X.; Zhao, G.; Wu, J.; Jiang, H.; Yao, X. Influence of Holding Time on Hot Deformation Behavior of Hard-Deformed Superalloy U 720Li. Rare Met. Mater. Eng. 2024, 53, 2446–2457. [Google Scholar]
- Ning, Y.; Yao, Z.; Fu, M.W.; Guo, H. Recrystallization of the hot isostatic pressed nickel-base superalloy FGH4096: I. Microstructure and mechanism. Mater. Sci. Eng. A 2011, 528, 8065–8070. [Google Scholar] [CrossRef]
- Ning, Y.; Fu, M.W.; Yao, W. Recrystallization of the hot isostatic pressed nickel-base superalloy FGH4096. II: Characterization and application. Mater. Sci. Eng. A 2012, 539, 101–106. [Google Scholar] [CrossRef]
- Yang, J.; Ma, X.; Guo, J.; Lu, Y.; Wang, S.; Dong, A. Thermal Deformation Behavior of Novel Ni-Based PM Superalloy Under Different Initial Conditions. Rare Met. Mater. Eng. 2022, 51, 651–660. [Google Scholar]
- Oh, S.I.; Semiatin, S.L.; Jonas, J.J. An analysis of the isothermal hot compression test. Metall. Trans. A 1992, 23, 963–975. [Google Scholar] [CrossRef]
- Guimaraes, A.A.; Jonas, J.J. Recrystallization and Aging Effects Associated with High Temperature Deformation of Waspaloy and Inconel 718. Metall. Trans. A 1981, 12, 1656–1666. [Google Scholar] [CrossRef]
- Sellars, C.M.; Whiteman, J.A. Recrystallization and grain growth in hot rolling. Met. Sci. 1979, 13, 187–194. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, C.; Cheng, J.; Guo, J. An Improved Grain Growth Model and Its Application in Gradient Heat Treatment of Aero-Engine Turbine Discs. Materials 2023, 16, 6584. [Google Scholar] [CrossRef]
- Yang, G.; Sun, X.; Yong, Q.; Li, Z.; Li, X. Austenite Grain Refinement and Isothermal Growth Behavior in a Low Carbon Vanadium Microalloyed Steel. J. Iron Steel Res. Int. 2014, 21, 757–764. [Google Scholar] [CrossRef]
- Zhu, Y.; Cao, Y.; He, Q.; Luo, R.; Zhang, J.; Di, H.; Huang, G.; Liu, Q.; Xiao, J. Machine learning neural-network identification for dynamic recrystallization grains during hot deformation of nickel-based superalloy. Mater. Charact. 2022, 191, 112108. [Google Scholar] [CrossRef]
- Jia, D.; Sun, W.; Xu, D.; Yu, L.; Xin, X.; Zhang, W.; Qi, F. Abnormal dynamic recrystallization behavior of a nickel based superalloy during hot deformation. J. Alloys Compd. 2019, 787, 196–205. [Google Scholar]
- Wagner, C. Theorie der Alterung von Niederschlaegen durch Umloesen (Oswald-Reifung). Berichte Der Bunsenges. Fuer Phys. Chem. 1961, 65, 7–8. [Google Scholar]
- Yao, X.; Ding, Q.; Wei, X.; Wang, J.; Zhang, Z.; Bei, H. The effects of key elements Re and Ru on the phase morphologies and microstructure in Ni-based single crystal superalloys. J. Alloys Compd. 2022, 926, 166835. [Google Scholar]
- Liu, Z.; Cheng, J.; Wang, C.; Guo, J. Quantitative Microstructure Prediction of Powder High-Temperature Alloy during Solution Heat treatment and its validation. Metals 2024, 14, 769. [Google Scholar] [CrossRef]
- Radis, R.; Schaffer, M.; Albu, M.; Gerald, K. Multimodal size distributions of γ′ precipitates during continuous cooling of UDIMET 720Li. Acta Mater. 2009, 57, 5739–5747. [Google Scholar]
- Masoumi, F.; Shahriari, D.; Jahazi, M.; Cormier, J.; Devaux, A. Kinetics and Mechanisms of γ′ Reprecipitation in a Ni-based Superalloy. Sci. Rep. 2016, 6, 28650. [Google Scholar]
- Papadaki, C.; Li, W.; Korsunsky, A. On the Dependence of γ′ Precipitate Size in a Nickel-Based Superalloy on the Cooling Rate from Super-Solvus Temperature Heat Treatment. Materials 2018, 11, 1528. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Ma, T.; Chang, T.; Zhang, P.; Fang, X.; Huang, K. Tailoring of nanoscale γ′ precipitates and unveiling their strengthening mechanisms in multimodal nickel-based superalloy GH4720Li. Mater. Charact. 2022, 188, 111918. [Google Scholar] [CrossRef]
- Collins, D.M.; Stone, H.J. A modelling approach to yield strength optimization in a nickel-base superalloy. Int. J. Plast. 2014, 54, 96–112. [Google Scholar]
- Galindo-Nava, E.I.; Connor, L.D.; Rae, C.M.F. On the prediction of the yield stress of unimodal and multimodal γ′ Nickel-base superalloys. Acta Mater. 2015, 98, 377–390. [Google Scholar]
- Goodfellow, A.J.; Galindo-Nava, E.I.; Christofidou, K.A.; Jones, N.G.; Martin, T.; Bagot, P.A.J.; Boyer, C.D.; Hardy, M.C.; Stone, H.J. Gamma Prime Precipitate Evolution During Aging of a Model Nickel-Based Superalloy. Metall. Mater. Trans. A 2017, 49, 718–728. [Google Scholar] [CrossRef]
- Goodfellow, A.J. Strengthening mechanisms in polycrystalline nickel-based superalloys. Mater. Sci. Technol. 2018, 34, 1793–1808. [Google Scholar]
- Goodfellow, A.J.; Galindo-Nava, E.I.; Schwalbe, C.; Stone, H.J. The role of composition on the extent of individual strengthening mechanisms in polycrystalline Ni-based superalloys. Mater. Des. 2019, 173, 107760. [Google Scholar]
- Smith, T.M.; Unocic, R.R.; Deutchman, H.; Mills, M.J. Creep deformation mechanism mapping in nickel base disk superalloys. Mater. High Temp. 2016, 33, 372–383. [Google Scholar]








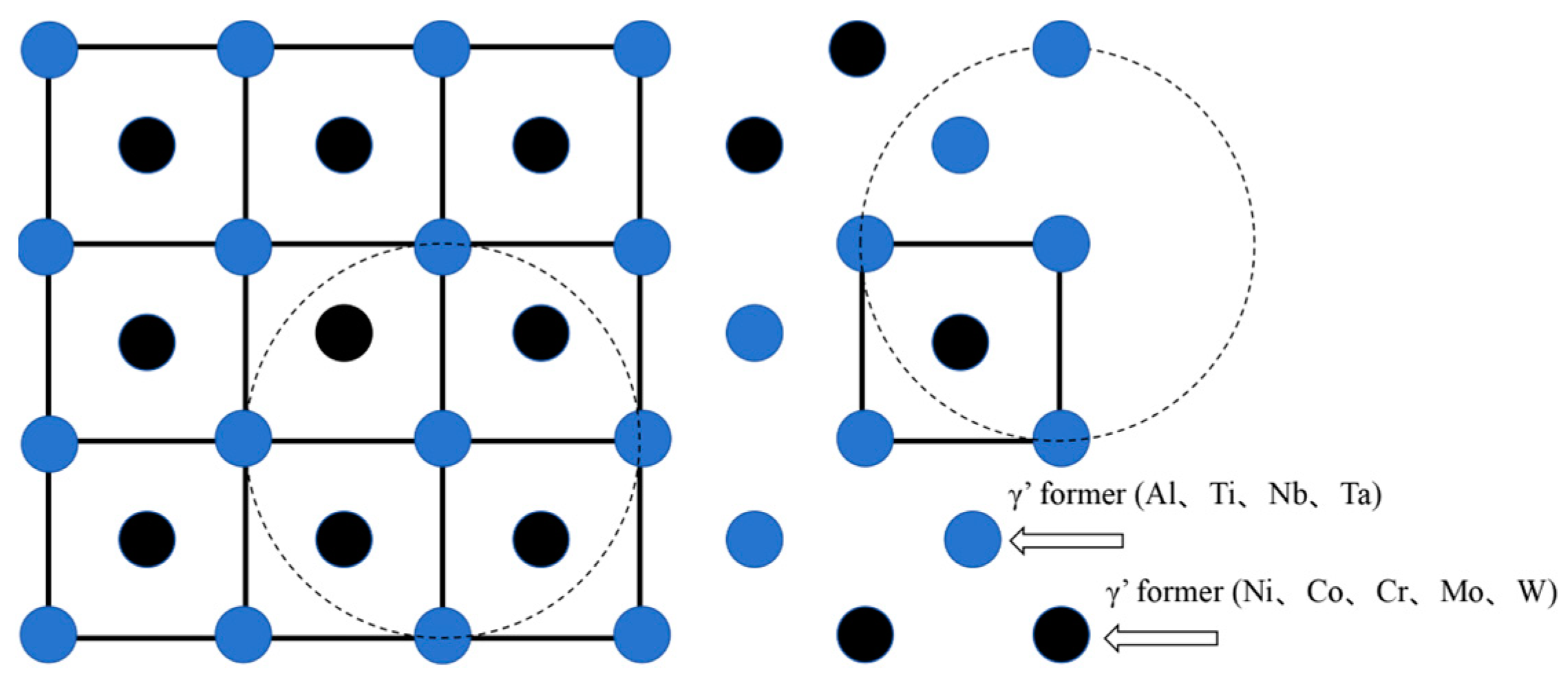
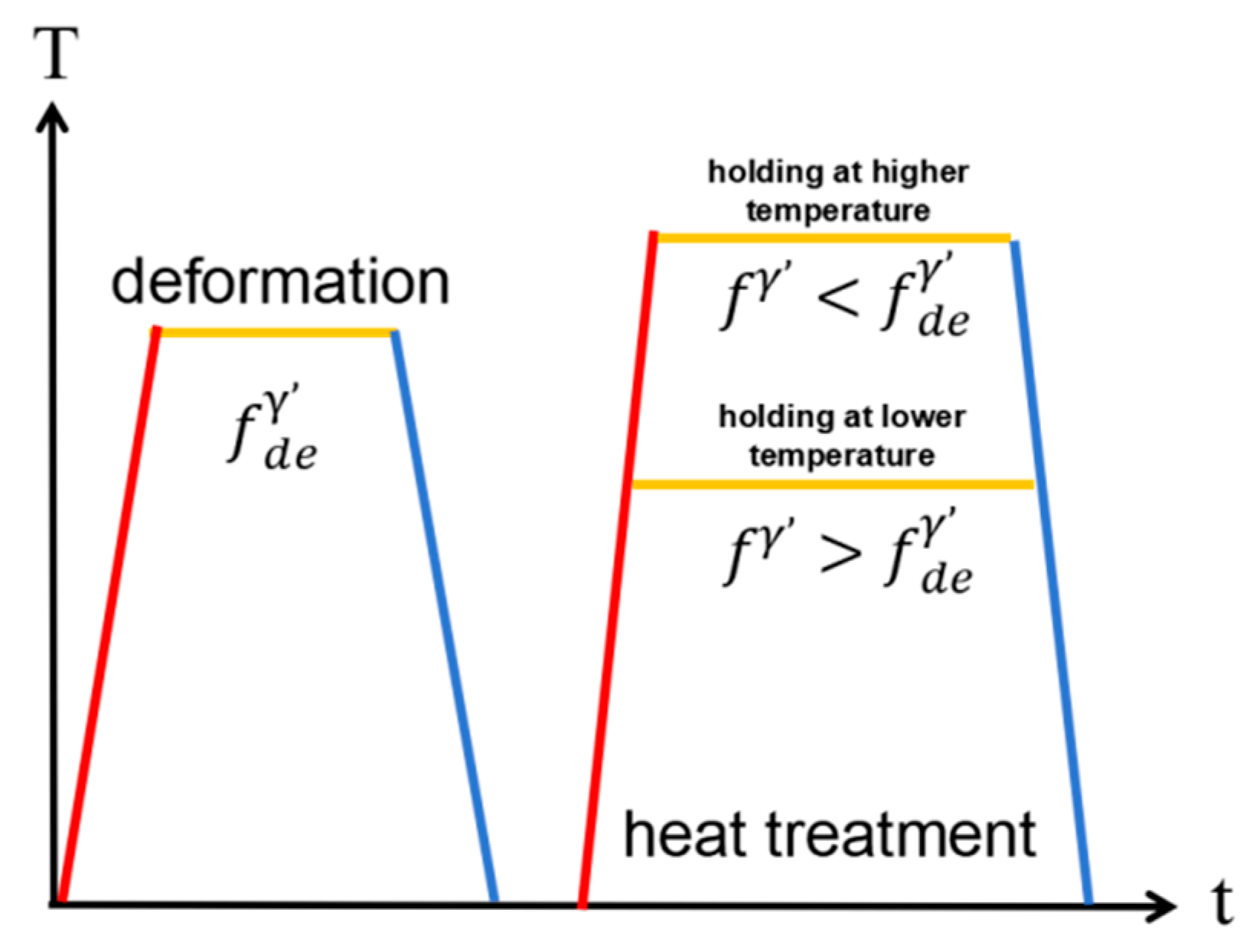
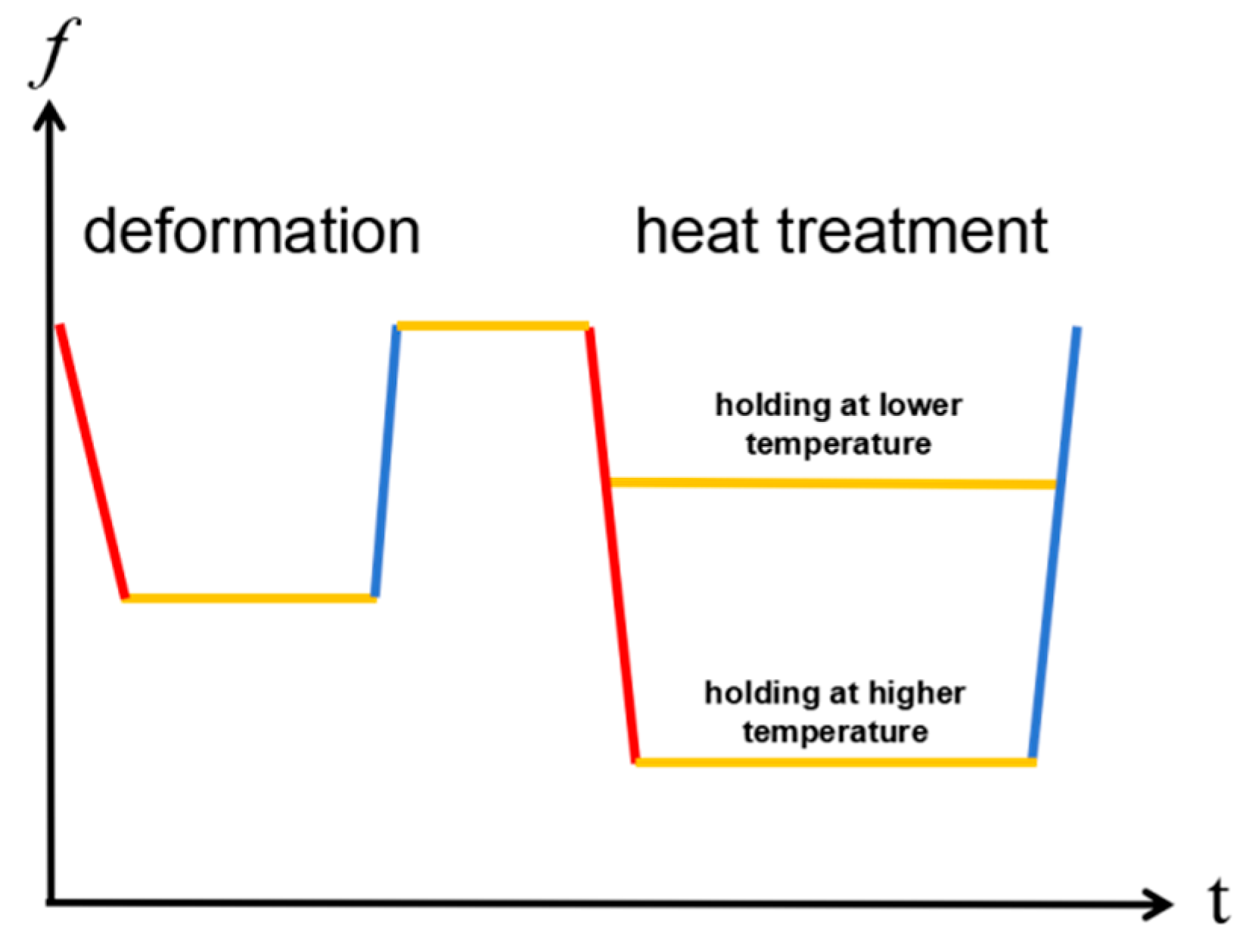
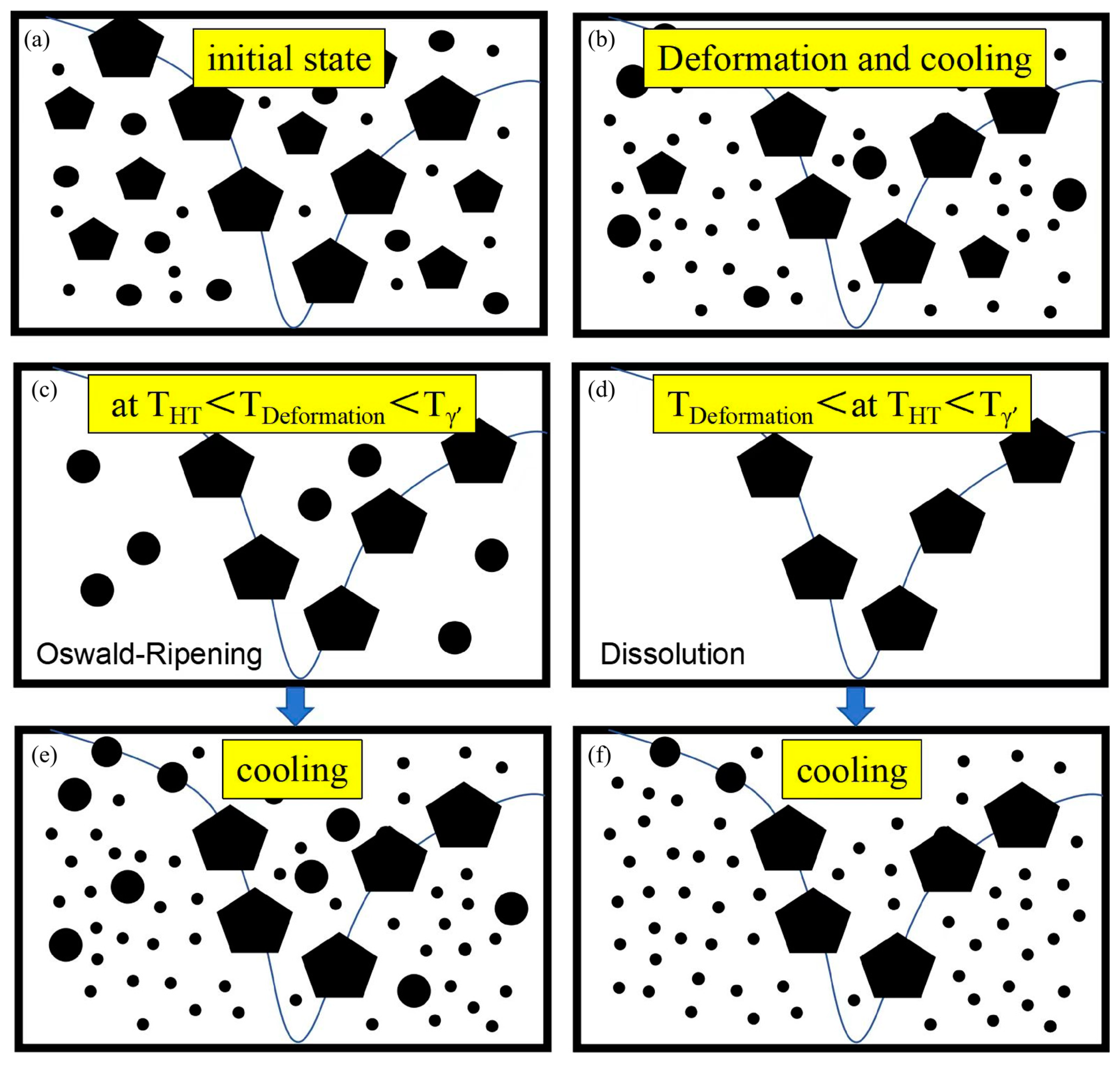
| Ni | Cr | Co | Mo | W | Ti | Al | Zr | C | B |
|---|---|---|---|---|---|---|---|---|---|
| 57 | 16 | 15 | 3 | 1.25 | 5 | 2.5 | 0.03 | 0.025 | 0.018 |
| DT | HT | |||||||
|---|---|---|---|---|---|---|---|---|
| 1100 °C | 15.7% | 13.5% | 29.2% | 1100 °C/4 h | 19.7% | 6.2% | 3.6% | 29.5% |
| 1120 °C/4 h | 14.0% | 1.3% | 5.7% | 21.0% | ||||
| 1110 °C | 11.2% | 14.2% | 25.4% | 1100 °C/4 h | 16.7% | 7.0% | 2.5% | 26.2% |
| 1120 °C/4 h | 11.7% | 0.7% | 7.4% | 19.8% | ||||
| 1120 °C | 4.6% | 15.6% | 20.2% | 1100 °C/4 h | 15.3% | 9.6% | 1.3% | 26.2% |
| 1120 °C/4 h | 12.7% | 3.9% | 3.2% | 19.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Xiong, J.; Long, A.; Xiao, L.; Ma, X.; Feng, G.; Guo, J. Influence of Hot Deformation Temperature on Grain Size and γ′ Phase in U720Li Alloy After Sub-Solvus Heat Treatment. Metals 2025, 15, 409. https://doi.org/10.3390/met15040409
Cheng J, Xiong J, Long A, Xiao L, Ma X, Feng G, Guo J. Influence of Hot Deformation Temperature on Grain Size and γ′ Phase in U720Li Alloy After Sub-Solvus Heat Treatment. Metals. 2025; 15(4):409. https://doi.org/10.3390/met15040409
Chicago/Turabian StyleCheng, Junyi, Jiangying Xiong, Anping Long, Lei Xiao, Xiangdong Ma, Ganjiang Feng, and Jianzheng Guo. 2025. "Influence of Hot Deformation Temperature on Grain Size and γ′ Phase in U720Li Alloy After Sub-Solvus Heat Treatment" Metals 15, no. 4: 409. https://doi.org/10.3390/met15040409
APA StyleCheng, J., Xiong, J., Long, A., Xiao, L., Ma, X., Feng, G., & Guo, J. (2025). Influence of Hot Deformation Temperature on Grain Size and γ′ Phase in U720Li Alloy After Sub-Solvus Heat Treatment. Metals, 15(4), 409. https://doi.org/10.3390/met15040409






