Prediction and Prevention of Edge Waves in Continuous Cold Forming of Thick-Wall High-Strength Welded Pipe
Abstract
1. Introduction
2. Technology Design
3. The FEM Modeling and Simulation
3.1. Finite Element Modeling
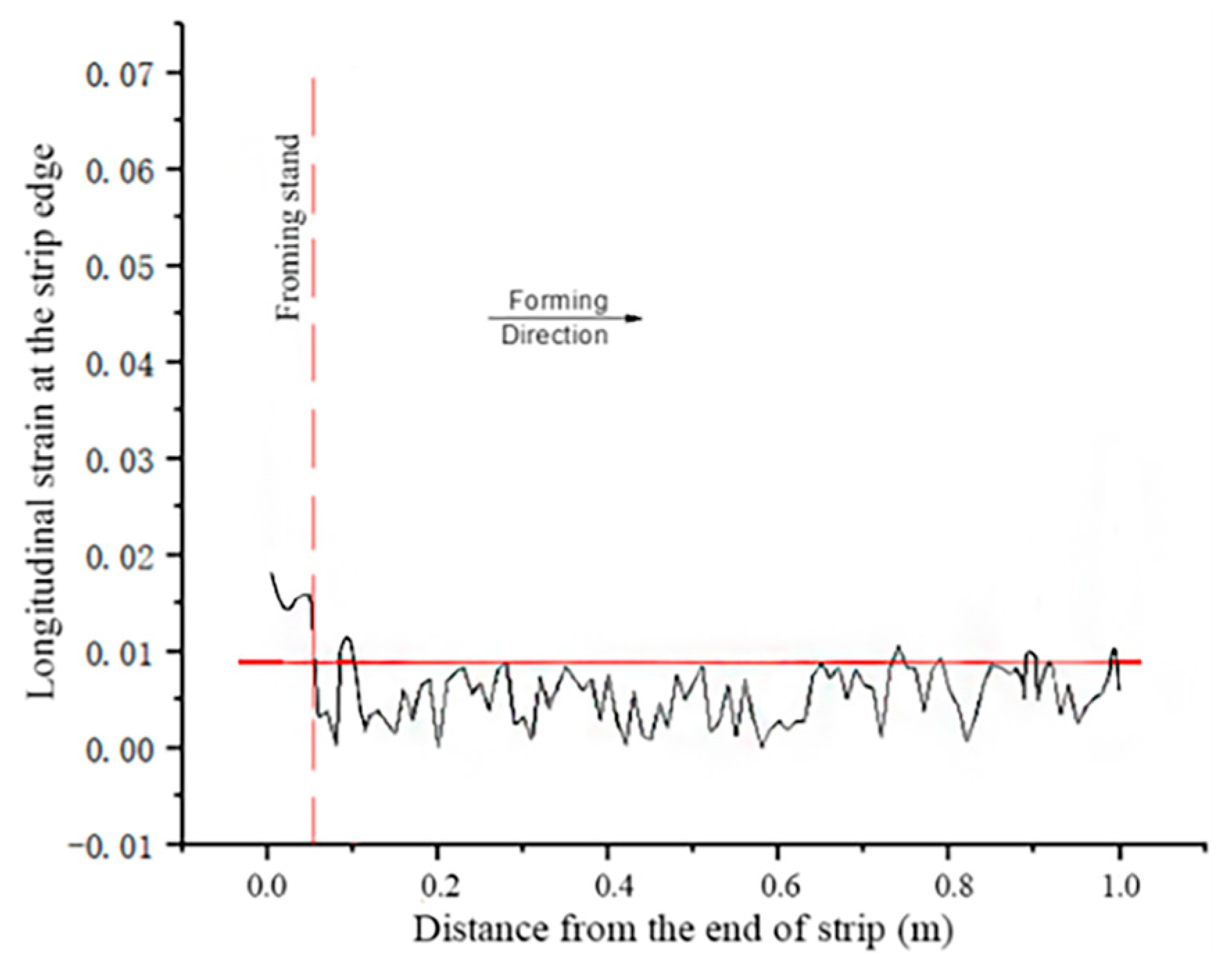
3.2. Validity of the Simulation
3.3. Process Optimization
3.3.1. The Goal of Optimization
3.3.2. Optimization Design
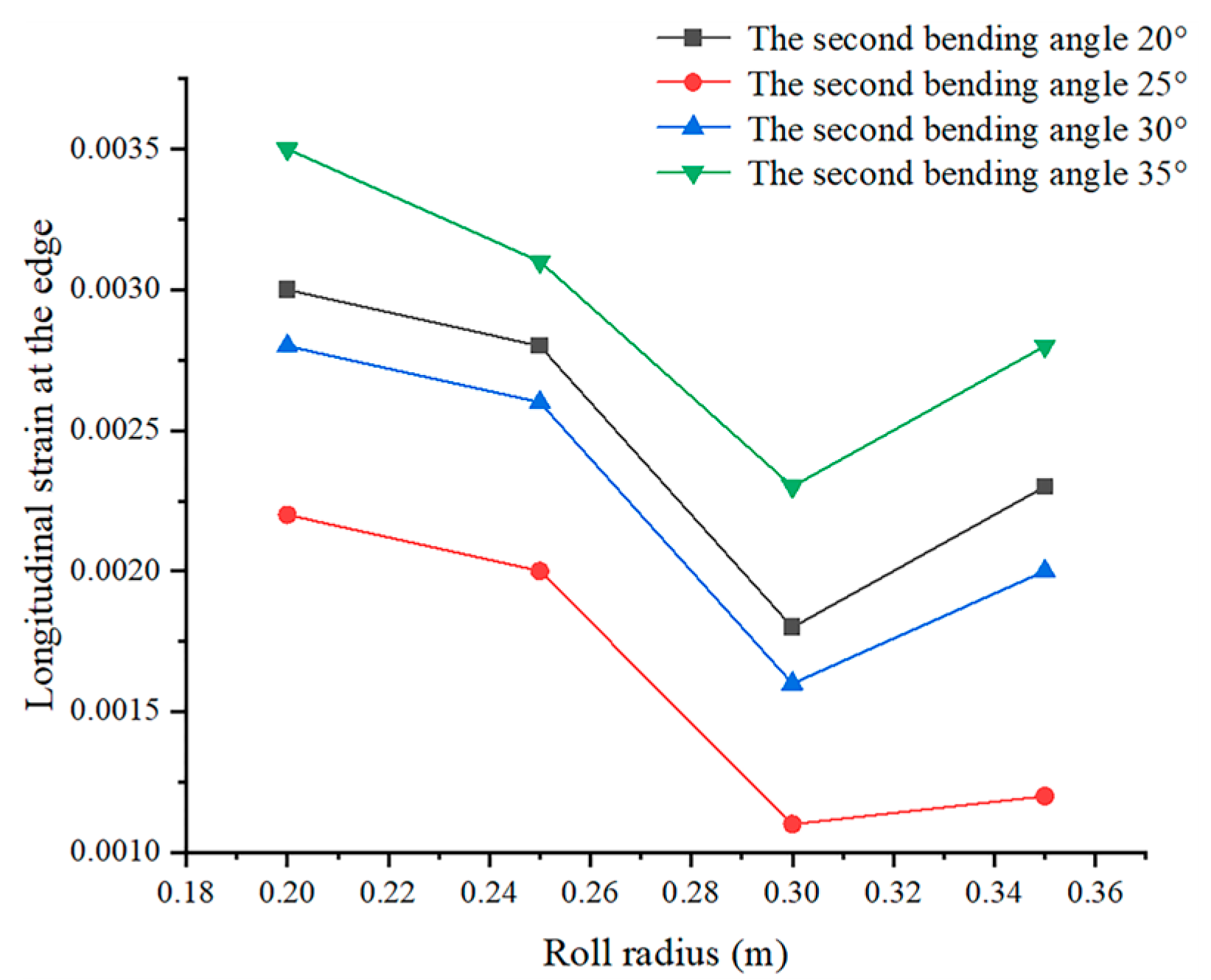
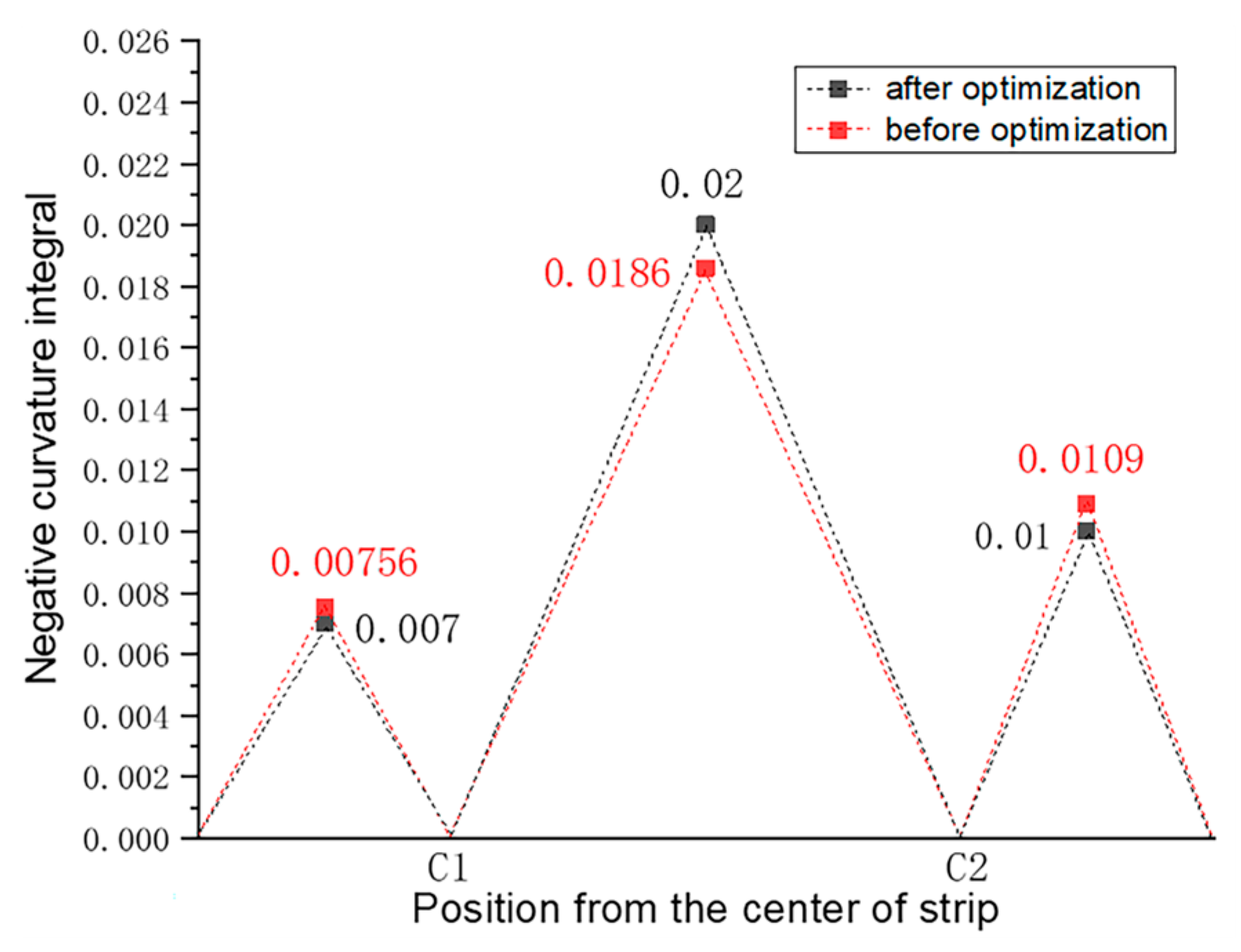
3.3.3. Simulation and Optimization Results
3.3.4. Results of the Full Simulation of Cold Roll Forming Using Optimized Data
4. Conclusions
- (1)
- In the current data range, the influence of the bending angle on the possible buckling of the strip edge in forming is higher than the influence of the roll diameter. A suitable distribution of the bending angles and roll diameter for each forming pass in cold bending can avoid the “Bauschinger effect” in forming and prevent edge buckling, which seriously affects the quality of welded joints.
- (2)
- This paper presents a combined numerical simulation and mathematical modeling method that, based on predicting edge buckling in strip forming, has the capability to optimize key process parameters before the production line is put into operation, minimizing the possible buckling of the strip edges in forming and reducing the losses that may be caused by design defects. The method can give full play to the capabilities of the cold bending unit and can also be applied to the optimization of multiple process parameters for other forming processes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, J.J.; Cao, J.G.; Zhao, J.W.; Liu, J.; Zhao, R.G.; Liu, S.Q. The flower pattern and rolls design for ERW pipes with the different specification in the flexible roll forming process. Thin-Wall Struct. 2020, 154, 106–809. [Google Scholar] [CrossRef]
- Ghiabakloo, H.; Kim, J.; Kang, B.S. An efficient finite element approach for shape prediction in flexibly-reconfigurable roll forming process. Int. J. Mech. Sci. 2018, 142–143, 339–358. [Google Scholar] [CrossRef]
- Park, J.W.; Kil, M.G.; Kim, J.; Kang, B.S. A Predictive Model of Flexibly-reconfigurable Roll Forming Process using Regression Analysis. Procedia Eng. 2017, 207, 1266–1271. [Google Scholar] [CrossRef]
- Sreenivas, A.; Abeyrathna, B.; Rolfe, B.; Weiss, M. Longitudinal strain and wrinkling analysis of variable depth flexible roll forming. J. Manuf. Process. 2022, 81, 414–432. [Google Scholar] [CrossRef]
- Sheu, J.J.; Liang, C.F.; Yu, C.H.; Hsu, W.C.; Lee, P.K. Flexible roll forming of U-section product with curved bending profile using advanced high strength steel. Procedia Manuf. 2018, 15, 782–787. [Google Scholar] [CrossRef]
- Kasaei, M.M.; Moslemi Naeini, H.; Azizi Tafti, R.; Salmani Tehrani, M. Prediction of maximum initial strip width in the cage roll forming process of ERW pipes using edge buckling criterion. J. Mater. Process. Technol. 2014, 214, 190–199. [Google Scholar] [CrossRef]
- Hu, S.D.; Pi, D.G.; Li, L.X. Influence of Technology on Deformation Behavior of Cold-formed High Frequency Induction Welded Steel Pipes. Adv. Mater. Res. 2013, 631–632, 704–707. [Google Scholar] [CrossRef]
- Hu, S.D.; Ye, B.; Li, L.X. Materials properties of thick-wall cold-rolled welded tube with a rectangular or square hollow section. Construction and Building. Materials 2011, 25, 2683–2689. [Google Scholar]
- Farzin, M.; Salmani Tehrani, M.; Shalemi, E. Determination of buckling limit strain in cold roll forming by the finite element analysis. J. Mater. Process. Technol. 2002, 125–126, 626–632. [Google Scholar] [CrossRef]
- Bhattacharyya, D.; Smith, P.D. The Development of Longitudinal Strain in Cold Roll Forming and its influence of Product Straightness. In Proceedings of the 1984 Advanced Tech of Plasticity, ATP, Tokyo, Japan, 3–5 September 1984; pp. 422–427. [Google Scholar]
- Woo, Y.Y.; Han, S.W.; Hwang, T.W.; Park, J.Y.; Moon, Y.H. Characterization of the longitudinal bow during flexible roll forming of steel sheets. J. Mater. Process. Technol. 2018, 252, 782–794. [Google Scholar] [CrossRef]
- Safdarian, R.; MoslemiNaeini, H. The effects of forming parameters on the cold roll forming of channel section. Thin-Wall Struct. 2015, 92, 130–136. [Google Scholar] [CrossRef]
- Li, D.J.; Xu, L.Q.; Li, L.J.; Yue, C.F.; Zhou, W.J.; Zhang, C.L. Finite element simulation for straightedge lineal roll forming process of high frequency welding pipe. Int. J. Interact. Des. Manuf. IJIDeM 2023, 19, 743–751. [Google Scholar] [CrossRef]
- Tehrani, M.S.; Naeini, H.M.; Hartley, P.; Khademizadeh, H. Localized edge buckling in cold roll-forming of circular tube section. J. Mater. Process. Tech. 2006, 177, 617–620. [Google Scholar] [CrossRef]
- Luo, Z.; Sun, M.; Zhang, Z.; Lu, C.; Zhang, G.; Fan, X. Finite element analysis of circle-to-rectangle roll forming of thick-walled rectangular tubes with small rounded corners. Int. J. Mater. Form. 2022, 15, 73. [Google Scholar] [CrossRef]
- DIN 6935:1975; Cold Bending of Flat Rolled Steel Products (FOREIGN STANDARD). Deutsches Institut für Normung: Berlin, Germany, 1975.
- Abeyrathna, B.; Ghanei, S.; Rolfe, B.; Taube, R.; Weiss, M. Optimising part quality in the flexible roll forming of an automotive component. Int. J. Adv. Manuf. Technol. 2021, 118, 3361–3373. [Google Scholar] [CrossRef]
- Cao, J.; Wang, X.; Ruan, K.; Cheng, J.; Wei, Z.; Zhao, R. Numerical simulation research on UDF flexible roll forming of multi-specification thin-walled circular tubes. Int. J. Adv. Manuf. Technol. 2023, 127, 4503–4517. [Google Scholar] [CrossRef]
- Gardner, L.; Saari, N.; Wang, F. Comparative experimental study of hot-rolled and cold-formed rectangular hollow sections. Thin-Walled Struct. 2010, 48, 495–507. [Google Scholar] [CrossRef]
- Yoon, J.S.; Kim, J.; Kim, H.H.; Kang, B.S. Feasibility study on flexibly reconfigurable roll forming process for sheet metal and its implementation. Adv. Mech. Eng. 2014, 6, 958925. [Google Scholar] [CrossRef]
- Chen, J.; Jin, W.L. Corner strength enhancement of high strength cold-formed steel at normal room and elevated temperatures. J. Zhejiang Univ. Sci. A 2008, 9, 1251–1257. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, X.; Liu, H.; Liu, J.; Zhao, R. Optimization of the Forming Method on Torsion Defect in Cold-Roll Forming of Z Section Steel. ACS Omega 2022, 7, 4804–4811. [Google Scholar] [CrossRef]
- Shirani Bidabadi, B.; Moslemi Naeini, H.; Safdarian, R.; Barghikar, H. Investigation of over-bending defect in the cold roll forming of U-channel section using experimental and numerical methods. Proc. Inst. Mech. Eng. 2022, 236, 1380–1392. [Google Scholar] [CrossRef]
- Liu, M.; Liu, Y.; Li, H. Deformation analysis of double wall brazed tube in the multi-pass roll forming: Cross-sectional variation, stress-strain evolution and roundness assessment. J. Manuf. Process. 2023, 85, 479–491. [Google Scholar] [CrossRef]
- Sreenivas, A.; Abeyrathna, B.; Rolfe, B.; Weiss, M. Analysing the reduction in buckling limit of a flexible roll formed flange due to shape imperfection. J. Mater. Process. Tech. 2025, 338, 118767. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Chan, T.M. Mechanical properties of corner material in cold-formed steel structure: From normal strength to high strength. Structures 2024, 59, 105651. [Google Scholar] [CrossRef]
- Lee, H.; Park, N.; Kim, M.; Lee, M.G.; Song, J.H. Recent Developments and Trends in Flexible Forming Technology. Int. J. Automot. Technol. 2022, 23, 741–763. [Google Scholar] [CrossRef]
- Du, F.S.; Fu, Z.Q.; Yu, H. Roll Flower Design and forming mechanism of rectangular tubes in cold roll forming processes. China Mech. Eng. 2016, 27, 2841–2845. [Google Scholar]
- Díaz, A.; Cuesta, I.I.; Alegre, J.M.; de Jesus, A.M.P.; Manso, J.M. Residual stresses in cold-formed steel members: Review of measurement methods and numerical modelling. Thin-Walled Struct. 2021, 159, 107335. [Google Scholar] [CrossRef]
- Xiao, L.H.; Li, Y.; Cao, Y.X.; Cao, Y.F. Mechanisms and influences of edge-wave in roll-forming for thin-walled channel steel parts. J. Plast. Eng. 2016, 23, 32–39. [Google Scholar]
- Abeyrathna, B.; Rolfe, B.; Taube, R.; Oxley, B.; Weiss, M. Part quality improvement in flexible roll forming of a combined variable width and depth component. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1284, 012010. [Google Scholar] [CrossRef]

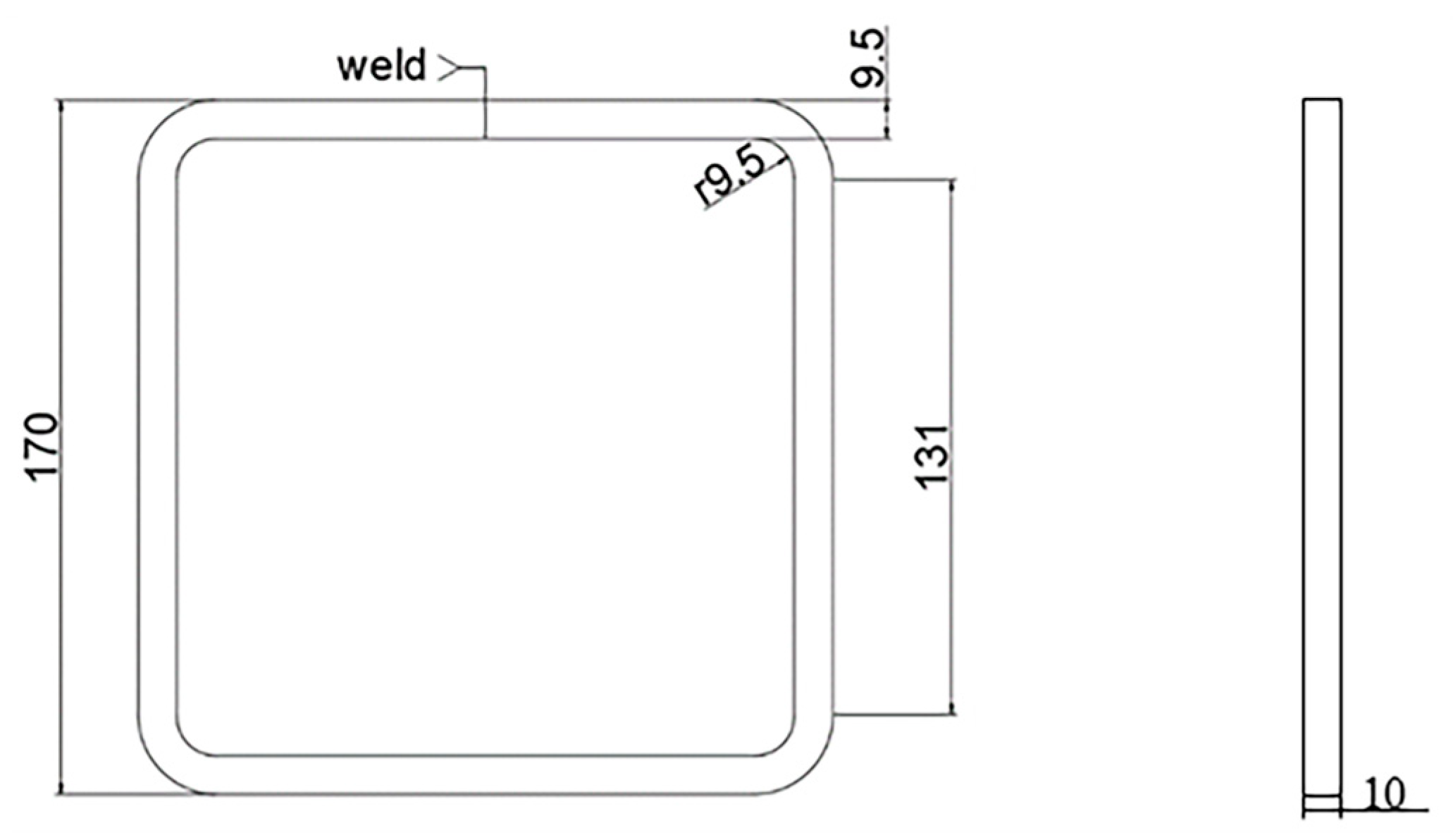

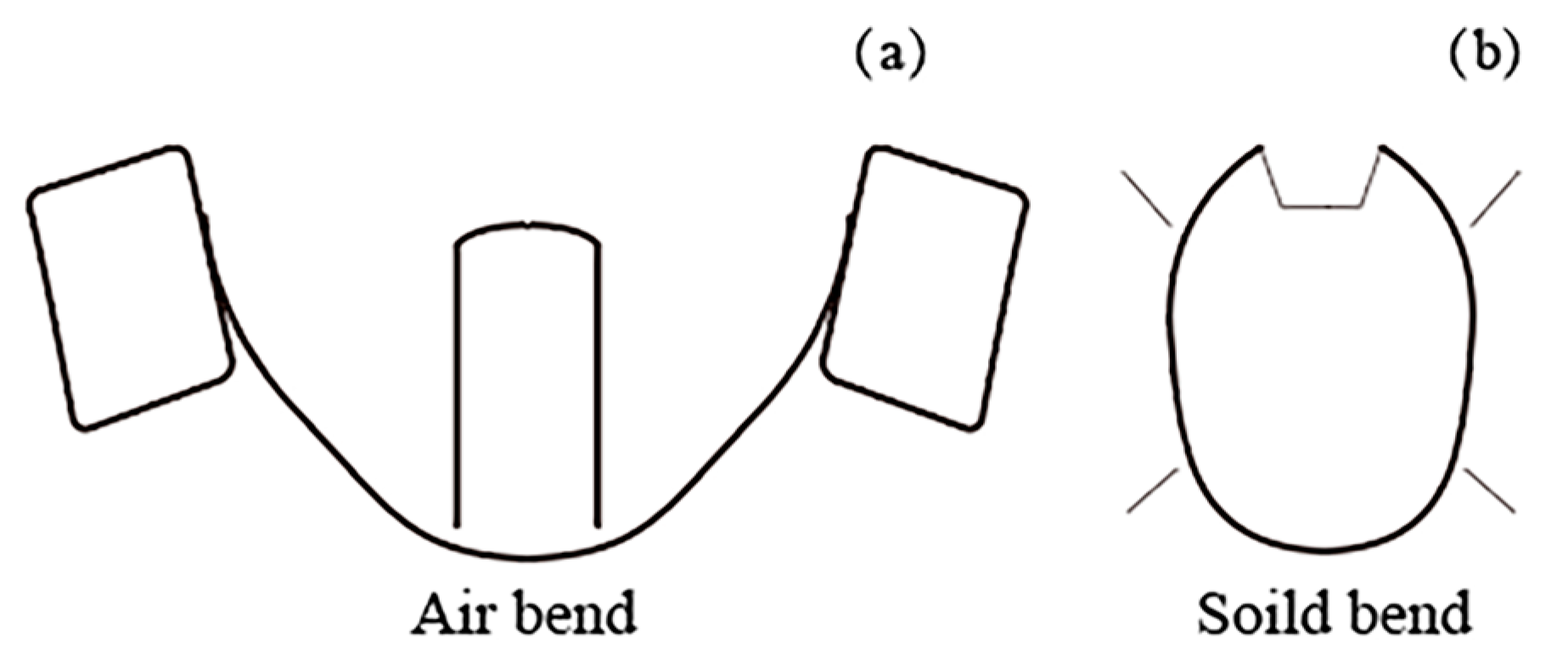
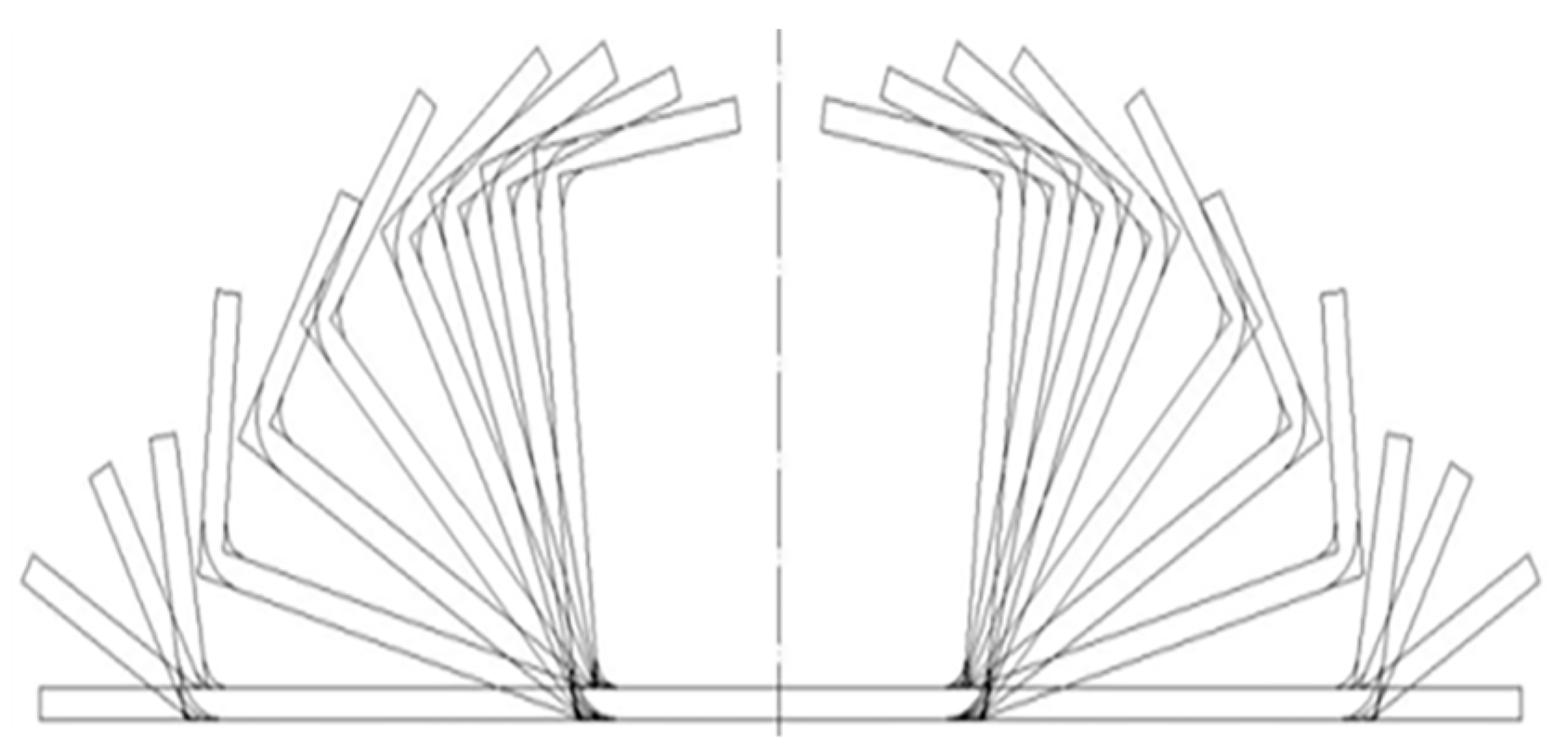
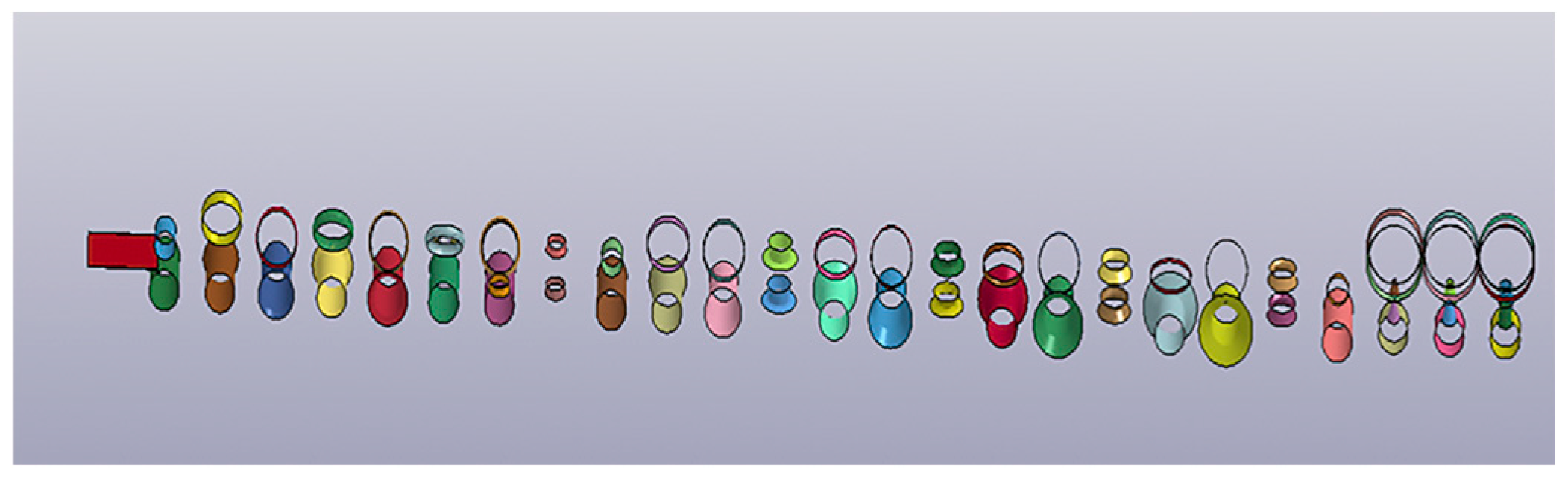
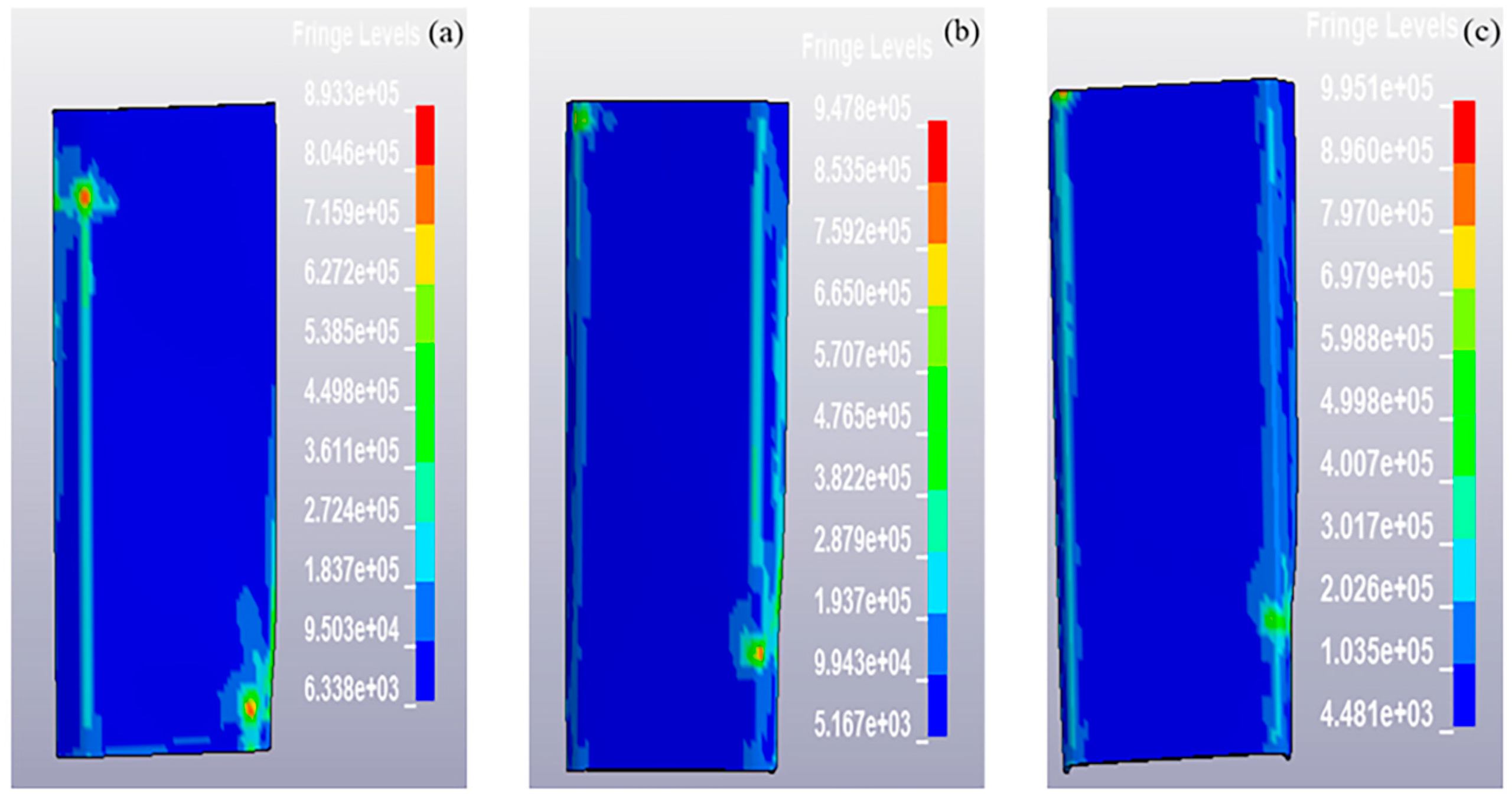
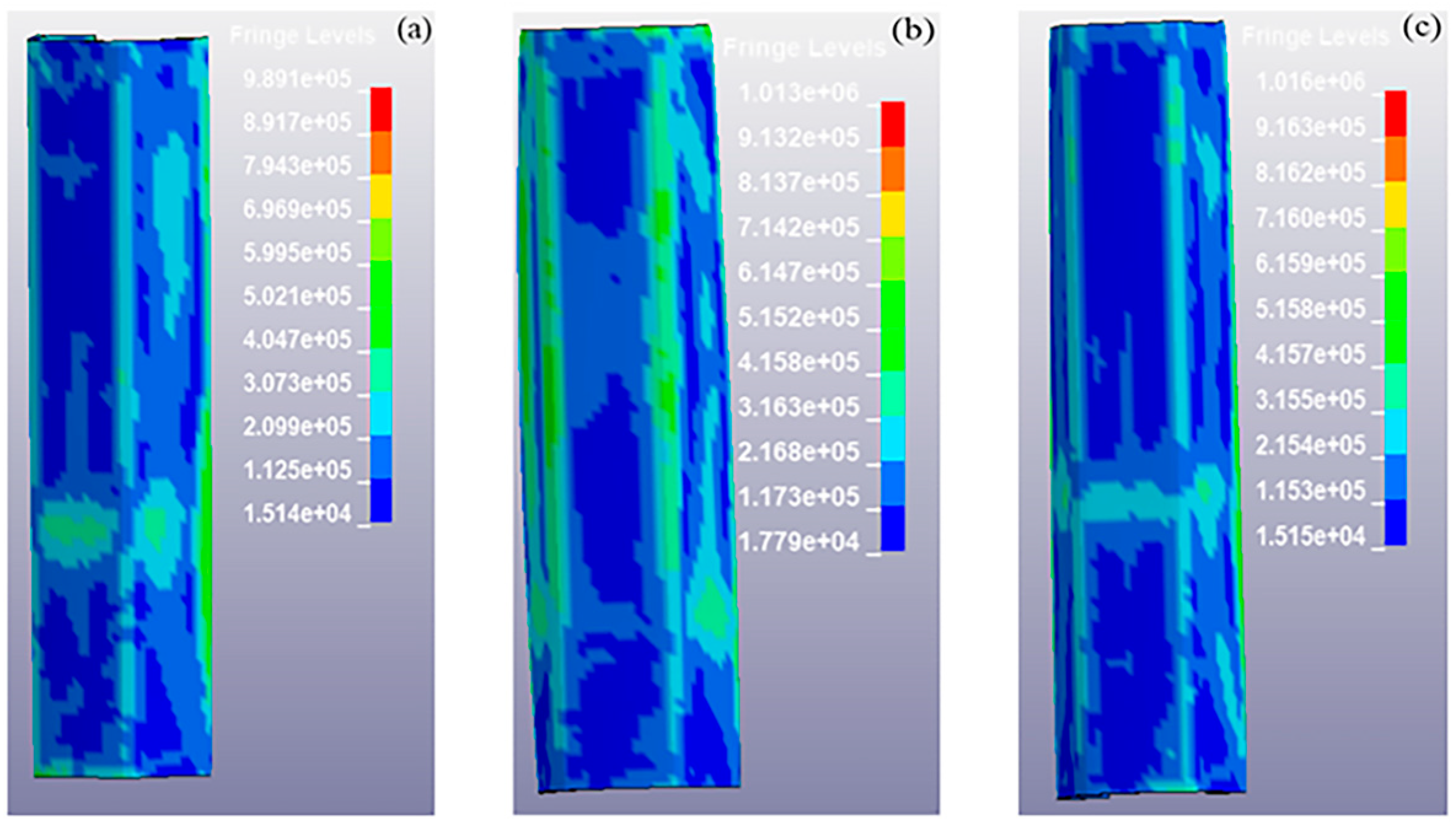


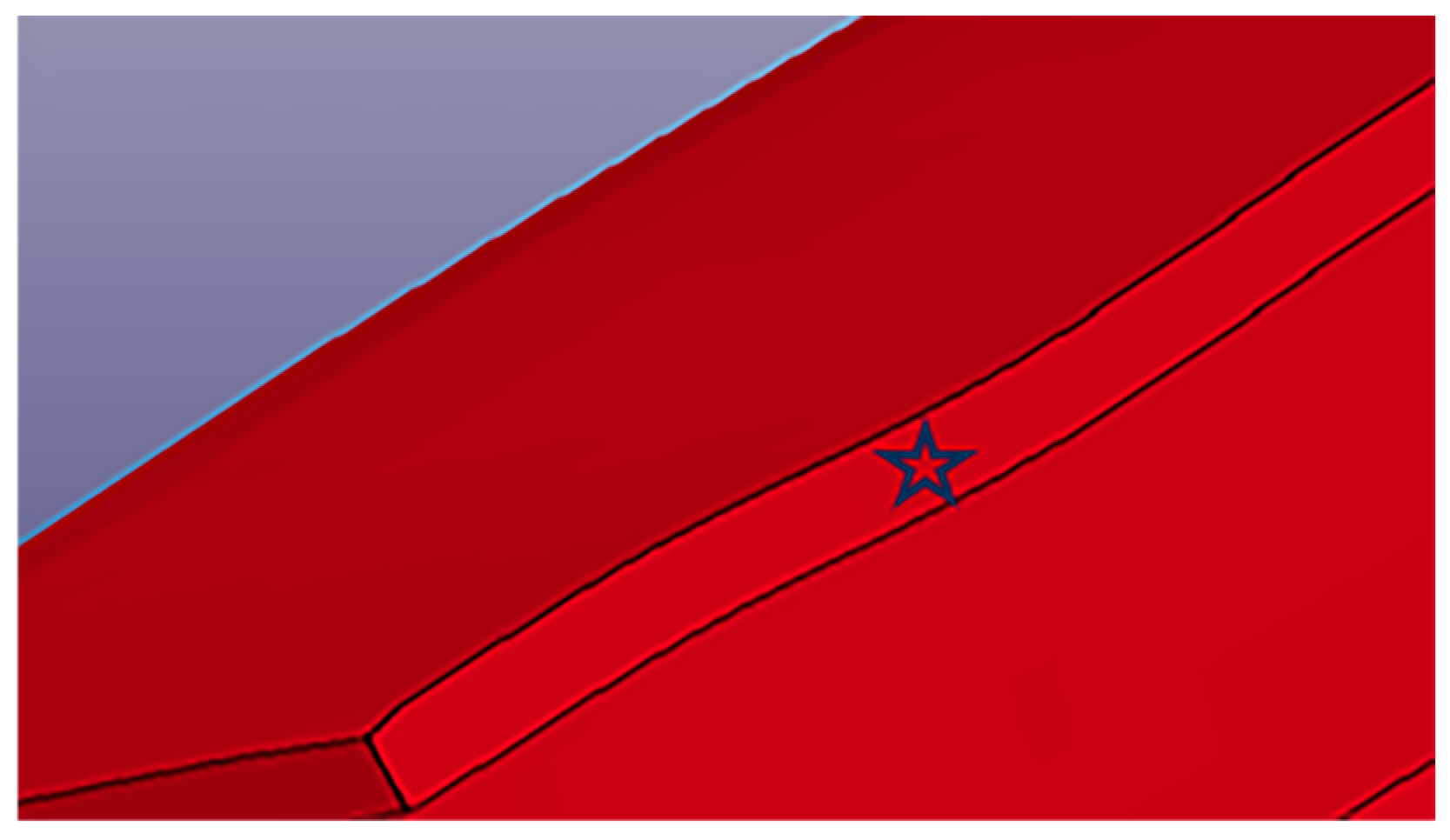
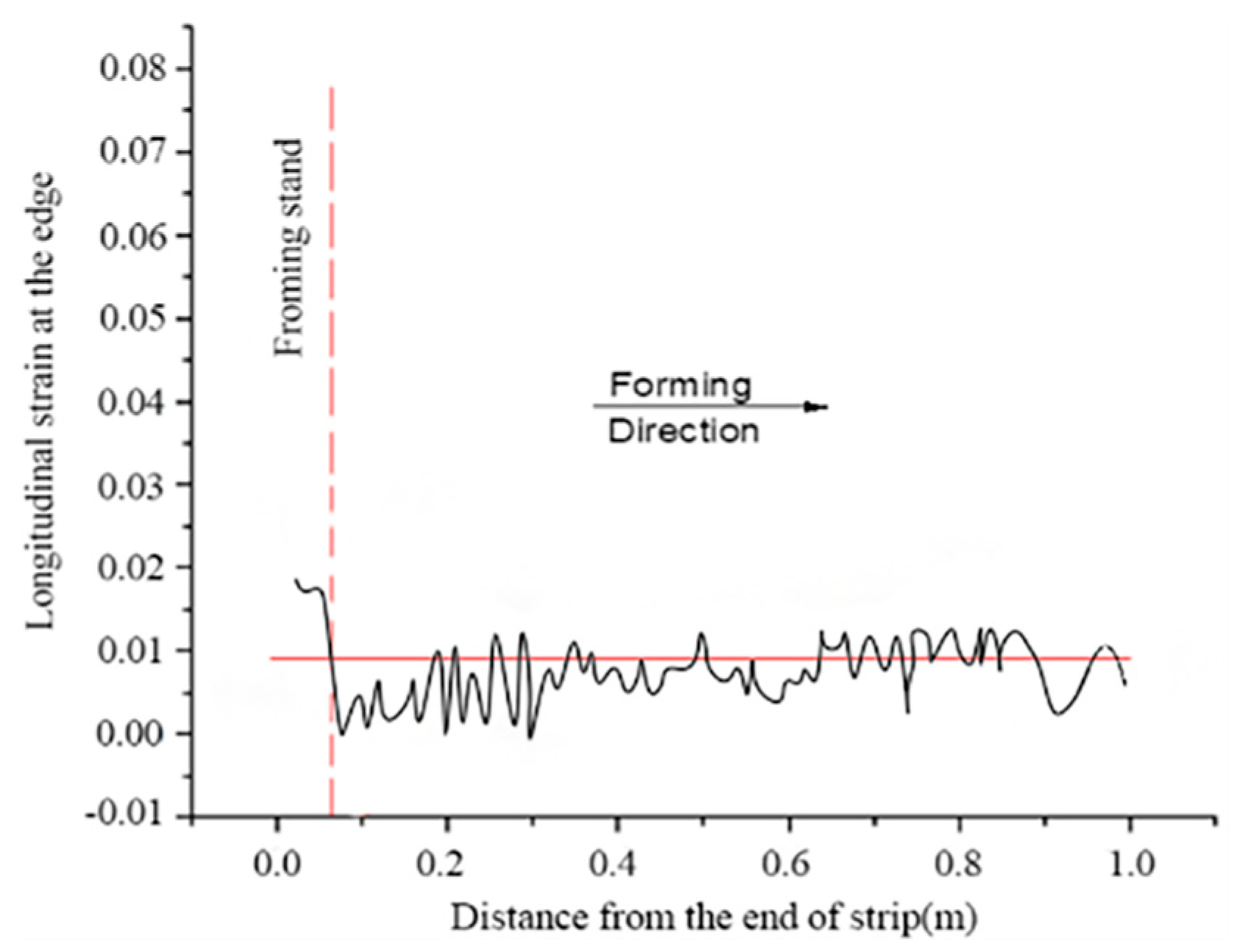
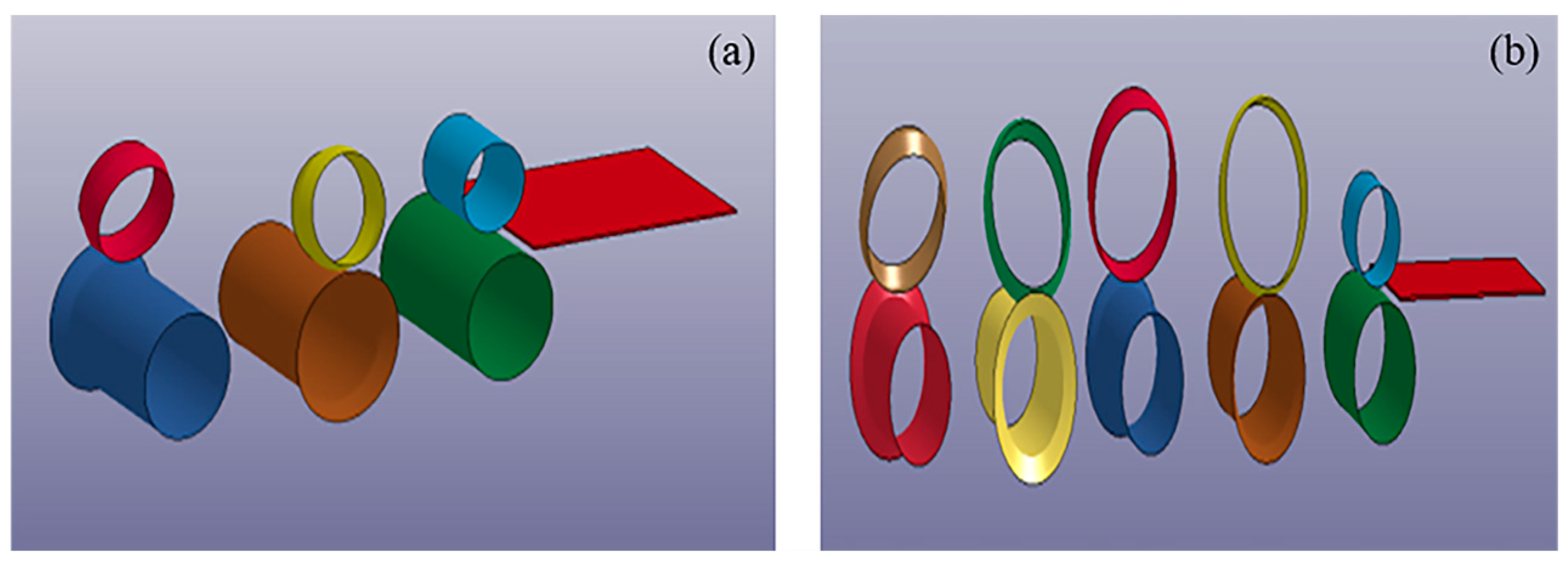
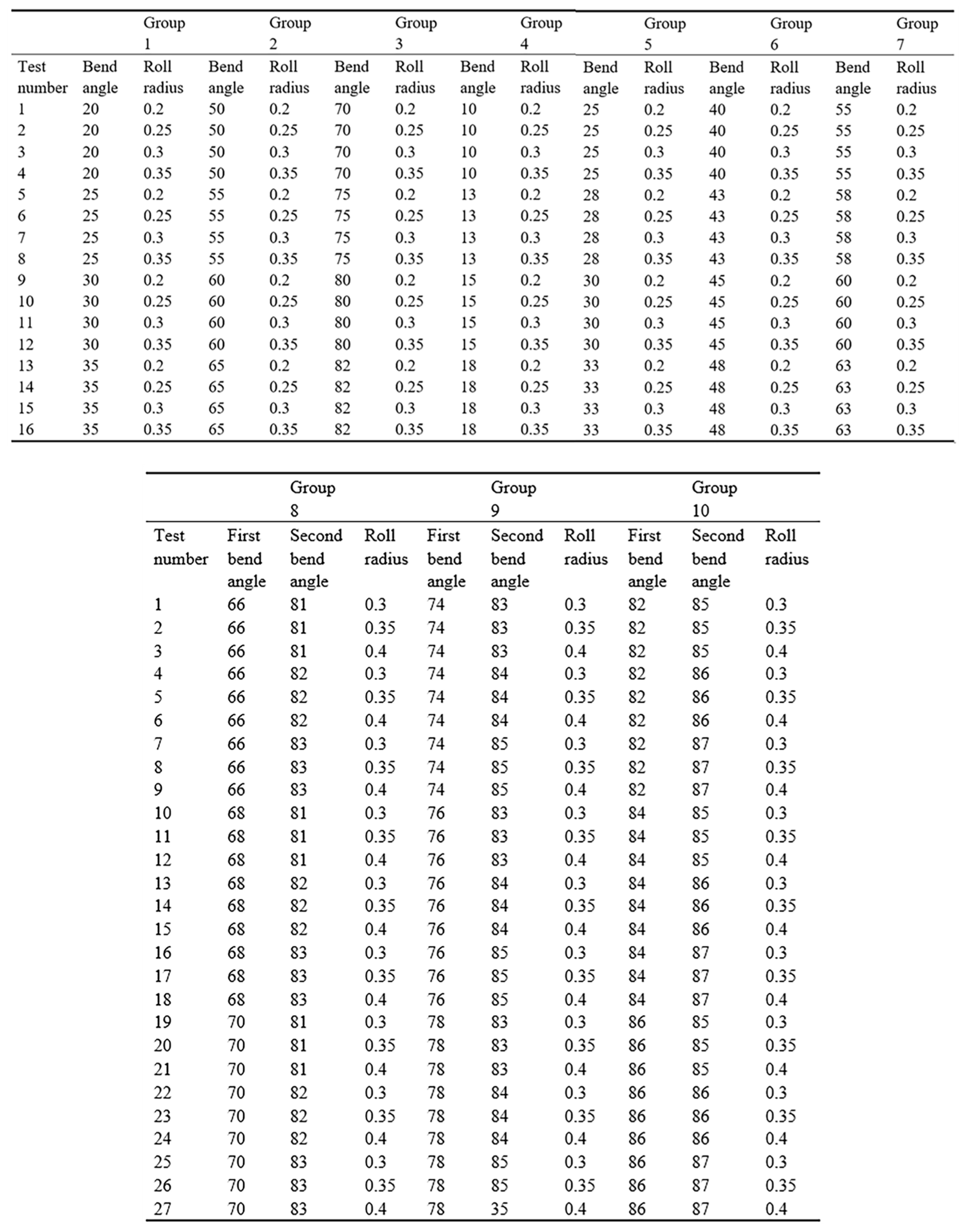
| Pass | Bending Angle | Degree |
|---|---|---|
| Pass 1 | Second bend angle for left | 30° |
| Pass 2 | Second bend angle for right | 30° |
| Pass 3 | Second bend angle for left | 60° |
| Pass 4 | Second bend angle for right | 60° |
| Pass 5 | Second bend angle for left | 80° |
| Pass 6 | Second bend angle for right | 80° |
| Pass 7 | First bend angle for left | 15° |
| Pass 8 | First bend angle for right | 15° |
| Pass 9 | First bend angle for left | 30° |
| Pass 10 | First bend angle for right | 30° |
| Pass 11 | First bend angle for left | 45° |
| Pass 12 | First bend angle for right | 45° |
| Pass 13 | First bend angle for left | 60° |
| Pass 14 | First bend angle for right | 60° |
| Pass 15 | First and second bend angle | 68° and 82° |
| Pass 16 | First and second bend angle | 76° and 84° |
| Pass 17 | First and second bend angle | 84° and 86° |
| Element | C | Mn | Si | Cr | Ni | Mo | Al | P | S | Cu | V |
| Content (%) | 0.2 | 1.5 | 0.5 | 0.9 | 1.0 | 0.25 | 0.04 | ≤0.02 | ≤0.01 | ≤0.3 | 0.05 |
| Specimen | Yield Stress/MPa | Mean/MPa | Standard Deviation/MPa |
|---|---|---|---|
| 84°-1 | 975.7 | ||
| 84°-2 | 965.4 | ||
| 84°-3 | 1001.3 | 980.8 | 18.5 |
| 86°-1 | 965.2 | ||
| 86°-2 | 999.4 | ||
| 86°-3 | 991.5 | 985.4 | 17.9 |
| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| ε | 0.31% | 0.27% | 0.18% | 0.24% | 0.22% | 0.20% | 0.12% | 0.14% |
| Number | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| ε | 0.28% | 0.26% | 0.17% | 0.21% | 0.35% | 0.31% | 0.22% | 0.28% |
| Non-Standardized Coefficients | R | R2 | Adjustment of R2 | Model Error | DW Value | ||
|---|---|---|---|---|---|---|---|
| B | Standard Error | ||||||
| Constants | 0.007 | 0.003 | 0.929 | 0.863 | 0.742 | 0.033% | 2.455 |
| −0.019 | 0.013 | ||||||
| −6.122 × 10−6 | 0.000 | ||||||
| 5.474 × 10−5 | 0.000 | ||||||
| −0.003 | 0.003 | ||||||
| −1.02 × 10−5 | 0.000 | ||||||
| −0.005 | 0.008 | ||||||
| 0.650 | 0.258 | ||||||
| First Bend Angle | Second Bend Angle | Roll Diameter | |
|---|---|---|---|
| Pass 1, Pass 2 | 0° | 27° | 669 mm |
| Pass 3, Pass 4 | 0° | 57° | 636 mm |
| Pass 5, Pass 6 | 0° | 74° | 578 mm |
| Pass 7, Pass 8 | 13° | 74° | 608 mm |
| Pass 9, Pass 10 | 29° | 74° | 572 mm |
| Pass 11, Pass 12 | 43° | 74° | 642 mm |
| Pass 13, Pass 14 | 59° | 74° | 552 mm |
| Pass 15 | 68° | 82° | 714 mm |
| Pass 16 | 75° | 84° | 672 mm |
| Pass 17 | 84° | 85° | 742 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Zhao, J.; Liu, Y. Prediction and Prevention of Edge Waves in Continuous Cold Forming of Thick-Wall High-Strength Welded Pipe. Metals 2025, 15, 455. https://doi.org/10.3390/met15040455
Hu S, Zhao J, Liu Y. Prediction and Prevention of Edge Waves in Continuous Cold Forming of Thick-Wall High-Strength Welded Pipe. Metals. 2025; 15(4):455. https://doi.org/10.3390/met15040455
Chicago/Turabian StyleHu, Shengde, Junhao Zhao, and Yu Liu. 2025. "Prediction and Prevention of Edge Waves in Continuous Cold Forming of Thick-Wall High-Strength Welded Pipe" Metals 15, no. 4: 455. https://doi.org/10.3390/met15040455
APA StyleHu, S., Zhao, J., & Liu, Y. (2025). Prediction and Prevention of Edge Waves in Continuous Cold Forming of Thick-Wall High-Strength Welded Pipe. Metals, 15(4), 455. https://doi.org/10.3390/met15040455






