Investigation on the Influence of Vacancy and Alloying Element Content on the Performance of Fe/NbN Interface
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
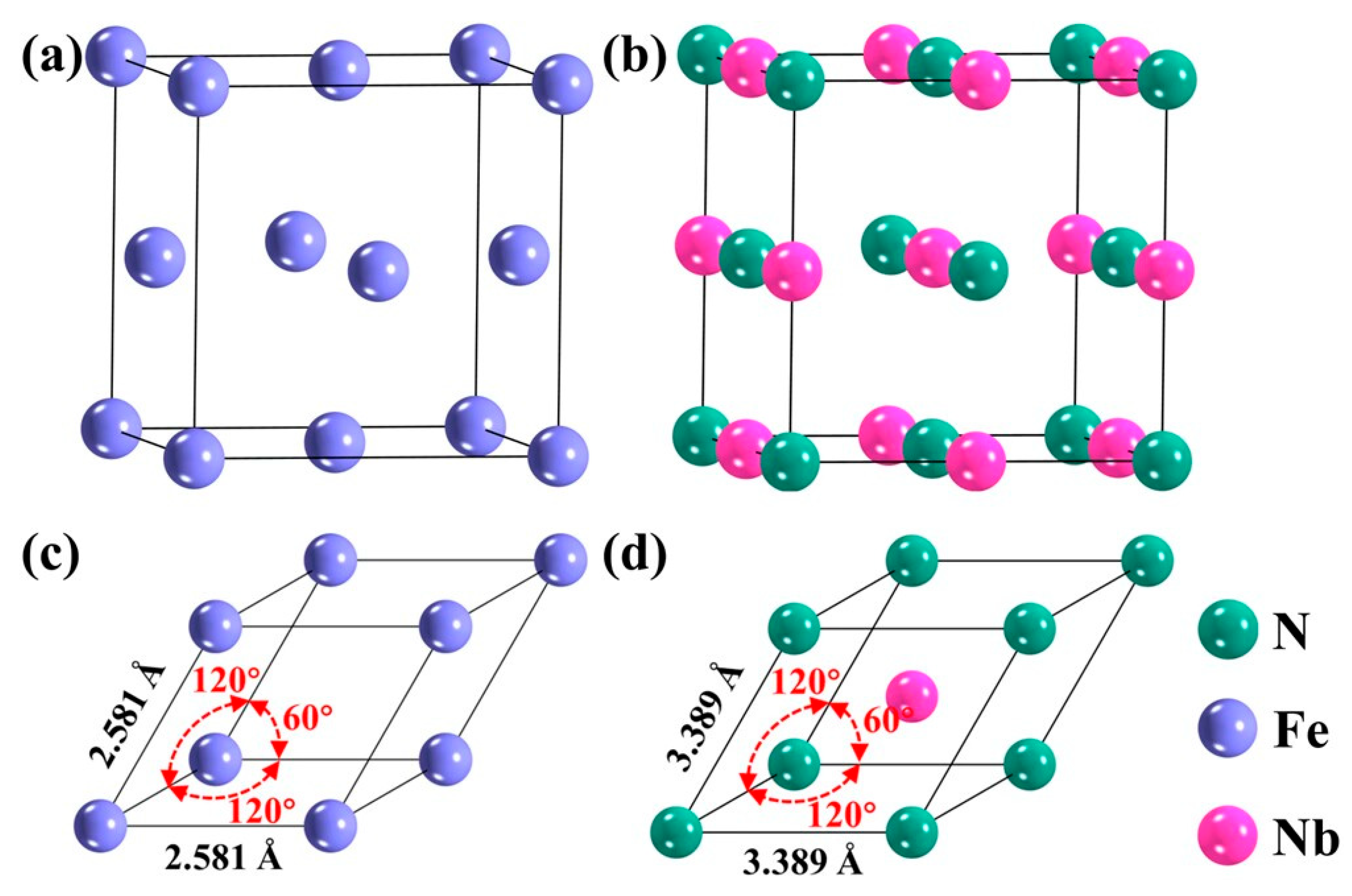
3.1. Bulk Phase fcc-Fe and NbN Model
3.2. Characterization of Bulk Phase fcc-Fe and NbN
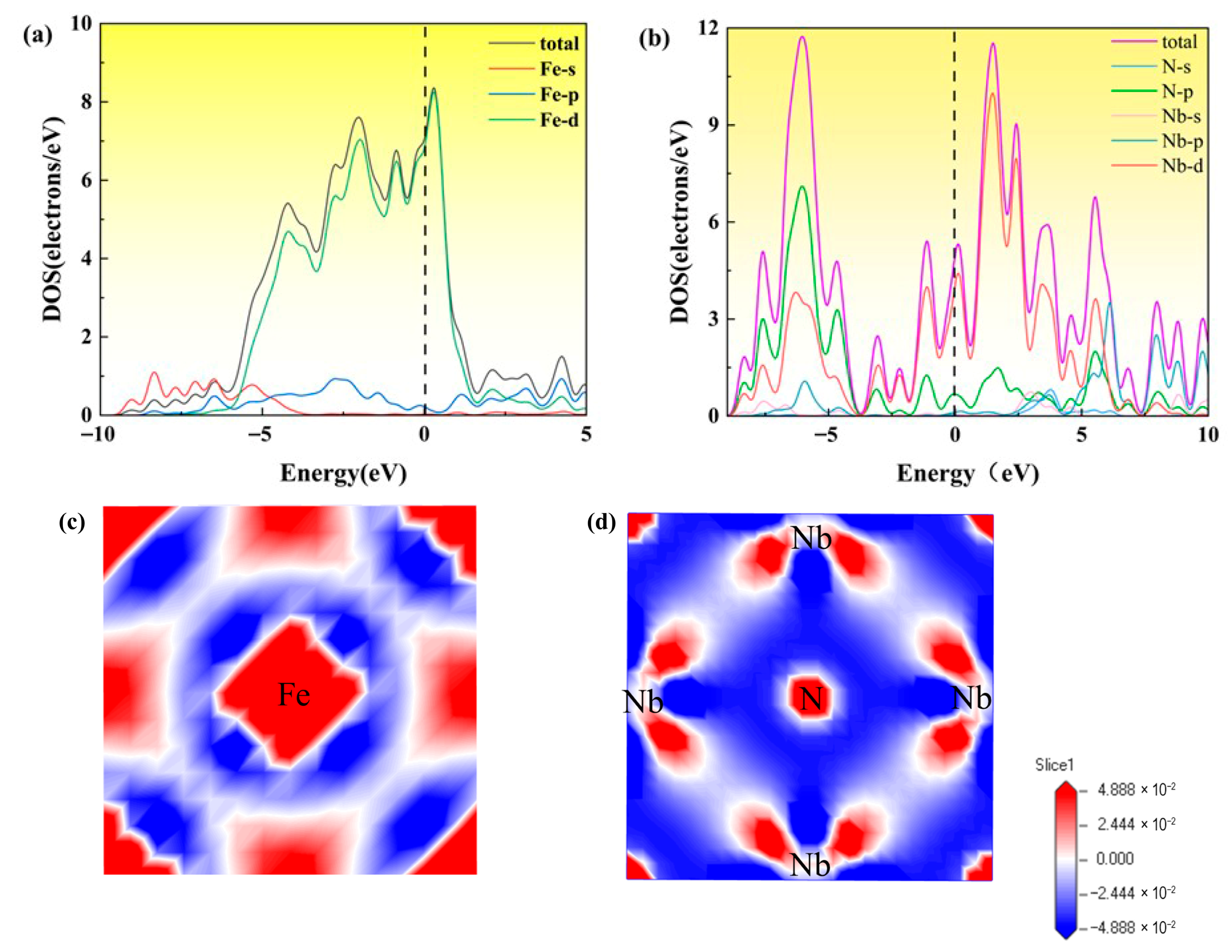
3.2.1. Electronic Property
3.2.2. Stretching Property
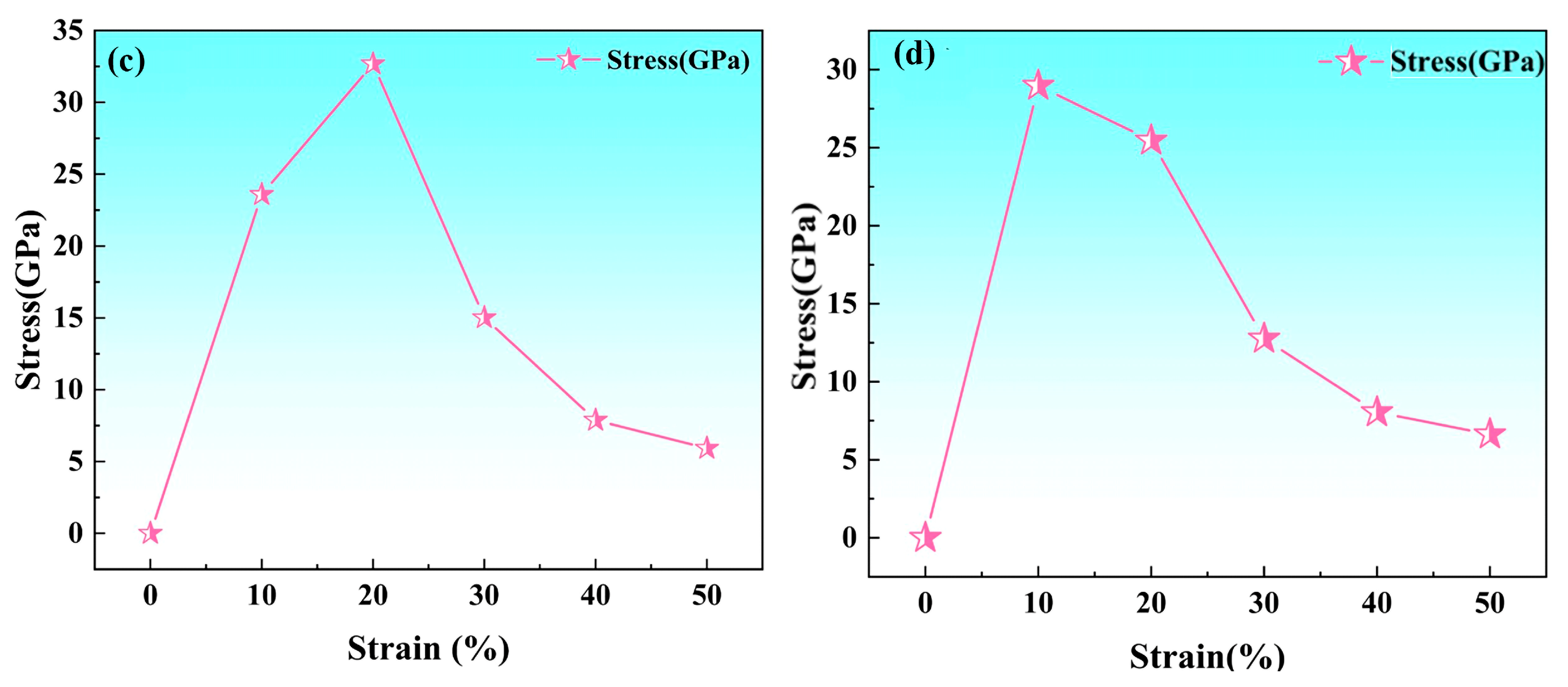
3.2.3. Stress-Strain Relationship
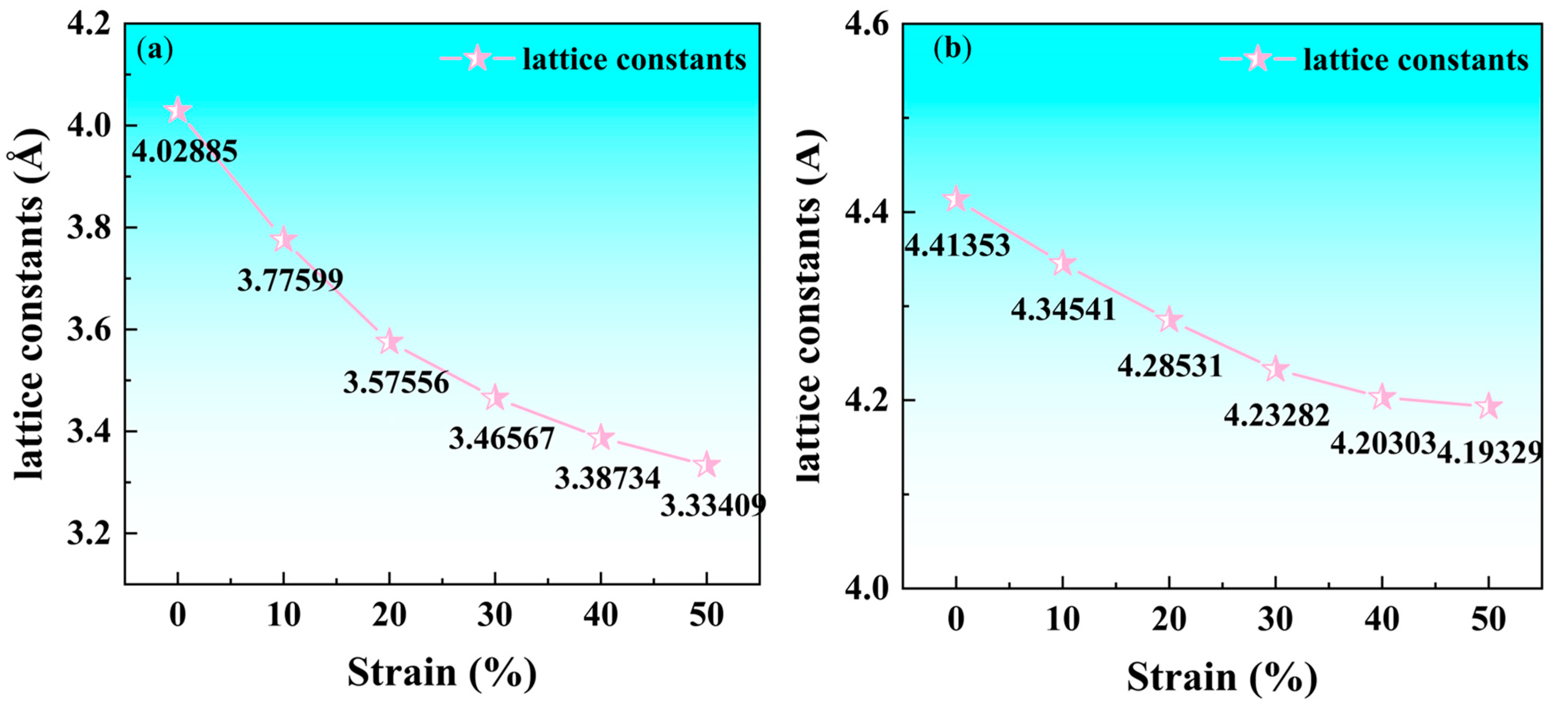
3.2.4. Lattice Constant
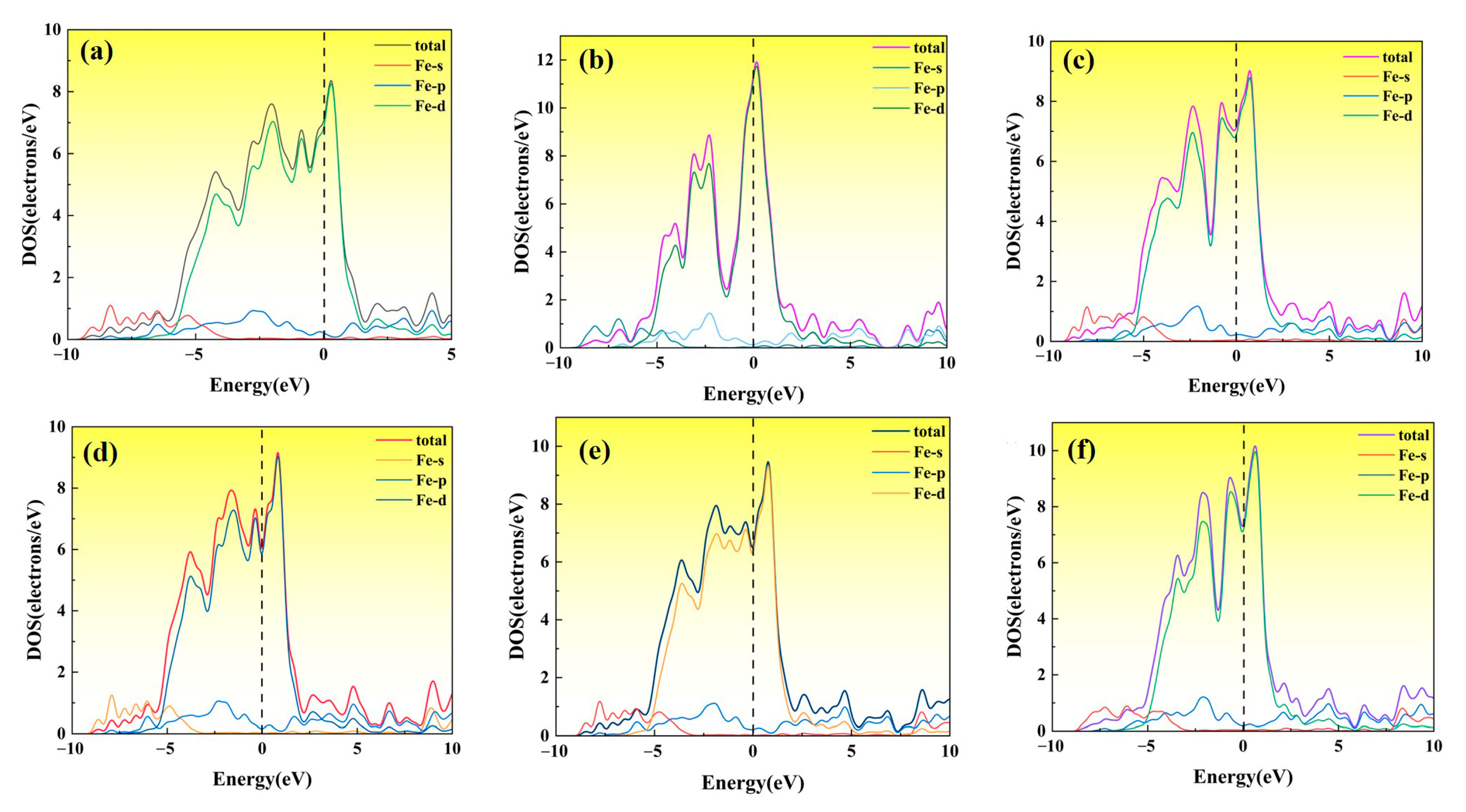
3.2.5. Density of States Under Strain
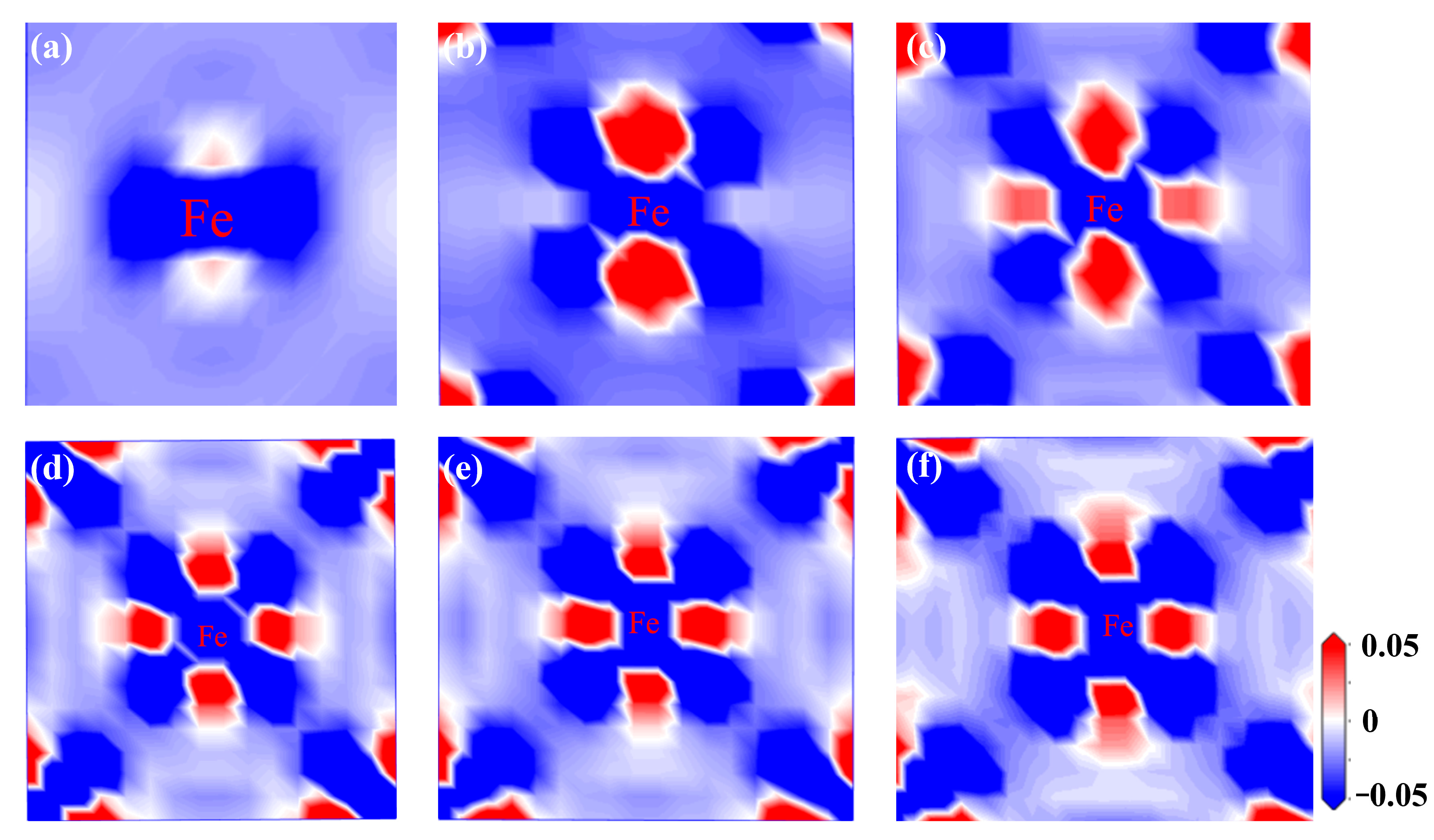
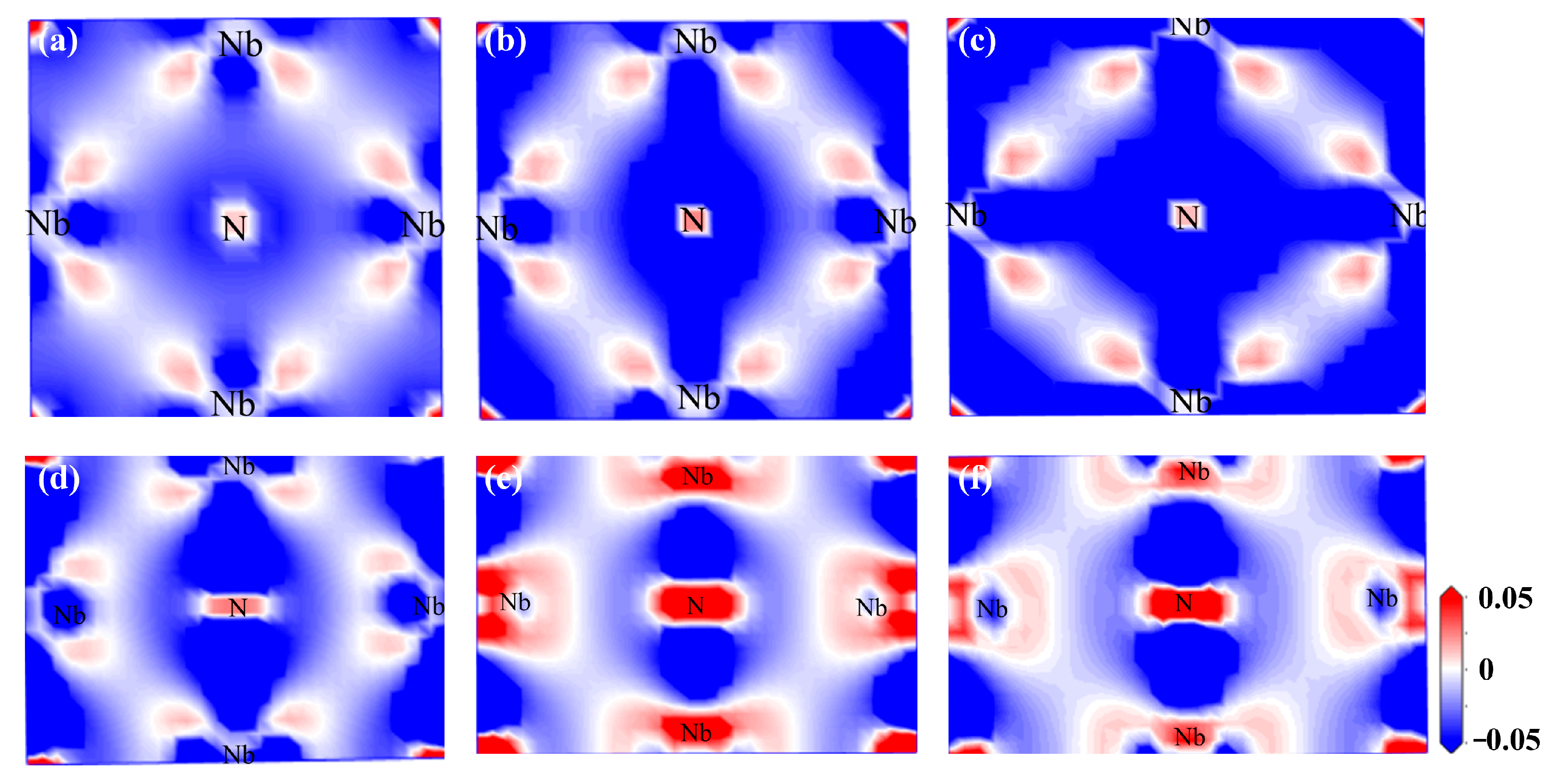
3.2.6. Differential Charge Density Under Strain
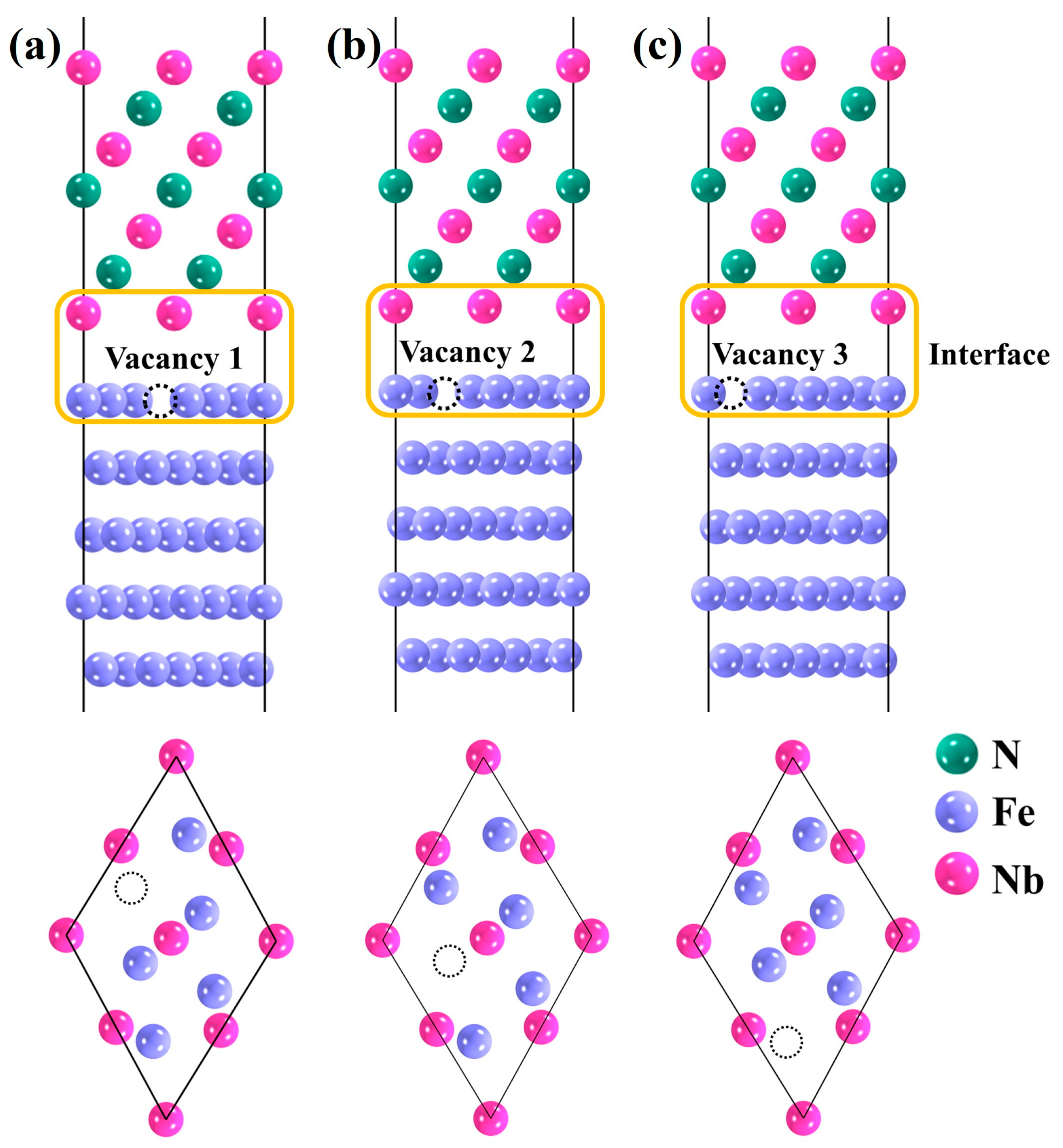
3.3. Defective Fe(111)/NbN(111) Interface Model
3.4. Nature of Fe(111)/NbN(111) Interface
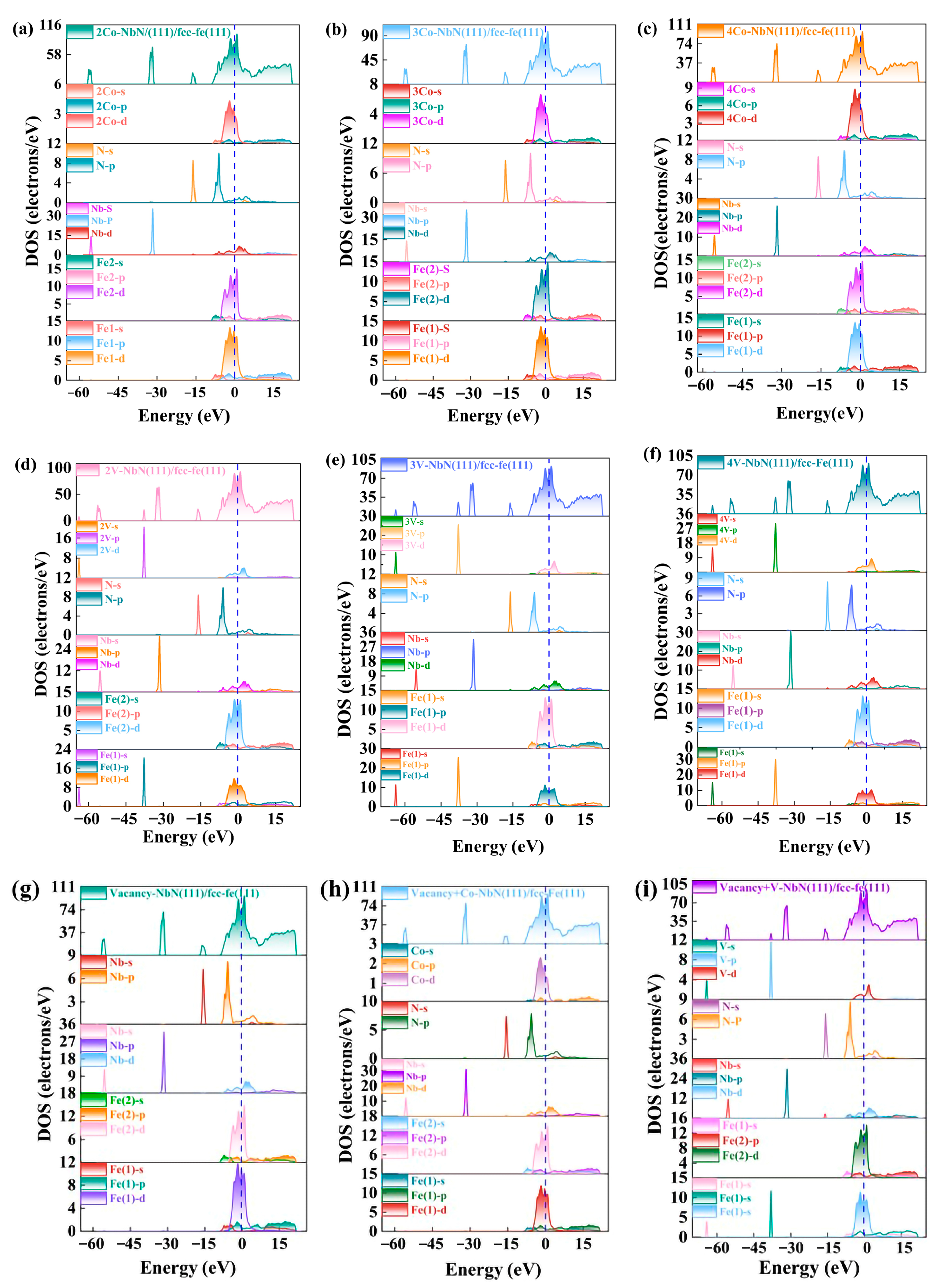
3.4.1. Density of States
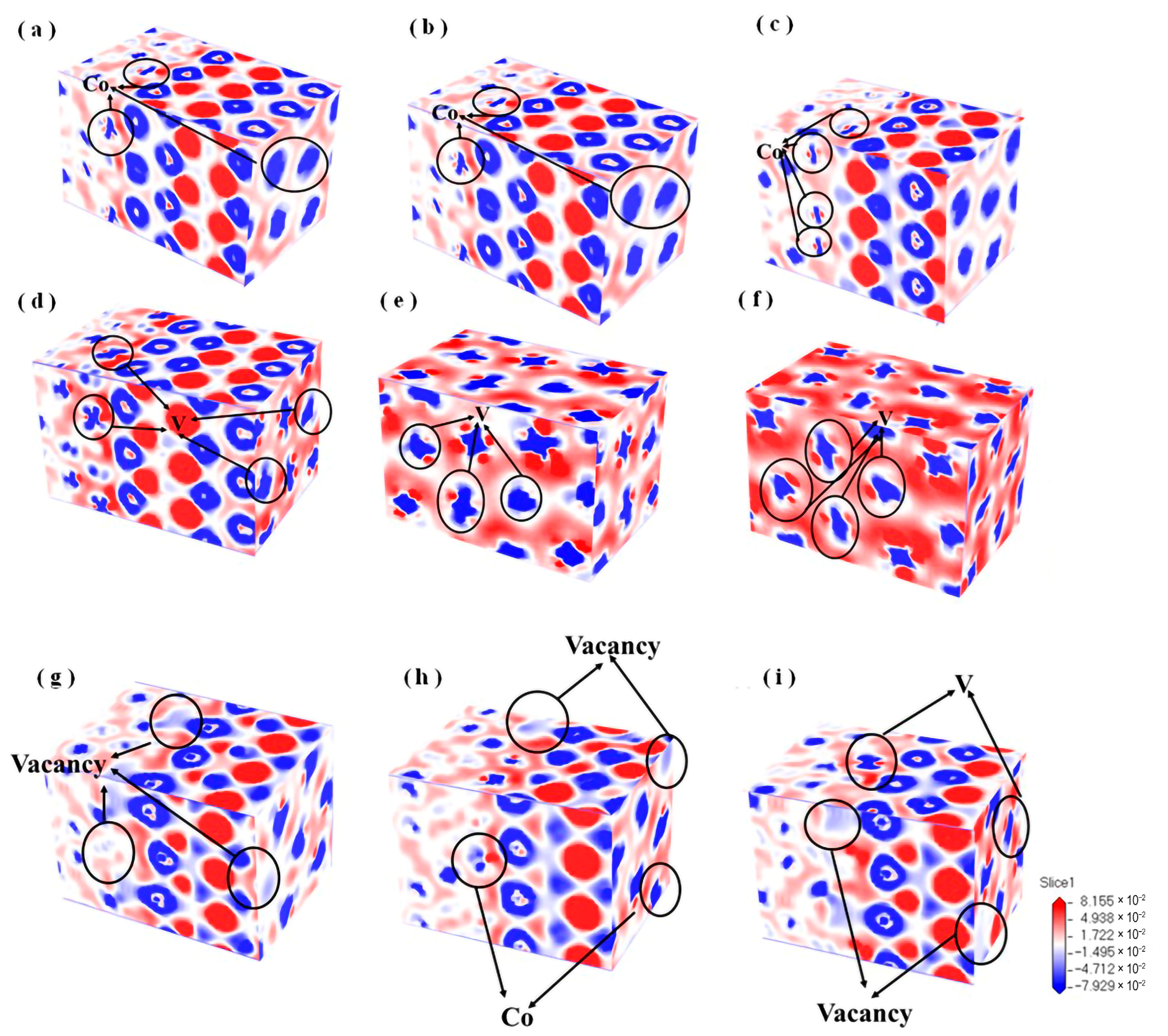
3.4.2. Differential Charge Density
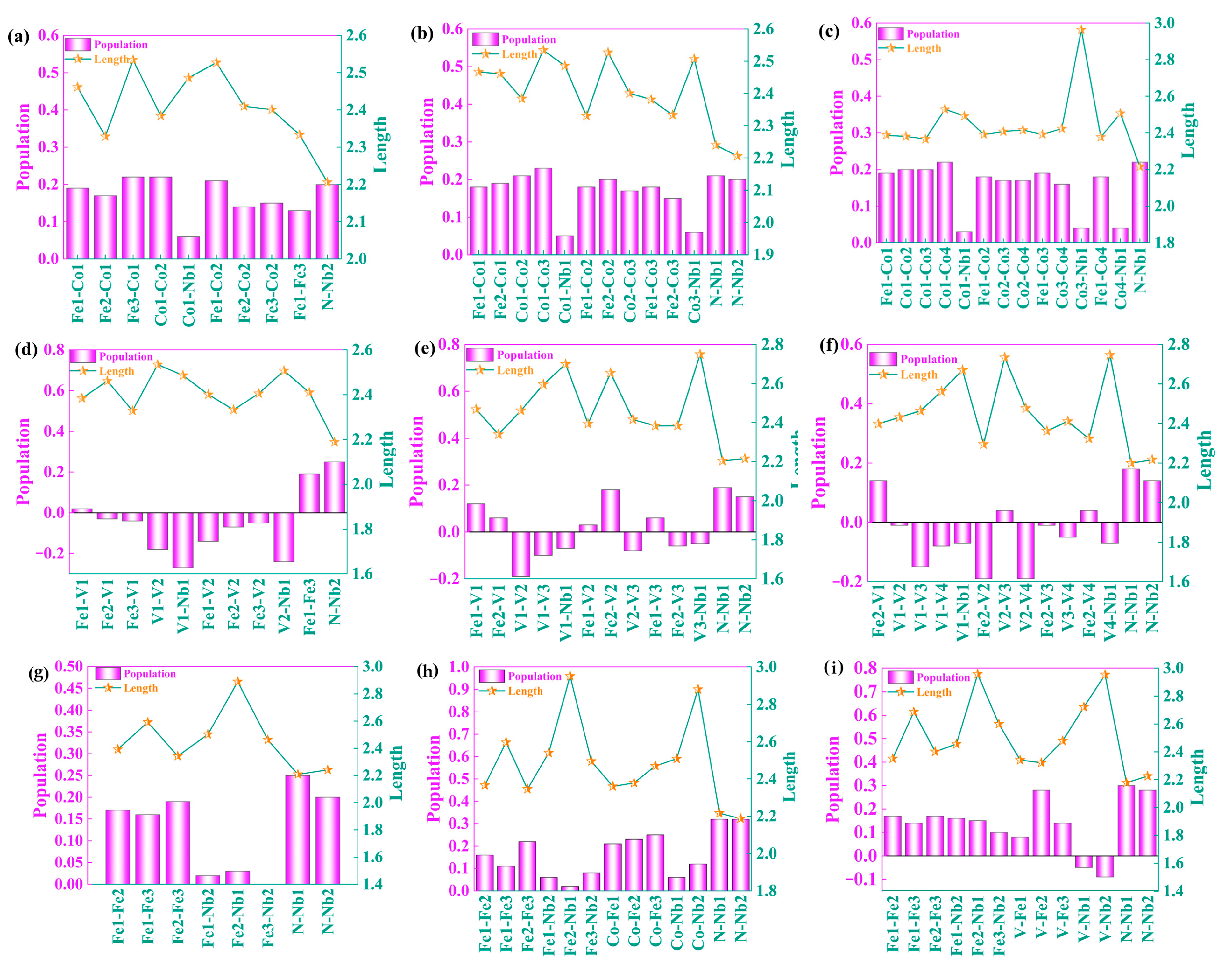
3.4.3. Population Analysis
4. Conclusions
- (1)
- For the bulk phases, the total density of states of fcc-Fe mainly comes from the contribution of the d-orbitals of Fe atoms, and NbN also has certain metallic features. The differential charge density maps indicate that the overall distribution of the two has a certain symmetry and high structural stability. The elastic modulus calculations indicate that both phases are elastically anisotropic and the degree of anisotropy in Young’s modulus, shear modulus, and Poisson’s ratio is more significant for NbN.
- (2)
- The fcc-Fe achieved a maximum tensile strength of 32.6 GPa when the tensile strain reaches 20%, and the stress gradually decreases as the strain increases when the strain exceeds 20%. While the maximum tensile strength of NbN is 29 GPa when the strain is 10%, and the stress decreases rapidly with the increase of strain. The unit cell lattice constants (b, c) decrease gradually with the increase of strain. Meanwhile, with the increasing of tensile strain, the fcc-Fe and NbN bulk phases experience the aggregation of charge, and the position of the intensity of the bonding peaks will undergo a change near the Fermi energy level. This indicates that the bulk phases suffer a large deformation with the increase of the strain, which leads to a decrease in the stability of the structure.
- (3)
- For the interface, the lowest formation energy of vacancy 3 is the optimal occupation site. The differential charge density results show that with the increase in the content of alloying element Co, the degree of charge density depletion around it gradually increases, and the covalent bonding characteristics between the interfacial atoms are significantly enhanced, resulting in enhanced stability of the interfacial structure. However, the increase in the content of alloying element V plays the opposite effect on the interfacial stability. At the same time, the introduction of vacancy leads to variations in the distribution of the surrounding electron clouds, enhancing the interactions between atoms and rendering the interface more stable.
- (4)
- The results of bond length and bond population are consistent with the results of DOS and DCD analysis. The increase of Co doping content can enhance the covalent bonding of atoms near the interface and further improve the binding ability of the interface. The optimal Co doping content is 3 atoms, and the optimal V doping content is 1 atom. The interfacial model containing vacancy and alloying element exhibits shorter bond length, larger bond population value and stronger covalence, which is conducive to improving the stability of the interface.
- (5)
- Looking ahead, adjusting the contents of Co and V appropriately in experiments can optimize interfacial properties. Notably, V is an alloying element effective in enhancing the thermal strength of steel, further improving the creep resistance of heat-resistant steels. Given the high cost of Co, which increases production expenses, leveraging the efficient strengthening properties of V as the primary means to enhance performance-supplemented by vacancy defect engineering to optimize interfacial stability-while controlling Co addition to achieve an optimal balance between cost and performance, provides actionable parameter guidance for engineering-scale steelmaking.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hou, J.; Gan, J.; Li, W.; Tian, H.; Luo, X.; Ju, J.; Zhou, Y.; Liu, S.; Yao, H.; Chen, Z.; et al. Exceptional high-temperature oxidation resistance and mechanisms of a novel chemically complex intermetallic alloy. Corros. Sci. 2023, 225, 111607. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Brady, M.P.; Lu, Z.P.; Liu, C.T.; Takeyama, M.; Maziasz, P.J.; Pint, B.A. Alumina-forming austenitic stainless steels strengthened by laves phase and MC carbide precipitates. Met. Mater. Trans. A 2007, 38, 2737–2746. [Google Scholar] [CrossRef]
- Nie, S.; Chen, Y.; Ren, X.; Sridharan, K.; Allen, T.R. Corrosion of alumina-forming austenitic steel Fe-20Ni-14Cr-3Al-0.6Nb-0.1Ti in supercritical water. J. Nucl. Mater. 2010, 399, 231–235. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, H.; Yang, R.; Liu, X.; Chen, X.; Qin, J.; McDonald, A.; Li, H. In-situ SEM investigation on stress-induced microstructure evolution of austenitic stainless steels subjected to cavitation erosion and cavitation erosion-corrosion. Mater. Des. 2022, 213, 110314. [Google Scholar] [CrossRef]
- Wan, L.; Wang, Q.; Ye, X.; Cao, X.; Jin, S.; Gao, T. Insight into structural stability and helium diffusion behavior of Fe-Cr alloys from first-principles. RSC Adv. 2020, 10, 3277–3292. [Google Scholar] [CrossRef]
- Çetin, M.; Günen, A.; Kalkandelen, M.; Karakas, M.S. Microstructural, wear and corrosion characteristics of boronized AISI 904L superaustenitic stainless steel. Vacuum 2021, 187, 110145. [Google Scholar] [CrossRef]
- Ajmal, M.; Lopez-Crespo, C.; Cruces, A.S.; Antunes, F.V.; Lopez-Crespo, P. On the use of the plastic component of the CTOD for fatigue analysis in austenitic stainless steel. Procedia Struct. Integr. 2022, 37, 964–976. [Google Scholar] [CrossRef]
- Panov, D.O.; Chernichenko, R.S.; Naumov, S.V.; Pertcev, A.S.; Stepanov, N.D.; Zherebtsov, S.V.; Salishchev, G.A. Excellent strength-toughness synergy in metastable austenitic stainless steel due to gradient structure formation. Mater. Lett. 2021, 303, 130585. [Google Scholar] [CrossRef]
- Zinovieva, O.; Zinoviev, A.; Romanova, V.; Balokhonov, R. Three-dimensional analysis of grain structure and texture of additively manufactured 316L austenitic stainless steel. Addit. Manuf. 2020, 36, 101521. [Google Scholar] [CrossRef]
- Kumar, P.; Jayaraj, R.; Suryawanshi, J.; Satwik, U.R.; McKinnell, J.; Ramamurty, U. Fatigue strength of additively manufactured 316L austenitic stainless steel. Acta Mater. 2020, 199, 225–239. [Google Scholar] [CrossRef]
- Kalal, S.; Gupta, M.; Rawat, R. N concentration effects on structure and superconductivity of NbN thin films. J. Alloys Compd. 2021, 851, 155925. [Google Scholar] [CrossRef]
- Ivashchenko, V.I.; Turchi, P.E.A.; Pavlova, N.Y.; Gorb, L.; Leszczynski, J. Temperature-and pressure-induced structural transformations in NbN: A first-principles study. Phys. B 2023, 663, 414998. [Google Scholar] [CrossRef]
- Wang, D.; Li, Q.; Jiao, X.; Ni, G.; Wang, S. Heterogeneous nucleation interface between NbN (111)and TiN (111) in high-nitrogen austenitic stainless steels: First-principles calculation. Mater. Today Commun. 2024, 40, 109554. [Google Scholar] [CrossRef]
- Banik, S.D.; Kumar, S.; Singh, P.K.; Bhattacharya, S.; Mahapatra, M.M. Distortion and residual stresses in thick plate weld joint of austenitic stainless steel: Experiments and analysis. J. Mater. Process. Technol. 2021, 289, 116944. [Google Scholar] [CrossRef]
- Lu, E.; Cao, X.; Jin, S.; Zhang, P.; Zhang, C.; Yang, J.; Wu, Y.; Guo, L.; Wang, B. Investigation of vacancy-type defects in helium irradiated FeCrNi alloy by slow positron beam. J. Nucl. Mater. 2015, 458, 240–244. [Google Scholar] [CrossRef]
- Iok, I.; Ishijima, Y.; Usami, K.; Sakuraba, N.; Kato, Y.; Kiuchi, K. Radiation hardening and IASCC susceptibility of extra high purity austenitic stainless steel. J. Nucl. Mater. 2011, 417, 887–891. [Google Scholar] [CrossRef]
- Edwards, D.J.; Garner, F.A.; Bruemmer, S.M.; Efsing, P. Nano-cavities observed in a 316SS PWR flux thimble tube irradiated to 33 and 70 dpa. J. Nucl. Mater. 2009, 384, 249–255. [Google Scholar] [CrossRef]
- Schvartzman, M.M.D.A.M.; Quinan, M.A.D.; Campos, W.R.D.C.; Lima, L.I.L. Stress corrosion cracking of the AISI 316L stainless steel HAZ in a PWR nuclear reactor environment. Weld. Int. 2011, 25, 15–23. [Google Scholar] [CrossRef]
- Katsura, R.; Morisawa, J.; Kawano, S.; Oliver, B.M. Post-irradiation annealing effect on helium diffusivity in austenitic stainless steels. J. Nucl. Mater. 2004, 329, 668–672. [Google Scholar] [CrossRef]
- Gong, Y.; Jin, S.; Zhu, T.; Cheng, L.; Cao, X.; You, L.; Lu, G.; Guo, L.; Wang, B. Helium self-trapping and diffusion behaviors in deformed 316L stainless steel exposed to high flux and low energy helium plasma. Nucl. Fusion 2018, 58, 046011. [Google Scholar] [CrossRef]
- Shen, Y.F.; Li, X.X.; Sun, X.; Wang, Y.D.; Zuo, L. Twinning and martensite in a 304 austenitic stainless steel. Mat. Sci. Eng. A-struct. 2012, 552, 514–522. [Google Scholar] [CrossRef]
- Sathiya, P.; Aravindan, S.; Haq, A.N. Mechanical and metallurgical properties of friction welded AISI 304 austenitic stainless steel. Int. J. Adv. Manuf. Technol. 2005, 26, 505–511. [Google Scholar] [CrossRef]
- Mierzejewska, Ż.A.; Oksiut, Z. Isolated fracture of the hip stem prosthesis made of austenitic steel-a literature review. Pol. Orthop. Traumatol. 2014, 79, 145–153. [Google Scholar]
- Hao, Y.; Yu, S.; Cao, P.J.; Li, K.J. Research status of failure mechanisms of heat-resistant steel in thermal power units. Heat Treat. Met. 2021, 46, 14–24. [Google Scholar]
- Vahrusheva, V.; Hlushkova, D.; Volchuk, V. Increasing the corrosion resistance of heat-resistant alloys for parts of power equipment. Boпpocы Aтoмнoй Нayки и Mexники 2022, 140, 137–140. [Google Scholar] [CrossRef]
- Liang, Z.; Gui, Y.; Wang, Y.; Zhao, Q. Corrosion performance of heat-resisting steels and alloys in supercritical carbon dioxide at 650 C and 15 MPa. Energy 2019, 175, 345–352. [Google Scholar] [CrossRef]
- Achmad, T.L.; Fu, W.; Chen, H.; Zhang, C.; Yang, Z.-G. Effects of alloying elements concentrations and temperatures on the stacking fault energies of Co-based alloys by computational thermodynamic approach and first-principles calculations. J. Alloys Compd. 2017, 694, 1265–1279. [Google Scholar] [CrossRef]
- Song, K.; Cao, S.; Bao, Y.; Qian, P.; Su, Y. Designing hydrogen embrittlement-resistant grain boundary in steel by alloying elements segregation: First-principles calculations. Appl. Surf. Sci. 2024, 656, 159684. [Google Scholar] [CrossRef]
- Labudovic, M.; Hu, D.; Kovacevic, R. A three dimensional model for direct laser metal powder deposition and rapid prototyping. J. Mater. Sci. 2003, 38, 35–49. [Google Scholar] [CrossRef]
- Appleyard, D. Powering up on powder technology. Met. Powder Rep. 2015, 70, 285–289. [Google Scholar] [CrossRef]
- Ren, J.; Hou, P.; Gao, Q.; Wang, Q.; Bai, Y.; Li, J.; Xue, H.; Lu, X.; Tang, F. A comparative study of the interfacial bonding properties and thermodynamic properties of bcc-Fe/MeAl (Me = Ni, Ti, Fe) interfaces based on first-principles methods. J. Phys. Chem. Solids 2025, 202, 112679. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, J.; Liu, D.; Chen, B.; Bai, Z.; Yang, P.; Ren, J.; Lu, X. Influence of alloying elements on the stability and segregation behavior of fcc-Fe/NbN interface by simulation. Vacuum 2024, 228, 113479. [Google Scholar] [CrossRef]

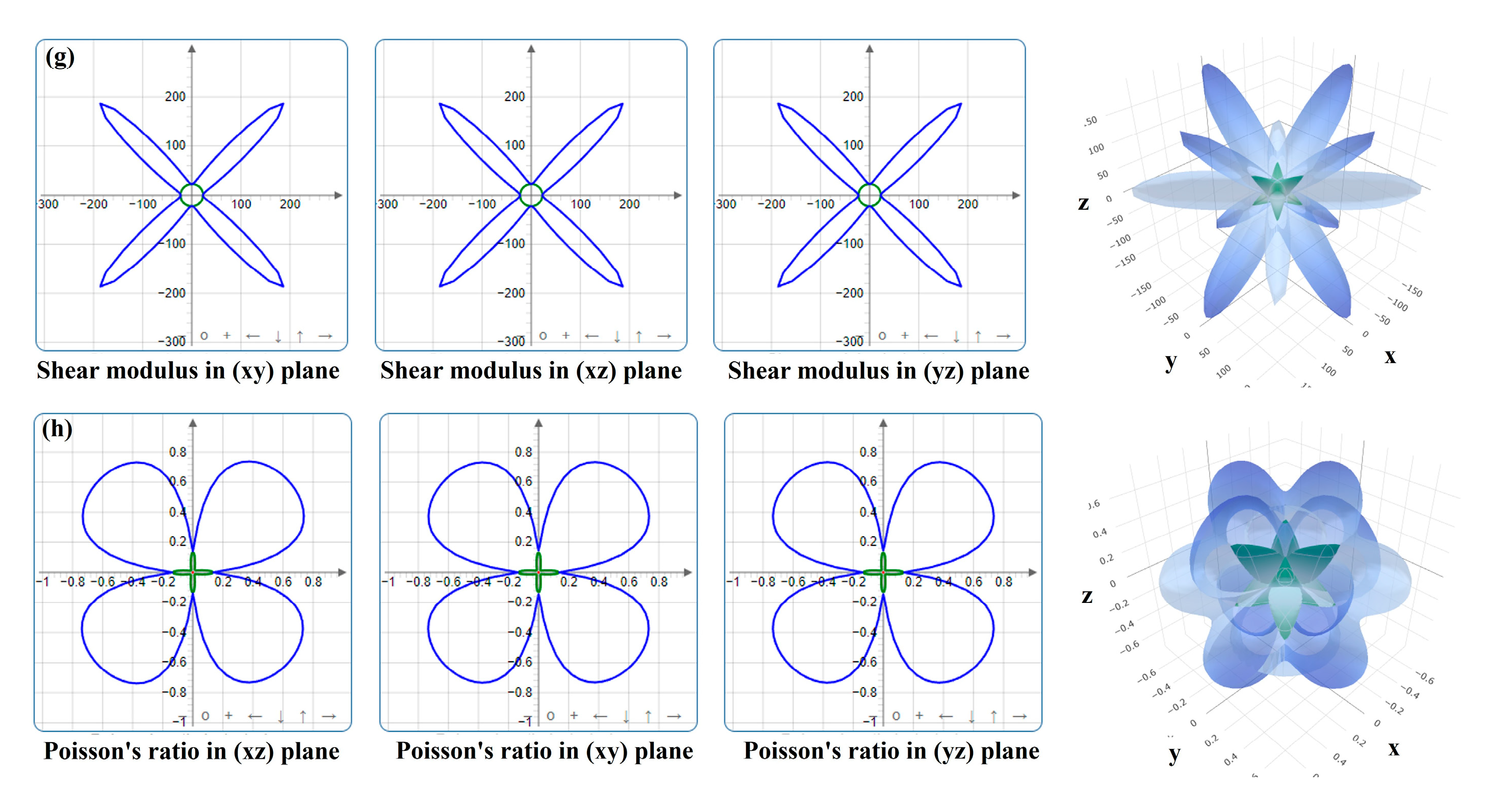




| Phases | Young’s Modulus (GPa) | Linear Coefficient (TPa−1) | Shear Modulus (GPa) | Poisson’s Ration | |||||
|---|---|---|---|---|---|---|---|---|---|
| Emin | Emax | βmin | βmax | Gmin | Gmax | υmin | υmax | ||
| fcc-Fe | Values | 322.53 | 616.36 | 1.16 | 1.16 | 122.80 | 269.98 | 0.01 | 0.48 |
| Anisotropy | 1.88 | 1 | 2.09 | ∞ | |||||
| NbN | Values | 66.63 | 599.25 | 1.16 | 1.28 | 22.92 | 263.44 | 0.02 | 0.88 |
| Anisotropy | 8.93 | 1.10 | 11.49 | 46.21 | |||||
| Vacancy | 1 | 2 | 3 |
|---|---|---|---|
| 0.664 | 0.649 | 0.648 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhao, X.; Zhang, J.; Sheng, J.; Ren, J.; Lu, X.; Tang, X. Investigation on the Influence of Vacancy and Alloying Element Content on the Performance of Fe/NbN Interface. Metals 2025, 15, 759. https://doi.org/10.3390/met15070759
Zhang S, Zhao X, Zhang J, Sheng J, Ren J, Lu X, Tang X. Investigation on the Influence of Vacancy and Alloying Element Content on the Performance of Fe/NbN Interface. Metals. 2025; 15(7):759. https://doi.org/10.3390/met15070759
Chicago/Turabian StyleZhang, Shuangwu, Xiaolong Zhao, Jiayin Zhang, Jie Sheng, Junqiang Ren, Xuefeng Lu, and Xingchang Tang. 2025. "Investigation on the Influence of Vacancy and Alloying Element Content on the Performance of Fe/NbN Interface" Metals 15, no. 7: 759. https://doi.org/10.3390/met15070759
APA StyleZhang, S., Zhao, X., Zhang, J., Sheng, J., Ren, J., Lu, X., & Tang, X. (2025). Investigation on the Influence of Vacancy and Alloying Element Content on the Performance of Fe/NbN Interface. Metals, 15(7), 759. https://doi.org/10.3390/met15070759






