CFD Modelling of Flow and Solids Distribution in Carbon-in-Leach Tanks
Abstract
:1. Introduction
2. Literature Review
3. Model Description
3.1. Governing Equations
| Description | Equations |
|---|---|
| Liquid-phase stress tensor | |
| Solid-phase stress tensor | |
| Solid shear viscosity | |
| Collisional viscosity | |
| Kinetic viscosity | |
| Frictional viscosity | |
| Solids pressure | |
| Radial distribution function | |
| Diffusion coefficient of granular temperature | |
| where | |
| Collision dissipation energy |
3.2. Turbulent Dispersion Force
3.3. Interphase Drag Force
4. Methodology and Boundary Conditions
4.1. Vessel Geometry

| Tank (m) | PBTD (m) | HA-715 | |||
|---|---|---|---|---|---|
| T | 0.288, 10 | D | T/2 | D | T/2, T/3 |
| H | T | Bl | 0.055 | Dshaft | 0.01152 |
| W | T/10 | Bw | 0.041 | - | - |
| Ci | T/2, T/3, T/4, T/6, T/8 | Dshaft | 0.01 | - | - |
| Dhub | 0.034 | - | - | ||
| Name of Case | X (wt. %) | N = Njs (RPM) | ρl (kg/m3) | µl (Pa·s) | ρp (kg/m3) | dp (mm) |
|---|---|---|---|---|---|---|
| PBTD-Validation | 40 | 589.8 | 1150 | 0.001 | 2585 | 3 |
| CIL tanks (Lab Scale) | 50 | 200–700 | 1000 | 0.001 | 2550 | 0.075 |
| CIL tanks (Full Scale) | 50 | 22.15 | 1000 | 0.001 | 2550 | 0.075 |
4.2. Numerical Simulations
5. Results and Discussion
5.1. Grid Independency and Validation
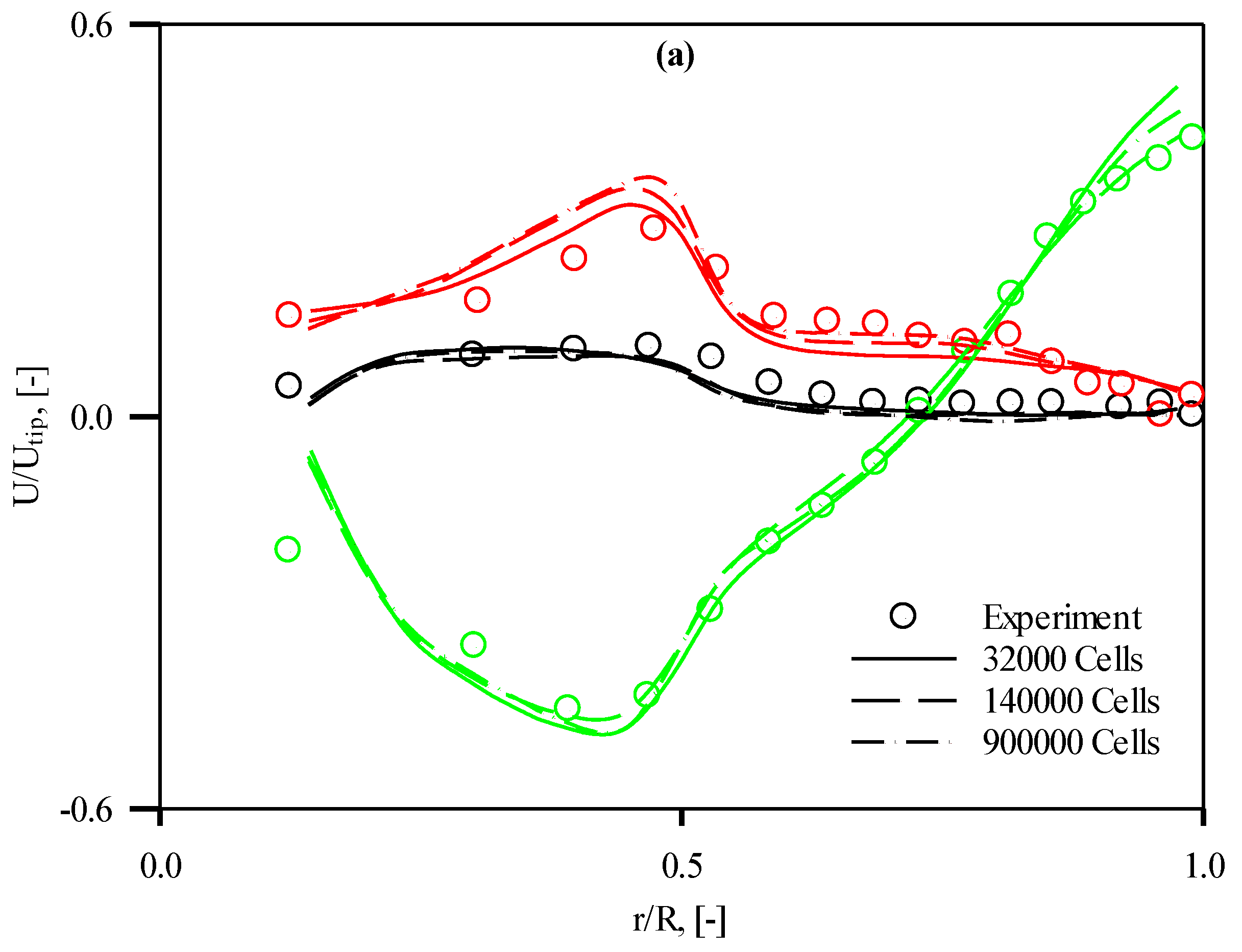

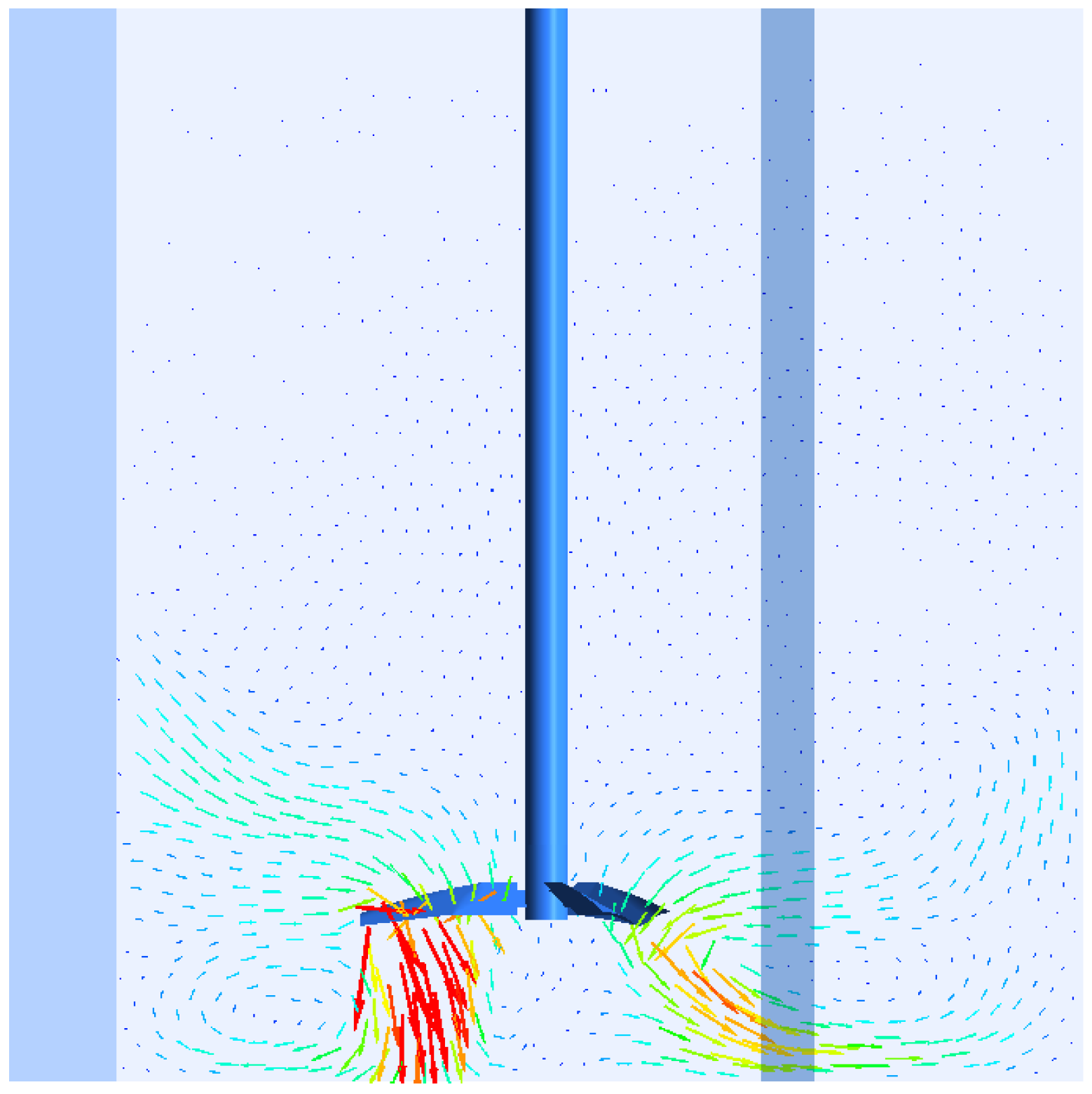
5.2. Flow Field

5.3. Concentration Profiles

5.4. Suspension Quality and Power Consumption

5.5. Scale-Up

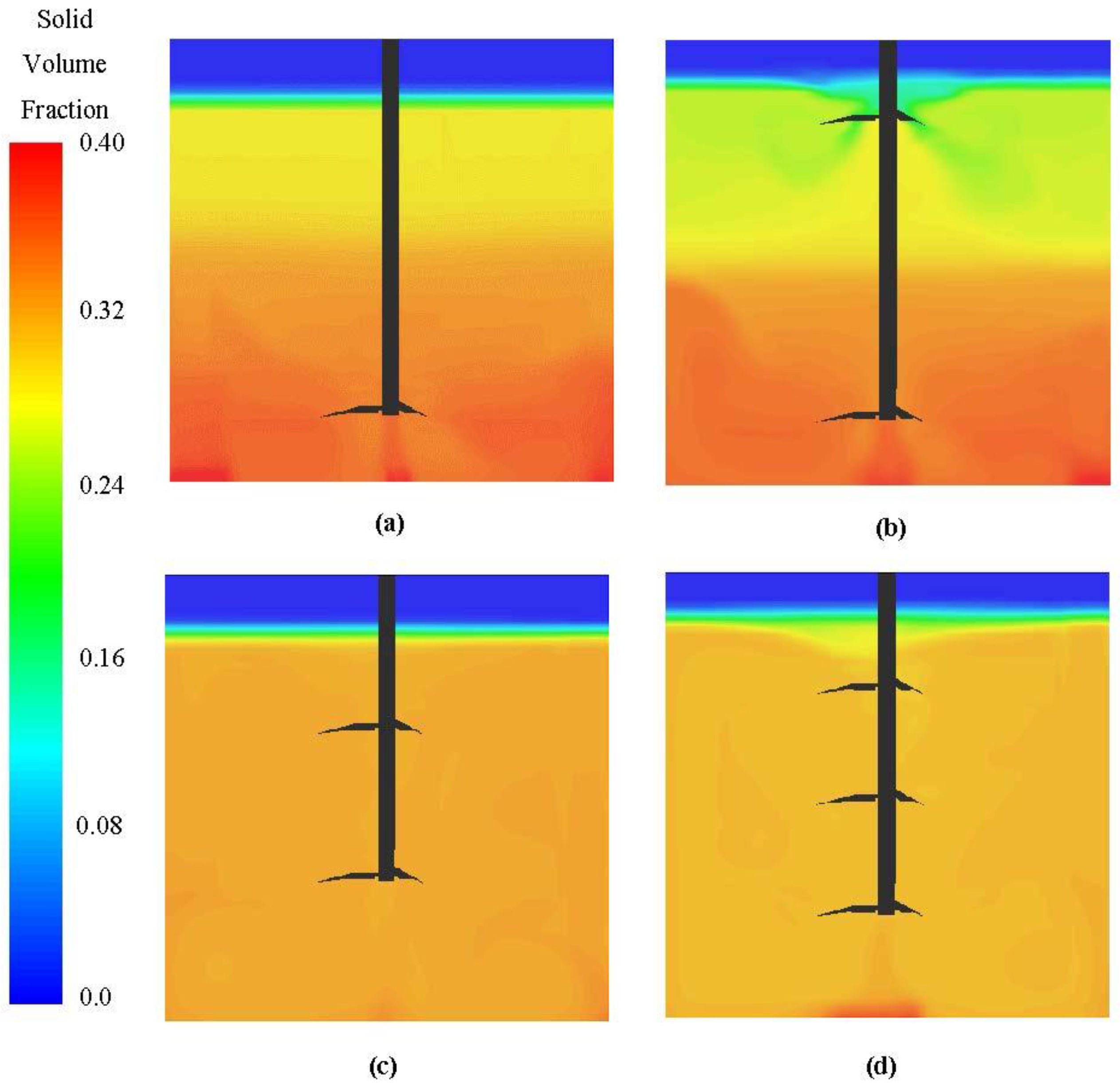
5.6. Multiple-Impeller Systems
| Variable | Twin-CT6 | Twin-CT3 | Triple-CT4 |
|---|---|---|---|
| Off-bottom clearance, Ci | T/6 | T/3 | T/4 |
| Distance between impellers, CiD | 2T/3 | T/3 | T/4 |
6. Conclusions
- The Euler-Euler simulation approach with KTGF, Syamlal drag model, RSM turbulence model and turbulent dispersion force model appropriately predict the local hydrodynamics in high solid loading stirred tank systems.
- For a given power consumption, the flow generated by the HA-715 impeller is more dominant than the PBTD.
- The low off-bottom clearance is favorable in achieving homogeneity at low impeller speed for lab scale CIL tanks.
- For scale-up, multiple impeller systems are necessary for providing kinetic energy in the upper half of the CIL tanks.
- While a low off-bottom clearance is suitable for solid suspension, solids can however accumulate at the bottom center in full scale CIL tanks due to weak secondary loops.
- The dual impeller configuration with T/3 clearance and triple impeller configuration with T/4 clearance minimize the problems encountered in the CIL tanks. Additional impellers require approximately 6 kW of extra power in CIL tanks.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Bl | blade length, m |
| Bw | blade width, m |
| Ci | impeller clearance, m |
| CiD | impeller-impeller distance, m |
| C | concentration in volume percent, (-) |
| Cav | average concentration in volume percent, (-) |
| CD | drag coefficient, (-) |
| CDo | particle drag coefficient in still fluid |
| CH | cloud height, m |
| D or Di | impeller diameter, m |
| Dshaft | shaft diameter, m |
| Dhub | hub diameter, m |
| dP | particle diameter, m |
| force due to turbulent dissipation, kg·m/s2 | |
| external force, kg·m/s2 | |
| lift force, kg·m/s2 | |
| virtual mass force, kg·m/s2 | |
| interphase interaction force, kg·m/s2 | |
| g | acceleration due to gravity, m/s2 |
| production of turbulence kinetic energy, kg·m2/s2 | |
| H | tank height, m |
| unit stress tensor, Pa | |
| k | turbulence kinetic energy per unit mass, m2/s2 |
| M | torque, N·m |
| N | impeller speed, 1/min |
| Njs | speed of just suspension, 1/min |
| NRe | Reynolds number, (-) |
| NP | power number, (-) |
| NQ | pumping number, (-) |
| p | pressure and is shared by both the phases, Pa |
| P | power delivered to the fluid, W |
| T | tank diameter, m |
| velocity vector, m/s | |
| drift velocity, m/s | |
| Utip | Impeller tip velocity, m/s |
| Greek Letters | |
| α | volume fraction |
| γ | shear rate, 1/s |
| ε | turbulence dissipation rate, m2/s3 |
| εb | bulk turbulence dissipation rate, m2/s3 |
| λ | Kolmogorov length scale, m |
| μ | shear viscosity, Pa·s |
| μt | turbulent viscosity, m2/s |
| ρ | density kg/m3 |
| σ | Prandtl numbers |
| σsl | dispersion Prandtl number |
| τ | shear stress, Pa |
| stress tensor, Pa | |
| θm | mixing time, s |
| υ | bulk viscosity |
| Subscripts | |
| 1 or l | continuous or primary phase |
| 2 or s | dispersed or secondary phase |
| m | mixture properties |
| z | axial point |
References
- Barigou, M. Particle tracking in opaque mixing systems: An overview of the capabilities of PET and PEPT. Chem. Eng. Res. Des. 2004, 82, 1258–1267. [Google Scholar] [CrossRef]
- Stevenson, R.; Harrison, S.T.L.; Mantle, M.D.; Sederman, A.J.; Moraczewski, T.L.; Johns, M.L. Analysis of partial suspension in stirred mixing cells using both MRI and ERT. Chem. Eng. Sci. 2010, 65, 1385–1393. [Google Scholar] [CrossRef]
- Guida, A.; Nienow, A.W.; Barigou, M. PEPT measurements of solid-liquid flow field and spatial phase distribution in concentrated monodisperse stirred suspensions. Chem. Eng. Sci. 2010, 65, 1905–1914. [Google Scholar] [CrossRef]
- Altway, A.; Setyawan, H.; Winardi, S. Effect of particle size on simulation of three-dimensional solid dispersion in stirred tank. Chem. Eng. Res. Des. 2001, 79, 1011–1016. [Google Scholar] [CrossRef]
- Micale, G.; Grisafi, F.; Rizzuti, L.; Brucato, A. CFD simulation of particle suspension height in stirred vessels. Chem. Eng. Res. Des. 2004, 82, 1204–1213. [Google Scholar] [CrossRef]
- Ochieng, A.; Lewis, A.E. Nickel solids concentration distribution in a stirred tank. Miner. Eng. 2006, 19, 180–189. [Google Scholar] [CrossRef]
- Fradette, L.; Tanguy, P.A.; Bertrand, F.; Thibault, F.; Ritz, J.-B.; Giraud, E. CFD phenomenological model of solid-liquid mixing in stirred vessels. Comput. Chem. Eng. 2007, 31, 334–345. [Google Scholar] [CrossRef]
- Ochieng, A.; Onyango, M.S. Drag models, solids concentration and velocity distribution in a stirred tank. Powder Technol. 2008, 181, 1–8. [Google Scholar] [CrossRef]
- Kasat, G.R.; Khopkar, A.R.; Ranade, V.V.; Pandit, A.B. CFD simulation of liquid-phase mixing in solid-liquid stirred reactor. Chem. Eng. Sci. 2008, 63, 3877–3885. [Google Scholar] [CrossRef]
- Fletcher, D.F.; Brown, G.J. Numerical simulation of solid suspension via mechanical agitation: Effect of the modelling approach, turbulence model and hindered settling drag law. Int. J. Comput. Fluid Dyn. 2009, 23, 173–187. [Google Scholar] [CrossRef]
- Tamburini, A.; Cipollina, A.; Micale, G.; Ciofalo, M.; Brucato, A. Dense solid-liquid off-bottom suspension dynamics: Simulation and experiment. Chem. Eng. Res. Des. 2009, 87, 587–597. [Google Scholar] [CrossRef]
- Tamburini, A.; Cipollina, A.; Micale, G.; Brucato, A.; Ciofalo, M. CFD simulations of dense solid-liquid suspensions in baffled stirred tanks: Prediction of suspension curves. Chem. Eng. J. 2011, 178, 324–341. [Google Scholar] [CrossRef]
- Tamburini, A.; Cipollina, A.; Micale, G.; Brucato, A.; Ciofalo, M. CFD simulations of dense solid-liquid suspensions in baffled stirred tanks: Prediction of the minimum impeller speed for complete suspension. Chem. Eng. J. 2012, 193–194, 234–255. [Google Scholar] [CrossRef]
- Gohel, S.; Joshi, S.; Azhar, M.; Horner, M.; Padron, G. CFD modeling of solid suspension in a stirred tank: Effect of drag models and turbulent dispersion on cloud height. Int. J. Chem. Eng. 2012. [Google Scholar] [CrossRef]
- Liu, L.; Barigou, M. Numerical modelling of velocity field and phase distribution in dense monodisperse solid-liquid suspensions under different regimes of agitation: CFD and PEPT experiments. Chem. Eng. Sci. 2013, 101, 837–850. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]
- Dagadu, C.P.K.; Akaho, E.H.K.; Danso, K.A.; Stegowski, Z.; Furman, L. Radiotracer investigation in gold leaching tanks. Appl. Radiat. Isot. 2012, 70, 156–161. [Google Scholar] [CrossRef] [PubMed]
- Dagadu, C.P.K.; Stegowski, Z.; Furman, L.; Akaho, E.H.K.; Danso, K.A. Determination of flow structure in a gold leaching tank by CFD simulation. J. Appl. Math. Phys. 2014, 2, 510–519. [Google Scholar] [CrossRef]
- Dagadu, C.P.K.; Stegowski, Z.; Sogbey, B.J.A.Y.; Adzaklo, S.Y. Mixing analysis in a stirred tank using computational fluid dynamics. J. Appl. Math. Phys. 2015, 3, 637–642. [Google Scholar] [CrossRef] [Green Version]
- Aubin, J.; Fletcher, D.F.; Xuereb, C. Modeling turbulent flow in stirred tanks with CFD: The influence of the modeling approach, turbulence model and numerical scheme. Exp. Therm. Fluid Sci. 2004, 28, 431–445. [Google Scholar] [CrossRef]
- Montante, G.; Magelli, F. Modelling of solids distribution in stirred tanks: Analysis of simulation strategies and comparison with experimental data. Int. J. Comput. Fluid Dyn. 2005, 19, 253–262. [Google Scholar] [CrossRef]
- Fan, L.; Mao, Z.; Wang, Y. Numerical simulation of turbulent solid-liquid two-phase flow and orientation of slender particles in a stirred tank. Chem. Eng. Sci. 2005, 60, 7045–7056. [Google Scholar] [CrossRef]
- Khopkar, A.R.; Kasat, G.R.; Pandit, A.B.; Ranade, V.V. Computational fluid dynamics simulation of the solid suspension in a stirred slurry reactor. Ind. Eng. Chem. Res. 2006, 45, 4416–4428. [Google Scholar] [CrossRef]
- Ljungqvist, M.; Rasmuson, A. Numerical simulation of the two-phase flow in an axially stirred vessel. Chem. Eng. Res. Des. 2001, 79, 533–546. [Google Scholar] [CrossRef]
- Micale, G.; Montante, G.; Grisafi, F.; Brucato, A.; Godfrey, J. CFD simulation of particle distribution in stirred vessels. Chem. Eng. Res. Des. 2000, 78, 435–444. [Google Scholar] [CrossRef]
- Murthy, B.N.; Joshi, J.B. Assessment of standard k-ε, RSM and LES turbulence models in a baffled stirred vessel agitated by various impeller designs. Chem. Eng. Sci. 2008, 63, 5468–5495. [Google Scholar] [CrossRef]
- Derksen, J.; Akker, V.D.; Harry, E.A. Large eddy simulations on the flow driven by a rushton turbine. AlChE J. 1999, 45, 209–221. [Google Scholar] [CrossRef]
- Burns, A.D.; Frank, T.; Hamill, I.; Shi, J.-M. The favre averaged drag model for turbulent dispersion in eulerian multi-phase flows. In Proceedings of the 5th International Conference on Multiphase Flow, ICMF, Yokohama, Japan, 30 May–4 June 2004. Paper No. 392.
- Syamlal, M.; Rogers, W.; O’Brien, T.J. Mfix Documentation: Theory Guide. Available online: https://mfix.netl.doe.gov/documentation/Theory.pdf (accessed on 26 October 2015).
- Del Valle, V.H.; Kenning, D.B.R. Subcooled flow boiling at high heat flux. Int. J. Heat Mass Transfer 1985, 28, 1907–1920. [Google Scholar] [CrossRef]
- Zwietering, T.N. Suspending of solid particles in liquid by agitators. Chem. Eng. Sci. 1958, 8, 244–253. [Google Scholar] [CrossRef]
- Hicks, M.T.; Myers, K.J.; Bakker, A. Cloud height in solids suspension agitation. Chem. Eng. Commun. 1997, 160, 137–155. [Google Scholar] [CrossRef]
- Bittorf, K.J.; Kresta, S.M. Prediction of cloud height for solid suspensions in stirred tanks. Chem. Eng. Res. Des. 2003, 81, 568–577. [Google Scholar] [CrossRef]
- Zhao, H.-L.; Lv, C.; Liu, Y.; Zhang, T.-A. Process optimization of seed precipitation tank with multiple impellers using computational fluid dynamics. JOM 2015, 67, 1451–1458. [Google Scholar] [CrossRef]
- Tamburini, A.; Cipollina, A.; Micale, G.; Brucato, A.; Ciofalo, M. CFD simulations of dense solid-liquid suspensions in baffled stirred tanks: Prediction of solid particle distribution. Chem. Eng. J. 2013, 223, 875–890. [Google Scholar] [CrossRef]
- Armenante, P.M.; Mazzarotta, B.; Chang, G.-M. Power consumption in stirred tanks provided with multiple pitched-blade turbines. Ind. Eng. Chem. Res. 1999, 38, 2809–2816. [Google Scholar] [CrossRef]
- Buurman, C.; Resoort, G.; Plaschkes, A. Scaling-up rules for solids suspension in stirred vessels. Chem. Eng. Sci. 1986, 41, 2865–2871. [Google Scholar] [CrossRef]
- Magelli, F.; Fajner, D.; Nocentini, M.; Pasquali, G. Solid distribution in vessels stirred with multiple impellers. Chem. Eng. Sci. 1990, 45, 615–625. [Google Scholar] [CrossRef]
- Montante, G.; Pinelli, D.; Magelli, F. Scale-up criteria for the solids distribution in slurry reactors stirred with multiple impellers. Chem. Eng. Sci. 2003, 58, 5363–5372. [Google Scholar] [CrossRef]
- Barresi, A.; Baldi, G. Solid dispersion in an agitated vessel. Chem. Eng. Sci. 1987, 42, 2949–2956. [Google Scholar] [CrossRef]
- Montante, G.; Bourne, J.R.; Magelli, F. Scale-up of solids distribution in slurry, stirred vessels based on turbulence intermittency. Ind. Eng. Chem. Res. 2008, 47, 3438–3443. [Google Scholar] [CrossRef]
- Ibrahim, S.; Nienow, A.W. Comparing impeller performance for solid-suspension in the transitional flow regime with newtonian fluids. Chem. Eng. Res. Des. 1999, 77, 721–727. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wadnerkar, D.; Pareek, V.K.; Utikar, R.P. CFD Modelling of Flow and Solids Distribution in Carbon-in-Leach Tanks. Metals 2015, 5, 1997-2020. https://doi.org/10.3390/met5041997
Wadnerkar D, Pareek VK, Utikar RP. CFD Modelling of Flow and Solids Distribution in Carbon-in-Leach Tanks. Metals. 2015; 5(4):1997-2020. https://doi.org/10.3390/met5041997
Chicago/Turabian StyleWadnerkar, Divyamaan, Vishnu K. Pareek, and Ranjeet P. Utikar. 2015. "CFD Modelling of Flow and Solids Distribution in Carbon-in-Leach Tanks" Metals 5, no. 4: 1997-2020. https://doi.org/10.3390/met5041997
APA StyleWadnerkar, D., Pareek, V. K., & Utikar, R. P. (2015). CFD Modelling of Flow and Solids Distribution in Carbon-in-Leach Tanks. Metals, 5(4), 1997-2020. https://doi.org/10.3390/met5041997






