Grain Boundary Assemblies in Dynamically-Recrystallized Austenitic Stainless Steel
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Stress-Strain Curves
3.2. Deformation Microstructures
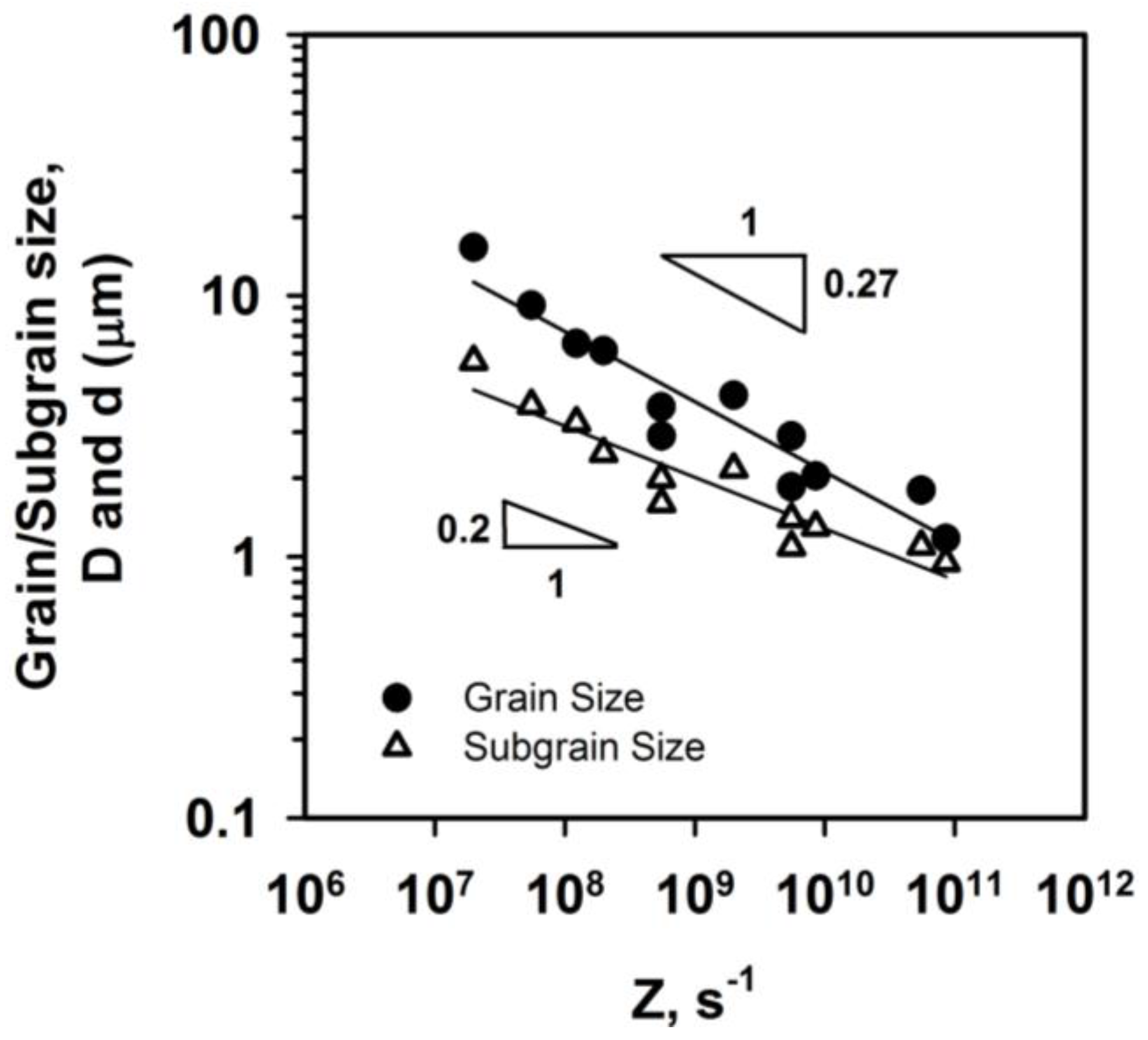
3.3. DRX Grains and Their Boundaries
4. Discussion
5. Conclusions
- The relationship between the DRX grain/subgrain size and flow stress can be expressed by power-law functions with different size exponents of −0.76 (grains) and −1.0 (subgrains), which is typical of discontinuous DRX under hot working conditions. Correspondingly, power-law functions with exponents of −0.27 and −0.2 are held for the effect of temperature-compensated strain rate (Z) on the grain and subgrain sizes, respectively.
- The fraction of ordinary high-angle boundaries in DRX microstructures increases from approx. 0.5 to 0.7, while the fraction of twin-related Σ3n CSL boundaries decreases from 0.25 to 0.05 as Z increases from 107 s−1 to 1011 s−1. Both the fraction of ordinary grain boundaries and the fraction of Σ3n CSL boundaries depend on the grain and subgrain sizes, i.e., D and d, and can be expressed by functions of the ratio of D/d.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sakai, T.; Jonas, J.J. Dynamic recrystallization: Mechanical and microstructural considerations. Acta Metall. 1984, 32, 189–209. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena; Elsevier Science: New York, NY, USA, 2004. [Google Scholar]
- Huang, K.; Logé, R.E. A review of dynamic recrystallization phenomena in metallic materials. Mater. Des. 2016, 111, 548–574. [Google Scholar] [CrossRef]
- McQueen, H.J.; Jonas, J.J. Recovery and Recrystallization during High Temperature Deformation. In Treatise on Materials Science and Technology; Arsenault, R.J., Ed.; Academic Press: New York, NY, USA, 1975; Volume 6, pp. 394–493. [Google Scholar]
- Maki, T.; Akasaka, K.; Okuno, K.; Tamura, I. Dnamic recrystallization of austenite in 18-8 stainless steel and 18 Ni maraging steel. Trans. Iron Steel Inst. Jpn. 1982, 22, 253–261. [Google Scholar] [CrossRef]
- Belyakov, A.; Sakai, T.; Miura, H.; Kaibyshev, R. Grain refinement under multiple warm deformation in 304 type austenitic stainless steel. ISIJ Int. 1999, 39, 592–599. [Google Scholar] [CrossRef]
- Sakai, T. Dynamic recrystallization microstrustures under hot working conditions. J. Mater. Process. Technol. 1995, 53, 349–361. [Google Scholar] [CrossRef]
- Belyakov, A.; Tikhonova, M.; Yanushkevich, Z.; Kaibyshev, R. Regularities of grain refinement in an austenitic stainless steel during multiple warm working. Mater. Sci. Forum 2013, 753, 411–416. [Google Scholar] [CrossRef]
- Dudova, N.; Belyakov, A.; Sakai, T.; Kaibyshev, R. Dynamic recrystallization mechanisms operating in a Ni-20%Cr alloy under hot-to-warm working. Acta Mater. 2010, 58, 3624–3632. [Google Scholar] [CrossRef]
- Tikhonova, M.; Belyakov, A.; Kaibyshev, R. Strain-induced grain evolution in an austenitic stainless steel under warm multiple forging. Mater. Sci. Eng. A 2013, 564, 413–422. [Google Scholar] [CrossRef]
- Wang, X.; Brunger, E.; Gottstein, G. The role of twinning during dynamic recrystallization in alloy 800 H. Scr. Mater. 2002, 46, 875–880. [Google Scholar] [CrossRef]
- Mahajan, S. Critique of mechanisms of formation of deformation, annealing and growth twins: Face-centered cubic metals and alloys. Scr. Mater. 2013, 68, 95–99. [Google Scholar] [CrossRef]
- Watanabe, T. Approach to Grain Boundary Design for Strong and Ductile Polycrystals. Res. Mech. 1984, 11, 47–84. [Google Scholar]
- Randle, V. Twinning-related grain boundary engineering. Acta Mater. 2004, 52, 4067–4081. [Google Scholar] [CrossRef]
- Fang, X.; Liu, Z.; Tikhonova, M.; Belyakov, A.; Wang, W. Evolution of texture and development of Σ3n grain clusters in 316 austenitic stainless steel during thermal mechanical processing. J. Mater. Sci. 2013, 48, 997–1004. [Google Scholar] [CrossRef]
- Cahoon, J.R.; Qiangyong, L.I.; Richards, N.L. Microstructural and processing factors influencing the formation of annealing twins. Mater. Sci. Eng. A 2009, 526, 56–61. [Google Scholar] [CrossRef]
- Pande, C.S.; Imam, M.A.; Rath, B.B. Study of Annealing Twins in FCC Metals and Alloys. Metall. Trans. A 1990, 21, 2891–2896. [Google Scholar] [CrossRef]
- Pande, C.S.; Imam, M.A. Grain growth and twin formation in boron-doped nickel polycrystals. Mater. Sci. Eng. A 2009, 512, 82–86. [Google Scholar] [CrossRef]
- Tikhonova, M.; Kuzminova, Y.; Fang, X.; Wang, W.; Kaibyshev, R.; Belyakov, A. Σ3 CSL boundary distributions in an austenitic stainless steel subjected to multidirectional forging followed by annealing. Philos. Mag. 2014, 94, 4181–4196. [Google Scholar] [CrossRef]
- Jonas, J.J.; Sellars, C.M.; Tegart, W.J. Strength and structure under hot-working conditions. Metall. Rev. 1969, 130, 1–33. [Google Scholar] [CrossRef]
- Belyakov, A.; Miura, H.; Sakai, T. Dynamic recrystallization under warm deformation of a 304 type austenitic stainless steel. Mater. Sci. Eng. A 1998, 255, 139–147. [Google Scholar] [CrossRef]
- Mackenzie, J.K. Second Paper on the Statistics Associated with the Random Disorientation of Cubes. Biometrika 1958, 45, 229–240. [Google Scholar] [CrossRef]
- Derby, B. The Dependence of Grain Size on Stress during Dynamic Recrystallization. Acta Metall. Mater. 1991, 39, 955–962. [Google Scholar] [CrossRef]
- Belyakov, A.; Gao, W.; Miura, H.; Sakai, T. Strain induced grain evolution in polycrystalline copper during warm deformation. Metall. Mater. Trans. A 1998, 29, 2957–2965. [Google Scholar] [CrossRef]
- Beladi, H.; Cizek, P.; Hodgson, P.D. On the Characteristics of Substructure Development through Dynamic Recrystallization. Metall. Mater. Trans. A 2009, 40, 1175–1189. [Google Scholar] [CrossRef]
- Cizek, P. The microstructure evolution and softening processes during high-temperature deformation of a 21Cr-10Ni-3Mo duplex stainless steel. Acta Mater. 2016, 106, 129–143. [Google Scholar] [CrossRef]
- Abson, D.J.; Jonas, J.J. Substructure strengthening in zirconium and zirconium-tin alloys. J. Nucl. Mater. 1972, 42, 73–85. [Google Scholar] [CrossRef]
- Frost, H.J.; Ashby, M.F. Deformation Echanism Maps; Pergamon press: Oxford, UK, 1982. [Google Scholar]
- Tikhonova, M.; Kaibyshev, R.; Fang, X.; Wang, W.; Belyakov, A. Grain boundary assembles developed in an austenitic stainless steel during large strain warm working. Mater. Charact. 2012, 70, 14–20. [Google Scholar] [CrossRef]
- Tikhonova, M.; Enikeev, N.; Valiev, R.Z.; Belyakov, A.; Kaibyshev, R. Submicrocrystalline Austenitic Stainless Steel Processed by Cold or Warm High Pressure Torsion. Mater. Sci. Forum 2016, 838–839, 398–403. [Google Scholar] [CrossRef]
- Belyakov, A.; Zherebtsov, S.; Salishchev, G. Three-stage relationship between flow stress and dynamic grain size in titanium in a wide temperature interval. Mater. Sci. Eng. A 2015, 628, 104–109. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Prangnell, P.B.; Bowen, J.R.; Gholinia, A.; Harris, C. Developing Stable Fine-Grain Microstructures by Large Strain Deformation. Philos. Trans. R. Soc. Lond. A 1999, 357, 1663–1681. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Langdon, T.G. Principles of equal-channel angular pressing as a processing tool for grain refinement. Prog. Mater. Sci. 2006, 51, 881–981. [Google Scholar] [CrossRef]









© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tikhonova, M.; Dolzhenko, P.; Kaibyshev, R.; Belyakov, A. Grain Boundary Assemblies in Dynamically-Recrystallized Austenitic Stainless Steel. Metals 2016, 6, 268. https://doi.org/10.3390/met6110268
Tikhonova M, Dolzhenko P, Kaibyshev R, Belyakov A. Grain Boundary Assemblies in Dynamically-Recrystallized Austenitic Stainless Steel. Metals. 2016; 6(11):268. https://doi.org/10.3390/met6110268
Chicago/Turabian StyleTikhonova, Marina, Pavel Dolzhenko, Rustam Kaibyshev, and Andrey Belyakov. 2016. "Grain Boundary Assemblies in Dynamically-Recrystallized Austenitic Stainless Steel" Metals 6, no. 11: 268. https://doi.org/10.3390/met6110268
APA StyleTikhonova, M., Dolzhenko, P., Kaibyshev, R., & Belyakov, A. (2016). Grain Boundary Assemblies in Dynamically-Recrystallized Austenitic Stainless Steel. Metals, 6(11), 268. https://doi.org/10.3390/met6110268






