Modeling and Simulation of the Gray-to-White Transition during Solidification of a Hypereutectic Gray Cast Iron: Application to a Stub-to-Carbon Connection Used in Smelting Processes
Abstract
:1. Introduction
2. Experimental Procedure
3. Modeling and Simulation
3.1. Thermal Model (Continuum Scale)
3.2. Microstructural Model
3.2.1. Phase Diagram Variables
3.2.2. Solidification Model
3.3. Simulation Data
3.3.1. Thermal Properties
3.3.2. Microstructural Properties
3.4. Summary of the Main Contributions of This Work
4. Results and Discussion
4.1. Experimental
4.1.1. Hardness Profile
4.1.2. Stress-Strain Curve
4.1.3. Microstructure
4.2. Simulation
4.2.1. Cooling Curves
4.2.2. Profile of Gray and White Fractions
4.2.3. Evolution of Gray and White Fractions, Eutectic Radii and Densities
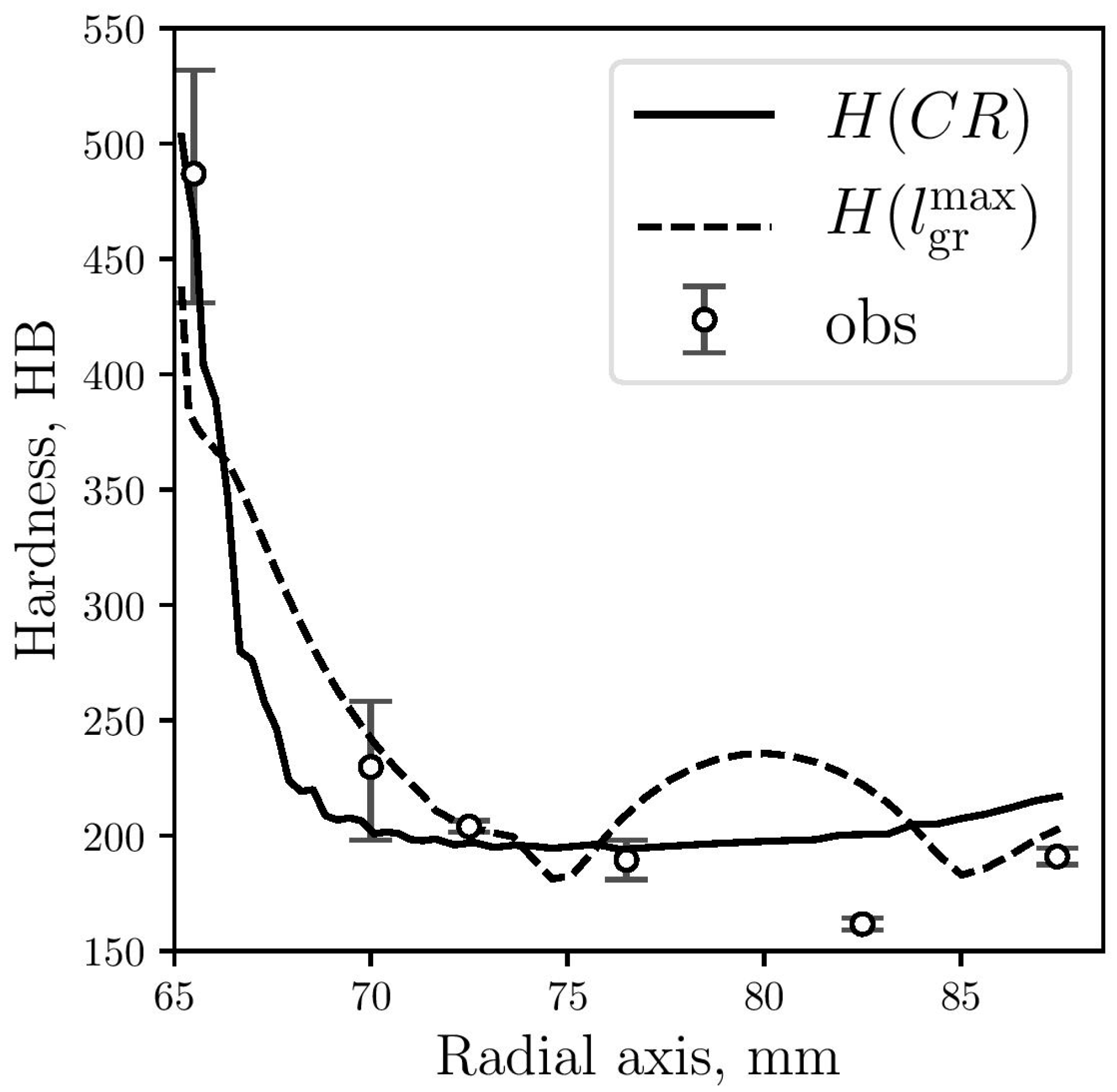
4.3. Hardness Prediction
5. Conclusions
- The measured hardness values and stress-strain curve were strongly affected by the observed microstructure.
- The computed GWT was consistent with the experimental data, thus validating the model prediction capabilities.
- Hardness was predicted via two methods that respectively consider cooling rates and microstructural parameters. When compared with the measured hardness values, predictions provided by the first method are in better agreement.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Table of Symbols | |
| ρ | Density |
| A | Nucleation parameter |
| B | Growth parameter |
| c | Specific heat |
| CE | Carbon equivalent |
| CR | Cooling rate |
| D | Diffusion coefficient |
| f | Volumetric fraction |
| fpt | Phase change function |
| H | Hardness |
| h | Effective heat transfer coefficient |
| k | Thermal conductivity |
| L | Latent heat |
| m | Growth exponent |
| N | Grain density |
| n | Nucleation exponent |
| R | Grain radius |
| T | Temperature |
| t | Time |
| Subscripts and Superscripts | |
| γ | Austenite |
| θ | Cementite |
| c | White eutectic |
| eut | Eutectic |
| g | Gray eutectic |
| gr | Graphite |
| l | Liquid |
| max | Maximum |
References
- Molenaar, D.; Ding, K.; Kapoor, A. Development of industrial benchmark finite element analysis model to study energy efficient electrical connections for primary aluminium smelters. In Proceedings of the TMS Light Metals, San Diego, CA, USA, 27 February–3 March 2011; pp. 985–990. [Google Scholar]
- Gunasegaram, D.R.; Molenaar, D. A Fully Coupled Thermal-Electrical-Mechanical Transient FEA Model for a 3D Anode Assembly. In Proceedings of the TMS Light Metals, San Antonio, TX, USA, 3–7 March 2013; pp. 1341–1346. [Google Scholar]
- Gunasegaram, D.R.; Molenaar, D. Towards improved energy efficiency in the electrical connections of Hall–Héroult cells through Finite Element Analysis (FEA) modeling. J. Clean. Prod. 2015, 93, 174–192. [Google Scholar] [CrossRef]
- Gunasegaram, D.R.; Molenaar, D. Rodding in Hall–Héroult Cells: An Fea Model that Predicts Room Temperature Mechanical Properties and Cracking Tendency of Thimbles. In Proceedings of the TMS Light Metals, San Diego, CA, USA, 16–20 February 2014; pp. 1287–1292. [Google Scholar]
- Fraś, E.; Górny, M.; López, H.F. The transition from gray to white cast iron during solidification: Part I. Theoretical background. Metall. Mater. Trans. A 2005, 36, 3075–3082. [Google Scholar] [CrossRef]
- Fraś, E.; Górny, M.; López, H.F. The Transition from gray to white cast iron during solidification: Part II. Experimental verification. Metall. Mater. Trans. A 2005, 36, 3083–3092. [Google Scholar] [CrossRef]
- Fraś, E.; Górny, M.; López, H.F. The transition from gray to white cast iron during solidification: Part III. Thermal analysis. Metall. Mater. Trans. A 2005, 36, 3093–3101. [Google Scholar] [CrossRef]
- Fraś, E.; Górny, M.; López, H.F. The effect of carbon on the transition from graphite to cementite eutectic in cast iron. Metall. Mater. Trans. A 2014, 45, 5601–5612. [Google Scholar] [CrossRef]
- Fraś, E.; López, H.F.; Kawalec, M.; Górny, M. Role of alloying additions in the solidification kinetics and resultant chilling tendency and chill of cast iron. Metals 2015, 5, 256–288. [Google Scholar] [CrossRef]
- Magnin, P.; Kurz, W. Competitive growth of stable and metastable Fe-C-X eutectics: Part I. experiments. Metall. Mater. Trans. A 1988, 19, 1955–1963. [Google Scholar] [CrossRef]
- Magnin, P.; Kurz, W. Competitive growth of stable and metastable Fe-C-X eutectics: Part II. Mechanisms. Metall. Mater. Trans. A 1988, 19, 1965–1971. [Google Scholar] [CrossRef]
- Maijer, D.; Cockcroft, S.L.; Patt, W. Mathematical modeling of microstructural development in hypoeutectic cast iron. Metall. Mater. Trans. A 1999, 30, 2147–2158. [Google Scholar] [CrossRef]
- Maijer, D.; Cockcroft, S.; Jacot, A. Modeling of microstructure and residual stress in cast iron calender rolls. Metall. Mater. Trans. A 2000, 31, 1201–1211. [Google Scholar] [CrossRef]
- Jacot, A.; Maijer, D.; Cockcroft, S.L. A two-dimensional model for the description of the columnar-to-equiaxed transition in competing gray and white iron eutectics and its application to calender rolls. Metall. Mater. Trans. A 2000, 31, 2059–2068. [Google Scholar] [CrossRef]
- Celentano, D.; Cruchaga, M. A thermally coupled flow formulation with microstructural evolution for hypoeutectic cast-iron solidification. Metall. Mater. Trans. B 1999, 30, 731–744. [Google Scholar] [CrossRef]
- Celentano, D.J.; Cruchaga, M.A.; Schulz, B.J. Thermal microstructural analysis of grey cast iron solidification: Simulation and experimental validation. Int. J. Cast Met. Res. 2005, 18, 237–247. [Google Scholar] [CrossRef]
- Urrutia, A.; Celentano, D.J.; Gunasegaram, D.R.; Deeva, N. Thermal microstructural multiscale simulation of solidification and eutectoid transformation of hypereutectic gray cast iron. Metall. Mater. Trans. A 2014, 45, 3954–3970. [Google Scholar] [CrossRef]
- Jelić, P.; Lazić, L.; Črnko, J. The effect of cooling rate on the properties of alloyed cast-iron sizing roll. Metalurgija 2010, 49, 45–48. [Google Scholar]
- Pluphrach, G. Study of the effect of solidification on graphite flakes microstructure and mechanical properties of an ASTM A-48 gray cast iron using steel molds. Sonklanakarin J. Sci. Technol. 2010, 32, 613–618. [Google Scholar]
- Samuelsson, D.P.B. Analysis of Microstructural Strain-Fields in Grey Cast Iron; Chalmers University of Technology: Göteborg, Sweden, 2011. [Google Scholar]
- Sahu, S.; Bhat, M.N.; Kumar, A.; Pratik, A.; Kumar, A. Effect of section thickness on the microstructure and hardness of gray cast iron (A simulation study). Int. J. Eng. Res. Technol. 2014, 3, 35–40. [Google Scholar]
- Jabbari Behnam, M.M.; Davami, P.; Varahram, N. Effect of cooling rate on microstructure and mechanical properties of gray cast iron. Mater. Sci. Eng. A 2010, 528, 583–588. [Google Scholar] [CrossRef]
- Wilberfors, F.; Svensson, I.L.; Elfsberg, J.; Richnau, K.; Ipek, N. Local chill as a mean of increasing strength in grey cast iron. Int. J. Cast Met. Res. 2016, 29, 40–46. [Google Scholar] [CrossRef]
- Stefanescu, D.M. Thermal analysis—Theory and applications in metalcasting. Int. J. Met. 2015, 9, 7–22. [Google Scholar] [CrossRef]
- Riposan, I.; Chisamera, M.; Stan, S.; Hartung, C.; White, D. Three-stage model for nucleation of graphite in grey cast iron. Mater. Sci. Technol. 2010, 26, 1439–1447. [Google Scholar] [CrossRef]
- Biswas, S.; Monroe, C.; Prucha, T. Use of published experimental results to validate approaches to gray and ductile iron mechanical properties prediction. Int. J. Met. 2017, 11, 656–674. [Google Scholar] [CrossRef]
- Collini, L.; Nicoletto, G.; Konečná, R. Microstructure and mechanical properties of pearlitic gray cast iron. Mater. Sci. Eng. A 2008, 488, 529–539. [Google Scholar] [CrossRef]
- Onsoien, M.I.; Skaland, T. Preconditioning of gray iron melts using ferrosilicon or silicon carbide. AFS Trans. 2001, 1, 1–12. [Google Scholar]
- Cooper, C.A.; Elliott, R.; Young, R.J. Investigation of elastic property relationships for flake and spheroidal cast irons using Raman spectroscopy. Acta Mater. 2002, 50, 4037–4046. [Google Scholar] [CrossRef]
- Seah, K.H.W.; Hemanth, J.; Sharma, S.C. Effect of the cooling rate on the dendrite arm spacing and the ultimate tensile strength of cast iron. J. Mater. Sci. 1998, 33, 23–28. [Google Scholar] [CrossRef]
- Hsu, C.-H.; Lee, S.-C.; Shy, Y.-H.; Chiou, W.-T. Relationship between dynamic and static toughness of flake and compacted graphite cast irons. Mater. Sci. Eng. A 2000, 282, 115–122. [Google Scholar] [CrossRef]
- Xu, W.; Ferry, M.; Wang, Y. Influence of alloying elements on as-cast microstructure and strength of gray iron. Mater. Sci. Eng. A 2005, 390, 326–333. [Google Scholar] [CrossRef]
- Goettsch, D.D.; Dantzig, J.A. Modeling microstructure development in gray cast irons. Metall. Mater. Trans. A 1994, 25, 1063–1079. [Google Scholar] [CrossRef]
- Yeh, C.-P.; Hwang, W.-S.; Lin, C.-H. Numerical simulation on hardness distribution for a FC250 gray cast iron brake disc casting and its experimental verification. Mater. Trans. 2009, 50, 2584–2592. [Google Scholar] [CrossRef]
- Catalina, A.; Guo, X.; Stefanescu, D.M.; Chuzhoy, L.; Pershing, M. Prediction of room temperature microstructure and mechanical properties in gray iron castings. AFS Trans. 2000, 108, 247–257. [Google Scholar]
- Sare, I.R. Abrasion resistance and fracture toughness of white cast irons. Met. Technol. 1979, 6, 412–419. [Google Scholar] [CrossRef]
- Berns, H. Comparison of wear resistant MMC and white cast iron. Wear 2003, 254, 47–54. [Google Scholar] [CrossRef]
- Wiengmoon, A.; Chairuangsri, T.; Brown, A.; Brydson, R.; Edmonds, D.V.; Pearce, J.T.H. Microstructural and crystallographical study of carbides in 30 wt.% Cr cast irons. Acta Mater. 2005, 53, 4143–4154. [Google Scholar] [CrossRef]
- Wu, X.; Xing, J.; Fu, H.; Zhi, X. Effect of titanium on the morphology of primary M7C3 carbides in hypereutectic high chromium white iron. Mater. Sci. Eng. A 2007, 457, 180–185. [Google Scholar] [CrossRef]
- Zhi, X.; Xing, J.; Fu, H.; Xiao, B. Effect of niobium on the as-cast microstructure of hypereutectic high chromium cast iron. Mater. Lett. 2008, 62, 857–860. [Google Scholar] [CrossRef]
- Daimaruya, M.; Kobayashi, H.; Fuad, K. Thermoelasto-plastic stresses and thermal distortions in a brake drum. J. Therm. Stress. 1997, 20, 345–361. [Google Scholar] [CrossRef]
- Stefanescu, D.M.; Katz, S. Thermodynamic properties of iron-base alloys. ASM Handb. 2008, 15, 41–55. [Google Scholar]
- Heine, R.W. The Fe-C-Si solidification diagram for cast irons. AFS Trans. 1986, 94, 391–402. [Google Scholar]
- Stefanescu, D.M.; Alonso, G.; Larrañaga, P.; Suarez, R. On the stable eutectic solidification of iron-carbon-silicon alloys. Acta Mater. 2016, 103, 103–114. [Google Scholar] [CrossRef]
- Johnson, W.C.; Smartt, H.B. The role of interphase boundary adsorption in the formation of spheroidal graphite in cast iron. Metall. Mater. Trans. A 1977, 8, 553–565. [Google Scholar] [CrossRef]
- Abaqus 6.13. Available online: http://dsk.ippt.pan.pl/docs/abaqus/v6.13/ (accessed on 18 September 2013).
- MatWeb: Online Materials Information Resource. Available online: http://www.matweb.com/search/datasheetText.aspx?bassnum=M1020A (accessed on 1 March 2017).
- Andersen, D.H.; Zhang, Z.L. Fracture and physical properties of carbon anodes for the aluminum reduction cell. Eng. Fract. Mech. 2011, 78, 2998–3016. [Google Scholar] [CrossRef]
- Celentano, D.J.; Cruchaga, M.A.; Schulz, B.J. On the effect of natural convection on the thermal-microstructural evolution in gray cast-iron solidification. Metall. Mater. Trans. B 2006, 37, 253–264. [Google Scholar] [CrossRef]
- Nastac, L.; Stefanescu, D.M. Prediction of the gray-to-white transition in cast iron through solidification modeling. AFS Trans. 1995, 103, 329–337. [Google Scholar]
- Josefson, B.L.; Hjelm, H.E. Modelling Elastoplastic Deformations in Grey Cast Iron. In Low Cycle Fatigue and Elasto-Plastic Behaviour of Materials—3; Rie, K.T., Grünling, H.W., König, G., Neumann, P., Nowack, H., Schwalbe, K.-H., Seeger, T., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 465–472. [Google Scholar]
- Altenbach, H.; Stoychev, G.B.; Tushtev, K.N. On elastoplastic deformation of grey cast iron. Int. J. Plast. 2001, 17, 719–736. [Google Scholar] [CrossRef]
- Stoychev, G. FE analysis of gray cast iron structural elements. Mach. Des. 2010, 2, 335–340. [Google Scholar]
- Angus, H.T. Cast Iron: Physical and Engineering Properties; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Elkem Foundry. Available online: http://www.elkemfoundry.com.cn/pdf/GraphiteStructuresInCI.pdf (accessed on 11 January 2017).
- Jiyang, Z. Color metallography of cast iron. China Foundry 2011, 8, 447–462. [Google Scholar]
- Khalil-Allafi, J.; Amin-Ahmadi, B. Effect of mold hardness on microstructure and contraction porosity in ductile cast iron. J. Iron Steel Res. Int. 2011, 18, 4447–4467. [Google Scholar] [CrossRef]
- Hillert, M. Comments on ‘‘Eutectic solidification of gray cast iron’’. Scr. Mater. 2005, 52, 249–250. [Google Scholar] [CrossRef]
- Kelly Pipe. Available online: http://www.kellypipe.com/assets/files/hardcon.pdf (accessed on 12 April 2017).
- Bates, C. Alloy element effect on lamellar iron properties: Part II. AFS Trans. 1986, 94, 889–905. [Google Scholar]











| C | Si | Mn | P | Cr | Co | Zr | Sn | Pb | S | V | Fe | CE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.00 | 3.93 | 0.74 | 0.036 | 0.031 | 0.022 | 0.022 | 0.019 | 0.016 | 0.015 | 0.015 | bal. | 5.3 |
| Transformation Temperatures | Equation | Reference | |
|---|---|---|---|
| Liquidus | Tl = 389.1(C + 0.31Si) − 505.8 | [42] | |
| Gray eutectic | Tg = 1135.06 + 13.89Si − 2.05Si2 | [12] | |
| White eutectic | Tc = 1147.2 − 6.93(Si + 2.5P) − 1.717(Si + 2.5P)2 | [12] | |
| Carbon concentrations | Eutectic | Ceut = 4.3 − 0.37Si + 0.02Si2 − 0.5P | [12] |
| Maximum in austenite | = 2.2 − 0.26Si − 0.01Si2 | [43] | |
| Solidification Model | Equation | Parameters | |
|---|---|---|---|
| Nucleation model | Ng/c = Ag/c (Tg/c − T)ng/c | Ng/c: eutectic grain density Ag/c: nucleation parameter ng/c: nucleation exponent | |
| Growth rate model | dRg/c/dt = Bg/c (Tg/c − T)mg/c | Rg/c: eutectic grain radius Bg/c: growth parameter mg/c: growth exponent | |
| Volumetric fractions | Gray/white fraction | - | |
| Graphite fraction | : graphite fraction in the eutectic grain | ||
| Cementite fraction | : cementite fraction in the eutectic grain | ||
| Austenite fraction | fγ = fg + fc − fgr − fθ | - | |
| Component | ρ (kg/m3) | T (°C) | k (J/(kg·°C)) | T (°C) | c (W/(m·°C)) |
|---|---|---|---|---|---|
| Thimble | 7300 | 280 | 44.1 | 20 | 500 |
| 420 | 40.9 | 600 | 750 | ||
| 560 | 37.1 | 800 | 750 | ||
| 700 | 33.6 | 1145 | 820 | ||
| 840 | 28.1 | 1155 | 840 | ||
| 980 | 22.5 | - | |||
| 1120 | 18.8 | - | - | ||
| 1250 | 100.0 * | - | - | ||
| Stub | 7870 | 30 | 40.6 | 1 | 422 |
| 300 | 40.2 | 100 | 496 | ||
| 400 | 37.7 | 200 | 544 | ||
| 500 | 34.3 | 300 | 580 | ||
| 600 | 31.4 | 400 | 621 | ||
| 700 | 28.9 | 500 | 683 | ||
| 800 | 26.4 | 600 | 780 | ||
| 900 | 26.4 | 700 | 931 | ||
| 1000 | 27.2 | 750 | 871 | ||
| 1100 | 27.6 | 800 | 716 | ||
| 1200 | 28 | 850 | 577 | ||
| - | - | 900 | 591 | ||
| - | - | 1000 | 617 | ||
| - | - | 1100 | 644 | ||
| - | - | 1200 | 670 | ||
| Anode | 1580 | 30 | 4 | 30 | 680 |
| 200 | 4.6 | 200 | 1180 | ||
| 400 | 5.2 | 400 | 1550 | ||
| 600 | 5.9 | 600 | 1750 | ||
| 800 | 6.4 | 800 | 1910 | ||
| 1000 | 6.8 | 1000 | 2000 | ||
| 1200 | 7 | 1200 | 2070 |
| Effective Heat Transfer Coefficient | T (K (°C)) | h (W·m−2·K−1) |
|---|---|---|
| Anode-thimble (solid) | 1373 (1100) | 500 |
| Anode-thimble (liquid) | 1473 (1200) | 1000 |
| Stub-thimble (solid) | 1373 (1100) | 500 |
| Stub-thimble (liquid) | 1473 (1200) | 1000 |
| Anode-stub | - | 500 |
| Anode/thimble/stub-air | - | 30 |
| Eutectic | Gray | White |
|---|---|---|
| Nucleation parameter (A) (nuclei m−3·K−n) | 2.0 × 107 | 9.0 × 106 |
| Growth parameter (B) (m·s−1·K−m) | 3.3 × 10−9 | 2.5 × 10−5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urrutia, A.; Celentano, D.J.; Gunasegaram, D.R. Modeling and Simulation of the Gray-to-White Transition during Solidification of a Hypereutectic Gray Cast Iron: Application to a Stub-to-Carbon Connection Used in Smelting Processes. Metals 2017, 7, 549. https://doi.org/10.3390/met7120549
Urrutia A, Celentano DJ, Gunasegaram DR. Modeling and Simulation of the Gray-to-White Transition during Solidification of a Hypereutectic Gray Cast Iron: Application to a Stub-to-Carbon Connection Used in Smelting Processes. Metals. 2017; 7(12):549. https://doi.org/10.3390/met7120549
Chicago/Turabian StyleUrrutia, Alejandro, Diego J. Celentano, and Dayalan R. Gunasegaram. 2017. "Modeling and Simulation of the Gray-to-White Transition during Solidification of a Hypereutectic Gray Cast Iron: Application to a Stub-to-Carbon Connection Used in Smelting Processes" Metals 7, no. 12: 549. https://doi.org/10.3390/met7120549
APA StyleUrrutia, A., Celentano, D. J., & Gunasegaram, D. R. (2017). Modeling and Simulation of the Gray-to-White Transition during Solidification of a Hypereutectic Gray Cast Iron: Application to a Stub-to-Carbon Connection Used in Smelting Processes. Metals, 7(12), 549. https://doi.org/10.3390/met7120549







