Numerical and Experimental Investigations of Solidification Parameters and Mechanical Property during Laser Dissimilar Welding
Abstract
1. Introduction
2. Experimental Procedure
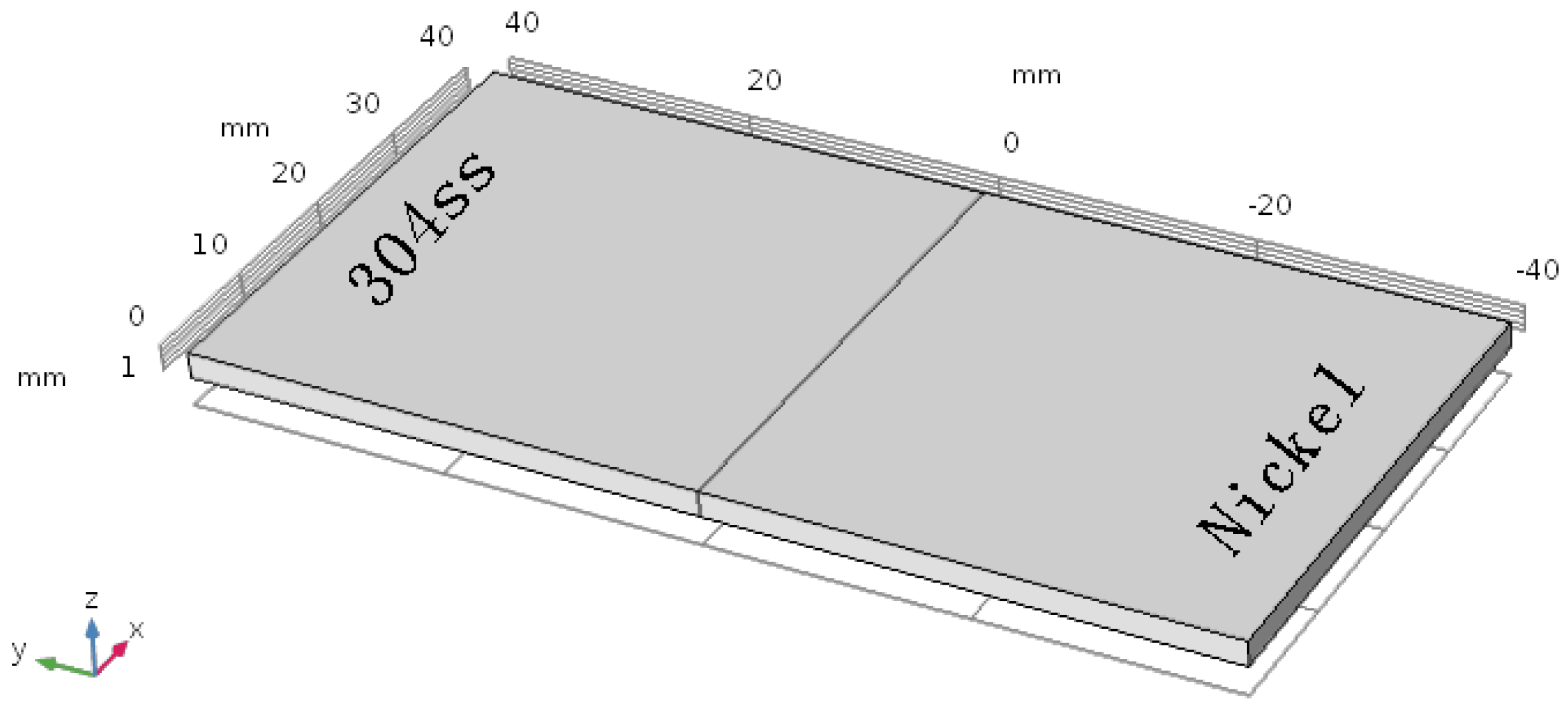
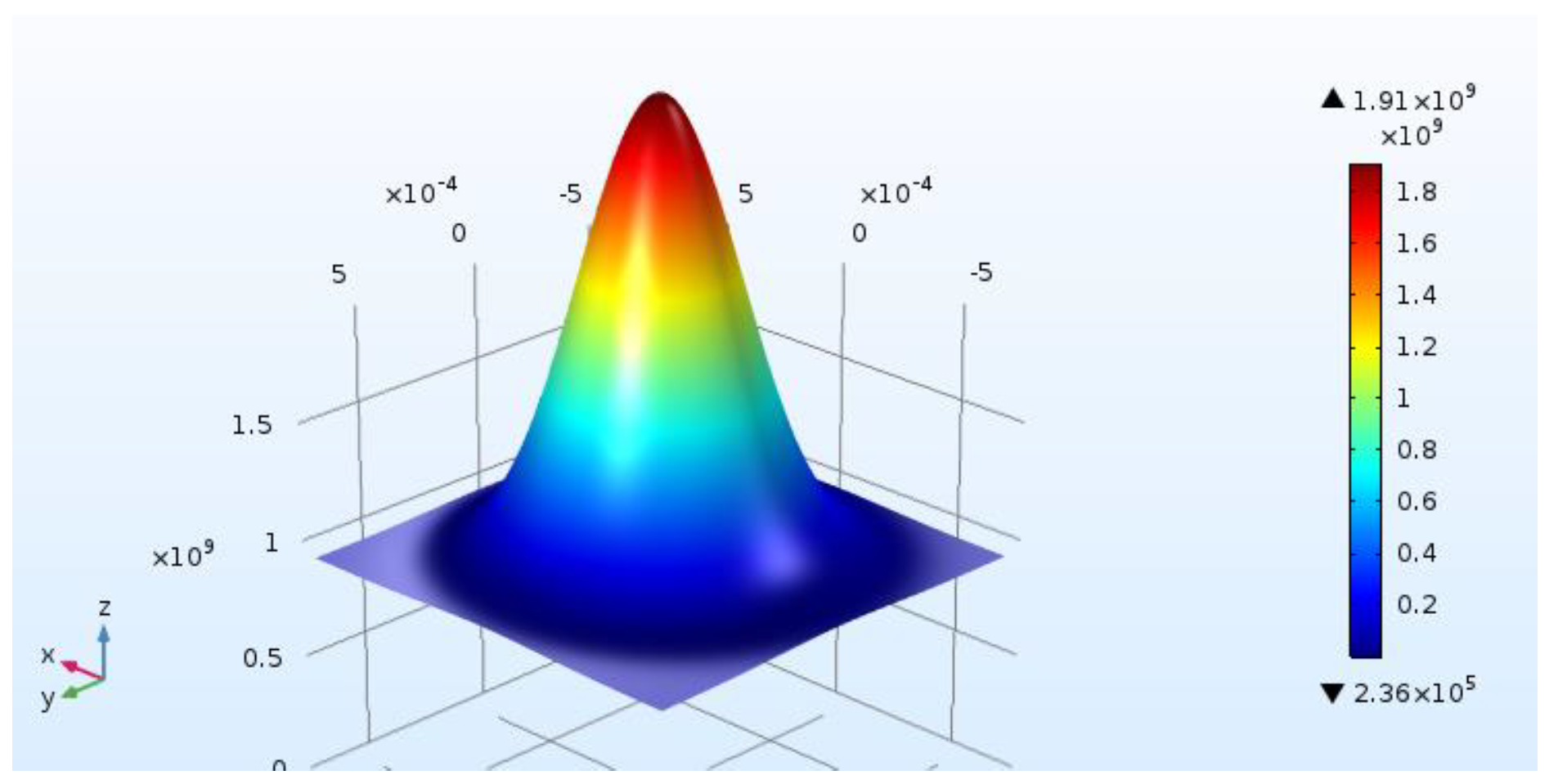
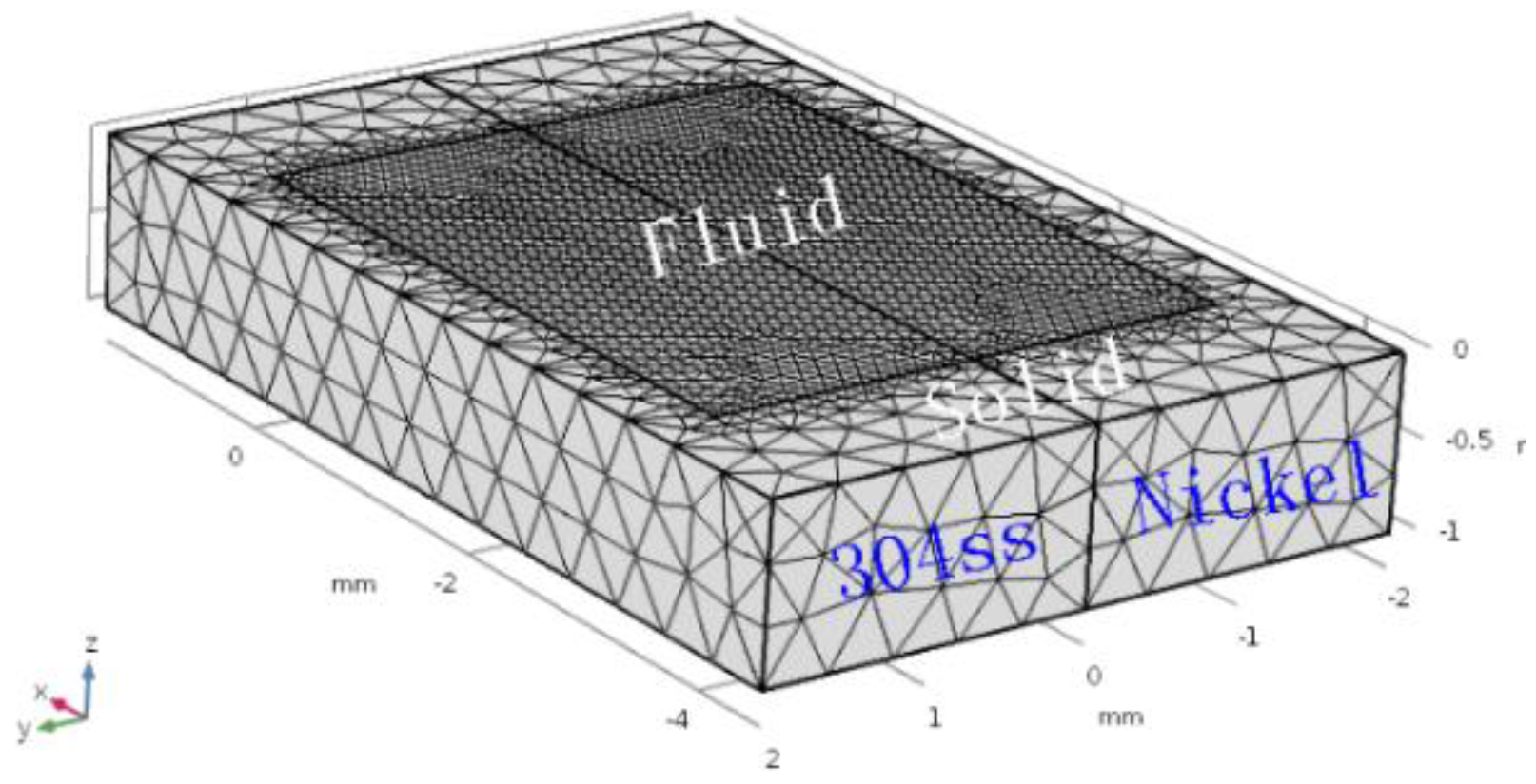
3. Numerical Model
4. Results and Discussion
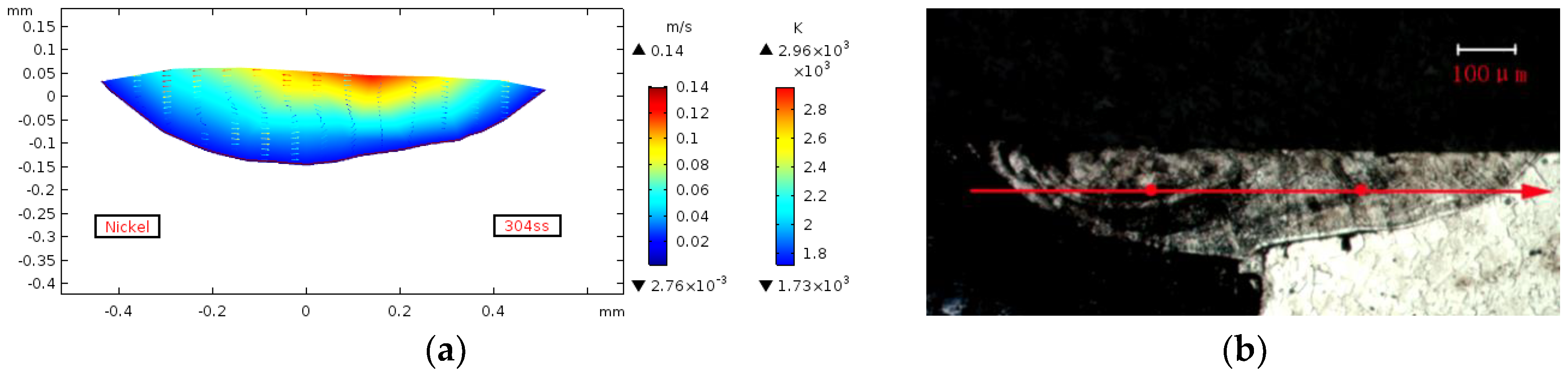
4.1. Influence of Heat Input on the Weld Formation
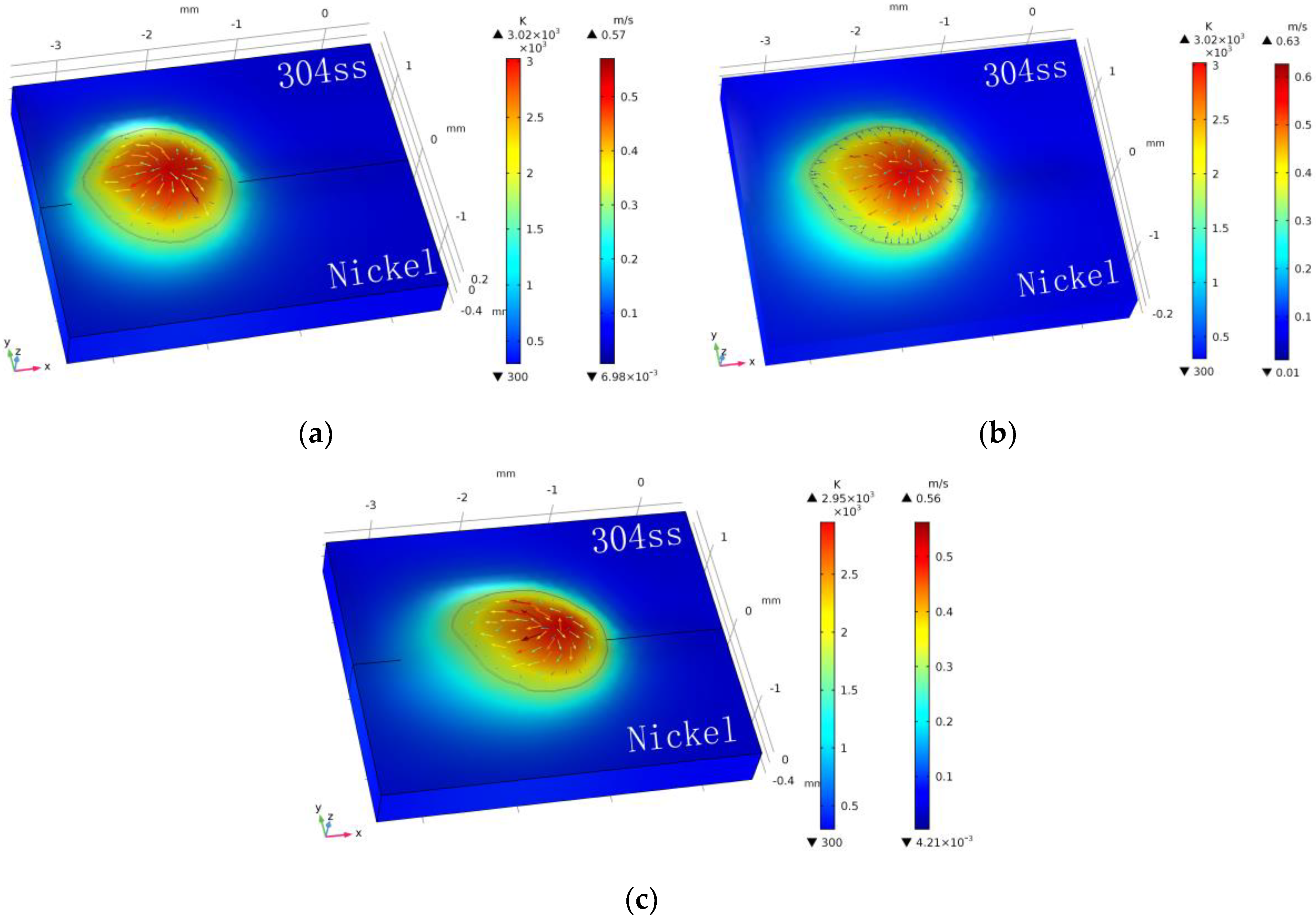
4.2. Influence of Heat Input on the Weld Pool Configuration
4.3. Influence of Heat Input on the Microstructure
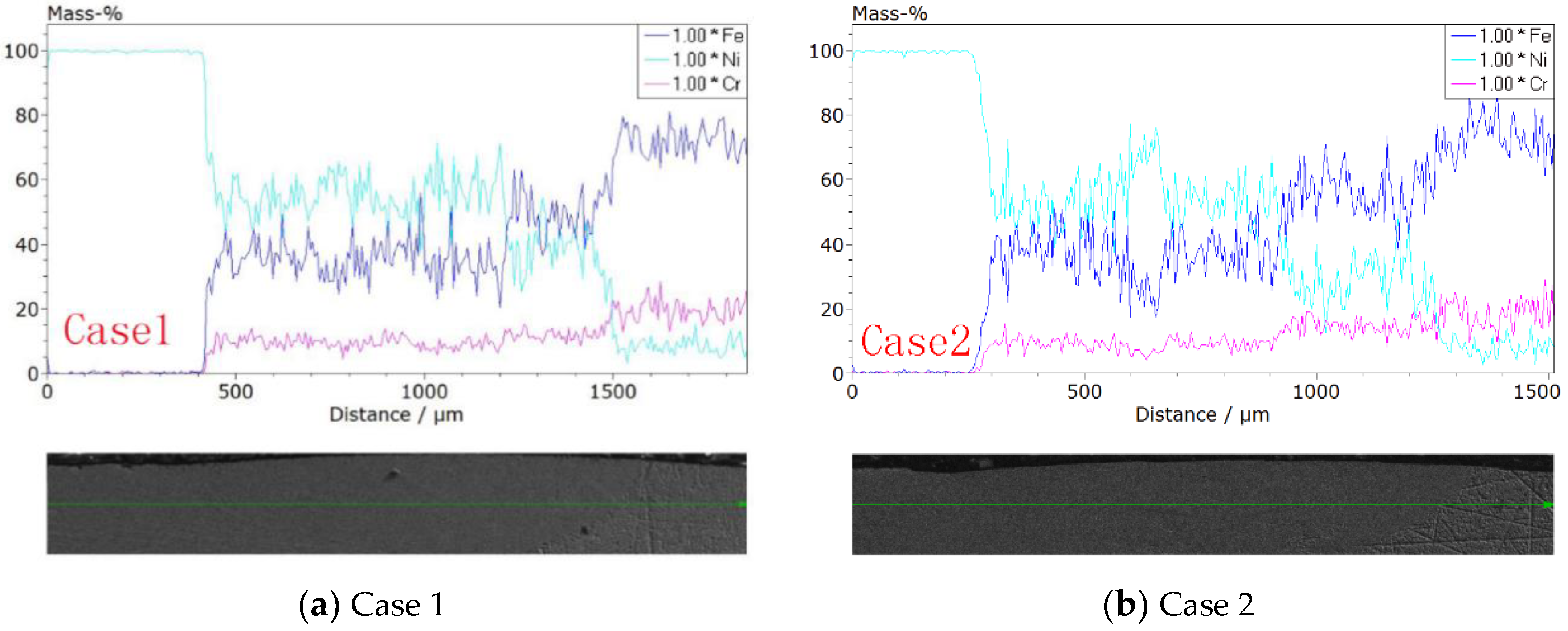
4.4. Influence of Heat Input on the Elements Distribution
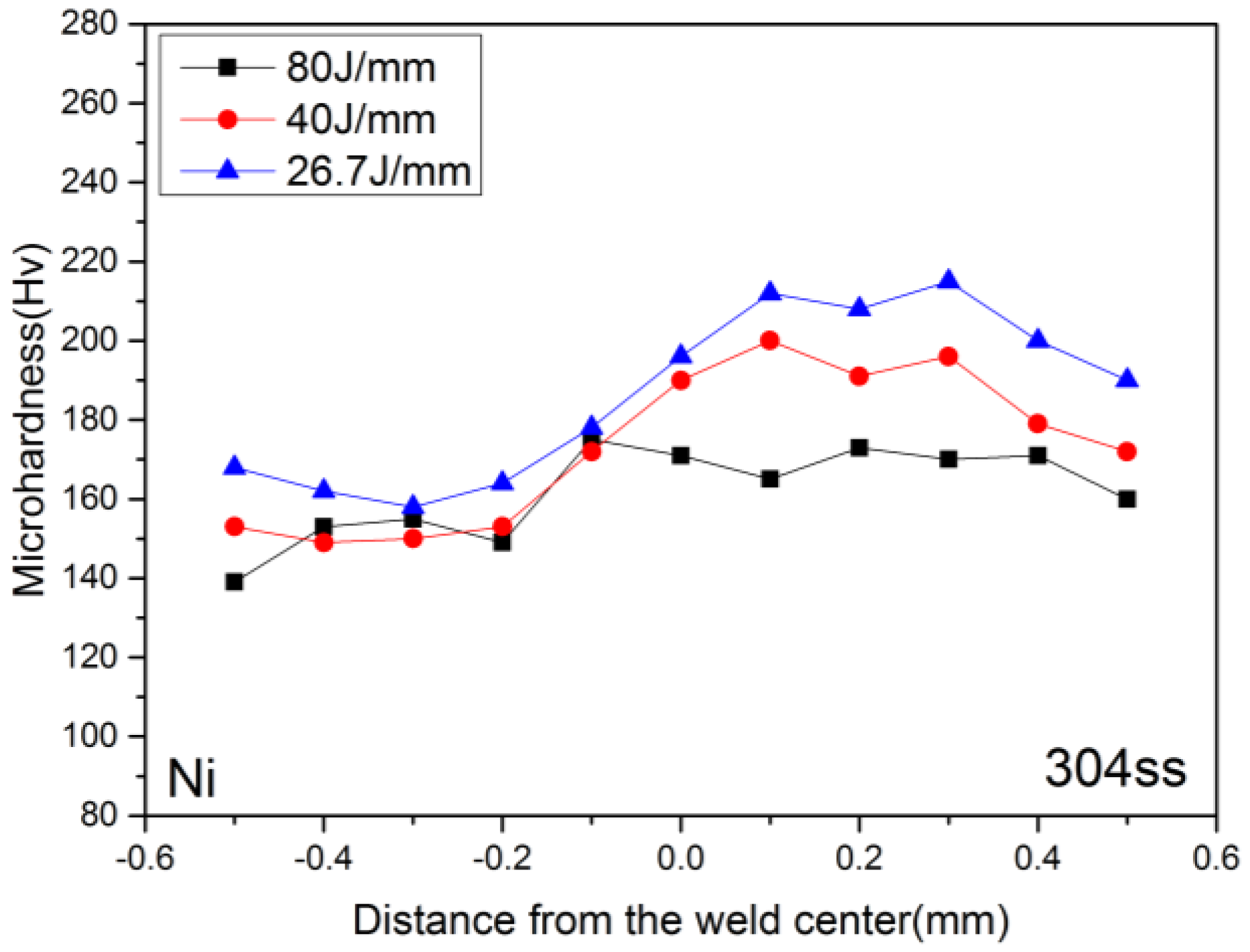
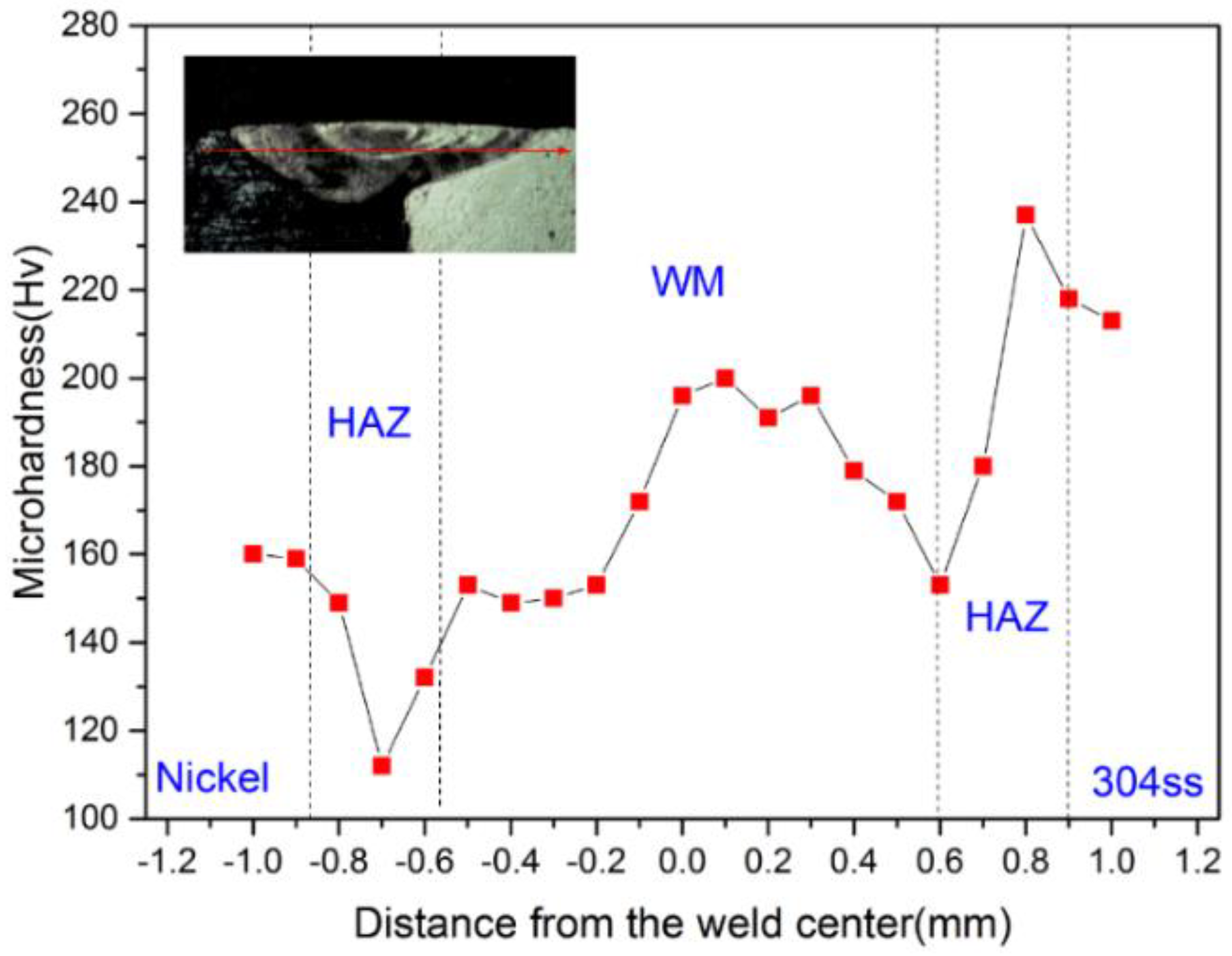
4.5. Influence of Heat Input on the Microhardness
5. Conclusions
- The joints produced by LBW are nearly defect-free, which proves that LBW is an effective fusion welding method for dissimilar welding of 304ss and nickel.
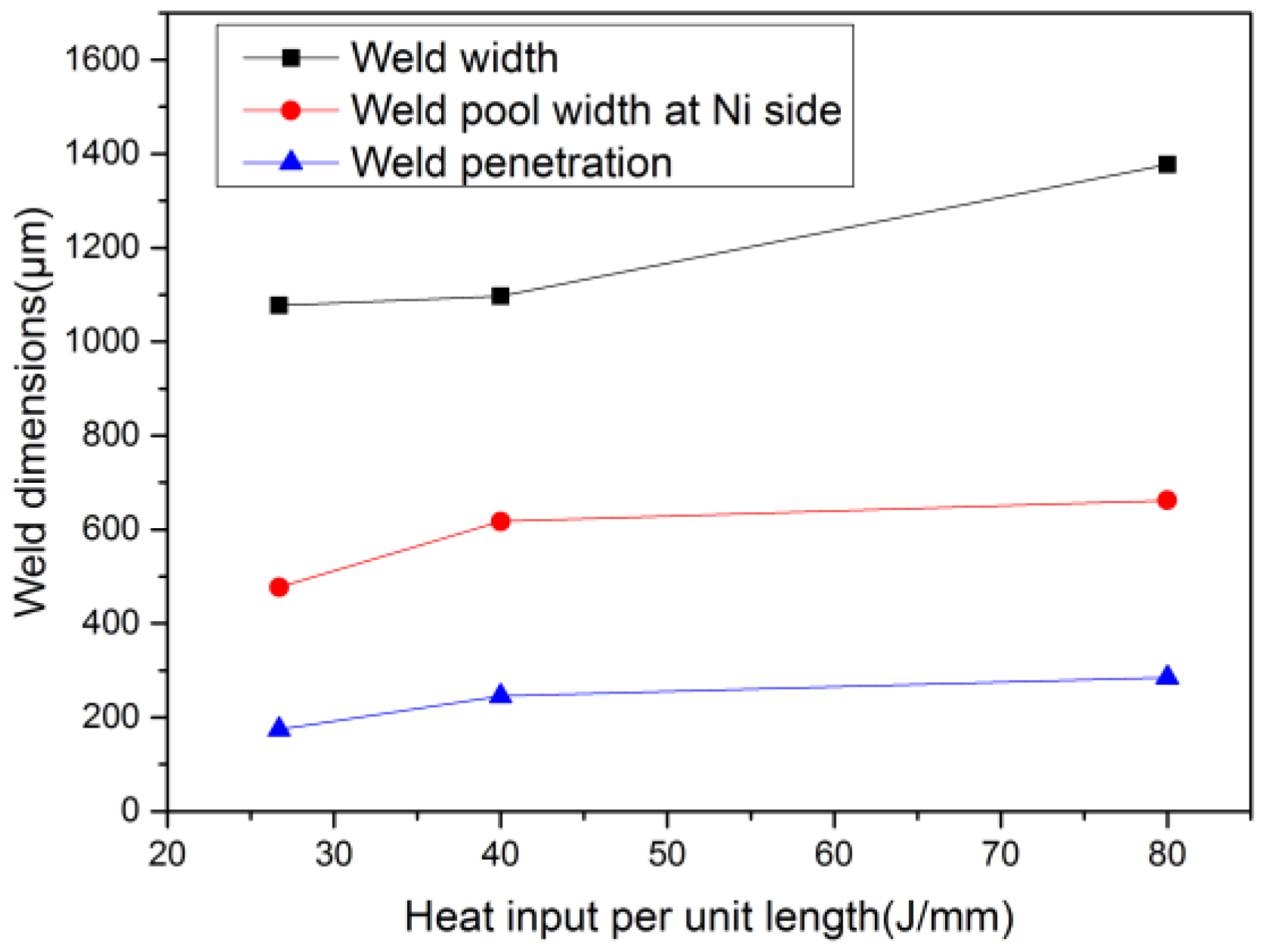
- With an increase of welding speed, both the weld width and weld penetration decrease. The change of the weld dimension from case 1 to case 2 is much larger than that from case 2 to case 3. It is demonstrated that the heat input per unit length is more efficient to characterize the effect of heat input compared with welding speed.
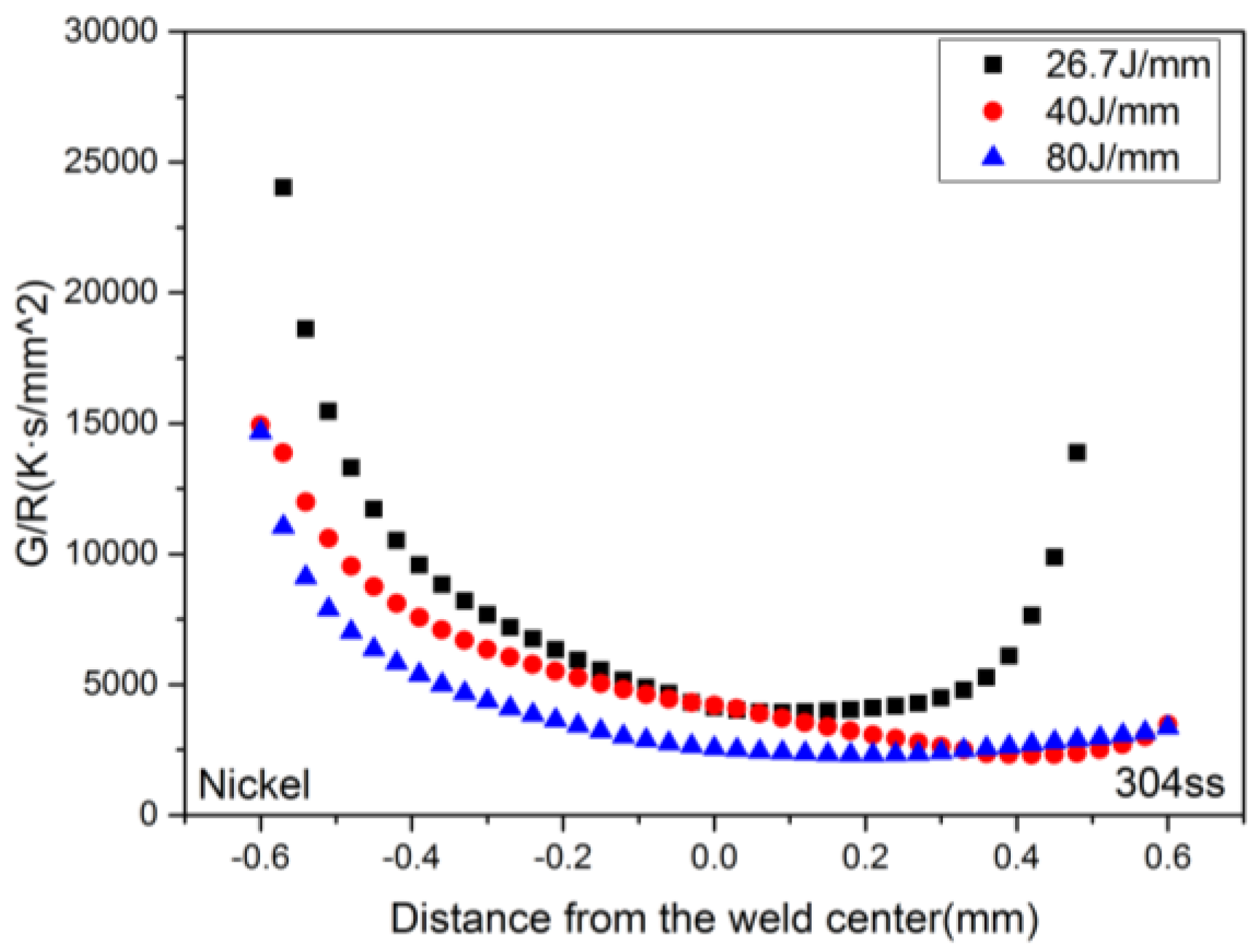
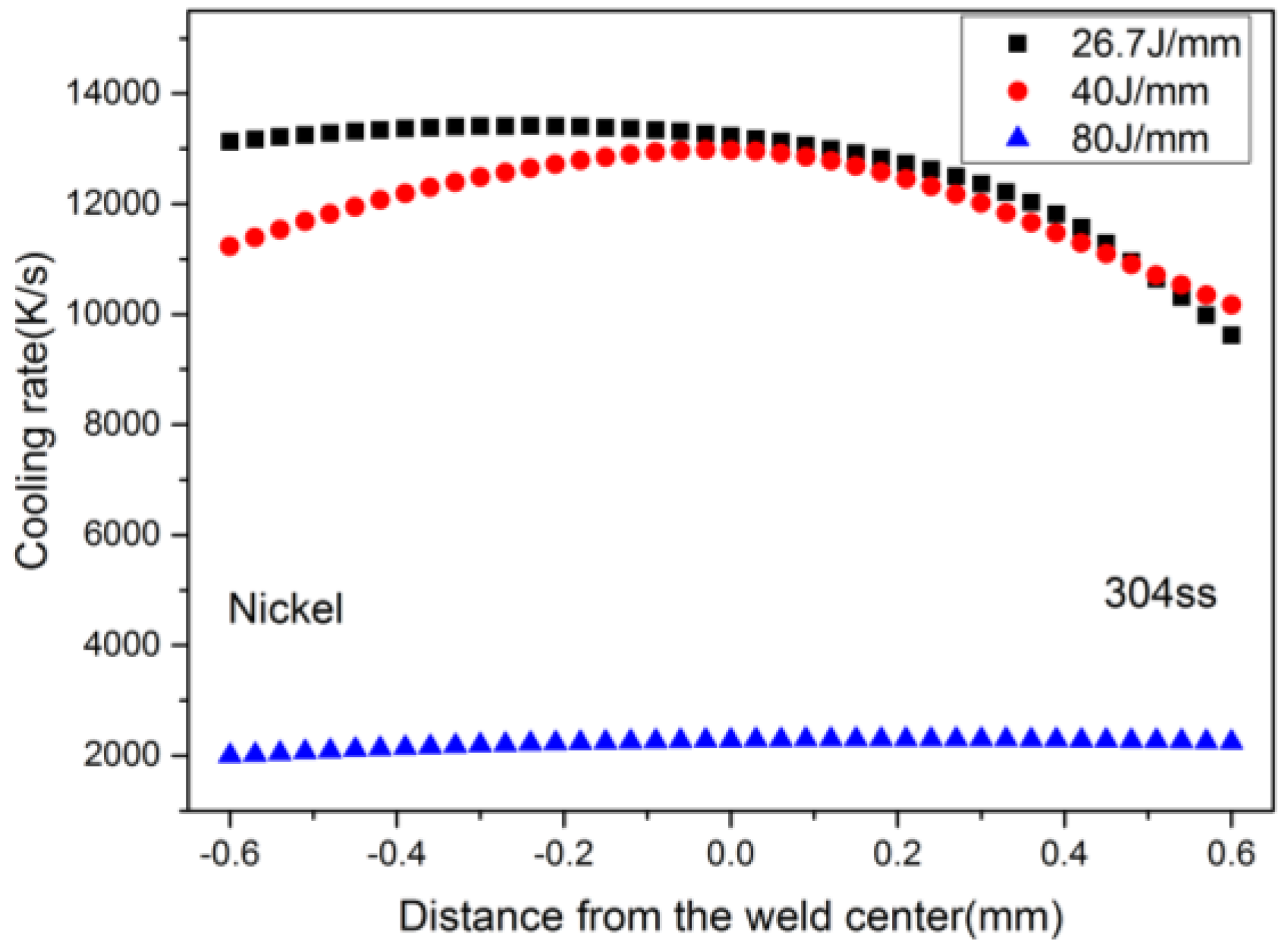
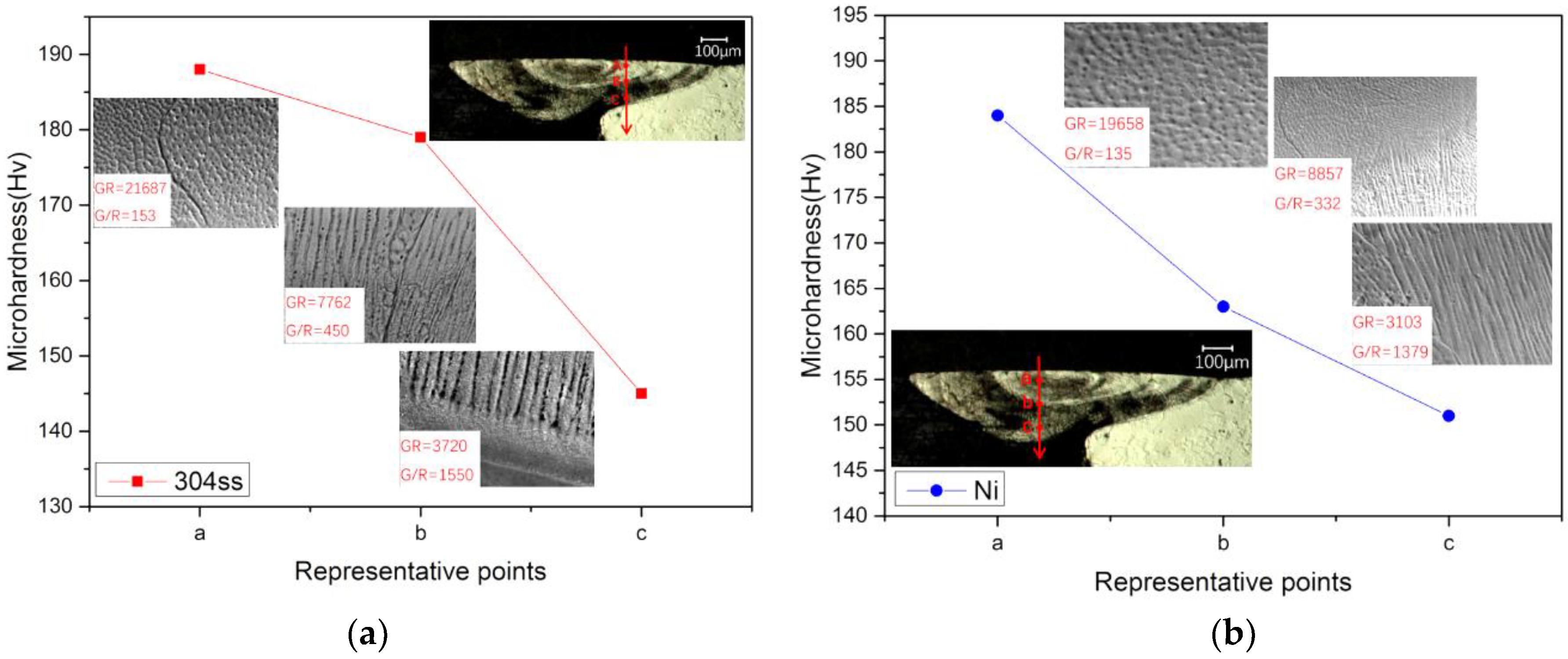
- The heat input has more influence on the cooling rate (GR) than the morphology parameter (G/R). As a result, the morphology of the solidified microstructure at different heat input in this study is similar, but the scale is quite different and the solidified structure for case 3 is the finest.
- The microhardness of the solidification structure is greatly affected by the grain dimension. In this investigation, the Vickers hardness of case 3 is the largest, followed by case 2 and case 1. It was found that the lower the heat input, the higher the hardness in the fusion zone.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bahrami, A.; Valentine, D.T.; Helenbrook, B.T.; Aidun, D.K. Study of mass transport in autogenous GTA welding of dissimilar metals. Int. J. Heat Mass Transf. 2015, 85, 41–53. [Google Scholar] [CrossRef]
- Mishin, O.V.; Gertsman, V.Y.; Alexandrov, I.V.; Valiev, R.Z. Grain boundary character distributions and mechanical properties of 304 stainless steel. Mater. Sci. Eng. A 1996, 212, 281–283. [Google Scholar] [CrossRef]
- Yu, G.; He, X.L.; Li, S.X. Laser Manufacturing and Its Application; National Defense Industry Press: Beijing, China, 2017; pp. 93–97. ISBN 978-7-118-10984-9. [Google Scholar]
- Boccarusso, L.; Arleo, G.; Astarita, A.; Bernardo, F.; De Fazio, P.; Durante, M.; Memola Capece Minutolo, F.; Sepe, R.; Squillace, A. A new approach to study the influence of the weld bead morphology on the fatigue behaviour of Ti–6Al–4V laser beam welded butt joints. Int. J. Adv. Manuf. Technol. 2017, 88, 75–88. [Google Scholar] [CrossRef]
- Hu, Y.; He, X.; Yu, G.; Zhao, S. Capillary convection in pulsed butt welding of miscible dissimilar couple. Mech. Sci. Technol. 2016, 231, 2429–2440. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, H.; Feng, Y.; Luo, B. 3D Multiphysical Modelling of Fluid Dynamics and Mass Transfer in Laser Welding of Dissimilar Materials. Metals-Basel 2018, 8, 443. [Google Scholar] [CrossRef]
- Kou, S. Welding Metallurgy; John Wiley & Sons: New York, NY, USA, 2003; pp. 170–195. ISBN 0-471-43491-4. [Google Scholar]
- He, X.L.; Fuerschbach, P.W.; DebRoy, T. Heat transfer and fluid flow during laser spot welding of 304 stainless steel. J. Phys. D Appl. Phys. 2003, 36, 1388–1398. [Google Scholar] [CrossRef]
- Farzadi, A.; Serajzadeh, S.; Kokabi, A.H. Modeling of heat transfer and fluid flow during gas tungsten arc welding of commercial pure aluminum. Int. J. Adv. Manuf. Technol. 2008, 38, 258–267. [Google Scholar] [CrossRef]
- Wang, L.L.; Wei, J.H.; Wang, Z.M. Numerical and experimental investigations of variable polarity gas tungsten arc welding. Int. J. Adv. Manuf. Technol. 2018, 95, 2421–2428. [Google Scholar] [CrossRef]
- Ahmad, J.Y.S.; Ozturk, F.; Jarrar, F.; Evis, Z. Thermal history and microstructure during friction stir welding of Al-Mg ally. Int. J. Adv. Manuf. Technol. 2016, 86, 1071–1081. [Google Scholar] [CrossRef]
- Yang, Z.; Tao, W.; Zhao, X.; Chen, Y.; Shi, C. Numerical modelling and experimental verification of thermal characteristics and their correlations with mechanical properties of double-sided laser welded T-joint. Int. J. Adv. Manuf. Technol. 2017, 92, 1609–1618. [Google Scholar] [CrossRef]
- Voller, V.; Prakash, C. A fixed grid numerical modelling methodology for convection–diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Brent, A.D.; Voller, V.R.; Reid, K.J. Eethalphy-Porosity technology for modeling convection-diffusion phase-change—Application to the melting of a pure metal. Numer. Heat Transf. 1988, 13, 297–318. [Google Scholar] [CrossRef]
- Mikaél’A, B. Infrared Radiation: A Handbook for Applications; Plenum: New York, NY, USA, 1968. [Google Scholar]
- Peckner, D.; Bernstein, I.M. Handbook of Stainless Steels; McGraw-Hill: New York, NY, USA, 1977. [Google Scholar]
- Zhang, Y.; Zhang, C.L.; Liu, Y.M.; Zhang, J.L.; Chen, H. Welding Technology of Dissimilar Metals; China Machine Press: Beijing, China, 2016; pp. 254–255. ISBN 978-7-111-53889-9. [Google Scholar]
- Bahrami, A.; Helenbrook, B.T.; Valentine, D.T.; Aidun, D.K. Fluid flow and mixing in linear GTA welding of dissimilar ferrous alloy. Int. J. Heat Mass Transf. 2016, 93, 729–741. [Google Scholar] [CrossRef]
- Souli, M.; Benson, D.J. Abitrary Lagrangian Eulerian and Fluid-Structure Interaction; Wiley: New York, NY, USA, 2010; pp. 3–45. ISBN 978-1-84821-131-5. [Google Scholar]
- Fuerschbach, P.W.; Eisler, G.R. Effect of laser spot weld energy and duration on melting and absorption. Sci. Technol. Weld. Join. 2002, 7, 241–246. [Google Scholar] [CrossRef]
- Chakraborty, N. The effects of turbulence on molten pool transport during melting and solidification processes in continuous conduction mode laser welding of copper nickel dissimilar couple. Appl. Therm. Eng. 2009, 9, 3618–3631. [Google Scholar] [CrossRef]
- Hu, Y.; He, X.; Yu, G.; Ge, Z.; Zheng, C.; Ning, W. Heat and mass transfer in laser dissimilar welding of stainless steel and nickel. Appl. Surf. Sci. 2012, 258, 5914–5922. [Google Scholar] [CrossRef]
- Wei, H.L.; Elmer, J.W.; DebRoy, T. Origin of grain orientation during solidification of an aluminum alloy. Acta Mater. 2016, 115, 123–131. [Google Scholar] [CrossRef]
- Sun, Z.; Ion, J.C. Laser welding of dissimilar metal combinations. J. Mater. Sci. 1995, 30, 4205–4214. [Google Scholar] [CrossRef]
- Lippold, J.C. Welding Metallurgy and Weldability; John Wiley & Sons: New York, NY, USA, 2014; p. 21. ISBN 978-1-118-23070-1. [Google Scholar]
- Zhang, Z.; Wu, Q.; Grujicic, M.; Wan, Z.Y. Monte Carlo simulation of grain growth and welding zones in friction stir welding of AA6082-T6. J. Mater. Sci. 2016, 51, 1882–1895. [Google Scholar] [CrossRef]
- Lehto, P.; Remes, H.; Saukkonen, T. Influence of grain size distribution on the Hall-Petch relationship of welded structural steel. Mater. Sci. Eng. A 2014, 592, 28–39. [Google Scholar] [CrossRef]




| Material | Ni | Fe | Cr | C | P | S |
|---|---|---|---|---|---|---|
| Ni | 99.7 | 0.062 | - | 0.08 | - | 0.015 |
| 304ss | 8.5 | Bal | 18~20 | 0.06 | 0.03 | 0.02 |
| Laser Spot | Shielding Gas | Laser Power | Welding Speed |
|---|---|---|---|
| 0.57 mm | Pure argon (15 L/min) | 800 W | 10–30 mm/s |
| Parameter | Value |
|---|---|
| Ambient temperature | 300 K |
| Emissivity | 0.2 |
| Stefan-Boltzmann constant | 5.67 × 10−8 (Wm-2·K-4) |
| Laser absorption coefficient | 0.26 |
| Convection heat transfer coefficient | 100 (W/m2·K) |
| Property | 304ss | Ni |
|---|---|---|
| Liquidus temperature (K) | 1727 | 1735 |
| Solidus temperature (K) | 1672 | 1730 |
| Heat of fusion (kJ/kg) | 272 | 290 |
| Specific heat of solid (J/kg·K) | 711.28 | 515 |
| Specific heat of liquid (J/kg·K) | 836.8 | 595 |
| Thermal conductivity of solid(W/m·K) | 19.2 | 60.7 |
| Effective thermal conductivity of liquid(W/m·K) | 50 | 150 |
| Solid density (kg/m3) | 7450 | 8900 |
| Liquid density (kg/m3) | 6910 | 8880 |
| Dynamic viscosity (kg/m·s) | 6.7 × 10−3 | 3.68 × 10−3 |
| Surface tension (N/m) | 1.872 | 1.778 |
| Temperature coefficient of surface tension (N/m·K) | −4.3 × 10−4 | −3.4 × 10−4 |
| Welding Parameters | Case1 | Case 2 | Case 3 |
|---|---|---|---|
| Welding speed (mm/s) | 10 | 20 | 30 |
| Heat input (J/mm) | 80 | 40 | 26.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Yu, G.; He, X.; Li, S.; Zhao, Y. Numerical and Experimental Investigations of Solidification Parameters and Mechanical Property during Laser Dissimilar Welding. Metals 2018, 8, 799. https://doi.org/10.3390/met8100799
Li Z, Yu G, He X, Li S, Zhao Y. Numerical and Experimental Investigations of Solidification Parameters and Mechanical Property during Laser Dissimilar Welding. Metals. 2018; 8(10):799. https://doi.org/10.3390/met8100799
Chicago/Turabian StyleLi, Zhiyong, Gang Yu, Xiuli He, Shaoxia Li, and Yao Zhao. 2018. "Numerical and Experimental Investigations of Solidification Parameters and Mechanical Property during Laser Dissimilar Welding" Metals 8, no. 10: 799. https://doi.org/10.3390/met8100799
APA StyleLi, Z., Yu, G., He, X., Li, S., & Zhao, Y. (2018). Numerical and Experimental Investigations of Solidification Parameters and Mechanical Property during Laser Dissimilar Welding. Metals, 8(10), 799. https://doi.org/10.3390/met8100799






