A Combined Method to Model Dynamic Recrystallization Based on Cellular Automaton and a Phenomenological (CAP) Approach
Abstract
:1. Introduction
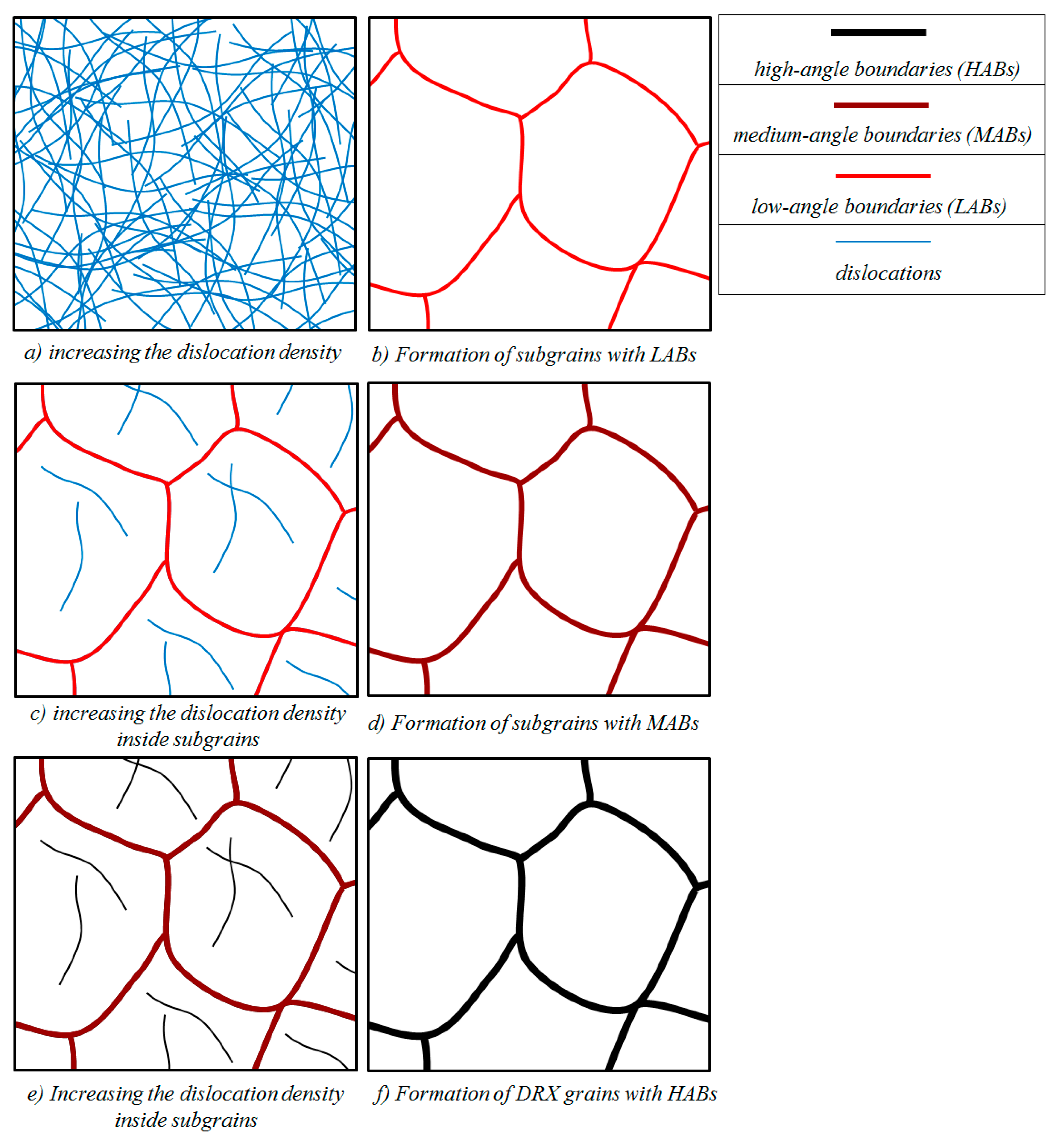
2. Continuous Dynamic Recrystallization (CDRX)
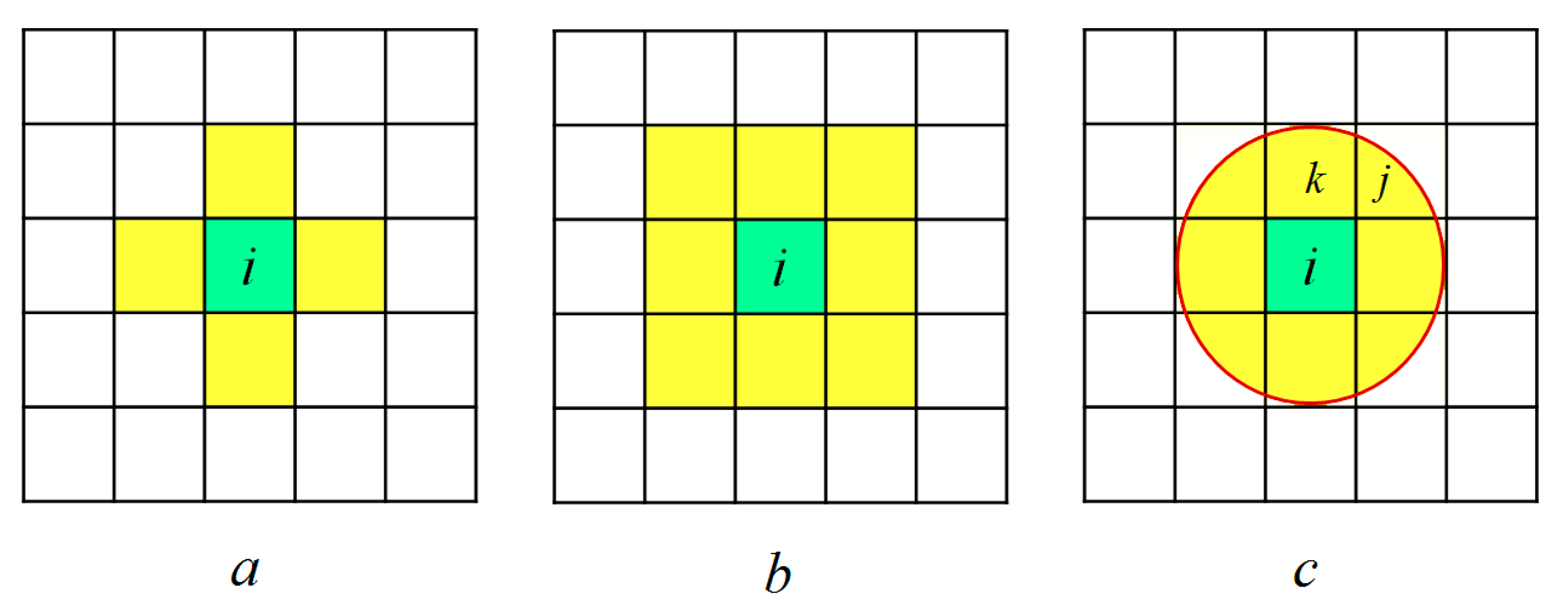
3. The CA Model Concept
3.1. Evolution of Dislocation Density
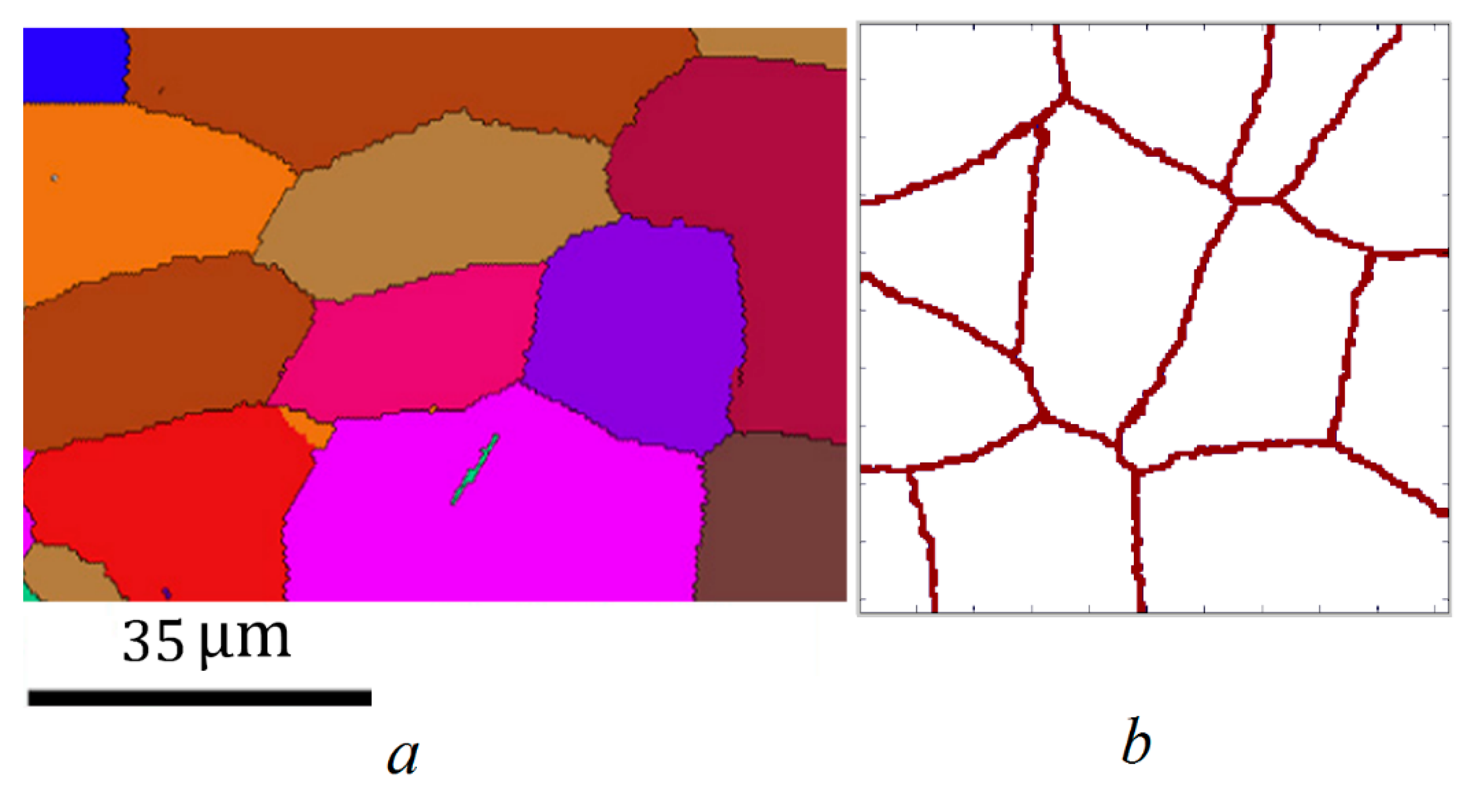
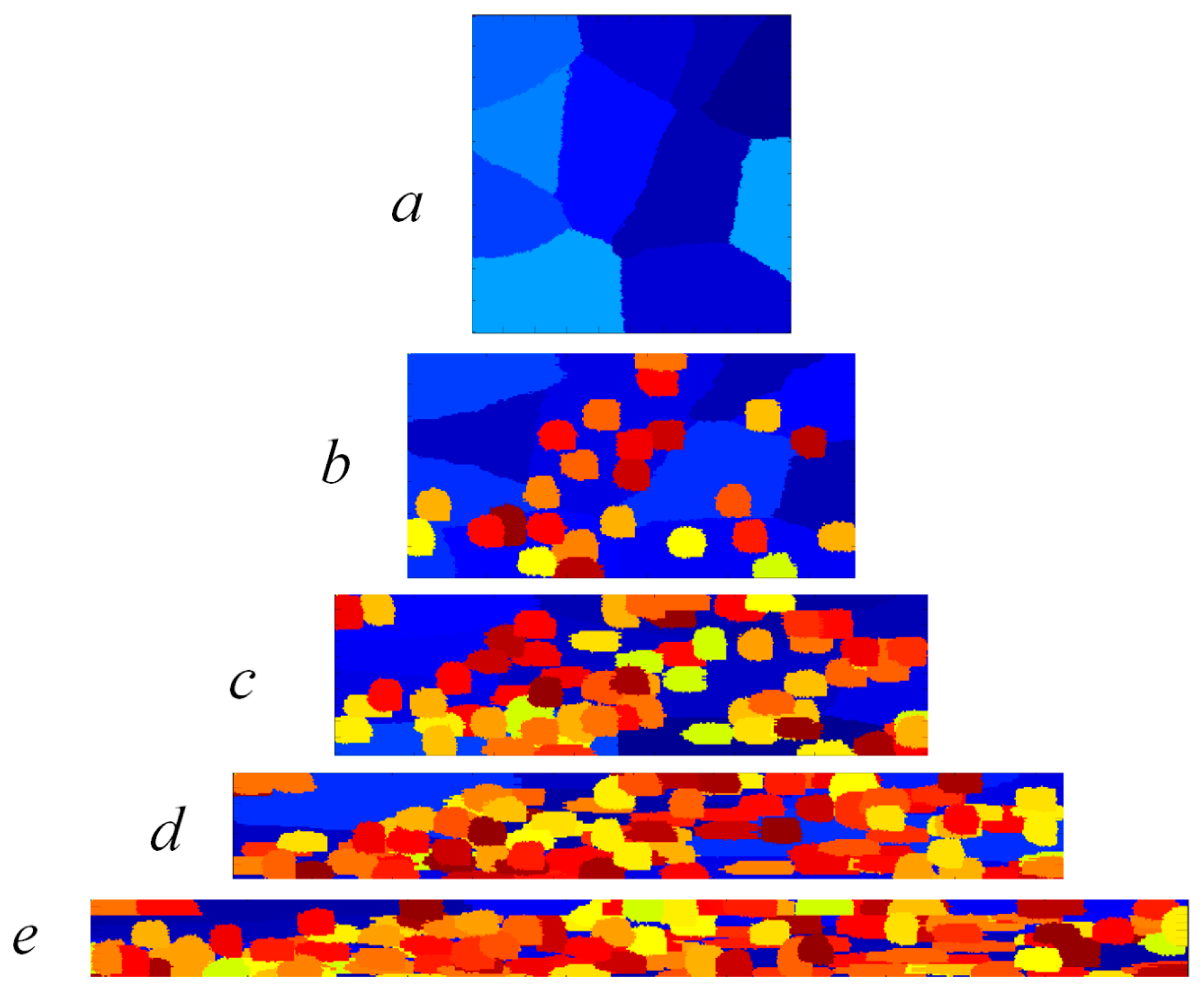
3.2. Generation of Initial Microstructure
3.3. Modeling of CDRX
3.4. The Module of Geometry Changes
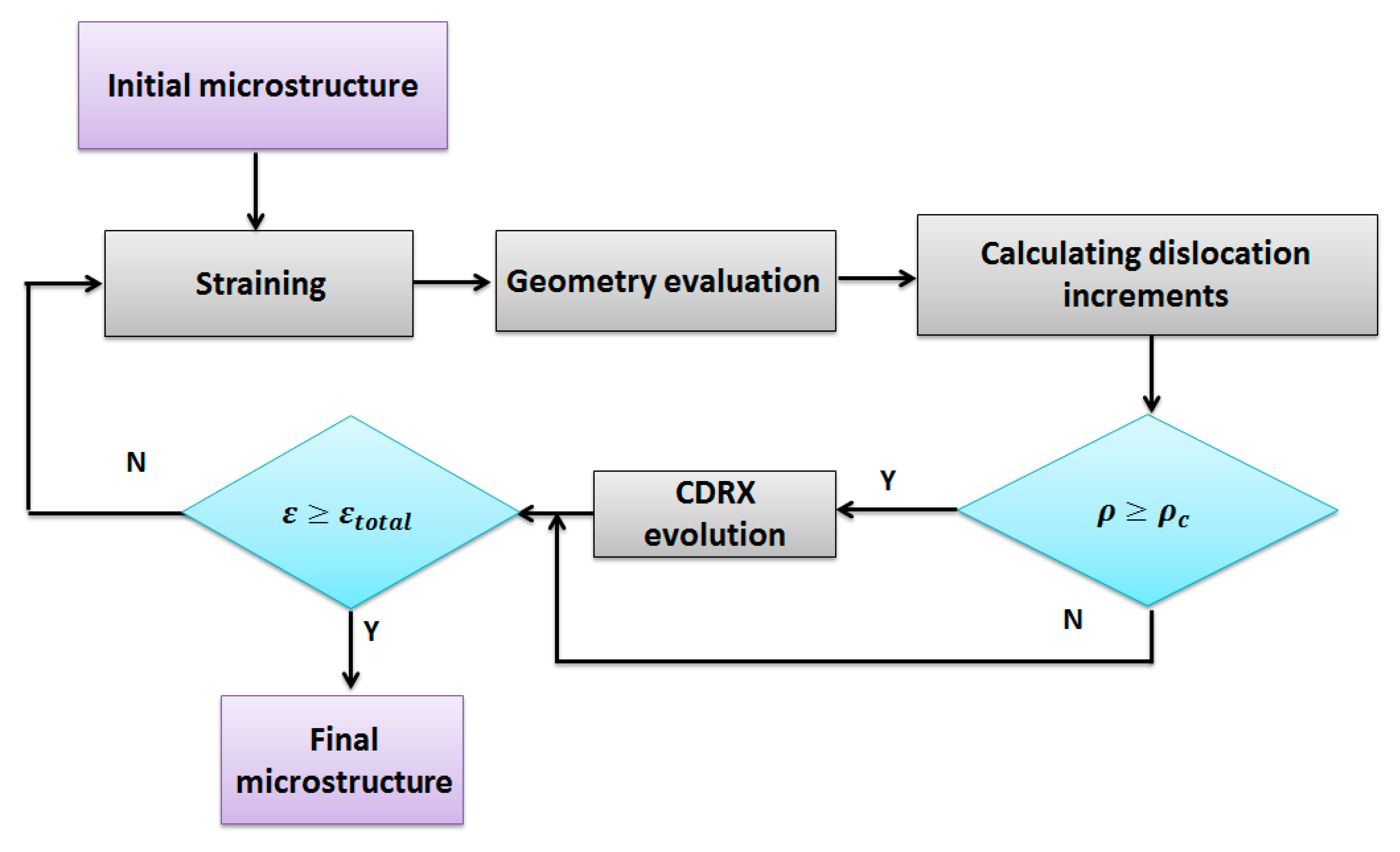
4. Simulation Stages
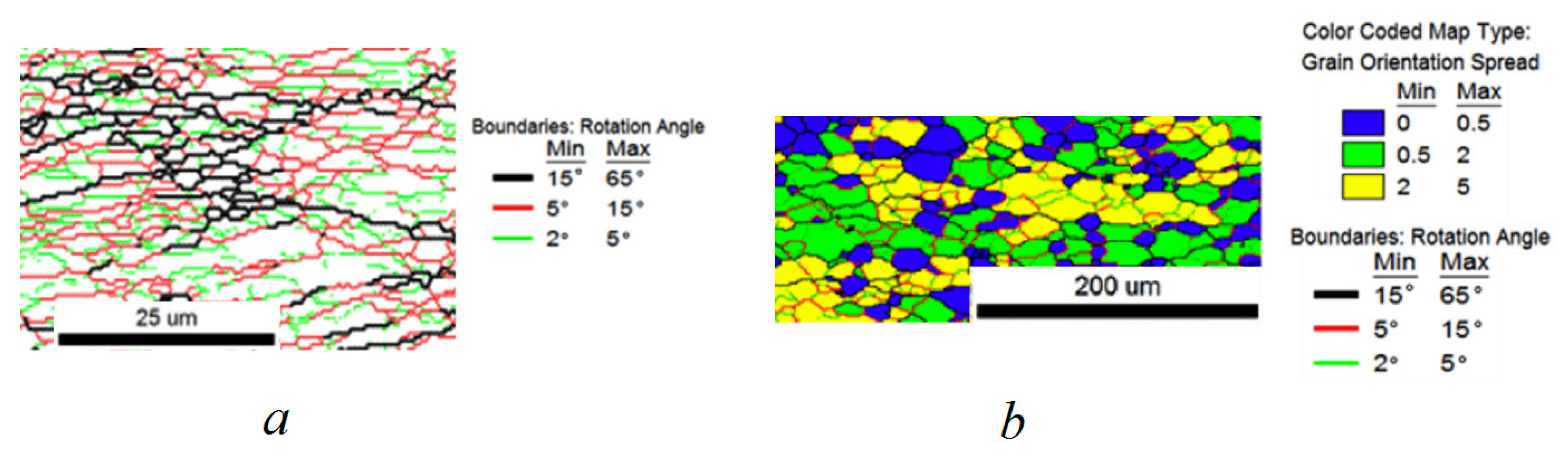
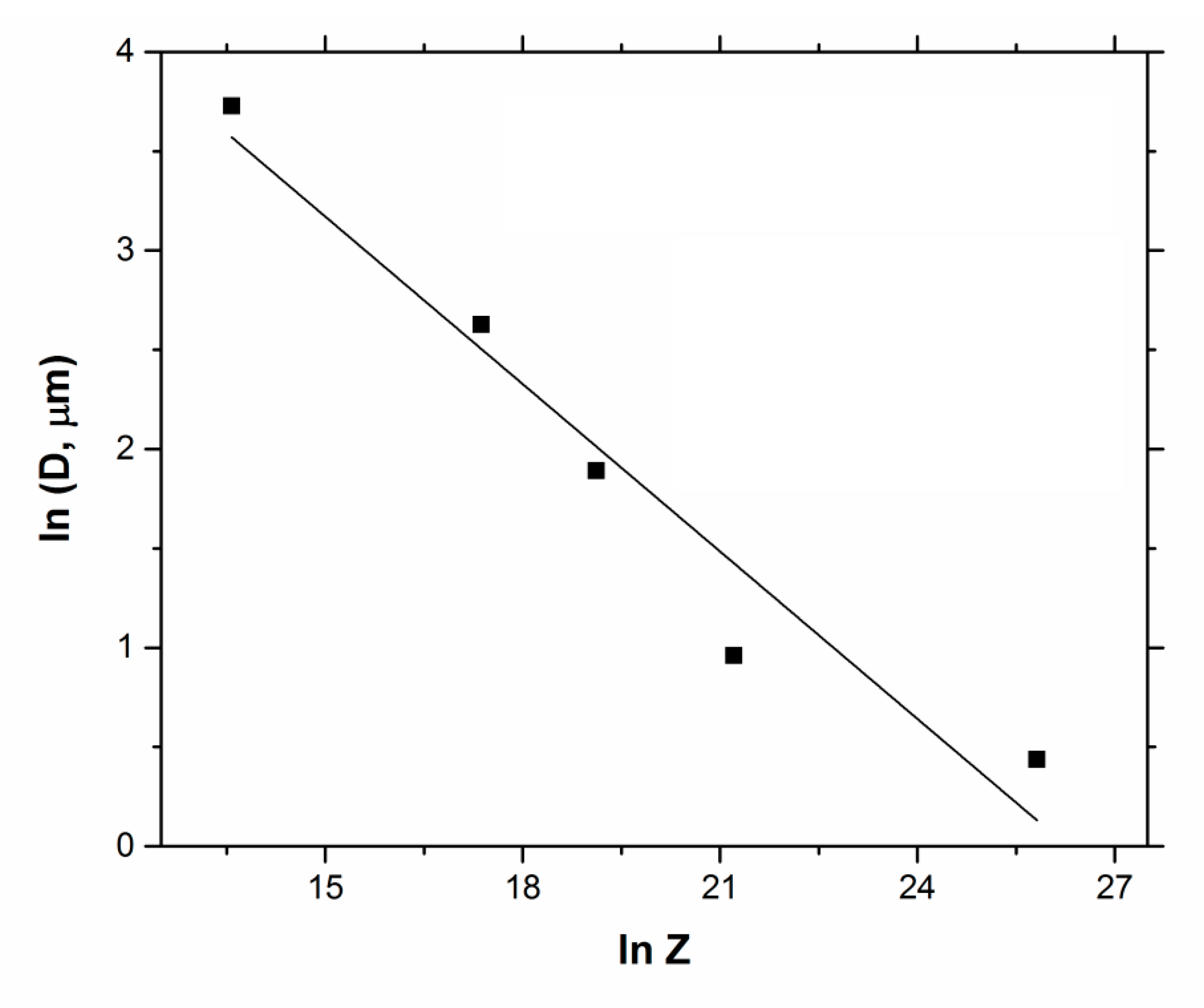
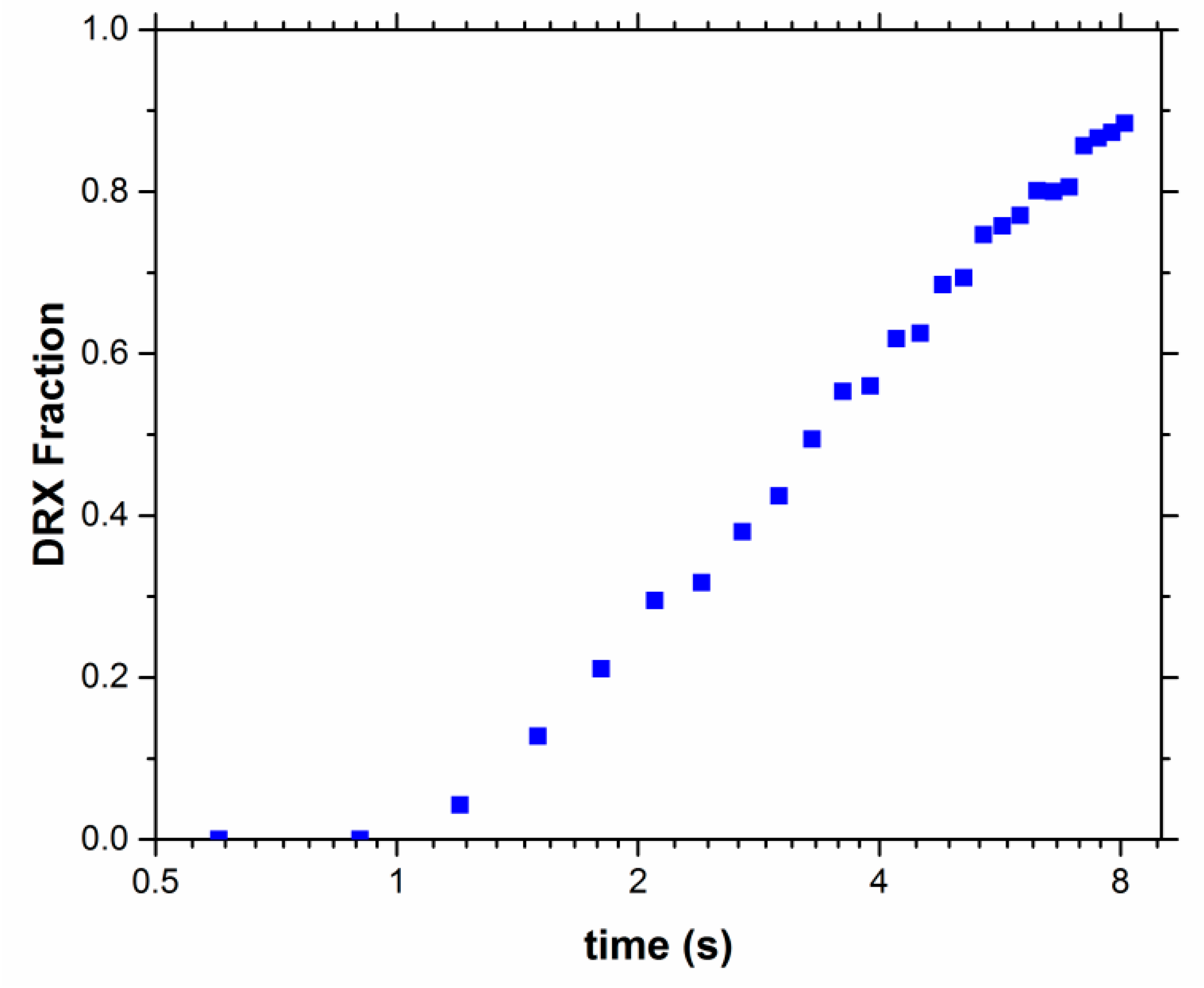
5. Simulation Results and Discussion
6. Conclusions
- -
- The recrystallization was considered as a one-step reaction without any large-scale growth, which is the characteristic of the CDRX phenomenon.
- -
- The size of CDRX grains was determined by using the subgrains’ size, which was formulated based on the phenomenological approach.
- -
- Volume fractions of the recrystallized area were well estimated by utilizing the proposed model.
- -
- Flow stress curves of the TiNiFe alloy were accurately forecasted by the presented CA model.
Author Contributions
Acknowledgments
Conflicts of Interest
Data Availability
Nomenclature
| Area of one cell | T | Temperature | |
| B | Burger’s vector | Tm | Melting point |
| C | A constant | Ix, Iy | Nominal deformation at two principal directions |
| Dsub | Subgrain size | The vector in the deformed position | |
| D | Average size of DRX grains | The vector in the undeformed position | |
| dε | Strain increment | Deformation matrix | |
| fDRX | DRX fraction | Dislocation interaction term | |
| K1 | A constant showing the effect of work hardening | 0 | Work hardening rate |
| K2 | A constant showing the effect of softening | Shear modulus | |
| Nucleation rate | Shear modulus at room temperature | ||
| Number of cells belonging to the given grain | Poisson’s ratio | ||
| NDRX | Total number of recrystallized cells | Dislocation density | |
| Ntotal | Total number of cells | Flow stress | |
| Q | Nucleation activation energy | Z | Zener–Hollomon parameter |
| R | Gas constant |
References
- Zhang, H.Y.; Zhang, S.H.; Li, Z.X.; Cheng, M. Hot die forging process optimization of superalloy IN718 turbine disc using processing map and finite element method. J. Eng. Manuf. 2010, 224, 103–110. [Google Scholar] [CrossRef]
- Raabe, D. Mesoscale simulation of recrystallization textures and microstructures. Adv. Eng. Mater. 2001, 3, 745–752. [Google Scholar] [CrossRef]
- Miodownik, M.A. A review of microstructural computer models used to simulate grain growth and recrystallisation in aluminium alloys. J. Light Met. 2002, 2, 125–135. [Google Scholar] [CrossRef]
- Cram, D.G.; Zurob, H.S.; Brechet, Y.J.M.; Hutchinson, C.R. Modelling discontinuous dynamic recrystallization using a physically based model for nucleation. Acta Mater. 2009, 57, 5218–5228. [Google Scholar] [CrossRef]
- Driver, J. The limitations of continuous dynamic recrystallization (CDRX) of aluminium alloys. Mater. Lett. 2018, 222, 135–137. [Google Scholar] [CrossRef]
- Zhang, Z.; Qu, S.; Feng, A.; Hu, X.; Shen, J. The Low Strain Rate Response of As-Cast Ti-6Al-4V Alloy with an Initial Coarse Lamellar Structure. Metals 2018, 8, 270. [Google Scholar] [CrossRef]
- Cram, D.G.; Fang, X.Y.; Zurob, H.S.; Bréchet, Y.J.M.; Hutchinson, C.R. The effect of solute on discontinuous dynamic recrystallization. Acta Mater. 2012, 60, 6390–6404. [Google Scholar] [CrossRef]
- Maire, L.; Fausty, J.; Bernacki, M.; Bozzolo, N.; Micheli, P.D.; Moussa, C. A new topological approach for the mean field modeling of dynamic recrystallization. Mater. Des. 2018, 146, 194–207. [Google Scholar] [CrossRef] [Green Version]
- Belyakov, A.; Tikhonova, M.; Dolzhenko, P.; Sakai, T.; Kaibyshev, R. On kinetics of grain refinement and strengthening by dynamic recrystallization. Adv. Eng. Mater. 2018. [Google Scholar] [CrossRef]
- Vondrous, A.; Bienger, P.; Schreijäg, S.; Selzer, M.; Schneider, D.; Nestler, B.; Helm, D.; Mönig, R. Combined crystal plasticity and phase-field method for recrystallization in a process chain of sheet metal production. Comput. Mech. 2015, 55, 439–452. [Google Scholar] [CrossRef]
- Takaki, T.; Yamanaka, A.; Tomita, Y. Phase-Field Modeling for Dynamic Recrystallization. In From Creep Damage Mechanics to Homogenization Methods; Altenbach, H., Matsuda, T., Okumura, D., Eds.; Springer: Basel, Switzerland, 2015; pp. 441–459. [Google Scholar]
- Hore, S.; Das, S.K.; Banerjee, S.; Mukherjee, S. Computational modelling of static recrystallization and two dimensional microstructure evolution during hot strip rolling of advanced high strength steel. J. Manuf. Process. 2015, 17, 78–87. [Google Scholar] [CrossRef]
- Madej, Ł.; Sitko, M. Parallelization of the Monte Carlo Static Recrystallization Model. In eScience on Distributed Computing Infrastructure; Bubak, M., Kitowski, J., Wiatr, K., Eds.; Springer: Basel, Switzerland, 2014; pp. 445–458. [Google Scholar]
- Fu, J.; Peng, B.; Xie, B.; Ye, Y. A modified monte-carlo potts model for dynamic recrystallization. Adv. Mater. Res. 2015, 1096, 280–287. [Google Scholar] [CrossRef]
- Fan, D.; Chen, L.Q. Computer simulation of grain growth using a continuum field model. Acta Mater. 1997, 45, 611–622. [Google Scholar] [CrossRef]
- Krill Iii, C.E.; Chen, L.Q. Computer simulation of 3-D grain growth using a phase-field model. Acta Mater. 2002, 50, 3059–3075. [Google Scholar] [CrossRef]
- Lusk, M.T. A phase–field paradigm for grain growth and recrystallization. Proc. Royal Soc. A 1999, 455, 677–700. [Google Scholar] [CrossRef]
- Piękoś, K.; Tarasiuk, J.; Wierzbanowski, K.; Bacroix, B. Generalized vertex model of recrystallization–Application to polycrystalline copper. Comput. Mater. Sci. 2008, 42, 584–594. [Google Scholar] [CrossRef]
- Mellbin, Y.; Hallberg, H.; Ristinmaa, M. Modeling of dynamic recrystallization at large deformations using a combined crystal plasticity and vertex model. In Proceedings of the 9th European Solid Mechanics Conference, Madrid, Spain, 6–10 July 2015. [Google Scholar]
- Reyes, L.A.; Páramo, P.; Zamarripa, A.S.; Garza, M.; Mata, M.P.G. Grain size modeling of a Ni-base superalloy using cellular automata algorithm. Mater. Des. 2015, 83, 301–307. [Google Scholar] [CrossRef]
- Zinoviev, A.; Zinovieva, O.; Ploshikhin, V.; Romanova, V.; Balokhonov, R. Evolution of grain structure during laser additive manufacturing. Simulation by a cellular automata method. Mater. Des. 2016, 106, 321–329. [Google Scholar] [CrossRef]
- Wang, L.; Fang, G.; Qian, L. Modeling of dynamic recrystallization of magnesium alloy using cellular automata considering initial topology of grains. Mater. Sci. Eng. 2018, 711, 268–283. [Google Scholar] [CrossRef]
- Timoshenkov, A.; Warczok, P.; Albu, M.; Klarner, J.; Kozeschnik, E.; Bureau, R.; Sommitsch, C. Modelling the dynamic recrystallization in C–Mn micro-alloyed steel during thermo-mechanical treatment using cellular automata. Comput. Mater. Sci. 2014, 94, 85–94. [Google Scholar] [CrossRef]
- Sommitsch, C.; Krumphals, A.; Candic, M.; Tian, B.; Stockinger, M. Modeling of grain growth in one and two phase materials by 2D cellular automata. J. Comput. Theor. Nanosci. 2012, 9, 1515–1524. [Google Scholar] [CrossRef]
- Lin, Y.C.; Liu, Y.X.; Chen, M.S.; Huang, M.H.; Ma, X.; Long, Z.L. Study of static recrystallization behavior in hot deformed Ni-based superalloy using cellular automaton model. Mater. Des. 2016, 99, 107–114. [Google Scholar] [CrossRef]
- Han, F.; Tang, B.; Kou, H.; Li, J.; Feng, Y. Cellular automata modeling of static recrystallization based on the curvature driven subgrain growth mechanism. J. Mater. Sci. 2013, 48, 7142–7152. [Google Scholar] [CrossRef]
- Sieradzki, L.; Madej, L. A perceptive comparison of the cellular automata and Monte Carlo techniques in application to static recrystallization modeling in polycrystalline materials. Comput. Mater. Sci. 2013, 67, 156–173. [Google Scholar] [CrossRef]
- Han, F.; Tang, B.; Kou, H.; Cheng, L.; Li, J.; Feng, Y. Static recrystallization simulations by coupling cellular automata and crystal plasticity finite element method using a physically based model for nucleation. J. Mater. Sci. 2014, 49, 3253–3267. [Google Scholar] [CrossRef]
- Jin, Z.; Cui, Z. Investigation on dynamic recrystallization using a modified cellular automaton. Comput. Mater. Sci. 2012, 63, 249–255. [Google Scholar] [CrossRef]
- Xiao, N.; Zheng, C.; Li, D.; Li, Y. A simulation of dynamic recrystallization by coupling a cellular automaton method with a topology deformation technique. Comput. Mater. Sci. 2008, 41, 366–374. [Google Scholar] [CrossRef]
- Chen, F.; Qi, K.; Cui, Z.; Lai, X. Modeling the dynamic recrystallization in austenitic stainless steel using cellular automaton method. Comput. Mater. Sci. 2014, 83, 331–340. [Google Scholar] [CrossRef]
- Azarbarmas, M.; Aghaie-Khafri, M. Dynamic recrystallization and texture modeling of IN718 superalloy. Model. Simul. Mater. Sci. Eng. 2017, 25, 075001. [Google Scholar] [CrossRef]
- Jin, Z.Y.; Juan, L.; Cui, Z.S.; Wei, D.L. Identification of nucleation parameter for cellular automaton model of dynamic recrystallization. Trans. Nonferrous Met. Soc. 2010, 20, 458–464. [Google Scholar] [CrossRef]
- Ji, H.P.; Zhang, L.G.; Liu, J.; Wang, T.Y. Cellular automaton modeling of dynamic recrystallisation microstructure evolution for 316LN stainless steel. Key Eng. Mater. 2016, 693, 548–553. [Google Scholar] [CrossRef]
- Zhang, T.; Lu, S.; Wu, Y.; Hai, G. Optimization of deformation parameters of dynamic recrystallization for 7055 aluminum alloy by cellular automaton. Trans. Nonferrous Met. Soc. 2017, 27, 1327–1337. [Google Scholar] [CrossRef]
- Li, J.; Xie, Z.; Li, S.; Zang, Y. Modeling on dynamic recrystallization of aluminium alloy 7050 during hot compression based on cellular automaton. J. Cent. South Univ. 2016, 23, 497–507. [Google Scholar] [CrossRef]
- Azarbarmas, M.; Aghaie-Khafri, M. A new cellular automaton method coupled with a rate-dependent (CARD) model for predicting dynamic recrystallization behavior. Metall. Mater. Trans. 2018, 49. [Google Scholar] [CrossRef]
- Azarbarmas, M.; Aghaie-Khafri, M.; Cabrera, J.M.; Calvo, J. Dynamic recrystallization mechanisms and twining evolution during hot deformation of Inconel 718. Mater. Sci. Eng. 2016, 678, 137–152. [Google Scholar] [CrossRef]
- Azarbarmas, M.; Aghaie-Khafri, M.; Cabrera, J.M.; Calvo, J. Microstructural evolution and constitutive equations of Inconel 718 alloy under quasi-static and quasi-dynamic conditions. Mater. Des. 2016, 94, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Vorhauer, A.; Pippan, R. On the onset of a steady state in body-centered cubic iron during severe plastic deformation at low homologous temperatures. Metall. Mater. Trans. 2008, 39, 417–429. [Google Scholar] [CrossRef]
- Kaibyshev, R.; Shipilova, K.; Musin, F.; Motohashi, Y. Continuous dynamic recrystallization in an Al–Li–Mg–Sc alloy during equal-channel angular extrusion. Mater. Sci. Eng. 2005, 396, 341–351. [Google Scholar] [CrossRef]
- Mishnev, R.; Shakhova, I.; Kaibyshev, R. Microstructure evolution in a Cu-Cr-Zr alloy during warm intense plastic straining. In Proceedings of the 6th International Conference on Nanomaterials by Severe Plastic Deformation, Metz, France, 30 June–4 July 2014; pp. 1–7. [Google Scholar]
- Shojaeefard, M.H.; Akbari, M.; Khalkhali, A.; Asadi, P.; Parivar, A.H. Optimization of microstructural and mechanical properties of friction stir welding using the cellular automaton and Taguchi method. Mater. Des. 2014, 64, 660–666. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Liu, X.; Li, L.X.; He, F.Y.; Zhou, J.; Zhu, B.W.; Zhang, L.Q. Simulation on dynamic recrystallization behavior of AZ31 magnesium alloy using cellular automaton method coupling Laasraoui–Jonas model. Trans. Nonferrous Met. Soc. 2013, 23, 2692–2699. [Google Scholar] [CrossRef]
- Chen, F.; Cui, Z.S.; Chen, J. Prediction of microstructural evolution during hot forging. Manuf. Rev. 2014, 1, 1–21. [Google Scholar] [CrossRef]
- Ma, X.; Zheng, C.W.; Zhang, X.G.; Li, D.Z. Microstructural depictions of austenite dynamic recrystallization in a low-carbon steel: A cellular automaton model. Acta Metall. Sin. 2016, 29, 1127–1135. [Google Scholar] [CrossRef]
- Chen, F.; Cui, Z.; Liu, J.; Chen, W.; Chen, S. Mesoscale simulation of the high-temperature austenitizing and dynamic recrystallization by coupling a cellular automaton with a topology deformation technique. Mater. Sci. Eng. 2010, 527, 5539–5549. [Google Scholar] [CrossRef]
- Sachs, G.Z. The plastic deformation mode of polycrystals. Z. Verein Deut. Ing. 1928, 72, 734. [Google Scholar]
- Taylor, G. Plastic strain in metals. J. Inst. Met. 1938, 62, 307–324. [Google Scholar]
- Yin, X.Q.; Park, C.H.; Li, Y.F.; Ye, W.J.; Zuo, Y.T.; Lee, S.W.; Yeom, J.T.; Mi, X.J. Mechanism of continuous dynamic recrystallization in a 50Ti-47Ni-3Fe shape memory alloy during hot compressive deformation. J. Alloys Compd. 2017, 693, 426–431. [Google Scholar] [CrossRef]
- Yin, X.Q.; Wang, S.J.; Li, Y.F.; Gao, B.D.; Kang, X.Y.; Mi, X.J. Hot deformation behavior of TiNiFe shape memory alloy: A study with processing map. Adv. Mater. Res. 2013, 631, 371–376. [Google Scholar] [CrossRef]
- Petrov, P.; Abbod, M. Analysis of rheological behavior of AL-CU-MG-FE-NI alloy at elevated temperatures using phenomenological flow stress model. Int. J. Mater. Form. 2009, 2, 371. [Google Scholar] [CrossRef]
- Svyetlichnyy, D.S.; Muszka, K.; Majta, J. Three-dimensional frontal cellular automata modeling of the grain refinement during severe plastic deformation of microalloyed steel. Comput. Mater. Sci. 2015, 102, 159–166. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.L.; Volinsky, A.A.; Tian, B.H.; Chai, Z.; Liu, P.; Liu, Y. Hot deformation and dynamic recrystallization behavior of the Cu-Cr-Zr-Y alloy. J. Mater. Eng. Perform. 2016, 25, 1150–1156. [Google Scholar] [CrossRef]
- Huang, L.J.; Qi, F.; Hua, P.T.; Yu, L.X.; Liu, F.; Sun, W.R.; Hu, Z.Q. Discontinuous dynamic recrystallization of inconel 718 superalloy during the superplastic deformation. Metall. Mater. Trans. 2015, 46, 4276–4285. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, W.Z.; Zhen, L.; Zhang, X.M. Microstructure evolution during dynamic recrystallization of hot deformed superalloy 718. Mater. Sci. Eng. 2008, 486, 321–332. [Google Scholar] [CrossRef]
- Chuan, W.; He, Y.; Wei, L.H. Modeling of discontinuous dynamic recrystallization of a near-α titanium alloy imi834 during isothermal hot compression by combining a cellular automaton model with a crystal plasticity finite element method. Comput. Mater. Sci. 2013, 79, 944–959. [Google Scholar] [CrossRef]
- Beygelzimer, Y.E.; Spuskanyuk, A.V. The thick yield surface: Idea and approach for investigating its structure. Philos. Mag. 1999, 79, 2437–2459. [Google Scholar] [CrossRef]
- Kotamala, S. Prestressing of Simply Supported Concrete Beam with Nitinol Shape Memory Alloy; University of Toledo: Toledo, OH, USA, 2004. [Google Scholar]
- Jaeger, J.D.; Solas, D.; Fandeur, O.; Schmitt, J.H.; Rey, C. 3D numerical modeling of dynamic recrystallization under hot working: Application to Inconel 718. Mater. Sci. Eng. 2015, 646, 33–44. [Google Scholar] [CrossRef]
- Churakova, A.; Gunderov, D. Increase in the dislocation density and yield stress of the Ti50Ni50 alloy caused by thermal cycling. Mater. Today Proc. 2017, 4, 4732–4736. [Google Scholar] [CrossRef]
- Wang, S.; Mi, X.; Yin, X.; Li, Y. Deformation behavior of TiNiFe alloy in isothermal compression. Rare Met. 2012, 31, 323–327. [Google Scholar] [CrossRef]
- Ding, R.; Guo, Z.X. Microstructural modelling of dynamic recrystallisation using an extended cellular automaton approach. Comput. Mater. Sci. 2002, 23, 209–218. [Google Scholar] [CrossRef]
- Liu, Y.G.; Li, M.Q.; Luo, J. The modelling of dynamic recrystallization in the isothermal compression of 300M steel. Mater. Sci. Eng. 2013, 574, 1–8. [Google Scholar] [CrossRef]
- Chen, D.D.; Lin, Y.C.; Zhou, Y.; Chen, M.S.; Wen, D.X. Dislocation substructures evolution and an adaptive-network-based fuzzy inference system model for constitutive behavior of a Ni-based superalloy during hot deformation. J. Alloys Compd. 2017, 708, 938–946. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.M.; Najafizadeh, A. Modeling and prediction of hot deformation flow curves. Metall. Mater. Trans. 2012, 43, 108–123. [Google Scholar] [CrossRef]
- Lin, Y.C.; He, D.G.; Chen, M.S.; Chen, X.M.; Zhao, C.Y.; Ma, X.; Long, Z.L. EBSD analysis of evolution of dynamic recrystallization grains and δ phase in a nickel-based superalloy during hot compressive deformation. Mater. Des. 2016, 97, 13–24. [Google Scholar] [CrossRef]
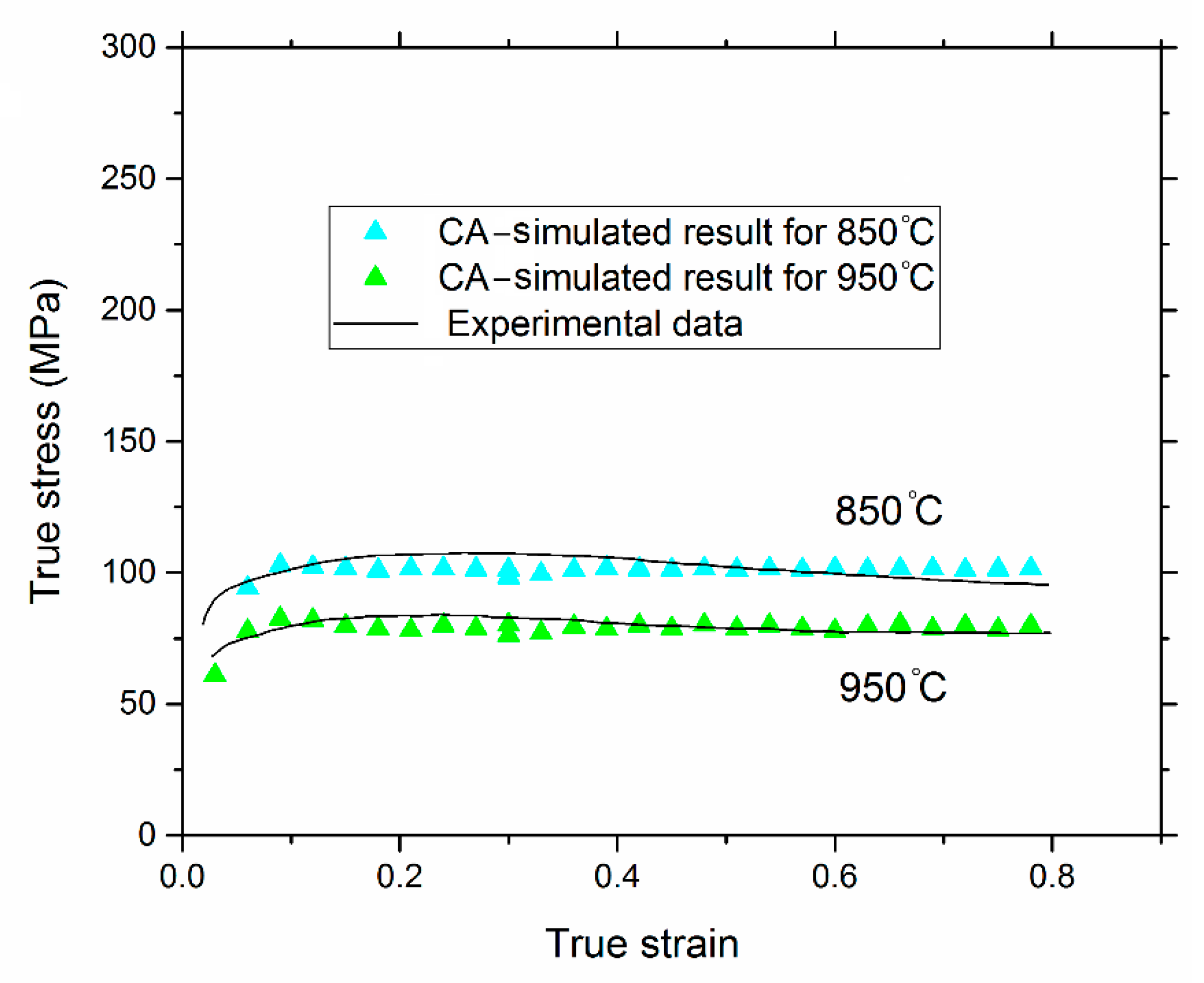
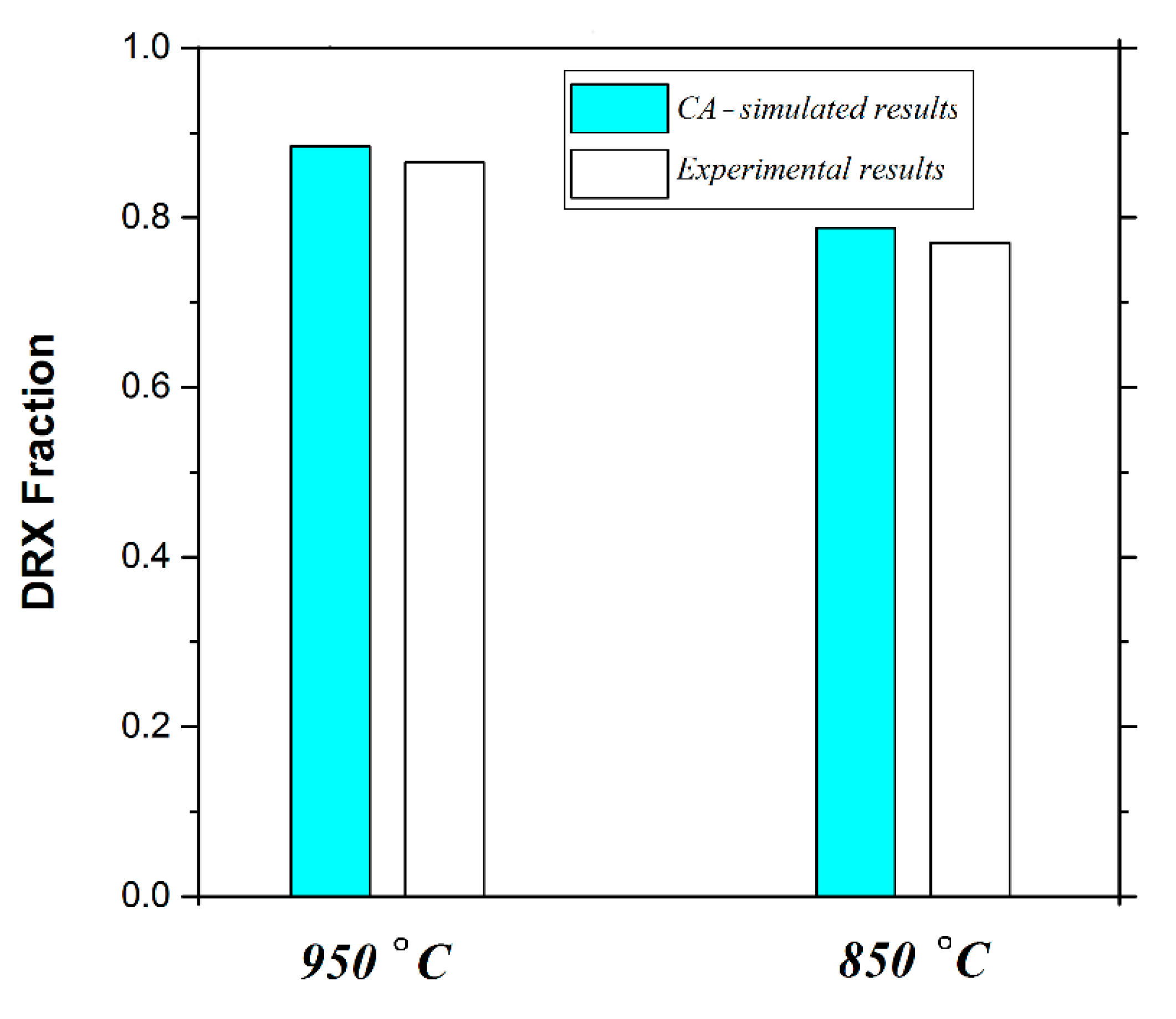
| Parameter | Value |
|---|---|
| Melting point (Tm) | 1275 °C [60] |
| Density of initial dislocations | 1013 m‒2 [61] |
| Room temperature shear modulus (μ0) | 2.15 × 1010 Pa [62] |
| Activation energy of nucleation (Q) | 429 kJ/mol [63] |
| Poisson’s ratio (ν) | 0.34 [61] |
| Burger’s vector (b) | 2.86 × 10‒10 m [64] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azarbarmas, M.; Mirjavadi, S.S.; Ghasemi, A.; Hamouda, A.M. A Combined Method to Model Dynamic Recrystallization Based on Cellular Automaton and a Phenomenological (CAP) Approach. Metals 2018, 8, 923. https://doi.org/10.3390/met8110923
Azarbarmas M, Mirjavadi SS, Ghasemi A, Hamouda AM. A Combined Method to Model Dynamic Recrystallization Based on Cellular Automaton and a Phenomenological (CAP) Approach. Metals. 2018; 8(11):923. https://doi.org/10.3390/met8110923
Chicago/Turabian StyleAzarbarmas, Morteza, Seyed Sajad Mirjavadi, Ali Ghasemi, and Abdel Magid Hamouda. 2018. "A Combined Method to Model Dynamic Recrystallization Based on Cellular Automaton and a Phenomenological (CAP) Approach" Metals 8, no. 11: 923. https://doi.org/10.3390/met8110923
APA StyleAzarbarmas, M., Mirjavadi, S. S., Ghasemi, A., & Hamouda, A. M. (2018). A Combined Method to Model Dynamic Recrystallization Based on Cellular Automaton and a Phenomenological (CAP) Approach. Metals, 8(11), 923. https://doi.org/10.3390/met8110923






