Substitution Versus Full-Heusler Segregation in TiCoSb
Abstract
:1. Introduction
2. Experiment
3. Results
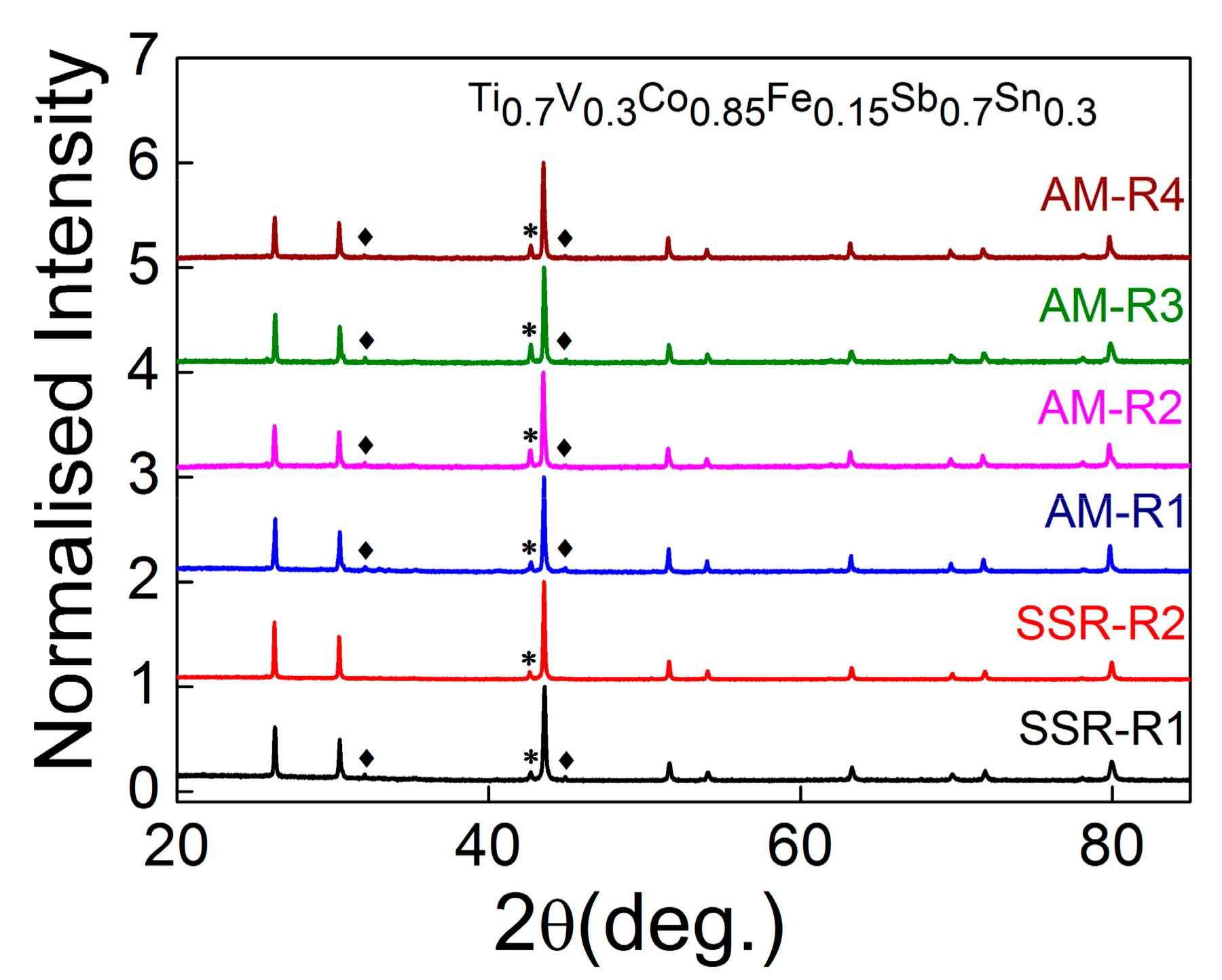
3.1. X-ray Powder Diffraction
3.2. Scanning Electron Microscopy
3.3. Electrical Properties
3.4. Thermal Conductivity and Figure of Merit
4. Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bos, J.W.G.; Downie, R.A. Half-Heusler thermoelectrics: A complex class of materials. J. Phys. Condens. Matter 2014, 26, 433201. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.J.; Fu, C.G.; Xie, H.H.; Liu, Y.T.; Zhao, X.B. High Efficiency Half-Heusler Thermoelectric Materials for Energy Harvesting. Adv. Energy Mater. 2015, 5, 1500588. [Google Scholar] [CrossRef]
- Rowe, D.M. Thermoelectrics and Its Energy Harvesting; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Schwall, M.; Balke, B. Phase separation as a key to a thermoelectric high efficiency. Phys. Chem. Chem. Phys. 2013, 15, 1868–1872. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Gao, S.; Zeng, X.; Dehkordi, A.M.; Tritt, T.M.; Poon, S.J. Uncovering high thermoelectric figure of merit in (Hf,Zr)NiSn half-Heusler alloys. Appl. Phys. Lett. 2015, 107, 041902. [Google Scholar] [CrossRef] [Green Version]
- Gurth, M.; Rogl, G.; Romaka, V.V.; Grytsiv, A.; Bauer, E.; Rogl, P. Thermoelectric high ZT half-Heusler alloys Ti1−x−yZrxHfyNiSn (0 ≤ x ≤ 1; 0 ≤ y ≤ 1). Acta Mater. 2016, 104, 210–222. [Google Scholar] [CrossRef]
- Barczak, S.A.; Halpin, J.E.; Buckman, J.; Decourt, R.; Pollet, M.; Smith, R.I.; MacLaren, D.A.; Bos, J.W.G. Grain-by-Grain Compositional Variations and Interstitial Metals-A New Route toward Achieving High Performance in Half-Heusler Thermoelectrics. ACS Appl. Mater. Interfaces 2018, 10, 4786–4793. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.A.; Joshi, G.; Liu, W.S.; Lan, Y.C.; Wang, H.; Lee, S.; Simonson, J.W.; Poon, S.J.; Tritt, T.M.; Chen, G.; et al. Enhanced Thermoelectric Figure of Merit of p-Type Half-Heuslers. Nano Lett. 2011, 11, 556–560. [Google Scholar] [CrossRef] [PubMed]
- Rausch, E.; Balke, B.; Ouardi, S.; Felser, C. Enhanced thermoelectric performance in the p-type half-Heusler (Ti/Zr/Hf)CoSb0.8Sn0.2 system via phase separation. Phys. Chem. Chem. Phys. 2014, 16, 25258–25262. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.G.; Bai, S.Q.; Liu, Y.T.; Tang, Y.S.; Chen, L.D.; Zhao, X.B.; Zhu, T.J. Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials. Nat. Commun. 2015, 6, 8144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, C.G.; Zhu, T.J.; Liu, Y.T.; Xie, H.H.; Zhao, X.B. Band engineering of high performance p-type FeNbSb based half-Heusler thermoelectric materials for figure of merit zT > 1. Energy Environ. Sci. 2015, 8, 216–220. [Google Scholar] [CrossRef]
- Hea, R.; Kraemer, D.; Mao, J.; Zeng, L.; Jie, Q.; Lan, Y.C.; Li, C.H.; Shuai, J.; Kim, H.S.; Liu, Y.; et al. Achieving high power factor and output power density in p-type half-Heuslers Nb1−xTixFeSb. Proc. Natl. Acad. Sci. USA 2016, 113, 13576–13581. [Google Scholar] [CrossRef] [PubMed]
- Xia, K.; Liu, Y.; Anand, S.; Snyder, G.J.; Xin, J.; Yu, J.; Zhao, X.; Zhu, T. Enhanced Thermoelectric Performance in 18-Electron Nb0.8CoSb Half-Heusler Compound with Intrinsic Nb Vacancies. Adv. Funct. Mater. 2018, 28, 1705845. [Google Scholar] [CrossRef]
- Ferluccio, D.A.; Smith, R.I.; Buckman, J.; Bos, J.W.G. Impact of Nb vacancies and p-type doping of the NbCoSn-NbCoSb half-Heusler thermoelectrics. Phys. Chem. Chem. Phys. 2018, 20, 3979–3987. [Google Scholar] [CrossRef] [PubMed]
- Graf, T.; Felser, C.; Parkin, S.S.P. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Downie, R.A.; MacLaren, D.A.; Smith, R.I.; Bos, J.W.G. Enhanced thermoelectric performance in TiNiSn-based half-Heuslers. Chem. Commun. 2013, 49, 4184–4186. [Google Scholar] [CrossRef] [PubMed]
- Birkel, C.S.; Douglas, J.E.; Lettiere, B.R.; Seward, G.; Verma, N.; Zhang, Y.C.; Pollock, T.M.; Seshadri, R.; Stucky, G.D. Improving the thermoelectric properties of half-Heusler TiNiSn through inclusion of a second full-Heusler phase: Microwave preparation and spark plasma sintering of TiNi1+xSn. Phys. Chem. Chem. Phys. 2013, 15, 6990–6997. [Google Scholar] [CrossRef] [PubMed]
- Chai, Y.W.; Kimura, Y. Microstructure evolution of nanoprecipitates in half-Heusler TiNiSn alloys. Acta Mater. 2013, 61, 6684–6697. [Google Scholar] [CrossRef]
- Douglas, J.E.; Birkel, C.S.; Verma, N.; Miller, V.M.; Miao, M.S.; Stucky, G.D.; Pollock, T.M.; Seshadri, R. Phase stability and property evolution of biphasic Ti-Ni-Sn alloys for use in thermoelectric applications. J. Appl. Phys. 2014, 115, 043720. [Google Scholar] [CrossRef]
- Downie, R.A.; Barczak, S.A.; Smith, R.I.; Bos, J.W.G. Compositions and thermoelectric properties of XNiSn (X = Ti, Zr, Hf) half-Heusler alloys. J. Mater. Chem. C 2015, 3, 10534–10542. [Google Scholar] [CrossRef] [Green Version]
- Downie, R.A.; Smith, R.I.; MacLaren, D.A.; Bos, J.W.G. Metal Distributions, Efficient n-Type Doping, and Evidence for in-Gap States in TiNiMySn (M = Co, Ni, Cu) half-Heusler Nanocomposites. Chem. Mater. 2015, 27, 2449–2459. [Google Scholar] [CrossRef] [Green Version]
- Berche, A.; Jund, P. Fully Ab-Initio Determination of the Thermoelectric Properties of Half-Heusler NiTiSn: Crucial Role of Interstitial Ni Defects. Materials 2018, 11, 868. [Google Scholar] [CrossRef] [PubMed]
- Dow, H.S.; Kim, W.S.; Shin, W.H. Effect of C and N Addition on Thermoelectric Properties of TiNiSn Half-Heusler Compounds. Materials 2018, 11, 262. [Google Scholar] [CrossRef] [PubMed]
- Levin, E.E.; Long, F.; Douglas, J.E.; Buffon, M.L.C.; Lamontagne, L.K.; Pollock, T.M.; Seshadri, R. Enhancing Thermoelectric Properties through Control of Nickel Interstitials and Phase Separation in Heusler/Half-Heusler TiNi1.1Sn Composites. Materials 2018, 11, 903. [Google Scholar] [CrossRef] [PubMed]
- Schwall, M.; Balke, B. On the Phase Separation in n-Type Thermoelectric Half-Heusler Materials. Materials 2018, 11, 649. [Google Scholar] [CrossRef] [PubMed]
- Asaad, M.; Buckman, J.; Smith, R.I.; Bos, J.W.G. Thermoelectric properties and high-temperature stability of the Ti1−xVxCoSb1−xSnx half-Heusler alloys. RSC Adv. 2016, 6, 56511–56517. [Google Scholar] [CrossRef]
- Tareuchi, N.; Gosho, K.; Hiroi, M.; Kawakami, M. The effect of V substitution on the properties of CoTiSb. Phys. B Condens. Matter 2005, 359, 1183–1185. [Google Scholar] [CrossRef]
- Sekimoto, T.; Kurosaki, K.; Muta, H.; Yamanaka, S. Thermoelectric properties of Sn-doped TiCoSb half-Heusler compounds. J. Alloys Compd. 2006, 407, 326–329. [Google Scholar] [CrossRef]
- Wu, T.; Jiang, W.; Li, X.; Zhou, Y.; Chen, L. Thermoelectric properties of p-type Fe-doped TiCoSb half-Heusler compounds. J. Appl. Phys. 2007, 102, 103705. [Google Scholar] [CrossRef]
- Mena, J.M.; Schoberth, H.G.; Gruhn, T.; Emmerich, H. Nanophase separation in CoSb-based half-Heusler thermoelectrics: A multiscale simulation study. Phys Status Solidi A Appl. Mater. Sci. 2016, 213, 706–715. [Google Scholar] [CrossRef]
- Mena, J.M.; Rausch, E.; Ouardi, S.; Gruhn, T.; Fecher, G.H.; Schoberth, H.G.; Emmerich, H.; Felser, C. Miscibility Gap in the Phase Diagrams of Thermoelectric Half-Heusler Materials CoTi1−xYxSb (Y = Sc, V, Mn, Fe). J. Electron. Mater. 2016, 45, 1382–1388. [Google Scholar] [CrossRef]
- Larson, A.C.; von Dreele, R.B. General Structure Analysis System (GSAS); Los Alamos National Laboratory Report LAUR 86-748; Los Alamos National Laboratory: Los Alamos, NM, USA, 2000. [Google Scholar]
- Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 210–213. [Google Scholar] [CrossRef]
- Skovsen, I.; Bjerg, L.; Christensen, M.; Nishibori, E.; Balke, B.; Felser, C.; Iversen, B.B. Multi-temperature synchrotron PXRD and physical properties study of half-Heusler TiCoSb. Dalton Trans. 2010, 39, 10154–10159. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-S.; Gibbs, Z.M.; Tang, Y.; Wang, H.; Snyder, G.J. Characterization of Lorenz number with Seebeck coefficient measurement. APL Mater. 2015, 3, 041506. [Google Scholar] [CrossRef]
- Barczak, S.A.; Buckman, J.; Smith, R.I.; Baker, A.R.; Don, E.; Forbes, I.; Bos, J.W.G. Impact of Interstitial Ni on the Thermoelectric Properties of the Half-Heusler TiNiSn. Materials 2018, 11, 536. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Chen, L.D.; Zhang, W.Q.; Feng, C.D. Disorder scattering effect on the high-temperature lattice thermal conductivity of TiCoSb-based half-Heusler compounds. J. Appl. Phys. 2005, 98, 013708. [Google Scholar] [CrossRef]
- Yang, J.; Meisner, G.P.; Chen, L. Strain field fluctuation effects on lattice thermal conductivity of ZrNiSn-based thermoelectric compounds. Appl. Phys. Lett. 2004, 85, 1140–1142. [Google Scholar] [CrossRef]
- Kübler, J.; Fecher, G.H.; Felser, C. Understanding the trend in the Curie temperatures of Co2-based Heusler compounds: Ab initio calculations. Phys. Rev. B 2007, 76, 024414. [Google Scholar] [CrossRef]
- Vanengen, P.G.; Buschow, K.H.J.; Erman, M. Magnetic-properties and magneto-optical spectroscopy of heusler alloys based on transition metals and Sn. J. Magn. Magn. Mater. 1983, 30, 374–382. [Google Scholar] [CrossRef]
- Data Underpinning. Available online: https://doi.org/10.17861/e6cdebd6-56ec-4606-881a-7eb3c4f12050 (accessed on 12 November 2018).



| Sample | a (Å) | Density (g·cm−3) | %Density | FH (%) | Sn (%) | ρ300k (mΩ·cm) | S300K (µV·K−1) | (S2/ρ)max (mW·m−1·K−2 ) | κ323K (W·m−1·K−1) |
|---|---|---|---|---|---|---|---|---|---|
| R1 | 5.8724(1) | 6.9(1) | 92(1) | 7.1(1) | 1.0(1) | 2.8 | −60.1 | 0.38 | - |
| R2 | 5.8711(1) | 7.1(1) | 95(1) | 8.2(3) | 0.2(1) | 4.1 | −85.3 | 0.32 | 4.6 |
| Sample | a (Å) | Density (g cm-3) | %Density | FH (%) | Sn (%) | ρ300k (mΩ·cm) | S300K (µV·K−1) | (S2/ρ)max (mW·m−1·K−2 ) | κ323K (W·m−1·K−1) |
|---|---|---|---|---|---|---|---|---|---|
| R1 | 5.8838(1) | 6.8(1) | 91(1) | 10.3(3) | 3.8(2) | 4.4 | −8.9 | 0.02 | - |
| R2 | 5.8835(1) | 7.0(1) | 93(1) | 12.8(2) | 2.7(3) | 2.7 | −21.7 | 0.02 | 5.8 |
| R3 | 5.8796(1) | 7.1(1) | 95(1) | 10.9(1) | 2.8(2) | 2.1 | −25.1 | 0.08 | 5.6 |
| R4 | 5.8838(1) | 6.8(1) | 91(1) | 10.2(2) | 2.5(2) | 3.2 | −8.3 | 0.01 | 6.9 |
| Sample | SSR (R1) | AM (R4) |
|---|---|---|
| HH phase | Ti0.73(3)V0.27(3)Co0.90(2)Fe0.10(2)Sb0.88(1)Sn0.12(1) (VEC = 18.1(8)) | Ti0.92(3)V0.08(3)CoSb0.88(1)Sn0.12(1) (VEC = 18.0(3)) |
| FH phase | V(Co0.64(1)Fe0.36(1))2Sn | V(Co0.59(1)Fe0.41(1))2Sn |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asaad, M.; Buckman, J.; Bos, J.-W.G. Substitution Versus Full-Heusler Segregation in TiCoSb. Metals 2018, 8, 935. https://doi.org/10.3390/met8110935
Asaad M, Buckman J, Bos J-WG. Substitution Versus Full-Heusler Segregation in TiCoSb. Metals. 2018; 8(11):935. https://doi.org/10.3390/met8110935
Chicago/Turabian StyleAsaad, Maryana, Jim Buckman, and Jan-Willem G. Bos. 2018. "Substitution Versus Full-Heusler Segregation in TiCoSb" Metals 8, no. 11: 935. https://doi.org/10.3390/met8110935
APA StyleAsaad, M., Buckman, J., & Bos, J. -W. G. (2018). Substitution Versus Full-Heusler Segregation in TiCoSb. Metals, 8(11), 935. https://doi.org/10.3390/met8110935






