The Instability Criterion for Bicrystal at Nanoscale
Abstract
:1. Introduction
2. Computational Methodology
2.1. Theory of Instability Criterion
2.2. Derivation of the Minimum Eigenvalue of Matrix A
- when h = g, i.e., the atoms are in the same dimension.(a) if m = j, : (b) if m ≠ j,
- when h ≠ g, i.e., the atoms are in different dimensions, . Therefore, the partial derivatives of E1 can be divided into two parts: = summation item + additional item.
- when m = n,
- when m ≠ n,
- When h = g, . In this case, the following is true.
- (a)
- If n ≠ m, j = n,
- (b)
- If n = m,
- When h ≠ g, . In this case, the following is true.
- (a)
- If n ≠ m, j = n,
- (b)
- If n = m,The expressions of all the above formulas are the values of matrix A.
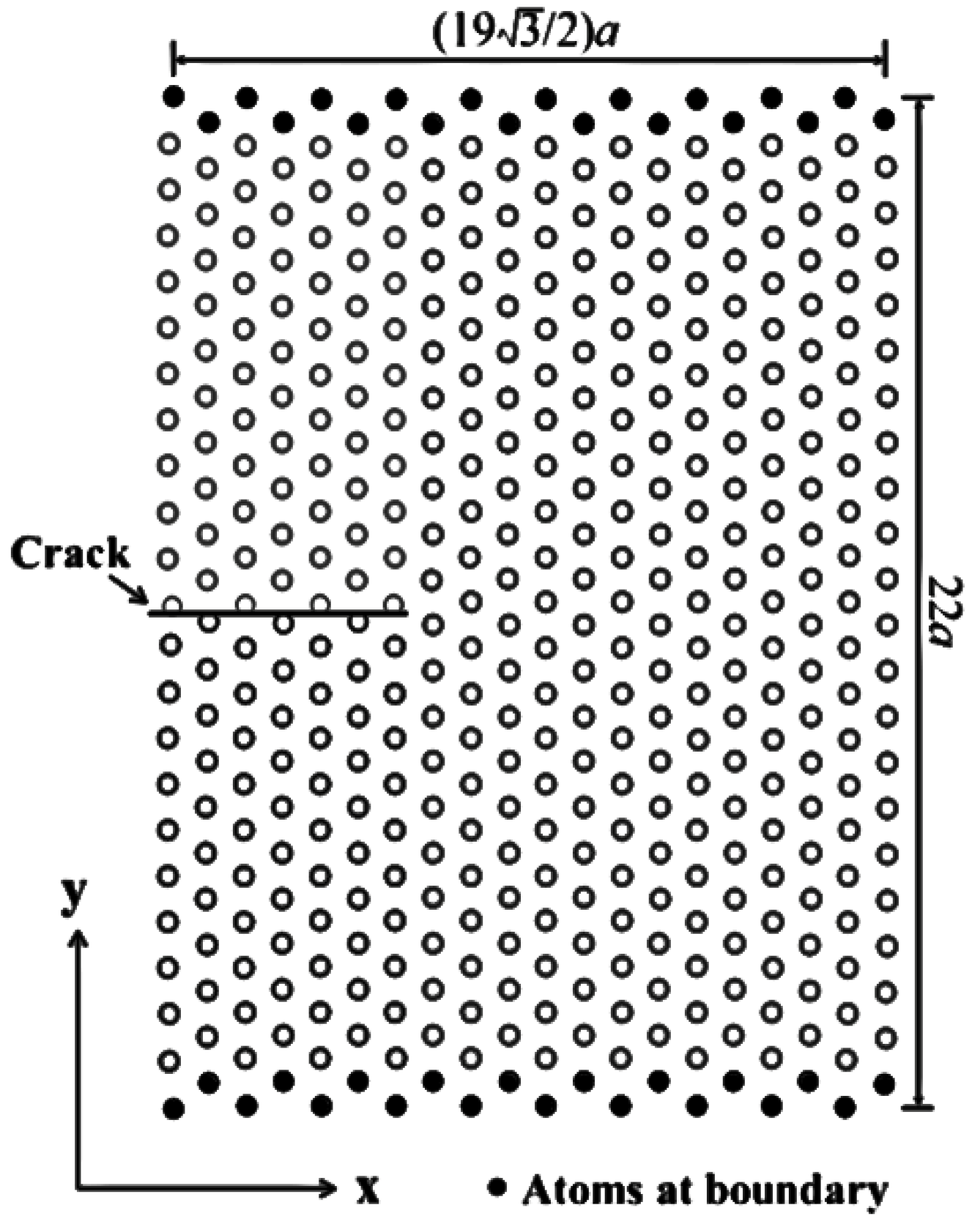
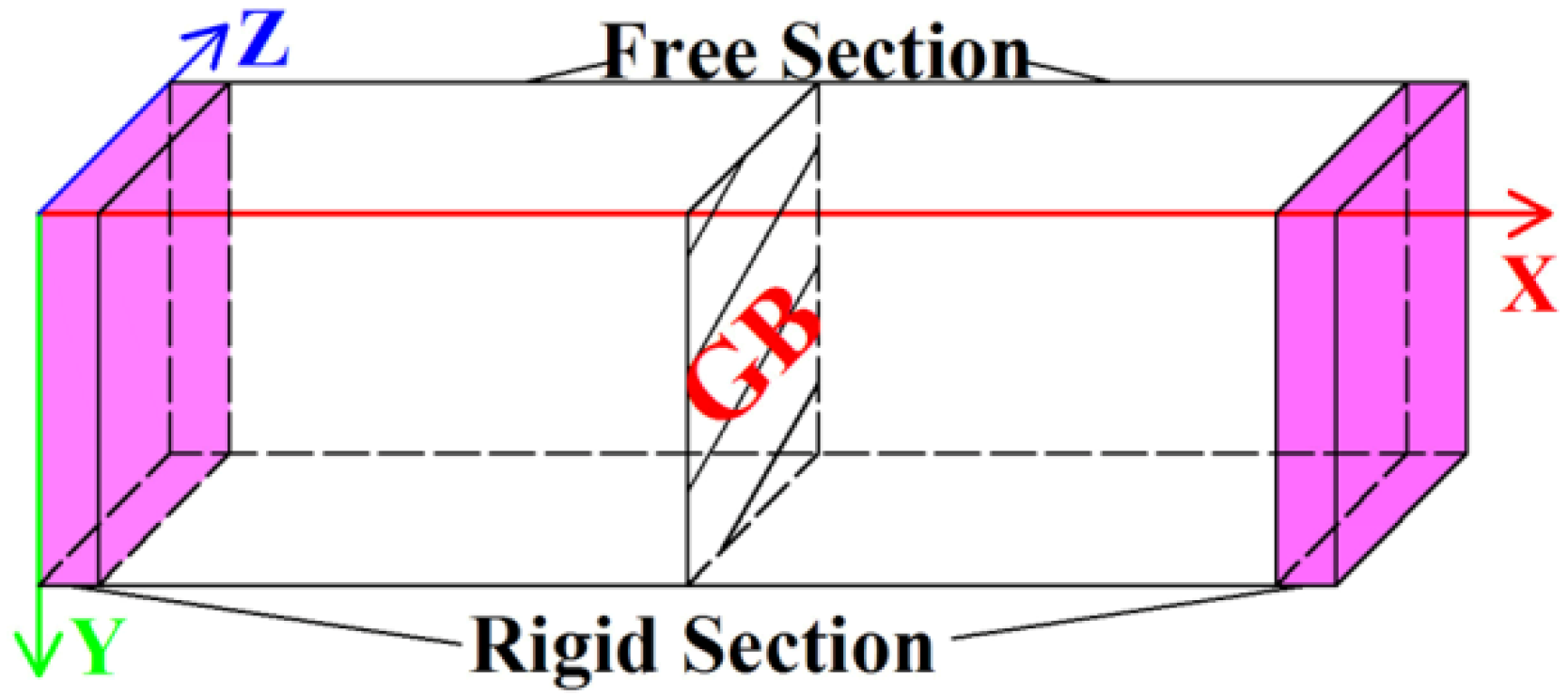
2.3. Simulation Methods
3. Yield Criterion under a Thermal Effect
4. The Instability Criterion for Bicrystals
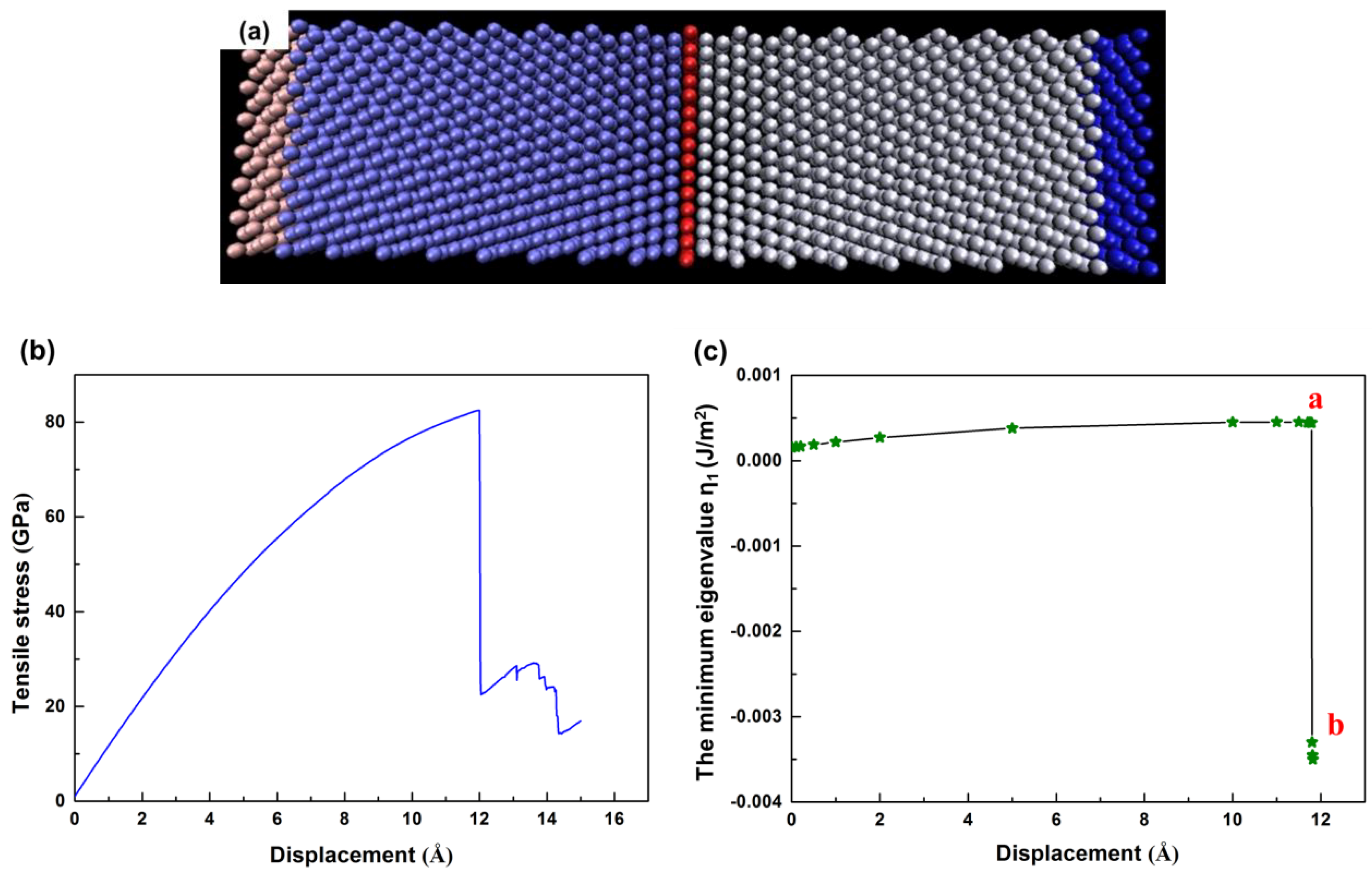
4.1. The Instability Criterion for a Bicrystal with a Coherent Twin Boundary
4.2. The Instability Criterion for a Bicrystal with a Symmetric Tilt Grain Boundary
4.3. The Instability Criterion for a Bicrystal with Asymmetric Tilt Grain Boundary
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Milstein, F.; Huang, K. Theory of the response of an fcc crystal to [110] uniaxial loading. Phys. Rev. B 1978, 18, 2529–2541. [Google Scholar] [CrossRef]
- Milstein, F.; Hill, R. Divergences among the born and classical stability criteria for cubic crystals under hydrostatic loading. Phys. Rev. Lett. 1979, 43, 1411–1423. [Google Scholar] [CrossRef]
- Wang, J.H.; Li, J.; Yip, S.; Phillpot, S.; Wolf, D. Mechanical instabilities of homogeneous crystals. Phys. Rev. B 1995, 52, 12627–12635. [Google Scholar] [CrossRef]
- Cerny, M.; Sob, M.; Pokluda, J.; Sandera, P. Ab initio calculations of ideal tensile strength and mechanical stability in copper. J. Phys. Condens. Matter 2004, 16, 1045–1052. [Google Scholar] [CrossRef]
- Van Vliet, K.J.; Li, J.; Zhu, T.; Yip, S. Quantifying the early stages of plasticity through nanoscale experiments and simulations. Phys. Rev. B 2003, 67, 104105. [Google Scholar] [CrossRef]
- Kolluri, K.; Gungor, M.R.; Maroudas, D. Molecular dynamics simulations of martensitic fcc-to-hcp phase transformations in strained ultrathin metallic films. Phys. Rev. B 2008, 78, 195408. [Google Scholar] [CrossRef]
- Kitamura, T.; Umeno, Y.; Tsuji, N. Internal atomic stress near ∑5 tilt grain boundary in aluminium under tension. Model Simul Mater. Sci. Eng. 2003, 11, 839–849. [Google Scholar] [CrossRef]
- Kitamura, T.; Umeno, Y.; Tsuji, N. Analytical evaluation of unstable deformation criterion of atomic structure and its application to nanostructure. Comput. Mater. Sci. 2004, 29, 499–510. [Google Scholar] [CrossRef]
- Miller, R.E.; Rodney, D. On the nonlocal nature of dislocation nucleation during nanoidentation. J. Mech. Phys. Solids 2008, 56, 1203–1223. [Google Scholar] [CrossRef]
- Yan, Y.B.; Kondo, T.; Shimada, T.; Sumigawa, T.; Kitamura, T. Criterion of mechanical instabilities for dislocation structures. Mater. Sci. Eng. A 2012, 534, 681–687. [Google Scholar] [CrossRef] [Green Version]
- Lich, L.V.; Shimada, T.; Wang, J.; Kitamura, T. Instability criterion for ferroelectrics under mechanical/electric multi-fields: Ginzburg-Landau theory based modeling. Acta Mater. 2016, 112, 1–10. [Google Scholar] [CrossRef]
- Shimada, T.; Ouchi, K.; Ikeda, I.; Ishii, Y.; Kitamura, T. Magnetic instability criterion for spin-lattice systems. Comput. Mater. Sci. 2015, 97, 216–221. [Google Scholar] [CrossRef]
- Umeno, Y.; Shimada, T.; Kitamura, T. Dislocation nucleation in a thin Cu film from molecular dynamics simulations: Instability activation by thermal fluctuations. Phys. Rev. B 2010, 82, 104108. [Google Scholar] [CrossRef]
- Zaefferer, S.; Kuo, J.-C.; Zhao, Z.; Winning, M.; Raabe, D. On the influence of the grain boundary misorientation on the plastic deformation of aluminum bicrystals. Acta Mater. 2003, 51, 4719–4735. [Google Scholar] [CrossRef]
- Spearot, D.E.; Jacob, K.I.; McDowell, D.L. Nucleation of dislocations from [0 0 1] bicrystal interfaces in aluminum. Acta Mater. 2005, 53, 3579–3589. [Google Scholar] [CrossRef]
- Zhang, R.F.; Wang, J.; Beyerlein, I.J.; Germann, T.C. Dislocation nucleation mechanisms from fcc/bcc incoherent interfaces. Scr. Mater. 2011, 65, 1022–1025. [Google Scholar] [CrossRef]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. Optimization 2004, 3, 284–289. [Google Scholar]
- Girifalco, L.A.; Weizer, V.G. Application of the Morse Potential Function to Cubic Metal. Phys. Rev. 1959, 114, 687–690. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Li, J. AtomEye: An efficient atomistic configuration viewer. Model. Simul. Mater. Sci. Eng. 2003, 11, 173–177. [Google Scholar] [CrossRef]
- Ackland, G.J.; Jones, A.P. Applications of local crystal structure measures in experiment and simulation. Phys. Rev. B 2006, 73, 054104. [Google Scholar] [CrossRef]
- Sangiovanni, D.G. Inherent toughness and fracture mechanisms of refractory transition-metal nitrides via density-functional molecular dynamics. Acta Mater. 2018, 151, 11–20. [Google Scholar] [CrossRef]
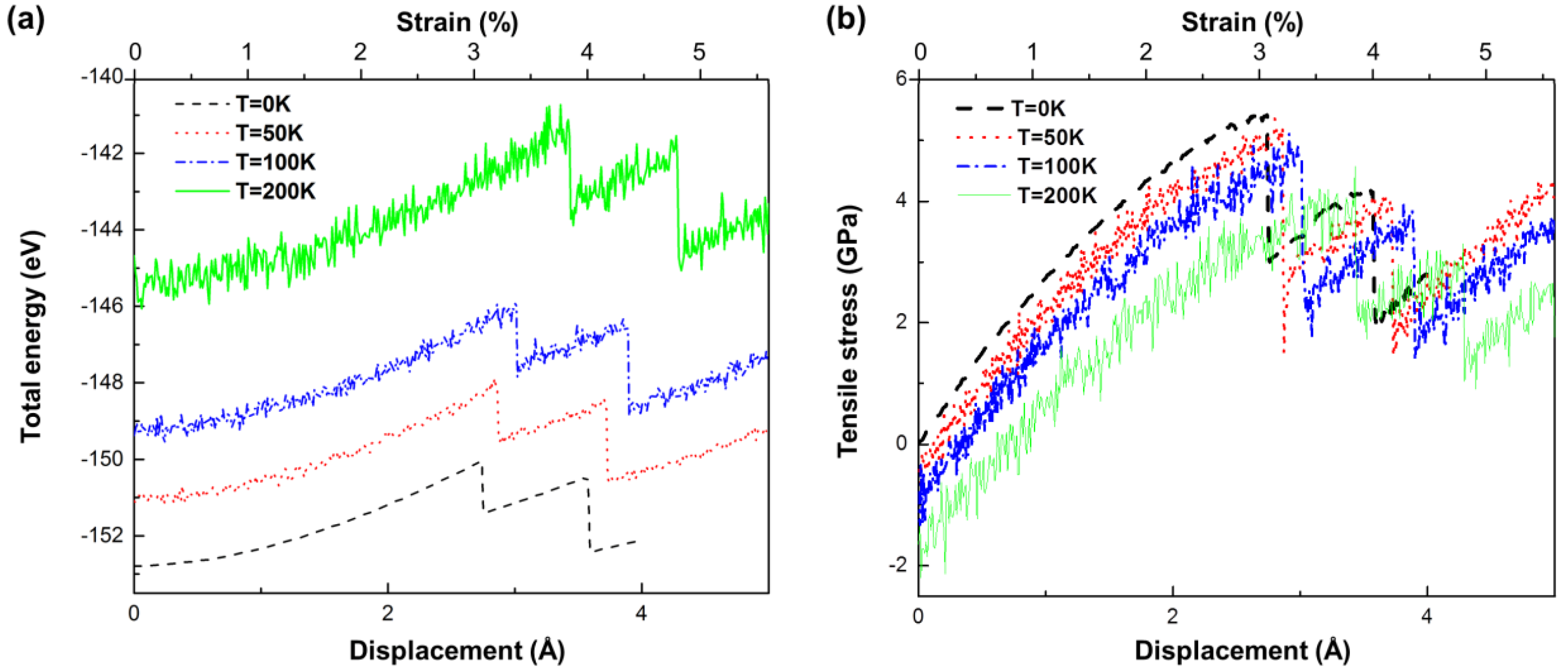





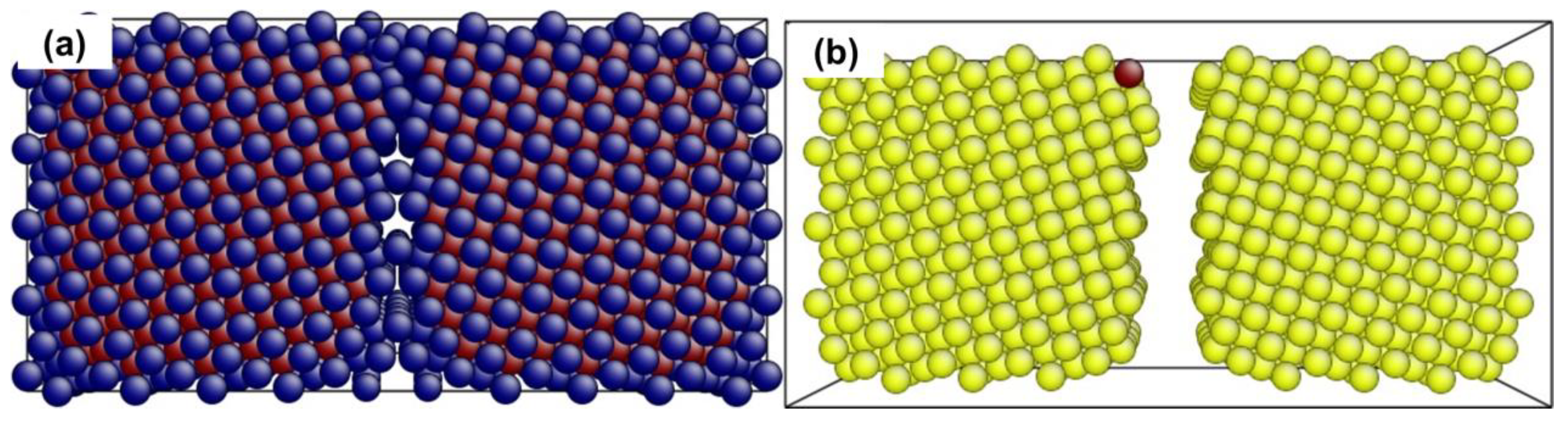
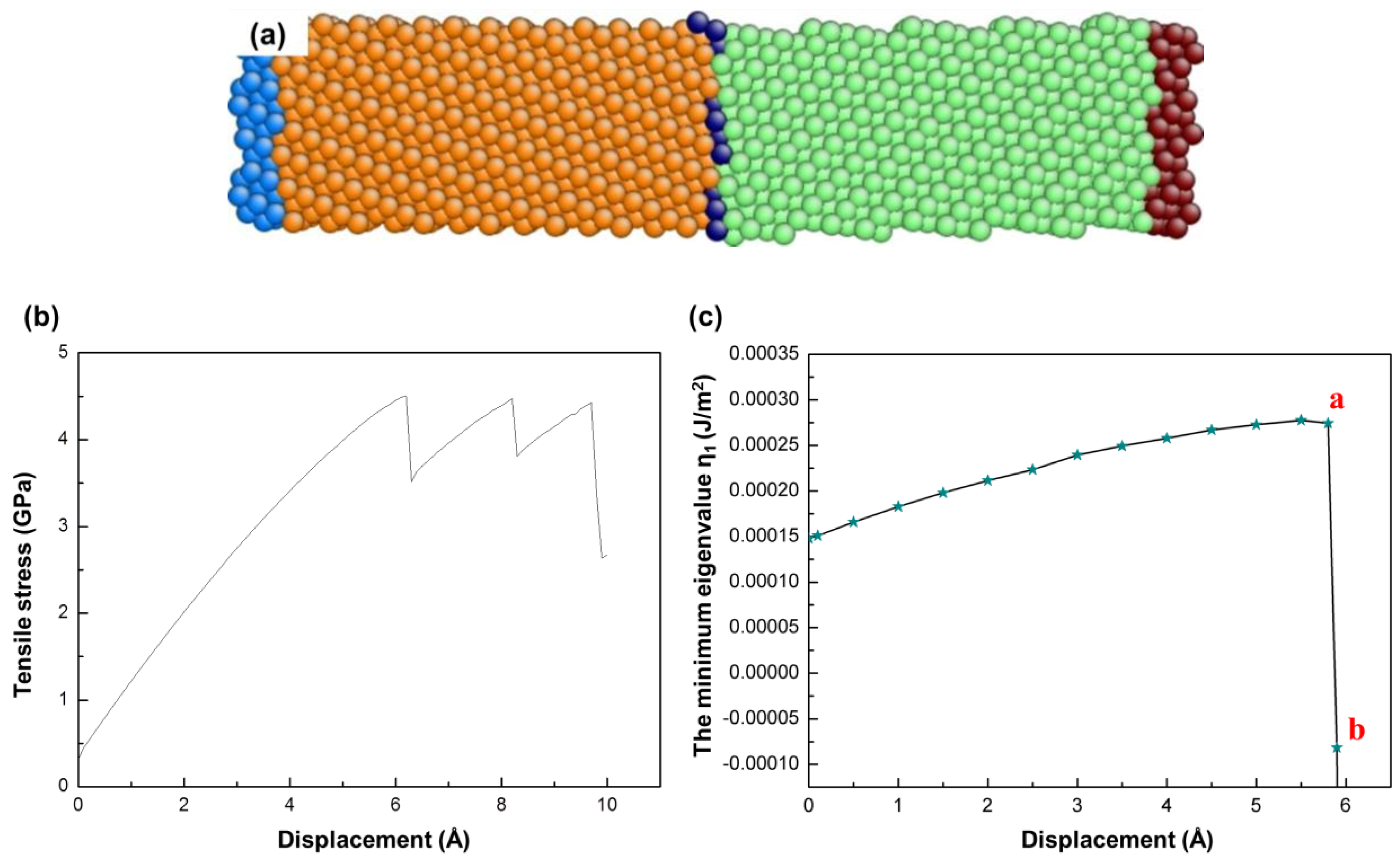

| Temperature (K) | 0 | 50 | 100 | 200 | |
|---|---|---|---|---|---|
| Displacement at the First Drop Point (Å) | |||||
| Total energy | 2.74 | 2.85 | 3.01 | 3.42 | |
| Tensile stress | 2.74 | 2.86 | 3.01 | 3.41 | |
| Minimum eigenvalue | 2.754 | 2.65 | 2.46 | disorder | |
| Model | GB | Lattice Orientation | Lx (nm) | Ly (nm) | Lz (nm) | Number of Atoms | |
|---|---|---|---|---|---|---|---|
| Left Grain | Right Grain | ||||||
| A | CTB | x y z | x [111] y z | 12.617 | 3.470 | 0.832 | 1982 |
| B | STGB | x y z | x y z | 6.143 | 3.071 | 2.024 | 2570 |
| C | ATGB | x y z | x y z | 13.949 | 3.288 | 0.572 | 1841 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, L.; Xu, C.; Zhang, J.; Shan, D.; Guo, B. The Instability Criterion for Bicrystal at Nanoscale. Metals 2018, 8, 986. https://doi.org/10.3390/met8120986
Yuan L, Xu C, Zhang J, Shan D, Guo B. The Instability Criterion for Bicrystal at Nanoscale. Metals. 2018; 8(12):986. https://doi.org/10.3390/met8120986
Chicago/Turabian StyleYuan, Lin, Chuanlong Xu, Jiangwei Zhang, Debin Shan, and Bin Guo. 2018. "The Instability Criterion for Bicrystal at Nanoscale" Metals 8, no. 12: 986. https://doi.org/10.3390/met8120986
APA StyleYuan, L., Xu, C., Zhang, J., Shan, D., & Guo, B. (2018). The Instability Criterion for Bicrystal at Nanoscale. Metals, 8(12), 986. https://doi.org/10.3390/met8120986




