Volatilization Behavior of β-Type Ti-Mo Alloy Manufactured by Electron Beam Melting
Abstract
:1. Introduction
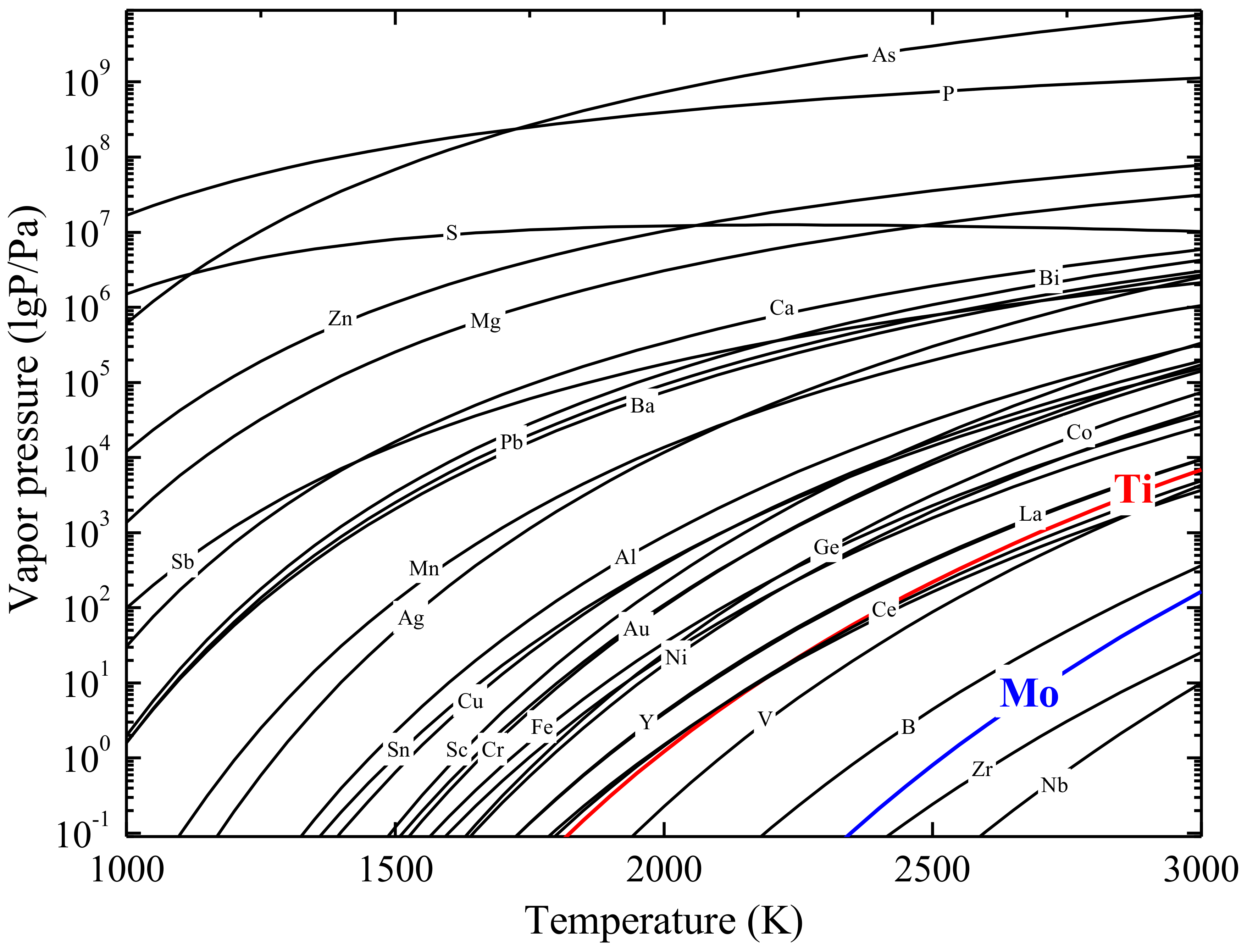
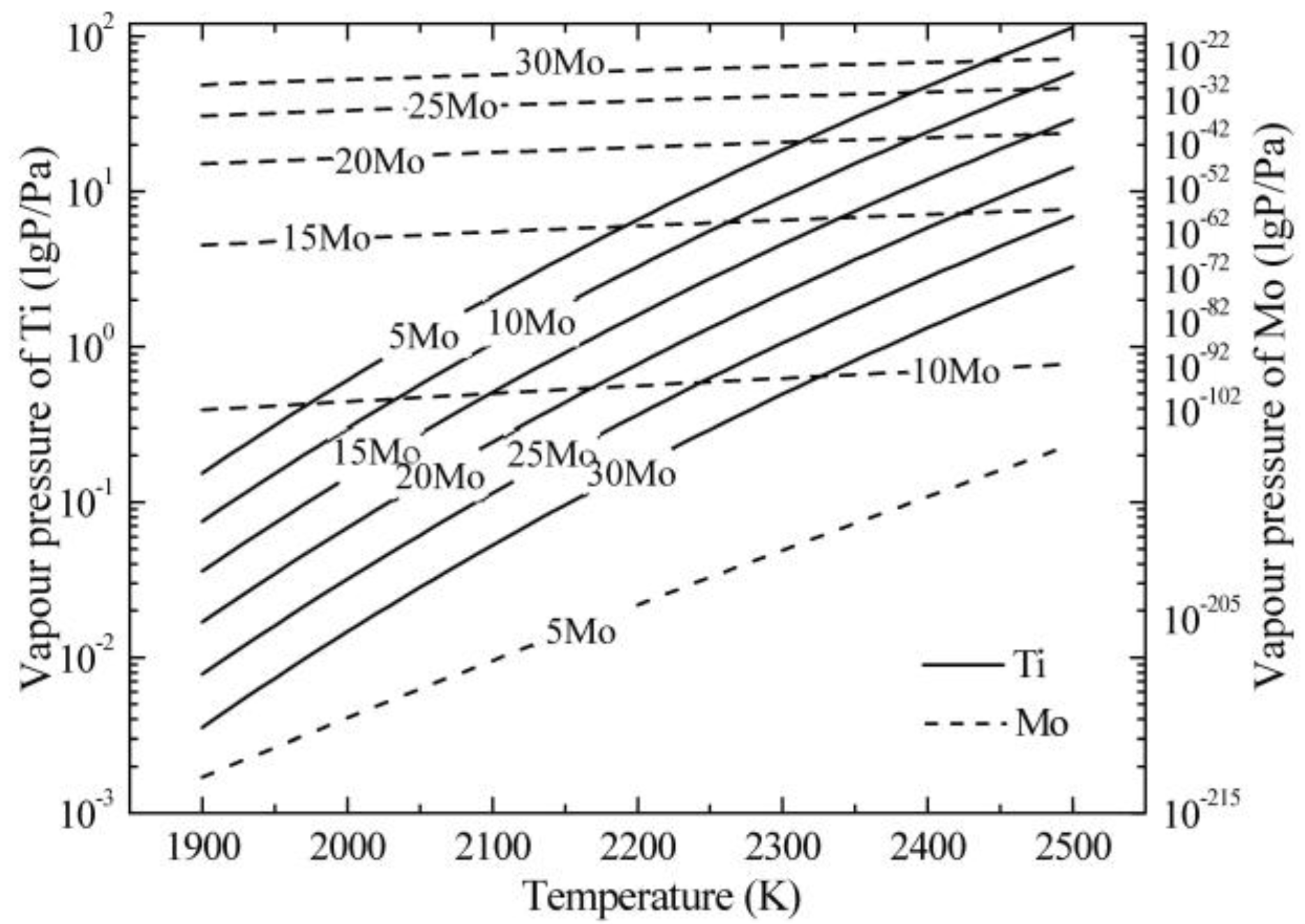
2. Theoretical Analysis of Element Volatilization
3. Experimental Section
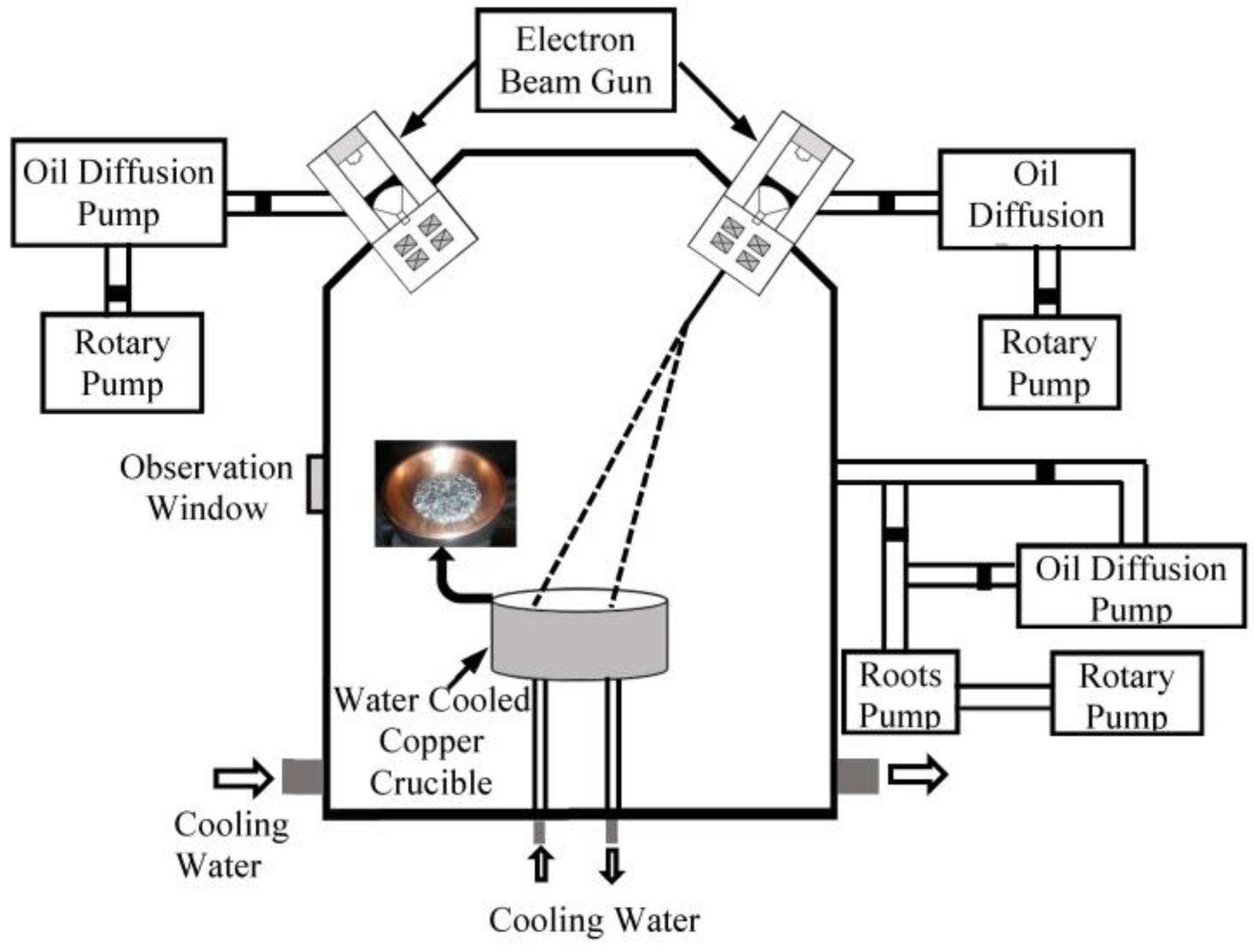
3.1. Electron Beam Melting Process
3.2. Microstructural Characterization
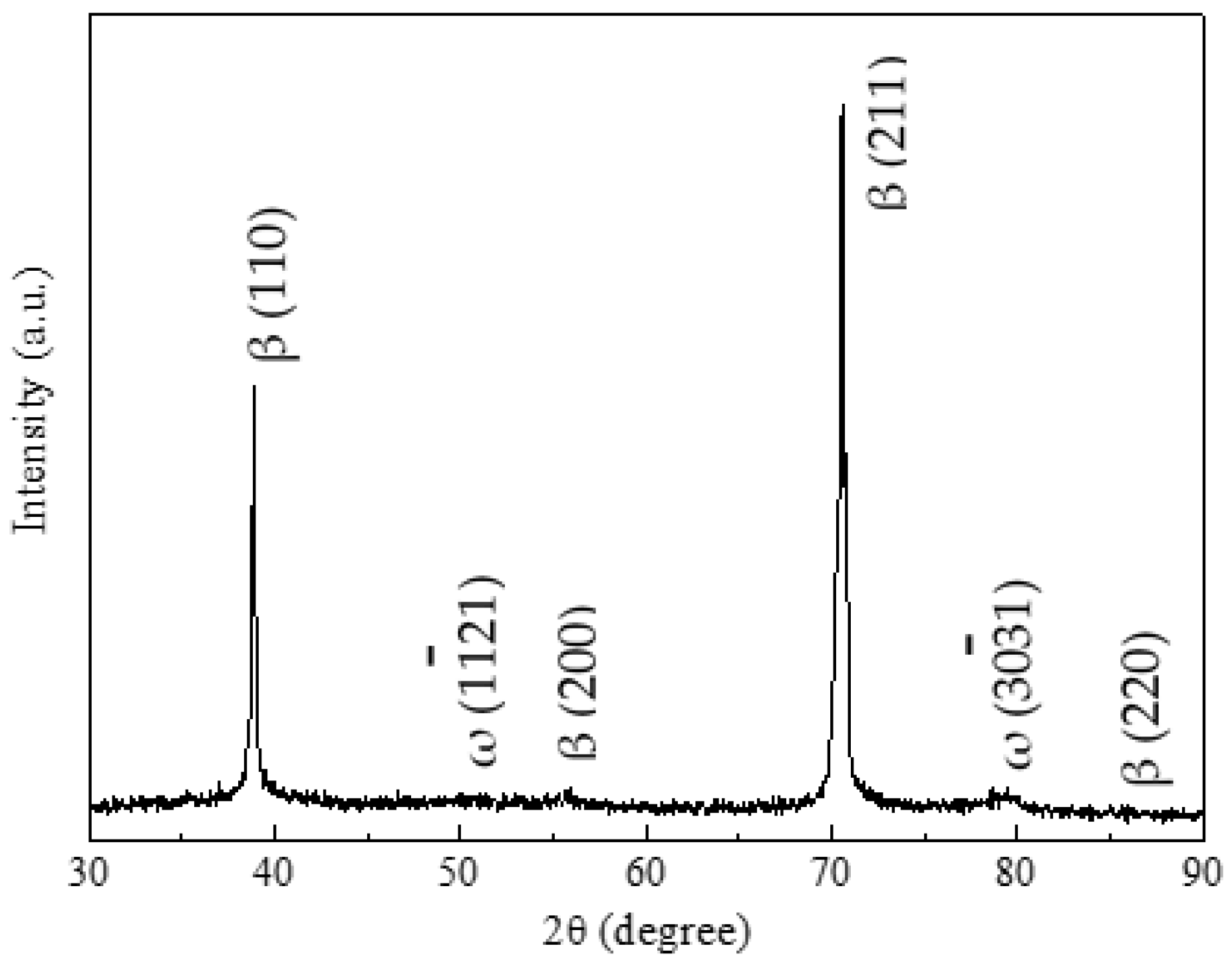
4. Results
5. Discussion
6. Conclusions
- (1)
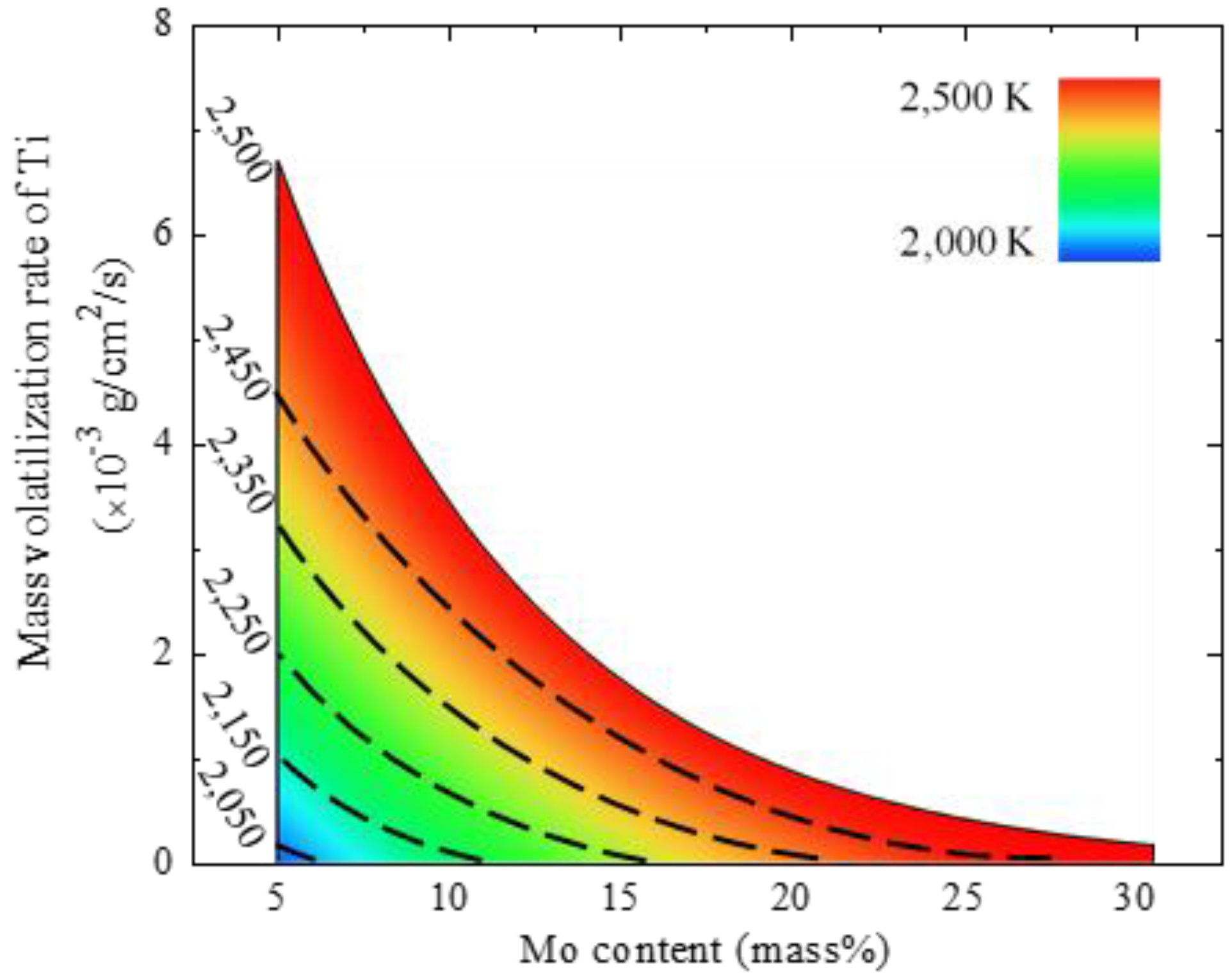
- Ti was the main volatilization element during the EBM process based on the calculation of vapor pressure and on analyses for mass losses and the chemical compositions of the ingots. The mass volatilization rate of Ti exhibited an increasing tendency with the increase of both the melting power and melting time.
- (2)
- The ingots without apparent metallurgical defects were fabricated via EBM technology, and they consisted of large and columnar grains at the bottom and top sections, respectively. The effects of the melting power and melting time on the ingots’ microstructures were negligible.
- (3)
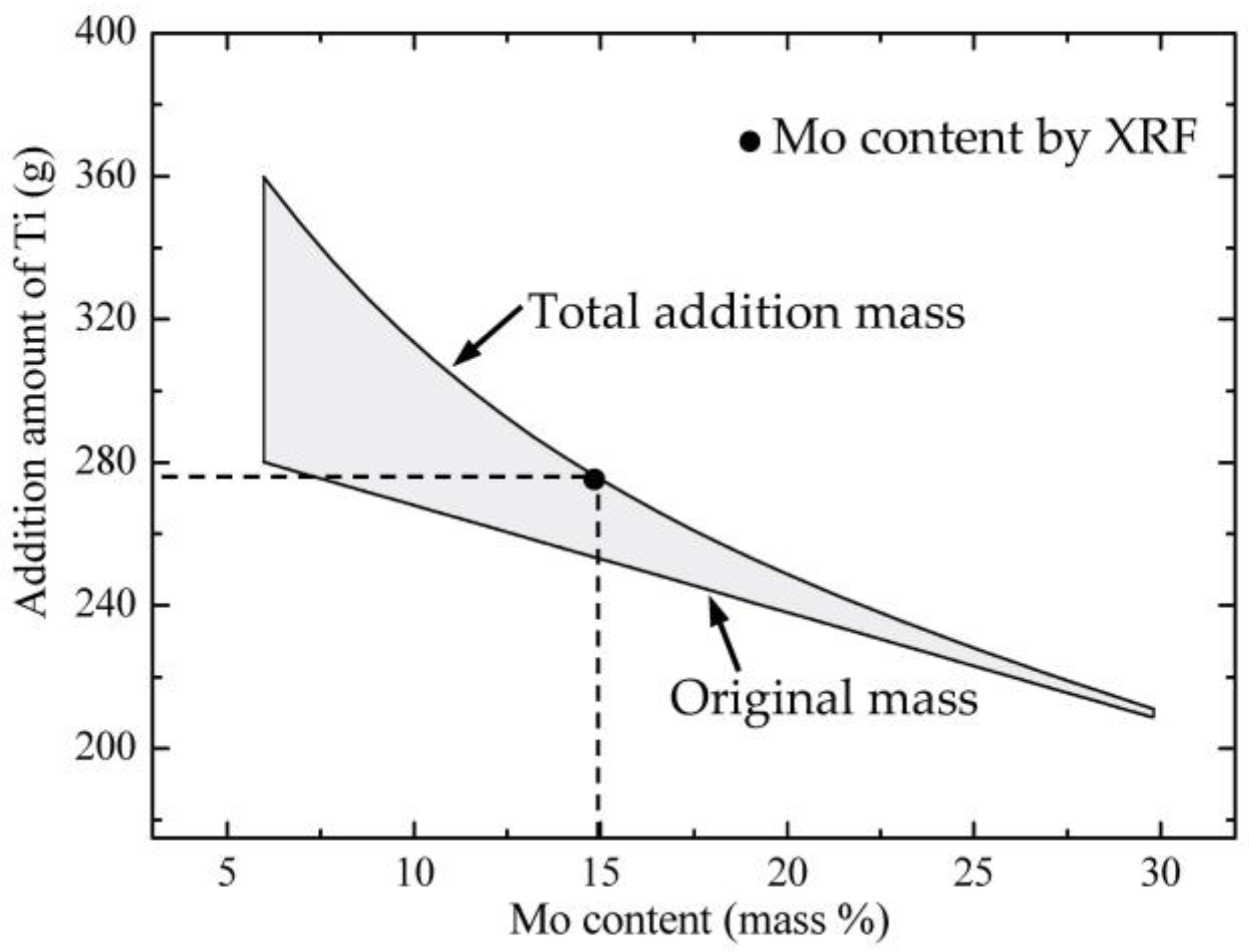
- Regardless of the melting time, Ti’s volatilization had the same pattern as that of the Ti-15Mo alloy. In terms of the pure Ti and Ti-32Mo intermediate alloys as raw materials, the considerable compensation method of the Ti element was established at the melting power of 10.5 kW for fabricating Ti-Mo binary alloys.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Weissa, I.; Semiatinb, S.L. Thermomechanical processing of beta titanium alloys—An overview. Mater. Sci. Eng. A 1998, 243, 46–65. [Google Scholar] [CrossRef]
- Banerjee, D.; Williams, J.C. Perspectives on Titanium Science and Technology. Acta Mater. 2013, 61, 844–879. [Google Scholar] [CrossRef]
- An, H.; Liu, J.L.; Fan, L.Y. Quality control in smelting titanium ingots in vacuum arc-melting furnace. World Nonferrous Met. 2007, 8, 25–27. [Google Scholar]
- Henry, J.L.; Hill, S.D.; Schaller, J.L.; Campbell, T.T. Nitride inclusions in titanium ingots: A study of possible sources in the production of magnesium-reduced sponge. Mater. Trans. 1973, 4, 1859–1864. [Google Scholar] [CrossRef]
- Nakajima, T.; Morimoto, Y.; Takaki, S.; Abiko, K. Preparation of Ultra-Pure Ti-Al Alloys. Phys. Status Solidi 2015, 167, 411–418. [Google Scholar] [CrossRef]
- Board, C.A. Aircraft Accident Report; National Transportation Safety Board: Washington, DC, USA, 2004.
- Choudhury, A.; Hensberger, E. Electron beam melting and refining of metals and alloys. ISIJ Int. 1992, 32, 673–681. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Zhou, L.; Sun, J.; Han, M.C.; Sun, Y.; Yang, J.C. The development of cold hearth melting technique. Titan. Ind. Prog. 2007, 24, 27–30. [Google Scholar]
- Schwab, H.; Prashanth, K.G.; Lober, L.; Kuhn, U.; Eckert, J. Selective laser melting of Ti-45Nb alloy. Metals 2015, 5, 686–694. [Google Scholar] [CrossRef]
- Smith, C.J.; Derguti, F.; Nava, E.H.; Thomas, M.; Williams, S.T.; Gulizia, S.; Fraser, D.; Todd, I. Dimensional accuracy of electron beam melting (EBM) additive manufacture with regard to weight optimized tress structures. J. Mater. Process. Technol. 2016, 229, 128–138. [Google Scholar] [CrossRef]
- Liu, Y.J.; Li, S.J.; Wang, H.L.; Hou, W.T.; Hao, Y.L.; Yang, R.; Sercombe, T.B.; Zhang, L.C. Microstructure, defects and mechanical behavior of beta-type titanium porous structures manufactured by electron beam melting and selective laser melting. Acta Mater. 2016, 113, 56–67. [Google Scholar] [CrossRef]
- Tan, Y.; You, X.G.; You, Q.F.; Li, J.Y.; Shi, S.; Li, P.T. Microstructure and deformation behavior of nickel based superalloy Inconel 740 prepared by electron beam smelting. Mater. Charact. 2016, 114, 267–276. [Google Scholar] [CrossRef]
- Tan, Y.; Shi, S.; Guo, X.L.; Jiang, D.C.; Dong, W.; Ren, S.Q. Effect of cooling rate on solidification of electron beam melted silicon ingots. Vacuum 2013, 89, 12–16. [Google Scholar] [CrossRef]
- Shi, S.; Dong, W.; Peng, X.; Jiang, D.C.; Tan, Y. Volatilization and removal mechanism of phosphorus from the surface of silicon melt during electron beam melting. Appl. Surf. Sci. 2013, 266, 344–349. [Google Scholar] [CrossRef]
- Jiang, D.C.; Tan, Y.; Shi, S.; Dong, W.; Gu, Z.; Zou, R.X. Removal of phosphorus in molten silicon by electron beam candle melting. Mater. Lett. 2012, 78, 4–7. [Google Scholar] [CrossRef]
- Choi, G.S.; Lim, J.W.; Munirathnam, N.R.; Kim, I.H.; Kim, J.S. Preparation of 5N grade tantalum by electron beam melting. J. Alloys Compd. 2009, 469, 298–303. [Google Scholar] [CrossRef]
- You, X.G.; Tan, Y.; You, Q.F.; Shi, S.; Li, J.Y.; Ye, F.; Wei, X. Preparation of Inconel 740 superalloy by electron beam smelting. J. Alloys Compd. 2016, 676, 202–208. [Google Scholar] [CrossRef]
- You, X.G.; Tan, Y.; Li, J.Y.; Li, P.T.; Dong, C.; Shi, S.; Liao, J.; Qin, S.Q. Effects of solution heat treatment on the microstructure and hardness of Inconel 740 superalloy prepared by electronbeam smelting. J. Alloys Compd. 2015, 638, 239–248. [Google Scholar] [CrossRef]
- Kanayama, H.; Kusamichi, T.; Muraoka, T.; Onouye, T.; Nishimura, T. Electron beam melting of sponge titanium. ISIJ Int. 1991, 31, 906–914. [Google Scholar] [CrossRef]
- Vutova, K.; Vassileva, V.; Koleva, E.; Georgieva, E.; Mladenov, G.; Mollov, D.; Kardjiev, M. Investigation of electron beam melting and refining of titanium and tantalum scrap. J. Mater. Process. Technol. 2010, 210, 1089–1094. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Sun, J.; Han, M.C.; Zhou, L.; Yang, J.C. Electron beam cold hearth melting of TC4. Aerosp. Mater. Technol. 2007, 5, 50–52. [Google Scholar]
- Akhonin, S.V.; Trigub, N.P.; Zamkov, V.N.; Semiatin, S.L. Mathematical modeling of aluminum evaporation during electron-beam cold-hearth melting of Ti-6Al-4V ingots. Metall. Mater. Trans. B 2003, 34, 447–454. [Google Scholar] [CrossRef]
- Han, M.C.; Zhang, Y.M.; Zhou, Y.G.; Zhao, T.F.; Yang, J.C.; Li, J.; Zhou, L. Elimination of LDI and HDI in TC4 alloy during electron beam cold hearth melting. Rare Met. Mater. Eng. 2008, 4, 665–669. [Google Scholar]
- Zhang, Y.M.; Zhou, L.; Sun, J.; Han, M.C.; Georg, R.; Jochen, F.; Yang, J.C.; Zhao, Y.Q. An investigation on electron beam cold hearth melting of Ti64 Alloy. Rare Met. Mater. Eng. 2008, 37, 1973–1977. [Google Scholar] [CrossRef]
- Mitchell, A.; Kawakami, A.; Cockcroft, S.L. Beta fleck and segregation in titanium alloy ingots. High Temp. Mater. Process. 2006, 25, 337–349. [Google Scholar] [CrossRef]
- Xiang, L.; Min, X.H.; Mi, G.B. Application and research process of body-centered-cubic Ti-Mo base alloys. J. Mater. Eng. 2017, 45, 128–136. [Google Scholar]
- Cotton, J.D.; Briggs, R.D.; Boyer, R.R.; Tamirisakandala, S.; Russo, P.; Shchetnikov, N.; Fanning, J.C. State of the art in beta titanium alloys for airframe applications. JOM 2015, 67, 1281–1303. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Luo, D.W. Microstructure and mechanical properties of Ti-Mo alloys cold-rolled and heat treatment. Mater. Charact. 2011, 62, 931–937. [Google Scholar] [CrossRef]
- Haghighi, S.E.; Cao, G.H.; Zhang, L.C. Nanoindentation study of mechanical properties of Ti based alloys with Fe and Ta additions. J. Alloys Compd. 2017, 692, 892–897. [Google Scholar] [CrossRef]
- Haghighi, S.E.; Liu, Y.J.; Cao, G.H.; Zhang, L.C. Influence of Nb on the β→α″ martensitic phase transformation and properties of the newly designed Ti-Fe-Nb alloys. Mater. Sci. Eng. C 2016, 60, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Lai, M.J.; Tasan, C.C.; Raabe, D. On the mechanism of {332} twinning in metastable β titanium alloys. Acta Mater. 2016, 111, 173–186. [Google Scholar] [CrossRef]
- Castany, P.; Ramarolahy, A.; Prima, F.; Laheurte, P.; Curfs, C.; Gloriant, T. In situ synchrotron X-ray diffraction study of the martensite transforamtion in superelastic Ti-24Nb-0.5N and Ti-24Nb-0.5O alloys. Acta Mater. 2015, 88, 102–111. [Google Scholar] [CrossRef]
- Yin, F.; Iwasaki, S.; Ping, D.; Nagai, K. Snoek-type high damping alloys realized in β-Ti alloys with high oxygen solid solution. Adv. Mater. 2006, 18, 1541–1544. [Google Scholar] [CrossRef]
- Min, X.H.; Tsuzaki, K.; Emura, S.; Tsuchiya, K. Enhancement of uniform elongation in high strength Ti–Mo based alloys by combination of deformation modes. Mater. Sci. Eng. A 2011, 528, 4569–4578. [Google Scholar] [CrossRef]
- Kubaschewshi, O.; Evans, F.L.L.; Alock, C.B. Metallurgical Thermochemistry, 5th ed.; Pergamon Press: New York, NY, USA, 1979. [Google Scholar]
- You, Q.F.; Shi, S.; You, X.G.; Tan, T.; Wang, Y.N.; Li, J.Y. Evaporation behavior of Ni, Cr and Fe in Inconel 718 superalloy during electron beam melting. Vacuum 2017, 135, 135–141. [Google Scholar] [CrossRef]
- Su, Y.Q.; Guo, J.J.; Liu, G.Z. Quality Control of Molten Alloy in Vacuum Melting Process of Nonferrous Alloys; Harbin Institute of Technology Press: Harbin, China, 2005. [Google Scholar]
- You, Q.F.; Yuan, H.; You, X.G.; Li, J.Y.; Zhao, L.H.; Shi, S.; Tan, Y. Segregation behavior of nickel-based superalloy after electron beam smelting. Vacuum 2017, 145, 116–122. [Google Scholar] [CrossRef]
- Ramirez-Ledesma, A.L.; Lopez, H.F.; Juarez-Islas, J.A. Evaluation of chill cast Co-Cr Alloys for biomedical applications. Metals 2016, 6, 188. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Min, X.H.; Emura, S.; Tsuchiya, K. Accommodative {332}<113> primary and secondary twinning in a slightly deformed β-type Ti-Mo alloy. Mater. Sci. Eng. A 2017, 684, 534–541. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Su, Y.Q.; Chen, D.Z.; Guo, J.J.; Fu, H.Z. Dynamic model for evaporation loss calculation of alloying elements. Foundry 2009, 58, 373–375. [Google Scholar]
- Maeda, M.; Kiwake, T.; Shibuya, K.; Ikeda, T. Activity of aluminum in molten Ti-Al alloys. Mater. Sci. Eng. A 1997, 239–240, 276–280. [Google Scholar] [CrossRef]
- Yan, J.W.; Luo, L.; Peng, A.F.; Zhang, C.S.; Cao, Q.H. Behavior of element vaporization and composition control of Fe-Ga alloy during vacuum smelting. J. Iron Steel Res. Int. 2015, 22, 983–989. [Google Scholar] [CrossRef]




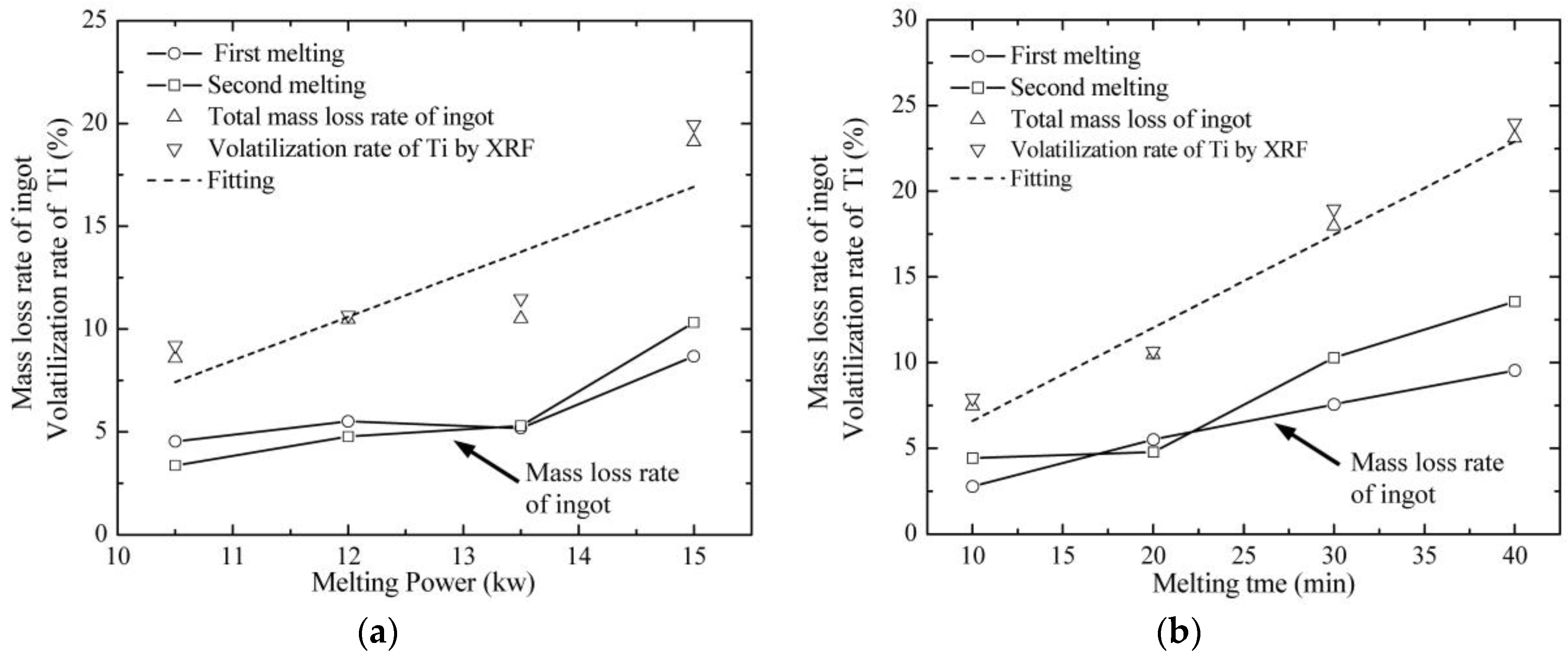
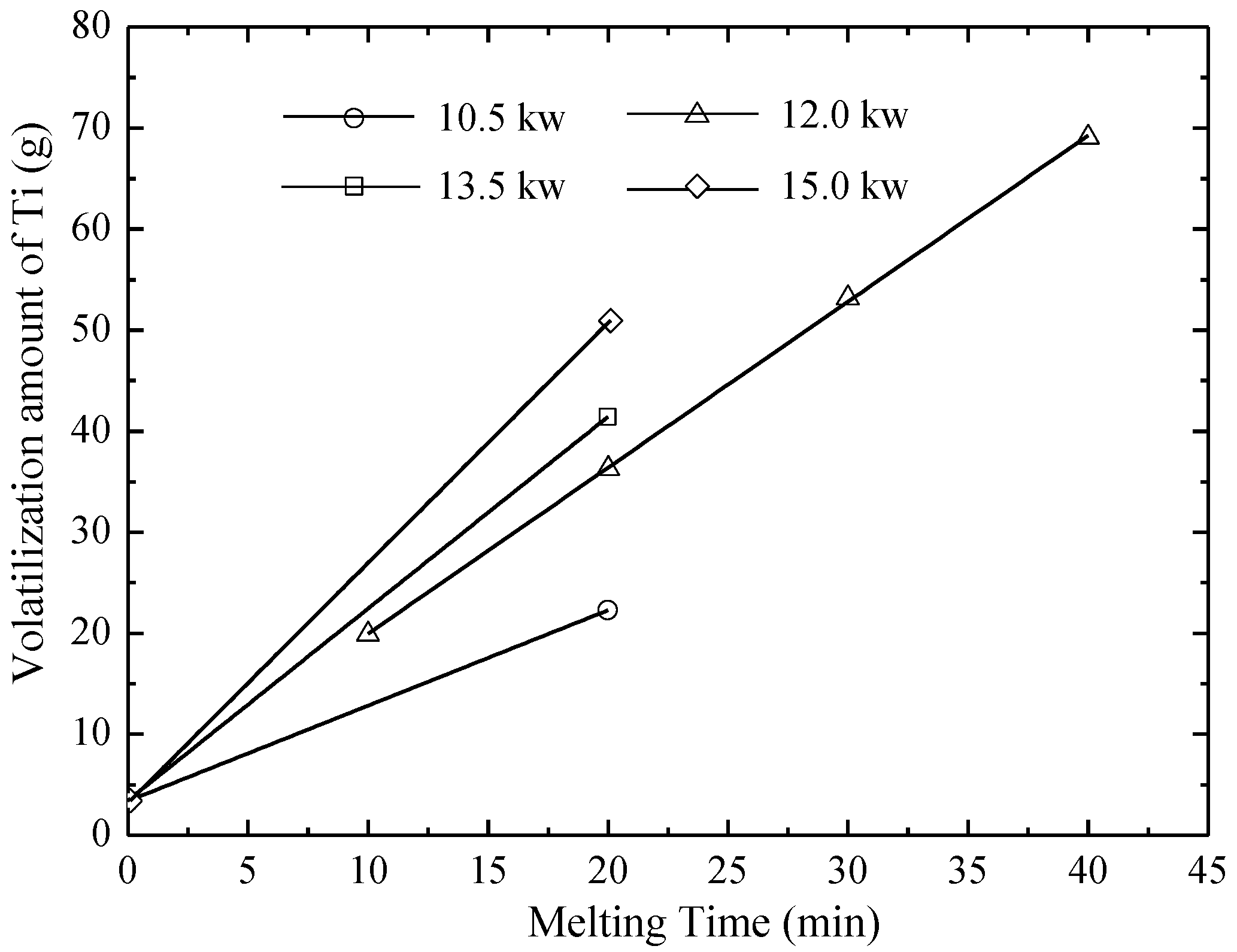
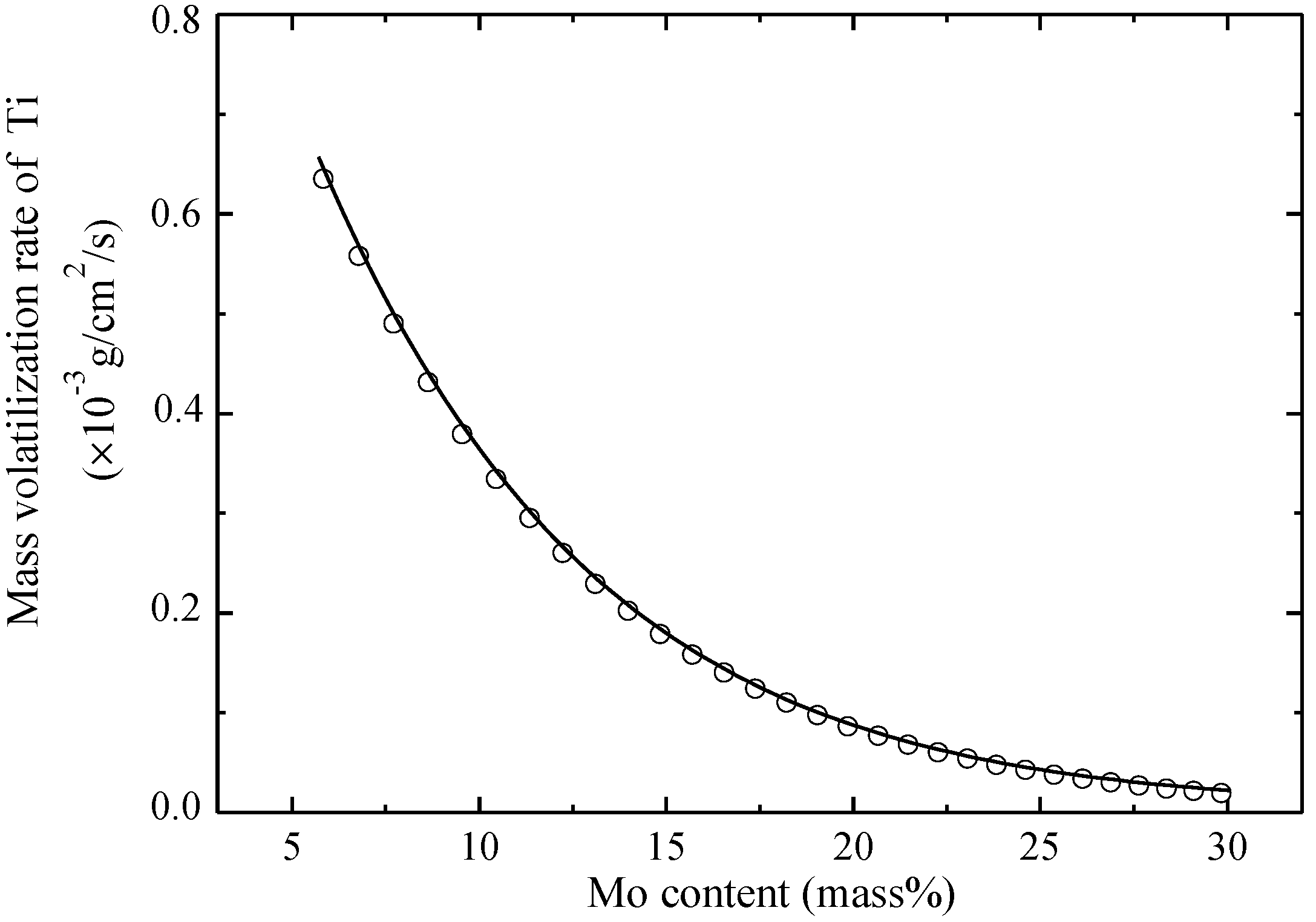
| Melting Power (kW) | Mass Loss Rate of First Time (%) | Mass Loss Rate of Second Time (%) | Total Mass Loss Rate of Ingot (%) | Volatilization Rate of Ti (%) |
|---|---|---|---|---|
| 10.5 | 4.5 | 3.5 | 8.0 | 9.2 |
| 12.0 | 5.5 | 4.8 | 10.3 | 10.7 |
| 13.5 | 5.2 | 5.3 | 10.5 | 11.5 |
| 15.0 | 8.7 | 10.3 | 19.0 | 19.9 |
| Melting Time (min) | Mass Loss Rate of First Time (%) | Mass Loss Rate of Second Time (%) | Total Mass Loss Rate of Ingot (%) | Volatilization Rate of Ti (%) |
|---|---|---|---|---|
| 10 | 2.8 | 4.4 | 7.2 | 7.9 |
| 20 | 5.5 | 4.8 | 10.3 | 10.7 |
| 30 | 7.6 | 10.3 | 17.9 | 19.0 |
| 40 | 9.5 | 13.5 | 23.0 | 24.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, K.; Min, X.; Shi, S.; Tan, Y. Volatilization Behavior of β-Type Ti-Mo Alloy Manufactured by Electron Beam Melting. Metals 2018, 8, 206. https://doi.org/10.3390/met8040206
Yao K, Min X, Shi S, Tan Y. Volatilization Behavior of β-Type Ti-Mo Alloy Manufactured by Electron Beam Melting. Metals. 2018; 8(4):206. https://doi.org/10.3390/met8040206
Chicago/Turabian StyleYao, Kai, Xiaohua Min, Shuang Shi, and Yi Tan. 2018. "Volatilization Behavior of β-Type Ti-Mo Alloy Manufactured by Electron Beam Melting" Metals 8, no. 4: 206. https://doi.org/10.3390/met8040206
APA StyleYao, K., Min, X., Shi, S., & Tan, Y. (2018). Volatilization Behavior of β-Type Ti-Mo Alloy Manufactured by Electron Beam Melting. Metals, 8(4), 206. https://doi.org/10.3390/met8040206





