Numerical Analysis of Stress Gradient and Traps Effects on Carbon Diffusion in AISI 316L during Low Temperature Gas Phase Carburization
Abstract
:1. Introduction
2. Material and Experimental Procedures
3. Diffusion Model
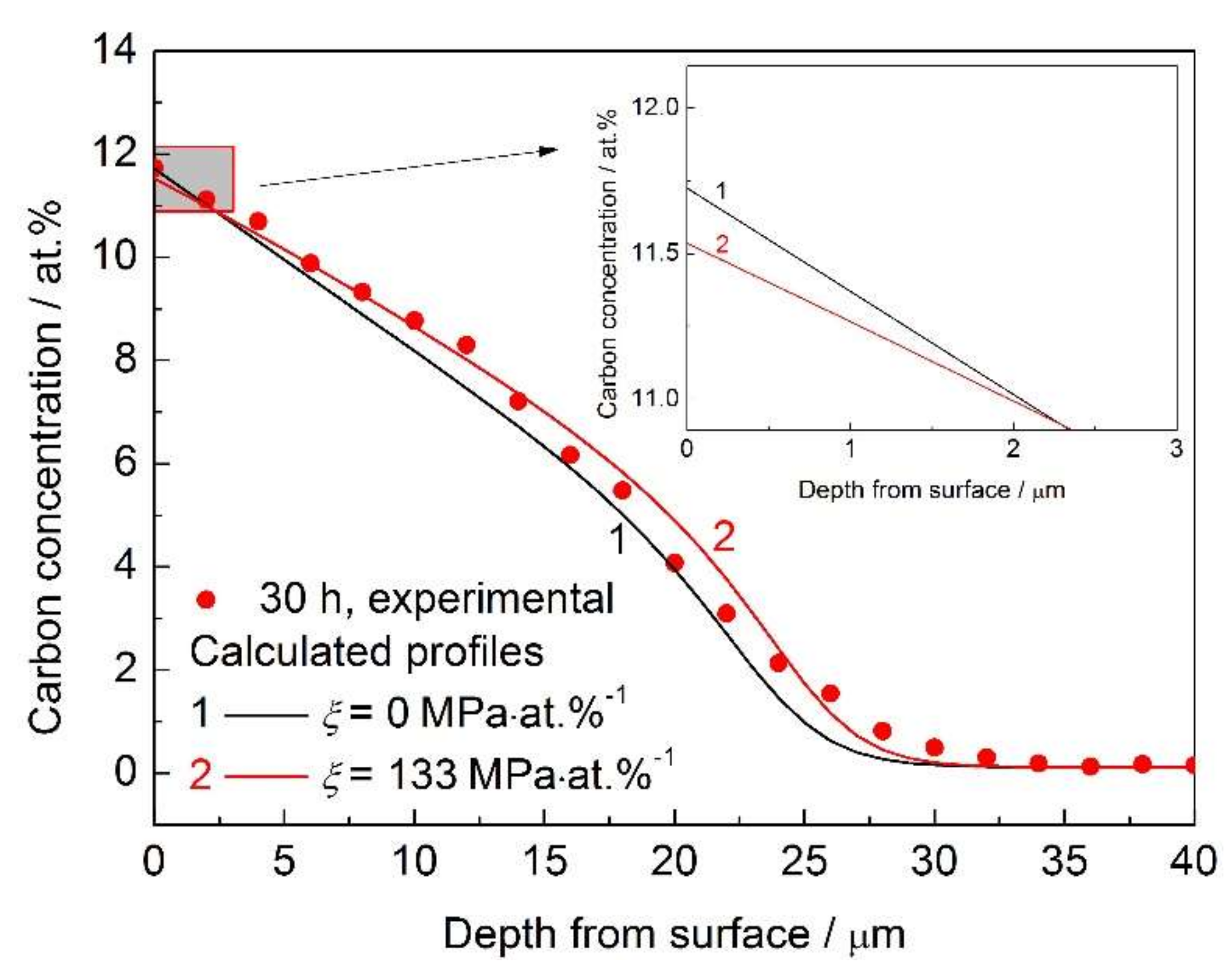
3.1. Composition-Induced Stress Gradient
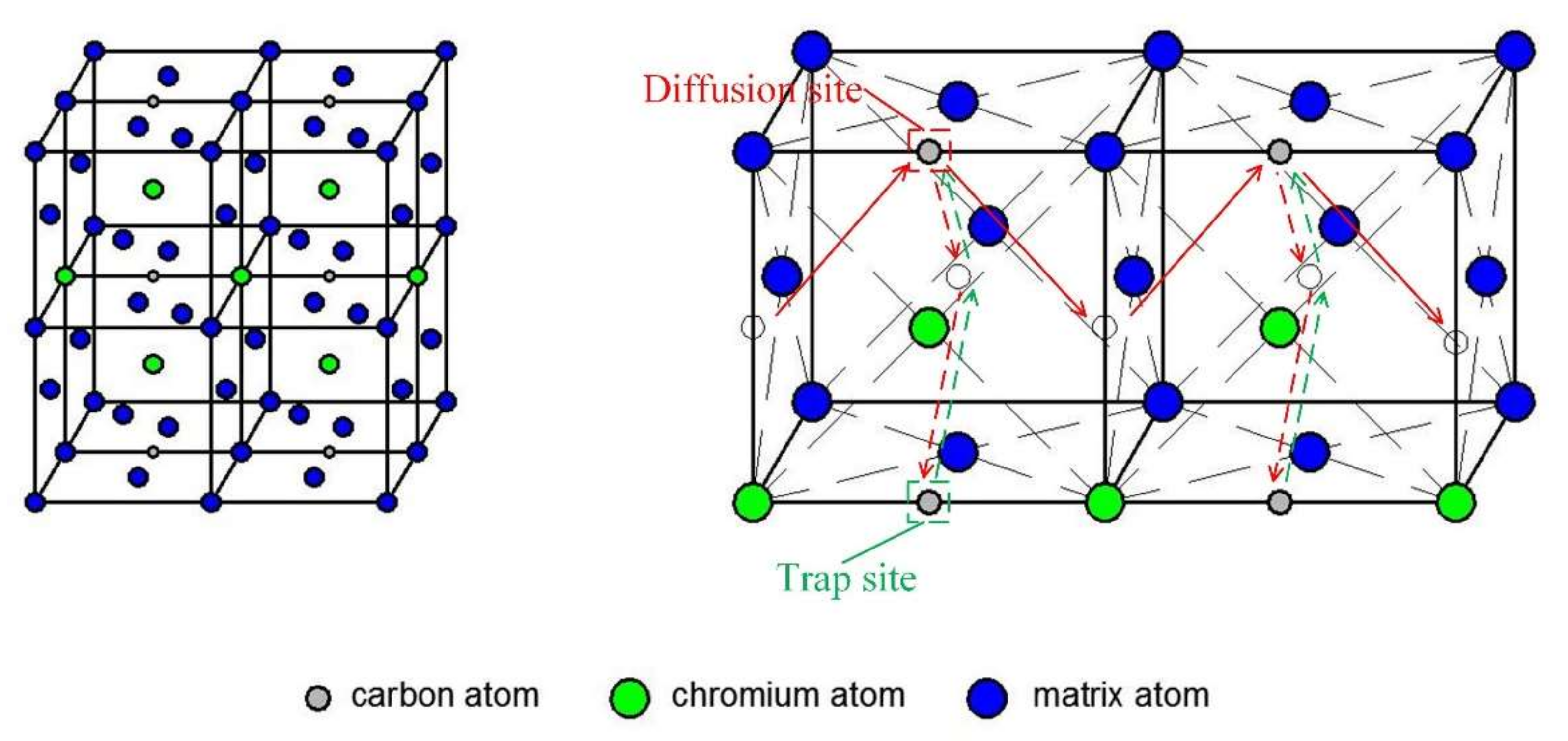
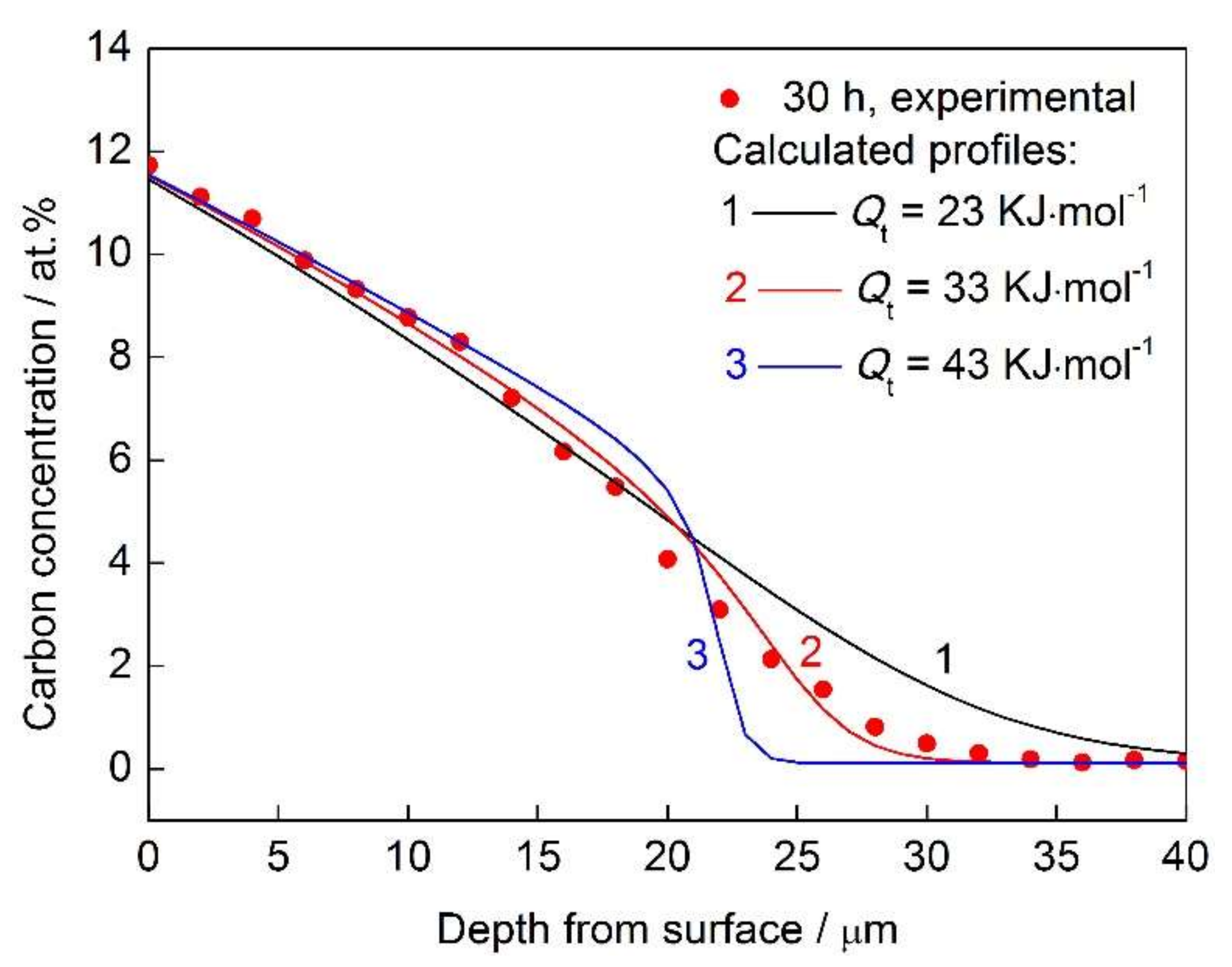
3.2. Trapping Effect
3.3. Boundary Conditions
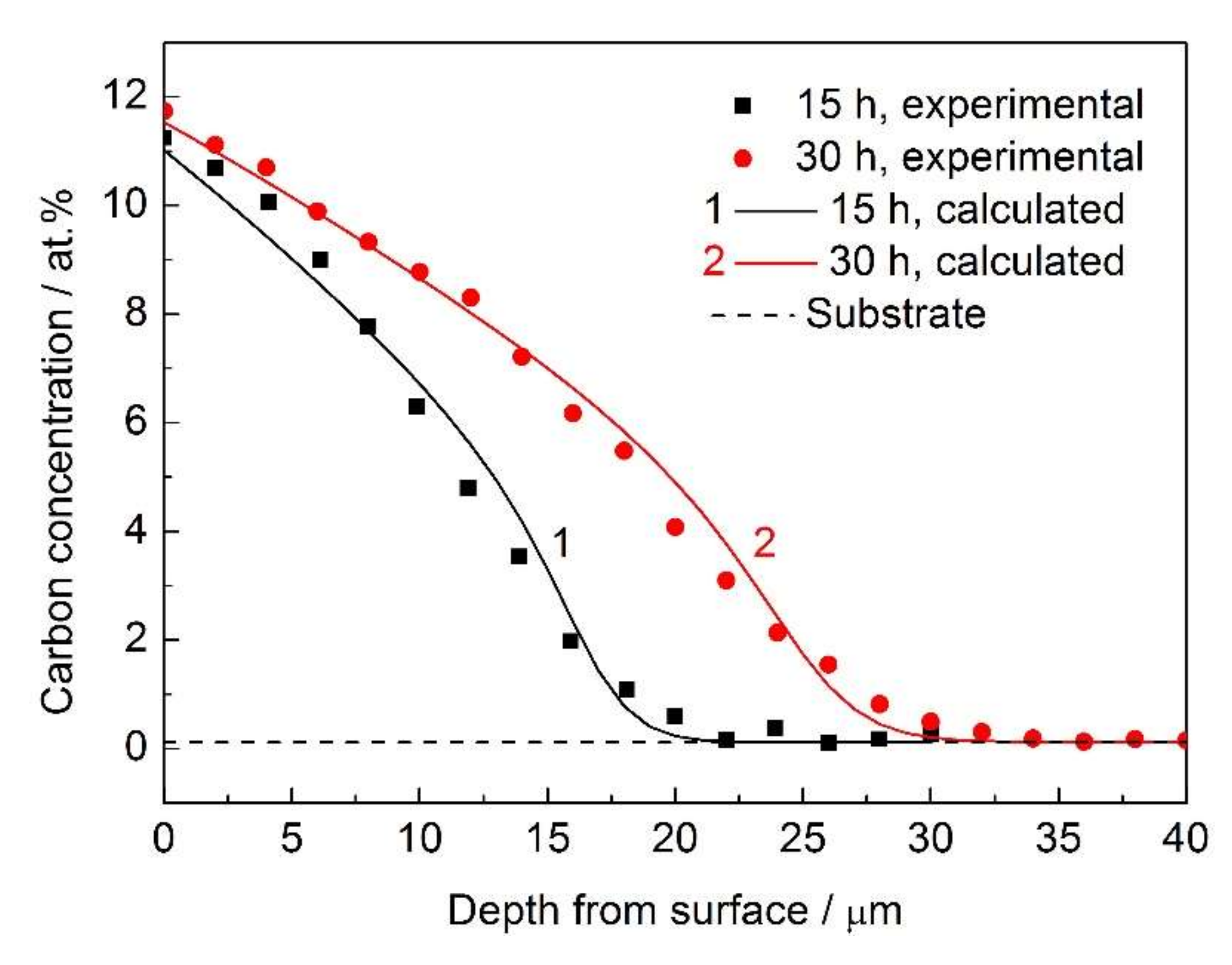
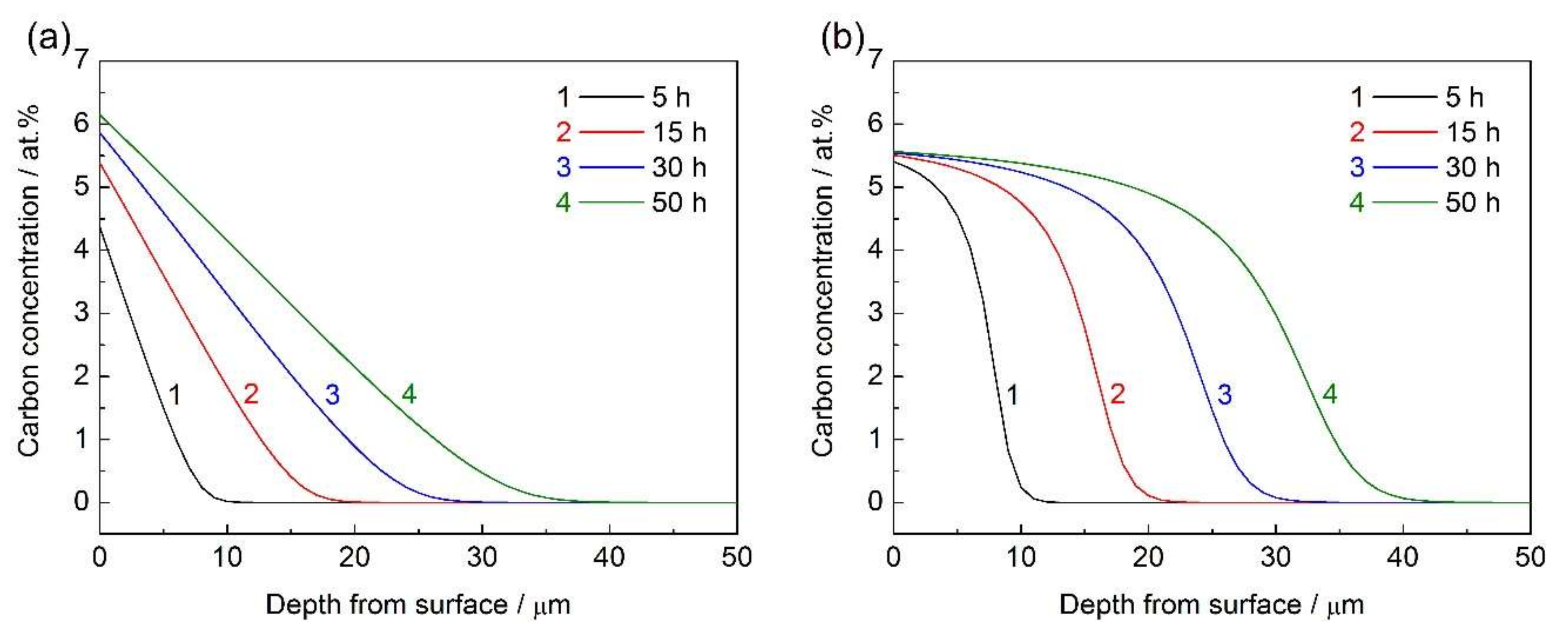
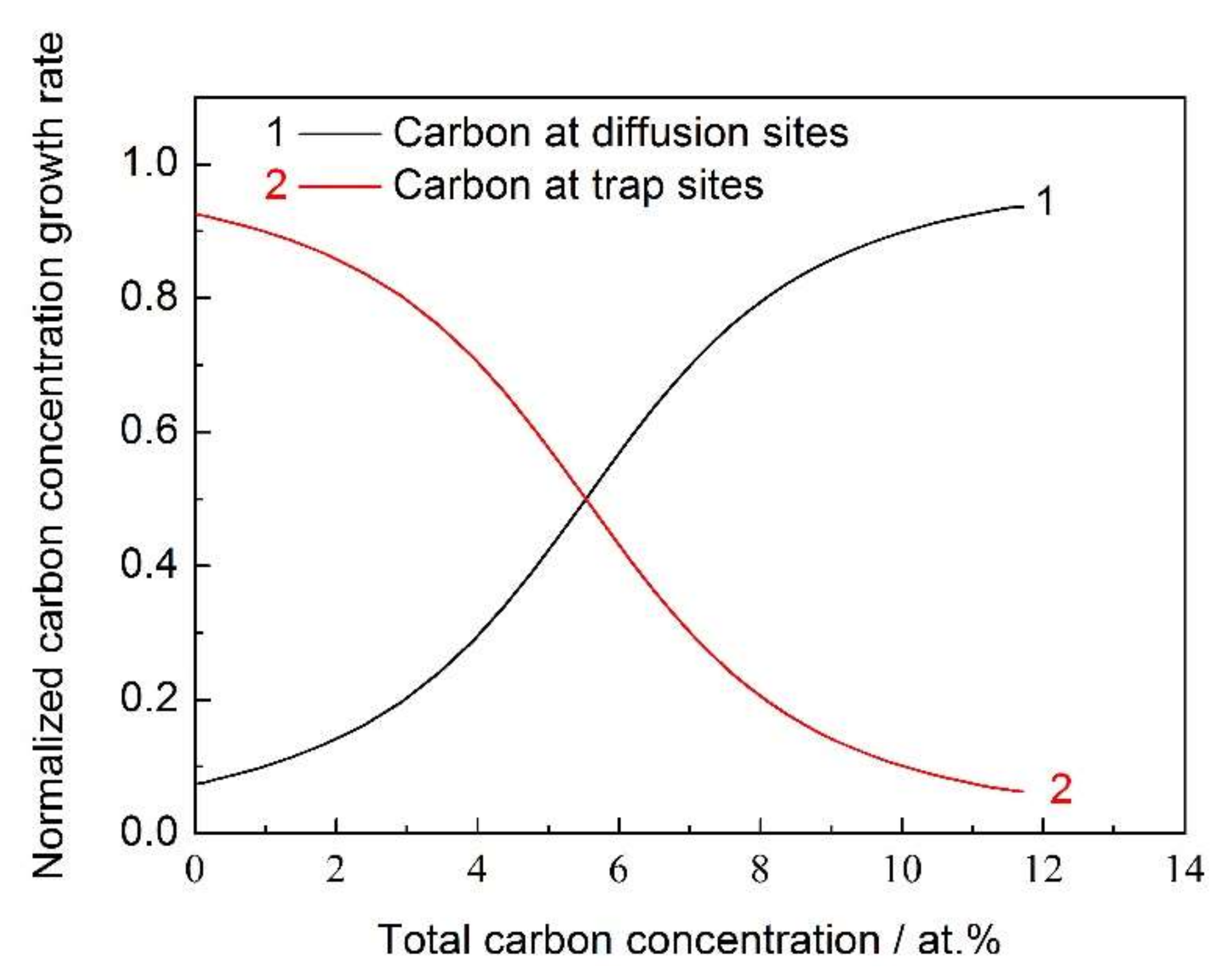
4. Results and Discussion
5. Conclusions
- The calculated carbon concentration–depth profiles based on the diffusion model considering the composition-induced stress gradient and the trapping effect by chromium were in good agreement with the experimental results.
- The composition-induced compressive stress gradient can enhance carbon diffusion in AISI 316L during low temperature gas phase carburization and reduce the surface carbon concentration. However, these effects are not remarkable.
- Carbon atoms prefer to occupy the trap sites, and the detrapping activation energy (Qt = 33 kJ·mol−1) was obtained from fitting the experimental data.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Davis, J.R. Metals Handbook: Desk Edition, 2nd ed.; ASM International Materials Park: Russell, OH, USA, 1998. [Google Scholar]
- Hsu, K.L.; Ahn, T.M.; Rigney, D.A. Friction, wear and microstructure of unlubricated austenitic stainless steels. Wear 1980, 60, 13–37. [Google Scholar] [CrossRef]
- Magee, J.H. Friction, lubrication and wear technology. In ASM Handbook; Blau, P.J., Ed.; ASM International Materials Park: Russell, OH, USA, 1998; Volume 18, pp. 710–724. [Google Scholar]
- Jones, N.G.; Ward-Close, C.M.; Brown, P.M.; Dye, D. An evaluation of the tensile properties of a supersaturated carbon layer via in situ synchrotron diffraction. Scr. Mater. 2010, 63, 85–88. [Google Scholar] [CrossRef]
- Michal, G.M.; Ernst, F.; Cao, Y.; Oba, F.; Agarwal, N.; Heuer, A.H. Carbon supersaturation due to paraequilibrium carburization: Stainless steels with greatly improved mechanical properties. Metall. Mater. Trans. A 2006, 54, 1597–1606. [Google Scholar] [CrossRef]
- Christiansen, T.; Somers, M.A.J. Low temperature gaseous nitriding and carburising of stainless steel. Surf. Eng. 2005, 21, 445–455. [Google Scholar] [CrossRef]
- Christiansen, T.L.; Somers, M.A.J. Low-temperature gaseous surface hardening of stainless steel: The current status. Int. J. Mater. Res. 2009, 100, 1361–1377. [Google Scholar] [CrossRef]
- Qu, J.; Blau, P.J.; Jolly, B.C. Tribological properties of stainless steels treated by colossal carbon supersaturation. Wear 2007, 263, 719–726. [Google Scholar] [CrossRef]
- Leyland, A.; Lewis, D.B.; Stevensom, P.R.; Matthews, A. Low temperature plasma diffusion treatment of stainless steels for improved wear resistance. Surf. Coat. Technol. 1993, 62, 608–617. [Google Scholar] [CrossRef]
- Dong, H. S-phase surface engineering of Fe-Cr, Co-Cr and Ni-Cr alloys. Int. Mater. Rev. 2010, 55, 65–98. [Google Scholar] [CrossRef]
- Li, W.; Li, X.; Dong, H. Effect of tensile stress on the formation of S-phase during low-temperature plasma carburizing of 316L foil. Acta Mater. 2011, 59, 5765–5774. [Google Scholar] [CrossRef]
- Li, W.; Guo, W.; Zhu, X.; Jin, X.; Li, X.; Dong, H. The effect of applied compressive stress on the diffusion of carbon in carbon supersaturated S-phase layer. Surf. Coat. Technol. 2017, 331, 1–6. [Google Scholar] [CrossRef]
- Christiansen, T.L.; Hummelshøj, T.S.; Somers, M.A.J. Expanded austenite crystallography and residual stress. Surf. Eng. 2010, 26, 242–247. [Google Scholar] [CrossRef]
- Christiansen, T.L.; Somers, M.A.J. Stress and composition of carbon stabilized expanded austenite on stainless steel. Metall. Mater. Trans. A 2009, 40, 1791–1798. [Google Scholar] [CrossRef]
- Rong, D.S.; Jiang, Y.; Gong, J.M. Residual stress in low temperature carburised layer of austenitic stainless steel. Mater. Sci. Technol. 2017, 33, 227–284. [Google Scholar] [CrossRef]
- Li, C.M. Physical chemistry of some microstructural phenomena. Metall. Mater. Trans. A 1978, 9, 1353–1380. [Google Scholar]
- Oddershede, J.; Christiansen, T.L.; Ståhl, K.; Somers, M.A.J. Extended X-ray absorption fine structure investigation of carbon stabilized expanded austenite and carbides in stainless steel AISI 316. Steel Res. Int. 2011, 82, 1248–1254. [Google Scholar] [CrossRef]
- Peng, Y.W.; Gong, J.M.; Jiang, Y.; Fu, M.H.; Rong, D.S. The effect of plastic pre-strain on low-temperature surface carburization of AISI 304 austenitic stainless steel. Surf. Coat. Technol. 2016, 304, 16–22. [Google Scholar] [CrossRef]
- Yang, F. Interaction between diffusion and chemical stresses. Mater. Sci. Eng. A 2005, 409, 153–159. [Google Scholar] [CrossRef]
- Karabelchtchikova, O.; Sisson, R.D. Carbon diffusion in steels: A numerical analysis based on direct integration of the flux. J. Phase Equilib. Diff. 2006, 27, 598–604. [Google Scholar] [CrossRef]
- Christiansen, T.; Somers, M.A.J. Avoiding ghost stress on reconstruction of stress- and composition-depth profiles from destructive X-ray diffraction depth profiling. Mater. Sci. Eng. A 2006, 424, 181–189. [Google Scholar] [CrossRef]
- Parascandola, S.; Möller, W.; Williamson, D.L. The nitrogen transport in austenitic stainless steel at moderate temperatures. Appl. Phys. Lett. 2000, 76, 2194–2196. [Google Scholar] [CrossRef]
- Martinavičius, A.; Abrasonis, G.; Möller, W. Influence of crystal orientation and ion bombardment on the nitrogen diffusivity in single-crystalline austenitic stainless steel. J. Appl. Phys. 2011, 110, 259. [Google Scholar] [CrossRef]
- Moskalioviene, T.; Galdikas, A.; Rivière, J.P.; Pichon, L. Modeling of nitrogen penetration in polycrystalline AISI 316L austenitic stainless steel during plasma nitriding. Surf. Coat. Technol. 2011, 205, 3301–3306. [Google Scholar] [CrossRef]
- Karabelchtchikova, O. Fundamentals of Mass Transfer in Gas Carburizing. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, November 2007. [Google Scholar]
- Hu, G.X.; Cai, X.; Rong, Y.H. Fundament of Materials Science, 3rd ed.; Shanghai Jiao Tong University Press: Shanghai, China, 2010; ISBN 9787313024800. [Google Scholar]
- Hummelshøj, T.S.; Christiansen, T.L.; Somers, M.A.J. Lattice expansion of carbon-stabilized expanded austenite. Scr. Mater. 2010, 63, 761–763. [Google Scholar] [CrossRef]
- Natesan, K.; Kassner, T.F. Thermodynamics of carbon in nickel, iron-nickel and iron-chromium-nickel alloys. Metall. Trans. 1973, 4, 2557–2566. [Google Scholar] [CrossRef]
- Gu, X. Numerical Simulations of Concentration-Depth Profiles of Carbon and Nitrogen in Austenitic Stainless Steel Based upon Highly Concentration Dependent Diffusivities. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, May 2011. [Google Scholar]
- Galdikas, A.; Moskalioviene, T. Stress induced nitrogen diffusion during nitriding of austenitic stainless steel. Comp. Mater. Sci. 2010, 50, 796–799. [Google Scholar] [CrossRef]
- Galdikas, A.; Moskalioviene, T. Modeling of stress induced nitrogen diffusion in nitrided stainless steel. Surf. Coat. Technol. 2011, 205, 3742–3746. [Google Scholar] [CrossRef]
- Christiansen, T.; Somers, M.A.J. Controlled dissolution of colossal quantities of nitrogen in stainless steel. Metall. Mater. Trans. A 2006, 37, 675–682. [Google Scholar] [CrossRef]
- Frnst, F.; Avishai, A.; Kahn, H.; Gu, X.; Michal, G.M.; Heuer, A.H. Enhanced carbon diffusion in austenitic stainless steel carburized at low temperature. Metall. Mater. Trans. A 2009, 40, 1768–1780. [Google Scholar]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Gong, J.; Chen, C.; Liu, Z.; Jiang, Y. Numerical Analysis of Stress Gradient and Traps Effects on Carbon Diffusion in AISI 316L during Low Temperature Gas Phase Carburization. Metals 2018, 8, 214. https://doi.org/10.3390/met8040214
Peng Y, Gong J, Chen C, Liu Z, Jiang Y. Numerical Analysis of Stress Gradient and Traps Effects on Carbon Diffusion in AISI 316L during Low Temperature Gas Phase Carburization. Metals. 2018; 8(4):214. https://doi.org/10.3390/met8040214
Chicago/Turabian StylePeng, Yawei, Jianming Gong, Chaoming Chen, Zhe Liu, and Yong Jiang. 2018. "Numerical Analysis of Stress Gradient and Traps Effects on Carbon Diffusion in AISI 316L during Low Temperature Gas Phase Carburization" Metals 8, no. 4: 214. https://doi.org/10.3390/met8040214
APA StylePeng, Y., Gong, J., Chen, C., Liu, Z., & Jiang, Y. (2018). Numerical Analysis of Stress Gradient and Traps Effects on Carbon Diffusion in AISI 316L during Low Temperature Gas Phase Carburization. Metals, 8(4), 214. https://doi.org/10.3390/met8040214




