Correction of Flow Curves and Constitutive Modelling of a Ti-6Al-4V Alloy
Abstract
:1. Introduction
2. Experimental Procedure and Corrected Approach
2.1. Experimental Procedure
2.2. Friction and Temperature Corrected Approach
3. Results and Discussion
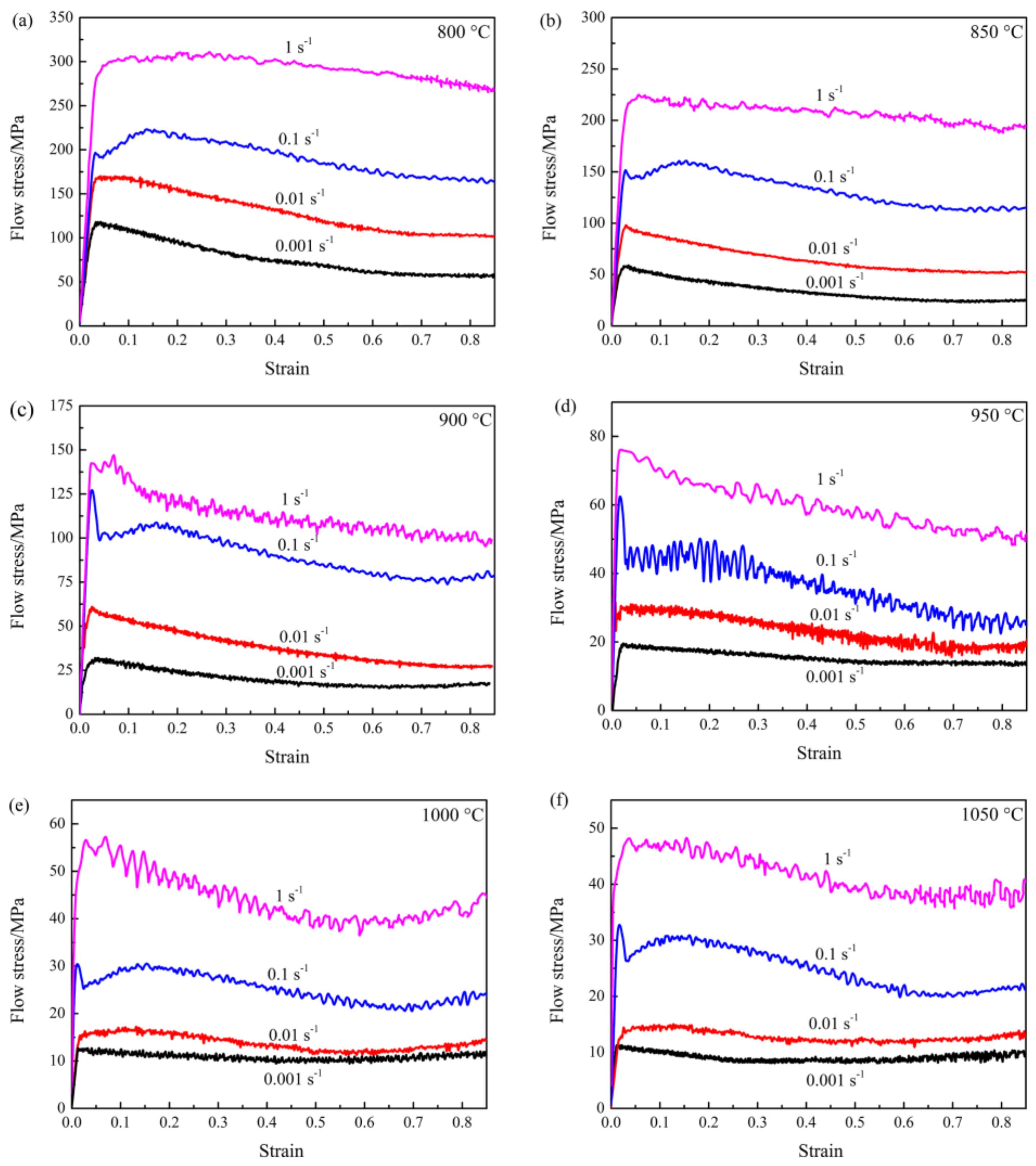
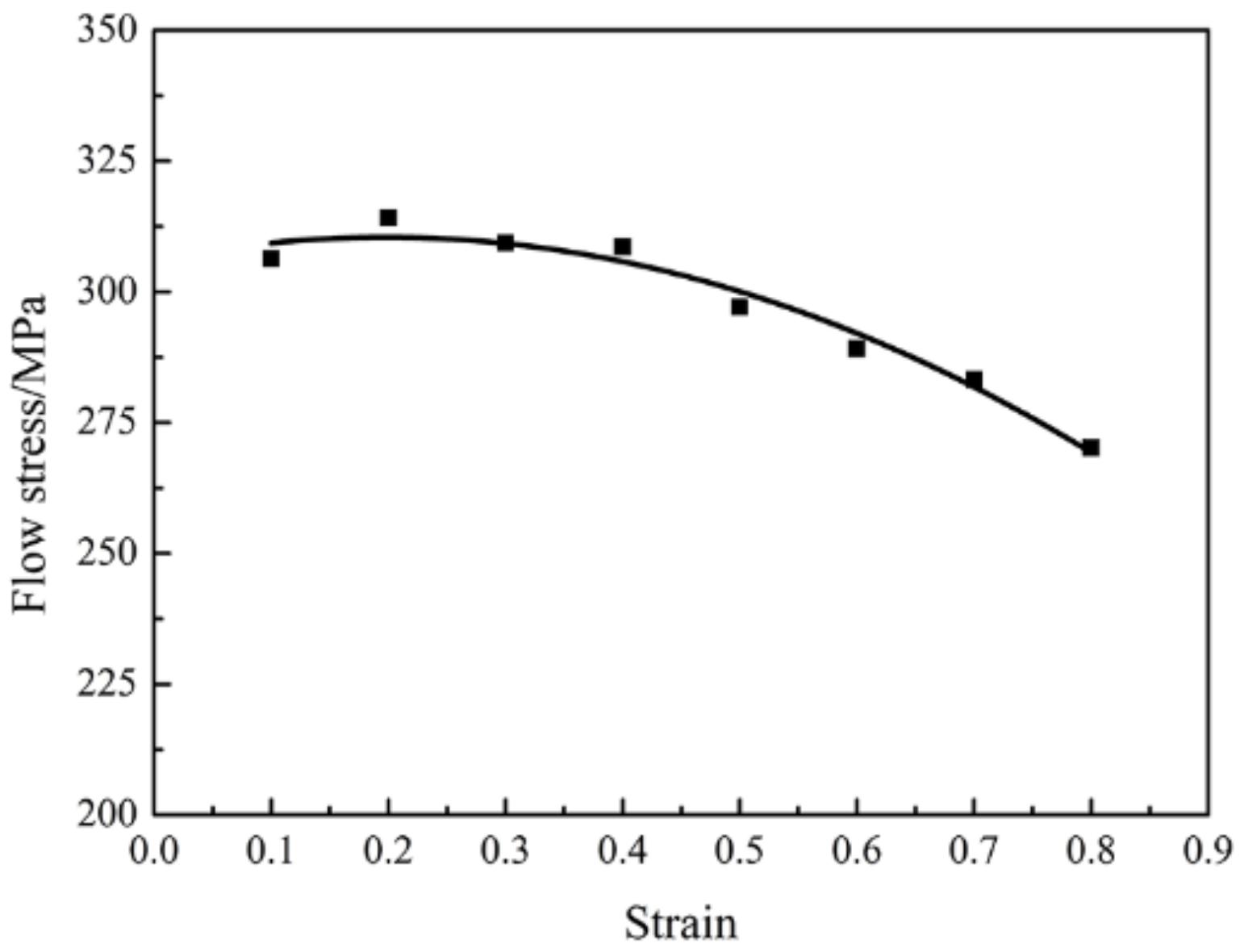
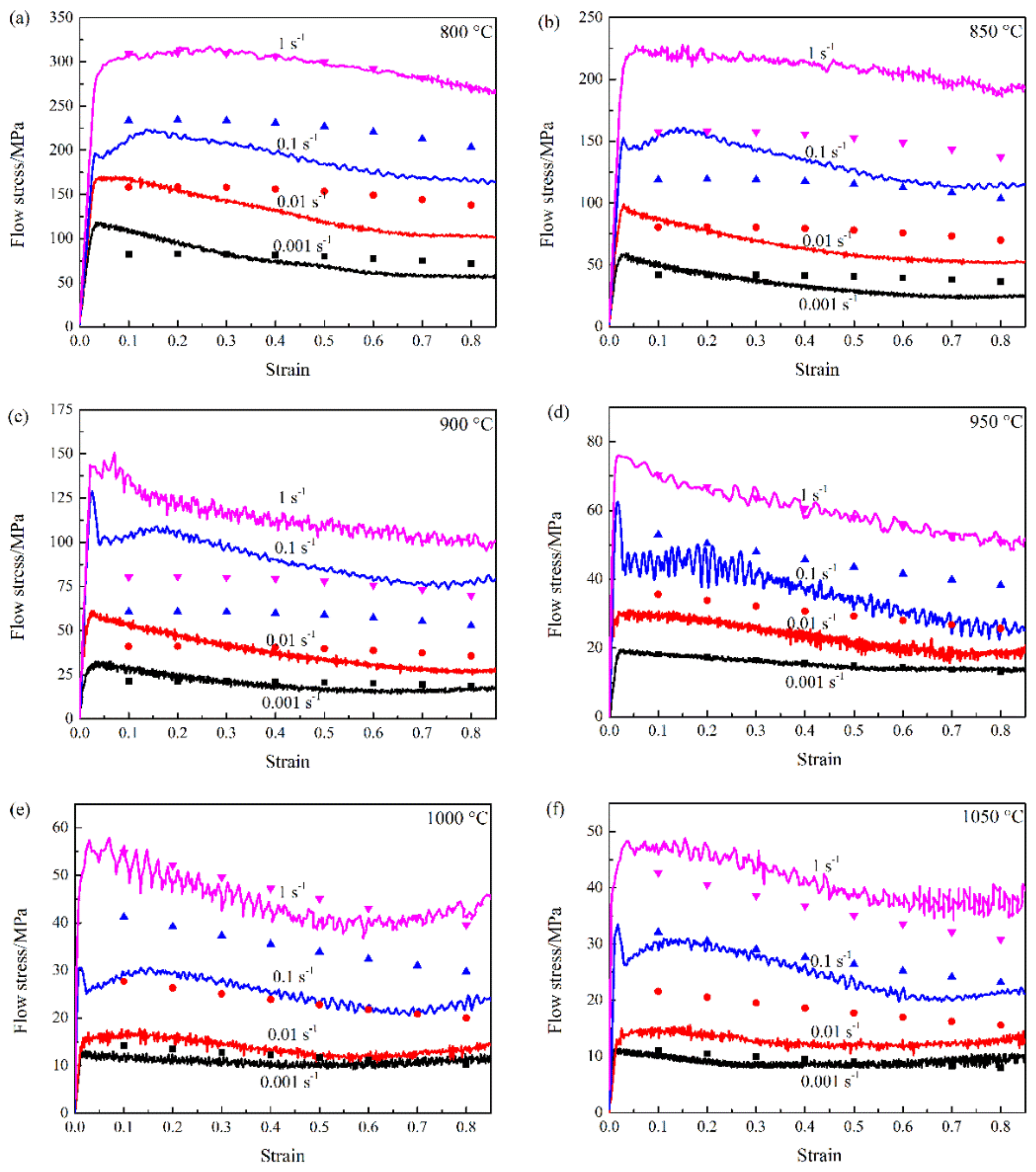
3.1. Corrected Flow Curves by Considering the Effect of Friction and Temperature Increasing
3.2. Constitutive Models
3.2.1. Modified Johnson-Cook Model
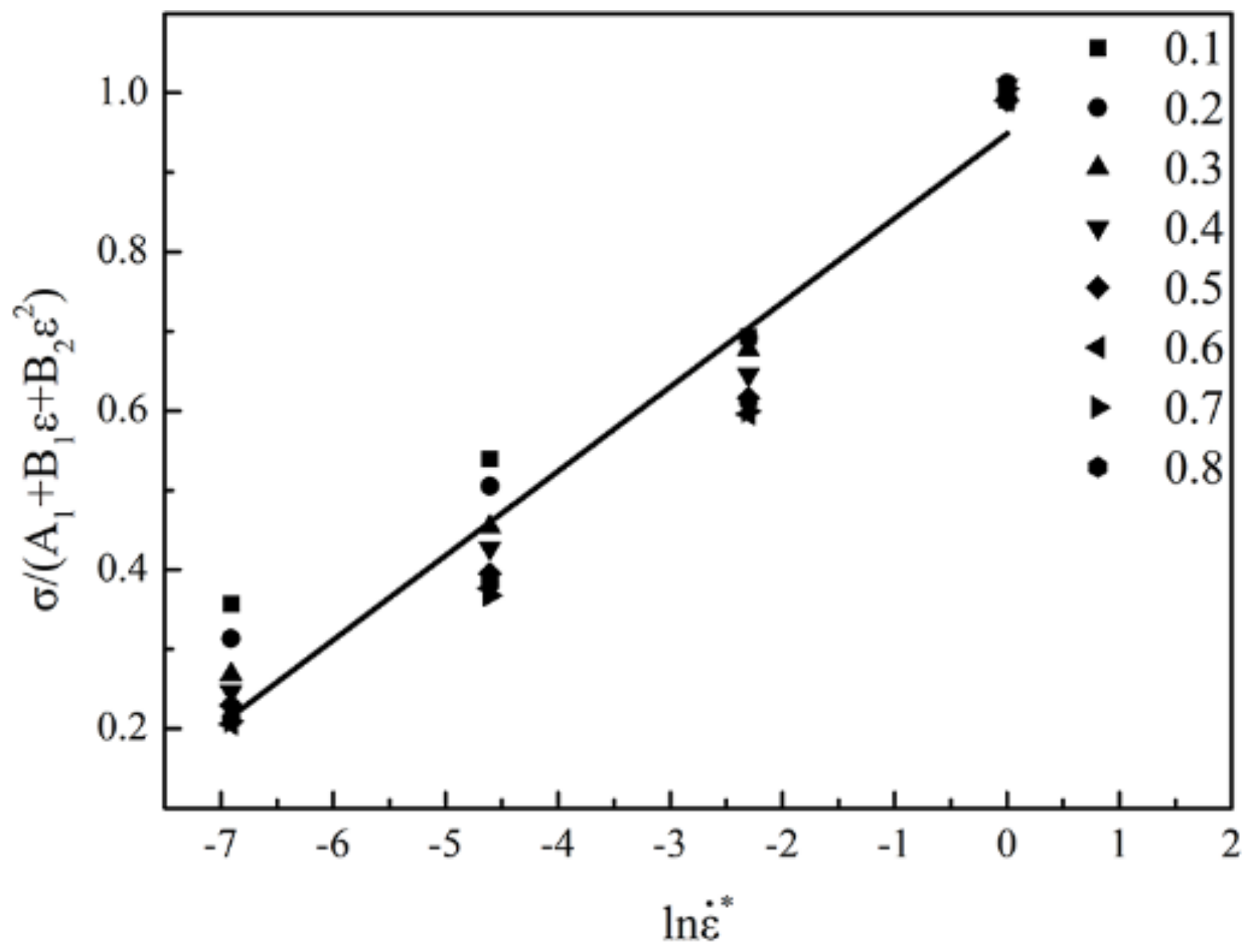
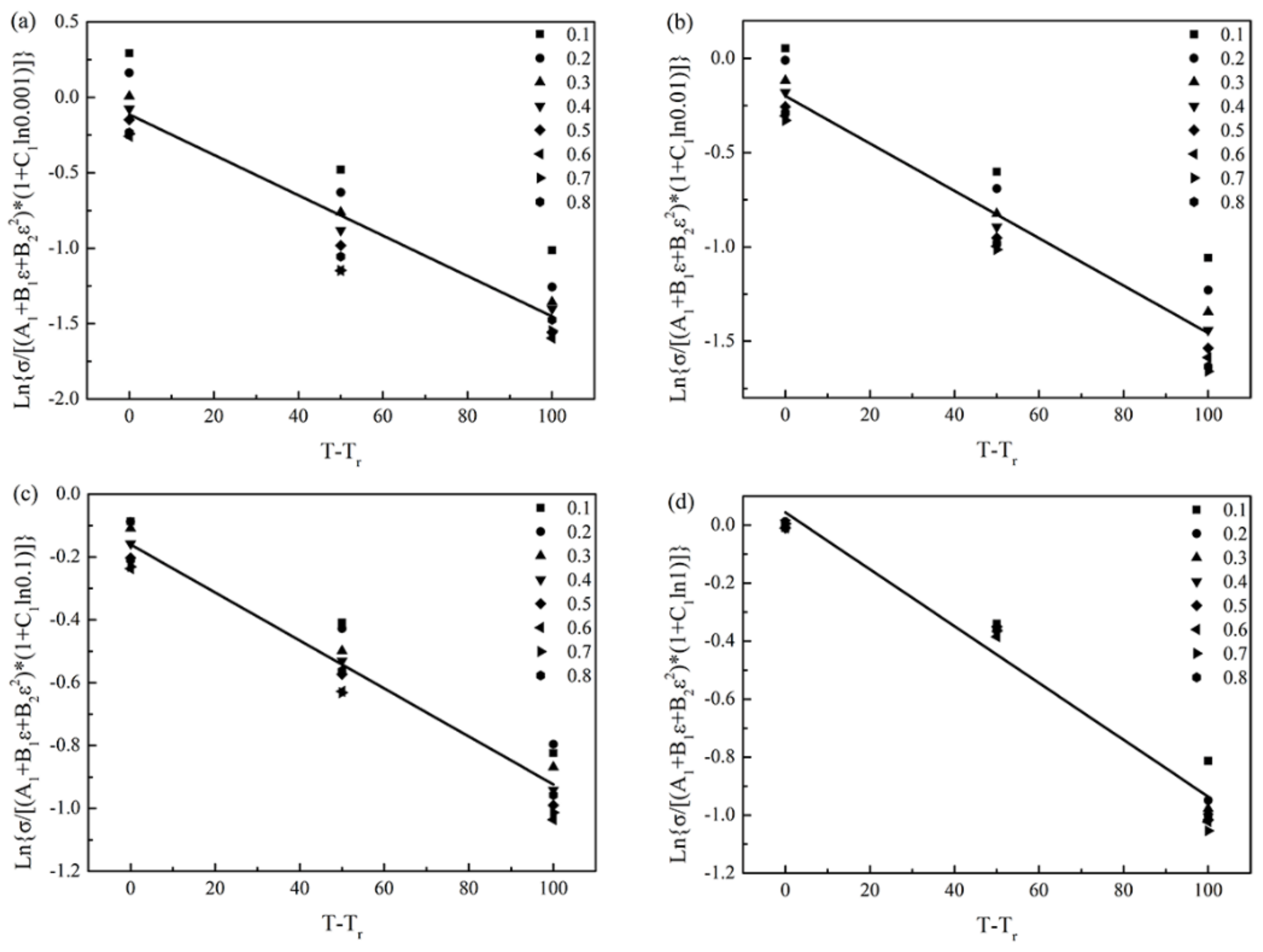
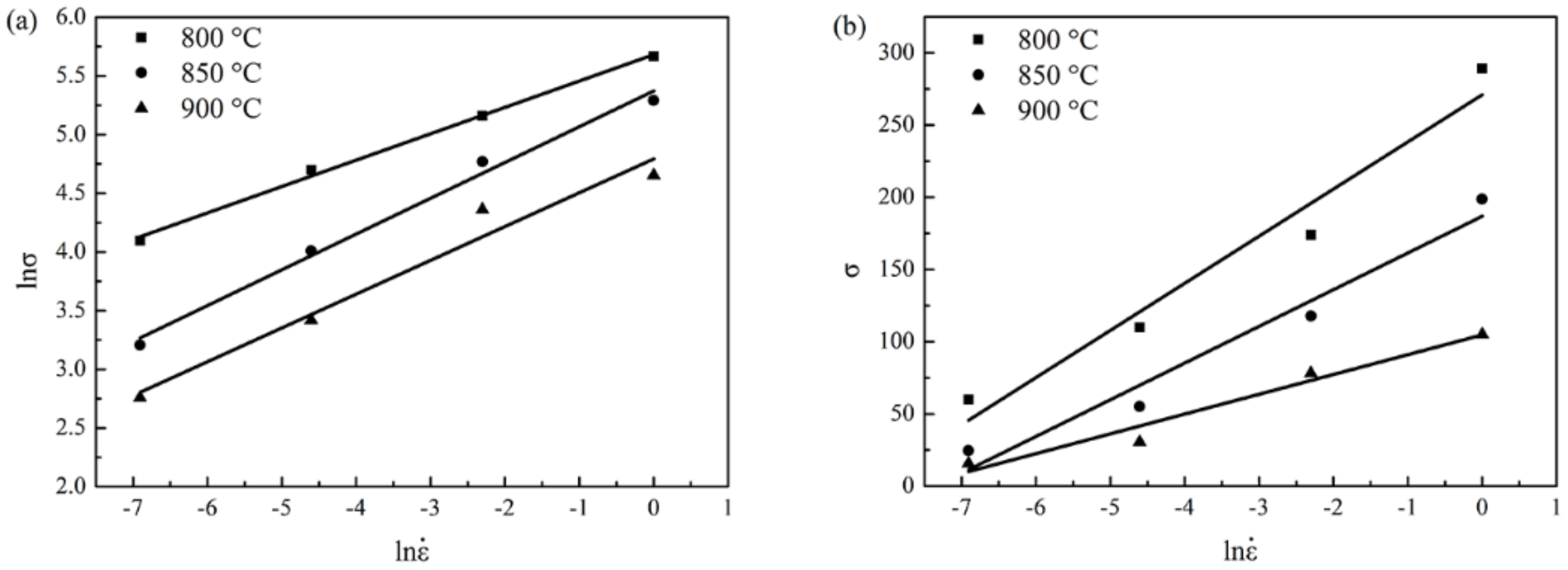
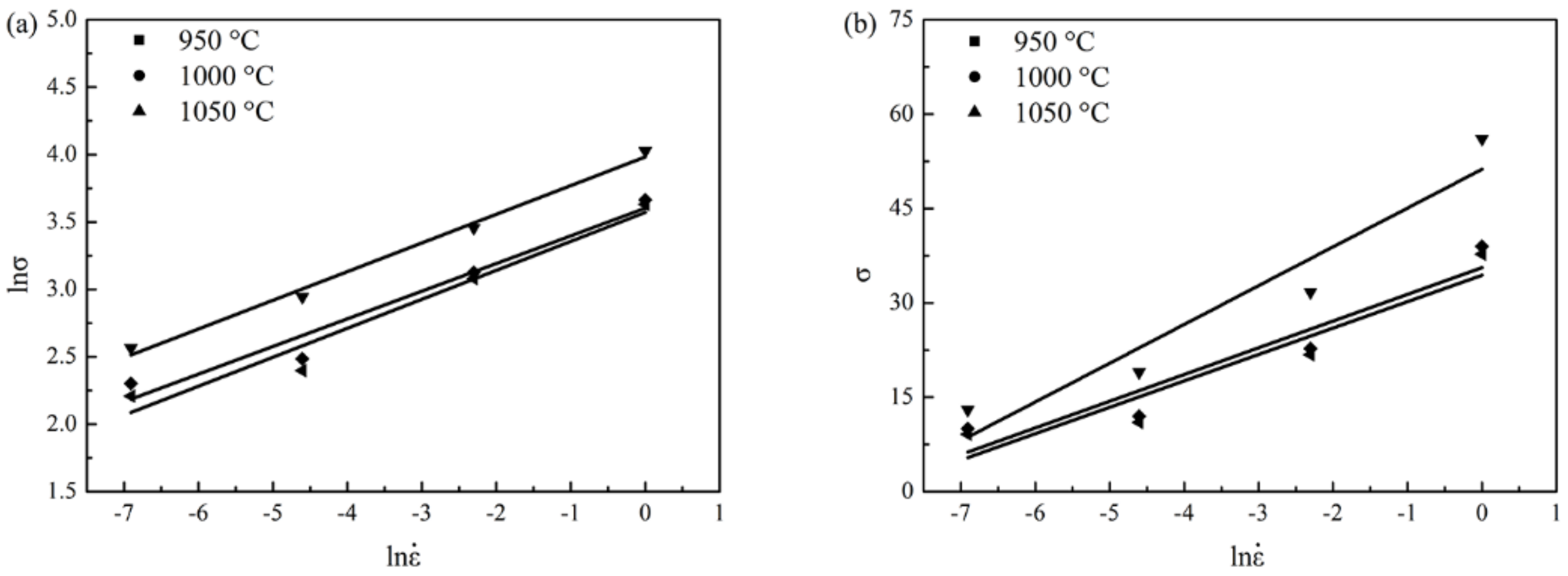
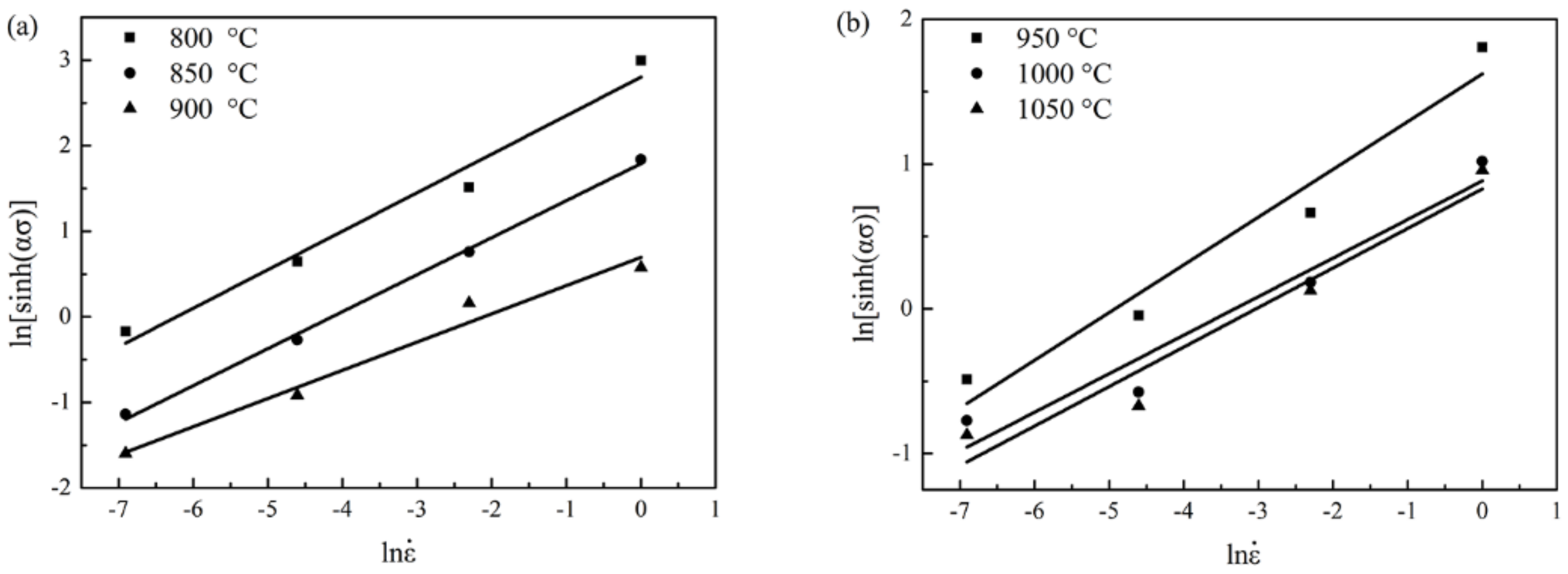
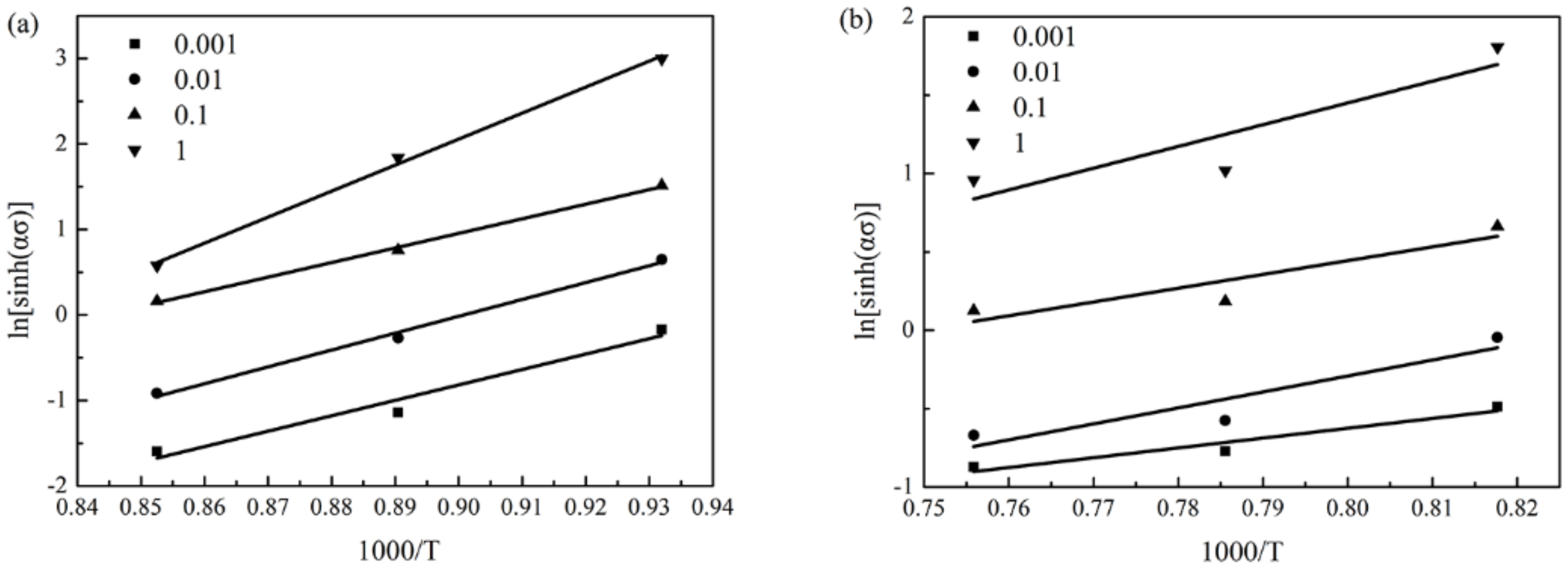
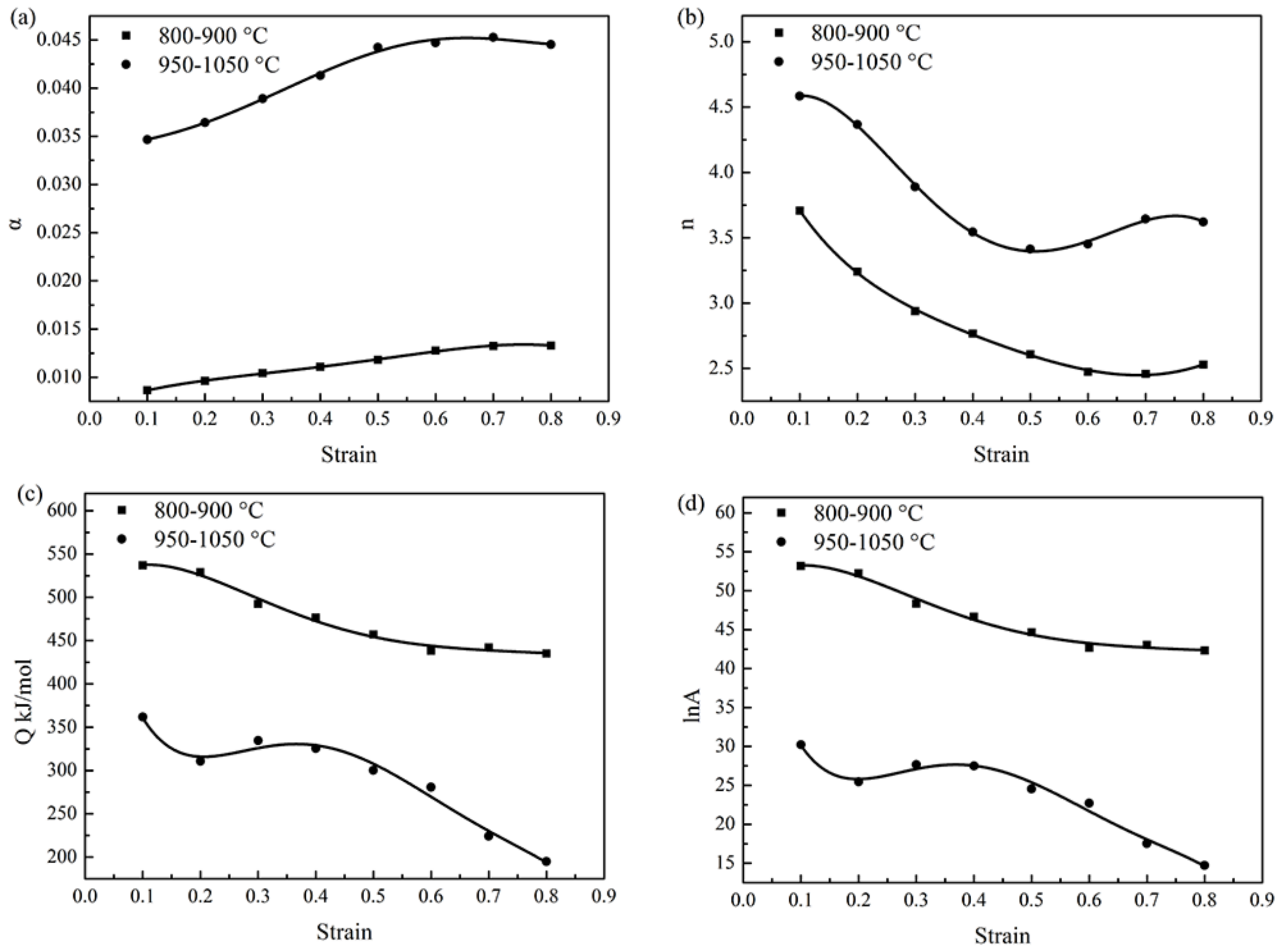
3.2.2. Strain Compensated Arrhenius-Type Constitutive Model
3.3. Formatting of Mathematical Components
4. Conclusions
- (1)
- The barreling coefficient B values are ≥1.1 in all temperatures and strain rates, which shows that friction has a significant influence on flow stress. The friction can result in a tested flow stress that is higher than the actual flow stress, while the temperature increasing is in contrast.
- (2)
- Based on the similarity of the flow stress curves, the constitutive model should be calculated in 800–900 °C and 950–1050 °C, separately.
- (3)
- The modified Johnson-Cook constitutive model only has a good agreement with the experimental data at reference deformation condition and strain rate of 0.001 s−1. But the agreement is not good with other deformation conditions. The correlation coefficient and average absolute relative error for the modified Johnson-Cook constitutive model are 0.924 and 22.673%.
- (4)
- The strain compensated Arrhenius-type constitutive model has a good agreement with the experimental data in most of the deformation conditions. The correlation coefficient and average absolute relative error for the strain compensated Arrhenius-type constitutive model are 0.986 and 9.168%. Thus, the strain compensated Arrhenius-type constitutive model has a better prediction capability than the modified Johnson-Cook constitutive.
Author Contributions
Conflicts of Interest
References
- Mirzadeh, H. Constitutive modeling and prediction of hot deformation flow stress under dynamic recrystallization conditions. Mech. Mater. 2015, 85, 66–79. [Google Scholar] [CrossRef]
- Gao, P.; Zhan, M.; Fan, X.; Lei, Z.; Cai, Y. Hot deformation behavior and microstructure evolution of TA15 titanium alloy with nonuniform microstructure. Mater. Sci. Eng. A 2017, 689, 243–251. [Google Scholar] [CrossRef]
- Mosleh, A.; Mikhaylovskaya, A.; Kotov, A.; Pourcelot, T.; Aksenov, S.; Kwame, J.; Portnoy, V. Modelling of the superplastic deformation of the near-alpha titanium alloy (Ti-2.5Al-1.8Mn) using Arrhenius-type constitutive model and artificial neural network. Metals 2017, 7, 568. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Effects of deformation temperatures on stress/strain distribution and microstructural evolution of deformed 42CrMo steel. Mater. Des. 2009, 30, 908–913. [Google Scholar] [CrossRef]
- Pu, E.; Zheng, W.; Song, Z.; Feng, H.; Dong, H. Hot deformation characterization of nickel-based superalloy UNS10276 through processing map and microstructural studies. J. Alloys Compd. 2017, 694, 617–631. [Google Scholar] [CrossRef]
- Cai, J.; Wang, K.; Zhai, P.; Li, F.; Yang, J. A modified Johnson-Cook constitutive equation to predict hot deformation behavior of Ti-6Al-4V alloy. J. Mater. Eng. Perform. 2015, 24, 32–44. [Google Scholar] [CrossRef]
- Jun, H.J.; Lee, K.S.; Kato, H.; Kim, H.S.; Chang, Y.W. Constitutive model for high temperature deformation behavior of Ti-Zr-Ni-Be bulk metallic glass in supercooled liquid region. Comput. Mater. Sci. 2012, 61, 213–223. [Google Scholar] [CrossRef]
- He, A.; Xie, G.; Zhang, H.; Wang, X. A comparative study on Johnson-Cook, modified Johnson-Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20crmo alloy steel. Mater. Des. 2013, 52, 677–685. [Google Scholar] [CrossRef]
- Hajari, A.; Morakabati, M.; Abbasi, S.M.; Badri, H. Constitutive modeling for high-temperature flow behavior of Ti-6242s alloy. Mater. Sci. Eng. A 2017, 681, 103–113. [Google Scholar] [CrossRef]
- Li, Y.; Onodera, E.; Chiba, A. Friction coefficient in hot compression of cylindrical sample. Mater. Trans. 2010, 51, 1210–1215. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Tan, J.Q.; Zhan, M.; Liu, S.; Huang, T.; Guo, J.; Yang, H. A modified Johnson-Cook model for tensile flow behaviors of 7050-T7451 aluminum alloy at high strain rates. Mater. Sci. Eng. A 2015, 631, 214–219. [Google Scholar] [CrossRef]
- Jonas, J.J.; Sellars, C.M.; Tegart, W.J.M. Strength and structure under hot-working conditions. Int. Mater. Rev. 1969, 14, 1–24. [Google Scholar] [CrossRef]
- Liang, R.Q.; Khan, A.S. A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures. Int. J. Plast. 1999, 15, 963–980. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M.; Liu, G. A modified Johnson–Cook model for tensile behaviors of typical high-strength alloy steel. Mater. Sci. Eng. A 2010, 527, 6980–6986. [Google Scholar] [CrossRef]
- Song, W.; Ning, J.; Mao, X.; Tang, H. A modified Johnson-Cook model for titanium matrix composites reinforced with titanium carbide particles at elevated temperatures. Mater. Sci. Eng. A 2013, 576, 280–289. [Google Scholar] [CrossRef]
- Trimble, D.; Shipley, H.; Lea, L.; Jardine, A.; O’Donnell, G.E. Constitutive analysis of biomedical grade Co-27Cr-5Mo alloy at high strain rates. Mater. Sci. Eng. A 2017, 682, 466–474. [Google Scholar] [CrossRef]
- Sellars, C.M.; Mctegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- Cai, J.; Li, F.; Liu, T.; Chen, B.; He, M. Constitutive equations for elevated temperature flow stress of Ti–6Al–4V alloy considering the effect of strain. Mater. Des. 2011, 32, 1144–1151. [Google Scholar] [CrossRef]
- Pilehva, F.; Zarei-Hanzaki, A.; Ghambari, M.; Abedi, H.R. Flow behavior modeling of a Ti-6Al-7Nb biomedical alloy during manufacturing at elevated temperatures. Mater. Des. 2013, 51, 457–465. [Google Scholar] [CrossRef]
- Li, J.; Li, F.; Cai, J.; Wang, R.; Yuan, Z.; Xue, F. Flow behavior modeling of the 7050 aluminum alloy at elevated temperatures considering the compensation of strain. Mater. Des. 2012, 42, 369–377. [Google Scholar] [CrossRef]
- Momeni, A.; Abbasi, S.M. Effect of hot working on flow behavior of Ti-6Al-4V alloy in single phase and two phase regions. Mater. Des. 2010, 31, 3599–3604. [Google Scholar] [CrossRef]
- Souza, P.M.; Beladi, H.; Singh, R.; Rolfe, B.; Hodgson, P.D. Constitutive analysis of hot deformation behavior of a Ti6Al4V alloy using physical based model. Mater. Sci. Eng. A 2015, 648, 265–273. [Google Scholar] [CrossRef]
- Wanjara, P.; Jahazi, M.; Monajati, H.; Yue, S.; Immarigeon, J.P. Hot working behavior of near-alpha alloy IMI834. Mater. Sci. Eng. A 2005, 396, 50–60. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Najafizadeh, A. A new method for evaluation of friction in bulk metal forming. J. Mater. Process. Technol. 2004, 152, 136–143. [Google Scholar] [CrossRef]
- Gholamadeh, A.; Taheri, A.K. The prediction of hot flow behavior of Al-6%Mg alloy. Mech. Res. Commun. 2009, 36, 252–259. [Google Scholar] [CrossRef]
- Roebuck, B.; Lord, J.D.; Brooks, M.; Loveday, M.S.; Sellars, C.M.; Evans, R.W. Measurement of flow stress in hot axisymmetric compression tests. Mater. High Temp. 2006, 23, 59–83. [Google Scholar] [CrossRef]
- Shafaat, M.A.; Omidvar, H.; Fallah, B. Prediction of hot compression flow curves of Ti-6Al-4V alloy in alpha plus beta phase region. Mater. Des. 2011, 32, 4689–4695. [Google Scholar] [CrossRef]
- Mirzadeh, H. Constitutive analysis of Mg-Al-Zn magnesium alloys during hot deformation. Mech. Mater. 2014, 77, 80–85. [Google Scholar] [CrossRef]
- Mandal, S.; Rakesh, V.; Sivaprasad, P.V.; Venugopal, S.; Kasiviswanathan, K.V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel. Mater. Sci. Eng. A 2009, 500, 114–121. [Google Scholar] [CrossRef]
- Haghdadi, N.; Zarei-Hanzaki, A.; Abedi, H.R. The flow behavior modeling of cast A356 aluminum alloy at elevated temperatures considering the effect of strain. Mater. Sci. Eng. A 2012, 535, 252–257. [Google Scholar] [CrossRef]




| Temperature (°C) | Strain Rate (s−1) | ||||
|---|---|---|---|---|---|
| 0.001 | 0.01 | 0.1 | 1 | 10 | |
| 800 | 1.23367 | 1.22045 | 1.22528 | 1.24138 | 1.19697 |
| 850 | 1.24819 | 1.247 | 1.24637 | 1.24822 | 1.20488 |
| 900 | 1.17906 | 1.21424 | 1.24033 | 1.27114 | 1.23279 |
| 950 | 1.18657 | 1.18411 | 1.18164 | 1.23693 | 1.24067 |
| 1000 | 1.16292 | 1.14611 | 1.12361 | 1.13064 | 1.21576 |
| 1050 | 1.18666 | 1.16968 | 1.21577 | 1.25549 | 1.16799 |
| A1 | B1 | B2 | C1 | λ1 | λ2 | |
|---|---|---|---|---|---|---|
| 800–900 °C | 305.9702 | 44.92423 | −113.465 | 0.10623 | −0.00969 | 0.000551 |
| 950–1050 °C | 74.03002 | −37.8908 | 11.0537 | 0.1073 | −0.00378 | 0.000178 |
| α | n | Q | lnA |
|---|---|---|---|
| D0 = 0.00694 | E0 = 4.59468 | F0 = 506.4186 | H0 = 50.30346 |
| D1 = 0.02219 | E1 = −11.8426 | F1 = 656.7189 | H1 = 64.77531 |
| D2 = −0.06088 | E2 = 35.76194 | F2 = −4249.11 | H2 = −434.195 |
| D3 = 0.09974 | E3 = −63.4781 | F3 = 8640.985 | H3 = 894.9239 |
| D4 = −0.05019 | E4 = 55.43269 | F4 = −7629.24 | H4 = −800.436 |
| D5 = −0.00901 | E5 = −17.3419 | F5 = 2514.97 | H5 = 267.9284 |
| α | n | Q | lnA |
|---|---|---|---|
| D0 = 0.03364 | E0 = 4.09854 | F0 = 584.4601 | H0 = 53.59972 |
| D1 = 0.00887 | E1 = 10.5984 | F1 = −3732.22 | H1 = −396.407 |
| D2 = −0.00285 | E2 = −69.7254 | F2 = 18,715.89 | H2 = 2033.636 |
| D3 = 0.22163 | E3 = 133.9525 | F3 = −41438.3 | H3 = −4591.96 |
| D4 = −0.4681 | E4 = −92.761 | F4 = 41,030.41 | H4 = 4648.483 |
| D5 = 0.25605 | E5 = 15.50738 | F5 = −15175.7 | H5 = −1758.81 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Dong, L.; Zhang, Z.; Lei, X.; Yang, R.; Sha, Y. Correction of Flow Curves and Constitutive Modelling of a Ti-6Al-4V Alloy. Metals 2018, 8, 256. https://doi.org/10.3390/met8040256
Hu M, Dong L, Zhang Z, Lei X, Yang R, Sha Y. Correction of Flow Curves and Constitutive Modelling of a Ti-6Al-4V Alloy. Metals. 2018; 8(4):256. https://doi.org/10.3390/met8040256
Chicago/Turabian StyleHu, Ming, Limin Dong, Zhiqiang Zhang, Xiaofei Lei, Rui Yang, and Yuhui Sha. 2018. "Correction of Flow Curves and Constitutive Modelling of a Ti-6Al-4V Alloy" Metals 8, no. 4: 256. https://doi.org/10.3390/met8040256
APA StyleHu, M., Dong, L., Zhang, Z., Lei, X., Yang, R., & Sha, Y. (2018). Correction of Flow Curves and Constitutive Modelling of a Ti-6Al-4V Alloy. Metals, 8(4), 256. https://doi.org/10.3390/met8040256





