1. Introduction
SGI (Spheroidal graphite cast irons) are mainly Fe-C-Si alloys. Therefore, the solid-state transformations taking place after the solidification step, i.e., the decomposition of austenite to ferrite (in the stable system) and to pearlite (in the metastable system), have been considered to occur as they do in Fe-C-Si steels [
1].
While it has long been recognized that the fundamental assumptions about pearlite nucleation and growth in steels can be extrapolated to this transformation in SGI [
1], it is also crucial to consider the structure after the solidification step as an input. Among the aspects inherited from the solidification that have to be accounted for in the pearlite transformation, the following should be highlighted: the austenite grain size, the eutectic cell size, the silicon—and alloying elements—concentration profiles, and the size and distribution of the graphite nodules.
To the best of the present author’s knowledge, no model has currently taken into account either these solidification outputs nor the carbon and silicon possible diffusion paths when dealing with the metastable transformation in SGI.
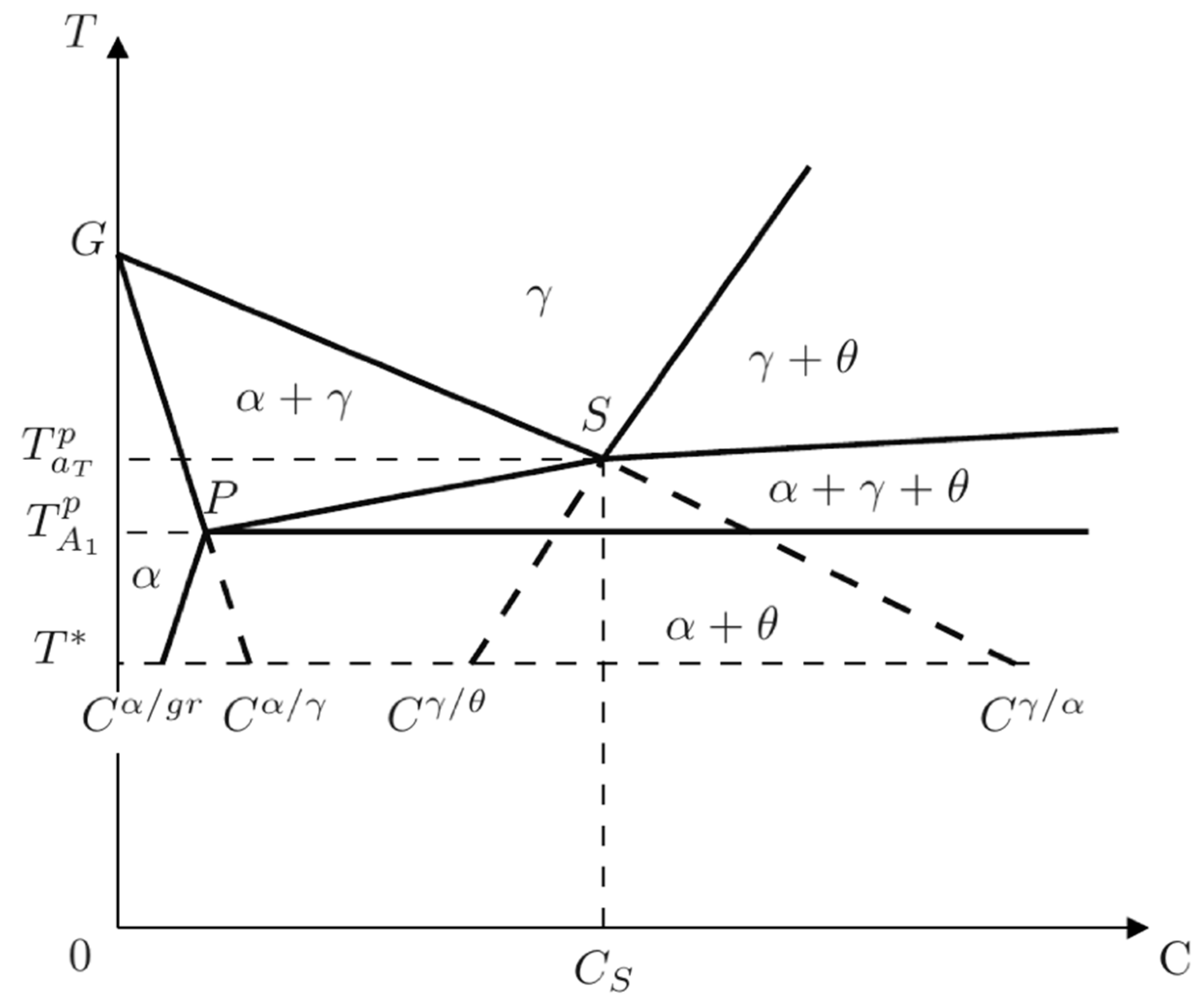
Based on the fact that no partitioning of substitutional elements has been reported to take place during the solid-state transformations, Lacaze et al. [
2] considered that the metastable transformation could be described by making use of a Fe-C binary isopleth section with the nominal percentage of silicon in the alloy (
Figure 1). Hence, they suggested that pearlite could only nucleate and grow at temperatures lower than the lowest limit of the three-phase field (
). According to Hillert [
3], at temperatures lower than
, two kinds of pearlite could develop: para-pearlite (non-partitioning of substitutional solutes between ferrite and cementite) and constant ortho-pearlite (partitioning of substitutional solutes between ferrite and cementite with constant interlaminar spacing).
Al-Salman et al. [
4] studied the pearlite growth in a 2 wt%-Si alloy and, making use of microprobe analysis, they were able to conclude that above 600 °C, pearlite grows with partitioning of silicon between ferrite and cementite at the reaction front. In addition, the Fe-C-Si isotherm sections exposed by Hillert in one of his papers [
3] presents evidence that pearlite growing with no partition of silicon between ferrite and cementite is only possible at temperatures lower than 650 °C.
All in all, at the temperatures at which pearlite is known to grow in SGI [
1], ortho-pearlite is the only possible pearlite structure to be considered. Accordingly, the difference in silicon content between the austenite/cementite and the austenite/ferrite interfaces drives the partitioning of silicon and it can be inserted in the binary theory for pearlite growth [
2]. This is exactly what Tewari and Sharma [
5] did: by assuming that cementite does not dissolve any silicon, they were able to reproduce the results of pearlite growth by Al-Salman et al. [
4].
Concerning the modelling of pearlite growth, Lacaze and Gerval [
6] are among the few who have proposed a continuous process for modelling pearlite nucleation. In addition, they made use of a semi-empirical law based on experimental results in order to describe its growth. This law is only a function of the undercooling from
and does not directly include the partitioning of silicon.
Stefanescu and Kanetkar [
7] modelled pearlite nucleation as a continuous process and they studied its growth as a function of the variation of free energy during the transformation of austenite to pearlite.
Liu et al. [
8] made use of an instantaneous nucleation law and modelled its growth as a function of the undercooling and the diffusion of carbon in the austenite volume.
Assuming that the stable and metastable transformations are two competitive processes that start at the same temperature, Almansour et al. [
9] calculated the growth velocity of pearlite employing the additivity rule to the Kolmogorov-Johnson-Mehl-Avrami equation.
This short literature review about the metastable transformation in SGI makes evident that it has been assumed to happen as it does in steels, without considering particular features of this kind of alloy. Among the aspects inherited from the solidification that have to be accounted for in the pearlite transformation, the following should be highlighted: the austenite grain size, the eutectic cell size, the silicon—and alloying elements—concentration profiles, and the size and distribution of the graphite nodules.
To the best of the present author’s knowledge, no model has currently taken into account either these solidification outputs nor the carbon and silicon possible diffusion paths when dealing with the metastable transformation in SGI.
The aim of the present work is to develop an integrated model for metastable eutectoid transformation. This model can be used to simulate the final microstructure of a eutectic SGI with a negligible percentage of alloying elements as the result of a continuous cooling process. To this end, the thermo-metallurgical solidification model, coupled with the solid-state transformations taking place from the end of the solidification, steps up to the upper temperature of the stable eutectoid intercritic [
10] and linked with the decomposition of austenite to ferrite reported in [
11], is extended in the present study to describe the pearlite reaction. This new model is expected to predict the size and distribution of the pearlite nodules, the interlaminar spacing, and the final pearlite fractions, considering its growth as controlled by the partitioning of silicon between ferrite and cementite at the pearlite/austenite interface.
This manuscript is organized as follows:
Section 2 presents the proposed model, that includes nucleation and growth of pearlite nodules, and its application to a casting sample; the results of the model are discussed and experimentally validated in
Section 3 and, finally,
Section 4 summarizes the concluding remarks drawn from this research.
3. Results and Discussion
Computed cooling curves and cooling rate curves at the central region of the specimen are shown in
Figure 6a,b, respectively. The computed cooling curves and cooling rate curves quantitatively agree with those corresponding to the three different experiments. In these figures, it can be seen that the metastable eutectoid transformation starts approximately at the same time in one of the experimental tests (exp3) and in the simulation: 470 s.
Comparing the region of the eutectoid transformation with the results reported in previous articles [
10,
11], in which pearlite reaction was modelled examining only the volume and the grain boundary diffusion of carbon in austenite, it can be seen that the present modelling results fit the experimental records more accurately.
In
Figure 7a, the simulated evolution of the pearlite volume fraction is shown for each of the studied zones. In this case, the time for the beginning of the metastable eutectoid transformation at node 3 was the shortest, while the temperature at which the decomposition of austenite to pearlite starts was the highest if compared with the nodes corresponding to the other four areas, i.e., nodes 1, 2, 4 and 5. The latter one presented similar pearlite fractions and transformation onsets. Indeed, the difference in the pearlite volume fractions was negligible for these four areas.
On the other hand, the calculated ferrite fractions presented in
Figure 7b showed an inverse behavior compared to the pearlite fractions.
In
Figure 8, the density of pearlite nodules per unit volume is plotted. Comparing
Figure 7a and
Figure 8, it is clear that the pearlite fraction obtained as the output of the simulation process did not have a direct relationship with the total density of pearlite nodules. In nodes 1, 2, 3 and 4, the nodule densities were of the same order, while in node 5 (central area of the specimen, next to the thermocouple), the density was considerably higher. If a ratio between the pearlite fraction and the nodule size distribution is recorded, it can be established that the zone with the highest pearlite fraction was the one with the highest percentage of large nodules, while the area that presents the lowest pearlite fraction was the one showing the lowest percentage of large nodules.
Unlike the previous work [
10], where only the graphite fraction in the central region was calculated, in this paper, the graphite fractions were experimentally measured and compared with the calculated results for the five nodes; see
Figure 9a. They showed good agreement. In
Figure 9b, the simulated ferrite fractions confirm to fit the experimental results in four of the five areas. The ferrite fractions were of vital importance when simulating the pearlite transformation, as they were an indication of the austenite fraction that is available for decomposing into pearlite.
Later, the interlaminar spacing was calculated and plotted in
Figure 10 at the end of the metastable transformation. As predicted by the theory, these measurements decreased as the undercooling increased.
Finally, the experimentally measured and the calculated pearlite fractions were correlated as shown in
Figure 11. Once more, they showed a good agreement except in the central area. On the other hand, concerning the experimental fractions, the difference between the maximum and minimum pearlite fractions was only 15.06%, whereas in case of simulated fractions—without taking into account the central node—the difference was 24%. In fact, these differences were within the expected standard deviations of the experimental results with respect to their mean value. As an example of the experimental measurement, a micrograph of the central section of the specimen is exposed in
Figure 12. It was decided to append only one since the experimental measurements do not significantly vary from one point to another in the specimen (
Figure 9 and
Figure 11).