Characterization of Deformation Mechanisms in Mg Alloys by Advanced Acoustic Emission Methods
Abstract
:1. Introduction
1.1. Magnesium Alloys
1.2. Acoustic Emission
2. Materials and Methods
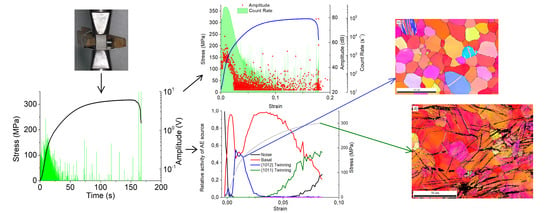
3. Results
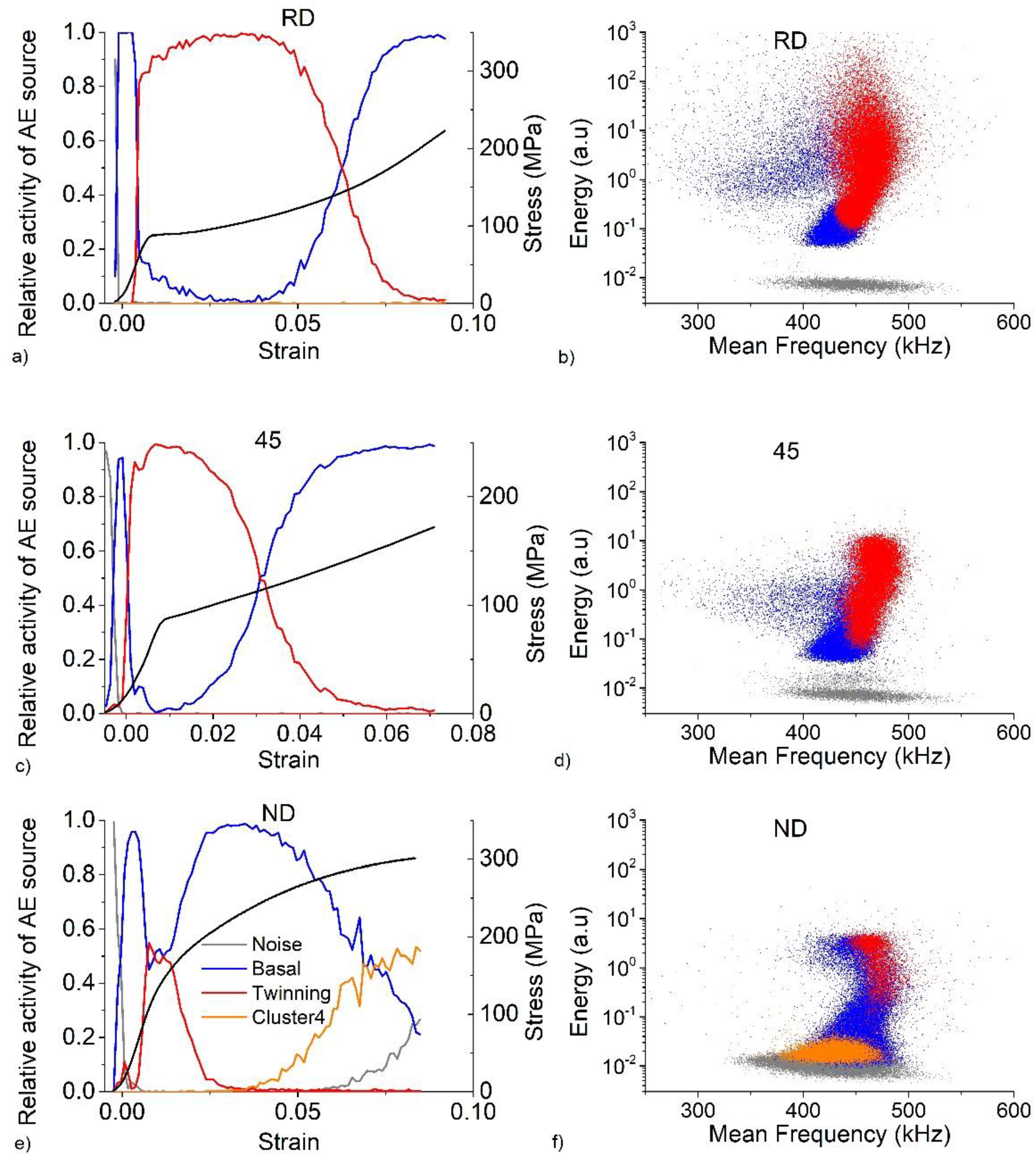
3.1. Hit-Based Evaluation
3.2. ASK Analysis
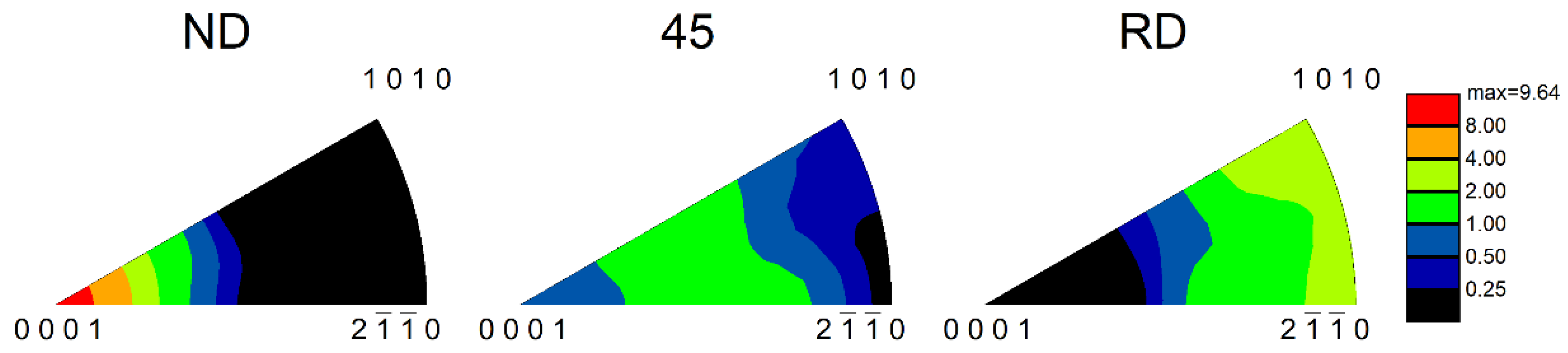
3.3. EBSD
4. Discussion
5. Conclusions
- Both methods were consistent for the RD and ND samples and successfully identified the deformation mechanisms which were shown to be the basal slip and deformation twinning. However, the 45 sample showed some differences. Additional experiments supported the conclusions of the ASK analysis.
- The ASK analysis together with microstructural observations identified an additional source of AE during the deformation of the ND sample, which was shown to be the double twinning.
- In this way, the ASK analysis proved to be a useful tool in discriminating between different sources of AE even if the classical hit-based approach reaches its limitations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nie, J.F.; Muddle, B.C. Characterisation of strengthening precipitate phases in a Mg–Y–Nd alloy. Acta Mater. 2000, 48, 1691–1703. [Google Scholar] [CrossRef]
- Janeček, M.; Král, R.; Dobroň, P.; Chmelík, F.; Šupík, V.; Holländer, F. Mechanisms of plastic deformation in AZ31 magnesium alloy investigated by acoustic emission and transmission electron microscopy. Mat. Sci. Eng. A-Struct. 2007, 462, 311–315. [Google Scholar] [CrossRef]
- Agnew, S.R.; Duygulu, O. Plastic anisotropy and the role of non-basal slip in magnesium alloy AZ31B. Int. J. Plast. 2005, 21, 1161–1193. [Google Scholar] [CrossRef]
- Christian, J.W.; Mahajan, S. Deformation Twinning. Prog. Mater. Sci. 1995, 39, 1–157. [Google Scholar] [CrossRef]
- Schmid, E.; Boas, W. Kristallplastizität (Struktur und Eigenschaften der Materie in Einzeldarstellungen), 1st ed.; Springer: Heidelberg/Berlin, Germany, 1935; p. 373. [Google Scholar]
- Huang, M.; Jiang, L.; Liaw, P.; Brooks, C.; Seelev, R.; Klarstrom, D. Using acoustic emission in fatigue and fracture materials research. JOM 1998, 50, 1–12. [Google Scholar]
- Chmelík, F.; Lukáč, P.; Janeček, M.; Moll, F.; Mordike, B.L.; Kainer, K.-U.; Langdon, T.G. An evaluation of the creep characteristics of an AZ91 magnesium alloy composite using acoustic emission. Mater. Sci. Eng. A 2002, 338, 1–7. [Google Scholar] [CrossRef]
- Lou, X.Y.; Li, M.; Boger, R.K.; Agnew, S.R.; Wagoner, R.H. Hardening evolution of AZ31B Mg sheet. Int. J. Plast. 2007, 23, 44–86. [Google Scholar] [CrossRef]
- Heiple, C.R.; Carpenter, S.H. Acoustic Emission Produced by Deformation of Metals and Alloys—A Review: Part I. J. Acoust. Em. 1987, 6, 177–204. [Google Scholar]
- Heiple, C.R.; Carpenter, S.H. Acoustic Emission Produced by Deformation of Metals and Alloys—A Review: Part II. J. Acoust. Em. 1987, 6, 215–237. [Google Scholar]
- Shashkov, I.V.; Lebedkina, T.A.; Lebyodkin, M.A.; Dobron, P.; Chmelik, F.; Kral, R.; Parfenenko, K.; Mathis, K. Acoustic-emission study of intermittency of plastic flow during twinning and dislocation glide. Acta Phys. Pol. A 2012, 122, 430–434. [Google Scholar] [CrossRef]
- Dobroň, P.; Bohlen, J.; Chmelík, F.; Lukáč, P.; Letzig, D.; Kainer, K.U. Acoustic emission during stress relaxation of pure magnesium and AZ magnesium alloys. Mat. Sci. Eng. A-Struct. 2007, 462, 307–310. [Google Scholar] [CrossRef] [Green Version]
- Chmelik, F.; Klose, F.B.; Dierke, H.; Sachl, J.; Neuhauser, H.; Lukac, P. Investigating the Portevin-Le Chatelier effect in strain rate and stress rate controlled tests by the acoustic emission and laser extensometry techniques. Mat. Sci. Eng. A Struct. 2007, 462, 53–60. [Google Scholar] [CrossRef]
- Scruby, C.; Wadley, H.; Sinclair, J.E. The origin of acoustic-emission during deformation of aluminum and an aluminum-magnesium alloy. Philos. Mag. A 1981, 44, 249–274. [Google Scholar] [CrossRef]
- Pomponi, E.; Vinogradov, A. A real-time approach to acoustic emission clustering. Mech. Syst. Sig. Process. 2013, 40, 791–804. [Google Scholar] [CrossRef]
- Vinogradov, A.; Lazarev, A.; Linderov, M.; Weidner, A.; Biermann, H. Kinetics of deformation processes in high-alloyed cast transformation-induced plasticity/twinning-induced plasticity steels determined by acoustic emission and scanning electron microscopy: Influence of austenite stability on deformation mechanisms. Acta Mater. 2013, 61, 2434–2449. [Google Scholar] [CrossRef]
- Chapuis, A.; Driver, J.H. Temperature dependency of slip and twinning in plane strain compressed magensium single crystals. Acta Mater. 2011, 59, 1986–1994. [Google Scholar] [CrossRef]
- Holt, J. Electronic noise in acoustic-emission measurements. Non-Destr. Test. 1976, 9, 66–70. [Google Scholar] [CrossRef]
- Drozdenko, D.; Bohlen, J.; Chmelík, F.; Lukáč, P.; Dobroň, P. Acoustic emission study on the activity of slip and twin mechanisms during compression testing of magnesium single crystals. Mat. Sci. Eng. A-Struct. 2016, 650, 20–27. [Google Scholar] [CrossRef] [Green Version]
- Mathis, K.; Capek, J.; Zdrazilova, Z.; Trojanova, Z. Investigation of tension-compression asymmetry of magnesium by use of the acoustic emission technique. Mat. Sci. Eng. A-Struct. 2011, 528, 5904–5907. [Google Scholar] [CrossRef]
- Mathis, K.; Csiszar, G.; Capek, J.; Gubicza, J.; Clausen, B.; Lukas, P.; Vinogradov, A.; Agnew, S.R. Effect of the loading mode on the evolution of the deformation mechanisms in randomly textured magnesium polycrystals—Comparison of experimental and modeling results. Int. J. Plast. 2015, 72, 127–150. [Google Scholar] [CrossRef]
- Vinogradov, A.; Vasilev, E.; Seleznev, M.; Máthis, K.; Orlov, D.; Merson, D. On the limits of acoustic emission detectability for twinning. Mater. Lett. 2016, 183, 417–419. [Google Scholar] [CrossRef]
- Barnett, M.R. Twinning and the ductility of magnesium alloys Part II. “Contraction” twins. Mat. Sci. Eng. A-Struct. 2007, 464, 8–16. [Google Scholar] [CrossRef]
- Lentz, M.; Risse, M.; Schaefer, N.; Reimers, W.; Beyerlein, I.J. Strength and ductility with {1011}—{1012} double twinning in a magnesium alloy. Nat. Commun. 2016, 7, 11068. [Google Scholar] [CrossRef] [PubMed]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čapek, J.; Knapek, M.; Minárik, P.; Dittrich, J.; Máthis, K. Characterization of Deformation Mechanisms in Mg Alloys by Advanced Acoustic Emission Methods. Metals 2018, 8, 644. https://doi.org/10.3390/met8080644
Čapek J, Knapek M, Minárik P, Dittrich J, Máthis K. Characterization of Deformation Mechanisms in Mg Alloys by Advanced Acoustic Emission Methods. Metals. 2018; 8(8):644. https://doi.org/10.3390/met8080644
Chicago/Turabian StyleČapek, Jan, Michal Knapek, Peter Minárik, Jan Dittrich, and Kristián Máthis. 2018. "Characterization of Deformation Mechanisms in Mg Alloys by Advanced Acoustic Emission Methods" Metals 8, no. 8: 644. https://doi.org/10.3390/met8080644
APA StyleČapek, J., Knapek, M., Minárik, P., Dittrich, J., & Máthis, K. (2018). Characterization of Deformation Mechanisms in Mg Alloys by Advanced Acoustic Emission Methods. Metals, 8(8), 644. https://doi.org/10.3390/met8080644