Constitutive Analysis on High-Temperature Flow Behavior of 3Cr-1Si-1Ni Ultra-High Strength Steel for Modeling of Flow Stress
Abstract
:1. Introduction
2. Approaches
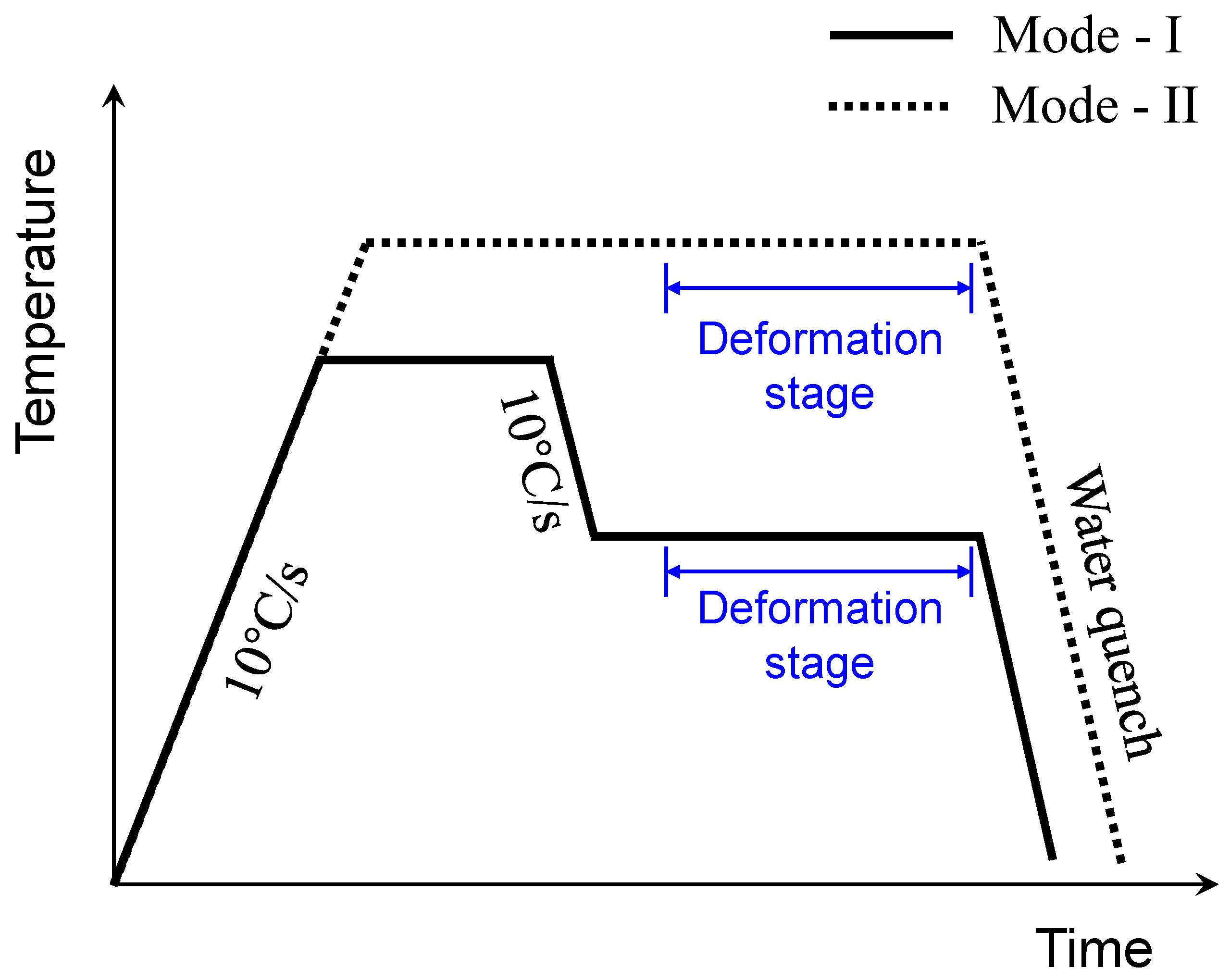
2.1. Experiments
2.2. Constitutive Model and Approaches to Determine the Constitutive Constants
3. Results and Discussion
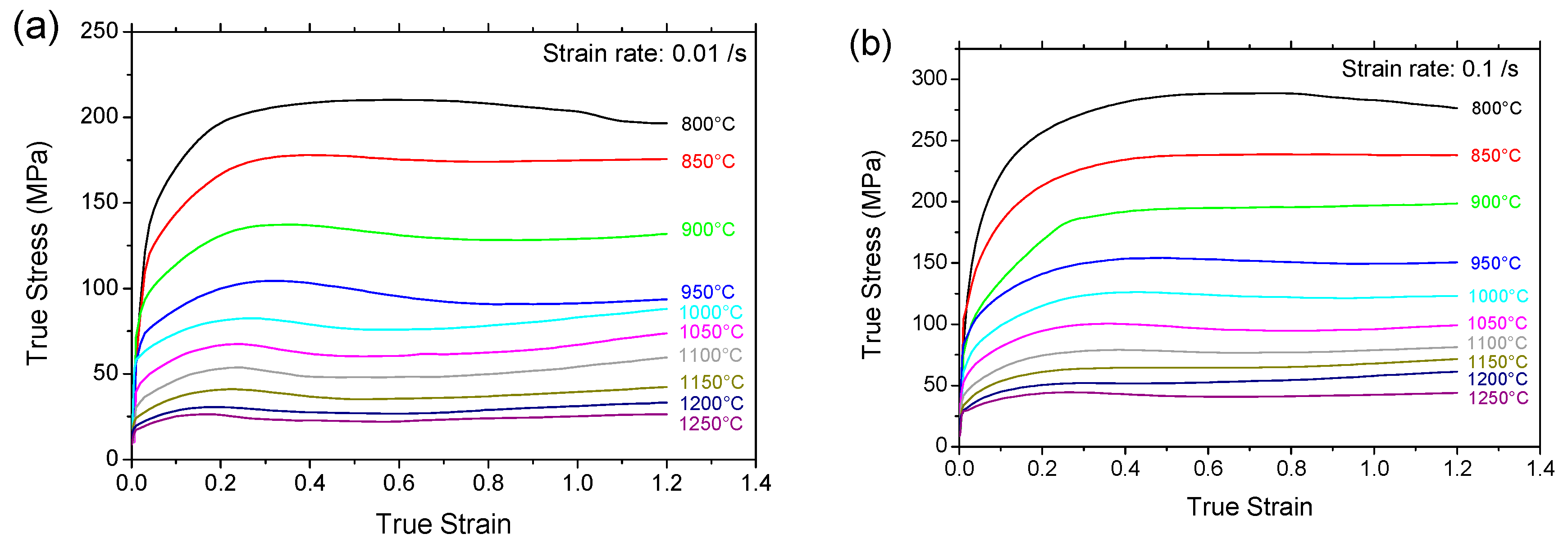
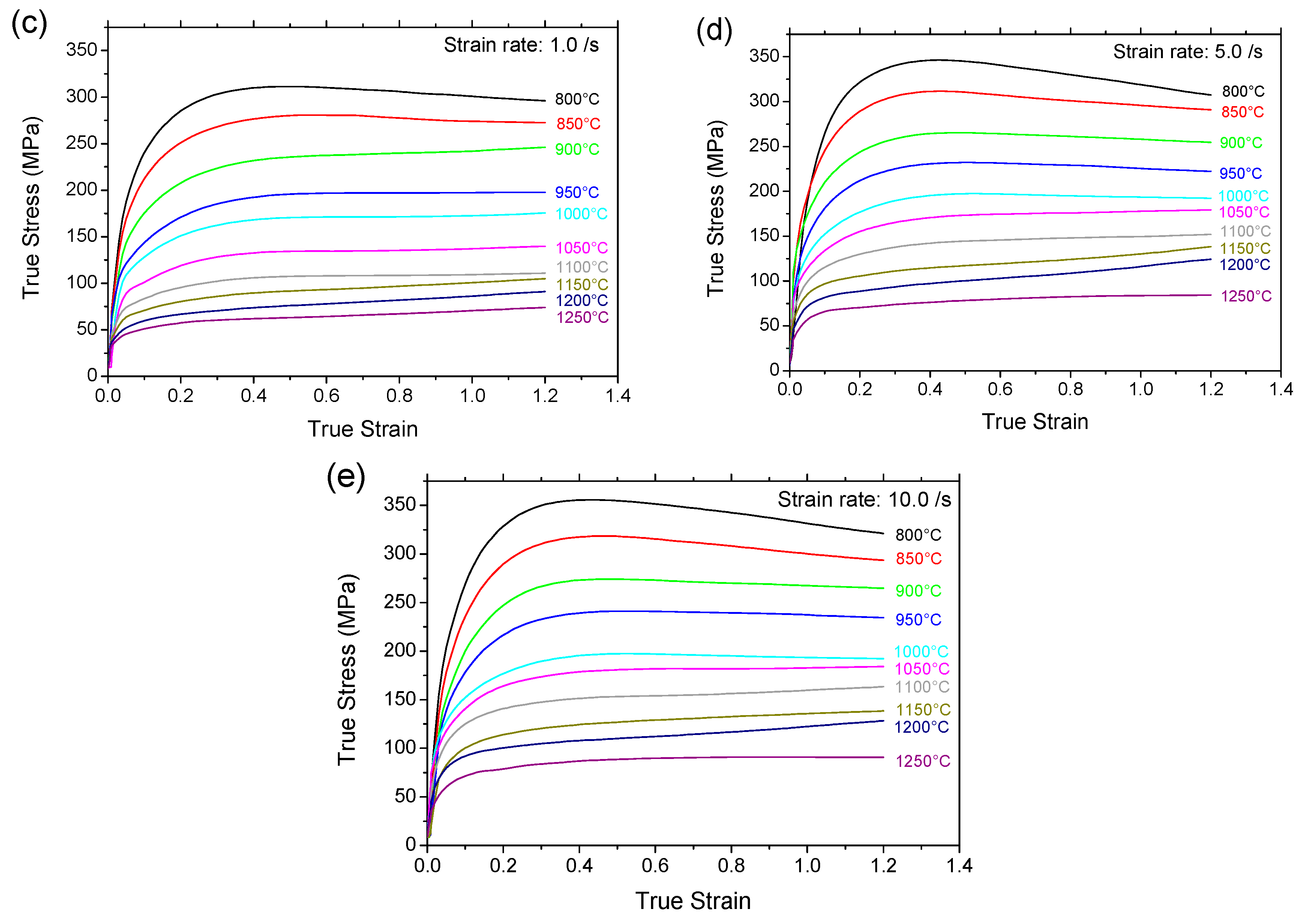
3.1. Measured Flow Stress
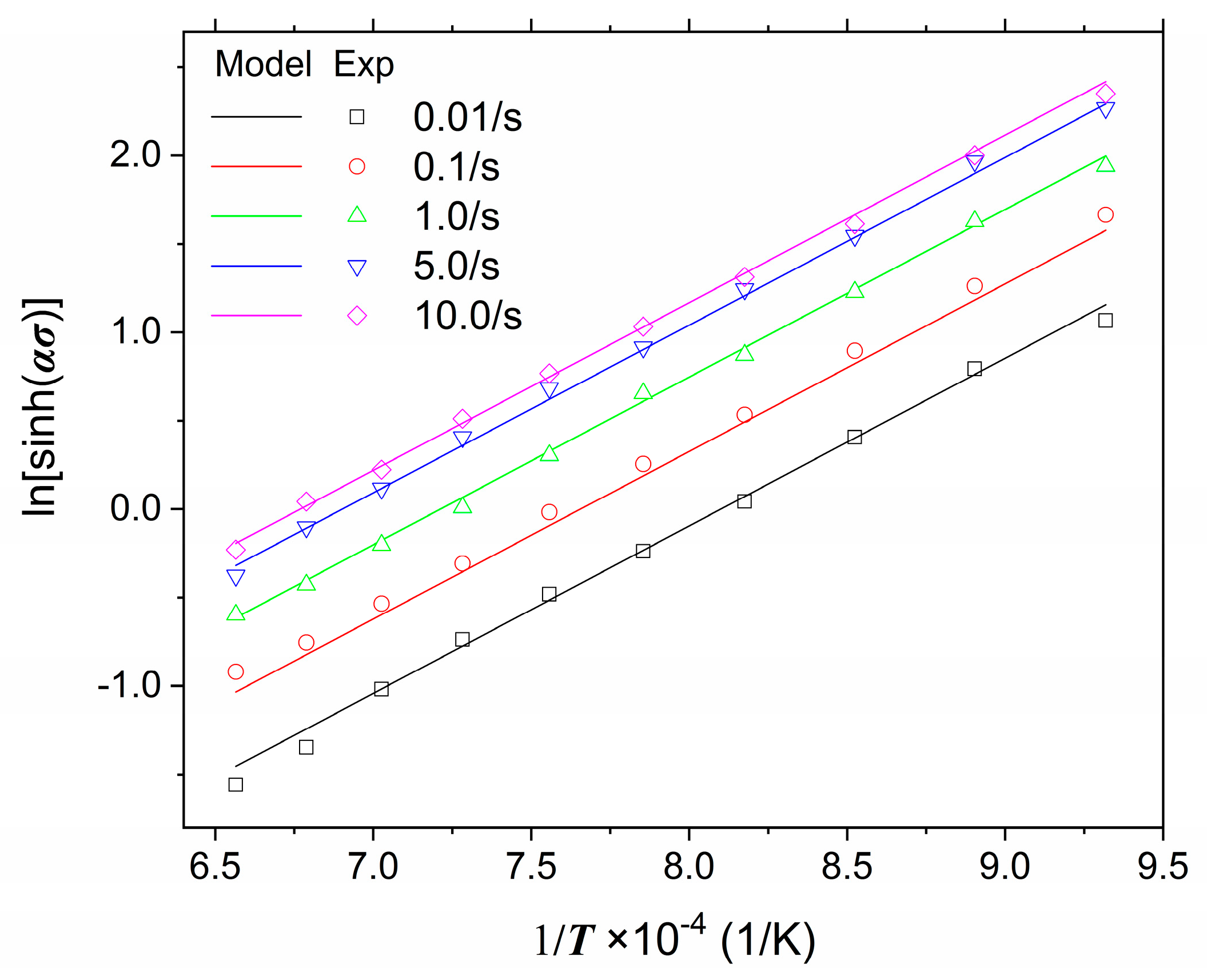
3.2. Determination of Constitutive Constants
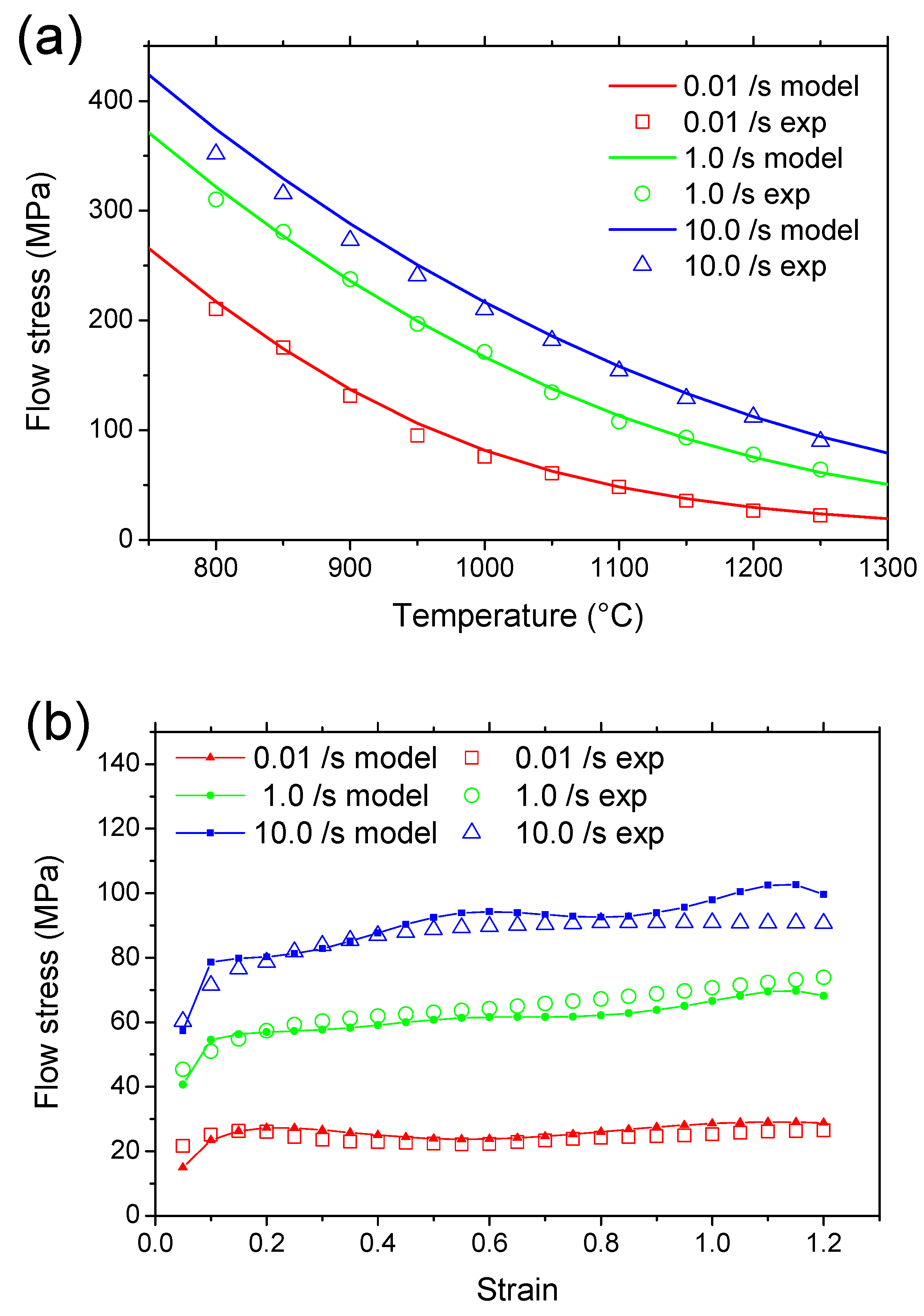
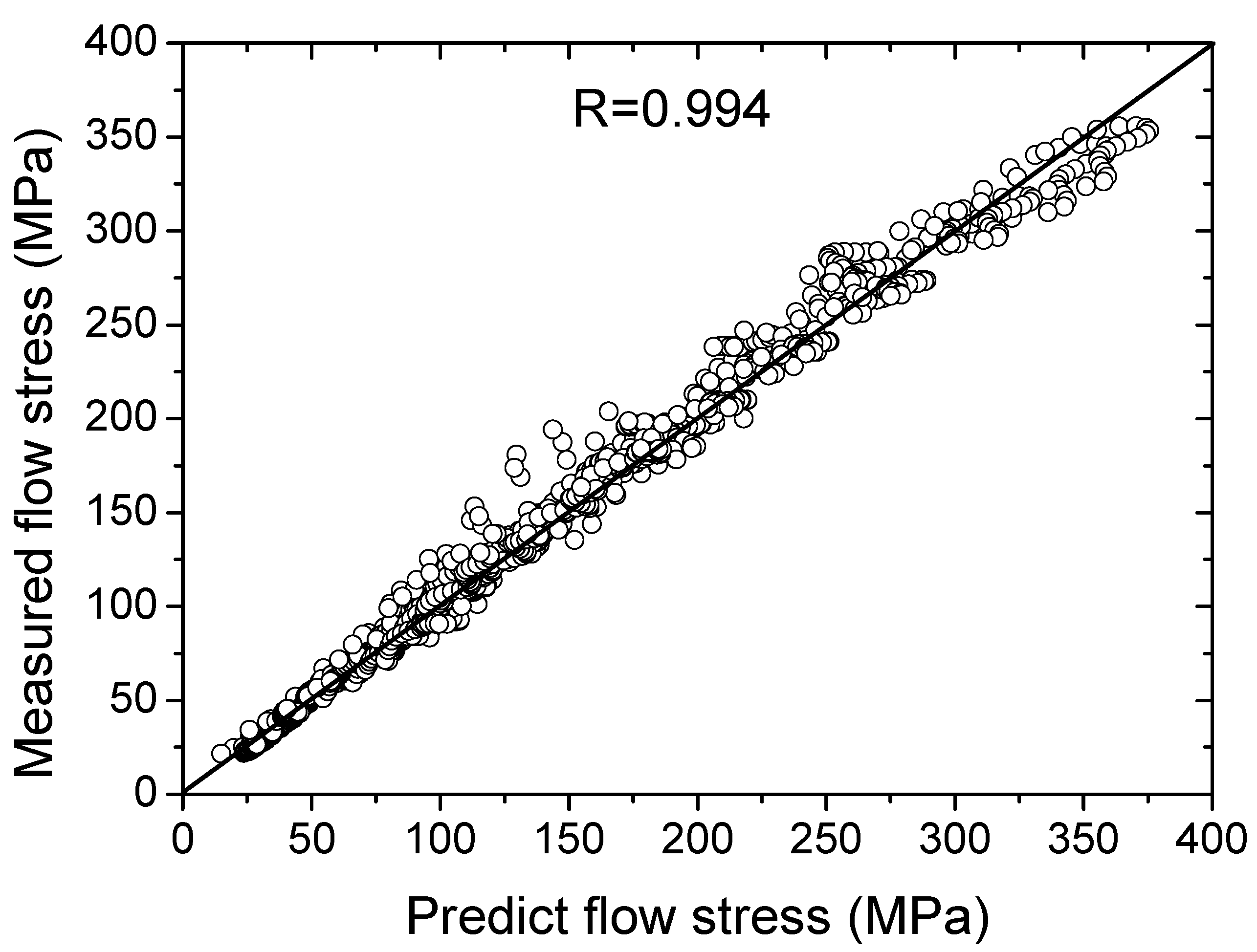
3.3. Verification of the Constitutive Equations
4. Conclusions
- (1)
- The exponent-type constitutive equation, in which the Zener-Hollomon parameter is used to represent the effect of temperature and strain rate on the flow stress. All the material constants are found to be significantly influenced by strain.
- (2)
- The influence of strain in the constitutive model is successfully implemented by introducing strain-dependent constants in the constitutive equations. Fifth-order polynomials are employed to represent the influence of strain on the constitutive constants.
- (3)
- The proposed constitutive equations which consider the compensation of strain is found to accurately predict flow stress. The constitutive equations have high accuracy and reliability, and can be applied to the field of numerical simulation for the related manufacturing processes.
Author Contributions
Funding
Conflicts of Interest
References
- Lee, H.H.; Yoon, J.I.; Kim, H.S. Single-roll angular-rolling: A new continuous severe plastic deformation process for metal sheets. Scr. Mater. 2018, 146, 204–207. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, G.; Chen, L. Analysis of longitudinal weld seam defects and investigation of solid-state bonding criteria in porthole die extrusion process of aluminum alloy profiles. J. Mater. Process. Technol. 2016, 237, 31–47. [Google Scholar] [CrossRef]
- Chen, J.; Fujii, H.; Sun, Y.; Morisada, Y.; Kondoh, K. Optimization of mechanical properties of fine-grained non-combustive magnesium alloy joint by asymmetrical double-sided friction stir welding. J. Mater. Process. Technol. 2017, 242, 117–125. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Shi, L.; Wu, C.S.; Gao, S.; Padhy, G.K. Modified constitutive equation for use in modeling the ultrasonic vibration enhanced friction stir welding process. Scr. Mater. 2016, 119, 21–26. [Google Scholar] [CrossRef]
- Tello, K.E.; Gerlich, A.P.; Mendez, P.F. Constants for hot deformation constitutive models for recent experimental data. Sci. Technol. Weld. Join. 2010, 15, 260–266. [Google Scholar] [CrossRef]
- McQueen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, G.; Yu, J.; Zhang, W. Constitutive analysis of homogenized 7005 aluminum alloy at evaluated temperature for extrusion process. Mater. Des. 2015, 66, 129–136. [Google Scholar] [CrossRef]
- Slooff, F.; Zhou, J.; Duszczyk, J.; Katgerman, L. Constitutive analysis of wrought magnesium alloy Mg–Al4–Zn1. Scr. Mater. 2007, 57, 759–762. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, M.-S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A. Constitutive analysis to predict high-temperature flow stress in modified 9Cr–1Mo (P91) steel. Mater. Des. 2010, 31, 981–984. [Google Scholar] [CrossRef]
- Shang, X.; He, A.; Wang, Y.; Yang, X.; Zhang, H.; Wang, X. Flow Behavior Modeling of a Nitrogen-Alloyed Ultralow Carbon Stainless Steel During Hot Deformation: A Comparative Study of Constitutive Models. J. Mater. Eng. Perform. 2015, 24, 4106–4118. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.; Prado, J.; Najafizadeh, A. Hot deformation behavior of a medium carbon microalloyed steel. Mater. Sci. Eng. A 2011, 528, 3876–3882. [Google Scholar] [CrossRef]
- Changizian, P.; Zarei-Hanzaki, A.; Roostaei, A.A. The high temperature flow behavior modeling of AZ81 magnesium alloy considering strain effects. Mater. Des. 2012, 39, 384–389. [Google Scholar] [CrossRef]
- Cai, Z.; Chen, F.; Guo, J. Constitutive model for elevated temperature flow stress of AZ41M magnesium alloy considering the compensation of strain. J. Alloys Compd. 2015, 648, 215–222. [Google Scholar] [CrossRef]
- Ciccarelli, D.; El Mehtedi, M.; Jäger, A.; Spigarelli, S. Analysis of flow stress and deformation mechanism under hot working of ZK60 magnesium alloy by a new strain-dependent constitutive equation. J. Phys. Chem. Solids 2015, 87, 183–195. [Google Scholar] [CrossRef]
- Trimble, D.; O’Donnell, G. Constitutive modelling for elevated temperature flow behaviour of AA7075. Mater. Des. 2015, 76, 150–168. [Google Scholar] [CrossRef]
- Li, J.-C.; Xie, Z.-Y.; Li, S.-P.; Zang, Y.-Y. Modeling on dynamic recrystallization of aluminium alloy 7050 during hot compression based on cellular automaton. J. Cent. South Univ. 2016, 23, 497–507. [Google Scholar] [CrossRef]
- Cai, J.; Li, F.; Liu, T.; Chen, B.; He, M. Constitutive equations for elevated temperature flow stress of Ti–6Al–4V alloy considering the effect of strain. Mater. Des. 2011, 32, 1144–1151. [Google Scholar] [CrossRef]
- Peng, X.; Guo, H.; Shi, Z.; Qin, C.; Zhao, Z. Constitutive equations for high temperature flow stress of TC4-DT alloy incorporating strain, strain rate and temperature. Mater. Des. 2013, 50, 198–206. [Google Scholar] [CrossRef]
- Xiao, Y.-H.; Guo, C.; Guo, X.-Y. Constitutive modeling of hot deformation behavior of H62 brass. Mater. Sci. Eng. A 2011, 528, 6510–6518. [Google Scholar] [CrossRef]
- Wang, Z.; Qi, L.; Zhou, J.; Guan, J.; Liu, J. A constitutive model for predicting flow stress of Al18B4O33w/AZ91D composite during hot compression and its validation. Comput. Mater. Sci. 2011, 50, 2422–2426. [Google Scholar] [CrossRef]
- Ahamed, H.; Senthilkumar, V. Hot deformation behavior of mechanically alloyed Al6063/0.75 Al2O3/0.75 Y2O3 nano-composite—A study using constitutive modeling and processing map. Mater. Sci. Eng. A 2012, 539, 349–359. [Google Scholar] [CrossRef]
- Zhu, R.; Liu, Q.; Li, J.; Xiang, S.; Chen, Y.; Zhang, X. Dynamic restoration mechanism and physically based constitutive model of 2050 Al–Li alloy during hot compression. J. Alloys Compd. 2015, 650, 75–85. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, G.; Chen, Q.; Han, F.; Zhao, Z. A physically-based constitutive modelling of a high strength aluminum alloy at hot working conditions. J. Alloys Compd. 2018, 743, 283–293. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of Strain Rate Upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Gao, S.; Wu, C.S.; Padhy, G.K.; Shi, L. Evaluation of local strain distribution in ultrasonic enhanced Al 6061-T6 friction stir weld nugget by EBSD analysis. Mater. Des. 2016, 99, 135–144. [Google Scholar] [CrossRef]
- Peng, X.K.; Wuhrer, R.; Heness, G.; Yeung, W.Y. Rolling strain effects on the interlaminar properties of roll bonded copper/aluminium metal laminates. J. Mater. Sci. 2000, 35, 4357–4363. [Google Scholar] [CrossRef]
- Arora, A.; Zhang, Z.; De, A.; Debroy, T. Strains and strain rates during friction stir welding. Scr. Mater. 2009, 61, 863–866. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A. A comparative study on Johnson Cook, modified Zerilli–Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr–1Mo steel. Comput. Mater. Sci. 2009, 47, 568–576. [Google Scholar] [CrossRef]
- Li, D.; Feng, Y.; Yin, Z.; Shangguan, F.; Wang, K.; Liu, Q.; Hu, F. Hot deformation behavior of an austenitic Fe–20Mn–3Si–3Al transformation induced plasticity steel. Mater. Des. 2012, 34, 713–718. [Google Scholar] [CrossRef]
- Chen, G.; Li, H.; Wang, G.; Guo, Z.; Zhang, S.; Dai, Q.; Wang, X.; Zhang, G.; Shi, Q. Effects of pin thread on the in-process material flow behavior during friction stir welding: A computational fluid dynamics study. Int. J. Mach. Tools Manuf. 2018, 124, 12–21. [Google Scholar] [CrossRef]
- Buffa, G.; Patrinostro, G.; Fratini, L. Using a neural network for qualitative and quantitative predictions of weld integrity in solid bonding dominated processes. Comput. Struct. 2014, 135, 1–9. [Google Scholar] [CrossRef]
- Shi, L.; Wu, C.S.; Sun, Z. An integrated model for analysing the effects of ultrasonic vibration on tool torque and thermal processes in friction stir welding. Sci. Technol. Weld. Join. 2017, 1–15. [Google Scholar] [CrossRef]
- Long, L.; Chen, G.; Zhang, S.; Liu, T.; Shi, Q. Finite-element analysis of the tool tilt angle effect on the formation of friction stir welds. J. Manuf. Process. 2017, 30, 562–569. [Google Scholar] [CrossRef]

| C | Mn | Si | S | P | Cr | Ni | Mo | Nb | W |
|---|---|---|---|---|---|---|---|---|---|
| 0.30 | 0.66 | 1.47 | 0.001 | 0.010 | 3.48 | 1.06 | 0.44 | 0.02 | 0.84 |
| Coefficients | Coefficients | Coefficients | Coefficients |
|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, B.; Chen, G.; Liu, K.; Wang, X.; Jiang, X.; Pan, J.; Shi, Q. Constitutive Analysis on High-Temperature Flow Behavior of 3Cr-1Si-1Ni Ultra-High Strength Steel for Modeling of Flow Stress. Metals 2019, 9, 42. https://doi.org/10.3390/met9010042
Lei B, Chen G, Liu K, Wang X, Jiang X, Pan J, Shi Q. Constitutive Analysis on High-Temperature Flow Behavior of 3Cr-1Si-1Ni Ultra-High Strength Steel for Modeling of Flow Stress. Metals. 2019; 9(1):42. https://doi.org/10.3390/met9010042
Chicago/Turabian StyleLei, Bingwang, Gaoqiang Chen, Kehong Liu, Xin Wang, Xiaomei Jiang, Jiluan Pan, and Qingyu Shi. 2019. "Constitutive Analysis on High-Temperature Flow Behavior of 3Cr-1Si-1Ni Ultra-High Strength Steel for Modeling of Flow Stress" Metals 9, no. 1: 42. https://doi.org/10.3390/met9010042
APA StyleLei, B., Chen, G., Liu, K., Wang, X., Jiang, X., Pan, J., & Shi, Q. (2019). Constitutive Analysis on High-Temperature Flow Behavior of 3Cr-1Si-1Ni Ultra-High Strength Steel for Modeling of Flow Stress. Metals, 9(1), 42. https://doi.org/10.3390/met9010042




