Dislocations Help Initiate the α–γ Phase Transformation in Iron—An Atomistic Study

Abstract

Using molecular dynamics simulation, we studied the influence of pre-existing dislocations on the austenitic and the martensitic phase transformations in pure iron. The simulations were performed in a thin-film geometry with (100) surfaces. We found that dislocations alleviate the transformation by lowering the austenitic transformation temperature and increasing the martensitic transformation temperature. In all cases, the new phase nucleates at the dislocations. The orientation relationships governing the nucleation process are dominated by the Burgers, Kurdjumov–Sachs, and Nishiyama–Wassermann pathways. However, upon growth and coalescence of the transformed material, the final microstructure consists of only few twinned variants separated by twin boundaries; this simple structure is dictated by the free surfaces which tend to form conserved planes under the transformation. After transformation, the material also contains abundant dislocations.

1. Introduction

The phase transformations of iron and steels are relevant in many areas of science and technology and have been studied intensely in the past [1,2,3]. Molecular dynamics (MD) simulation has contributed to the atomistic analysis of the processes occurring under the transformation, and several characteristics—such as the transformation pathway or the kinetics of the transformation—could be successfully analyzed [4,5,6]. Besides the thermally induced transformation, the effect of applied stresses was also studied [7,8,9,10], to analyze how and to what extent such stresses may trigger and influence the transformation.

While many available studies focus on the phase transformation behavior of ideal crystals of pure iron [11,12,13] or iron alloys [14,15,16,17], crystal defects may play a major role in the transformation behavior of iron. The influence of surfaces—in thin-film or nanowire geometries—was studied early on [5,18,19,20]. In addition, it was found that grain boundaries and phase boundaries may act as nucleation centers for the new phase [21,22], as well as planar defects [23].

The influence that dislocations exert on the transformation has been known for a long period of time. Fairly early on, Cahn [24] calculated—on the basis of an elastic model—that the low value of the nucleation energy around a dislocation favors heterogeneous phase nucleation in its vicinity; these results were corroborated later by Dollins [25]. More recently, Malygin [26] proposed a phenomenological model, in which the elastic energy of dislocations—in particular via their elastic strain field—influences the transformation temperature. Quite generally, Sharma et al. [27] report that the probability for phase nucleation during the austenitic transformation increases with the number of special orientation relationships available. Because a large number of orientation relationships are possible around the distorted cores of dislocations, we expect that dislocations may indeed alleviate the phase transformation process. However, this phenomenon appears to have been only little investigated in the past by MD simulations.

In this paper, we used MD simulation to study the influence of pre-existing dislocations on the thermally induced transformation behavior of pure iron. The use of the Meyer–Entel potential [14] allowed us to study both the austenitic and the martensitic transformation processes. By using a multitude of samples with varying dislocation densities, we could systematically study the influence of the dislocation density on the transformation temperatures.

2. Simulation Method

We modeled pure Fe using the Meyer–Entel interaction potential [14], as it implements the phase transition between the $\alpha$- and $\gamma$-phases of Fe [28]. It has been used repeatedly to study the atomistic details of the martensitic and austenitic transformations in Fe and Fe alloys [11,15,16,17,20,23,29]. The equilibrium transition temperature $T_c$ of the $\alpha$–$\gamma$ transition amounts to $550\pm 50$ K for this potential, as was determined by both free-energy calculations [18,28] and dynamic MD simulations [11,13].

This potential allows us to build both stable face-centered-cubic (fcc) and body-centered-cubic (bcc) crystals at the appropriate temperatures. For our simulations, we used cubic samples with a size of approximately 182 Å × 182 Å × 182 Å containing roughly 500,000 atoms (bcc sample) and 172 Å × 172 Å × 172 Å containing 432,000 atoms (fcc sample). The edges of the simulation box were aligned with the $\langle 100\rangle$ crystal axes. Periodic boundary conditions were applied in the x and y directions. In the z direction, free surfaces were introduced so as to implement a thin-film geometry.

For introducing dislocations into the crystal, we proceeded as follows. First, straight edge dislocations were introduced using the edge2 algorithm of the free software atomsk [30]. As a second step, these dislocations were relaxed by annealing at a high temperature. The fcc samples were annealed for 100 ps at 1000 K, while the bcc samples could only be heated up to 500 K without transforming; they were also annealed for 100 ps and then cooled back to 10 K. After relaxation, the initially straight edge dislocations had reacted with each other and formed a dislocation network. The dislocations were of a mixed type of edge and screw dislocation. During relaxation, the network lost around 50 % of its length both in the fcc and bcc crystallites.

We measured the dislocation density $\rho$ by dividing the total dislocation line length $L_{\mathrm{disl}}$ by the volume V of the sample:

$$\rho =\frac{L_{\mathrm{disl}}}{V}.$$

(1)

In total, we constructed 20 bcc and 20 fcc samples with various starting numbers of edge dislocations and various dislocation configurations. After annealing, the bcc crystals used for our simulations had dislocation densities of between $0.35\times {10}^{12}$ and $5.93\times {10}^{12}$ cm${}^{-2}$; as more dislocations can be introduced into fcc crystals, their $\rho$ value varied between $3.16\times {10}^{12}$ and $27.69\times {10}^{12}$ cm${}^{-2}$.

In Figure 1a,b, an example of a relaxed bcc sample with a dislocation density of $4.5\times {10}^{12}$ cm${}^{-2}$ is shown, and similarly in Figure 1c,d is an example of an fcc sample with a dislocation density of $13.56\times {10}^{12}$ cm${}^{-2}$.

The martensitic phase transformation was studied by cooling the fcc crystal from its start temperature of 1000 K down to almost 0 K. Analogously, the austenitic transformation was simulated by heating the bcc crystals from their starting temperature of 10 K up to 1300 K. In each case, the heating/cooling rate amounted to 1 K/ps. It is known [15] that simulated transformation temperatures depend on the heating/cooling rates applied; higher rates delay the transformation. From simulations of selected systems, we expected that this effect would change our results by around 30 K when reducing the rate by a factor of 10; for even smaller rates, the influence would become negligible. The occurrence of the phase transformation is monitored via the change of the system volume, or equivalently, by one of its edge lengths: a sudden jump in the volume identifies the transition temperature $T_c$ [21,22].

We performed the calculations using the open-source Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) code [31]. The temperature control was performed by using the Nose–Hoover thermostat [32,33]. During this process, we kept the pressure components in each Cartesian direction constant using a barostat. For the atomistic analysis, we used the free software tool Open Visualization Tool (OVITO) [34]. The local crystal structure was analyzed using the common-neighbor analysis [35,36]. For an analysis of the dislocation network, we used the dislocation extraction analysis algorithm (DXA) [37].

3. Results

Figure 2 displays how the phase-transformation temperature $T_c$ depends on the dislocation density. The austenitic temperature (Figure 2a) decreased from a value of 919 K for a dislocation-free crystal to values of 750 ± 50 K when $\rho$ reached a value of around $2\times {10}^{12}$ cm${}^{-2}$ and then stayed roughly constant. The observed spread in $T_c$ was caused by the statistical nature of the dislocation networks generated. The martensitic temperature (Figure 2b) rose from around 120 K for the lowest density studied, $3.16\times {10}^{12}$ cm${}^{-2}$, to around 180 K for the highest densities, $\rho >20\times {10}^{12}$ cm${}^{-2}$. We thus conclude that the presence of dislocations assists in inducing both martensitic and austenitic transformations.

Clearly, the austenitic temperature is always above the equilibrium transformation temperature of 550 K, and the martensitic temperature is always below it. We note that the equilibrium temperature is characterized by the fact that the free energies of the two phases are identical at this temperature. In a thermally induced transformation, the finite heating/cooling rate delays the transformation as a result of kinetic effects; this is not a simulation artifact—it also occurs in reality [38].

We note that the ideal fcc thin film—in the absence of any dislocations—does not transform at all. The occurrence of the transformation depends in particular on the surface orientation chosen and the thin-film thickness. In previous work [39], we showed that the martensitic transition temperature of ideal thin films decreases with the thin-film thickness, such that the transformation does not occur at all for films that are too thick; this is the case in the present study.

In Figure 2c,d, we plot the total potential energy of the defective crystals as a function of the dislocation density introduced. Clearly, larger defect densities lead to an increase in the potential energy. We note, however, that this increase is linear in the dislocation density for fcc crystals (Figure 2d), while it appears to saturate for bcc crystals. We suspect that the reason is that bcc crystals do not sustain as high defect densities as fcc crystals, such that further disordering of the crystal by introducing more dislocations cannot further increase the defect energy. This saturation aligns very satisfactorily with the saturation of the austenitic transition temperatures and suggests that the energy density stored in the dislocations is the dominant factor in determining the transition temperature.

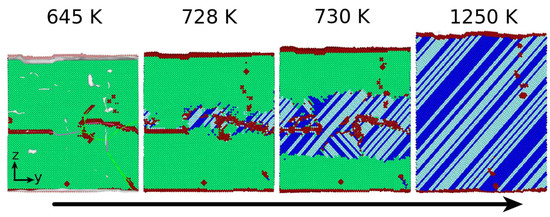
3.1. The Austenitic Transformation

As a reference case, we first study the transformation of a dislocation-free sample. Figure 3 shows that the new phase nucleates at the free surfaces of the thin film and grows from there into the interior. The final structure is an almost defect-free fcc crystallite; only a band of hcp-phase material runs along a $\left\{111\right\}$ plane through the fcc material. We note that the energetic difference between fcc- and hcp-phases in the Meyer–Entel potential is small [13,40]. The emergence of both close-packed phases, fcc and hcp, is well known from simulational studies of the austenitic transformation in Fe [8,9,41]. We therefore denote the occurrence of either of the phases, fcc and hcp, as ‘close-packed’ (cp). The transition temperature amounts to $T_c=918$ K. We note that the transformation proceeds quickly and is terminated within 10 ps.

Next we discuss the case of a small dislocation density, $1.72\times {10}^{12}$ cm${}^{-2}$. Figure 4 shows how the transformation proceeds. In contrast to the dislocation-free case, the transformation does not start at the free surfaces, but in the crystal interior. Indeed, the new phase nucleates at the dislocations at a temperature of 728 K and grows from there towards the surfaces, as seen in the snapshot at 730 K, until the entire specimen has transformed. The transformation took more time, 20 ps, to complete; however, it occurred already at a lower temperature, 730 K. A higher fraction of the hcp-phase was generated than in the dislocation-free case.

Finally, Figure 5 shows the transformation in a sample containing a high dislocation density, $4.5\times {10}^{12}$ cm${}^{-2}$; in this case, we show views on the cp ${\left(110\right)}_{\mathrm{bcc}}$ plane. In Figure 5a, the dislocations running through the initial bcc specimen are clearly observed. Upon the start of the transformation (Figure 5b), a cp nucleus forms in the region of high dislocation density. Figure 5d highlights this region by removing all original bcc atoms from the plot. We see that the nucleus is indeed plate-like and is bounded by dislocation lines.

The final structure of the sample (Figure 5c) looks similar to the previous cases; however, several defects—recognizable as ‘unidentified atoms’—remain in the structure. We discuss in Section 3.3 below that these consist mainly of dislocations in the transformed phase.

The transition temperature amounts to 768 K, a similar value as in the case discussed in Figure 4. However, the transformation needs considerably more time, 145 ps. The transformation does not proceed continuously; the creation of the planar nuclei takes 90 ps, but their growth is inhibited for another 40 ps, before the final coalescence of the grown nuclei is completed quickly, within 15 ps. Correspondingly, the temperature interval during which the transformation proceeds is broad; the first planar nuclei are observed at 625 K, while the coalescence process occurs at 768 K. This latter temperature was taken as the transition temperature in this case.

Dislocations act as nucleation centers for the creation of the new phase. Figure 6a demonstrates this for the case of the austenitic transformation.

We study the transformation path for the example of Figure 4: $\rho =1.72\times {10}^{12}$ cm${}^{-2}$. It is analyzed in Figure 7, which shows a view on the ${\left(0\overline{1}1\right)}_{\mathrm{bcc}}\parallel {\left(0001\right)}_{\mathrm{hcp}}$ plane. In this plane, the ${\left[\overline{1}11\right]}_{\mathrm{bcc}}$ direction transforms into the ${\left[11\overline{2}0\right]}_{\mathrm{hcp}}$. We also note that every second ${\left(0001\right)}_{\mathrm{hcp}}$ plane is shifted in the ${\left[1\overline{1}0\right]}_{\mathrm{bcc}}$ direction. This process leads to the stacking sequence typical of the hcp structure. The transformation fulfils the Burgers orientation relationship [42]:

$$\begin{array}{c}{\left(0\overline{1}1\right)}_{\mathrm{bcc}}\parallel {\left(0002\right)}_{\mathrm{hcp}},{\left[\overline{1}11\right]}_{\mathrm{bcc}}\parallel {\left[11\overline{2}0\right]}_{\mathrm{hcp}}.\hfill \end{array}$$

(2)

This is the bcc–hcp analogue to the Kurdjumov–Sachs pathway [43].

We note that in this transformation, the ${\left(001\right)}_{\mathrm{bcc}}$ surface plane is not conserved. However, after completion of the transformation, the surface plane, ${\left(001\right)}_{\mathrm{bcc}}$, transforms into the ${\left(001\right)}_{\mathrm{fcc}}$ plane. This is shown in Figure 7b,c. The ${\left[100\right]}_{\mathrm{bcc}}$ direction transforms into the ${\left[110\right]}_{\mathrm{fcc}}$ direction, the ${\left[010\right]}_{\mathrm{bcc}}$ direction into the ${\left[1\overline{1}0\right]}_{\mathrm{fcc}}$ direction. This is the classical Bain orientation relationship [44]. The Bain orientation relationship can be written as

$${\left(001\right)}_{\mathrm{fcc}}\parallel {\left(001\right)}_{\mathrm{bcc}}\mathrm{and}{\left[110\right]}_{\mathrm{fcc}}\parallel {\left[100\right]}_{\mathrm{bcc}}.$$

This transformation favors fcc as the transformed phase, while the local nucleation process favored the hcp-phase. Indeed, for this example, the transformed material contained only around 30% fcc-phase after nucleation; the fraction increased to 55% after completion of the transformation. We conclude that while dislocations act as nucleation centers and their presence decreases the transition temperature, the growth of the transformed phase is governed by the boundary conditions of the specimen—in this case by the surfaces.

3.2. The Martensitic Transformation

We study the martensitic phase transformation for the representative example of a dislocation density of $\rho =10.34\times {10}^{12}$ cm${}^{-2}$. Figure 8a shows the temporal evolution of the system temperature during the phase transformation. Because we applied a thermostat cooling with 1 K/ps, we expected a linearly decreasing temperature. Instead, the system heated up during the transformation; this is the signature of the latent heat of transformation that is liberated during the transition. Initially, the temperature rose fairly steadily, indicating a rapid transformation; the ensuing temperature fluctuations indicated the discontinuous evolution of the transformation where martensite growth alternated with phases where the growth was halted. The completion of the transition was signaled by the linear temperature decrease at late times.

We note that the entire transformation took a time of around 50 ps. This was somewhat slower than in previous studies of martensitic transformations in systems of a similar size: 10–20 ps for the evolution at a flat $\alpha$–$\gamma$ phase boundary [45], and 34 ps for the transformation in the vicinity of a grain boundary [21]. Evidently, the multitude of nucleation centers at dislocations and the irregular shape of the dislocation cores preclude a swift growth of the martensite phase.

As mentioned above, an ideal dislocation-free crystal will not transform; in other words, neither does the surface help to nucleate the new phase nor do we observe homogeneous nucleation in the bulk. As soon as dislocations are present, these act as nucleation centers. This is demonstrated in Figure 6b, which shows the martensite phase at the beginning of the transformation process, at the time corresponding to Figure 8c; the new phase directly follows the dislocation cores.

In Figure 8a, several instances of time are marked, and the transformation was monitored in the snapshots provided in Figure 8b–f. The transformation was not homogeneous but started at the dislocations; nuclei were created at several times and at several places (Figure 8b,c). Growth of the nuclei is observed in Figure 8d; in Figure 8e,f, the transformed grains start coalescing, forming a large number of grain boundaries. However, these finally coalesce, and the final state of the transformed specimen displayed in Figure 8g shows a simplified microstructure characterized by a few columnar grains, separated by twin boundaries.

In Figure 9, we look into the atomistic details of the transformation that allow us to discuss the orientation relationships obeyed. Figure 9a zooms into the transformation at the time corresponding to Figure 8e; the top left part of the figure is shown in an enlarged and rotated view. It provides a view on a ${\left(111\right)}_{\mathrm{fcc}}$ plane that is transforming to the ${\left(110\right)}_{\mathrm{bcc}}$ plane. The white arrows highlight the cp ${\left[\overline{1}10\right]}_{\mathrm{fcc}}$ direction that is transformed into the ${\left[\overline{1}11\right]}_{\mathrm{bcc}}$ direction. This conserved plane and directions signal the orientation relationships of the Kurdjumov–Sachs pathway [43]:

$${\left(111\right)}_{\mathrm{fcc}}\parallel {\left(110\right)}_{\mathrm{bcc}},$$

$${\left[10\overline{1}\right]}_{\mathrm{fcc}}\parallel {\left[11\overline{1}\right]}_{\mathrm{bcc}}\mathrm{or}{\left[01\overline{1}\right]}_{\mathrm{fcc}}\parallel {\left[1\overline{1}\overline{1}\right]}_{\mathrm{bcc}}.$$

The existence of two variants provides for the building of twin structures by the transformation. Their occurrence is marked in Figure 9a. The twin boundaries correspond to the ${\left[1\overline{1}2\right]}_{\mathrm{bcc}}$ plane.

We find these Kurdjumov–Sachs orientation relationships obeyed in most material nucleated in the vicinity of the dislocations; occasionally, the Nishiyama–Wassermann orientation relationships [46,47] are also encountered:

$${\left(111\right)}_{\mathrm{fcc}}\parallel {\left(110\right)}_{\mathrm{bcc}}\mathrm{and}{\left[11\overline{2}\right]}_{\mathrm{fcc}}\parallel {\left[01\overline{1}\right]}_{\mathrm{bcc}}.$$

While the local nuclei lead to the observation of Kurdjumov–Sachs and Nishiyama–Wassermann orientation relationships, the final structure of the new phase is governed by a different principle based on the proposition that the free surface of the thin film must be conserved over the transformation [39]. We call, for simplicity, the final evolving structure the ‘global phase’, as it will eventually cover all of the thin film and was encountered in all cases studied here irrespective of the initial dislocation density. We provide more details in Figure 9b. It shows the processes occurring after the bcc-phase that grows from the bottom surface upwards—the global phase—encounters the transformed material in about the middle of the thin film; this snapshot corresponds to a time intermediate between Figure 8e,f. When colliding with the nanotwinned microstructure building around the dislocations, the growth of the variants aligning with the global phase is favored, while the variants, which are not in registry with it, shrink. This encounter is highlighted by the red arrows in Figure 9b.

At the end of this process, the nanotwinned structure vanished, and only four twins remained; this happened for all 20 crystallites investigated by us. To understand the orientation relationships of the global phase, we compare in Figure 9c,d the orientation relationships between the sample before and after the phase transformation. These fulfil the Pitsch orientation relationships [48]:

$${\left(001\right)}_{\mathrm{fcc}}\parallel {\left(1\overline{1}0\right)}_{\mathrm{bcc}}\mathrm{and}{\left[110\right]}_{\mathrm{fcc}}\parallel {\left[111\right]}_{\mathrm{bcc}}.$$

The occurrence of the Pitsch orientation relationships was caused by our choice of free surfaces for the thin film studied; as they were ${\left(001\right)}_{\mathrm{fcc}}$ planes, the transformation attempted to conserve these planes. As a result, the transformed film had ${\left(110\right)}_{\mathrm{bcc}}$ surfaces. Figure 9b,c verifies this behavior: the ${\left(001\right)}_{\mathrm{fcc}}$ plane is transformed into the ${\left(1\overline{1}0\right)}_{\mathrm{bcc}}$ plane and the ${\left[110\right]}_{\mathrm{fcc}}$ direction into the ${\left[111\right]}_{\mathrm{bcc}}$ direction. Additionally, the resulting twin structure is typical of the Pitsch transformation. In our case, we observed the occurrence of four ${\left(11\overline{2}\right)}_{\mathrm{bcc}}$ twin boundaries.

We conclude that while the local transformations starting at the nuclei at the dislocations obey mostly Kurdjumov–Sachs (and in some cases Nishiyama–Wassermann) orientation relationships, the final structure of the thin film is governed by the surface orientation of the thin film and follows the Pitsch path. When the transformation is completed, the complex microstructure resulting from the multiple nuclei is simplified, and a simple microstructure consisting of twins remains. We note that in all the 20 samples that we studied, the final structure of the sample was always the same: the surface was a ${\left(1\overline{1}0\right)}_{\mathrm{bcc}}$ plane, as is characteristic for the Pitsch path, and the microstructure showed the twins characteristic for this path.

3.3. Dislocations in the Transformed Phase

After completion of the transformation, dislocations were also present in the material. Figure 10a shows that after the austenitic transformation, the dislocation density in fact had grown. Figure 10b,c compares the dislocation network before and after the transformation for a representative example, $\rho =3.63\times {10}^{12}$ cm${}^{-2}$. During the martensitic transformation, on the other hand, the dislocation density shrinked (Figure 11a). An example for a representative case, $\rho =10.34\times {10}^{12}$ cm${}^{-2}$, is provided in Figure 11b,c. The difference between the two transformations suggests that fcc crystals can host a higher dislocation density than bcc crystals.

During the austenitic transformation, in some cases, we observed that the dislocations generated were organized in grain boundaries. These cases are marked in Figure 10a. These were cases in which excessively high values of dislocation densities were generated.

When comparing in detail the structures of the dislocation networks before and after the transformations, one can observe similarities in the dislocation structures. For the austenitic transformation, Figure 10b,c exemplifies that at places where initially dislocations were absent, the transformed crystal shows no dislocations either. Newly generated dislocations appeared primarily in regions which were already, in the bcc-phase, filled with dislocations. As fcc crystals sustain higher dislocation densities, these plastically deformed regions featured, after transformation, a highly plastified fcc crystallite. One particular example, for which an original dislocation appeared to have been transferred as an individual entity in the transformed crystal, is marked as the middle circle in Figure 10b,c; the Burgers vector changed from $1/2{\langle 111\rangle }_{\mathrm{bcc}}$ to $1/2{\langle 110\rangle }_{\mathrm{fcc}}$.

Because the density of dislocations is increasing during an austenitic transformation, one may wonder whether the energy needed for dislocation creation will not impede the phase transformation. Indeed, as Figure 2a shows, the austenitic transformation temperature stagnates for dislocation densities above $2\times {10}^{12}$ cm${}^{-2}$. This is in contrast to the martensitic transformation, for which dislocations are destroyed during the transformation and hence no energy needs be dispensed in generating dislocation structures.

4. Conclusions

Using MD simulation, we studied the influence of pre-existing dislocations on the martensitic and austenitic phase transformations in pure iron. The simulations were performed in a thin-film geometry with (100) surfaces. We found the following results.

• The presence of dislocations alleviates the transformation in the sense that the martensitic transformation temperature is increased and the austenitic transformation temperature is decreased. For the martensitic transformation, a dislocation-free crystal would not transform at all under the simulation conditions (system size and cooling rate); here the presence of dislocations is essential in inducing the transformation.
• For the martensitic transformation, a roughly linear dependence of the transformation temperature on the dislocation density was found. For the austenitic transformation, on the other hand, a saturation of the transformation temperature at dislocation densities above around $\rho =2\times {10}^{12}$ cm${}^{-2}$ was observed. These trends correlate well with the potential energy stored in the dislocations, which exhibits the same dependence on dislocation energy as the transition temperature.
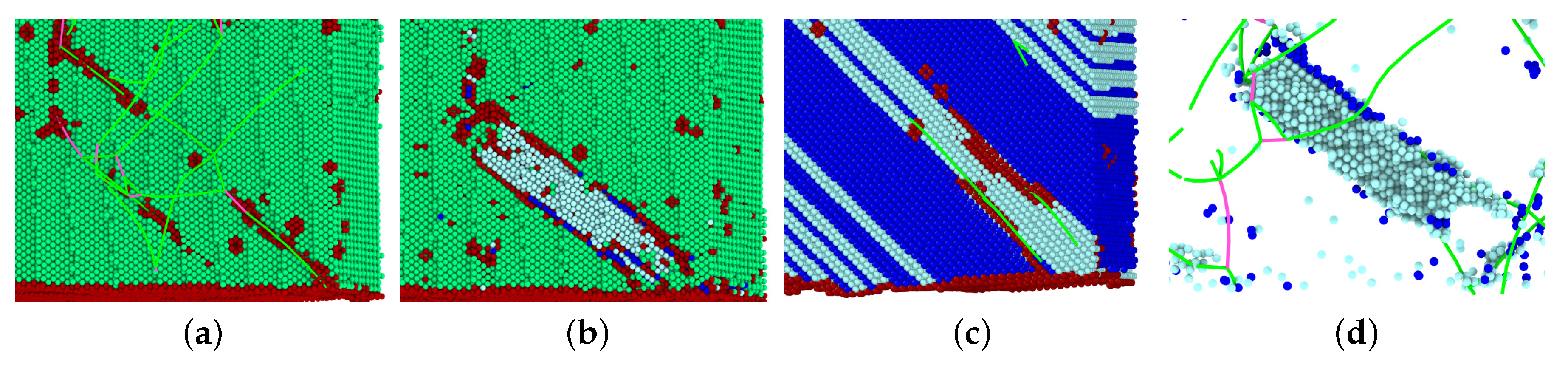
• In all cases, the new phase nucleated at the dislocations. In the absence of dislocations, the new phase would nucleate at the surface (if at all). Nucleation at the dislocations is in agreement with previous MD findings for NiAl alloys [49], which show that the lattice distortion induced by the stress exerted by the dislocation configurations assists in the nucleation of the new phase, and also with other studies of defective pure Fe crystals that report phase nucleation in the vicinity of defects, such as grain boundaries [21] and phase boundaries [22]. However, Karewar et al. [23] found a more complex nucleation pattern in their study of the influence of planar defects on the martensitic transformation, depending on the resolved shear stresses in the available slip systems; depending on the configuration of the planar defects, these may increase or decrease the barrier for slip and hence for the coordinated atomic movement necessary for the martensitic transformation.
• The orientation relationships governing the transformation in the nuclei at the dislocations are governed by the Burgers path and the Kurdjumov–Sachs and Nishiyama–Wassermann paths; these pathways have also been identified to dominate the transformation behavior of pure iron in other simulational studies [50]. However, when, after growth and coalescence of the nuclei, the entire sample has transformed, a simple microstructure results. After the martensitic transformation, the bcc-phase is characterized by a homogeneous phase consisting of only few twinned grains separated by twin boundaries; the austenitic phase, on the other hand, is single-crystalline, containing planar defects such as stacking-fault planes and plates of hcp material. This simple microstructure is the consequence of the free surfaces of the thin film, which tend to form conserved planes under the transformation [39]. As a consequence, the final orientation relationships of the transformed sample are characterized by the Bain and the Pitsch pathway.
• While the new phase nucleates earlier when dislocations are present, the duration of the transformation is slowed down, as multiple nuclei compete in their growth.
• The transformed crystal contains abundant dislocations. The dislocation density becomes reduced in the case of the martensitic transformation but may even increase during the austenitic transformation. A detailed analysis demonstrates that the dislocations in the novel structure are ‘inherited’ from the original phase.