Spreading Process Maps for Powder-Bed Additive Manufacturing Derived from Physics Model-Based Machine Learning
Abstract
1. Introduction
1.1. Powder Spreading Studies
1.2. AM Machine Learning Studies
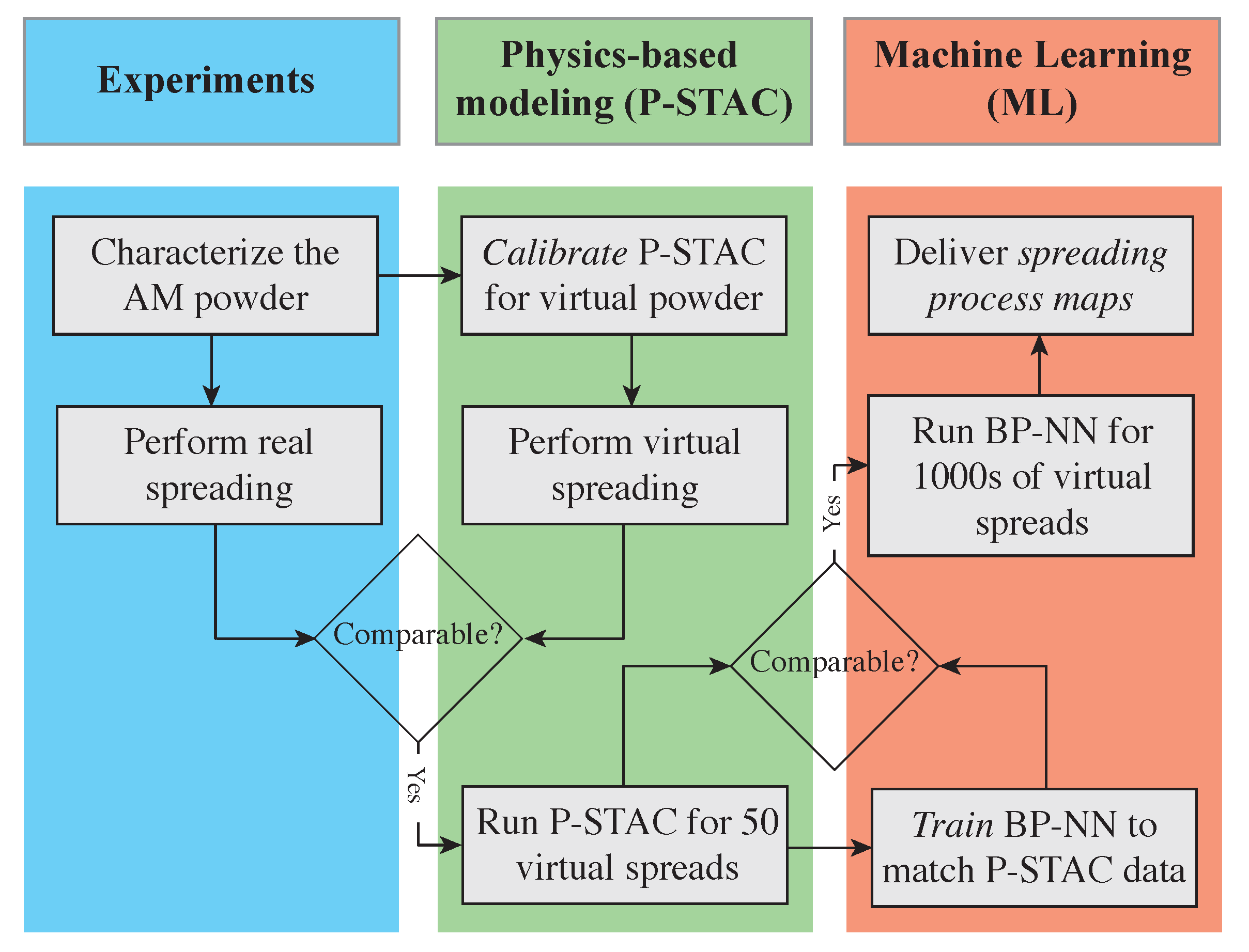
2. Methodology
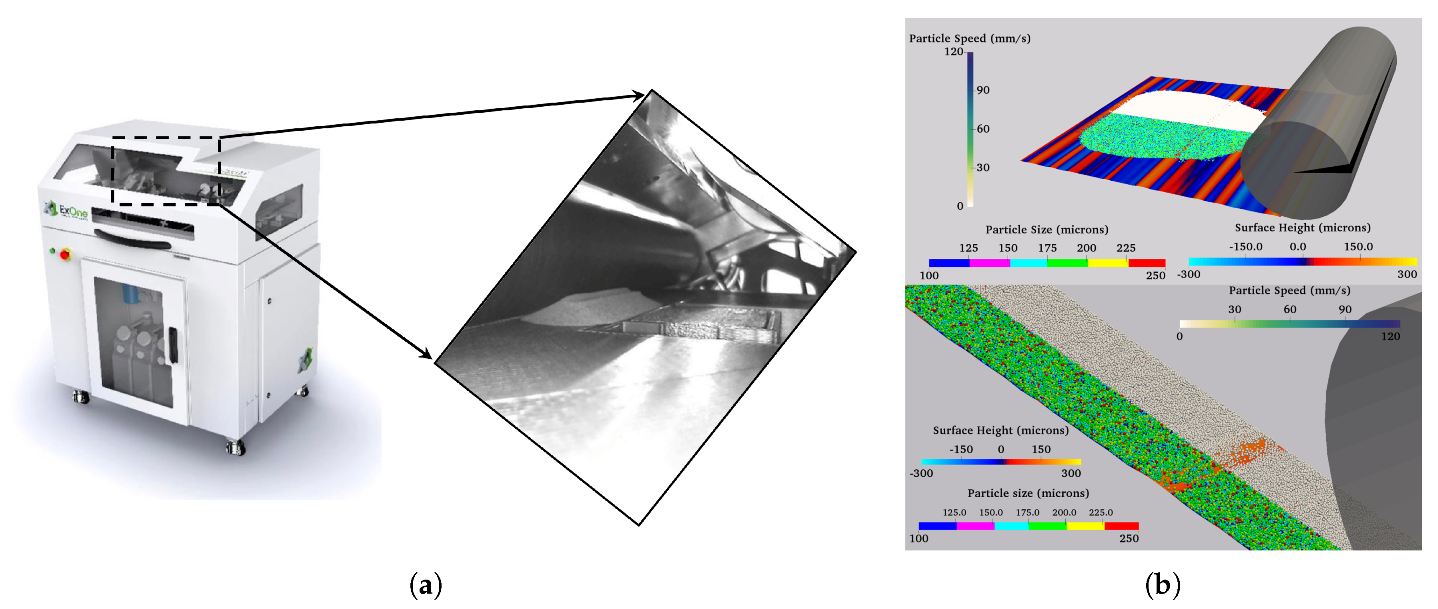
2.1. Physics-Based Polydispersed DEM Model
Spread Layer Characterization
2.2. Design of Simulations for Virtual Spreading
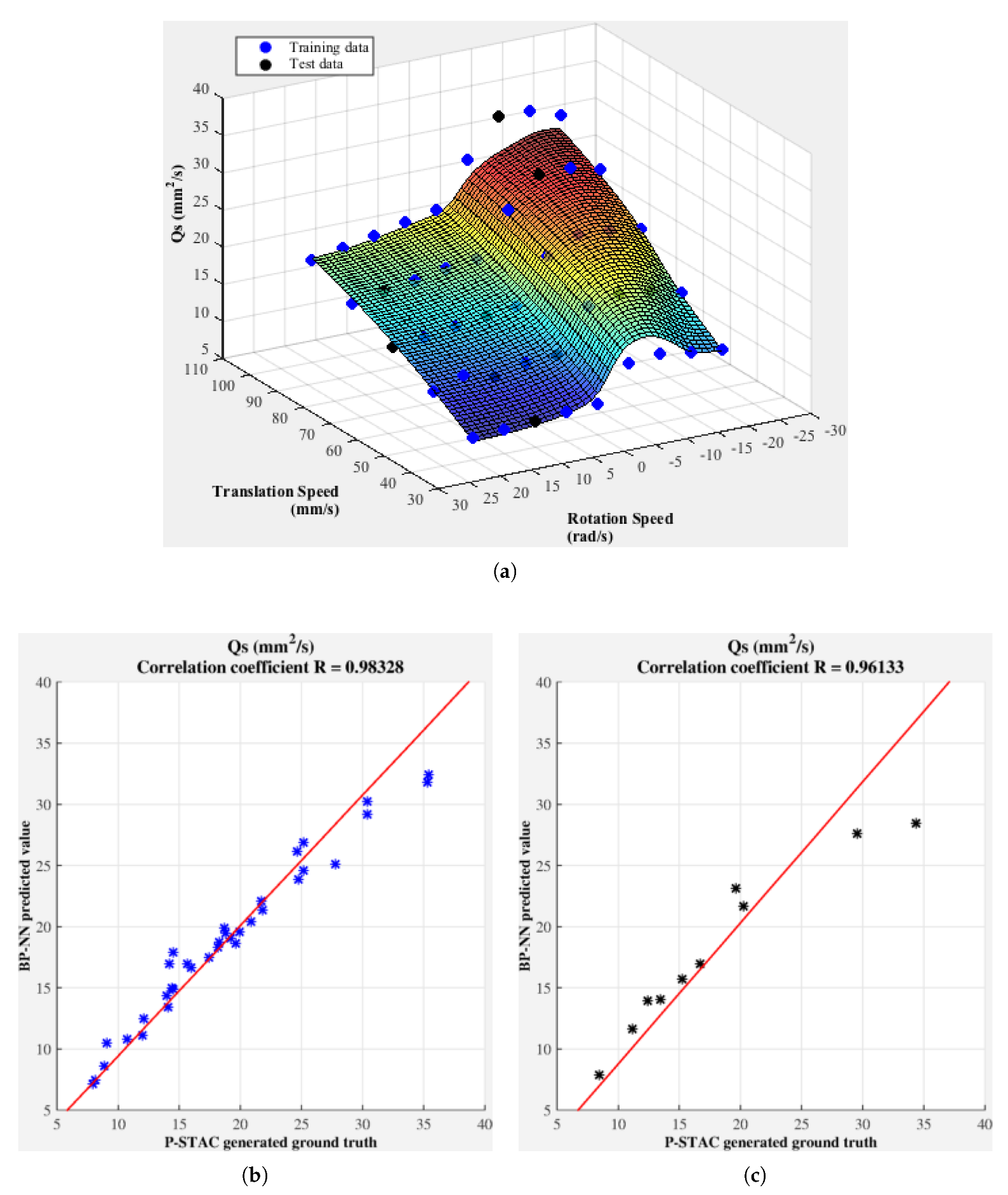
2.3. Physics Model-Based Machine Learning Enabled Surrogate Model
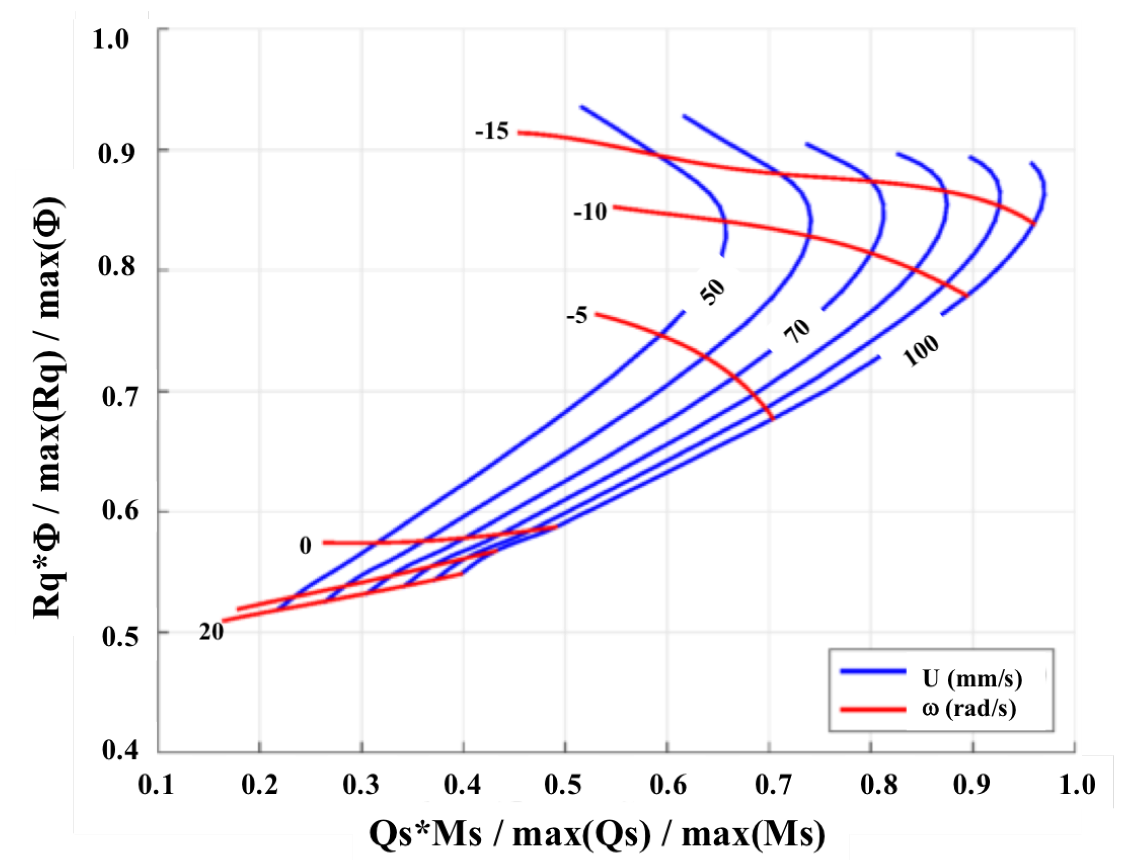
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Frazier, W.E. Metal additive manufacturing: A review. J. Mater. Eng. Perform. 2014, 23, 1917–1928. [Google Scholar] [CrossRef]
- ASTM International. ASTM Committee F42 on Additive Manufacturing Technologies; Subcommittee F42. 91 on Terminology. Standard Terminology for Additive Manufacturing Technologies; ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Snow, Z.; Martukanitz, R.; Joshi, S. On The Development of Powder Spreadability Metrics and Feedstock Requirements for Powder Bed Fusion Additive Manufacturing. Addit. Manuf. 2019, 28, 78–86. [Google Scholar] [CrossRef]
- Desai, P.S. Tribosurface Interactions involving Particulate Media with DEM-calibrated Properties: Experiments and Modeling. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2017. [Google Scholar]
- Herbold, E.; Walton, O.; Homel, M. Simulation of Powder Layer Deposition in Additive Manufacturing Processes Using the Discrete Element Method; Technical Report; Lawrence Livermore National Lab (LLNL): Livermore, CA, USA, 2015. [Google Scholar]
- Parteli, E.J.; Pöschel, T. Particle-based simulation of powder application in additive manufacturing. Powder Technol. 2016, 288, 96–102. [Google Scholar] [CrossRef]
- Mindt, H.; Megahed, M.; Lavery, N.; Holmes, M.; Brown, S. Powder bed layer characteristics: The overseen first-order process input. Metall. Mater. Trans. A 2016, 47, 3811–3822. [Google Scholar] [CrossRef]
- Steuben, J.C.; Iliopoulos, A.P.; Michopoulos, J.G. Discrete element modeling of particle-based additive manufacturing processes. Comput. Methods Appl. Mech. Eng. 2016, 305, 537–561. [Google Scholar] [CrossRef]
- Haeri, S.; Wang, Y.; Ghita, O.; Sun, J. Discrete element simulation and experimental study of powder spreading process in additive manufacturing. Powder Technol. 2017, 306, 45–54. [Google Scholar] [CrossRef]
- Haeri, S. Optimisation of blade type spreaders for powder bed preparation in Additive Manufacturing using DEM simulations. Powder Technol. 2017, 321, 94–104. [Google Scholar] [CrossRef]
- Mindt, H.W.; Desmaison, O.; Megahed, M.; Peralta, A.; Neumann, J. Modeling of powder bed manufacturing defects. J. Mater. Eng. Perform. 2018, 27, 32–43. [Google Scholar] [CrossRef]
- Markl, M.; Körner, C. Powder layer deposition algorithm for additive manufacturing simulations. Powder Technol. 2018, 330, 125–136. [Google Scholar] [CrossRef]
- Nan, W.; Pasha, M.; Bonakdar, T.; Lopez, A.; Zafar, U.; Nadimi, S.; Ghadiri, M. Jamming during particle spreading in additive manufacturing. Powder Technol. 2018, 338, 253–262. [Google Scholar] [CrossRef]
- Nan, W.; Ghadiri, M. Numerical simulation of powder flow during spreading in additive manufacturing. Powder Technol. 2019, 342, 801–807. [Google Scholar] [CrossRef]
- Desai, P.S.; Mehta, A.; Dougherty, P.S.; Higgs, F.C., III. A rheometry based calibration of a first-order DEM model to generate virtual avatars of metal Additive Manufacturing (AM) powders. Powder Technol. 2019, 342, 441–456. [Google Scholar] [CrossRef]
- Escano, L.I.; Parab, N.D.; Xiong, L.; Guo, Q.; Zhao, C.; Fezzaa, K.; Everhart, W.; Sun, T.; Chen, L. Revealing particle-scale powder spreading dynamics in powder-bed-based additive manufacturing process by high-speed X-ray imaging. Sci. Rep. 2018, 8, 15079. [Google Scholar] [CrossRef] [PubMed]
- Escano, L.I.; Parab, N.D.; Xiong, L.; Guo, Q.; Zhao, C.; Sun, T.; Chen, L. Investigating Powder Spreading Dynamics in Additive Manufacturing Processes by In-situ High-speed X-ray Imaging. Synchrotron Radiat. News 2019, 32, 9–13. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, C.; Escano, L.I.; Young, Z.; Xiong, L.; Fezzaa, K.; Everhart, W.; Brown, B.; Sun, T.; Chen, L. Transient dynamics of powder spattering in laser powder bed fusion additive manufacturing process revealed by in-situ high-speed high-energy X-ray imaging. Acta Mater. 2018, 151, 169–180. [Google Scholar] [CrossRef]
- Everton, S.K.; Hirsch, M.; Stravroulakis, P.; Leach, R.K.; Clare, A.T. Review of in-situ process monitoring and in-situ metrology for metal additive manufacturing. Mater. Des. 2016, 95, 431–445. [Google Scholar] [CrossRef]
- Baumann, F.W.; Sekulla, A.; Hassler, M.; Himpel, B.; Pfeil, M. Trends of machine learning in additive manufacturing. Int. J. Rapid Manuf. 2018, 7, 310–336. [Google Scholar] [CrossRef]
- Mies, D.; Marsden, W.; Warde, S. Overview of additive manufacturing informatics: “A digital thread”. Integr. Mater. Manuf. Innov. 2016, 5, 6. [Google Scholar] [CrossRef]
- Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A Review of the Application of Machine Learning and Data Mining Approaches in Continuum Materials Mechanics. Front. Mater. 2019, 6, 110. [Google Scholar] [CrossRef]
- Kamath, C. Data mining and statistical inference in selective laser melting. Int. J. Adv. Manuf. Technol. 2016, 86, 1659–1677. [Google Scholar] [CrossRef]
- Zhao, X.; Rosen, D.W. A data mining approach in real-time measurement for polymer additive manufacturing process with exposure controlled projection lithography. J. Manuf. Syst. 2017, 43, 271–286. [Google Scholar] [CrossRef]
- DeCost, B.L.; Jain, H.; Rollett, A.D.; Holm, E.A. Computer vision and machine learning for autonomous characterization of am powder feedstocks. JOM 2017, 69, 456–465. [Google Scholar] [CrossRef]
- Yao, X.; Moon, S.K.; Bi, G. A hybrid machine learning approach for additive manufacturing design feature recommendation. Rapid Prototyp. J. 2017, 23, 983–997. [Google Scholar] [CrossRef]
- Uhlmann, E.; Pontes, R.P.; Laghmouchi, A.; Bergmann, A. Intelligent pattern recognition of a SLM machine process and sensor data. Procedia Cirp 2017, 62, 464–469. [Google Scholar] [CrossRef]
- Gu, G.X.; Chen, C.T.; Richmond, D.J.; Buehler, M.J. Bioinspired hierarchical composite design using machine learning: Simulation, additive manufacturing, and experiment. Mater. Horiz. 2018, 5, 939–945. [Google Scholar] [CrossRef]
- Wu, D.; Wei, Y.; Terpenny, J. Surface Roughness Prediction in Additive Manufacturing Using Machine Learning. In Proceedings of the ASME 2018 13th International Manufacturing Science and Engineering Conference, College Station, TX, USA, 18–22 June 2018. [Google Scholar]
- Gobert, C.; Reutzel, E.W.; Petrich, J.; Nassar, A.R.; Phoha, S. Application of supervised machine learning for defect detection during metallic powder bed fusion additive manufacturing using high resolution imaging. Addit. Manuf. 2018, 21, 517–528. [Google Scholar] [CrossRef]
- Bessa, M.; Pellegrino, S. Design of ultra-thin shell structures in the stochastic post-buckling range using Bayesian machine learning and optimization. Int. J. Solids Struct. 2018, 139, 174–188. [Google Scholar] [CrossRef]
- Scime, L.; Beuth, J. A multi-scale convolutional neural network for autonomous anomaly detection and classification in a laser powder bed fusion additive manufacturing process. Addit. Manuf. 2018, 24, 273–286. [Google Scholar] [CrossRef]
- He, H.; Yang, Y.; Pan, Y. Machine learning for continuous liquid interface production: Printing speed modelling. J. Manuf. Syst. 2019, 50, 236–246. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Z.; Shi, J.; Wu, D. Prediction of surface roughness in extrusion-based additive manufacturing with machine learning. Robot. Comput. Integr. Manuf. 2019, 57, 488–495. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Gao, R.X. Deep learning-based tensile strength prediction in fused deposition modeling. Comput. Ind. 2019, 107, 11–21. [Google Scholar] [CrossRef]
- Zhang, W.; Mehta, A.; Desai, P.S.; Higgs, C.F., III. Machine Learning enabled Powder Spreading Process Map for Metal Additive Manufacturing (AM). In Proceedings of the 28th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 7–9 August 2017; pp. 1235–1249. [Google Scholar]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Zeltmann, S.E.; Gupta, N.; Tsoutsos, N.G.; Maniatakos, M.; Rajendran, J.; Karri, R. Manufacturing and security challenges in 3D printing. JOM 2016, 68, 1872–1881. [Google Scholar] [CrossRef]
- Tang, P.; Puri, V. Methods for minimizing segregation: A review. Part. Sci. Technol. 2004, 22, 321–337. [Google Scholar] [CrossRef]
- Dougherty, P.S.; Marinack, M.C., Jr.; Sunday, C.M.; Higgs, C.F., III. Shear-induced particle size segregation in composite powder transfer films. Powder Technol. 2014, 264, 133–139. [Google Scholar] [CrossRef]






| Parameter | Range of Values |
|---|---|
| Spreader diameter (mm) | 30 |
| Spreader length (mm) | 70 |
| Spreader translation speed, U (mm/s) | 40, 55, 70, 85, 100 |
| Spreader rotation speed, (rad/s) | 0, 5, 10, 15, 20, −5, −10, −15, −20 |
| Substrate roughness (μm) | 79 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Number of training samples | 35 | Activation function for hidden layer | Sigmoid |
| Number of test samples | 10 | Activation function for output layer | Linear |
| Number of hidden layers | 1 | Learning rate | 0.0001 |
| Number of hidden nodes | 200 | L2-regularization parameter | 0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Desai, P.S.; Higgs, C.F., III. Spreading Process Maps for Powder-Bed Additive Manufacturing Derived from Physics Model-Based Machine Learning. Metals 2019, 9, 1176. https://doi.org/10.3390/met9111176
Desai PS, Higgs CF III. Spreading Process Maps for Powder-Bed Additive Manufacturing Derived from Physics Model-Based Machine Learning. Metals. 2019; 9(11):1176. https://doi.org/10.3390/met9111176
Chicago/Turabian StyleDesai, Prathamesh S., and C. Fred Higgs, III. 2019. "Spreading Process Maps for Powder-Bed Additive Manufacturing Derived from Physics Model-Based Machine Learning" Metals 9, no. 11: 1176. https://doi.org/10.3390/met9111176
APA StyleDesai, P. S., & Higgs, C. F., III. (2019). Spreading Process Maps for Powder-Bed Additive Manufacturing Derived from Physics Model-Based Machine Learning. Metals, 9(11), 1176. https://doi.org/10.3390/met9111176





