Abstract
In the context of lattice-based design and manufacturing, the problem of physical realization of density maps into lattices of a particular family is central. Density maps are prescribed by design optimization algorithms, which seek to fulfill structural demands on a workpiece, while saving material. These density maps cannot be directly manufactured since local graded densities cannot be achieved using the bulk solid material. Because of this reason, existing topology optimization approaches bias the local voxel relative density to either 0 (void) or 1 (filled). Additive manufacturing opens possibilities to produce graded density individuals belonging to different lattice families. However, voxel-level sampled boundary representations of the individuals produce rough and possibly disconnected shells. In response to this limitation, this article uses sub-voxel sampling (largely unexploited in the literature) to generate lattices of graded densities. This sub-voxel sampling eliminates the risk of shell disconnections and renders better surface continuity. The manuscript devises a function to produce Schwarz cells that materialize a given relative density. This article illustrates a correlation of continuity against stress concentration by simulating and inter-lattice continuity. The implemented algorithm produces implicit functions and thus lattice designs which are suitable for metal additive manufacturing and able to achieve the target material savings. The resulting workpieces, produced by outsource manufacturers, are presented. Additional work is required in the modeling of the mechanical response (stress/strain/deformation) and response of large lattice sets (with arbitrary geometry and topology) under working loads.
1. Introduction
The industrial technologies ecosystem has been enriched with the new Industry 4.0 paradigm, introducing smart technologies into the production lines. Among all these new industrial technological advances, the additive manufacturing is one of the most disruptive technologies, as it enables new manufacturing methods of parts. The evolution of additive manufacturing has been very fast—from plastic prototyping to metal prototyping and, recently, to working metal parts. The fast-paced evolution of additive manufacturing in the technological part is not matched by the changes in the CAD–CAM design of the parts [1]. Additive manufacturing makes feasible the production of complex and intricate geometric features. However, the high production costs limit the application range of this technology. In this context, topology optimization plays a major role in the production of lightweight parts that reduce material usage and, consequently, production costs [2,3]. Existing topology optimization algorithms deliver density maps as the result of the optimization. These density maps cannot be directly manufactured since the density of a bulk solid material cannot be locally graded. In order to overcome this limitation, additive manufacturing takes advantage of its geometrical freedom to enable the physical realization of these density maps into real pieces, using lattice structures [3].
Lattice structures are families of repetitive architectures whose distribution of void/filled sections can be controlled. Moreover, the attractiveness of lattice structures lies in their ability to retain good mechanical properties (e.g., high strength-to-weight ratio, energy absorption) while saving material [4,5,6]. Current works aim to use surface lattice materials for converting density maps into manufacturable workpieces. Surface lattices are a particular family of lattice structures that can be generated as isosurfaces of an implicit function that controls the shape of the structure. However, the materialization of density maps into surface lattice structures poses different challenges: (a) a procedure to control the density of surface lattice structures must be established, (b) the mass of the given density map must be preserved, and (c) stress concentration in terms of inter-lattice continuity is to be considered.
Initially, the manuscript presents how to generate surface lattice structures of variable density from a general perspective. Then, the manuscript addresses, in a formal and intuitive manner, the problem of controlling the density of the variable-density surface lattices, so that the arrangement of the void/filled regions of the lattice structure resembles the given density map. This is achieved by deriving the relationship between the iso-value (tuning parameter to produce the isosurface) used to generate the surface lattice and its corresponding density for the family of Schwarz lattices. The produced structures are effectively manufactured via three processes of additive manufacturing: fused deposition modeling, binder jetting and selective laser melting.
It is important to remark that in additive manufacturing, the problems of geometrical planning, material consolidation, residual stress, micro-defects and porosity, and overall stress vs. strain performance are correlated. However, at the present status of computing power, even the sub-problems of geometric modeling are intractable. The aim of this manuscript is not the mechanical characterization of lattice domains. FEA simulation of even small domains presents considerable challenges for FEA mesh generation and FEA solution itself. This is a vast, mostly unexplored research field, and the purpose of future investigation.
With the aim of guiding the reader through the manuscript, the basic terminology is graphically presented here. Figure 1a shows the initial or rectangular prismatic design domain (), of width w, depth d, and height h. The domain is partitioned into two different sets. One corresponds to the finite element mesh, built by cubic finite elements or voxels (Figure 1b). On the other hand, the domain is also divided into cubic lattices that are larger than voxels. A lattice is composed by an array of k x k x k voxels (Figure 1c). Finally, the space occupied by a cubic lattice becomes a Schwarz Primitive cell. So, the final surface lattice domain can be seen as the union of all the produced Schwarz Primitive cells (Figure 1d). It is important to clarify that (a) Figure 1c is merely illustrative and, in reality, it is usual that , and (b) the triangular mesh or full boundary representation (B-Rep) for the domain is generated by devising an overall piecewise implicit Schwarz family function and then by making the mesh explicit using a Marching Cubes algorithm.
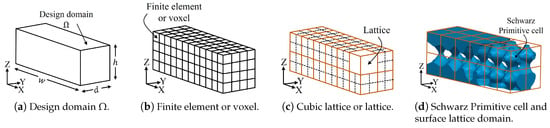
Figure 1.
Definition of the basic geometric entities used in the manuscript.
The remainder of this article is organized as follows: Section 2 provides a review of the relevant related work. Section 3 describes the methodology to generate surface lattice structures and presents the algorithm to convert density maps into lattice materials with controlled density. Section 4 presents and evaluates the results obtained following the presented approach. Advantages and limitations of the implemented algorithm are discussed. Section 5 concludes the manuscript and presents potential research lines to extend this work.
2. Literature Review
2.1. Topology Optimization in Additive Manufacturing
Additive manufacturing offers more geometrical freedom than traditional subtractive manufacturing techniques. This geometrical flexibility confers to additive manufacturing the capacity to exploit and materialize the complex results of topology optimization [2,3].
There are three mainly used topology optimization algorithms used in additive manufacturing applications [7]. The first is Solid Isotropic Material with Penalization (SIMP) or density-based topology optimization, which iteratively adjusts the density of localized neighborhoods [8,9]. The second strategy acts by removing and adding material in different locations of the domain. It is called bi-directional evolutionary structural optimization [10,11]. Finally, the third approach only modifies the boundary of the domain, which is represented by level set functions [12].
Topology optimization in additive manufacturing seeks to (1) design lightweight and functional pieces [8,10], (2) suppress or minimize the amount of support structures needed during the manufacturing stage [13,14], and (3) define optimal infill strategies for existing designs [15,16].
2.2. Lattice Structures in Additive Manufacturing
Besides being lightweight and keeping a high strength-to-weight ratio, lattice structures possess important characteristics which make them appropriate in engineering. Among these properties are: energy absorption [4], heat transfer [5], and vibration and acoustic damping [6]. Authors also evaluate specific mechanical characteristics. References [17,18] study the elastic properties of surface-based and Kelvin lattices, respectively. Reference [19] analyzes the feasibility of surface-based lattices for acoustic isolation by obtaining their vibration bandgaps. Applications of lattice structures can be found in bioengineering, automotive, aeronautic, and aerospace industries [20].
Regarding additive manufacturing, lattice structures are beneficial because they save material and time, reduce material wasting on supports, and diminish energy expenses during manufacturing [20]. In particular, surface-based lattices serve in biomedical [21,22] or industrial applications [15,23]. Surface-based structures are also employed as supports during the building process [24]. Research also focuses on the characterization of surface-based lattice structures fabricated via additive manufacturing. Reference [25] investigated the elastic and plastic deformation under compression of polymer surface-based lattices. Besides, Ref. [26] assesses manufacturability and mechanical performance of metal surface-based lattices.
2.3. Explicit Realization of the Results of Topology Optimization into Surface-Based Lattices
As stated before, density-based topology optimization is commonly used in additive manufacturing applications. The outcome of this kind of algorithms is a density map onto the finite element mesh. The drawback then is that this density map does not have a direct physical realization, due to the density of a material cannot be graded. Since the filled-void proportion of lattices can be manipulated, lattices have emerged as a plausible alternative to solve this issue.
In order to adapt the results of topology optimization into a lattice domain, the related literature relies on the concept of controlling the density (filled-void relation) of the lattice structure, so that it resembles the density map of topology optimization. In this realm, Refs. [27,28,29] propose solutions using different 2D lattice structures and Ref. [30] introduces a density mapping using 3D trusses. Likewise, surface lattices are also adopted for this task. References [15,23,29,31,32] employ surface lattices to materialize the results of topology optimization. Nevertheless, these works have some limitations: (1) the lack of a formal definition of the problem of mapping the densities of topology optimization into surface lattices, (2) the size of the finite elements affects the geometrical quality of the obtained surface (except for Ref. [29]), and (3) the mass of the produced lattice structure differs from the mass determined by the given density map.
2.4. Conclusions of the Literature Review
The literature review has shown that the development of topology optimization is one of the key points for the progress of additive manufacturing. Different topology optimization techniques (namely SIMP, evolutionary structural, and level set-based) are used to exploit the geometrical versatility brought by additive manufacturing. However, the problem of materializing the output of topology optimization into a manufacturable model is still an open research question.
In order to solve this problem, different authors propose to convert the results of the SIMP optimization algorithm into lattice domains, particularly surface-based lattices. However, there are three aspects that need to be revised: (1) the formalization of the problem of mapping the densities of topology optimization into surface lattices, (2) the generation of surface lattice domains whose qualities are not restricted by the mesh used for the optimization, and (3) the preservation of the mass dictated in the optimization stage.
This work focuses on the formalization of the problem in an accurate and intuitive manner. The proposed solution to the stated problem detaches the geometrical resolution of the generated surface lattice from the initial mesh used for the optimization. Likewise, this work proposes a solution for the problem of mass preservation by considering the characteristics of the surface lattices during the optimization stage.
The purpose of this manuscript is not the mechanical characterization of lattice sets. FEA mesh generation and simulations of lattice domains are intractable. Future work is to be dedicated to address the stress-strain prediction for lattice sets, which is in itself a very difficult problem, open for research.
3. Methodology
3.1. Formulation of SIMP
Structural optimization aims to minimize the amount of material of a design while keeping its functionality. SIMP-based (also called density-based) methodology seeks the optimal distribution of the relative density () along the domain.
The classic formulation of density-based topology optimization methods targets the minimization of the compliance , which is a measure of the total strain energy. SIMP relies on finite element analysis (FEA) to perform the simulations. Equation (1) presents the problem of compliance minimization for a rectangular prismatic domain , meshed with N cubic FEA elements (also called voxels) [9,33]:
where are the relative densities associated to the FEA elements, is the global displacement vector, is the global force vector, is the global stiffness matrix, is the initial domain volume, is the maximum proportion of volume of the optimal design, and is the domain volume, calculated as per Equation (2) ([9,33]),
The formulation of density-based topology optimization adopts the rule in Equation (3) ([9,33]):
where and are the elastic moduli of the i-th element and the raw material, respectively, and p is a penalization parameter that makes tends to either 0 or 1.
The outcome of density-based topology optimization is a density () map onto the FEA elements, with . Intuitively, represents the presence and the absence of material. However, intermediate densities—i.e., densities that are not 0 or 1—do not have a physical meaning and cannot be manufactured. In this realm, the junction of additive manufacturing and lattice materials offers a practical solution: the relative density (occupied volume) of the lattice structure can be adjusted to tailor the density map obtained from topology optimization.
This work assesses, formulates, and describes the process of explicitly realizing the density map given by topology optimization into variable-density surface lattice structures. Therefore, this work does not need to correct intermediate densities and chooses (no penalization).
3.2. Morphology of Schwarz Primitive Lattice Structures
Section 3.2, Section 3.3 and Section 3.4 address geometrical and topological considerations, such as the generation of Schwarz Primitive structures. Section 3.2 presents the geometric characteristics of the matrix-phase (cells with internal cavities) and network-phase (cells without internal cavities) Schwarz Primitive structures. The geometric characteristics of the Schwarz structures are related to the tuning parameter t, which is an iso-value used to generate the Schwarz Primitive lattices as isosurfaces of the function in Equation (4) [34]. On the other hand, Section 3.3 presents the mathematical relation between the iso-value t and the relative density of the Schwarz Primitive cells. This relation allows the generation of Schwarz architectures of a prescribed density. In addition, if interested in the minutia of the derivation of this function, the reader may visit Section 3.4, which describes in detail the derivation of this relation. On the contrary, if interested in the generation of variable-density Schwarz (also called Schwarz-modified) lattice structures, the reader may skip Section 3.4 and go directly to Section 3.5.
This manuscript contributes to the Schwarz lattice geometry because it presents higher stiffness, when compared to other basic geometries [35]. The Schwarz lattice geometry is also quite well addressed in the relevant literature [36]. Schwarz Primitive lattice structures are generated as isosurfaces of the function shown in Equation (4), in which L denotes the length of the cell [34]. This article studies two types of Schwarz Primitive lattices: network-phase and matrix-phase cells (Figure 2), whose main difference is that the latter has an internal cavity and the first does not.
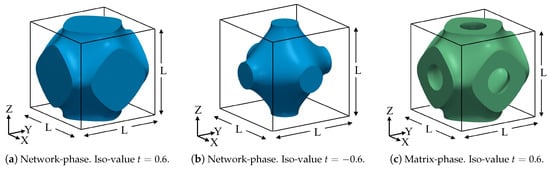
Figure 2.
Geometry of Schwarz Primitive triply periodic surface.
In order to generate network-phase Schwarz structures, first the isosurface of the function F in Equation (4) corresponding to the iso-value t is generated. Then, the isosurface must be closed. The space enclosed in the formed shape corresponds to a network-phase cell. This enclosed space is represented by the inequality in Equation (5). The iso-value t must be in the range . Figure 2a,b shows Schwarz Primitive network-phase cells for () and ().
In the case of the matrix-phase cells, it is necessary to generate two isosurfaces corresponding to the iso-values t and . The space enclosed by these two isosurfaces is represented by the inequality in Equation (6). In this case, only non-negative iso-values t are considered, i.e., . Figure 2c shows the matrix-cell associated to (). From Figure 2, the reader may notice that is the result of the Boolean difference between and (). A matrix-phase Schwarz Primitive cell can be built as the Boolean difference between two network-phase cells.
The relative density (or volume fraction) of a lattice cell is the ratio of its volume and the volume of the lattice . Figure 3 shows five samples of network-phase Schwarz Primitive cells. Each sample is associated to a different iso-value t, reported in the figure. Notice that the larger the value of t, the higher the relative density. The cell corresponding to (Figure 3a) is totally contained within the depicted cube and would not have connections with neighbor cells. Therefore, it cannot be used for the explicit realization of density maps into surface lattice structures. This phenomenon appears when the iso-value is lower than (), which corresponds to a relative density .
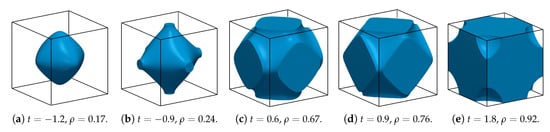
Figure 3.
Geometry of Schwarz Primitive network-phase cells.
Figure 4 reproduces five examples of matrix-phase cells. As in the case of network-phase cells, a larger t produces cells with larger relative density. On the other hand, for every , there is a region of the cell that allows the connectivity with their neighbors. In this case, the manufacturing technique and its capacity to produce fine details dictate the minimum value of t suitable for manufacturing. However, when (Figure 4d,e), an internal cavity appears in the cell. This cavities would trap the raw material in processes such as powder bed fusion, but do not represent an issue in processes where the raw material is deposited, such as directed energy deposition or fused deposition modeling.
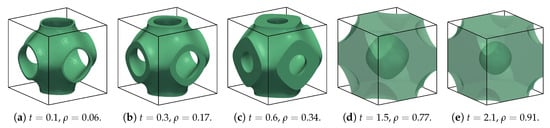
Figure 4.
Geometry of Schwarz Primitive matrix-phase cells.
3.3. Relation between the Iso-Value and the Relative Density of Schwarz Primitive Cells
In order to control the relative density of the generated surface lattice domain, it is necessary to express the iso-value t as a function of the relative density . This section addresses this task for the network and matrix-phase Schwarz Primitive cells.
3.3.1. Network-Phase Cells
Network-phase Schwarz Primitive cells are generated using an iso-value . To determine the relationship between t and , the interval may be discretized (sampled) and the relative density associated to each value of t must be inspected. In this work, the selected size of the sample was 19. That is, 19 network-phase cells were generated using different values of t in Equation (5). The iso-values were . The corresponding relative density of each cell was measured. The results are shown in Figure 5a. Moreover, for , and for , .
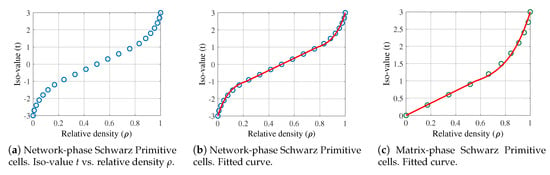
Figure 5.
Establishment of the relation between the iso-value t vs. and the relative density for Schwarz Primitive cells.
The reader may observe that (1) there is a linear behavior for and a non-linear behavior out of this range, (2) for , , and (3) the graph is symmetric with respect to the point . Considering these findings and the relationship between t and for the studied specimens, a function is adjusted to the data. The function has the form of Equation (7), with a linear zone and two non-linear portions. The values of the parameters are listed in Table 1. Figure 5b compares the experimental data and the fitted curve. Notice that the obtained function has two properties that are indispensable for the current application: (1) it is continuous, and (2) it is monotonically increasing.
3.3.2. Matrix-Phase Cells
Matrix-phase cells can be generated with the Boolean difference among two network-phase cells. Therefore, the relative density of a matrix-phase cell associated with the iso-value t may be written in terms of the relative density of two network-phase cells (), as follows:
The relationship stated in Equation (8) and the function fitted for the network-phase cells (Equation (7)) are used to construct a function that associates t with for the matrix-phase Schwarz Primitive cells. The function in Equation (9) shows the obtained result. Figure 5c shows the concordance between the fitted function and the experimental relative density measured for some samples of matrix-phase cells.
The two function in Equations (7) and (9) allow to retrieve the iso-value that produces a Schwarz Primitive cell with a prescribed relative density . The reader may refer to Section 3.4 to find a more detailed explanation on how and were inferred.
3.4. Derivation of the Lattice Iso-Value as Function of the Relative Density
To establish the relationship between the iso-value t and the relative density of Schwarz Primitive cells, it was necessary to fit the functions and (Equations (7) and (9)). The following sections give more insights on how these functions were constructed.
3.4.1. Network-Phase Cells
For the network-phase Schwarz Primitive cells, a sample of 19 specimens was generated. Every specimen was associated to a different value of (see Figure 5b). According to the experimental results, the fitted function had to fulfill the following criteria: (1) linearity for and non-linearity for , (2) symmetry with respect to the point , (3) , and (4) and .
Considering criteria (2) and (3), Equation (10) was deduced. Moreover, using the symmetry stated in criterion (2), only the relationship for was analyzed.
Criteria (1) and (4) were used to obtain the piece-wise continuous function (), shown in Equation (11). The values of the parameters are listed in Table 1. Figure 6 compares the experimental data and the fitted curve. Notice that, for the obtained function: (1) , (2) , (3) it is continuous, and (4) it is monotonically increasing.
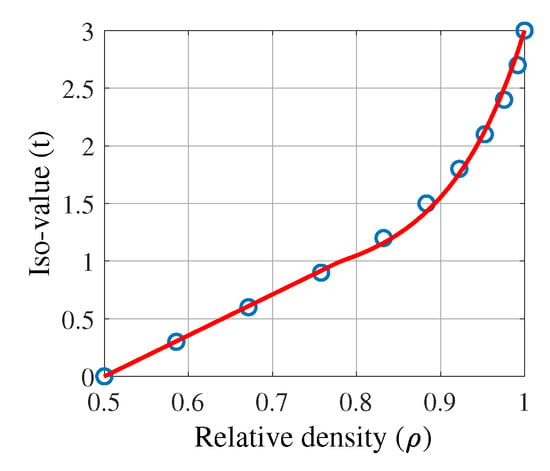
Figure 6.
Fitting of the iso-value t as a function of () for the network-phase Schwarz Primitive cell.
3.4.2. Matrix-Phase Cells
Since the matrix-phase cell with iso-value t can be generated as the Boolean difference between the network-phase cells of iso-values t and , the relative density of a matrix-phase cell is given by the difference of the relative densities of the network-phase cells (Equation (12)), where and .
3.5. Generation of Variable-Density Surface Lattice Structures
The manuscript has discussed how to generate periodic surface lattice structures (such as Schwarz Primitive). This section introduces how to develop variable-density lattice structures. This procedure can be applied to several types of surface lattice structures (e.g., Schwarz Primitive or gyroid) that are approximated with implicit functions, as the one in Equation (4).
In order to generate surface lattice structures (Schwarz Primitive) with variable density, let
where is a function that defines the shape of the lattice structure (as the given in Equation (4)) and is an iso-level function that fulfills . The function T is the one that determines the relative density of the structure. Variable-density Schwarz lattices are simply non-periodic Schwarz lattices (or Schwarz-modified lattices).
Figure 7 depicts a diagram to describe the generation of variable-density surface lattice structures in network-phase for a prismatic rectangular domain . The process is divided into three steps:
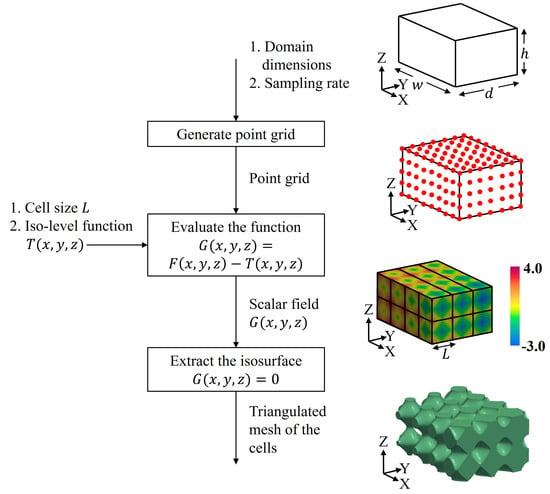
Figure 7.
Work-flow for the generation of variable-density surface lattices. Images are merely illustrative. The surface lattice was generated with a denser point grid.
- Generation of the point grid: the first step is to sample , given its dimensions and the grid sampling rate in which must be sampled. The output of this step is a point grid.
- Evaluation of the function : the function G is evaluated in the point grid obtained in the previous step. Apart from the point grid, it is necessary to provide (1) the size of the cell (L in Equation (4)), and (2) the iso-level function T. The outcome of this step is the scalar field .
- Extraction of the isosurface : the final step is to retrieve the isosurface from the scalar field generated in step 2 using Marching Cubes algorithm. This algorithm returns a triangular mesh that approximates the required isosurface.
To generate matrix-phase cells, the process must be performed twice, using the functions and . Additionally, T must be non-negative, that is, .
3.6. Explicit Realization of a Density Field into Variable-Density Surface Lattice Structures: Problem Statement
The previous section described how to generate variable-density Schwarz Primitive cells. However, it has not been yet shown how to transform a given density field (as the obtained with topology optimization) into a surface lattice structure. Intuitively, and using the knowledge acquired in Section 3.5, Section 3.6 and Section 3.7 shows how to construct an iso-level function T that resembles a given density map. The key point is to generate a function T that serves as the input of the second step of the procedure in Section 3.5 to create variable-density surface lattice domains.
The iso-value function T is a scalar function defined on a rectangular prismatic domain orthogonally oriented with respect to the World Coordinate System. The function T must be continuous and fulfill the density requirements dictated by the given density map. The isosurface (B-Rep of the lattice domain) that generates the implicit function must be (a) continuous and smooth, (b) approximately periodic, and (c) satisfy the local volume occupancy (density) prescribed by the density map. This problem can be stated using the following Given/Goal scheme:
Given
- A prismatic rectangular domain orthogonally oriented with respect to the World Coordinate System.
- A set E of cubic voxels, which partition , defined by a regular orthogonal grid. This set of voxels serve as FEA elements in the topology optimization.
- A density map defined on E, that is, , where represents the relative density of the i-th voxel (e.g., the dictated by the topology optimization algorithms).
Goal
- To generate a scalar (iso-value) function such that:
- (a)
- T is bounded. In the Schwarz-modified case used in this work, , to ensure that the domain is not devoid of material.
- (b)
- T is continuous.
- (c)
- , where denotes the relative density of a periodic Schwarz cell with tuning parameter t. That is, for every point , the density induced at that point by the function T must be equal to the density of the voxel to which the point belongs.
The stated mathematical problem does not have a solution, since criteria (b) and (c) imposed on T collide. This work proposes an approximated solution of the problem by: (1) relaxing to continuity on T, and (2) transforming voxel densities into vertex densities. This work presents the solution to the relaxed problem. The manuscript generates a continuous iso-value function T that for each point , if and , then , that is, the density at p is approximately equal to the density of the voxel to which the point belongs.
3.7. Explicit Realization of a Density Field into Variable-Density Surface Lattice Structures: Problem Solution
This section describes the procedure for generating lattice domains that resemble the volume distribution prescribed by a density map. The procedure is based on an approximated solution to the problem in Section 3.6. The proposed algorithm is divided into two main phases: () the construction of the iso-level function T using the known functions and (Equations (7) and (9)), and () the application of T to generate a variable-density surface lattice structure. Figure 8 summarizes the steps of the two phases of the algorithm.
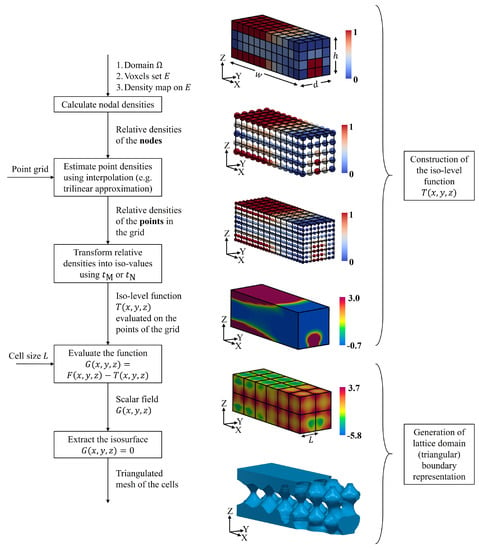
Figure 8.
Work-flow for the explicit realization of density maps into surface lattice structures. Images are merely illustrative. The generated surface lattice structure correspond to a denser finite element analysis (FEA) mesh and a denser point grid.
The first phase of the proposed method has three stages. The output of this phase is an iso-level function T that enables the generation of a surface lattice structure of variable and controlled density. A detailed explanation of each stage follows.
- Calculation of the vertex densities: in this step, the densities of the vertices Q of the voxels are computed. Let be a vertex that belongs to the voxels . The density of q is defined in Equation (16).
- Estimation of the densities of the points in the grid: once the vertex densities are calculated, these can be used to estimate the density of every point . Assuming (1) are the vertices of voxel , (2) are the vertex densities and (3) , the relative density of the point p is given by , (), where H is an interpolation function. This work uses trilinear interpolation for the simulations.
- Transformation of the relative densities into iso-values: the relative density of each point of the grid must be transformed into its corresponding iso-value. The function (or ) in Equation (7) (or Equation (9)) is used for this task. Therefore, the iso-level function of element is . If the number of voxels is N, the obtained iso-level function T is:It is important to remark that the function in Equation (17) is a piece-wise continuous function.
The second phase of the process is to use the provided function T (phase ) to generate a variable-density surface lattice structure, following the procedure described in Section 3.5 to generate the isosurface and obtain a triangulated mesh (B-Rep) of the surface lattice domain.
The following computing tools were used in this investigation: (1) The topology optimization algorithm SIMP and FEA were implemented in C++ by the authors. (2) All the methods presented in Section 3.5, Section 3.6 and Section 3.7 (except the Marching Cubes algorithm) were also programmed in C++ by the authors (i.e., from the generation of the point grid to the evaluation of the function ). (3) The extraction of the isosurface was carried out in ParaView, which includes an implementation of the Marching Cubes algorithm. ParaView was also used for visualization purposes. (4) The mesh generation and FEA simulation of the triangular B-Reps of the lattice domains were executed in ANSYS.
4. Results
4.1. Density Field into Surface Lattice Structures. Applications in Topology Optimization
A rectangular prismatic domain of size 12 cm × 4 cm × 4 cm was used to test the algorithm described in Section 3.7 for the explicit realization of density maps into surface lattice structures of variable density. The generated density maps correspond to the results of topology optimization on . The domain of 12 cm × 4 cm × 4 cm was divided into lattices. Every lattice was formed by cubic elements (voxels). The size of each element was cm × cm × cm. The domain was discretized into the mesh M, composed by cubic elements and nodes. The sizes of the domain, lattice and voxel were selected to be in concordance with the values found in the related literature [15,23] in order to facilitate comparison.
First, the SIMP algorithm was applied to optimize under the loads in Figure 9a. The selected volume fraction to run SIMP was , therefore, the target volume of the optimized domain was 96 cm. Since the key point was to test the performance of the algorithm for converting a density map into surface lattice structures, it was not necessary to force the SIMP algorithm to produce relative densities close to 0 or 1. Therefore, the value of the penalization factor was set to , which means that no penalization was imposed on the intermediate densities. The retrieved density map with the optimal density distribution dictated by the SIMP algorithm is shown in Figure 9b. Notice that this density map is defined over the densities of and, therefore, it is not continuous.
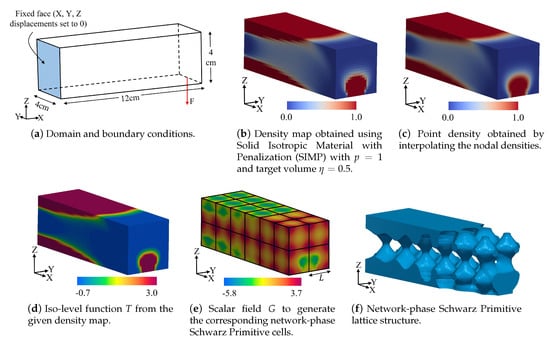
Figure 9.
Explicit realization of the results of topology optimization into surface lattice structures. The procedure was applied over a point grid of points.
After SIMP delivered the density map over the elements of the mesh M, it was necessary to construct the iso-level function T to generate the equivalent surface lattice domain, using the algorithm in Section 3.7. Therefore, a grid of points was generated. Then, the element densities were converted into nodal densities and tri-linear interpolation was used to obtain the density associated to each point of the grid. The outcome of this stage is shown in Figure 9c. In this figure can be seen that, in contrast with the element densities, the point densities generate a continuous variation of the density along the domain.
The density of each point of the grid was converted into the corresponding iso-value using the function (Equation (7)), i.e., the iso-level function T was generated. Due to the limitation of network-phase Schwarz Primitive cells to deal with small densities, all point densities below were set to this value. The resultant iso-level function T is depicted in Figure 9d. Then, using the result of the previous step and the characteristic function F of Schwarz Primitive cells (Equation (4)), the scalar field was produced. The size of the cells was defined as cm. In Figure 9e can be seen the scalar field G. Finally, the isosurface was generated using ParaView [37]. The resultant network-phase domain is depicted in Figure 9f.
Following a similar procedure, the density map given by SIMP in Figure 9b was used to generate the other two Schwarz-modified lattice structures. Figure 10 shows the three lattice structures generated from the density map in Figure 9b. In contrast to the network-phase lattice in Figure 10a, the lattice structure in Figure 10b was generated using a grid of points, which coincide with the nodes of the mesh M. It can be seen that the surface generated with the denser point grid is smoother, that is, surface in Figure 10a is smoother than surface in Figure 10b. It shows the advantage of implementing an algorithm that allows the presence of points in the grid that do not coincide with the FEA nodes (i.e., sub-voxel sampling). It represents a main difference with most of the algorithms found in the literature, where the nodes of M are used as the point grid to generate the surface lattice domain.
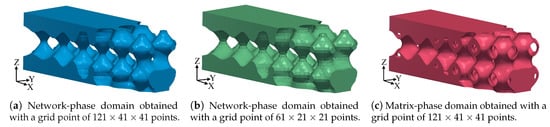
Figure 10.
Schwarz-modified Primitive domains obtained from density map in Figure 9b.
On the other hand, Figure 10c displays a matrix-phase lattice structure that resembles the density map in Figure 9b. Despite the fact that matrix-phase Schwarz cells are well-suited for mapping low density values, in order to avoid numerical issues when computing the corresponding isosurface, densities below were set to this value. Table 2 lists the volume, material saving, and difference between the material saving and the target volume for the three lattice domains. Observe that the intended material savings are not necessarily fulfilled. Several reasons lead to this situation: (a) Levels of density that are too low (e.g., in this case) produce disconnected floating solid domain regions, impossible to realize. (b) The translation from densities to iso-values (functions and in Equations (7) and (9)) is approximated. (c) The generation of the isosurface (triangular B-Rep) assumes a linear interpolation (i.e., Marching Cubes), which is itself an approximation. (d) The synthesis of the iso-level function T contains constraints other than the target density itself, such as the need of continuity. Therefore, the obtained volume occupancy is likely to depart from the target value.

Table 2.
Volume, material saving, and percentage of over-volume of the generated surface lattice domains. The target material saving was .
The use of arbitrary thresholds for suppressing small values of densities produced by SIMP (as the previously used ) is common in the literature [15,29]. Nevertheless, results have shown that this approach diminishes material savings. For this reason, this work evaluated a simple approach in which the thresholds for low densities are included directly in the optimization stage. Therefore, the topology optimization algorithm generates a density field that does not contain small density values.
In order to produce density maps without densities below , the formulation of SIMP was modified, so that the range of in Equation (1) is (instead of ), where is the minimum permitted value of density. Figure 11a shows the resultant density field when . In comparison with the results produced by the non-modified SIMP algorithm, it can be seen that the density distribution is similar but small densities () disappeared. Figure 12a,b shows the magnitude of the displacements on the two density maps generated by the modified and non-modified SIMP. The reader may observe that the magnitude and distribution of the deformation are visually identical. This result shows that reasonable restrictions on do not modify the global theoretical behavior of the density maps given by SIMP.
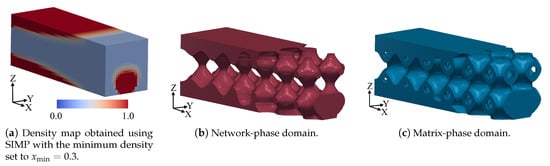
Figure 11.
Schwarz-modified Primitive domains obtained from density map in Figure 11a, which has minimum density of .

Figure 12.
Displacement fields using two Solid Isotropic Material with Penalization (SIMP) modified algorithms. (a) Algorithm SIMP modified to avoid relative density polarization to 0 and 1. Density map in Figure 9b. (b) Algorithm SIMP modified by avoiding relative densities below 0.3. Density map in Figure 11a.
The new density map was used to generate the lattice domains in Figure 11. Figure 11b,c exhibits the resultant network and matrix versions of Schwarz Primitive lattice domains, respectively. In Table 2, the volume and material savings of these two lattice domains can be seen. The material savings reached and for the network-phase and matrix-phase, respectively. Observe that the cells which yield smallest error in the target volume are the matrix-phase (with internal cavities) ones.
4.2. Physical Realization of the Devised Lattice Structures
The manufacturing of an overall domain of the implicit Schwarz-modified continuous B-Rep (Figure 11) would be unfeasible using traditional subtractive techniques (e.g., CNC machining). However, this domain is natural in additive manufacturing. As proof of manufacturability, the full lattice domains (Figure 11) were additively manufactured using Fused Deposition Modeling. Two lattice types were produced: (a) network-phase (without cavities), and (b) matrix-phase (with cavities). The machine, bulk material, and manufacturing parameters are given in Table 3. The build direction corresponds to the orientation in which the material is deposited. In this case, support structures were added in the overhanging zones of the network-phase domain. Supports were not required neither outside nor inside the cavities of the matrix-phase domain.

Table 3.
Experimental set-up for additive manufacturing tests.

Figure 13.
Explicit realization of the results of topology optimization. Manufactured Schwarz Primitive domains using Fused Deposition Modeling.
Partial lattice domain B-Reps (Figure 14a) were additively manufactured using Binder Jetting (Figure 14b,d), and Selective Laser Melting (Figure 14c,e). The pieces were produced by outsourced manufacturers. The used machines, materials, and manufacturing parameters are listed in Table 3. Both pieces were manufactured in commercial stainless steel distributed by the corresponding machine-builder company.

Figure 14.
Metal additive manufacturing of the matrix-phase Schwarz-modified structures produced from topology optimization.
In the Binder Jetting-processed piece (Figure 14b,d), supports were automatically added in the internal cavities of the lattice and were manually removed after completing all the manufacturing process (printing, debinding, and sintering). To remove the binding agent, the piece was heated at C for 12 h. The piece was sintered (to reduce porosity) at a peak temperature of 1400 C for 24 h.
The piece produced by Selective Laser Melting (Figure 14c,e) was built in an Argon inert atmosphere to prevent oxidation. The power of the laser was set to 200 W and the plate was pre-heated at C. Minimal mandatory scaffold was used between the piece and the basis plate. Supports were not necessary inside the cavities of the piece. To relieve the residual stress generated during material deposition, the piece was treated at C for 2 h.
4.3. Stress Concentration in Variable-Density Surface Lattice Structures
Previous Section 4.1 and Section 4.2 have shown how discrete density maps can become physical objects using surface lattice functions. The first phase of this process involves the generation of a continuous iso-level function T from the given discontinuous density map. Herein, this article shows the importance of producing a continuous iso-level function. Three surface lattice structures were generated using a (1) discontinuous (), (2) continuous (), and (3) smooth () iso-level function. The corresponding surface lattice domains and the respective iso-level functions can be seen in Figure 15. The size of the domain was 20 mm × 20 mm × 20 mm and the cell size was mm.
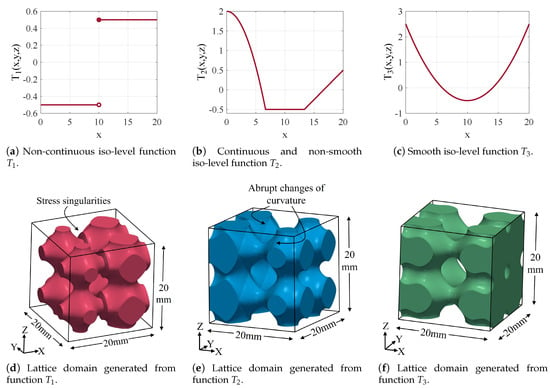
Figure 15.
Variable-density Schwarz Primitive domains generated from different analytic iso-level functions.
The only difference in the generation of the three lattice domains was the iso-level function T used for each one. The reader may notice that the iso-level function not only determines the density distribution, but also establishes the characteristics of continuity and smoothness of the obtained surface lattice domain. In Figure 15f can be seen that the the smooth function generated a smooth surface. Likewise, Figure 15e shows that the continuous and non-smooth function generated a continuous domain where some abrupt changes of curvature in the points where the partial derivatives of are not continuous. On the other hand, sharp corners appeared in the lattice domain generated with the discontinuous function (Figure 15d) at , which coincides with the discontinuity of .
The sharp corners in the domain generated with tend to concentrate the mechanical stress and favor material failure. In order to analyze the effect of the sharp corners, the simulation shown in Figure 16a was executed. All domains were subjected to a tension load in x direction of 12 kN. The material selected for the simulations was the titanium alloy Ti–6Al–4V because it is widely used in additive manufacturing for aerospace and biomedical industries. Accordingly, the material properties used in the simulations were Young’s modulus GPa and Poisson’s ratio [22,38].
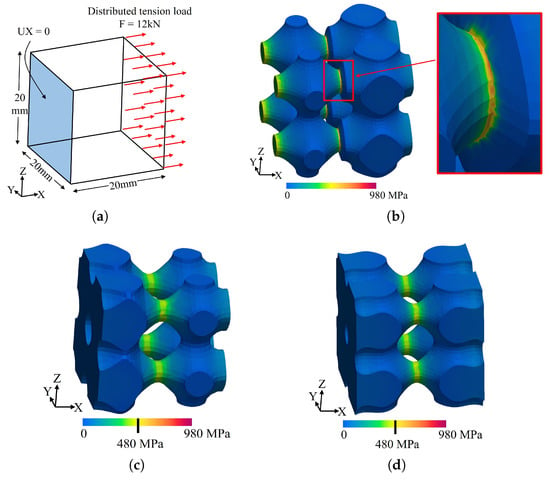
Figure 16b–d shows the stress in the x direction for the three domains. In all cases, the maximum stress is reached at . Moreover, the three domains have the same cross-sectional area, since at . The maximum stress for the domains generated with continuous functions and is 480 MPa. On the other hand, the maximum stress for the domain generated with the discontinuous function is 980 MPa, which doubles the stress of the other two domains. It is noticeable that the stress is completely concentrated in the sharp corners. Figure 17a–c show the displacement in the direction of the x axis for the three domains. It can be seen that the displacements are in the same order of magnitude. The differences in the x displacements are related to the area that is fixed at . These results show that non-continuous iso-level functions may generate stress concentrations in the locations of the discontinuities, even if the deformation is similar. It explains the relevance of the continuity requirement imposed on the iso-level functions generated in this work.
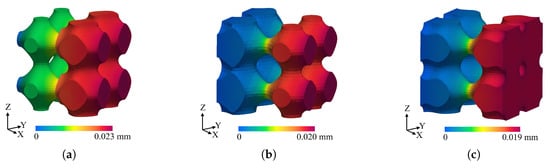
As stated in Section 3.6 and Section 3.7, the iso-level function that generates the algorithm proposed in this article is continuous. However, its partial derivatives are not continuous at the intersection of the FEA elements. Therefore, its behavior is analogous to the behavior of . The executed experiments have not shown any effects on the mechanical stress of the non-smooth transitions of the generated lattice domains. However, numerical and physical tests should be done in the future to test the mechanical response of the surface lattice structures generated with the proposed methodology.
5. Conclusions
This manuscript presents a procedure to effectively transform density maps (as generated by topology optimization algorithms) into manufacturable surface lattice structures, such as Schwarz Primitive architectures. The results show that the generated surface lattice domains (1) effectively resemble the given density map and (2) can be fabricated using additive manufacturing techniques. The results also reveal that the network-phase (architecture without internal cavities) lattice structures have limitations to map small density values, due to the generation of disconnections in the boundary of the cells. On the other hand, matrix-phase (architecture with internal cavities) structures have the capacity to map along the range of densities . In this case, the minimum density that can be represented is dictated by the manufacturing technology and the limitations associated with the machine (minimum detail that can be accurately reproduced).
The presented implementation removes the limitation of the SIMP algorithm, which polarizes the FEA relative densities to either 0 or 1 by allowing a real number in the interval . These intermediate densities are achievable by using the sub-voxel implicit functions presented in this manuscript. The smoothness in the spatial element density field is important because abrupt changes of density may lead to high stress concentrations.
This study also contributes the derivation of a function that expresses the Schwarz Primitive iso-value as a function of the relative density. This function allows to control the relative density of the Schwarz Primitive domain and may be used in future applications of Schwarz Primitive cells.
However, at the present status of CAD–CAM design and simulation, the mechanical analysis of lattice domains presents considerable challenges. Therefore, future research is needed in the modeling of mechanical response (stress/strain/deformation) of large sets of lattices under working loads, with arbitrary topology and geometry of the lattice-based workpiece. Likewise, further efforts are required in the mechanical characterization of physical surface lattice samples produced by additive manufacturing techniques.
Author Contributions
D.M.-Z., A.M. and O.R.-S. conceptualized the algorithm. D.M.-Z. and J.P.-C. carried out and validated the simulations A.M., J.P. and O.R.-S. supervised the Computational Geometry and Manufacturing aspects and applications of this research. All the authors contributed to the writing of the article.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this article:
| B-Rep: | Boundary representation of a solid object in . | |
| FEA: | Finite element analysis. | |
| SIMP: | Solid isotropic material with penalization, which is a topology optimization algorithm. | |
| : | , , denotes the compliance or total strain energy of a domain with vector of relative densities (J). | |
| : | Penalty factor aimed to polarize element relative densities around 0 and 1. | |
| : | Fraction of volume to be retained (or target volume) in the final design. | |
| V: | , , denotes the volume of a domain with vector of relative densities (mm or cm). | |
| : | Volume of the design domain (mm or cm). | |
| : | Young’s modulus of the bulk material (Pa). | |
| : | Young’s modulus of the i-th element of the mesh (Pa). | |
| L: | Length of the surface lattice cell (mm or cm). | |
| : | Relative density or volume fraction of a Schwarz Primitive. | |
| : | The function returns the relative density of a Schwarz Primitive cell generated with an iso-value t. | |
| (or ): | The function (or ) returns the relative density of a network-phase (or matrix-phase) Schwarz Primitive cell generated with an iso-value t. | |
| (or ): | The function (or ) gives the relative density of an element (or node ) of the mesh. | |
| : | Iso-value to generate a Schwarz Primitive cell. Tuning parameter related but not equal to the thickness of the walls of the cell. | |
| : | The function returns the iso-value that generates a Schwarz Primitive cell of relative density . | |
| (or ): | The function (or ) returns the iso-value that generates a network-phase (or matrix-phase) Schwarz Primitive cell of relative density . | |
| : | is the implicit function that characterizes the Schwarz Primitive surfaces. | |
| : | The iso-level function () used to produce variable-density surface lattice structures. The function T is the generalization of the value t. | |
| : | Scalar field that is evaluated to generate variable-density surface lattice structures. | |
| : | Rectangular prismatic subset of , which represents the design domain. | |
| : | Width, depth and height of (mm or cm). | |
| : | Partition of into voxels. The set denotes the voxels and the set denotes the vertices of the voxels. | |
| H: | Interpolation function. In this manuscript refers to tri-linear interpolation of point p given the values . | |
| : | Vector of relative densities of the N elements of the mesh M. | |
Appendix A. Iso-Level Functions
The iso-levels functions used in Section 4.3 are presented in Table A1. The explicit version of the function is associated to the corresponding figures where it is employed. The value of the cell size is mm.

Table A1.
Iso-level functions used in Section 4.3.
Table A1.
Iso-level functions used in Section 4.3.
| Figure Numbers | Iso-Level Function |
|---|---|
| Figure 15a,d | |
| Figure 15b,e | |
| Figure 15c,f |
References
- Posada, J.; Toro, C.; Barandiaran, I.; Oyarzun, D.; Stricker, D.; de Amicis, R.; Pinto, E.B.; Eisert, P.; Döllner, J.; Vallarino, I. Visual Computing as a Key Enabling Technology for Industrie 4.0 and Industrial Internet. IEEE Comput. Graph. Appl. 2015, 35, 26–40. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, Y.; Ramanujan, D.; Ramani, K.; Chen, Y.; Williams, C.B.; Wang, C.C.; Shin, Y.C.; Zhang, S.; Zavattieri, P.D. The status, challenges, and future of additive manufacturing in engineering. Comput.-Aided Des. 2015, 69, 65–89. [Google Scholar] [CrossRef]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.L.; et al. Current and future trends in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2457–2483. [Google Scholar] [CrossRef]
- Hou, W.; Yang, X.; Zhang, W.; Xia, Y. Design of energy-dissipating structure with functionally graded auxetic cellular material. Int. J. Crashworthin. 2018, 23, 366–376. [Google Scholar] [CrossRef]
- Maloney, K.J.; Fink, K.D.; Schaedler, T.A.; Kolodziejska, J.A.; Jacobsen, A.J.; Roper, C.S. Multifunctional heat exchangers derived from three-dimensional micro-lattice structures. Int. J. Heat Mass Transf. 2012, 55, 2486–2493. [Google Scholar] [CrossRef]
- Yin, S.; Wu, L.; Yang, J.; Ma, L.; Nutt, S. Damping and low-velocity impact behavior of filled composite pyramidal lattice structures. J. Compos. Mater. 2014, 48, 1789–1800. [Google Scholar] [CrossRef]
- Liu, J.; Ma, Y. A survey of manufacturing oriented topology optimization methods. Adv. Eng. Softw. 2016, 100, 161–175. [Google Scholar] [CrossRef]
- Montoya-Zapata, D.; Acosta, D.A.; Moreno, A.; Posada, J.; Ruiz-Salguero, O. Sensitivity Analysis in Shape Optimization using Voxel Density Penalization. In Spanish Computer Graphics Conference (CEIG); Casas, D., Jarabo, A., Eds.; The Eurographics Association: Geneve, Switzerland, 2019. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 line topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Montoya-Zapata, D.; Acosta, D.A.; Ruiz-Salguero, O.; Posada, J.; Sanchez-Londono, D. A General Meta-graph Strategy for Shape Evolution under Mechanical Stress. Cybern. Syst. 2019, 50, 3–24. [Google Scholar] [CrossRef]
- Tang, Y.; Kurtz, A.; Zhao, Y.F. Bidirectional Evolutionary Structural Optimization (BESO) based design method for lattice structure to be fabricated by additive manufacturing. Comput.-Aided Des. 2015, 69, 91–101. [Google Scholar] [CrossRef]
- Liu, J.; Yu, H.; To, A.C. Porous structure design through Blinn transformation–based level set method. Struct. Multidiscip. Optim. 2018, 57, 849–864. [Google Scholar] [CrossRef]
- Langelaar, M. Topology optimization of 3D self–supporting structures for additive manufacturing. Addit. Manuf. 2016, 12, 60–70. [Google Scholar] [CrossRef]
- Vanek, J.; Galicia, J.A.G.; Benes, B. Clever Support: Efficient Support Structure Generation for Digital Fabrication. Comput. Graph. Forum 2014, 33, 117–125. [Google Scholar] [CrossRef]
- Panesar, A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for functionally graded lattice structures derived using topology optimisation for Additive Manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- Wu, J.; Wang, C.C.; Zhang, X.; Westermann, R. Self-supporting rhombic infill structures for additive manufacturing. Comput.-Aided Des. 2016, 80, 32–42. [Google Scholar] [CrossRef]
- Lee, D.W.; Khan, K.A.; Al-Rub, R.K.A. Stiffness and yield strength of architectured foams based on the Schwarz Primitive triply periodic minimal surface. Int. J. Plast. 2017, 95, 1–20. [Google Scholar] [CrossRef]
- Montoya-Zapata, D.; Cortés, C.; Ruiz-Salguero, O. FE-simulations with a simplified model for open-cell porous materials: A Kelvin cell approach. J. Comput. Methods Sci. Eng. 2019, 19, 989–1000. [Google Scholar] [CrossRef]
- Elmadih, W.; Syam, W.P.; Maskery, I.; Chronopoulos, D.; Leach, R. Mechanical vibration bandgaps in surface-based lattices. Addit. Manuf. 2019, 25, 421–429. [Google Scholar] [CrossRef]
- Helou, M.; Kara, S. Design, analysis and manufacturing of lattice structures: an overview. Int. J. Comput. Integr. Manuf. 2018, 31, 243–261. [Google Scholar] [CrossRef]
- Melchels, F.P.; Bertoldi, K.; Gabbrielli, R.; Velders, A.H.; Feijen, J.; Grijpma, D.W. Mathematically defined tissue engineering scaffold architectures prepared by stereolithography. Biomaterials 2010, 31, 6909–6916. [Google Scholar] [CrossRef]
- Ataee, A.; Li, Y.; Fraser, D.; Song, G.; Wen, C. Anisotropic Ti-6Al-4V gyroid scaffolds manufactured by electron beam melting (EBM) for bone implant applications. Mater. Des. 2018, 137, 345–354. [Google Scholar] [CrossRef]
- Li, D.; Liao, W.; Dai, N.; Dong, G.; Tang, Y.; Xie, Y.M. Optimal design and modeling of gyroid-based functionally graded cellular structures for additive manufacturing. Comput.-Aided Des. 2018, 104, 87–99. [Google Scholar] [CrossRef]
- Strano, G.; Hao, L.; Everson, R.M.; Evans, K.E. A new approach to the design and optimisation of support structures in additive manufacturing. Int. J. Adv. Manuf. Technol. 2013, 66, 1247–1254. [Google Scholar] [CrossRef]
- Afshar, M.; Anaraki, A.P.; Montazerian, H.; Kadkhodapour, J. Additive manufacturing and mechanical characterization of graded porosity scaffolds designed based on triply periodic minimal surface architectures. J. Mech. Behav. Biomed. Mater. 2016, 62, 481–494. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Hao, L.; Hussein, A.; Raymont, D. Evaluations of cellular lattice structures manufactured using selective laser melting. Int. J. Mach. Tools Manuf. 2012, 62, 32–38. [Google Scholar] [CrossRef]
- Brackett, D.; Ashcroft, I.; Hague, R. Topology optimization for additive manufacturing. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2011; Volume 1, pp. 348–362. [Google Scholar]
- Song, G.H.; Jing, S.K.; Zhao, F.L.; Wang, Y.D.; Xing, H.; Zhou, J.T. Design Optimization of Irregular Cellular Structure for Additive Manufacturing. Chin. J. Mech. Eng. 2017, 30, 1184–1192. [Google Scholar] [CrossRef]
- Zhang, P.; Toman, J.; Yu, Y.; Biyikli, E.; Kirca, M.; Chmielus, M.; To, A.C. Efficient Design–Optimization of Variable-Density Hexagonal Cellular Structure by Additive Manufacturing: Theory and Validation. J. Manuf. Sci. Eng. 2015, 137, 021004. [Google Scholar] [CrossRef]
- Alzahrani, M.; Choi, S.K.; Rosen, D.W. Design of truss-like cellular structures using relative density mapping method. Mater. Des. 2015, 85, 349–360. [Google Scholar] [CrossRef]
- Liu, X.; Shapiro, V. Sample–Based Design of Functionally Graded Material Structures. In Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016; p. 02. [Google Scholar] [CrossRef]
- Savio, G.; Meneghello, R.; Concheri, G. Design of variable thickness triply periodic surfaces for additive manufacturing. Prog. Addit. Manuf. 2019, 4, 281–290. [Google Scholar] [CrossRef]
- Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef]
- Wohlgemuth, M.; Yufa, N.; Hoffman, J.; Thomas, E.L. Triply Periodic Bicontinuous Cubic Microdomain Morphologies by Symmetries. Macromolecules 2001, 34, 6083–6089. [Google Scholar] [CrossRef]
- Maskery, I.; Sturm, L.; Aremu, A.; Panesar, A.; Williams, C.; Tuck, C.; Wildman, R.; Ashcroft, I.; Hague, R. Insights into the mechanical properties of several triply periodic minimal surface lattice structures made by polymer additive manufacturing. Polymer 2018, 152, 62–71. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Al-Rub, R.K.A. Multifunctional Mechanical Metamaterials Based on Triply Periodic Minimal Surface Lattices. Adv. Eng. Mater. 2019, 21. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. ParaView: An End-User Tool for Large-Data Visualization. In Visualization Handbook; Hansen, C.D., Johnson, C.R., Eds.; Butterworth-Heinemann: Burlington, MA, USA, 2005; pp. 717–731. [Google Scholar] [CrossRef]
- Liu, S.; Shin, Y.C. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).