Next Article in Journal
Formation Process of the Passivating Products from Arsenopyrite Bioleaching by Acidithiobacillus ferrooxidans in 9K Culture Medium
Next Article in Special Issue
First Principles Investigation on Thermodynamic Properties and Stacking Fault Energy of Paramagnetic Nickel at High Temperatures
Previous Article in Journal
Influence of Post-Weld Heat Treatments on Microstructure and Mechanical Properties of Laser Beam Welded 2060-T3/2099-T3Al-Li T-Joints
Previous Article in Special Issue
Large-Scale Molecular Dynamics Simulations of Homogeneous Nucleation of Pure Aluminium
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 9
Issue 12
10.3390/met9121319
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Alloying Element Segregation and Grain Boundary Reconstruction, Atomistic Modeling

by
Lidia Karkina
1,
Iliya Karkin
1,
Andrey Kuznetsov
1,2,* and
Yuri Gornostyrev
1,2,3
1
Institute of Metal Physics of Ural Branch of RAS, 620108 Ekaterinburg, Russia
2
Ural Federal University, 620002 Ekaterinburg, Russia
3
Institute of Quantum Materials Science, 620007 Ekaterinburg, Russia
*
Author to whom correspondence should be addressed.
Metals 2019, 9(12), 1319; https://doi.org/10.3390/met9121319
Submission received: 8 November 2019 / Revised: 27 November 2019 / Accepted: 4 December 2019 / Published: 6 December 2019
(This article belongs to the Special Issue Atomistic Modelling and Simulation of Structural and Phase Stability in Metals and Alloys)
Browse Figures
Versions Notes

Abstract

:
Grain boundary (GB) segregation is an important phenomenon that affects many physical properties, as well as microstructure of polycrystals. The segregation of solute atoms on GBs and its effect on GB structure in Al were investigated using two approaches: First principles total energy calculations and the finite temperature large-scale atomistic modeling within hybrid MD/MC approach comprising molecular dynamics and Monte Carlo simulations. We show that the character of chemical bonding is essential in the solute–GB interaction, and that formation of directed quasi-covalent bonds between Si and Zn solutes and neighboring Al atoms causes a significant reconstruction of the GB structure involving a GB shear-migration coupling. For the solutes that are acceptors of electrons in the Al matrix and have a bigger atomic size (such as Mg), the preferred position is determined by the presence of extra volume at the GB and/or reduced number of the nearest neighbors; in this case, the symmetric GB keeps its structure. By using MD/MC approach, we found that GBs undergo significant structural reconstruction during segregation, which can involve the formation of single- or double-layer segregations, GB splitting, and coupled shear-migration, depending on the details of interatomic interactions.

1. Introduction

Grain boundary (GB) segregation affects essentially many phenomena in polycrystals, such as recrystallization, strength and plasticity, decomposition of solid solution, and new phase nucleation [1]. The role of GB segregation becomes especially important in ultrafine grained materials (UFG), where the fractions of GB and bulk atoms are comparable [2,3]. In this case, the formation of segregations at GBs significantly changes the conditions of the phase equilibrium [3,4,5,6] and thermal stability of grained structure [7,8,9,10]. Although the problem of GB segregation has been in the focus of researchers for many years [1], the physical mechanisms that control the solute–GB interaction and the effect of alloying elements on GB structure and properties remain the subject of debates (see, for example, Refs. [11,12,13,14]).
The problem of GB chemistry is challenging for both experiment [3,15,16] and theoretical modeling [10,11,17,18,19]. Recently, important progress has been done on the study of GB segregation by 3D atom probe tomography [20,21,22]. It turned out that unusually broad regions near GBs enriched in alloying elements are observed in UFG alloys subjected to severe plastic deformation [23,24,25]. It is commonly believed that such broad segregations may belong to a special so-called non-equilibrium structure of a GB [2,3]. Other mechanism of the formation of such broad enriched regions is recently discussed in connection with the segregation induced GB structural transitions [14,26,27,28,29,30,31].
Al-Mg and Al-Zn alloys give the bright example of the dramatic dependence of segregations on the chemistry of alloying elements. In particular, for an Al-Mg system it was observed that Mg atoms tend to form heterogeneous agglomerations at GBs [5,32], and it results in extra-hardening. In contrast, Zn atoms are distributed homogeneously along the GBs in the UFG Al-Zn alloy [3,8]. These specific segregations are thought to be a reason for GB sliding enhancement in UFG Al-Zn at relatively low temperatures, which resulted in unusual super-ductility [33,34,35]. However, the nature of the observed peculiarities of segregation is still not exactly known.
In general, the mechanism of solute–GB interaction depends on a number of factors, and is rather complex. It depends on the type of the GB and contains the deformation (related to size effect and lattice distortions) as well as the electronic (related to changes in the chemical bonding) contributions, which are not easy to separate from each other. As commonly believed, the electronic contribution is dominant in most cases. However, recent studies have shown that the size effect [11,35], and also changes in the bond order [17], may have a decisive influence on behavior of solutes at GBs. First principles calculations provide the most reliable information about the GB structure, energetics, and solute-GB interactions [11,12,35,36,37,38,39,40,41,42]. However, they require advanced computational resources, and mostly special type (ST) GBs can be studied. Atomistic simulation methods (molecular dynamics (MD) and Monte Carlo (MC)) allow one to implement large scale modeling. Unfortunately, used interatomic interaction potentials have limited reliability.
The results of atomistic simulations of impurity segregation at the ST GBs allow us to identify the important parameters related to the GB characteristics (GB energy, structure, and excess volume) or to the characteristics of the impurity atom (solution enthalpy, ionic radius). New important information has been obtained in recent years using hybrid simulation MD/MC approach, in which MD and MC runs are alternating with each other [14,30,43,44,45]. It was shown that in addition to local changes in chemical composition, another effect of dopant segregation to a GB can be realized, namely an alteration of GB structure. To describe such GB structural reconstruction, the concept “grain boundary complexions” was introduced [46,47,48], which consider an interfacial state that can exist only in the presence of adjacent grains. The different types of complexion have been proposed in Ref. [46], and unusual broad enriched GB regions observed in UFG alloys [21,22,23] can be classified as nanoscale intergranular films. At the same time, the question about the role of chemistry of alloying elements in segregation and the peculiar interface state formation continues to be open for debate.
In this paper, we present results of atomistic modeling of the segregation formation in Al alloys, which may cause the reconstruction of GB structure. First (Section 3.1), we consider the interaction of solute with ST GB by using first-principle electronic structure and total energy calculations. Next, in Section 3.2, we present the results of large-scale finite temperature MD/MC modeling and demonstrate that segregation can result in different types of GB reconstruction in dependence on chemistry of solute atoms. General trends of segregation formation and GB reconstruction are discussed in Section 4.

2. Methods of Modeling

In this paper, interaction of a single solute atom with a tilt ST GB in Al alloys is studied using two approaches. The first one is first principles calculations of a crystallite with a ST GB and a solute atom. The second approach involves atomistic MD/MC simulations of a rather large polycrystal with GB and solute atoms. This approach allows simulations at finite temperatures using many-body interatomic potentials developed within the framework of embedded atom method (EAM). Ab initio calculations give reliable information about solute–special type GB interaction at zero K, while MD/MC approach allows large-scale modeling at finite temperature, but is limited by the use of the semi-empirical interatomic potentials. Employing these two methods, we obtain a comprehensive picture of the phenomena under consideration.
We chose the alloying elements which are typically used as additions in Al-based alloys. Reliable interatomic potentials are known now for Mg, Ni, Cu, Pb (see Section 2.2), and there are no such for Si and Zn. Therefore, we employ ab-initio calculations for Si, Zn, and for Mg; the latter was chosen for the comparison of results of different approaches.

2.1. Ab Initio Calculations of the Solute-GB Interaction

The total energy of a crystallite containing a Σ5{210}<001> tilt GB and a solute atom (Mg, Si, or Zn) was calculated using DFT based package VASP (Vienna Ab-initio Simulation Package [49,50]) and using projector augmented plane wave (PAW) method [51]. The exchange-correlation energy was calculated in the generalized gradient approximation (GGA), the formalism proposed in Refs. [52] was used. Kinetic-energy cutoff of plane waves was 520 eV. The reciprocal space was sampled with the 8 × 4 × 2 k-point Γ-centered meshes [53]. The convergence criterion for energy was 1 × 10−5. A 48-atom supercell had the dimensions 8.2a × 1.6a × 1.0a, periodic boundary conditions were used (a is Al lattice parameter). The lattice parameter coincided with the experimental value a = 0.405 nm within 0.2%. The supercell contained two crystallites (see Figure 1a,b) misoriented (tilted) by 53.1° about the [001] axis with respect to each other. Shifted GB was obtained by relative displacement of adjacent grains to a local minimum of energy along the GB plane in one direction perpendicular to the tilt axis <100> of the GB, with subsequent relaxation.
An Al atom occupying one of the sites 1–8 beside the GB was replaced by a Mg, Si, or Zn (see Figure 1a,b), and the total energy of the crystallite was calculated using structural relaxation. The segregation energy Εseg(R) was determined as the energy difference between the crystallite with the impurity at a distance R from the GB plane and the crystallite containing the same impurity situated on most remote site from the GB plane.

2.2. MD/MC Finite Temperature Simulations

The hybrid MD/MC approach was used for the calculations of the solute interactions X (X = Mg, Ni, Cu, Pb) with special type GBs Σ5{210}<001> and Σ5{310}<001>, modeling the segregation formation and related structural changes. Initially, the distribution of solute atoms in the crystallite was random, in accordance with a given average concentration (3at.%). We used Metropolis scheme, which included additionally on each MC step the MD relaxation of a crystallite with the solute atom in a new trial position, and the probability of an atomic jump was determined by accounting the change in energy due to relaxation. This scheme differs from that used in the papers [29,30], where MD was carried out after each 103 MC steps. As it follows from the results presented below, the stepwise relaxation in the MC/MD simulation plays an essential role in the correct description of the structural reconstruction of GB. Total energy convergence criterion was 10−4 eV/at. The total number of steps in the MC procedure was about 106.
In the MD/MC calculations, we used LAMMPS (Sandia National Laboratories) package [54]. To describe the interatomic interactions, we employ many-body EAM potentials: EAM/FS potential [55] for Al-Mg alloys, EAM/alloy potential [56] for Al-Ni, EAM/adp potential [57] for Al-Cu, EAM/alloy potential [58] for Al-Pb. All potentials are listed in [59] in adapted for LAMMPS form. The interatomic potentials used in MD/MC simulations provided a reliable description of the basic properties of Al, and the lattice parameter coincided with the experiment value within 1%. The used crystallite contained about 80,000 atoms; its dimensions along the main directions <100>, <012>, and <013> were multiple of translations for a given crystallographic axes, and amounted to a, √5a, and 1/2√10a, respectively. GB was located in its center, and periodic boundary conditions were applied along three directions. The simulation was carried out at a temperature of 450 K, which is typical in the experimental study of aging processes in aluminum alloys.

3. Results

To reveal the microscopic features of the segregation formation and GB reconstruction in considered polycrystalline Al alloys, the atomistic modeling was done by using two mentioned above different scale approaches, namely, first principles zero K total energy calculations and finite temperature MD/MC simulations.

3.1. First Principles Modeling of Solute–GB Interactions and GB Reconstruction

The calculated segregation energies Eseg(R) of the solute atoms (Mg, Si, Zn) to different positions near the Σ5{210}<001> tilt GB in Al are presented in Figure 1b,d as functions of distance R from the GB plane for symmetric GB structure (Figure 1a) and for shifted GB obtained by relative displacement of adjacent grains (Figure 1c) to a local minimum of energy. The short-ranged character of the interaction between substitutional atoms and the GB (concentrated in a few layers near the GB) is seen in Figure 1b,d. Additionally, non-monotonic variance of these segregation energies with the distance is possible, especially in the case of a Si and Zn impurities near shifted GB. Frequently observed [39,60,61] oscillations of the segregation energy Eseg(R) may be caused by two reasons: The first is heterogeneity of local distortions, and the second is Friedel electron density oscillations near the GB [60]. As it will be seen below, the oscillations of segregation energy in the case of Si and Zn (Figure 1d) are related to reconstruction of GB structure.
We found that the biggest energy gain was obtained for Si, with one extra p-electron and about 10% smaller atomic radius than that of Al. At the same time, the interaction with the GB of Mg, with one less p-electron and 20% greater atomic radius than that of Al, is weaker than of Si. Finally, for Zn, the segregation energy behavior Eseg(R) is similar to Si. As it discussed in [34], the atomic relaxation contribution (deformation mechanism) in solute–GB interaction is dominate in case of Mg, while electronic contribution associated with a charge transfer and change in chemical bonding is the most significant in case of Si and Zn. The distribution of valence electron density (Figure 2a,d) indicates that strong covalent Si–Al bonds are formed by the Si impurity with its neighbors. Similar distribution of valence electron density is obtained also for Zn atom near GB (Figure 2b,e). However, the picture in the case of Mg is quite different (Figure 2c,f); in this case, there is a reduction of the electron density near the segregated atoms, which indicates the chemical bond weakening.
An important feature of results presented in Figure 2a,d,b,e is similarity in GB structure, which is formed after relaxation with solute atom in position 3, regardless of remarkable difference of initial GB configurations (symmetric or shifted). Moreover, the distribution of valence electron density turned out to be similar for Si (Figure 2a,d) and Zn (Figure 2b,e) solutes, though it is very different from that in case of Mg (Figure 2c,f). The Si and Zn solutes form strong quasi-covalent bonds with neighboring Al atoms (red regions in Figure 2a,d,b,e) that is the driving force behind considerable reconstruction of the GB, which results in the same GB structure, independent on initial configuration. Wherein, the GB plane turns out to be shifted from initial (shown by dashed line) to new position, passing through solute atoms. It should be noted that the segregation of the Si or Zn atom leads to severe heterogeneity in GB structure and distribution of electron density with alternating enriched and depleting regions. As a result, new preferable places for segregated atoms appear.
In contrast to Si and Zn atoms, the substitution of Al by Mg atom results in depletion of electron density and weakening of chemical bonds (Figure 2c,f). In this case, the GB structure formed after relaxation strongly depends on initial configuration. While in case of symmetric GB (Figure 2c), the relaxation results in local displacement and movement of Mg atoms in the GB center, in case of shifted GB (Figure 2f), the GB center turns out to be substantially displaced perpendicular to the GB plane from the initial position.
The results shown in Figure 2 correspond to the most representative case, when the solute atom was initially placed at position 3 (Figure 1a,c). Driven by the formation by the solute of the quasi-covalent bonds, a reconstruction of GB structure is going on, also when Si or Zn solute atoms are initially located at positions 1 and 2 in case of symmetric GB. It is not the case for position 2 in shifted GB, when strong chemical bonds do not form, and energy gain due to segregation appears to be rather small (Figure 1d). In contrast with Si or Zn solutes, a preferred position of Mg is determined by the presence of extra volume or a reduced number of nearest neighbors. As a result, sites 1–4 appear preferable for substitution of Al by Mg; while Mg segregation does not lead to significant reconstruction in case of symmetric GB, it causes structural changes and GB displacement for Mg in position 3 (Figure 2f) or 4 in case of shifted GB.
Thus, the presented results of ab initio modeling reveal an important feature of GB segregation, namely solute–GB interaction can result in significant reconstruction of GB structure and even displacement of the GB to a new position. As a result, solute–GB interaction cannot be fully understood based only on consideration of the fixed GB structure. This issue will be discussed in more detail in the next Section using MD/MC simulations.

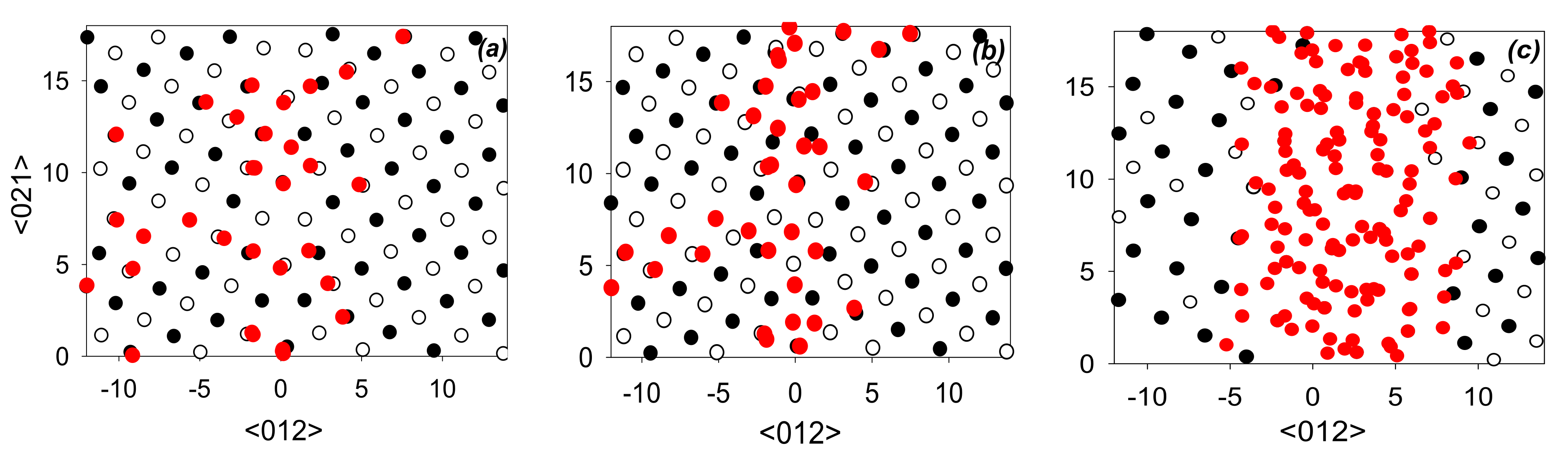
3.2. MD/MC Simulations of the Segregation Formation and GB Reconstruction

The results of ab initio calculations showed that interaction between solute atoms and GB results not only in local distortions but can cause a significant change in the GB structure that may be accompanied by partial sliding of grains and/or a displacement of the GB. To investigate realistic processes of the segregation formation and the GB reconstruction, we employed a combined approach, which included molecular dynamics and Monte Carlo simulations (MD/MC) as described in Section 2.2. We considered the interaction of different solute atoms (Mg, Ni, Cu, Pb) with the Σ5 {012}<100> and Σ5 {013}<100> GBs in Al matrix.
The structure of the Σ5{013}<100> GB in Al-3%Mg alloy after 106 MD/MC runs is shown in Figure 3a. As it seen, the Mg atoms fill all energetically preferable positions in the GB center (energy gain is about 0.4 eV). This is the case when the segregation formation does not lead to the GB reconstruction. Essentially, a different picture is realized for the Σ5{012}<100> GB (Figure 3b). In this case, energetically preferable position for substitution of Al by Mg is located in the next to the nearest atomic plane with respect to the center of the GB. During atomic relaxation, the GB moves to the next atomic plane, accompanied by relative sliding of the grains. As this takes place, the atomic structure in the GB center becomes significantly different from that in the initial position. Thus, even segregation of Mg can result in significant reconstruction of the GB structure, when energetically preferable position is not in the initial center of the GB. Note, that MD/MC and ab initio simulations (Section 3.1) lead to different structural states of the GB. We believe that this difference is due to the fact that ab initio relaxation gives a local minimum of energy, while MD/MC provides achievement of a global minimum.
Results of MD/MC simulations for Al-3%Ni alloy with the Σ5 GB are shown in Figure 4. As it is seen, the segregation of Ni results in reconstruction of the Σ5{012}<100> GB structure (Figure 4b), which is similar to the case of Mg segregation. This is due to the fact that in both cases, energetically preferable position of solute atom is the same and located next to the nearest atomic plane to the center of the GB. In contrast to the Mg, the segregation of Ni atoms on the Σ5{013}<100> GB results in reconstruction of the GB structure (Figure 4a) and formation of the multilayer configuration with set of structural units filled by solute atoms. This feature is due to the presence of two equivalent energetically preferable positions of Ni near the Σ5{013}<100> GB, and is associated with details of interatomic Ni-Al interaction near the GB. Strictly speaking, the question about reliability of used interatomic potentials for description of solute-GB interaction is open to discussion. Nevertheless, we believe that main qualitative features of the GB reconstruction are reproduced correctly.
In case of Al-3%Cu, we found that decomposition of alloy occurs in two stages. Initially (after 105 MD/MC steps), the Cu clusters located in the {100} plane (Guinier–Preston zones [62]) are formed inside the grains and near the GB. The formation of Guinier–Preston zones within similar MD/MC approach was obtained earlier in Ref. [63], and indicates that the used potentials reliably reproduce complex features of interatomic interactions in this system [64]. Further MD/MC runs result in redistribution of Cu atoms and formation of the segregation in case of the Σ5{013}<100> GB. Wherein the GB structure transforms to the multilayer configuration, which is similar to shown in Figure 4a. However, in contrast with Al-Ni alloy, the GB reconstruction is driven by interactions between Cu atoms. Note, in case of the Σ5{012}<100> GB, we did not find segregation due to the lack of attraction between Cu atoms and GB of this type.
For Al-Pb alloy, we found that energies of solute–GB interaction are very high for all positions located in three layers adjacent to the GB plane. This feature originated apparently from a large difference in lattice parameters of Pb and Al that results in significant deformation contribution in solute–GB interaction. As a result, segregations of Pb on the GB appear already in the early MD/MC runs (Figure 5a); in the next stage, the concentration of Pb atoms in GB region increases, and is accompanied by disordering of the crystal lattice (Figure 5b), apparently, due to the considerable local stress. After completion of the MD/MC runs, all Pb atoms are located in the center of the crystallite (near former GB), and the resulting layer of Pb atoms has an amorphous-like structure (Figure 5c). The driving force of this kind of decomposition process is a rather large attraction between Pb atoms in Al matrix (interaction energy between nearest-neighbor Pb atoms in Al for used interatomic potentials is about −0.3 eV).
In Figure 5, we show the results of MD/MC modeling of Al-Pb alloy with the Σ5{012}<100> GB; similar evolution of GB structure and decomposition of alloy was found also for the Σ5{013}<100> GB. An amorphous layer in the GB region was previously observed in MD/MC modeling of the segregation in systems Al-Cu, Cu-Zr [30], and discussed in terms of the complexions formation. Note, the process of amorphization in Al-Pb alloy near the GB is not associated with local melting, because a similar picture was obtained in our simulations at a temperature lower than expected for GB melting.
Thus, presented results of our MD/MC simulations at finite temperature support the conclusion about significant reconstruction of GB structure caused by segregation of solute atoms and demonstrate the variety of possible scenarios of this process; from GB enrichment to the formation of amorphous layer.

4. Discussion

The problem of GB chemistry has been discussed in the literature for many years based mostly on considering of a single solute atom and a GB with fixed structure. As a result, the microscopic mechanisms determining the solute–GB interaction and the effect of solute atoms on GB cohesive properties were identified [11,12,18,19,34,35]. However, the formation of GB segregations turns out to be a more difficult issue, and continues to be under discussion. As it was recently suggested, the GBs can exist in multiple states called complexions, which are characterized by different segregation capacity [13,46,47,48]. Thus, the consideration of interaction of a single solute atom with a GB is not enough for understanding segregation, and a reconstruction of the GB should be taken into account for further progress. In addition, the bottleneck in the investigation of this phenomenon with atomistic modeling is the lack of a reliable computational tool for interface structure prediction.
We employ here different scale methods of atomistic modeling to reveal a microscopic mechanism of the segregation formation and related GB reconstruction in Al alloys. By using ab initio calculations, we show that the character of chemical bonding is essential in the solute–GB interaction. Si or Zn solutes with extra p or d electrons form directed quasi-covalent bonds with neighboring Al atoms (chemical contribution) and causes a significant reconstruction of the GB structure (Figure 2) regardless of the initial GB configuration. This reconstruction involves GB coupled shear-migration processes, as it was discussed in Ref. [65]. For the solutes that have a bigger atomic size and accept electrons from the matrix (such as Mg), one can assume that the deformation contribution will be dominant. In this case, the symmetric GB keeps its structure (Figure 2c), but shifted GB may undergo the significant shear-migration coupled reconstruction (Figure 2f). In the latter case, a preferred position of Mg is determined by the extra volume at the GB and/or reduced number of nearest neighbors. Thus, the results of ab initio calculations give reliable evidence of the GB reconstruction due to segregation formation. Wherein, the presence of directional bonds and multiple GB states plays an important role.
It is important to note that by using ab initio calculations we simulate here fictitious segregations arising due to periodic boundary conditions along GB. At the same time, the alternating arrangement of solutes on both sides of the boundary (as it is shown in Figure 4a) may be more energetically preferable and results in two-layer GB segregations. Though MD/MC simulation does not provide completely reliable results, it allows realizing large-scale simulation of the segregation at finite temperatures, which is not available in the framework of ab initio calculations. The modeling of the interaction of different solute atoms (Mg, Ni, Cu, Pb) with the Σ5{012}<100> and Σ5{013}<100> GBs in Al matrix has shown that GBs undergo significant structural reconstruction during segregation in the most of the considered cases (Section 3.2). During the MD/MC runs, the structure of the GB itself, its spatial position, and the type of describing GB structural units may vary. The nature of the GB reconstruction is determined by preferable positions of solute atoms near the GB, which depend on features of solute–Al interactions. We found that single layer segregations are preferable in case of Mg in agreement with the results of ab initio modeling. At the same time, the double layer segregations form in case of Ni and Cu addition. Finally, the rather wide amorphous layer is formed in the GB area in case of Al-Pb alloy. It should be noted that the choice of the alternation of MC and MD runs plays a significant role in the reconstruction of the studied GBs, and presented results were obtained by using MD relaxation after each MC step.
In general, the solute–GB interaction is rather complex: It includes the deformation as well as the electronic contributions, and may result in GB reconstruction. Nevertheless, one should expect the deformation solute–GB interaction without GB reconstruction for solutes whose addition results in significant concentration increase in alloys. On the other hand, the segregation of transition elements with small solubility in bulk can lead to significant GB reconstruction.

5. Conclusions

To summarize, the presented results clearly show that segregation of solute atoms can be accompanied by a significant GB reconstruction, which, depending on the features of chemical bonding, may involve the GB splitting or shear-migration coupled reconstruction and complexions formation. In the case of solutes, for which the deformation contribution is dominant (such as Mg), one can expect that symmetric GB keeps its structure. At the same time, solutes with extra p or d electrons form directed quasi-covalent bonds with neighboring Al atoms (chemical contribution to solute–GB interaction) and cause a significant reconstruction of GB structure. The GB splitting and double layer segregations are possible in case of Ni and Cu addition, and the formation of rather wide amorphous layer in the GB area was found in case of Al-Pb alloy. The effect of such modified GBs on the properties of polycrystalline materials remains poorly understood by now.

Author Contributions

Conceptualization, Y.G. and L.K.; methodology, Y.G.; software, I.K. and A.K; validation, L.K., and Y.G.; formal analysis, I.K. and A.K.; investigation, L.K., and A.K.; data curation, Y.G.; writing–original draft preparation, L.K.; writing–review & editing, Y.G. and A.K., visualization, L.K. and A.K.

Funding

The research has been performed in the framework of the state assignment of the Ministry of Education and Science of the Russian Federation (topic “Structure”, No. A18-118020190116-6 and “Pressure”, No. A18-118020190104-3).

Acknowledgments

The results of the work were obtained using computational resources of MCC NRC “Kurchatov Institute”, http://computing.nrcki.ru/.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lejček, P. Grain Boundary Segregation in Metals; Springer: Berlin, Germany, 2010. [Google Scholar]
  2. Valiev, R.Z. Nanostructuring of metals by severe plastic deformation for advanced properties. Nat. Mater. 2004, 3, 511–516. [Google Scholar] [CrossRef]
  3. Sauvage, X.; Wilde, G.; Divinski, S.V.; Horita, Z.; Valiev, R.Z. Grain boundaries in ultrafine in ultrafine grained materials processed by severe plastic deformation and related phenomena. Mater. Sci. Eng. A 2012, 540, 1–12. [Google Scholar] [CrossRef] [Green Version]
  4. Raabe, D.; Sandlobes, S.; Millan, J.; Ponge, D.; Assadi, H.; Herbig, M.; Choi, P.-P. Segregation engineering enables nanoscale martensite to austenite phase transformation at grain boundaries: A pathway to ductile martensite. Acta Mater. 2013, 61, 6132–6152. [Google Scholar] [CrossRef]
  5. Chatterjee, P.P.; Pabi, S.K.; Manna, I. An allotropic transformation induced by mechanical alloying. J. Appl. Phys. 1999, 86, 5912–5914. [Google Scholar] [CrossRef]
  6. Ben Makhlouf, M.; Bachaga, T.; Suñol, J.J.; Mohamed Dammak, M.; Khitouni, M. Synthesis and characterization of nanocrystalline Al-20 at% Cu powders produced by mechanical alloying. Metals 2016, 6, 145. [Google Scholar] [CrossRef] [Green Version]
  7. Weissmuller, J. Alloy effects in nanostructures. Nanostruct. Mater. 1993, 3, 261–272. [Google Scholar] [CrossRef]
  8. Kirchheim, R. Grain coarsening inhibited by solute segregation. Acta Mater. 2002, 50, 413–419. [Google Scholar] [CrossRef]
  9. Trelewicz, J.R.; Schuh, C.A. Grain boundary segregation and thermodynamically stable binary nanocrystalline alloys. Phys. Rev. B 2009, 79, 094112. [Google Scholar] [CrossRef]
  10. Chookajorn, T.; Murdoch, H.A.; Schuh, C.A. Design of stable nanocrystalline alloys. Science 2012, 337, 951–954. [Google Scholar] [CrossRef] [Green Version]
  11. Lozovoi, A.Y.; Paxton, A.T.; Finnis, M.W. Structural and chemical embrittlement of grain boundaries by impurities: A general theory and first-principles calculations for copper. Phys. Rev. B 2006, 74, 155416. [Google Scholar] [CrossRef] [Green Version]
  12. Wachowicz, E.; Ossowski, T.; Kiejna, A. Cohesive and magnetic properties of grain boundaries in bcc Fe with Cr additions. Phys. Rev. B 2010, 81, 094104. [Google Scholar] [CrossRef] [Green Version]
  13. Zhu, Q.; Samanta, A.; Li, B.; Rudd, R.E.; Frolov, T. Predicting phase behavior of grain boundaries with evolutionary search and machine learning. Nat. Commun. 2018, 9, 467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Pan, Z.; Rupert, T.J. Amorphous intergranular films as toughening structural features. Acta Mater. 2015, 89, 205–214. [Google Scholar] [CrossRef] [Green Version]
  15. Krakauer, B.W.; Seidman, D.N. Subnanometer scale study of segregation at grain boundaries in an Fe(Si) alloy. Acta Mater. 1998, 46, 6145–6161. [Google Scholar] [CrossRef]
  16. Salem, A.A.; Langdon, T.G.; McNelley, T.R.; Kalidindi, S.R.; Semiatin, S.L. Strain-path effects on the evolution of microstructure and texture during the severe-plastic deformation of aluminum. Metall. Mater. Trans. A 2006, 37, 2879–2891. [Google Scholar] [CrossRef]
  17. Braithwaite, J.S.; Rez, P. Grain boundary impurities in iron. Acta Mater. 2005, 53, 2715–2726. [Google Scholar] [CrossRef]
  18. Zhang, S.; Kontsevoi, O.Y.; Freeman, A.J.; Olson, G.B. Sodium-induced embrittlement of an aluminum grain boundary. Phys. Rev. B 2010, 82, 224107. [Google Scholar] [CrossRef]
  19. Scheiber, D.; Razumovskiy, V.I.; Puschnig, P.; Pippanc, R.; Romaner, L. Ab initio description of segregation and cohesion of grain boundaries in W–25 at% Re alloys. Acta Mater. 2015, 88, 180–189. [Google Scholar] [CrossRef]
  20. Miller, M.K.; Cerezo, A.; Hetherlington, M.G.; Smith, G.D.W. Atom Probe Field Ion Microscopy; Oxford Science: Oxford, UK, 1996. [Google Scholar]
  21. Cerezo, A.; Clifton, P.H.; Lozano-Perez, S.; Panayi, P.; Sha, G.; Smith, G.D.W. Overview: Recent Progress in Three-Dimensional Atom Probe Instruments and Applications. Microsc. Microanal. 2007, 13, 408–417. [Google Scholar] [CrossRef]
  22. Blavette, D.; Cadel, E.; Pereige, C.; Deconihout, B.; Caron, P. Phase Transformation and Segregation to Lattice Defects in Ni-Base Superalloys. Microsc. Microanal. 2007, 13, 464–483. [Google Scholar] [CrossRef]
  23. Sha, G.; Marceau, R.K.W.; Gao, X.; Muddle, B.C.; Ringer, S.P. Nanostructure of aluminum alloy 2024: Segregation, clustering and precipitation processes. Acta Mater. 2011, 59, 1659–1670. [Google Scholar] [CrossRef]
  24. Sha, G.; Yao, L.; Liao, X.; Ringer, S.P.; Duan, Z.C.; Langdon, T.G. Segregation of solute elements at grain boundaries in an ultrafine grained Al-Zn-Mg-Cu alloy. Ultramicroscopy 2011, 111, 500–505. [Google Scholar] [CrossRef] [PubMed]
  25. Savage, X.; Ganeev, A.; Ivanisenko, Y.; Enikeev, N.; Murashkin, M.; Valiev, R. Grain Boundary Segregation in UFG Alloys Processed by Severe Plastic Deformation. Adv. Eng. Mater. 2012, 14, 968–974. [Google Scholar] [CrossRef] [Green Version]
  26. Udler, D.; Seidman, D.N. Congruent Phase Transition at a Twist Boundary Induced by Solute Segregation. Phys. Rev. Lett. 1996, 77, 3379. [Google Scholar] [CrossRef] [Green Version]
  27. Creuze, J.; Berthier, F.; Tétot, R.; Legrand, B. Wetting and Structural Transition Induced by Segregation at Grain Boundaries: A Monte Carlo Study. Phys. Rev. Lett. 2001, 86, 5735. [Google Scholar] [CrossRef] [PubMed]
  28. Kogtenkova, O.; Straumal, B.; Korneva, A.; Czeppe, T.; Wierzbicka-Miernik, A.; Faryna, M.; Zieba, P. Grain Boundary Complexions and Phase Transformations in Al- and Cu-Based Alloys. Metals 2019, 9, 10. [Google Scholar] [CrossRef] [Green Version]
  29. Pan, Z.; Rupert, T.J. Effect of grain boundary character on segregation-induced structural transitions. Phys. Rev. B 2016, 93, 134113. [Google Scholar] [CrossRef] [Green Version]
  30. Pan, Z.; Rupert, T.J. Atomistic modeling of interfacial segregation and structural transitions in ternary alloys. J. Mater. Sci. 2019, 54, 3975–3993. [Google Scholar]
  31. Khalajhedayati, A.; Pan, Z.L.; Rupert, T.J. Manipulating the interfacial structure of nanomaterials to achieve a unique combination of strength and ductility. Nat. Commun. 2016, 7, 10802. [Google Scholar] [CrossRef] [Green Version]
  32. Sauvage, X.; Enikeev, N.; Valiev, R.; Nasedkina, Y.; Murashkin, M. Atomic-scale analysis of the segregation and precipitation mechanisms in a severely deformed Al–Mg alloy. Acta Mater. 2014, 72, 125–136. [Google Scholar] [CrossRef]
  33. Bobruk, E.V.; Sauvage, X.; Enikeev, N.A.; Straumal, B.B.; Valiev, R.Z. Ultrafine Grained Structures Resulting from SPD-Induced Phase Transformation in Al-Zn Alloys. Rev. Adv. Mater. Sci. 2015, 43, 45–51. [Google Scholar]
  34. Karkina, L.E.; Karkin, I.N.; Kuznetsov, A.R.; Razumov, I.K.; Korzhavyi, P.A.; Gornostyrev, Y.N. Solute-grain boundary interaction and segregation formation in Al: First principles calculations and molecular dynamics modeling. Comput. Mater. Sci. 2016, 112, 18–26. [Google Scholar] [CrossRef]
  35. Petrik, M.V.; Kuznetsov, A.R.; Enikeev, N.; Gornostyrev, Y.N.; Valiev, R.Z. Peculiarities of Interactions of Alloying Elements with Grain Boundaries and the Formation of Segregations in Al–Mg and Al–Zn Alloys. Phys. Met. Metallogr. 2018, 119, 607–612. [Google Scholar] [CrossRef]
  36. Schweinfest, R.; Paxton, A.T.; Finnis, M.W. Bismuth embrittlement of copper is an atomic size effect. Nature 2004, 432, 1008–1011. [Google Scholar] [CrossRef]
  37. Yamaguchi, M.; Shiga, M.; Kaburaki, H. Grain Boundary Decohesion by Impurity Segregation in a Nickel-Sulfur System. Science 2005, 21, 393–397. [Google Scholar] [CrossRef]
  38. Zhang, L.; Shu, X.; Jin, S.; Zhang, Y.; Lu, G.H. First-principles study of He effects in a bcc Fe grain boundary: Site preference, segregation and theoretical tensile strength. J. Phys. Condens. Matter. 2010, 22, 375401. [Google Scholar] [CrossRef]
  39. Liu, X.; Wang, X.; Wang, J.; Zhang, H.J. First-principles investigation of Mg segregation at Σ = 11(113) grain boundaries in Al. J. Phys. Condens. Matter. 2005, 17, 4301–4308. [Google Scholar] [CrossRef]
  40. Christensen, M.; Angeliu, T.M.; Ballard, J.D.; Vollmer, J.; Najafabadi, R.; Wimmer, E. Effect of impurity and alloying elements on Zr grain boundary strength from first-principles computations. J. Nucl. Mater. 2010, 404, 121–127. [Google Scholar] [CrossRef]
  41. Yuasa, M.; Mabuchi, M.J. Effects of segregated Cu on an Fe grain boundary by first-principles tensile tests. J. Phys. Condens. Matter. 2010, 22, 505705. [Google Scholar] [CrossRef]
  42. Wachowicz, E.; Kiejna, A. Effect of impurities on grain boundary cohesion in bcc iron. Comput. Mater. Sci. 2008, 43, 736–743. [Google Scholar] [CrossRef]
  43. Pun, G.P.; Yamakov, V.; Mishin, Y. Interatomic potential for the ternary Ni–Al–Co system and application to atomistic modeling of the B2–L10 martensitic transformation. Model. Simul. Mater. Sci. Eng. 2015, 23, 065006. [Google Scholar]
  44. Koju, R.K.; Darling, K.A.; Kecskes, L.J.; Mishin, Y. Zener pinning of grain boundaries and structural stability of immiscible alloys. JOM 2016, 68, 1596–1604. [Google Scholar] [CrossRef]
  45. Li, A.; Szlufarska, I. Morphology and mechanical properties of nanocrystalline Cu/Ag alloy. J. Mater. Sci. 2017, 52, 4555–4567. [Google Scholar] [CrossRef] [Green Version]
  46. Dillon, S.J.; Tang, M.; Carter, W.C.; Harmer, M.P. Complexion: A new concept for kinetic engineering in materials science. Acta Mater. 2007, 55, 6208–6218. [Google Scholar] [CrossRef]
  47. Harmer, M.P. The phase behavior of interfaces. Science 2011, 332, 182–183. [Google Scholar] [CrossRef] [PubMed]
  48. Cantwell, P.R.; Tang, M.; Dillon, S.J.; Luo, J.; Rohrer, G.S.; Harmer, M.P. Grain boundary complexions. Acta Mater. 2014, 62, 1–48. [Google Scholar] [CrossRef]
  49. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  50. Kresse, G.; Hafner, J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys. Condens. Matter 1994, 6, 8245–8258. [Google Scholar] [CrossRef]
  51. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  52. Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
  53. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  54. LAMMPS Molecular Dynamics Simulator. Available online: http://lammps.sandia.gov/index.html (accessed on 18 January 2019).
  55. Mendelev, M.I.; Asta, M.; Rahman, M.J.; Hoyt, J.J. Development of interatomic potentials appropriate for simulation of solid–liquid interface properties in Al–Mg alloys. Philos. Mag. 2009, 89, 3269–3285. [Google Scholar] [CrossRef]
  56. Purja Pun, G.P.; Mishin, Y. Development of an interatomic potential for the Ni-Al system. Phil. Mag. 2009, 89, 3245–3267. [Google Scholar] [CrossRef]
  57. Apostol, F.; Mishin, Y. Interatomic potential for the Al-Cu system. Phys. Rev. B 2011, 83, 54116. [Google Scholar] [CrossRef] [Green Version]
  58. Landa, A.; Wynblatt, P.; Siegel, D.J.; Adams, J.B.; Mryasov, O.N.; Liu, X.-Y. Development of glue-type potentials for the Al-Pb system: Phase diagram calculation. Acta Mater. 2000, 48, 1753–1761. [Google Scholar] [CrossRef]
  59. Interatomic Potentials (Force Fields). Available online: http://www.ctcms.nist.gov/potentials/ (accessed on 20 January 2019).
  60. Guyot, P.; Simon, J.-P. Theoretical aspects of the interaction between grain-boundaries and impurities. J. Phys. Colloq. 1975, 36, 141–149. [Google Scholar] [CrossRef]
  61. Trautt, Z.T.; Mishin, Y. Grain Boundary Migration and Grain Rotation Studied by Molecular Dynamics. Acta Mater. 2012, 60, 2407–2424. [Google Scholar] [CrossRef]
  62. Guinier, A. Heterogeneities in Solid Solutions. Solid State Phys. 1959, 9, 293–398. [Google Scholar]
  63. Joshi, K.; Chaudhuri, S. Empirical force field-based kinetic Monte Carlo simulation of precipitate evolution and growth in Al–Cu alloys. Model. Simul. Mater. Sci. Eng. 2016, 24, 075012. [Google Scholar] [CrossRef]
  64. Gorbatov, O.I.; Gornostyrev, Y.N.; Korzhavyi, P.A. Many-body mechanism of Guinier-Preston zones stabilization in Al–Cu alloys. Scr. Mater. 2017, 138, 130–133. [Google Scholar] [CrossRef]
  65. Karkina, L.E.; Karkin, I.N.; Kuznetsov, A.R.; Gornostyrev, Y.N. Grain boundary shear-migration coupling in Al bicrystalls. Atomistic modeling. Phys. Solid State 2018, 60, 1916–1923. [Google Scholar] [CrossRef]
Metals 09 01319 g001 550
Figure 1. Calculated segregation energies of Mg, Si, Zn solute atoms in dependence on distance from symmetric (b) and shifted (d) grain boundary (GB). The structure of symmetric and shifted GBs is shown in fragments (a) and (c), respectively. Numbers correspond to positions of solute substituting an Al atom. Bigger and smaller balls in fragments (a,c) correspond to Al atom located in adjacent (001) planes. The supercell is doubled along the vertical axis for clarity.
Figure 1. Calculated segregation energies of Mg, Si, Zn solute atoms in dependence on distance from symmetric (b) and shifted (d) grain boundary (GB). The structure of symmetric and shifted GBs is shown in fragments (a) and (c), respectively. Numbers correspond to positions of solute substituting an Al atom. Bigger and smaller balls in fragments (a,c) correspond to Al atom located in adjacent (001) planes. The supercell is doubled along the vertical axis for clarity.
Metals 09 01319 g001
Metals 09 01319 g002 550
Figure 2. Charge density distribution after atomic relaxation of the crystalline containing the Σ5{210}[001] GB and solute atom Si (a,d), Zn (b,e), and Mg (c,f) in position 3. Fragments (a,b,c) and (d,e,f) correspond to symmetric and shifted GBs, respectively. The dashed line shows the initial position of the GB. The supercell is doubled along the vertical axis for clarity.
Figure 2. Charge density distribution after atomic relaxation of the crystalline containing the Σ5{210}[001] GB and solute atom Si (a,d), Zn (b,e), and Mg (c,f) in position 3. Fragments (a,b,c) and (d,e,f) correspond to symmetric and shifted GBs, respectively. The dashed line shows the initial position of the GB. The supercell is doubled along the vertical axis for clarity.
Metals 09 01319 g002
Metals 09 01319 g003 550
Figure 3. The fragment of the crystalline with the Σ5{013}<100> GB (a) and Σ5{012}<100>GB (b) in Al-3%Mg alloy after 106 MD/MC runs. Dashed lines show the initial position of the GB plane. Black and red circles mark Al and Mg atoms, respectively. Filed and open circles correspond to atoms, located in adjacent {001} planes.
Figure 3. The fragment of the crystalline with the Σ5{013}<100> GB (a) and Σ5{012}<100>GB (b) in Al-3%Mg alloy after 106 MD/MC runs. Dashed lines show the initial position of the GB plane. Black and red circles mark Al and Mg atoms, respectively. Filed and open circles correspond to atoms, located in adjacent {001} planes.
Metals 09 01319 g003
Metals 09 01319 g004 550
Figure 4. The fragment of the crystalline with the Σ5{013}<100> GB (a) and Σ5{012}<100> GB (b) in Al-3%Ni alloy after 106 MD/MC runs. Dashed lines show the initial position of the GB plane. Black and red circles mark Al and Ni atoms, respectively. Filed and open circles correspond to atoms, located in adjacent {001} planes.
Figure 4. The fragment of the crystalline with the Σ5{013}<100> GB (a) and Σ5{012}<100> GB (b) in Al-3%Ni alloy after 106 MD/MC runs. Dashed lines show the initial position of the GB plane. Black and red circles mark Al and Ni atoms, respectively. Filed and open circles correspond to atoms, located in adjacent {001} planes.
Metals 09 01319 g004
Metals 09 01319 g005 550
Figure 5. The fragment of the crystalline with the Σ5{012}<100> GB in Al-3%Pb alloy after 2 × 102 (a), 103 (b), and 106 (c) MD/MC steps. Black and red circles mark Al and Pb atoms, respectively. Filed and open circles correspond to Al atoms, located in adjacent {001} planes. Pb atoms form an amorphous plate and fill different positions without separation into layers.
Figure 5. The fragment of the crystalline with the Σ5{012}<100> GB in Al-3%Pb alloy after 2 × 102 (a), 103 (b), and 106 (c) MD/MC steps. Black and red circles mark Al and Pb atoms, respectively. Filed and open circles correspond to Al atoms, located in adjacent {001} planes. Pb atoms form an amorphous plate and fill different positions without separation into layers.
Metals 09 01319 g005

Share and Cite

MDPI and ACS Style

Karkina, L.; Karkin, I.; Kuznetsov, A.; Gornostyrev, Y. Alloying Element Segregation and Grain Boundary Reconstruction, Atomistic Modeling. Metals 2019, 9, 1319. https://doi.org/10.3390/met9121319

AMA Style

Karkina L, Karkin I, Kuznetsov A, Gornostyrev Y. Alloying Element Segregation and Grain Boundary Reconstruction, Atomistic Modeling. Metals. 2019; 9(12):1319. https://doi.org/10.3390/met9121319

Chicago/Turabian Style

Karkina, Lidia, Iliya Karkin, Andrey Kuznetsov, and Yuri Gornostyrev. 2019. "Alloying Element Segregation and Grain Boundary Reconstruction, Atomistic Modeling" Metals 9, no. 12: 1319. https://doi.org/10.3390/met9121319

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop