Power Spinning of the Curved Head with Tailor Welded Aluminum Alloy Blank: Deformation, Microstructure, and Property
Abstract
:1. Introduction
2. Material and Method
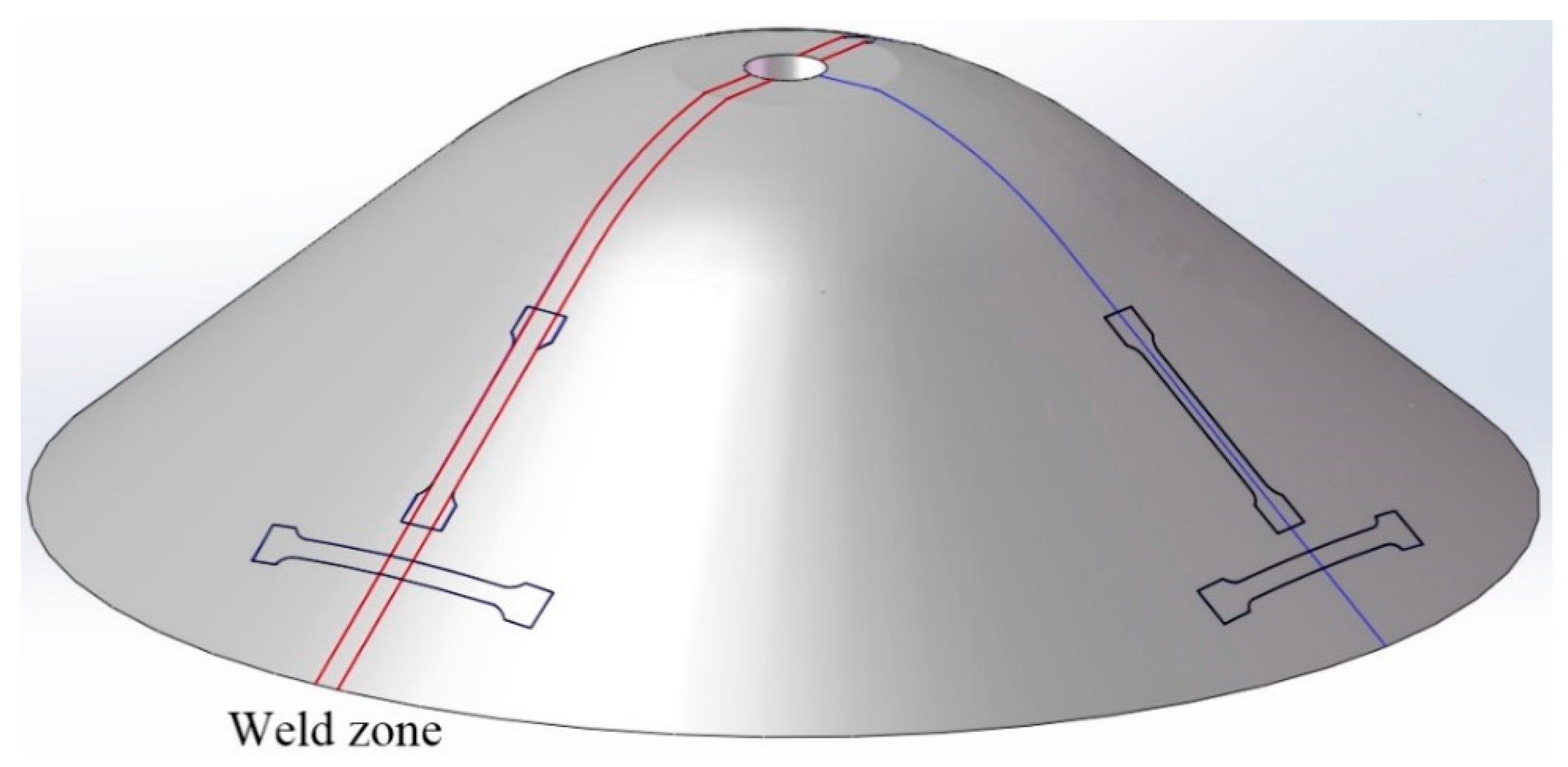
2.1. Material and Curved Head Component
2.2. FE Modelling of the Power Spinning with TWB
2.3. Experimental Validation of the FE Model
3. Results and Discussion
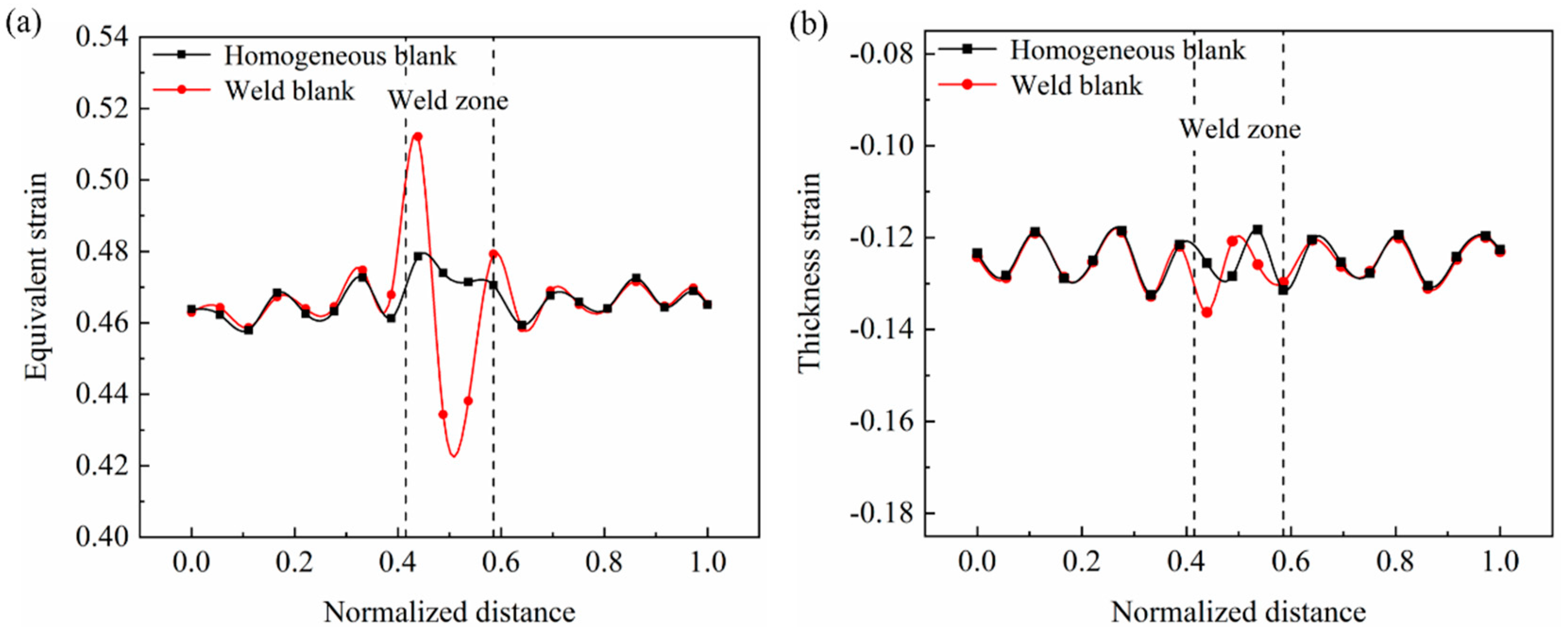
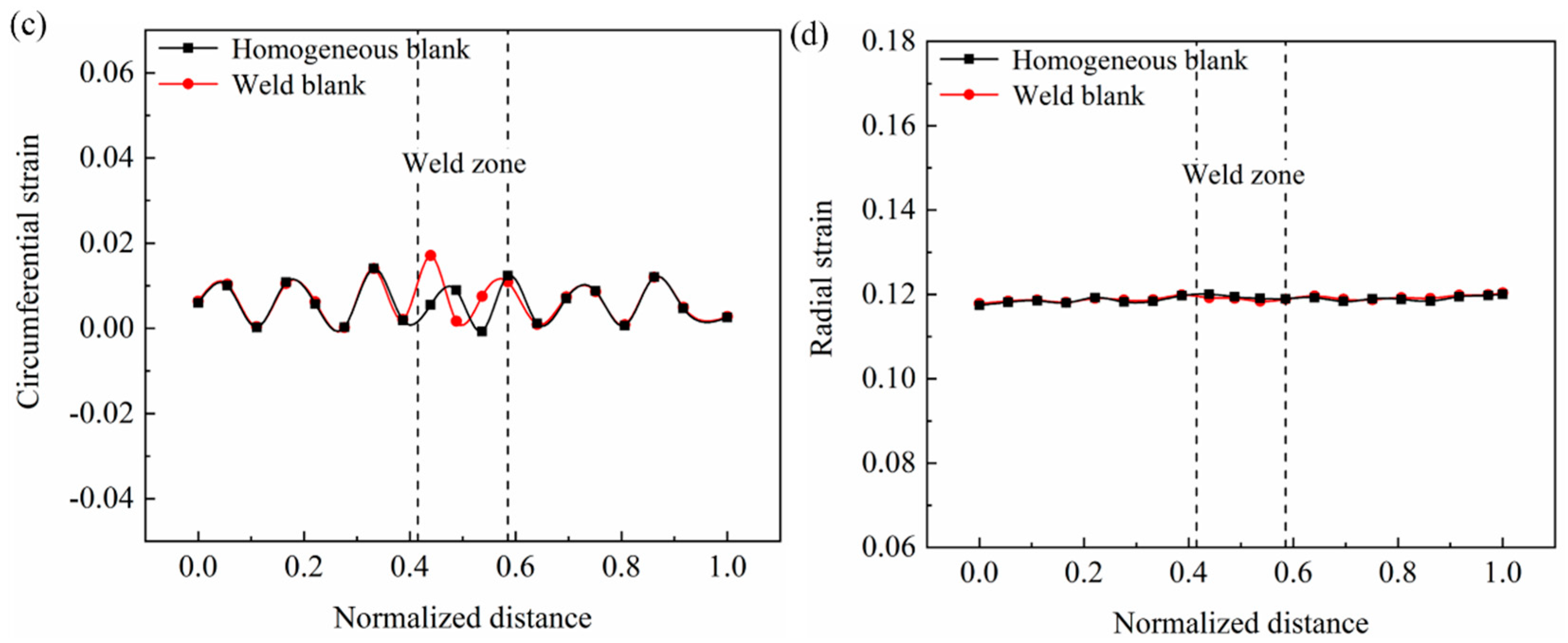
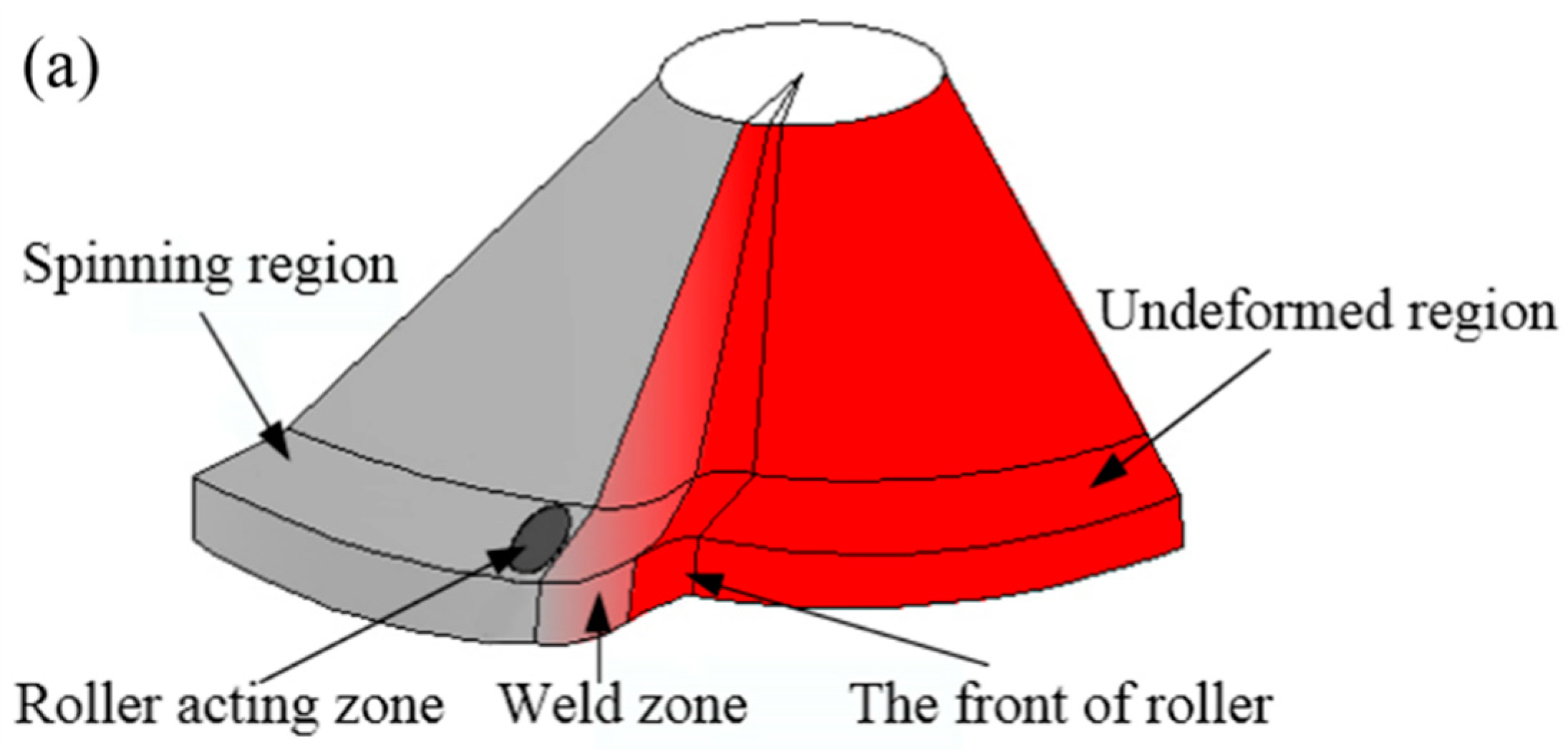
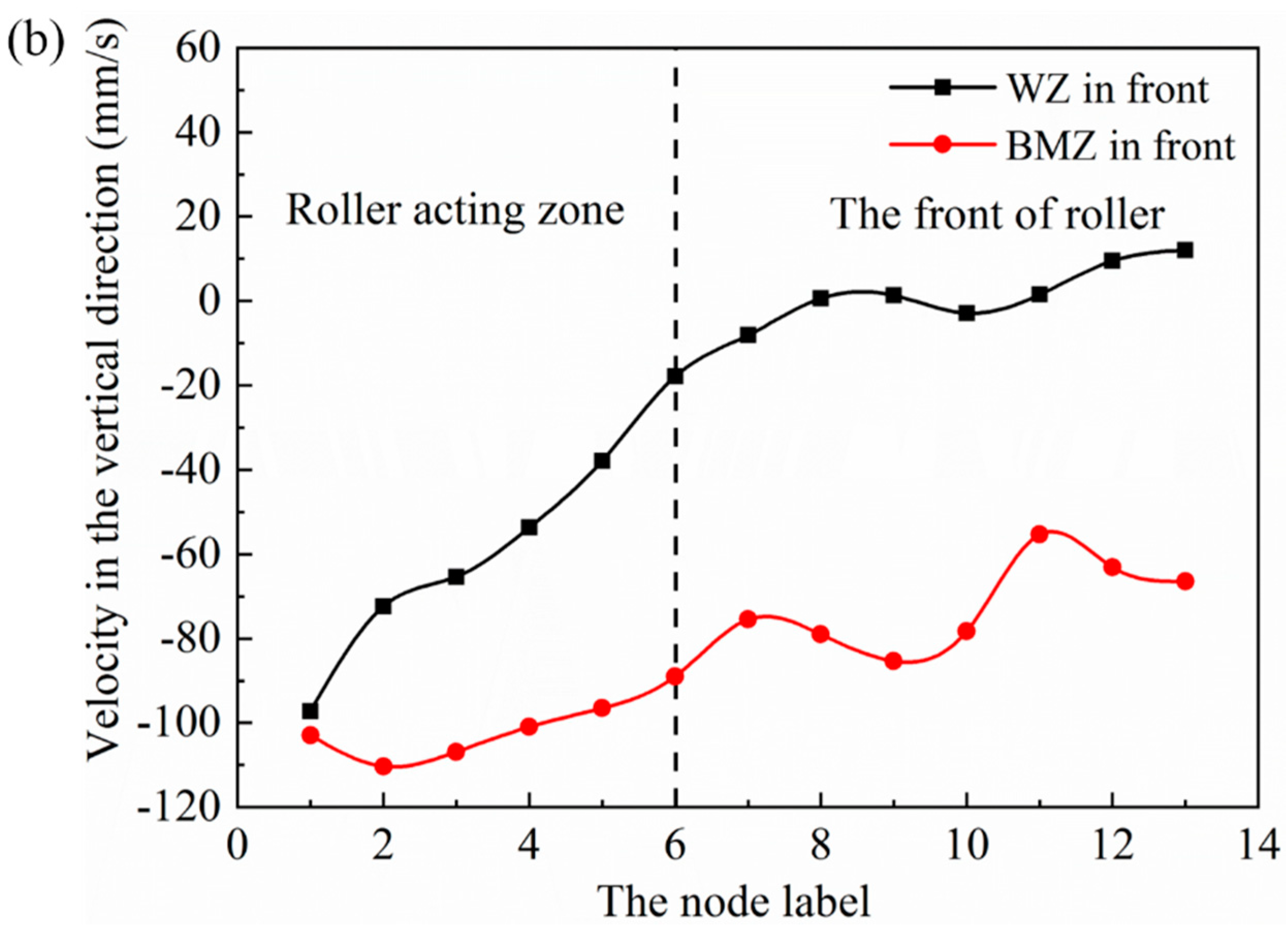
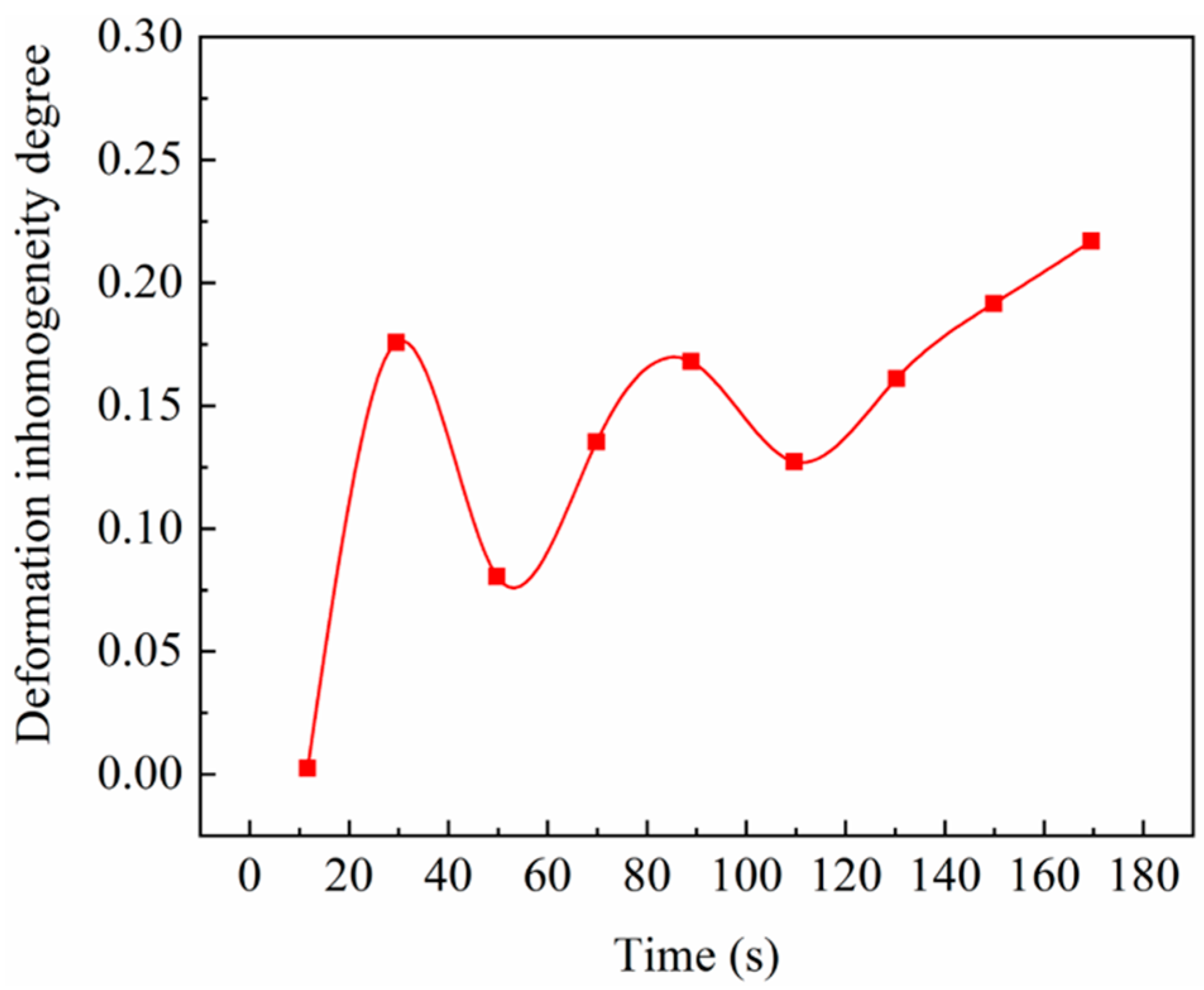
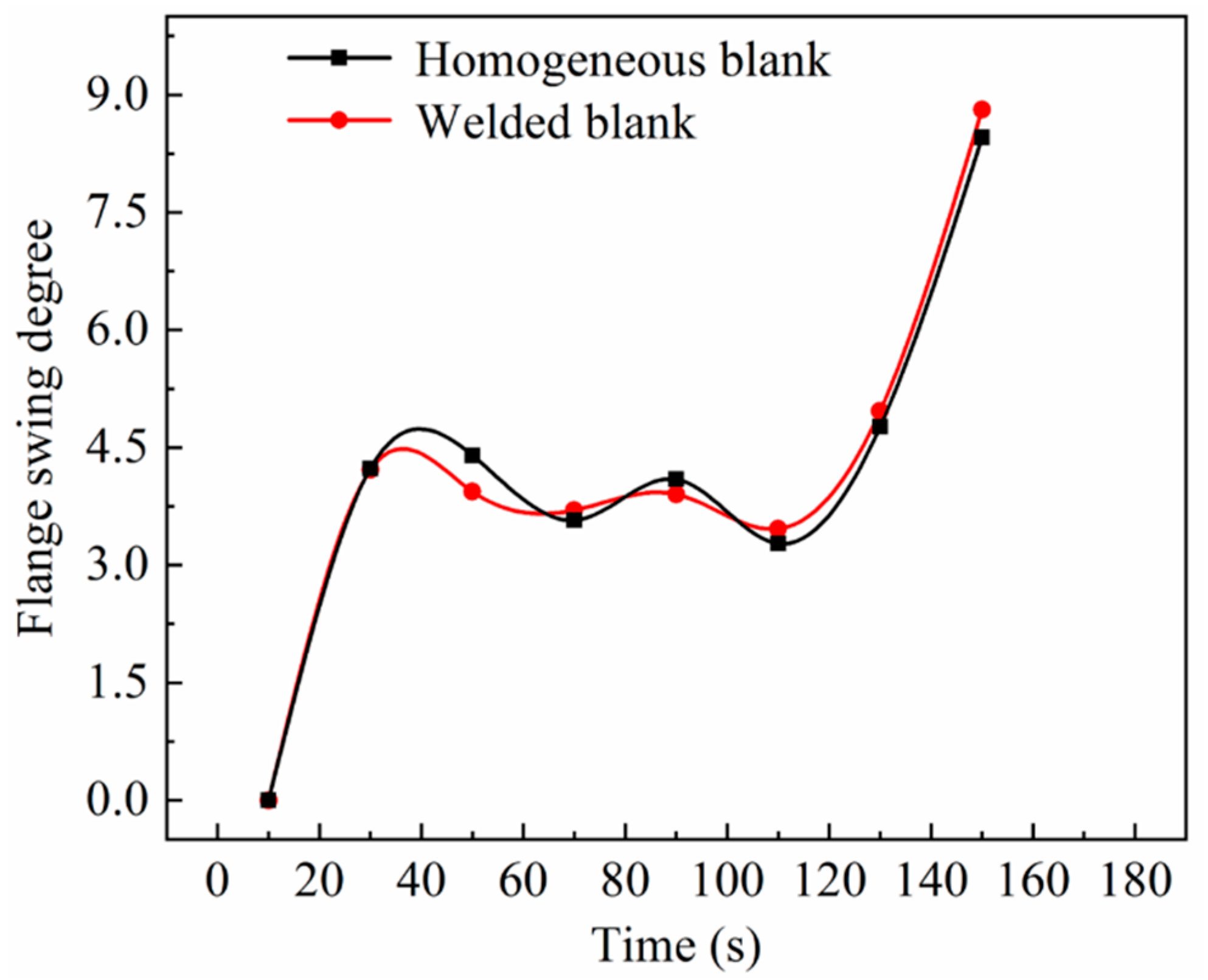
3.1. Deformation Characteristics
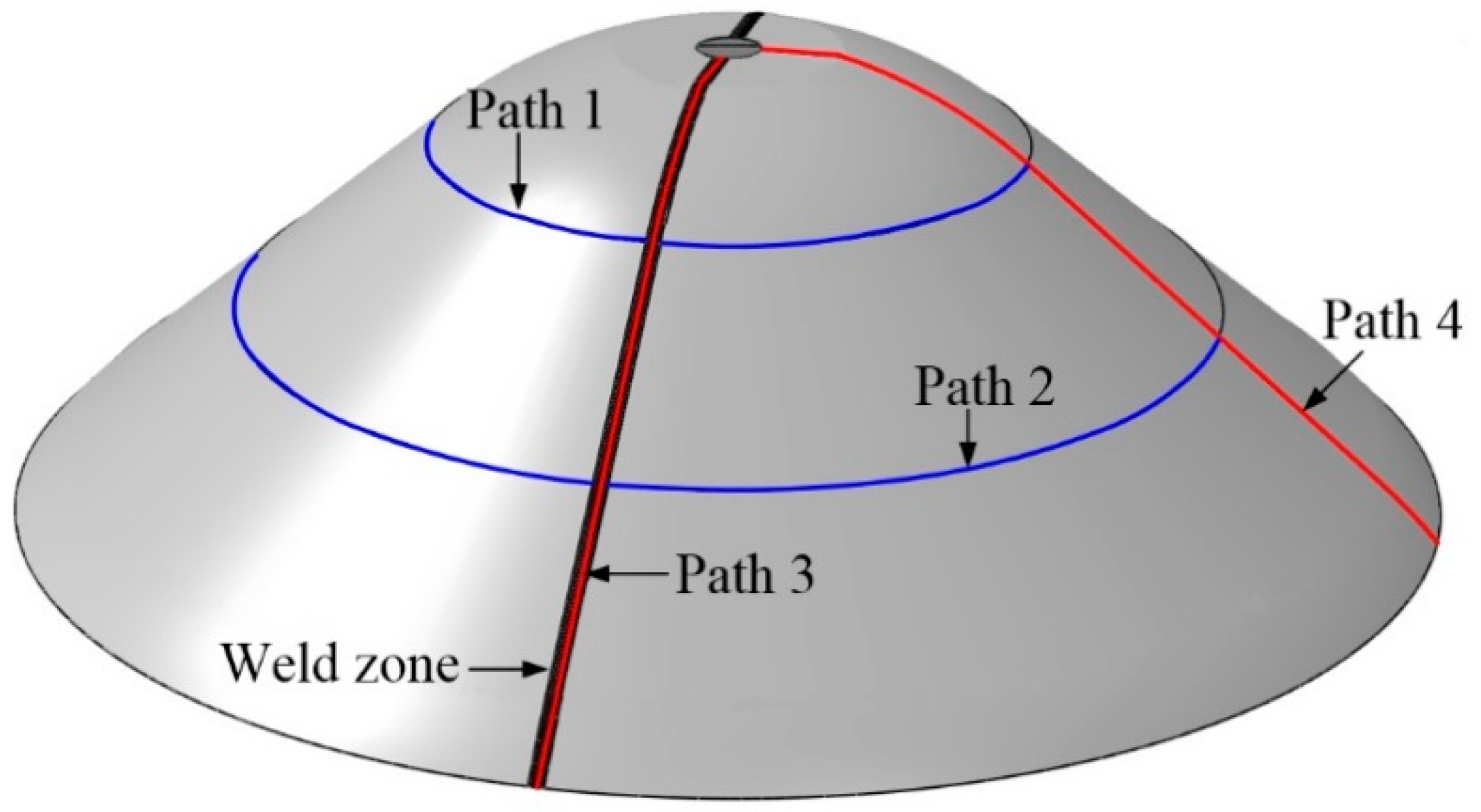
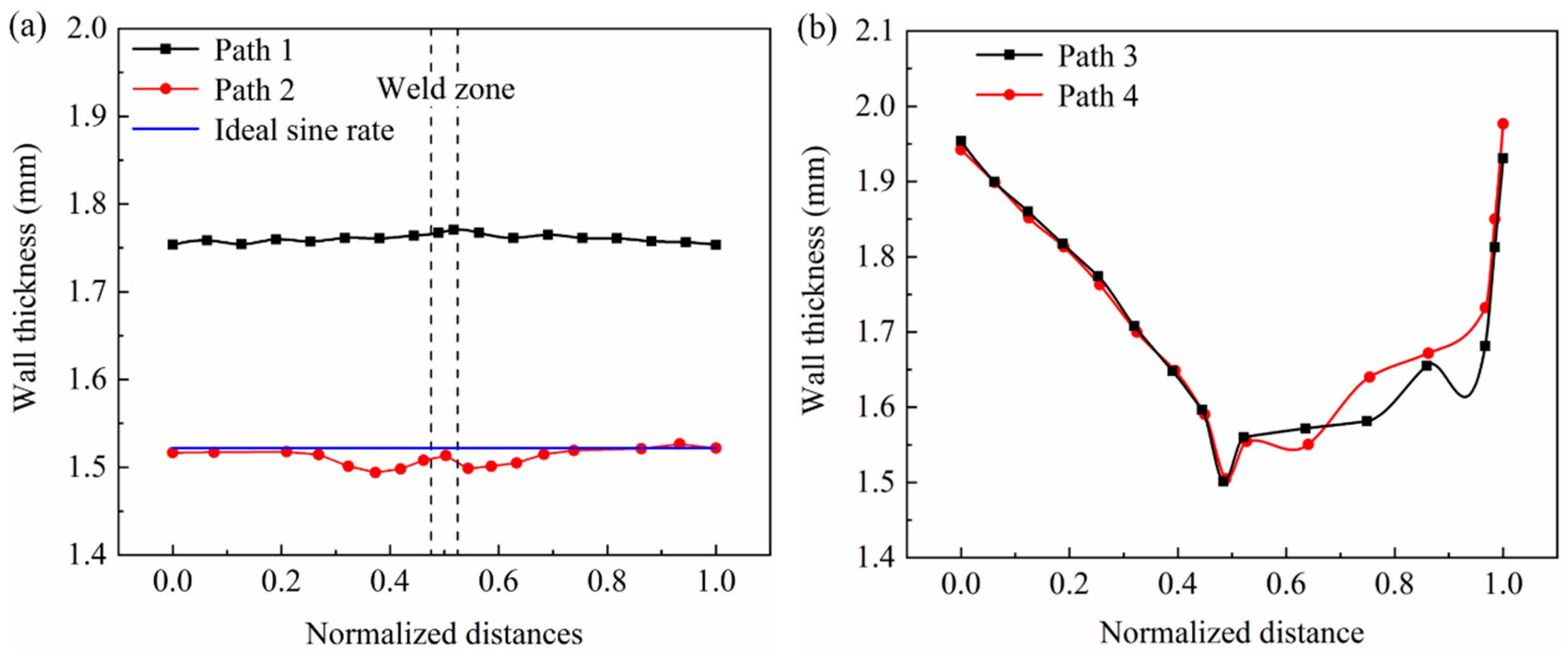
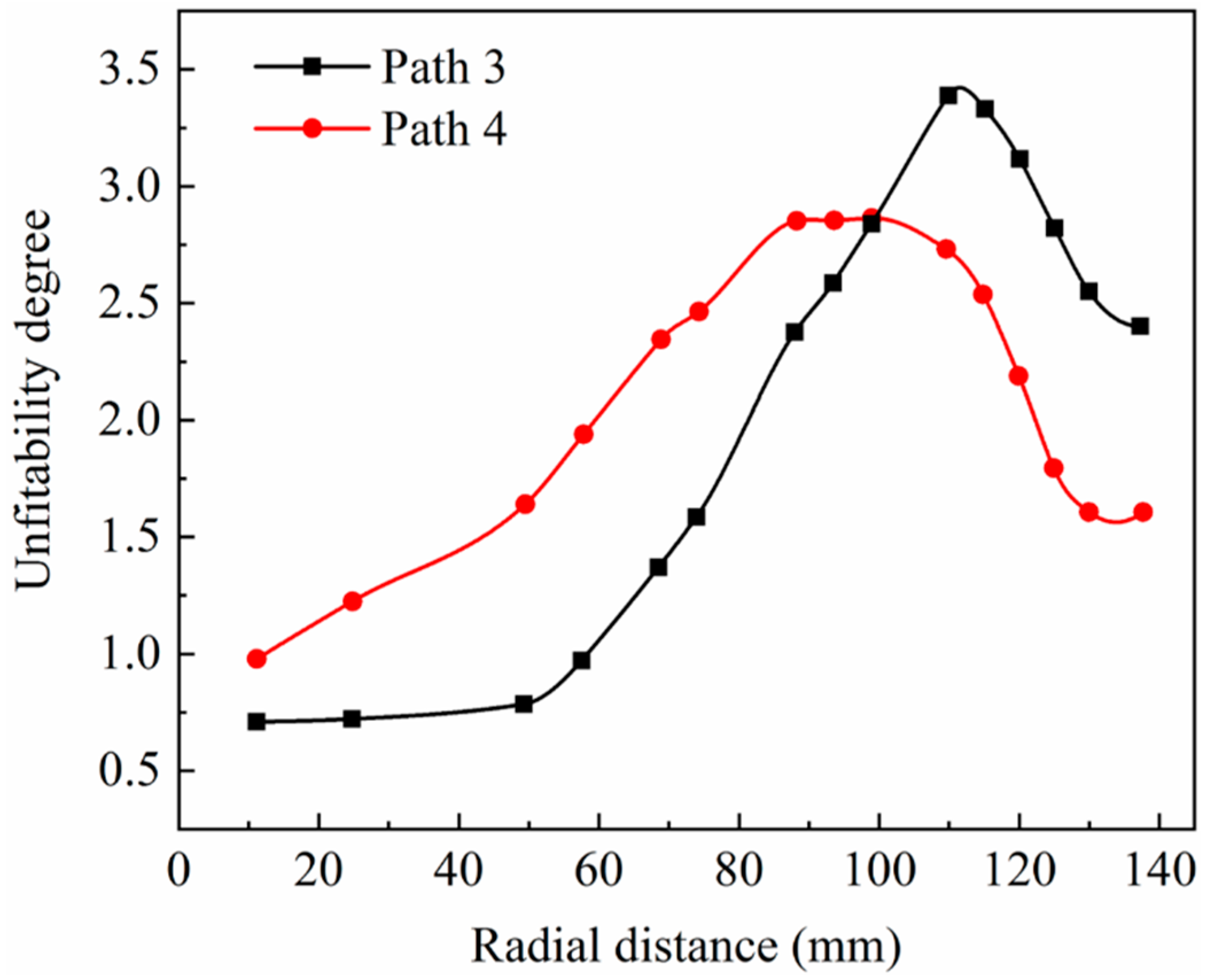
3.2. Wall Thickness and Unfitability Distribution
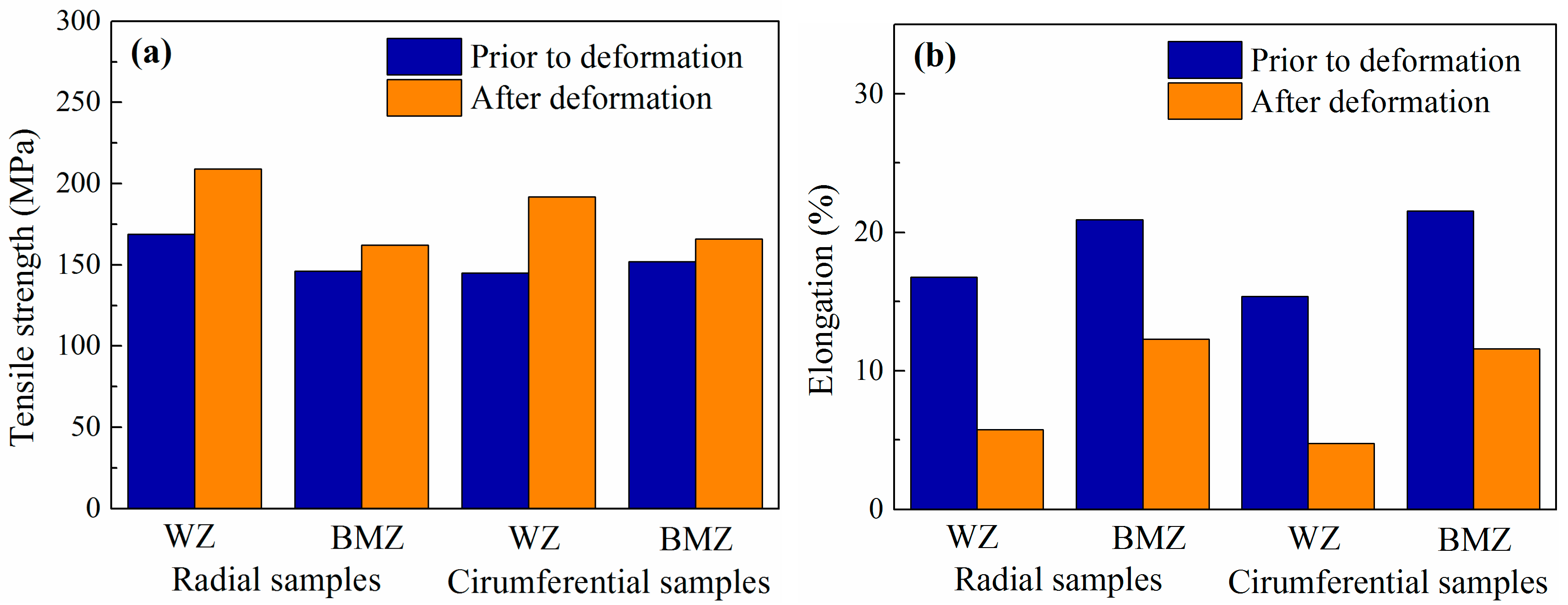
3.3. Microstructure and Mechanical Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xia, Q.X.; Xiao, G.F.; Long, H.; Cheng, X.Q.; Sheng, X.F. A review of process advancement of novel metal spinning. Int. J. Mach. Tools Manuf. 2014, 85, 100–121. [Google Scholar] [CrossRef]
- Music, O.; Allwood, J.M.; Kawai, K. A review of the mechanics of metal spinning. J. Mater. Process. Technol. 2010, 210, 3–23. [Google Scholar] [CrossRef]
- Threadgill, P.L.; Leonard, A.J.; Shercliff, H.R.; Withers, P.J. Friction stir welding of aluminium alloys. Int. Mater. Rev. 2013, 54, 49–93. [Google Scholar] [CrossRef]
- Xu, W.F.; Liu, J.H.; Luan, G.H.; Dong, C.L. Microstructure and mechanical properties of friction stir welded joints in 2219-T6 aluminum alloy. Mater. Des. 2009, 30, 3460–3467. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, B.L.; Ma, Z.Y. Effect of welding parameters on microstructure and mechanical properties of friction stir welded 2219Al-T6 joints. J. Mater. Sci. 2012, 47, 4075–4086. [Google Scholar] [CrossRef]
- Mishra, R.S.; De, P.S.; Kumar, N. Friction Stir Welding and Processing: Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Kosturek, R.; Sniezek, L.; Wachowski, M.; Torzewski, J. The influence of post-weld heat treatment on the microstructure and fatigue properties of Sc-modified AA2519 friction stir-welded joint. Materials 2019, 12, 583. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.F.; Fu, M.W.; Zhan, M.; Lei, Z.N.; Li, Y.X. Deformation behavior and microstructure evolution of titanium alloys with lamellar microstructure in hot working process: A review. J. Mater. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Gao, P.F.; Qin, G.; Wang, X.X.; Li, Y.X.; Zhan, M.; Li, G.J.; Li, J.S. Dependence of mechanical properties on the microstructural parameters of TA15 titanium alloy with tri-modal microstructure. Mater. Sci. Eng. A 2019, 739, 203–213. [Google Scholar] [CrossRef]
- Zhang, J.H.; Zhan, M.; Yang, H.; Jiang, Z.Q.; Han, D. 3D-FE modeling for power spinning of large ellipsoidal heads with variable thicknesses. Comput. Mater. Sci. 2012, 53, 303–313. [Google Scholar] [CrossRef]
- Zhan, M.; Yang, H.; Zhang, J.H.; Xu, Y.L.; Ma, F. Research on variation of stress and strain field and wall thickness during cone spinning. Mater. Sci. Forum 2006, 532, 149–152. [Google Scholar] [CrossRef]
- Zhan, M.; Yang, H.; Zhang, J.H.; Xu, Y.L.; Ma, F. 3D FEM analysis of influence of roller feed rate on forming force and quality of cone spinning. J. Mater. Process. Technol. 2007, 187, 486–491. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Xu, W.C.; Shan, D.B. Study on the spinning process of thin-walled aluminum alloy vessel head. Forg. Stamp. Technol. China 2006, 3, 74–78. [Google Scholar]
- Gan, T.; Yu, Z.Q.; Zhao, Y.X.; Evsyukov, S.A.; Lai, X.M. Effects of backward path parameters on formability in conventional spinning of aluminum hemispherical parts. Trans. Nonferr. Metal. Soc. 2018, 28, 328–339. [Google Scholar] [CrossRef]
- Heo, Y.M.; Wang, S.H.; Kim, H.Y.; Seo, D.G. The effect of the drawbead dimensions on the weld-line movements in the deep drawing of tailor welded blanks. J. Mater. Process. Technol. 2001, 113, 686–691. [Google Scholar] [CrossRef]
- Liu, J.; Gao, G.X.; Fakir, O.E.; Wang, L.L.; Lin, J.G. Hot stamping of AA6082 tailor welded blanks: Experiment and FE simulation. Manuf. Rev. 2016, 3, 8. [Google Scholar] [CrossRef] [Green Version]
- Wang, A.L.; Liu, J.; Gao, H.X.; Wang, L.L.; Masen, M. Hot stamping of AA6082 tailor welded blanks: Experiments and knowledge-based cloud–finite element (KBC-FE) simulation. J. Mater. Process. Technol. 2017, 250, 228–238. [Google Scholar] [CrossRef]
- Lee, W.; Chung, K.H.; Kim, D.Y.; Kim, J.; Kim, C.M.; Okamoto, K.; Wagoner, R.H.; Chung, K. Experimental and numerical study on formability of friction stir welded TWB sheets based on hemispherical dome stretch tests. Int. J. Plast. 2009, 25, 1626–1654. [Google Scholar] [CrossRef]
- Habibi, M.; Hashemi, R.; Tafti, F.M.; Assempour, A. Experimental investigation of mechanical properties, formability and forming limit diagrams for tailor-welded blanks produced by friction stir welding. J. Manuf. Process. 2018, 31, 310–323. [Google Scholar] [CrossRef]
- Ren, N.; Zhan, M.; Yang, H.; Zhang, Z.Y.; Qin, Y.T.; Jiang, H.M.; Diao, K.S.; Chen, X.P. Constraining effects of weld and heat-affected zone on deformation behaviors of welded tubes in numerical control bending process. J. Mater. Process. Technol. 2012, 212, 1106–1115. [Google Scholar] [CrossRef]
- Mennecart, T.; Güner, A.; Khalifa, N.B.; Tekkaya, A.E. Effects of Weld zone in Deep Drawing of Tailor Welded Blanks of High Strength Steels. Key Eng. Mater. 2014, 611, 955–962. [Google Scholar] [CrossRef]
- Ren, N. Study on Deformation Compatibility and Bending Limit in Steel Welded Tube NC Bending Processes. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2013. [Google Scholar]
- Xing, L.; Zhan, M.; Gao, P.F.; Ma, F. A method for establishing a continuous constitutive model of welded metals. Mater. Sci. Eng. A 2018, 718, 228–240. [Google Scholar] [CrossRef]
- Zhang, J.H. Deformation Laws of Power Spinning of D406A Large Ellipsoidal Heads with Variable Thicknesses. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2012. [Google Scholar]
- Zhan, M.; Wang, X.X.; Long, H. Mechanism of grain refinement of aluminum alloy in shear spinning under different deviation ratios. Mater. Des. 2016, 108, 207–216. [Google Scholar] [CrossRef]
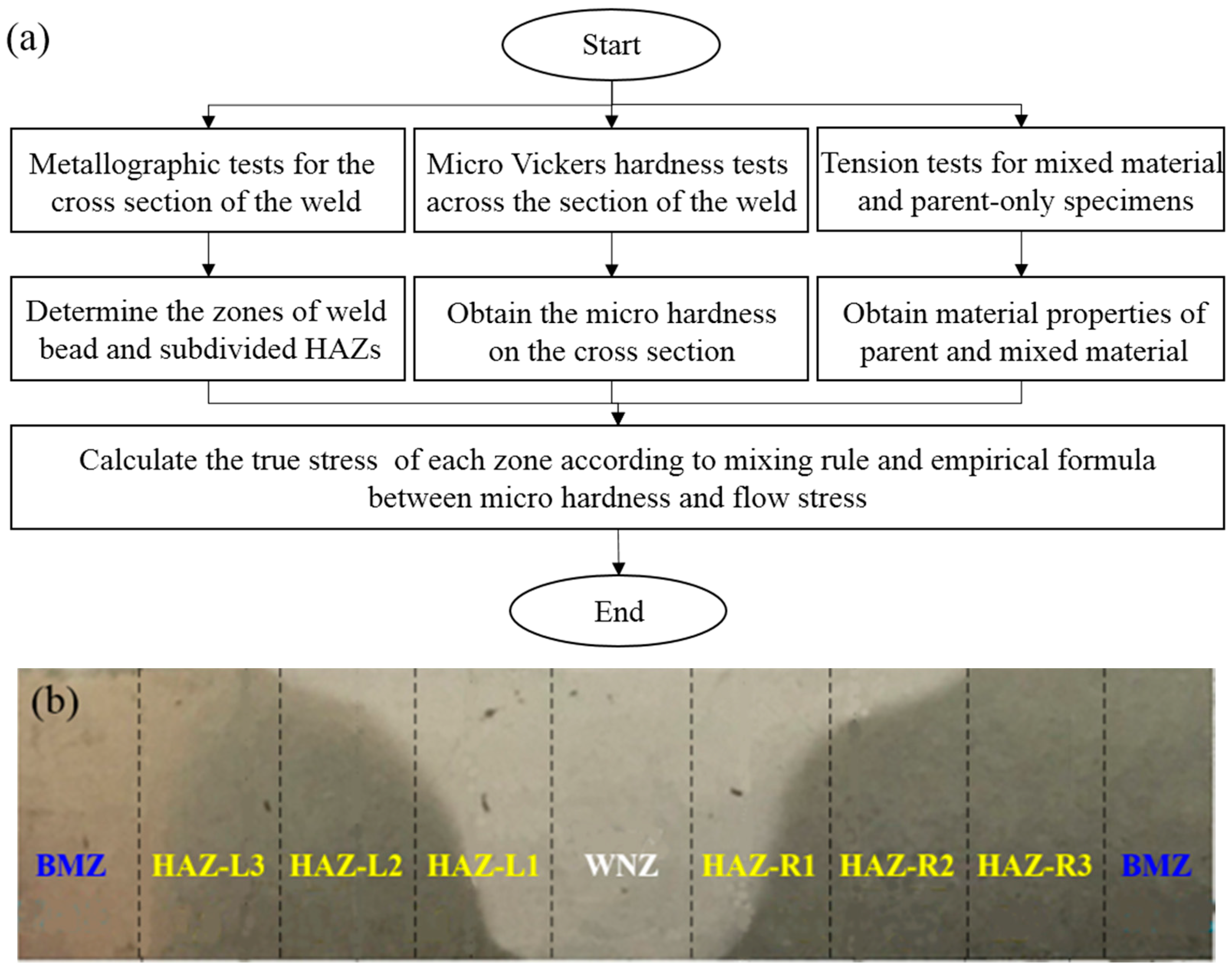

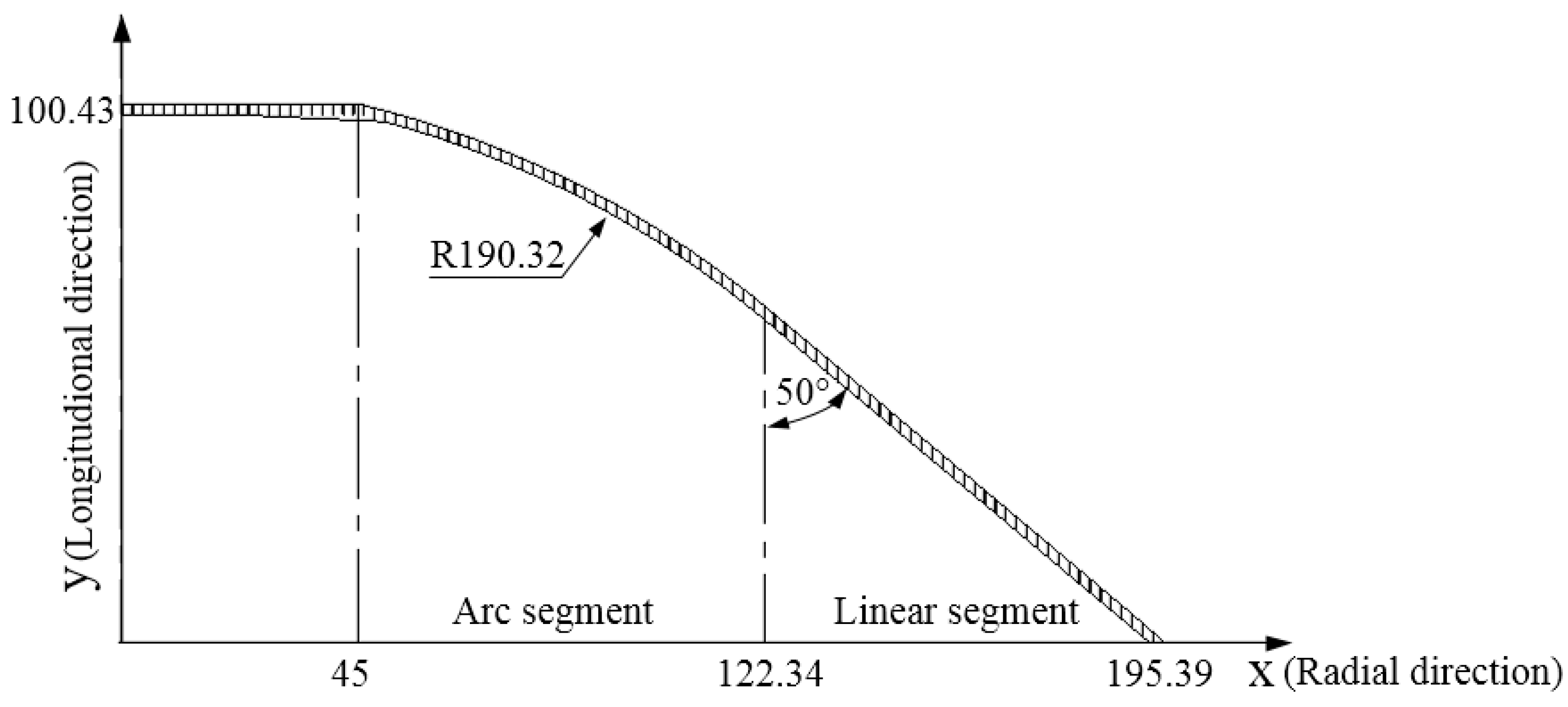
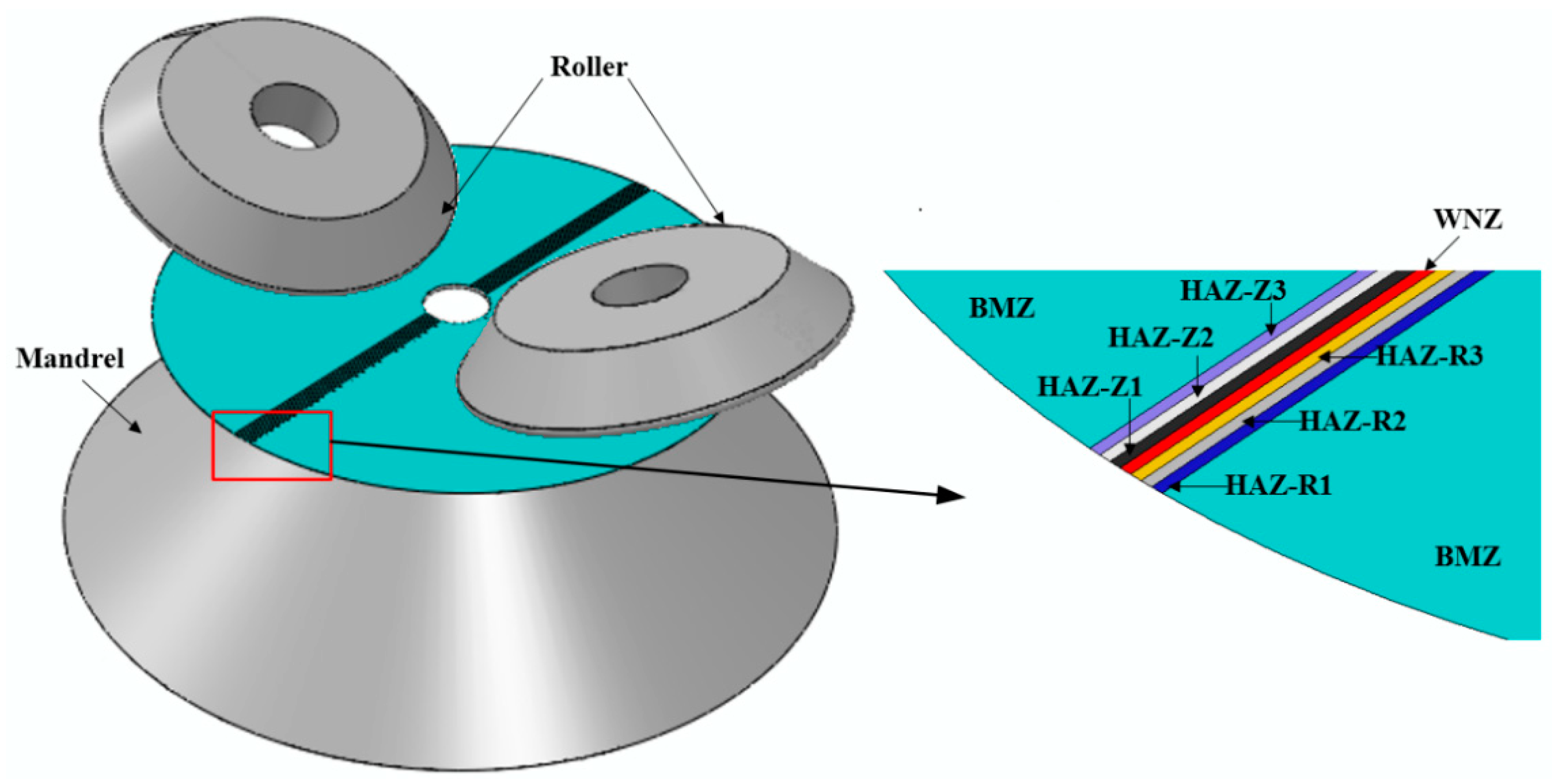
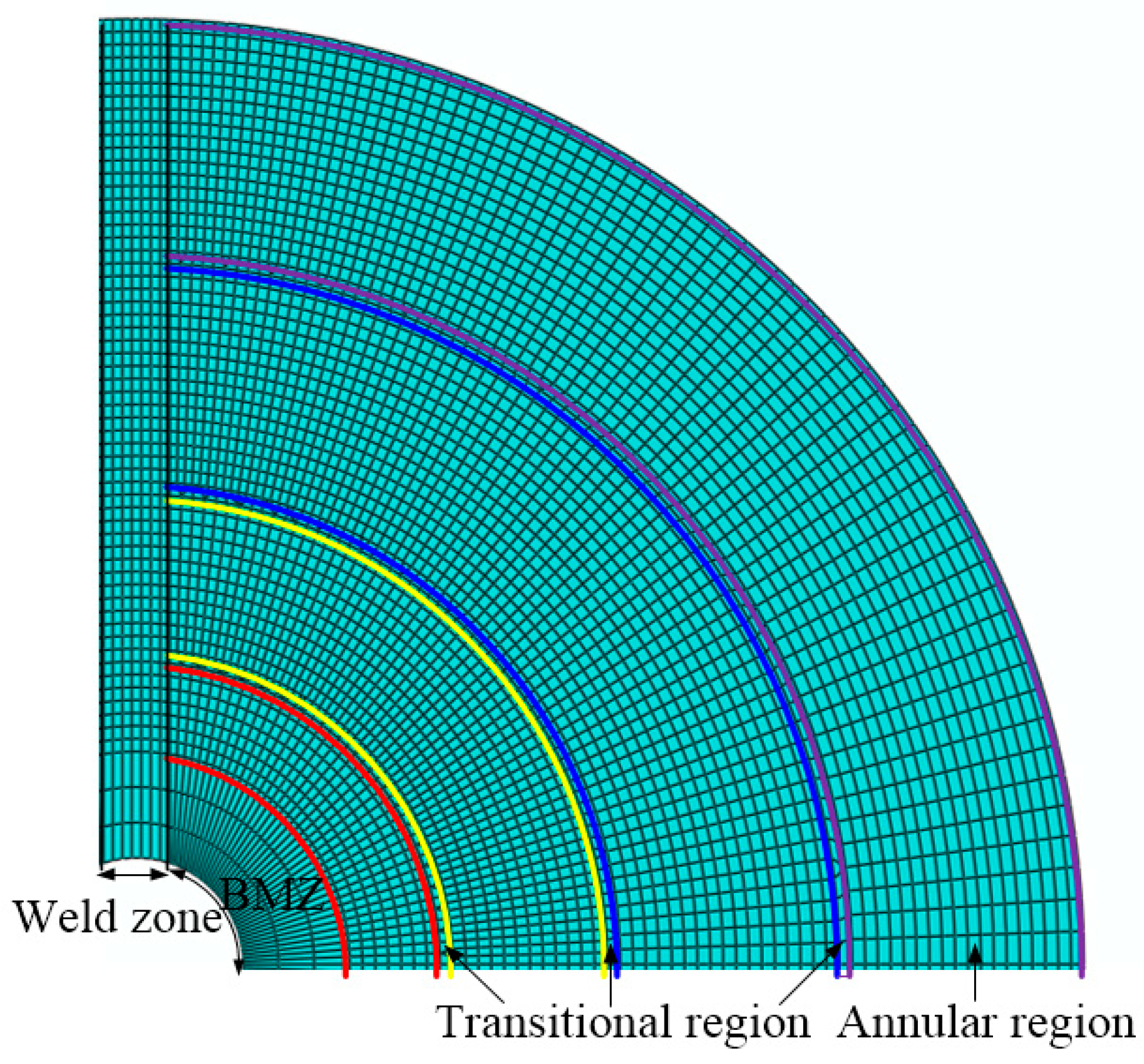






| Mechanical Properties | BMZ | HAZ-L1 | HAZ-L2 | HAZ-L3 | WNZ | HAZ-R1 | HAZ-R2 | HAZ-R3 |
|---|---|---|---|---|---|---|---|---|
| Young’s modulus E (MPa) | 57,982 | 62,305 | 64,093 | 64,729 | 60,416 | 60,604 | 63,629 | 64,412 |
| Yield strength σs (MPa) | 88.35 | 74.67 | 83.01 | 86.39 | 67.59 | 73.09 | 80.66 | 84.78 |
| Microhardness (HV) | 48 | 55 | 53 | 50 | 67 | 58 | 54 | 52 |
| Parameters | Values |
|---|---|
| Mandrel speed nM (rpm) | 80 in arc segment and 60 in line segment |
| Feed rate f (mm/r) | 1 |
| Roller nose radius ρ (mm) | 4 |
| Roller diameter DR (mm) | 200 |
| Deviation rate | 0 |
| Roller oblique angle β (°) | 20 |
| Friction coefficient | 0.05 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, F.; Gao, P.; Ma, P.; Zhan, M. Power Spinning of the Curved Head with Tailor Welded Aluminum Alloy Blank: Deformation, Microstructure, and Property. Metals 2019, 9, 1359. https://doi.org/10.3390/met9121359
Ma F, Gao P, Ma P, Zhan M. Power Spinning of the Curved Head with Tailor Welded Aluminum Alloy Blank: Deformation, Microstructure, and Property. Metals. 2019; 9(12):1359. https://doi.org/10.3390/met9121359
Chicago/Turabian StyleMa, Fei, Pengfei Gao, Pengyu Ma, and Mei Zhan. 2019. "Power Spinning of the Curved Head with Tailor Welded Aluminum Alloy Blank: Deformation, Microstructure, and Property" Metals 9, no. 12: 1359. https://doi.org/10.3390/met9121359
APA StyleMa, F., Gao, P., Ma, P., & Zhan, M. (2019). Power Spinning of the Curved Head with Tailor Welded Aluminum Alloy Blank: Deformation, Microstructure, and Property. Metals, 9(12), 1359. https://doi.org/10.3390/met9121359




