Thermodynamic Modelling on Nanoscale Growth of Magnesia Inclusion in Fe-O-Mg Melt
Abstract
:1. Introduction
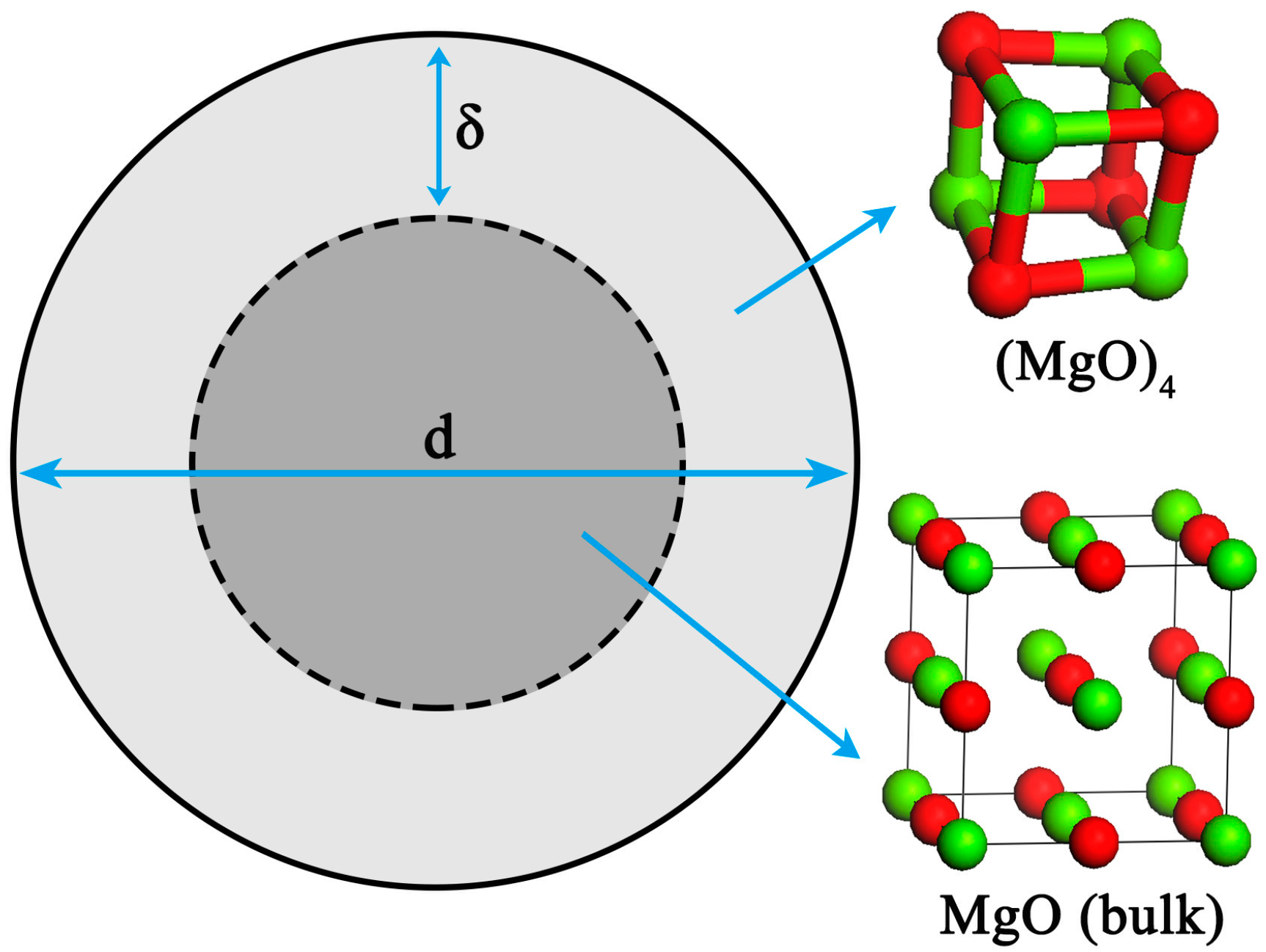
2. Theoretical Modeling for Nano-MgO in Liquid Iron
2.1. Thermodynamic Modeling
2.2. Calculation Method
3. Results and Discussions
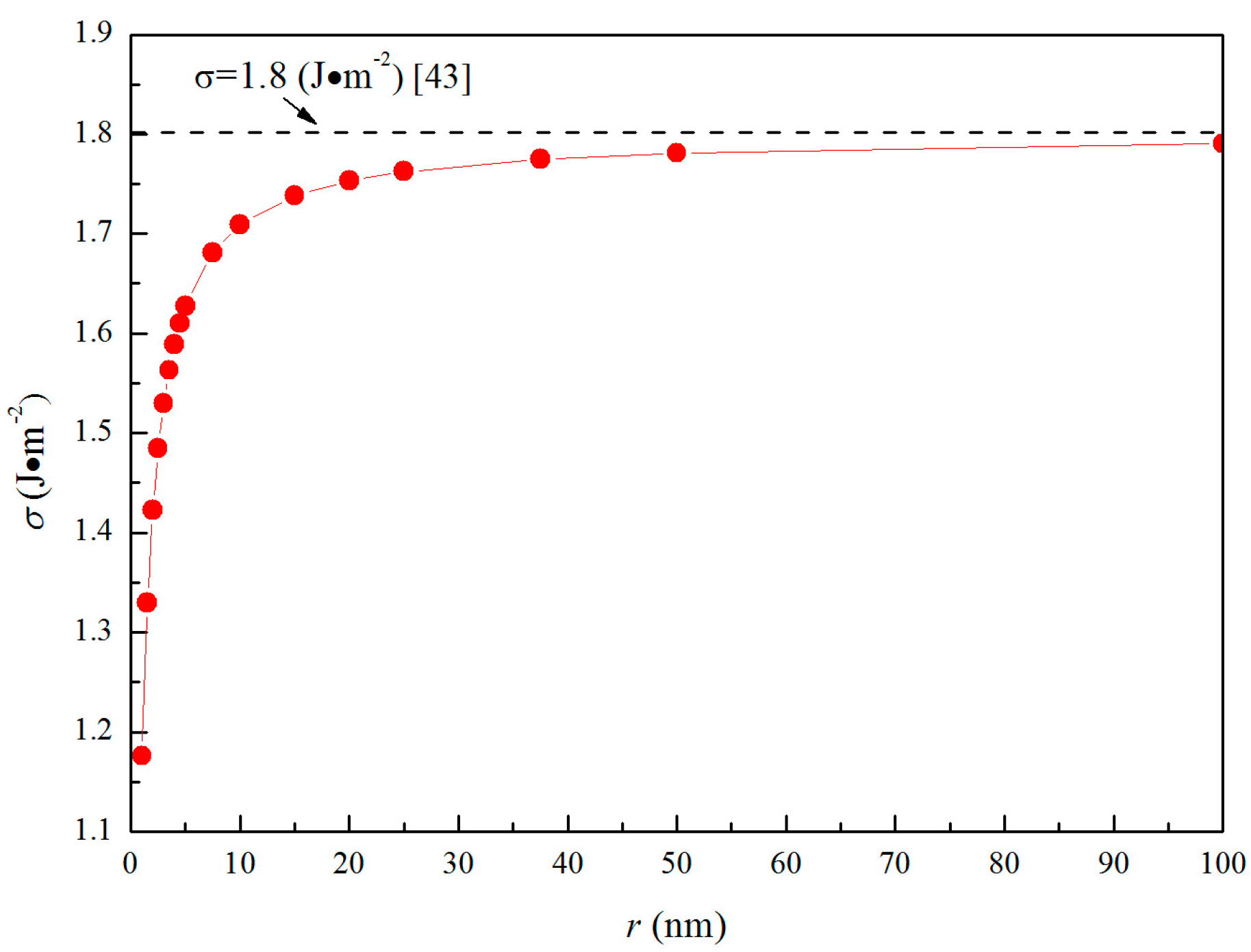
3.1. Thermodynamic Properties of Nano-MgO
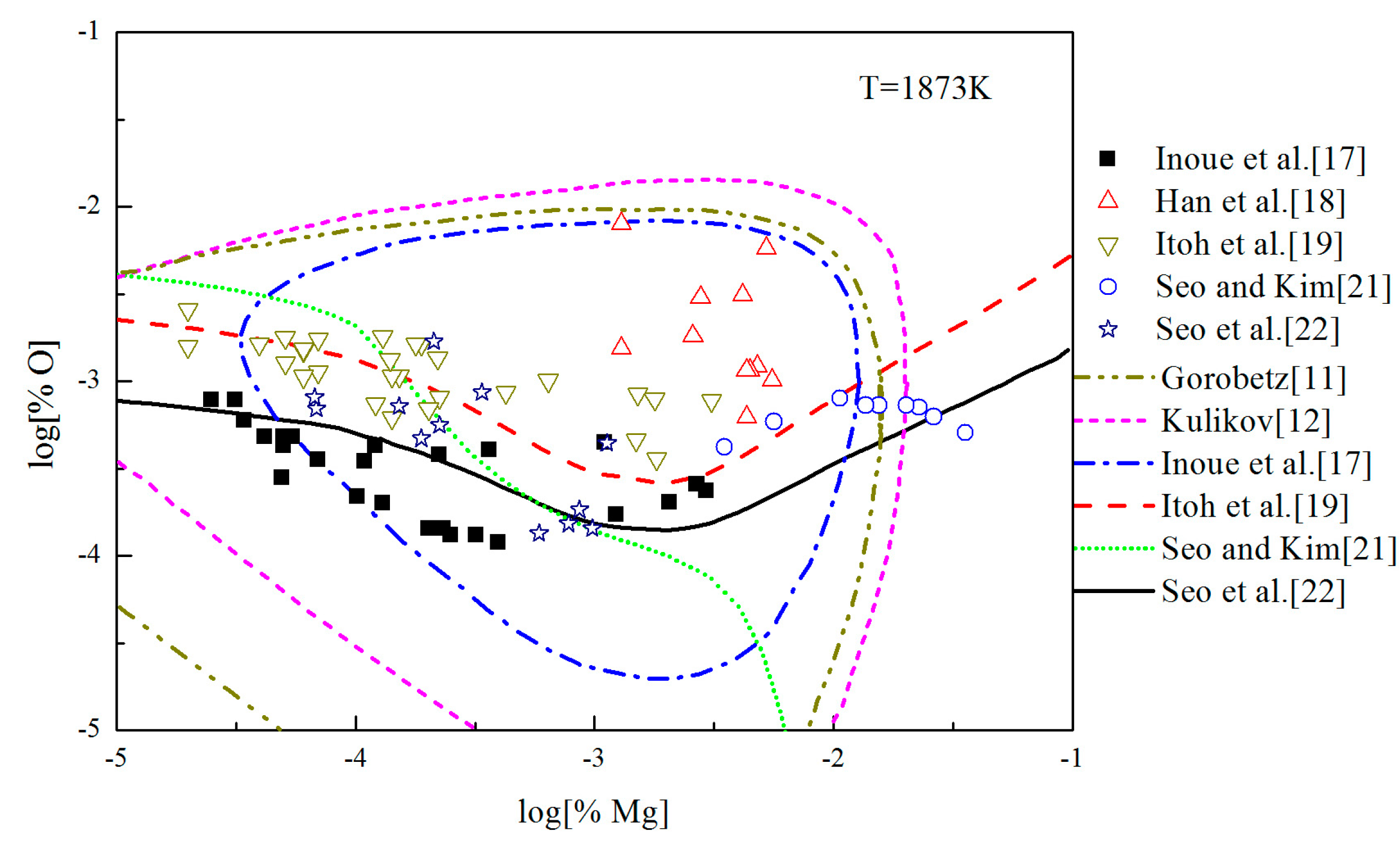
3.2. Nucleation and Excess Oxygen for Mg-Deoxidation Reaction in Fe-O-Mg Melt
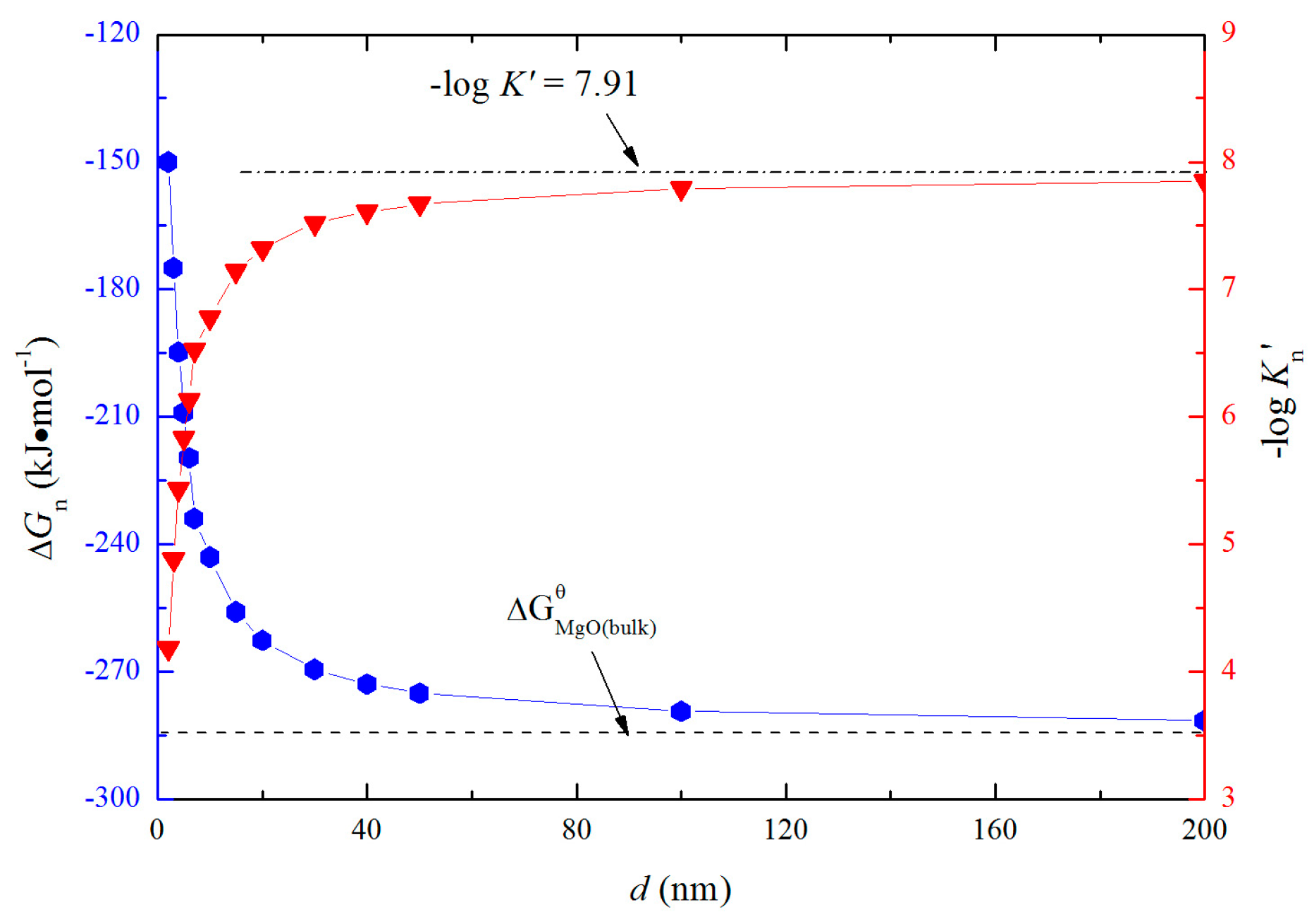
3.3. Gibbs Free Energy Changes for the Formation of Nano-MgO in Liquid Iron
3.4. Multi-Equilibria Thermodynamics of MgO in Liquid Iron
4. Conclusions
- (1)
- It is difficult for nano-magnesia to grow up into final bulk magnesia in final stage of Mg-deoxidation in liquid iron. The existence of the residual nanoscale magnesia is one of the important reason for the supersaturation ratio or the excess oxygen for MgO formation in liquid iron.
- (2)
- Numerical calculation results suggest that the solubility product of magnesium and oxygen for nano-MgO in liquid iron increased with the increasing magnesia products size. The experimental data about Mg-deoxidation in liquid iron are covered by the region between the thermodynamic curves of 2 nm magnesia and bulk-magnesia.
- (3)
- The previous Mg-deoxidation experiments are in the different thermodynamic states, and many previous experiments are close to the final equilibrium between bulk magnesia and liquid iron, but do not reach the final equilibrium because their partial product is nano-magnesia.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jiang, Z.; Zhuang, Y.; Li, Y.; Li, S. Effect of modification treatment on inclusions in 430 stainless steel by Mg-Al alloys. J. Iron Steel Res. Int. 2013, 20, 6–10. [Google Scholar] [CrossRef]
- Wang, L.; Yang, S.; Li, J.; Zhang, S.; Ju, J. Effect of Mg addition on the refinement and homogenized distribution of Inclusions in steel with different Al contents. Metall. Mater. Trans. B 2017, 48, 805–818. [Google Scholar] [CrossRef]
- Liu, C.; Yagi, M.; Gao, X.; Kim, S.J.; Huang, F.; Ueda, S.; Kitamura, S. Kinetics of transformation of Al2O3 to MgO·Al2O3 spinel inclusions in Mg-Containing steel. Metall. Mater. Trans. B 2018, 49, 113–122. [Google Scholar] [CrossRef]
- Zhang, T.; Min, Y.; Liu, C.; Jiang, M. Effect of Mg addition on the evolution of inclusions in Al-Ca deoxidized melts. ISIJ Int. 2015, 55, 1541–1548. [Google Scholar] [CrossRef]
- Ma, W.; Bao, Y.; Wang, M.; Zhao, L. Effect of Mg and Ca treatment on behavior and particle size of inclusions in bearing steels. ISIJ Int. 2014, 54, 536–542. [Google Scholar] [CrossRef]
- Lowe, J.H.; Mitchell, A. Zero Inclusion Steels. In Proceedings of the Clean Steel: Superclean Steel-Conference Proceedings, London, UK, 6–7 March 1995; p. 223. [Google Scholar]
- Sarma, D.S.; Karasev, A.V.; Jonsson, P.G. On the role of non-metallic inclusions in the nucleation of acicular ferrite in steels. ISIJ Int. 2009, 49, 1063–1074. [Google Scholar] [CrossRef]
- Liu, Z.; Kobayashi, Y.; Yin, F.; Kuwabara, M.; Nagai, K. Nucleation of acicular ferrite on sulfide inclusion during rapid solidification of low carbon steel. ISIJ Int. 2007, 47, 1781–1788. [Google Scholar] [CrossRef]
- Lupis, C.H.P.; Elliott, J.F. Generalized interaction coefficients: Part I: Definitions. Acta Metall. 1966, 14, 529–538. [Google Scholar] [CrossRef]
- Sigworth, G.K.; Elliott, J.F. The thermodynamics of liquid dilute iron alloys. Metal Sci. 1974, 8, 298–310. [Google Scholar] [CrossRef]
- Gorobets, A.P. Investigation into the thermodynamics of the deoxidation of iron by a magnesium solution. Metall. Koksokhim 1980, 69, 34–37. [Google Scholar]
- Kulikov, I.S. Iron deoxidation by alkaline-earth metals. Izv. Akad. Nauk SSSR Met. 1985, 6, 9–15. [Google Scholar]
- Nadif, M.; Gatellier, C. Influence of calcium or manganese on the solubility of oxygen and sulphur in liquid steel. Rev. Metall. CIT 1986, 83, 377–394. [Google Scholar] [CrossRef]
- Turkdogan, E.T. Possible failure of emf oxygen sensor in liquid iron containing dissolved calcium or magnesium. Steel Res. 1991, 62, 379–382. [Google Scholar] [CrossRef]
- Satoh, N.; Taniguchi, T.; Mishima, S.; Oka, T.; Miki, T.; Hino, M. Prediction of nonmetallic inclusion formation in Fe-40mass% Ni-5mass% Cr alloy production process. Tetsu-to-Hagane 2009, 95, 827–836. [Google Scholar] [CrossRef]
- Teplitskii, E.B.; Vladimirov, L.P. Thermodynamics of the Interaction of Mg with O in an Fe Melt. Zh. Fiz. Khim 1977, 51, 831–833. [Google Scholar]
- Inoue, R.; Suito, H. Thermodynamics of O, N, and S in liquid Fe equilibrated with CaO-Al2O3-MgO slags. Metall. Mater. Trans. B 1994, 25, 235–244. [Google Scholar] [CrossRef]
- Han, Q.; Zhou, D. Determination of dissolved sulfur and Mg-S, Mg-O equilibria in molten iron. Steel Res. 1997, 68, 9–14. [Google Scholar] [CrossRef]
- Itoh, H.; Hino, M.; Ban-Ya, S. Thermodynamics on the formation of spinel nonmetallic inclusion in liquid steel. Metall. Mater. Trans. B 1997, 28, 953–956. [Google Scholar] [CrossRef]
- Ohta, H.; Suito, H. Deoxidation equilibria of calcium and magnesium in liquid iron. Metall. Mater. Trans. B 1997, 28, 1131–1139. [Google Scholar] [CrossRef]
- Seo, J.D.; Kim, S.H. Thermodynamic assessment of Mg deoxidation reaction of liquid iron and equilibria of [Mg]-[Al]-[O] and [Mg]-[S]-[O]. Steel Res. 2000, 71, 101–106. [Google Scholar] [CrossRef]
- Seo, W.G.; Han, W.H.; Kim, J.S. Deoxidation equilibria among Mg, Al and O in liquid iron in the presence of MgO· Al2O3 spinel. ISIJ Int. 2003, 43, 201–208. [Google Scholar] [CrossRef]
- Xiao, Y.; Lei, H.; Yang, B.; Wang, G.; Wang, Q.; Jin, W. Nucleation and growth for magnesia inclusion in Fe-O-Mg melt. RSC Adv. 2018, 8, 38336. [Google Scholar] [CrossRef]
- Wasai, K.; Mukai, K. Thermodynamics of nucleation and supersaturation for the aluminum-deoxidation reaction in liquid iron. Metall. Mater. Trans. B 1999, 49, 1065–1074. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Q.; Li, S.; Ai, X.; Li, D. A Multi-step thermodynamic model for alumina formation during aluminum deoxidation in Fe-O-Al melt. Acta Metall. Sin. 2015, 28, 272–280. [Google Scholar] [CrossRef]
- Zong, N.; Yang, L.; He, P. Learning about the nucleation pathway of MgO·Al2O3 spinel from an Fe-O-Al-Mg melt using a two-step nucleation mechanism. RSC Adv. 2015, 5, 48382–48390. [Google Scholar] [CrossRef]
- Meng, Q.; Zhou, N.; Rong, Y.; Chen, S.; Hsu, T.Y. Size effect on the Fe nanocrystalline phase transformation. Acta Mater. 2002, 50, 4563–4570. [Google Scholar] [CrossRef]
- Zu, X.; Birringer, R.; Herr, U.; Gleiter, H. X-ray diffraction studies of the structure of nanometer-sized crystalline materials. Phys. Rev. B 1987, 35, 9085. [Google Scholar] [CrossRef]
- Sui, M.; Lu, K.; Deng, W.; Xiong, L.; Patu, S.; He, Y. Positron-lifetime study of polycrystalline Ni-P alloys with ultrafine grains. Phys. Rev. B 1991, 44, 6466. [Google Scholar] [CrossRef]
- Herr, U. Metastable phases in interface controlled materials. Contemp. Phys. 2000, 41, 93–104. [Google Scholar] [CrossRef]
- Dash, J.G. Surface melting. Contemp. Phys. 1989, 30, 89–100. [Google Scholar] [CrossRef]
- Thomas, G.J.; Siegel, R.W. Grain boundaries in nanophase palladium: High resolution electron microscopy and image simulation. Scr. Metall. 1990, 24, 201–206. [Google Scholar] [CrossRef]
- Waniewska, A.S.; Greneche, J.M. Magnetic interfaces in Fe-based nanocrystalline alloys determined by Mössbauer spectrometry. Phys. Rev. B 1997, 56, 8491. [Google Scholar] [CrossRef]
- Phillpot, S.R.; Wolf, D.; Gleiter, H. Molecular dynamics study of the synthesis and characterization of a fully dense, three-dimensional nanocrystalline material. J. Appl. Phys. 1995, 78, 847–861. [Google Scholar] [CrossRef]
- Chen, M.; Andrew, R.F.; Dixon, D.A. Structures and Stabilities of (MgO)n Nanoclusters. J. Phys. Chem. A 2014, 118, 3136–3146. [Google Scholar] [CrossRef] [PubMed]
- Haertelt, M.; Fielicke, A.; Meijer, G.; Kwapien, K.; Sierka, M.; Sauer, J. Structure determination of neutral MgO clusters-hexagonal nanotubes and cages. Phys. Chem. Chem. Phys. 2012, 14, 2849–2856. [Google Scholar] [CrossRef] [PubMed]
- Kwapien, K.; Sierka, M.; Dobler, J.; Sauer, J. Reactions of H2, CH4, C2H6, and C3H8 with [(MgO)n]+ clusters studied by density functional theory. ChemCatChem 2010, 2, 819–826. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, Y.H.; Song, Y.; Chen, H.S. Structures and bonding characters of (MgO)3n (n = 2-8) clusters. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 355–359. [Google Scholar] [CrossRef]
- Gueddim, A.; Bouarissa, N.; Villesuzanne, A. First-principles determination of structural properties of MgO. Phys. Scr. 2009, 80, 055702. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Wilson, E.B.; Decius, J.C.; Cross, P.C. Molecular Vibrations; Dover: New York, NY, USA, 1980. [Google Scholar]
- Hirano, T. MOPAC Manual, 7th ed.; Stewart, J.J.P., Ed.; US Air Force Academy: Colorado Springs, CO, USA, 1993. [Google Scholar]
- Nakajima, K. Estimation of interfacial tensions between phases in the molten iron-slag-inclusion (alumina) system. Tetsu-to-Hagané 1994, 80, 383–388. [Google Scholar] [CrossRef]
- Defay, R.; Prigogine, I. Surface Tension and Adsorption, Translated by D.H. Everet; John Wiley and Sons, Inc.: New York, NY, USA, 1966; p. 319. [Google Scholar]
- Suito, H.; Ohta, H. Characteristics of particle size distribution in early stage of deoxidation. ISIJ Int. 2006, 46, 33–41. [Google Scholar] [CrossRef]
- Jung, I.H.; Decterov, S.A.; Pelton, A.D. A thermodynamic model for deoxidation equilibria in steel. Metall. Mater. Trans. B 2004, 35, 493–507. [Google Scholar] [CrossRef]
- Wang, G.C.; Xiao, Y.Y.; Zhao, C.M.; Li, J.; Shang, D.L. Atomic cluster aggregates in nucleation of solid alumina inclusion in the aluminum deoxidation for liquid iron. Metall. Mater. Trans. B 2018, 49, 282–290. [Google Scholar] [CrossRef]
- Wang, G.C.; Wang, Q.; Li, S.L.; Ai, X.G.; Fan, C.G. Evidence of multi-step nucleation leading to various crystallization pathways from an Fe-O-Al melt. Sci. Rep. 2014, 4, 5082. [Google Scholar] [CrossRef] [PubMed]
- Wasai, K.; Mukai, K.; Miyanaga, A. Observation of inclusion in aluminum deoxidized iron. ISIJ Int. 2002, 42, 459–466. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, G.; Shang, D.; Lei, H.; Wang, Q.; Cao, L. Mechanisms on superfine alumina inclusions formation by Al-deoxidation reaction for liquid iron. Steel Res Int. 2018, 89, 18000255. [Google Scholar] [CrossRef]






| Author | logK | Year | ||||||
|---|---|---|---|---|---|---|---|---|
| Thermodynamic calculation | ||||||||
| Sigworth et al. [10] | 7.86 | - | - | - | - | - | - | 1974 |
| Gorobetz [11] | 9.24 | −250 | −380 | - | - | - | - | 1980 |
| Kulikov [12] | 8.54 | −160 | −243 | - | - | - | - | 1985 |
| Nadif et al. [13] | 7.75 | - | - | - | - | - | - | 1986 |
| Turkdogan [14] | 7.74 | - | - | - | - | - | - | 1991 |
| Satoh et al. [15] | 7.59 | - | - | - | - | - | - | 2009 |
| Experiment result | ||||||||
| Teplitskii et al. [16] | 5.12 | - | - | - | - | - | - | 1977 |
| Nadif et al. [13] | 5.70 | - | - | - | - | - | - | 1986 |
| Inoue et al. [17] | 7.8 ± 0.2 | −190 ± 60 | −290 ± 90 | - | - | - | - | 1994 |
| Han et al. [18] | 6.03 | −106 | −161 | - | - | - | - | 1997 |
| Itoh et al. [19] | 6.8 | −280 | −430 | −20,000 | 350,000 | 462,000 | −61,000 | 1997 |
| Ohta et al. [20] | 7.86 | −300 | −460 | 16,000 | 37,000 | 48,000 | 48,000 | 1997 |
| Seo and Kim [21] | 7.21 | −370 | −560 | 59,000 | 145,000 | 191,400 | 17,940 | 2000 |
| Seo et al. [22] | 7.24 | −266 | −404 | −40,000 | 527,000 | 696,000 | −122,000 | 2003 |
| [%O] | [%Mg] | |||
|---|---|---|---|---|
| 0.01 | 0.001 | 0.0005 | 0.0001 | |
| 0.01 | 1737.801 | 173.780 | 86.890 | 17.378 |
| 0.005 | 868.900 | 86.890 | 43.445 | 8.689 |
| 0.0025 | 434.450 | 43.445 | 21.723 | 4.345 |
| 0.001 | 173.780 | 17.378 | 8.689 | 1.738 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Lei, H.; Yang, B.; Wang, G.; Wang, Q.; Jin, W. Thermodynamic Modelling on Nanoscale Growth of Magnesia Inclusion in Fe-O-Mg Melt. Metals 2019, 9, 174. https://doi.org/10.3390/met9020174
Xiao Y, Lei H, Yang B, Wang G, Wang Q, Jin W. Thermodynamic Modelling on Nanoscale Growth of Magnesia Inclusion in Fe-O-Mg Melt. Metals. 2019; 9(2):174. https://doi.org/10.3390/met9020174
Chicago/Turabian StyleXiao, Yuanyou, Hong Lei, Bin Yang, Guocheng Wang, Qi Wang, and Wei Jin. 2019. "Thermodynamic Modelling on Nanoscale Growth of Magnesia Inclusion in Fe-O-Mg Melt" Metals 9, no. 2: 174. https://doi.org/10.3390/met9020174




