Modeling Electrical Resistivity of Naturally Aged Al–Mg–Si Alloys

Abstract

Isothermal ageing of Al–Mg–Si alloys, stored at room temperature for more than 5 months, is associated with an unexpected significant increase in the overall electrical resistivity. This unexpected anomalous increase is not observed in alloys with shorter storage (natural ageing) times. This phenomenon is explained with a scenario, based on the evolution of the size distribution of Guinier–Preston (GP) zones during natural ageing and during subsequent artificial ageing. The proposed scenario can explain the contribution of natural ageing atomic clusters to this anomalous increase in the electrical resistivity. A physically based combined precipitation–electrical resistivity model, with the former being based on simultaneous nucleation-growth-coarsening reactions and the latter based on the Bragg scattering of electrons from atomic clusters, has been used to explain the electrical resistivity evolution. It is shown that the proposed model is capable of reproducing the experimental data in both short natural ageing (less than 5 months) and long natural ageing (more than 5 months) regimes.

1. Introduction

The heat treatable Al–Mg–Si alloys are widely used in structural, automotive, and aerospace industries, since they show an optimum combination of weldability, formability, corrosion resistance, and mechanical properties [1]. The mechanical properties of Al–Mg–Si alloys are very sensitive to the precipitation hardening and precipitation sequence. The precipitation sequence in these alloys is generally believed [2,3,4] to be:

SSS→Atomic Clusters→(GP-I zones)→GP (GP-II) zones→β′′→β′→β,

where SSS is the supersaturated solid solution, GP-I zones are very tiny (less than 2 nm [5]) spherical co-clusters of both Mg and Si atoms with disordered crystal structures and uncertain compositions [6]. Guinier–Preston (GP)-II zones, on the other hand, are atomic clusters with a structure similar to β′′ but with, to some extent, different positions for Mg atoms along the <100>_Al direction [5]. These precipitates have needle-shaped morphologies with the composition of Mg_2+xSi_2+yAl_7-x-y [7]. β′′, the most influential precipitate when it comes to the strengthening, is also a needle-shaped precipitate, elongated in the <100>_Al direction with a monoclinic structure [3]. β′ and β (Mg₂Si) are precipitates, which are formed after peak-age, when the coarsening reaction is prevailing. The former is a metastable species and the latter is a stable one [6]. The main point of controversy about the precipitation sequence in the literature is related to the formation and transformation of GP-I to GP-II zones. For a long time, it was conventionally believed that this transformation is successive [8]. Yet, recent theories [9,10,11] show that the formations of GP-I and/or GP-II zones are competitive and parallel. Saga et al. [10] showed that temperatures below 67 °C are more favorable for precipitation of GP-I while above 67 °C GP-II precipitates are more likely to form. In real industrial production routes, sometimes it is practical to perform peak-ageing (T6) treatment on Al–Mg–Si samples immediately after the solution treatment. In many factories, the samples are commonly stored at room temperature a couple of hours up to several months. It is also a common practice to buy profiles after a few months of storage and transportation and do an immediate artificial ageing (without any extra solutionizing in between). Natural ageing obviously results in the formation of very small GP-I zones. The effect of these GP-I zones on the hardness and formability evolution of Al–Mg–Si alloys during subsequent isothermal ageing or during paint bake-heat treatment has been comprehensively investigated [12,13,14,15], while the influence of these early-stage precipitates on the electrical resistivity evolution in these alloys has rarely been studied. In the present investigation, the effects of initial GP-I zones, precipitated during natural ageing, on the subsequent precipitation behavior and on the evolution of electrical resistivity was studied using electrical resistivity and hardness measurements. A modeling approach was also used to predict the evolution of electrical resistivity in these alloys.

2. Modeling Approach

2.1. Multi-Component Model for the Formation/Dissolution of GP Zones

The MatCalc software [16,17,18,19] was used to calculate the number density and size of GP zones, formed during natural ageing. MatCalc, a modeling package developed at the University of Vienna in Austria, has the ability to simulate precipitation in different domains, meaning that different precipitate phases can be defined in a matrix, each of which having its own interfacial energy, preferred nucleation sites, and nucleus composition. In this case, only GP zone was of interest. This software is based on the finite difference method (FDM) in which an array of size classes is defined and assigned to each precipitate type. Each precipitate size class consists of a number of precipitates of the same radius. The total number of precipitates in each size class changes during ageing due to nucleation, growth, coarsening, and dissolution. In every time step, and for each precipitate phase, the nucleation rate is evaluated, and newly formed precipitates are added to the relevant size class. In the meantime, the growth/dissolution kinetics and the change in composition/numbers of precipitates in all existing size classes are evaluated. In aged Al–Mg–Si alloys, the system is a matrix in which precipitates of various chemical compositions, sizes, and crystallographic structures are in contact with the matrix. Assume that there are S alloying elements in the system and N_i (i = 1,…,S) is the molar concentration of alloying element i. There are m spherical precipitates in the system, each of which having a different radius r_k (k = 1,…,m). In such a system with S components and m precipitates, the total Gibbs energy is expressed as [19]:

$$G_{total}={\displaystyle \sum _{i=1}^S{N}_i{\mu }_i+\frac{4}{3}\pi {\displaystyle \sum _{k=1}^m{r}_k^3}}({\lambda }_k+{\displaystyle \sum _{i=1}^S{c}_{ki}{\mu }_{ki})+4\pi {\displaystyle \sum _{k=1}^m{r}_k^2}}{\gamma }_k,$$

(1)

where c_ki is the concentration of the alloying element i in the precipitate k, μ_i is the chemical potential of the alloying element in the matrix, μ_ki is the chemical potential of the alloying element in the precipitate, λ_k is the strain energy, and γ_k is the precipitate/matrix interface energy (it was chosen to be 0.1 J/m² [20]). In the abovementioned total Gibbs free energy equation, the first term describes the Gibbs energy of the matrix by summing up the contributions from alloying elements in the matrix. The second energy term is due to the precipitates, where the specific quantities for the mechanical free energy contribution, λ_k, are also included. The third term takes into account the increase in the energy of the system due to the formation of precipitate–matrix interfaces. Essentially there are three different possibilities for Gibbs free energy dissipation during precipitation.

Table 1. Dissipation rate mechanism [18].

Gibbs Free Energy Dissipation Rate	Equation Number
Dissipation by the precipitate-matrix interface movement during growth-dissolution of precipitates	(2)
Dissipation by diffusion of alloying elements inside the precipitate	(3)
Dissipation by diffusion of alloying elements inside the matrix	(4)

summarizes these three mechanisms for dissipation rates. Based on the Onsager’s thermodynamic extremal principle, a thermodynamic system will evolve toward equilibrium in such a way that it produces maximum entropy or the maximum Gibbs free energy dissipation rate [19]. The numerical way to use these equations to calculate the total Gibbs free energy of the system is explained in [17].

$$Q_1={\displaystyle \sum _{k=1}^m\frac{4\pi r_k^2}{M_k}}{(\frac{d{r}_k}{dt})}^2$$

(2)

M_k: the mobility of the interface

$$Q_2={{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{i=1}^S\frac{4\pi RT{r}_k^5}{45c_{ki}{D}_{ki}}(\frac{d{c}_{ki}}{dt})}}}^2$$

(3)

D_ki is the diffusion rate of alloying element i in the precipitate k

$$Q_3={{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{i=1}^S\frac{4\pi RT{r}_k^5}{45c_i{D}_i}\left(\frac{d{r}_k}{dt}(c_i-c_{ki})+\frac{r_k}{3}\frac{d{c}_{ki}}{dt}\right)}}}^2$$

(4)

c_i and D_i being the concentration and diffusion rate of alloying element i in the matrix

The nucleation rate of precipitates in the model was calculated from:

$$J=Z{\beta }^{*}{N}_c\exp (\frac{-\Delta G^{*}}{k_{B}T})\exp (\frac{-1}{2Z^2{\beta }^{*}t})$$

(5)

with the second exponential term being due to the transient nucleation rate, Z being the Zeldovich factor, β the atomic attachment rate for the critical nucleus, N_C is the number of available nucleation sites, k_B is the Boltzmann constant, and ΔG* is the nucleation energy barrier given by [18]:

$$\frac{d{r}_k}{dt}=\frac{F_k-\left(\frac{2{\gamma }_k}{r_k}\right)}{RT{r}_k}{\left[{\displaystyle \sum _{i=1}^n\frac{{(c_{ki}-c_i)}^2}{c_i{D}_i}}\right]}^{-1}$$

(6)

The factor $F_k-\left(\frac{2{\gamma }_k}{r_k}\right)$ represents the balance between the driving force (obtained from the thermodynamic database of the software) and the surface tension. The growth kinetics was assumed to be diffusion-controlled. Bulk diffusion coefficients of Mg and Si in the aluminum matrix were given by:

$$\{\begin{array}{l}{D}_{Mg}=(5.7\times {10}^{-5} m^2/s)\exp (\frac{-112.5kJ/mol}{RT})\\ D_{Si}=(1.4\times {10}^{-5} m^2/s)\exp (\frac{-126.7kJ/mol}{RT})\end{array}$$

(7)

There is a term in MatCalc which accounts for the faster diffusion of elements due to the presence of quenched-in vacancies. This parameter is called the matrix diffusion enhancement factor (MDEF). The diffusion coefficient is multiplied by the MDEF parameter (this was chosen as 100 [20]). In this model, the stoichiometry of GP zones was assumed to be Mg₂Si₃Al₆ [20].

2.2. Modeling Electrical Resistivity

Knowing that the relaxation time for scattering from atomic clusters of the size R is ${\tau }_R(k)$, then the electrical resistivity due to these atomic clusters was given by [21]:

$${\rho }_R=\frac{m}{n{e}^2(N{\tau }_R)}$$

(8)

where m is the electron mass, n is the electron density, e is electron charge, and N is the number density of atomic clusters. Taking into account the anisotropy of Bragg scattering rate modeled by two values in the k-space, the elementary transport theory of free electrons yields [22]:

$${\rho }_R\propto {\displaystyle \int (1-\cos {\theta }_{k{k}^{\prime }}}){\left|w(k-k^{\prime })\right|}^2{S}_R(k-k^{\prime })$$

(9)

where w is the potential function and $S(k-k^{\prime })$ is the structure factor given by [23,24]:

$$S{(k-k^{\prime })}_R=\frac{1}{10R}{\displaystyle \sum _{soluteatoms}{e}^{-i(k-k^{\prime })r_i}}={\displaystyle \prod _{j=1}^3[\frac{\sin \frac{{(10R)}^{1/3}}{2}(k-k^{\prime }).d_j}{\sin \frac{1}{2}(k-k^{\prime }).d_j}}{]}^2(\mathrm{if}R\mathrm{is}\mathrm{nm})$$

(10)

where $r_i$ is the position of solute atom in the atomic cluster and $d_j$ is the primitive translation vectors of the atomic clusters structure. Integration of Equation (9) with some simplifications yields [22]:

$${\rho }_R=\alpha .N.R^{4/3}(\alpha \text{is proportionality constant})$$

(11)

For atomic clusters of the size of R, if scattering occurs over a fraction $f_R$ of Fermi surface, then the total resistivity is given by [21]:

$$\rho ={\left(\frac{1-{\left(1+\frac{R}{5}\right)}^{-\frac{2}{3}}}{{\rho }_0+{\displaystyle \sum _{j=Fe,Cu,Mn}{c}_j{\rho }_j+{\displaystyle \sum _{i=Mg,Si}(c_i-\frac{N}{6}\pi R^3{C}_{pi}){\rho }_i}}}+\frac{{\left(1+\frac{R}{5}\right)}^{-\frac{2}{3}}}{{\rho }_0+{\displaystyle \sum _{j=Fe,Cu,Mn}{c}_j{\rho }_j+{\displaystyle \sum _{i=Mg,Si}(c_i-\frac{N}{6}\pi R^3{C}_{pi}){\rho }_i+{\rho }_R}}}\right)}^{-1}$$

(12)

where $C_i$ is the initial concentration of alloying element, $C_p$ is the concentration of alloying element in the matrix, and ${\rho }_0=2.6$, ${\rho }_{Si}=1.02$, ${\rho }_{Mg}=0.54$, and ${\rho }_{Cu}=0.344\mu \mathsf{\Omega }.cm/wt\%$ [25].

3. Materials and Methods

The alloy used for this study was 1-mm thick AA6061 (Al–0.6wt%Si–0.95wt%Mg–0.2wt%Cu) sheet, solutionized at 560 °C for 20 min, naturally aged at room temperature for periods up to one year, and re-aged at temperatures between 170 to 190 °C for various times. The electrical resistivity measurements were performed by the eddy currents technique using a Sigmatest D 2.068^® (Foerster Instruments, Reutlingen, Germany) at room temperature at a rate of 60 Hz. The evolution of hardness was monitored by Vickers hardness measurements (KB Prüftechnik, Hochdorf-Assenheim, Germany) using a 300-gr load, with a measurement error of $\pm 4$ VHN.

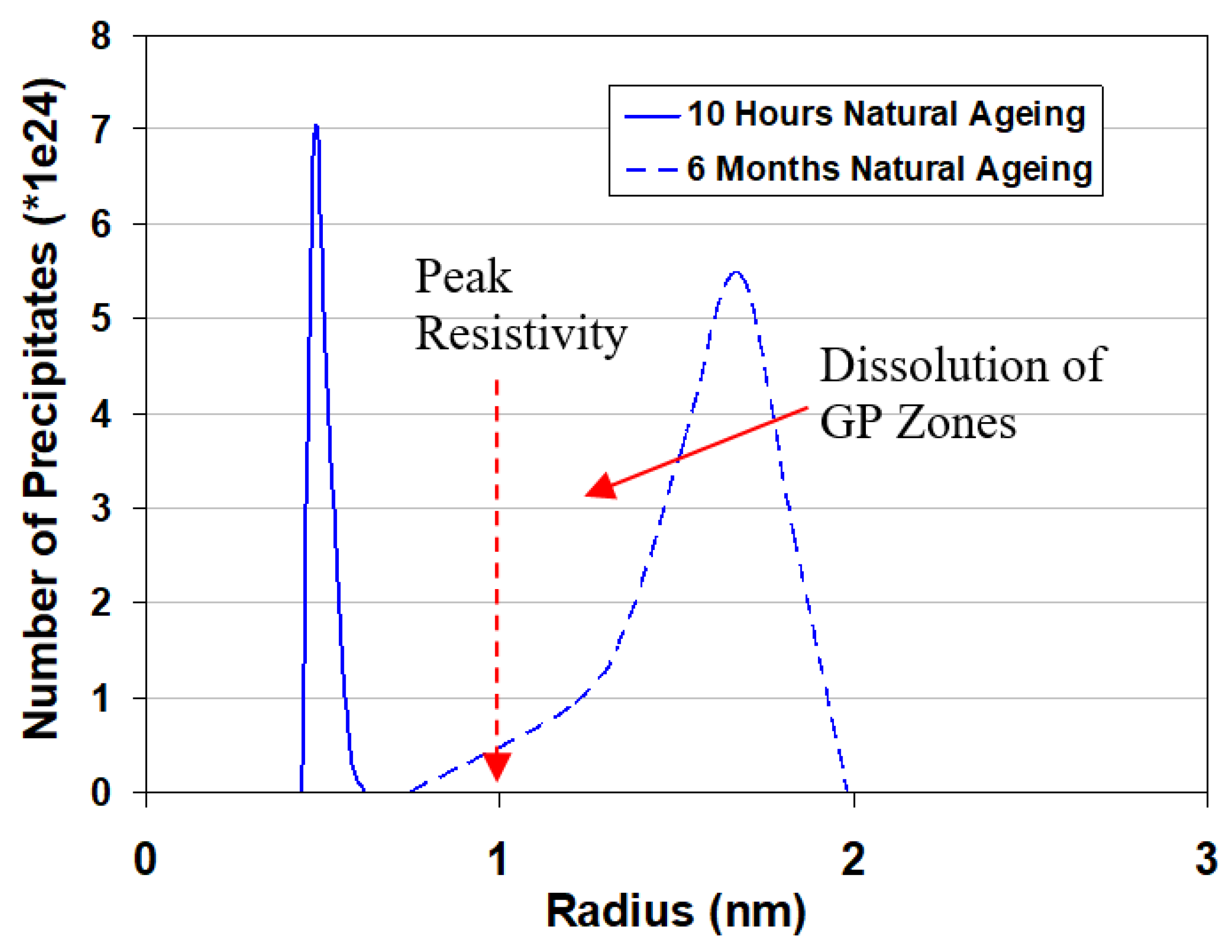
4. Results and Discussion

The hardness and resistivity evolutions of the as-solutionized samples during ageing at 170 and 190 °C are shown in Figure 1. The evolutions of hardness and resistivity could be divided into four distinct stages which are explained as follows:

• A→ B: In this stage, both hardness and resistivity slightly increased. This slight increase in both hardness and resistivity was due to the nucleation of GP-II zones [9,10,11]. In the beginning, GP-II zones were still very small and coherent. Therefore, they could not have a significant contribution to the mechanical properties. A few minutes after nucleation of GP-II zones, their sizes were in the range of the wavelength of conduction electrons at the Fermi level. In this condition, small nuclei of GP-II zones caused strong scattering of free electrons, which resulted in the observed increase in the resistivity [26,27].
• B→ C: During this stage, the hardness increased considerably from 80 VHN to around 110 VHN. This fast increase in the hardness of Al–Mg–Si alloy during ageing was related to the growth of GP-II precipitates [7]. During their growth in the <100> direction, GP-II precipitates caused a distortion in the surrounding matrix, and therefore they could obviously inhibit the movement of dislocations and consequently enhanced the mechanical strength. The growth of GP-II zones was associated with the depletion of alloying elements from the matrix which resulted in a drop of resistivity.
• C→ D: After the initial fast increase in the hardness, the hardness increased with a slower kinetic up to the formation of β′′ precipitates. The transformation of GP-II zone to β′′ precipitate was a process in which the Si/Mg ratio increased. The increase in the Si/Mg ratio of GP-II zones was associated with the dissolution of some of the existing particles. As a result, the hardening rate during transition of GP-II zones to β′′ precipitates decreased [7]. The decrease of resistivity in this stage indicates that the solute depletion was the governing phenomenon.
• D→ E: During this stage, both hardness and resistivity decreased. It is conventionally believed [2] that after peak hardness, the transformation of β′′ to β′ and β is the main reaction. These reactions are accompanied with the coarsening of precipitates. During coarsening, smaller precipitates dissolve while the larger ones grow. The coarsening results in a decrease in the number density of precipitates, which is deleterious for mechanical properties. Figure 1 shows that the resistivity kept decreasing after peak aging. This means that even after peak aging, there was the possibility of growth and alloy depletion.

Figure 2 shows the effects of natural-ageing time on the evolution of hardness and resistivity in the alloy AA6061 aged at 170 °C. It is seen that the hardness and resistivity evolutions of samples naturally aged for 5 months and more were different compared to those of samples naturally aged for 24 h and 1 month. For example, it is seen that there were two hardness peaks and one anomalous resistivity peak during subsequent ageing of samples naturally aged for 5 months and three years. In this paper, the main objective is to provide an explanation for the anomalous behavior of samples naturally aged for more than 5 months. The evolution of resistivity and hardness of the alloy AA6061, naturally aged for almost 3 years during ageing at 170 and 190 °C, is shown Figure 3. For the sake of comparison, the evolution of resistivity and hardness of the as-solutionized alloy is also given. Obviously, the presence of natural-ageing GP-I zones at the beginning of isothermal ageing has some general consequences as compared to the as-solutionized samples, i.e., decreasing the peak-age hardness, decreasing the hardening kinetics, and increasing the overall resistivity. From Figure 3 it is seen that at the beginning of ageing, both hardness and resistivity levels of naturally aged alloy were higher than those of as-solutionized ones. It was mainly due to the fact that a high density of small GP-I zones had formed during the holding time at room temperature after the solution treatment [27]. Small GP-I zones had a positive contribution to the resistivity. The fact that small initial GP-I zones increased the resistivity is very well described by the Bragg scattering of free electrons by coherent clusters and small GP zones [26]. During the initial 30 min of artificial ageing of the naturally pre-aged alloy at 170 °C and 190 °C, the hardness and resistivity slightly decreased. There has been a long discussion about the stability and the kinetics of transformation of natural-ageing GP-I zones during the initial stage of subsequent ageing [28,29,30,31,32]. It is more likely to assume that a part of natural-ageing GP-I zones act as nucleation sites for the precipitation of other phases, while other GP-I zones dissolve during subsequent artificial ageing. That the resistivity decreased during the initial stage of ageing (shown in Figure 3) could be attributed to the partial dissolution of initial GP-I zones at relatively high-ageing temperature. It is also worth noting that the rates of resistivity and hardness decrease were extremely slow indicating the slow dissolution kinetics of GP-I zones. Initial GP-I zones significantly decreased the level of supersaturation, the concentration of quenched-in vacancies, and consequently the driving force for nucleation [33]. The partial dissolution of subcritical initial GP-I zones at the beginning of subsequent ageing releases some alloying elements and vacancies, and therefore increases the driving force for nucleation and growth of GP-II zones [6]. Formation of GP-II zones is associated with a fast increase in hardness [7] and a drop in resistivity in such a way that the hardness reaches a peak and the resistivity reaches a trough. During their growth, GP-II zones consume alloying elements provided by the matrix and the initial dissolution of pre-existing GP-I zones. This solute depletion was the main reason for the resistivity drop. It is seen from Figure 3 that the increase in the hardness of naturally aged alloy due to the formation of GP-II zones was nearly half of that in the as-solutionized alloy. Therefore, one can conclude that the number density and volume fraction of GP-II zones in the naturally aged alloy was lower than in the as-solutionized sample. This conclusion is in accordance with the observation of Esmaeili et al. [33]. They showed that the volume fraction of β′′ precipitates, formed at peak age, was lower for the naturally aged material. This was due to the fact that the concentration of quenched-in vacancies in the supersaturated condition and the driving force for nucleation was lower in the naturally aged alloy. At the end of this stage, the hardness drops and resistivity increases unexpectedly. This stage is associated with the transformation of GP-II zones to β′′. In principle, this transformation should lead to an increase in hardness and a decrease in resistivity. This opposite behavior could be very well explained by the following scenario: GP-II zones, present in the microstructure, have a tendency to transform to β′′. During this transformation, the Si content of GP-II zones should increase. Yet, most of the alloying elements and vacancies have been consumed by the nuclei of GP-II zones and the pre-existing GP-I zones. One way that system can provide new a Si source for this transformation is the dissolution of pre-existing GP-I zones. At this stage, the dissolution of GP-I zones initially decreases the hardness temporarily. Yet, as soon as there is enough supersaturation for GP-II→β′′ transformation, the hardness again starts increasing.

Regarding the anomalous increasing of resistivity after the trough, there is a proposed theory according to which the maximum resistivity is reached when the atomic cluster size attains a critical and definite value which is equal to the wavelength of conduction electrons at the Fermi level so as to maximize the Bragg scattering [34,35]. Panseri and Federighi [36] reported that the critical size of clusters in Al–Mg–Si alloys is around 10 Å. Figure 4 shows that natural ageing for more than 5 months (dashed line in Figure 4 represents 5 months ageing) results in the formation of GP-I zones bigger than this critical size. It seems that in these alloys during artificial ageing up to peak-hardness (around 100 min), the average size of remaining natural ageing GP-I zones is higher than the critical value. At this point, GP-I zones do not have their strongest positive contribution to the resistivity and the resistivity evolution is mainly controlled by solute depletion due to the growth of GP-II zones. Yet, due to the intermediate dissolution of GP-I zones (needed to provide Si), the average size of GP-I zones becomes equal to the critical value, which results in a strong scattering and the anomalous resistivity peak. Obviously, when the dissolution of GP-I goes on, the average size of GP-I zones goes below the critical value and the resistivity starts decreasing again. This has been shown in Figure 5 in which the size distribution of GP-I zones after 10 h and 6 months of natural ageing are compared.

It is also interesting to note that the resistivity level of the naturally aged alloy even in the overaged condition is still higher than that of the as-solutionized one, meaning that a small part of the initial GP-I zones remains stable even after peak ageing and during over-ageing. Figure 6 shows the prediction of the proposed combined precipitation–electrical resistivity model for two cases; the artificial ageing of the alloy aged for 24 h and the one aged for 5 months. Clearly the model is capable of reproducing both normal and anomalous electrical resistivity evolution.

5. Conclusions

From the results of this study, the following conclusions could be drawn:

-

Isothermal ageing of Al–Mg–Si alloys, naturally aged for more than 5 months, was associated with an unexpected significant increase in the overall electrical resistivity.

-

Natural ageing in initial GP-I zones decreased the hardening kinetics, decreased the peak-age hardness, and increased the overall resistivity of the alloy during subsequent ageing.

-

The initial stage of ageing in the as-solutionized alloy was associated with the nucleation and growth of GP-II zones, while in the naturally aged alloy it was associated with the initial partial dissolution of GP-I zones and then the formation of GP-II zones. During subsequent ageing of the naturally aged alloy, the supersaturation needed for the further growth of GP-II zones and the transformation of GP-II zones to other precipitates was partially provided by the dissolution of smaller GP-I zones. The intermediate dissolution of GP-I zones temporarily decreased the hardness. Yet, as soon as the dissolution of GP-I zones provided enough supersaturation for further growth of GP-II zones, the hardness started increasing again.

-

The intermediate dissolution of GP-I zones resulted in an anomalous resistivity peak. It seems that during ageing, there was a moment that the average size of GP-I zones was nearly equal to a critical value in which GP-I zones can strongly scatter free electrons which leads to the appearance of the anomalous resistivity peak.