On the Design of Innovative Heterogeneous Sheet Metal Tests Using a Shape Optimization Approach †
Abstract
:1. Introduction
2. Methodology
2.1. Constitutive Model
2.2. Indicator and Cost Function
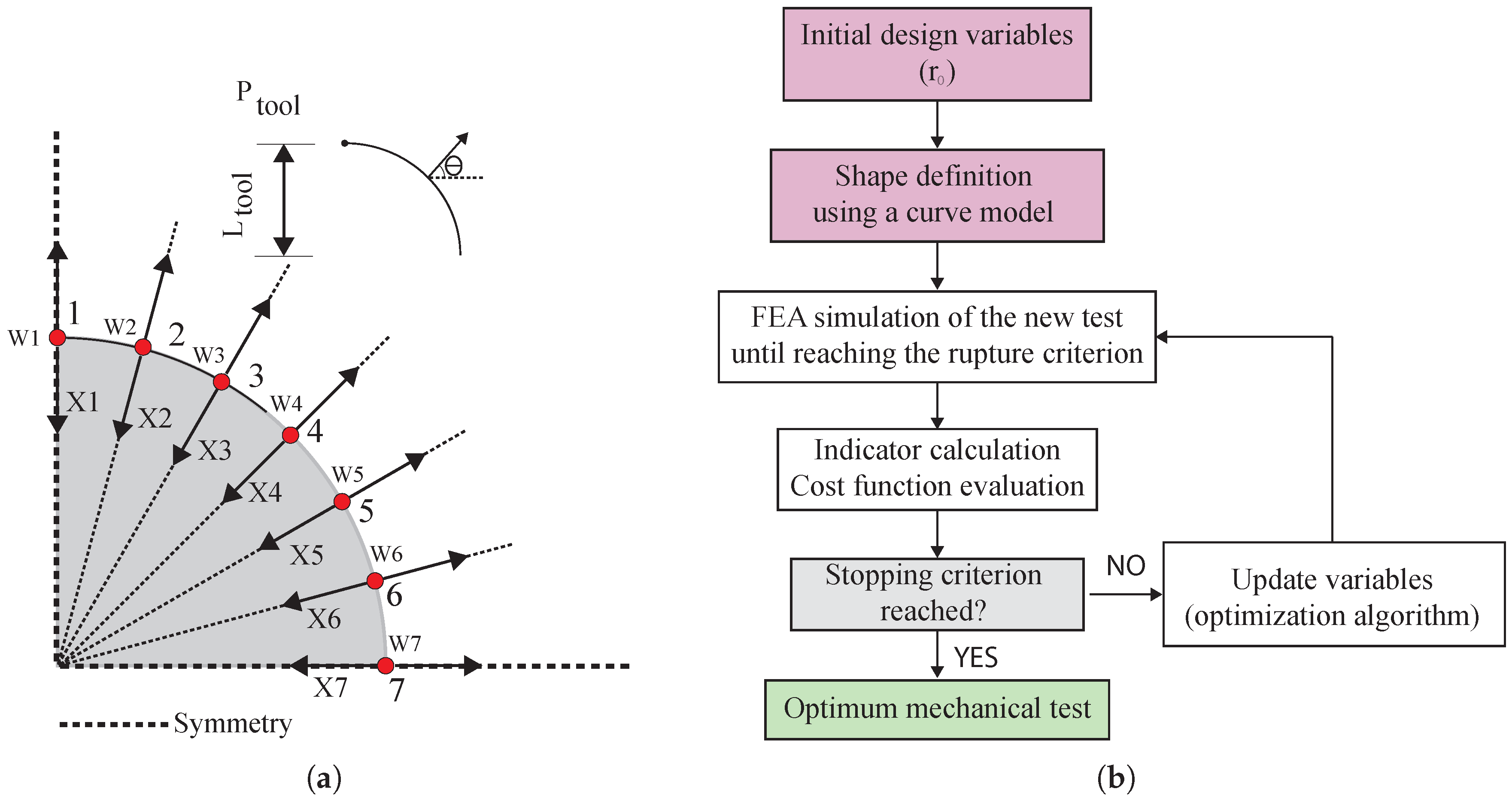
3. Optimization Features and Geometry Definition
3.1. Geometry Definition Using a Curve Model
- Cubic splines: Define a curve as a set of connected piecewise simple polynomial functions. The control points are interpolated, and no local control is considered in the geometry, only global. Therefore, abrupt variations can be observed on consecutive control points’ positions during the optimization, leading to unrealistic specimen shapes and to premature strain localization and rupture [4]. In order to avoid this drawback, a penalty function to constrain these variations was created. This penalty function is defined by:with:and:where , the parameter defines the admissible variation, and represents the control point.
- B-splines can be set as a single piecewise curve defined as a linear combination of control points and a B-spline basis function . The B-spline can be described as:For the normalized B-spline basis function of order k, the basis function is defined by:and:where are elements of a knot vector. In this work, B-splines of fourth order are used. Notice that, when using fourth order B-splines, the penalty function (2) is unnecessary because the curve becomes smoother. The knot vector assumes the following form: , where n + 1 is the number of control points;
- NURBS are functions that have the same properties as B-splines and are capable of representing a wider class of geometries. A NURBS curve is represented as a combination of control points and rotational basis functions and can be defined by:with:where is a weighting factor for the control points. If the weights of the control points are equal to one, the resulting curve is a B-spline. For more details concerning curve models, see [19].
3.2. Numerical Method and Test Design
- The geometry definition and discretization: This feature is related to the numerical simulation, the number of elements, the number of control points used, the curve model, the parametrization used, etc.
- The optimization method: This defines the robustness of the process and can influence the final result.
- The cost function parameters: A modification of these parameters can lead to different results. A very robust cost function can provide better results. However, this is not the object of study in this work.
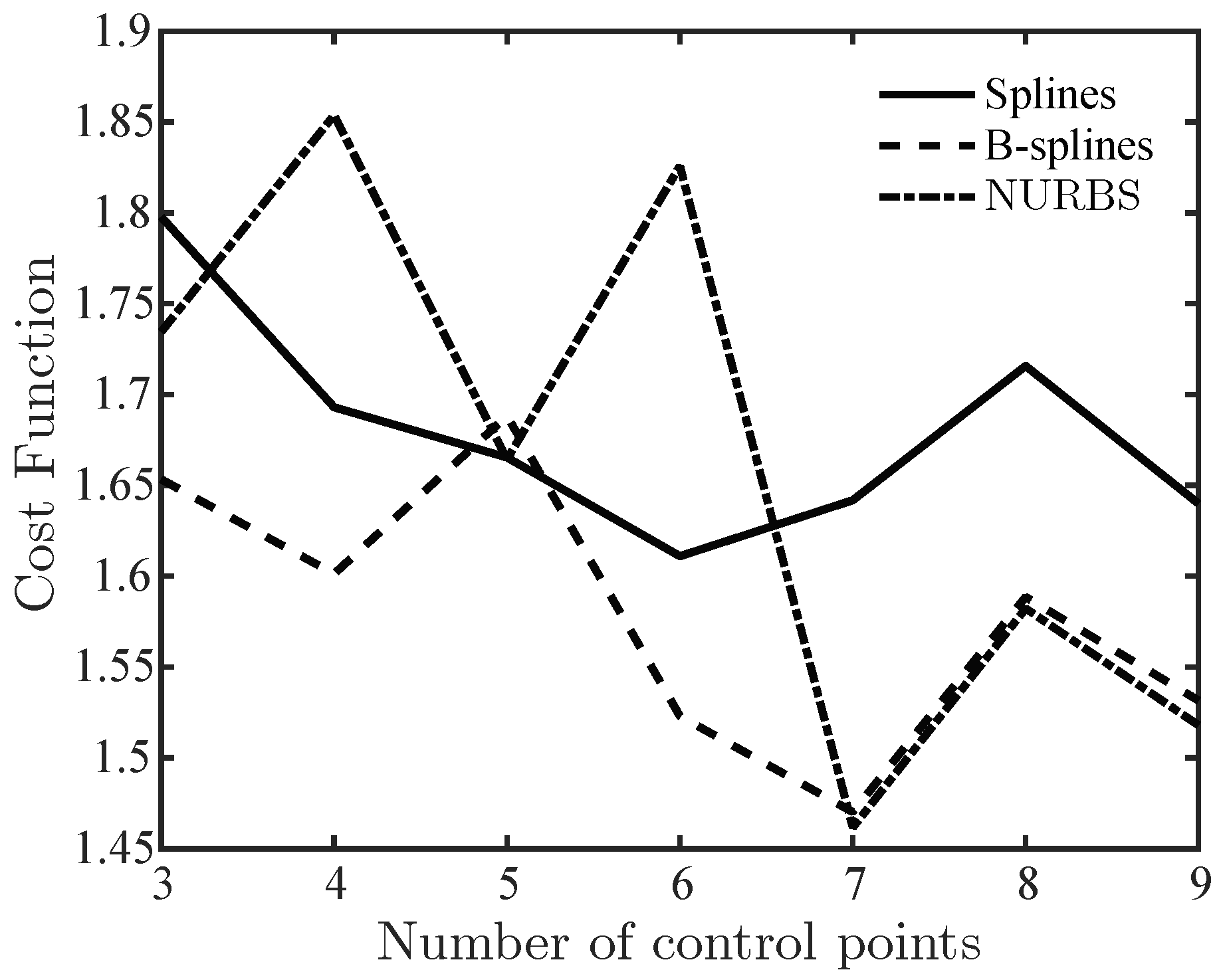
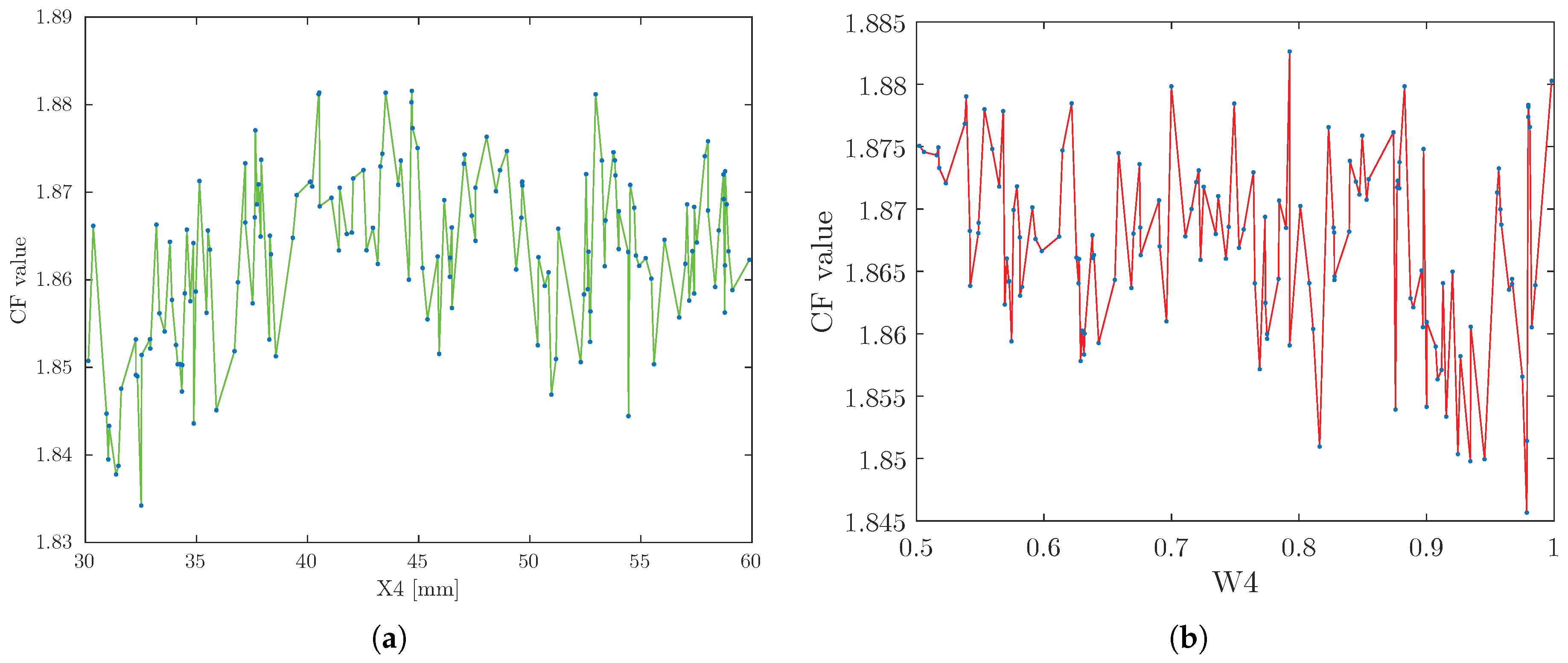
3.3. Number of Control Points and Sensitivity Analysis
3.4. Optimization Strategy
3.4.1. CMA-ES
3.4.2. SDBOX
3.4.3. Nelder–Mead
3.4.4. Pattern Search
4. Results and Discussion
4.1. Ritz Method and Sensitivity Analysis
4.2. Optimization Algorithms Performance Evaluation
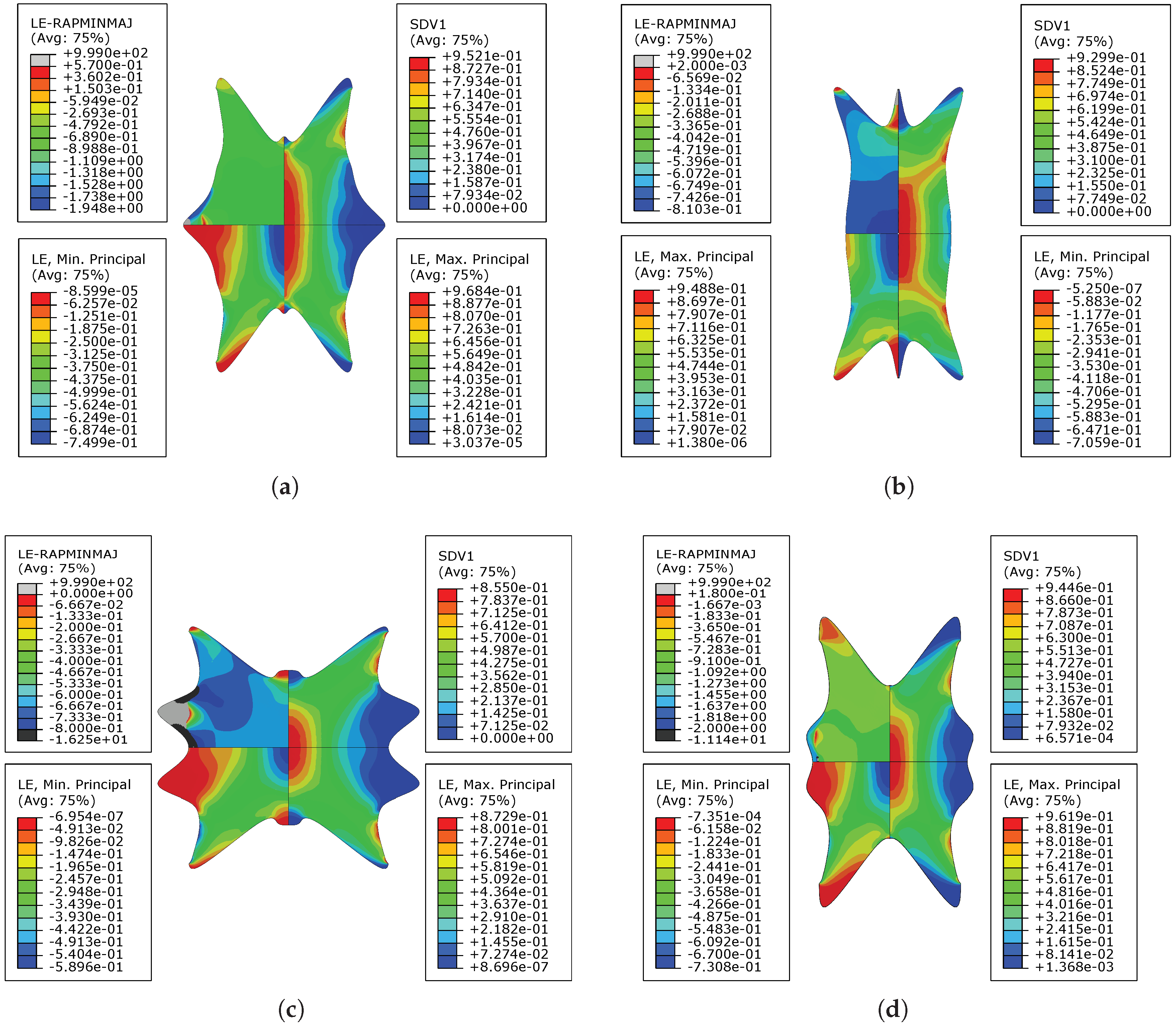
4.3. Test Design: Optimization Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| B-splines | Basis spline |
| CF | Cost Function |
| CMA-ES | Covariance Matrix Adaptation Evolution Strategy |
| DIC | Digital Image Correlation |
| EGM | Equation Gap Method |
| FEA | Finite Element Analysis |
| FEMU | Finite Element Model Updating |
| FFM | Full Filed Method |
| LE | Principal strain |
| LE-RAPMINMAJ | Ratio between the minor and major principal strains |
| NM | Nelder–Mead |
| SDBOX | Globally-convergent derivative-free algorithm for the minimization of a continuously |
| differentiable function | |
| SDV1 | State Variable, which stands for the equivalent plastic strain |
| NURBS | Non-Uniform Rational Basis Spline |
| VFM | Virtual Field Method |
References
- Ablat, M.A.; Qattawi, A. Numerical simulation of sheet metal forming: A review. Int. J. Adv. Manuf. Technol. 2016, 1235–1250. [Google Scholar] [CrossRef]
- Teaca, M.; Charpentier, I.; Martiny, M.; Ferron, G. Identification of sheet metal plastic anisotropy using heterogeneous biaxial tensile tests. Int. J. Mech. Sci. 2010, 52, 572–580. [Google Scholar] [CrossRef]
- Zhang, S.; Leotoing, L.; Guines, D.; Thuillier, S. Potential of the Cross Biaxial Test for Anisotropy Characterization Based on Heterogeneous Strain Field. Exp. Mech. 2015, 55, 817–835. [Google Scholar] [CrossRef] [Green Version]
- Souto, N. Computational Design of a Mechanical Test for Material Characterization by Inverse Analysis. Ph.D. Thesis, University of Aveiro, Aveiro, Portugal, 2015. [Google Scholar]
- Avril, S.; Bonnet, M.; Bretelle, A.S.; Grédiac, M.; Hild, F.; Ienny, P.; Latourte, F.; Lemosse, D.; Pagano, S.; Pagnacco, E.; et al. Overview of identification methods of mechanical parameters based on full-field measurements. Exp. Mech. 2008, 48, 381–402. [Google Scholar] [CrossRef]
- Syed-Muhammad, K.; Toussaint, E.; Grédiac, M. Optimization of a mechanical test on composite plates with the virtual fields method. Struct. Multidiscip. Optim. 2009, 38, 71–82. [Google Scholar] [CrossRef]
- Souto, N.; Andrade-Campos, A.; Thuillier, S. Mechanical design of a heterogeneous test for material parameters identification. Int. J. Mater. Form. 2017, 10, 353–367. [Google Scholar] [CrossRef]
- Helfrick, M.N.; Niezrecki, C.; Avitabile, P.; Schmidt, T. 3D digital image correlation methods for full-field vibration measurement. Mech. Syst. Signal Process. 2011, 25, 917–927. [Google Scholar] [CrossRef]
- Meuwissen, M.; Oomens, C.; Baaijens, F.; Petterson, R.; Janssen, J. Determination of the elasto-plastic properties of aluminium using a mixed numerical–experimental method. J. Mater. Process. Technol. 1998, 75, 204–211. [Google Scholar] [CrossRef]
- Banabic, D.; Barlat, F.; Cazacu, O.; Kuwabara, T. Advances in anisotropy and formability. Int. J. Mater. Form. 2010, 3, 165–189. [Google Scholar] [CrossRef]
- Pottier, T.; Vacher, P.; Toussaint, F.; Louche, H.; Coudert, T. Out-of-plane Testing Procedure for Inverse Identification Purpose: Application in Sheet Metal Plasticity. Exp. Mech. 2012, 52, 951–963. [Google Scholar] [CrossRef]
- Souto, N.; Thuillier, S.; Andrade-Campos, A. Design of an indicator to characterize and classify mechanical tests for sheet metals. Int. J. Mech. Sci. 2015, 101–102, 252–271. [Google Scholar] [CrossRef]
- Prates, P.A.; Pereira, A.F.G.; Sakharova, N.A.; Oliveira, M.C.; Fernandes, J.V. Inverse Strategies for Identifying the Parameters of Constitutive Laws of Metal Sheets. Adv. Mater. Sci. Eng. 2016, 2016, 4152963. [Google Scholar] [CrossRef]
- Aquino, J.; Andrade Campos, A.; Souto, N.; Thuillier, S. Experimental validation of a new heterogeneous mechanical test design. AIP Conf. Proc. 2018, 1960, 090002. [Google Scholar] [Green Version]
- Souto, N.; Thuillier, S.; Andrade-Campos, A. Design of a mechanical test to characterize sheet metals—Optimization using B-splines or cubic splines. AIP Conf. Proc. 2016, 1769. [Google Scholar] [CrossRef]
- Aquino, J.; Andrade Campos, A.; Souto, N.; Thuillier, S. On the design of innovative heterogeneous tests using a shape optimization approach. AIP Conf. Proc. 2018, 1960, 110001. [Google Scholar]
- Souto, N.; Andrade-Campos, A.; Thuillier, S. Material parameter identification within an integrated methodology considering anisotropy, hardening and rupture. J. Mater. Process. Technol. 2015, 220, 157–172. [Google Scholar] [CrossRef]
- Abedini, A.; Butcher, C.; Rahmaan, T.; Worswick, M. Evaluation and calibration of anisotropic yield criteria in shear Loading: Constraints to eliminate numerical artefacts. Int. J. Solids Struct. 2018, 151, 118–134. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Simulia: Providence, RI, USA, 2009. [Google Scholar]
- Sirisena, H.; Chou, F. Convergence of the Control Parameterization Ritz Method for Nonlinear Optimal Control Problems. J. Optim. Theory Appl. 1979, 29, 369–382. [Google Scholar] [CrossRef]
- Lucidi, S.; Sciandrone, M. On the Global Convergence of Derivative-Free Methods for Unconstrained Optimization. SIAM J. Optim. 2002, 13, 97–116. [Google Scholar] [CrossRef] [Green Version]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef] [Green Version]
- Rios, L.M.; Sahinidis, N.V. Derivative-free optimization: A review of algorithms and comparison of software implementations. J. Glob. Optim. 2013, 56, 1247–1293. [Google Scholar] [CrossRef]
- Hooke, R.; Jeeves, T.A. “Direct Search” Solution of Numerical and Statistical Problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Liberti, L.; Sergei, K. Comparison of deterministic and stochastic approaches to global optimization. Int. Trans. Oper. Res. 2005, 12, 263–285. [Google Scholar] [CrossRef] [Green Version]
- Cavazzuti, M. Optimization Methods: From Theory to Design: Scientific and Technological Aspects in Mechanics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef] [Green Version]
- Audet, C.; Custódio, A.L.; Dennis, J.E. Erratum: Mesh Adaptive Direct Search Algorithms for Constrained Optimization. SIAM J. Optim. 2008, 18, 1501–1503. [Google Scholar] [CrossRef] [Green Version]
- Mohr, D.; Henn, S. Calibration of Stress-triaxiality Dependent Crack Formation Criteria: A New Hybrid Experimental–Numerical Method. Exp. Mech. 2007, 47, 805–820. [Google Scholar] [CrossRef]
- Abedini, A.; Butcher, C.; Worswick, M.J. Fracture Characterization of Rolled Sheet Alloys in Shear Loading: Studies of Specimen Geometry, Anisotropy, and Rate Sensitivity. Exp. Mech. 2017, 57, 75–88. [Google Scholar] [CrossRef]





| Isotropic hardening: |
| Kinematic hardening: |
| Yld2004-18p yield criterion: |
| Rupture criterion: |
| Parameter | Value | Units | Parameter | Value | Units |
|---|---|---|---|---|---|
| 1.264 | - | 0.974 | - | ||
| 1.242 | - | 1.049 | - | ||
| 0.578 | - | 0.708 | - | ||
| 1.000 | - | 1.365 | - | ||
| 0.793 | - | 0.672 | - | ||
| 0.838 | - | 0.929 | - | ||
| 0.996 | - | 0.768 | - | ||
| 1.000 | - | 0.678 | - | ||
| 100.030 | MPa | 210.268 | MPa | ||
| 5.917 | 102.729 | MPa | |||
| 1018.425 | MPa | 22.85 | - | ||
| 27,439.960 | MPa | 258.38 | - | ||
| 145.246 | MPa | 0.0258 | - |
| Strain state range and heterogeneity: |
| Diversity of the mechanical information, |
| Strain state range covered by the mechanical test, |
| Deformation heterogeneity of the specimen, |
| Strain Level: |
| Maximum strain achieved, |
| Average deformation over the specimen, |
| 1 | 4 | 0.25 | 0.8 | 0.4 | 0.13 | 0.02 | 0.25 | 0.35 | 0.25 |
| Strain State | Range |
|---|---|
| Uniaxial tension | |
| Simple shear | |
| Plain strain tension | |
| Equibiaxial tension | |
| Uniaxial compression |
| B-Splines | CMA-ES | Nelder | Pattern | SDBOX |
|---|---|---|---|---|
| Mead | Search | |||
| 0.0273 | 0.0438 | 0.0249 | 0.0327 | |
| 0.0100 | 0.0115 | 0.0092 | 0.0109 | |
| 0.1277 | 0.0908 | 0.0747 | 0.1345 | |
| 0.1070 | 0.0897 | 0.0864 | 0.1021 | |
| 0.2273 | 0.1178 | 0.1455 | 0.2352 | |
| CF Minimum | 1.5007 | 1.6464 | 1.6592 | 1.4846 |
| 0.5346 | 0.3231 | 0.3674 | 0.4108 | |
| 0 | 0 | 0 | 0 | |
| 0.0102 | 0.0038 | 0.0012 | 0.0145 | |
| 0.0012 | 0.0149 | 0.0302 | 0.0042 | |
| 0.0154 | 0.0141 | 0.0094 | 0.0274 | |
| 0.9058 | 0.8741 | 0.7761 | 0.9439 | |
| NURBS | CMA-ES | Nelder | Pattern | SDBOX |
| Mead | Search | |||
| 0.0313 | 0.0448 | 0.0357 | 0.0163 | |
| 0.0138 | 0.0098 | 0.0082 | 0.0041 | |
| 0.1465 | 0.0699 | 0.0970 | 0.1098 | |
| 0.1069 | 0.0807 | 0.0972 | 0.1047 | |
| 0.2634 | 0.0991 | 0.1391 | 0.3050 | |
| CF Minimum | 1.4380 | 1.6956 | 1.6228 | 1.4601 |
| 0.4517 | 0.2323 | 0.4469 | 0.4628 | |
| 0 | 0 | 0 | 0 | |
| 0.0112 | 0.0055 | 0.0024 | 0 | |
| 0.0282 | 0.0359 | 0.0184 | 0.0501 | |
| 0.0244 | 0.0055 | 0.0208 | 0 | |
| 0.9502 | 0.8281 | 0.8446 | 0.9226 | |
| Splines | CMA-ES | Nelder | Pattern | SDBOX |
| Mead | Search | |||
| 0.0293 | 0.0347 | 0.0364 | 0.0319 | |
| 0.0120 | 0.0094 | 0.0082 | 0.0105 | |
| 0.0970 | 0.0853 | 0.0884 | 0.0889 | |
| 0.0931 | 0.0865 | 0.0849 | 0.0927 | |
| 0.1943 | 0.1546 | 0.1349 | 0.1649 | |
| CF Minimum | 1.5741 | 1.6294 | 1.6472 | 1.6110 |
| 0.3543 | 0.3460 | 0.2944 | 0.3421 | |
| 0 | 0 | 0 | 0 | |
| 0.0047 | 0.00134 | 0.0080 | 0.0073 | |
| 0.0271 | 0.0812 | 0.0055 | 0.0573 | |
| 0.0204 | 0.00851 | 0.0191 | 0.0147 | |
| 0.8500 | 0.83976 | 0.8370 | 0.8501 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrade-Campos, A.; Aquino, J.; Martins, J.M.P.; Coelho, B. On the Design of Innovative Heterogeneous Sheet Metal Tests Using a Shape Optimization Approach. Metals 2019, 9, 371. https://doi.org/10.3390/met9030371
Andrade-Campos A, Aquino J, Martins JMP, Coelho B. On the Design of Innovative Heterogeneous Sheet Metal Tests Using a Shape Optimization Approach. Metals. 2019; 9(3):371. https://doi.org/10.3390/met9030371
Chicago/Turabian StyleAndrade-Campos, António, José Aquino, João M. P. Martins, and Bernardete Coelho. 2019. "On the Design of Innovative Heterogeneous Sheet Metal Tests Using a Shape Optimization Approach" Metals 9, no. 3: 371. https://doi.org/10.3390/met9030371
APA StyleAndrade-Campos, A., Aquino, J., Martins, J. M. P., & Coelho, B. (2019). On the Design of Innovative Heterogeneous Sheet Metal Tests Using a Shape Optimization Approach. Metals, 9(3), 371. https://doi.org/10.3390/met9030371





