Next Article in Journal
Thermodynamic and Experimental Studies on Al Addition of 253MA Steel
Previous Article in Journal
Friction Performance of Aluminum-Silicon Alloy Cylinder Liner after Chemical Etching and Laser Finishing
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 9
Issue 4
10.3390/met9040432
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Zn and P Alloying Effect in Sub-Rapidly Solidified LaFe11.6Si1.4 Magnetocaloric Plates

by
Pingxia Jin
1,2,
Yuqiang Li
1,2,
Yuting Dai
1,2,
Zhishuai Xu
1,2,
Changjiang Song
1,2,
Zhiping Luo
3,
Qijie Zhai
1,2,
Ke Han
4 and
Hongxing Zheng
1,2,*
1
School of Materials Science and Engineering, Shanghai University, Shanghai 200444, China
2
Center for Advanced Solidification Technology, Shanghai University, Shanghai 200444, China
3
Department of Chemistry and Physics, Fayetteville State University, Fayetteville, NC 28301, USA
4
National High Magnetic Field Laboratory, Florida State University, Tallahassee, FL 32310, USA
*
Author to whom correspondence should be addressed.
Metals 2019, 9(4), 432; https://doi.org/10.3390/met9040432
Submission received: 28 March 2019 / Revised: 8 April 2019 / Accepted: 10 April 2019 / Published: 11 April 2019
Browse Figures
Versions Notes

Abstract

:
The occupation mechanism and magnetic transition behavior of trace Zn and P alloying in the sub-rapidly solidified LaFe11.6Si1.4 magnetocaloric plates were investigated. The LaFe11.6Si1.4, LaFe11.6Si1.4Zn0.03, and LaFe11.6Si1.4P0.03 plates were fabricated using the centrifugal casting method in the present work. Experimental results showed that both Zn and P elements were distributed in the La5Si3 and LaFeSi phases during sub-rapid solidification. After annealed at 1373 K for 72 h, the LaFe11.6Si1.4 plate underwent a second-order magnetic transition, while both the LaFe11.6Si1.4Zn0.03 and LaFe11.6Si1.4P0.03 plates underwent a first-order transition. In combination with X-ray diffraction results, it was proposed that both Zn and P atoms prefer to enter the 96i site substituting for FeII/Si atoms according to the density-functional reconstruction of crystallographic structure. The Zn addition led to a slight decrease in magnetic entropy change from 7.0 to 5.9 J/(kg⋅K), while the P addition strikingly enhanced this property to 31.4 J/(kg⋅K) under a magnetic field change of 3 T. The effective refrigeration capacity of the annealed LaFe11.6Si1.4P0.03 plate reached 189.9 J/kg.

1. Introduction

Solid-state magnetic refrigeration has been considered to be a highly competitive alternative to the conventional vapor-compression technology based on the magnetocaloric effect [1]. As early as 1976, Brown discovered that the heavy rare-earth Gd demonstrated a magnetic entropy change as high as 13.17 J/(kg⋅K) under a magnetic field change of 7 T in the vicinity of 293 K [2]. Since then, heavy rare-earth Gd has been taken as an important benchmark for the research and development of room-temperature magnetocaloric materials [3,4]. During the past two decades, a few promising candidates, including Gd5Si2Ge2 [5,6,7], MnFeP1−xAsx(Si) [8,9], Heusler Ni2MnX (X = Ga, Sn, In) [10,11,12], La(Fe,Si)13 [13,14], LaMnO3 magnetite [15,16], and R2Fe17 system [17,18], were found, among which La(Fe,Si)13 attracted significant attention due to the advantages afforded by its non-toxic constituent elements, giant magnetocaloric effect, small thermal/magnetic hysteresis, and high thermal conductivity [19].
A lot of effort has been spent on the synthesis of La(Fe,Si)13. The main advantage of powder metallurgy [20,21,22] lies in its flexible gradient compositional control, which is beneficial for broadening the refrigeration temperature window; however, high-temperature annealing is still needed for the diffusion-controlled formation of the La(Fe,Si)13 (τ1) phase [23]. Although melt spinning could directly produce a high proportion of τ1 phase during rapid solidification, and the resultant refined grains greatly shorten the post-annealing procedure, it was hard to achieve practical application due to its flake-like shape [24,25]. Researchers have tried to integrate brittle La(Fe,Si)13 particles into a continuous matrix (epoxy resin [26,27] or molten Sn [28,29], SnBi [30]) or cladded them with a thin seamless austenitic steel jacket through the powder-in-tube (PIT) technology [31]. Unfortunately, more unexpected problems arose, such as slimsy interface bonding, low thermal conductivity, and dramatic decay of magnetocaloric capacity. The only exception is that Wang et al. [32] observed excellent magnetocaloric effect with durable service life in the La(Fe,Si)13Hy/In composite where they hot pressed La(Fe,Si)13Hy particles with solid-state indium powder at 413 K (lower than the melting point 430 K of indium element). Additionally, the centrifugal casting method [33] was also employed to produce a sub-rapidly solidified La(Fe,Si)13 thin plate.
On the other hand, fourth elemental alloying has been extensively attempted to adjust the magnetic transition, including C [34], H [35], Co [36], Ni [37], Cu [38], Nd [39], Ce [40], etc. For instance, Anh et al. [41] reported that the characteristic temperature of magnetic transition in the LaFe11.44Si1.56 alloy linearly increased with Nd partially replacing La, and was accompanied by volume shrinkage of the unit-cell. However, the occupation mechanism for the fourth elements in La(Fe,Si)13 remains unclear, and even controversial. Rosca et al. [42] proposed H atoms preferred the 48f interstitial site (a FeII/Si-based asymmetric pyramid with one La vertex [43]) in LaFe11.31Si1.69H1.45 based on neutron diffraction results, while Bao et al. [44] suggested the 24d interstitial site (an octahedral site with four FeII/Si and two La nearest neighbors [45]) based on the fact that all Fe–Fe bonds become longer, and the shortest inter-cluster bond (B4) changes the most [46]. One more example is that Phejar et al. [47] concluded that C atoms entered the 48f interstitial site, which differs from the viewpoint of Hai et al. [43] who argue in favor of the 24d interstitial site. Our recent work [48] supported the 24d interstitial site for C alloying in LaFe11.6Si1.4 according to the crystallographic structure reconstruction based on density-functional theory (DFT) [49,50,51], and it was proven that density-functional reconstruction is an effective tool to explain the magnetic transition behavior by quantitatively measuring the length change of Fe–Fe bonds. Save for these limited studies on light elements, it was simply taken for granted that rare-earth elements (Nd [52], Ce [53,54], and Pr [55]) substitute for La and transition-metals (Co [56,57], Mn [58,59,60], Ni [61], and Cu [38]) for Fe when alloying La(Fe,Si)13, although no supporting evidence was provided. Against this background, trace Zn (metallic element) and P (non-metallic element) alloying was studied in a sub-rapidly solidified La(Fe,Si)13 plate in the present work, with an emphasis on the magnetic transition behavior and occupation mechanism.

2. Experimental

Three button ingots with a weight of about 120 g and nominal compositions of LaFe11.6Si1.4, LaFe11.6Si1.4Zn0.03, and LaFe11.6Si1.4P0.03 (at.%) were prepared using levitation melting from commercial pure La (99.9 wt.%), Fe (99.99 wt.%), Si (99.999 wt.%), and Zn (99.8 wt.%). All ingots were remelted four times to ensure homogeneity. The obtained ingots were then spun into plates with a dimension of ~60 × 40 × 2.5 mm3 using a centrifugal casting setup in argon under a cooling rate of ~5000 K/s. Experimental details have been described elsewhere [62]. Half of the plates were sealed in quartz tubes and annealed at 1373 K for 72 h, followed by water quenching.
Microstructure and elemental analyses were performed using an electron probe microanalyzer (EPMA-8050G, Shimadzu, Tokyo, Japan) equipped with a wavelength-dispersive spectrometer (WDS). Differential scanning calorimetric measurements (DSC, Netzsch 404 F3, NETZSCH-Gerätebau GmbH, Selb, Germany) were carried out to clarify high-temperature phase transition behavior at a heating/cooling rate of 20 K/min. X-ray diffraction (XRD, Dlmax-2500, Rigaku, Osaka, Japan) with Cu Kα radiation was conducted to detect the phase and crystal structure. Magnetic properties were measured using a physical property measurement system (PPMS-9, Quantum Design, San Diego, CA, USA).

3. Results and Discussion

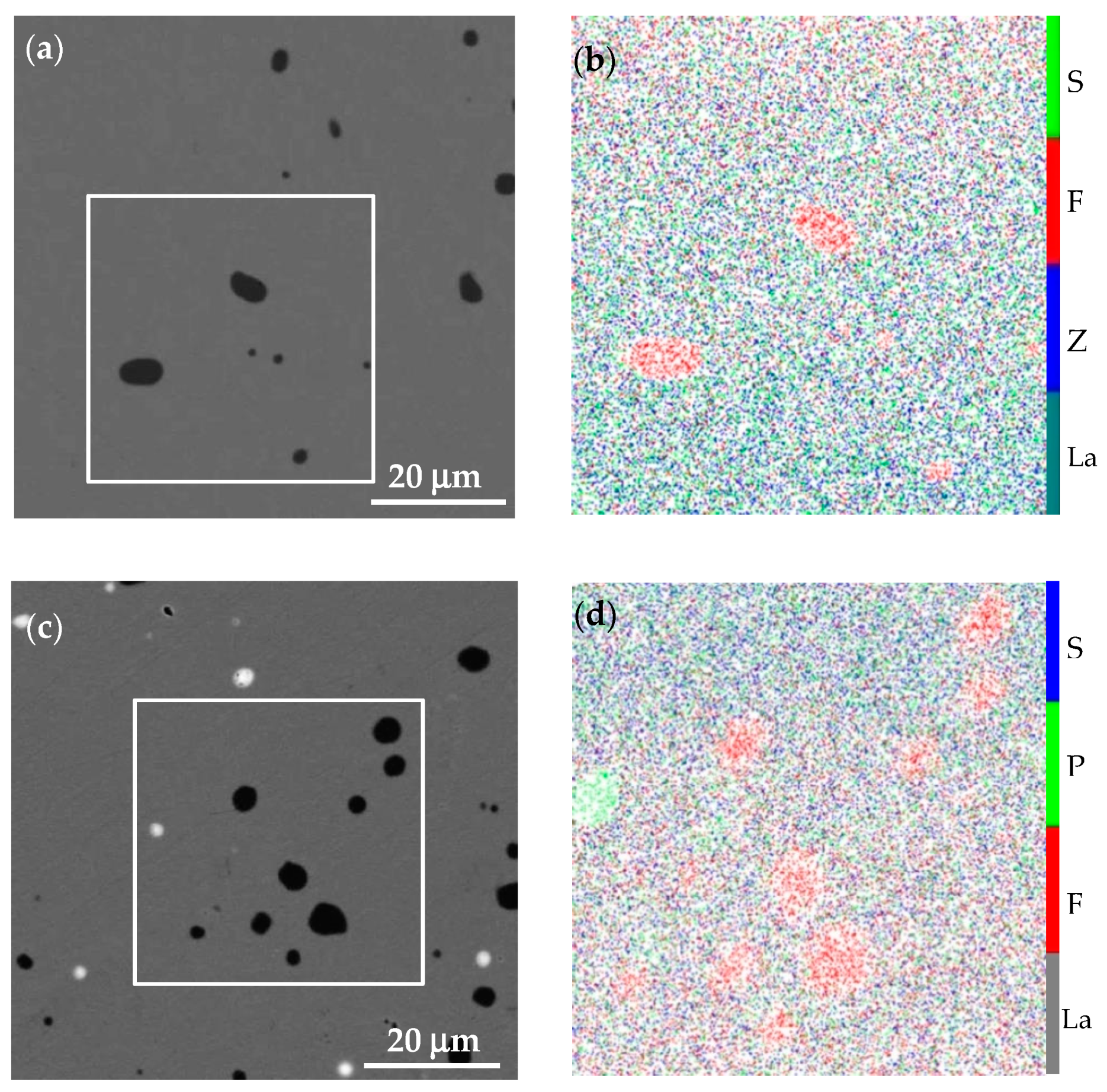
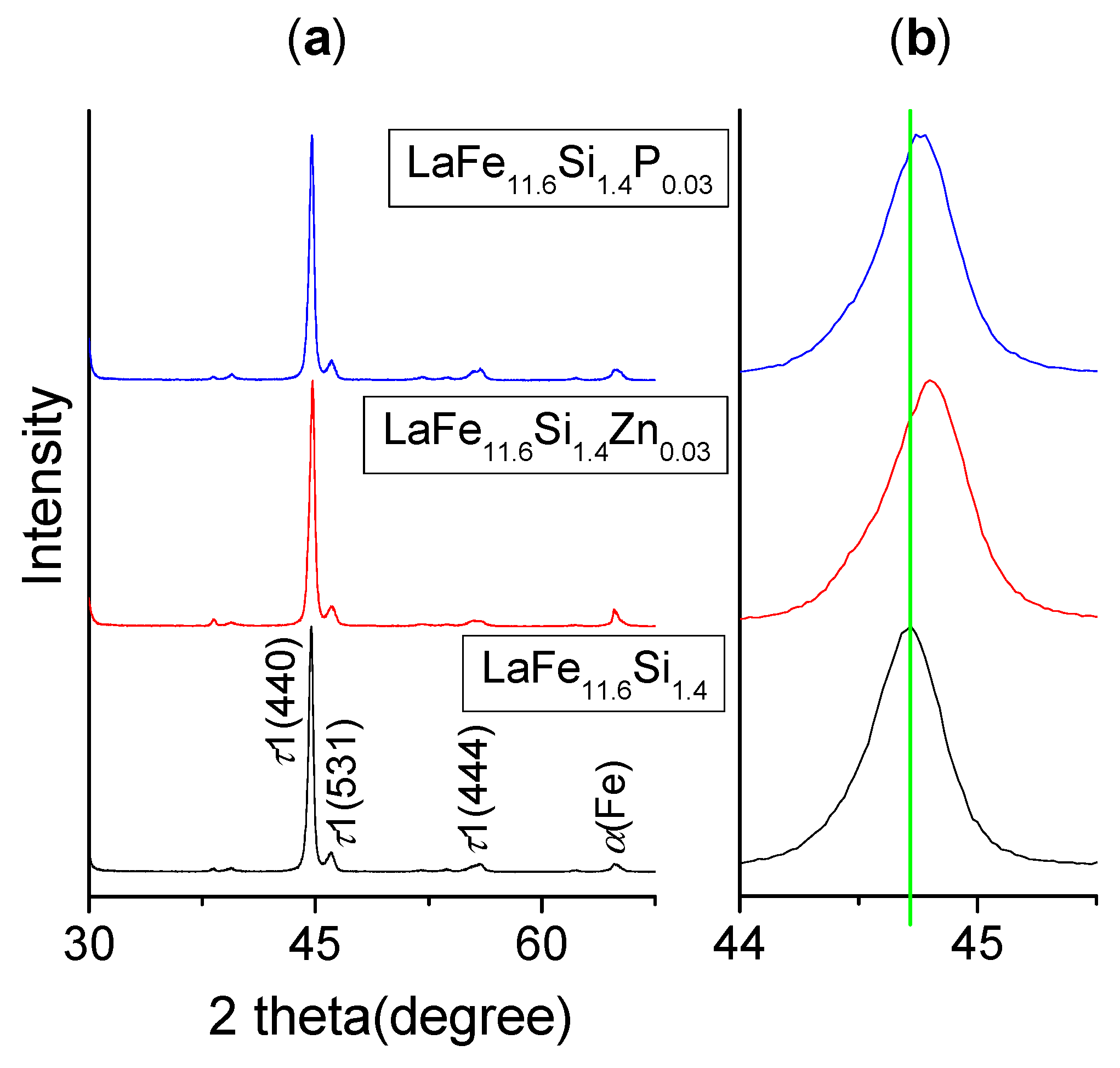
3.1. Phase and Microstructure

A typical honeycomb-like refined microstructure of the sub-rapidly solidified LaFe11.6Si1.4 plate is shown in Figure 1a, which is different from the coarse dendrites usually obtained in conventional arc-melted alloy [63]. WDS analyses reveal that the black, grey, and white areas represent α(Fe), LaFeSi, and La5Si3 phases, respectively, as marked by red arrows in Figure 1b. Similar SEM images of the LaFe11.6Si1.4Zn0.03 and LaFe11.6Si1.4P0.03 plates were not shown for clarity. Both Zn/P elements were distributed in the LaFeSi and La5Si3 phases, and no Zn/P element was detected in the α(Fe) phase. The elemental mappings of La, Fe, Si, and Zn in the sub-rapidly solidified LaFe11.6Si1.4Zn0.03 plate are shown in Figure 1c (similar elemental mappings of LaFe11.6Si1.4P0.03 are not shown here).
DSC measurements for the sub-rapidly solidified plates were used to analyze their high-temperature phase transition behavior. Here, using LaFe11.6Si1.4 as an example, a magnetic transition of the α(Fe) phase happens around 1018 K upon heating, and reverse transition occurs at 991 K upon cooling (marked by circles in Figure 2). According to previous investigation [64], solid LaFeSi, τ1, and α(Fe) phases melt at 1394, 1558, and 1682 K, respectively, upon heating. The primary α(Fe) phase first forms at 1682 K upon cooling, and then τ1 phase through a α(Fe) + LLa → τ1 peritectic reaction [65]. With Zn/P alloying, there is almost no difference for the high-temperature transition behaviors (not shown here). The formation τ1 phase in all three sub-rapidly solidified plates annealed at 1373 K is fully completed through peritectoid interdiffusion between the α(Fe) and LaFeSi phases [62]. A few weak exothermic peaks close to 1464 K correspond to the formation of La5Si3 phase from residual liquid τ1 phase, which can be easily confirmed by the shrinkage cavities. All annealed plates consist of τ1 matrix phase and a small amount of black α(Fe) phase, with a few white areas indicating LaFeSi phase visible in the LaFe11.6Si1.4P0.03 plate (Figure 3a,c). One can observe that both Zn and P elements homogeneously dissolved into the τ1 matrix according to the WDS analyses (Figure 3b,d).
X-ray diffraction peaks shown in Figure 4a are well indexed to be τ1 and α(Fe) phases [66]. The main diffraction peak at 44.7° from τ1 phase for both Zn/P-alloyed plates shifts towards higher angle regime in contrast to that of LaFe11.6Si1.4, as shown in Figure 4b (enlarged image), which implies that the unit-cell shrank with Zn/P alloying. Using the least square method, the lattice parameters of the τ1 phase for the annealed LaFe11.6Si1.4, LaFe11.6Si1.4Zn0.03, and LaFe11.6Si1.4P0.03 plates are calculated to be 1.1473 ± 0.006, 1.1468 ± 0.0059, and 1.1471 ± 0.0052 nm, respectively.

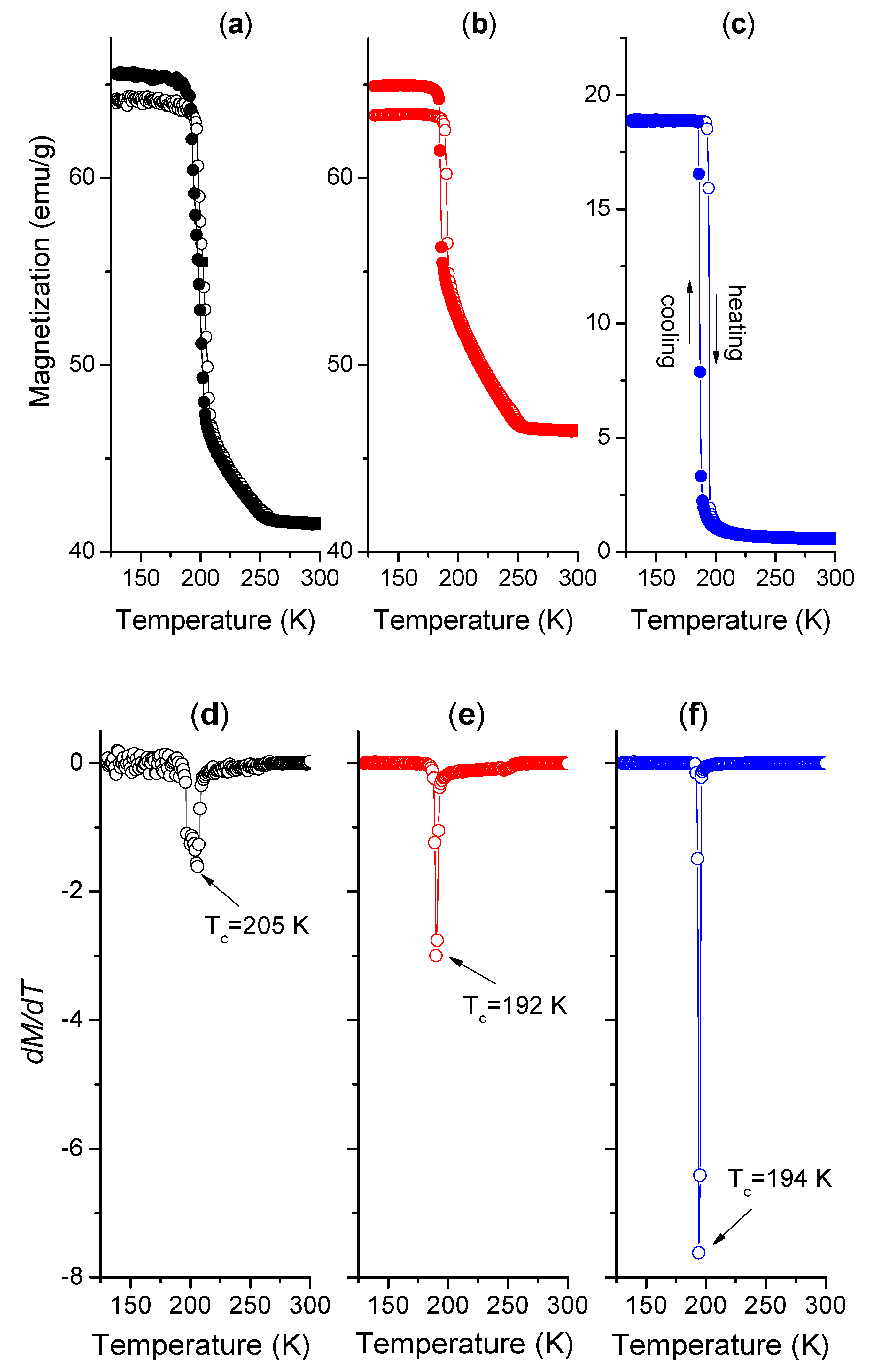
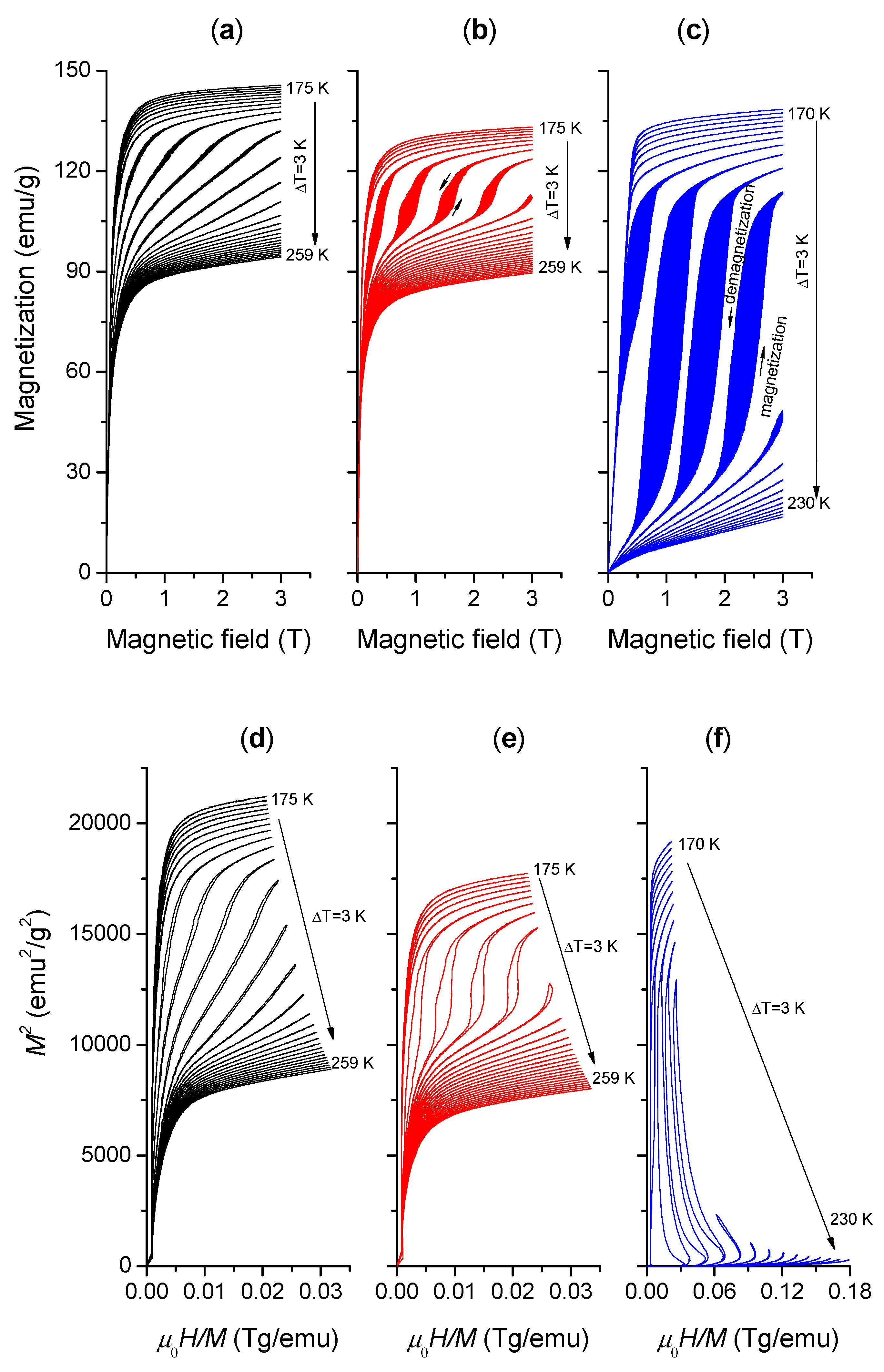
3.2. Magnetic Transition and Magnetocaloric Effect

Magnetization curves as a function of temperature (M-T) were measured under a low magnetic field of 0.05 T (Figure 5a–c). The Curie temperature of LaFe11.6Si1.4, LaFe11.6Si1.4Zn0.03, and LaFe11.6Si1.4P0.03 were determined to be 205, 192, and 194 K, respectively, from the dM/dT curves upon heating (Figure 5d–f). All the annealed plates show a drop of magnetization intensity upon heating, which corresponds to a ferromagnetic-paramagnetic transition, and reverse transition upon cooling [67]. The characteristic transition temperature decreased by 13 and 11 K, respectively, with Zn and P alloying compared to that of LaFe11.6Si1.4. This agrees to the principle that the Curie temperature always increases with expansion of the unit-cell and decreases with shrinkage in La(Fe,Si)13 [68], although some unknown factors cannot be excluded. We will discuss the occupation mechanism in Section 3.3. It should be noted that the M(T) curve of LaFe11.6Si1.4P0.03 is different for both LaFe11.6Si1.4 and LaFe11.6Si1.4Zn0.03. A clear slope change for LaFe11.6Si1.4 and LaFe11.6Si1.4Zn0.03 can be observed, in contrast to the sharp decrease in LaFe11.6Si1.4P0.03, and the nonzero remnant magnetization above the Curie temperature is associated with the residual α(Fe) phase [69].
Several selected isothermal magnetization curves (M-H) around the magnetic transition (near the Curie temperature) under a magnetic field change of 3 T were measured at an interval of 3 K (Figure 6a–c). One can observe that the magnetization curves for the LaFe11.6Si1.4 plate have characteristics of a second-order transition, while both the LaFe11.6Si1.4Zn0.03 and LaFe11.6Si1.4P0.03 plates show S-shaped magnetization curves, which are a typical feature for the first-order itinerant electro-metamagnetism [70]. The magnetic hysteresis effects (shadowed areas marked in Figure 6b,c) also confirm the first-order nature of the magnetic transition, and the LaFe11.6Si1.4 plate underwent a second-order transition without any hysteresis (Figure 6a). Additionally, it was also well accepted that the type of phase transition can be judged using the Arrott plots (Figure 6d–f) [71,72] according to the Inoue-Shimizu model [73]. The free energy of a magnetic system is expressed by the Landau expansion in powers of magnetization in this model. The type of phase transition is closely related to the sign of the Landau coefficient at the Curie temperature, which can be obtained from the Arrott plots. If there are “S-bend” Arrott curves near the Curie temperature, the Landau coefficient is negative and the transition is first order; otherwise, it is positive, and the transition is second order. As seen in Figure 6d–f, a second-order transition happened in the LaFe11.6Si1.4 plate with regard to an almost linear behavior in the Arrott plots, while the magnetic transition in both the LaFe11.6Si1.4Zn0.03 and LaFe11.6Si1.4P0.03 plates changed from the second order to the first order according to the characteristic “S-bend” Arrott plots.
The magnetic entropy change (ΔSM) can be estimated using the classical Maxwell Equation Δ S M ( T , H ) = μ 0 ∫ 0 H ( ∂ M ∂ T ) H d H [50], as shown in Figure 7a–c. The second-order transition occurred with Zn alloying in LaFe11.6Si1.4, and as a result, the maximum |ΔSM| value decreased from 7.0 to 5.9 J/(kg⋅K) under a magnetic field change of 3 T. P alloying led to a complete first-order magnetic transition, and thus, the maximum |ΔSM| value reached to 31.4 J/(kg⋅K), which is higher than those of the LaFe11.6Si1.4 plate (22.2 J/(kg⋅K) annealed at 1373 K for 3 h [62]) and the suction-cast rod (27.8 J/(kg⋅K) annealed at 1373 K for 100 h [48]). Additionally, refrigeration capacity (RC) was taken as another important indicator to assess magnetocaloric effect. RC represents the amount of heat that can be transferred between the cold sink and the hot sink within one thermodynamic cycle, which systematically takes into account both peak values and temperature intervals of ΔSM, and is defined as RC = ∫ T cold T hot | Δ S M ( T ) | d T [16,18], where Thot and Tcold are the corresponding temperatures at full width half the maximum peak value of ΔSM (as shown by stripped area in Figure 7a). After subtracting average hysteresis losses, the effective RCeff values for the annealed LaFe11.6Si1.4, LaFe11.6Si1.4Zn0.03, and LaFe11.6Si1.4P0.03 are 89.3, 72.7, and 189.9 J/kg, respectively.

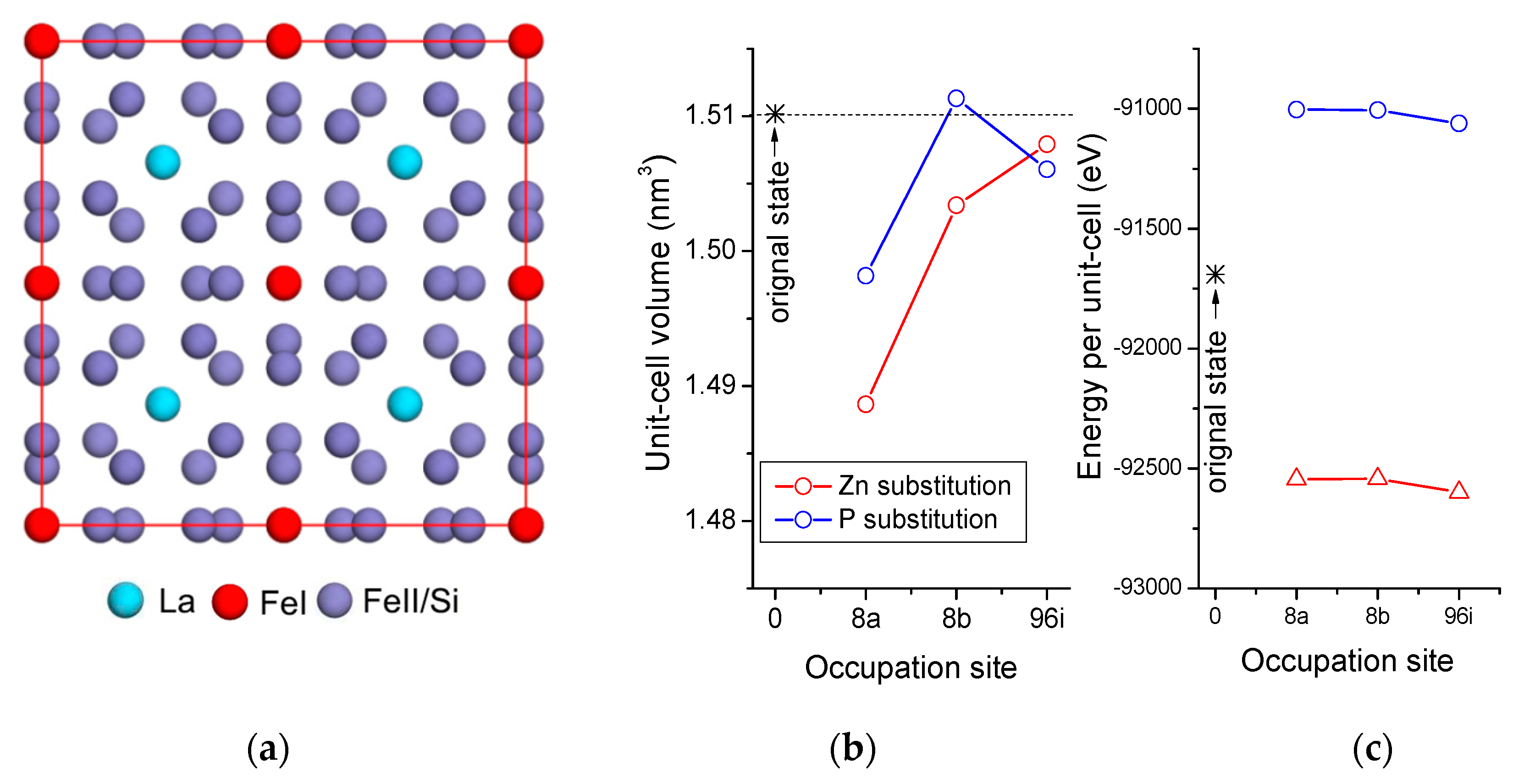
3.3. Occupation Mechanism

DFT was introduced to reconstruct the crystallographic structure of the unit-cell so as to explore the occupation mechanism of Zn/P alloying in LaFe11.6Si1.4. An ideal crystallographic unit-cell of NaZn13-type LaFe11.6Si1.4 consists of 112 atoms, where the positions of 8a, 8b, and 96i are occupied by La, FeI, and FeII/Si atoms, respectively (Figure 8a). In the present work, commercial CASTEP code [74] was used based on the plane wave ultrasoft pseudopotential. The generalized gradient approximation (GGA) with the Perdew-Wang 1991 (PW91) functional [75] within the framework of density functional theory was adopted. The plane-wave cutoff energy was set to be 330 eV, and the number of k-points is 2 × 2 × 2. The electron configurations for La, Fe, Si, P, and Zn atoms were 5d16s2, 3d64s2, 3s23p2, 3s23p3, and 3d104s2, respectively. Geometric optimization of the convergence tolerances of geometry optimizations were listed as follows: (1) the total energy change within 5 × 10−6 eV per atom; (2) the maximum force smaller than 0.1 eV/nm; (3) the maximum stress of 0.02 GPa; and (4) the maximum displacement of 5 × 10−5 nm. BFGS minimizer24 was used to optimize the unit-cell, and we reconstructed the crystal structure using Materials Studio with lattice parameters a = b = c = 1.1488 nm.
A coefficient k = 1.133 was introduced so as to coordinate the X-ray diffraction experimental results and DFT reconstruction data. The calculated unit-cell volume and energy data with various Zn/P occupation sites are plotted in Figure 8b,c. Firstly, the atomic radii [76,77] of La, Fe, Si, Zn, and P are 0.187, 0.126, 0.111, 0.131, and 0.106 nm, respectively. It seems unreasonable that the substitution of Zn for 8b (FeI) or 96i (FeII/Si) would lead to the volume shrinkage in LaFe11.6Si1.4 since Zn atoms are larger than Fe and Si atoms. Similarly, replacing 8b (FeI) with P would result in a slight expansion of the unit-cell, although the P atom is smaller than the Fe atom, which indicates that besides the atomic radius, chemical bonds and electronegativity or other factors should be taken into consideration for the DFT calculation. According to X-ray diffraction experimental results (volume shrinkage), all of the other five occupation sites seem possible for Zn/P alloying except the P substitution for 8b (FeI) (Figure 8b). Based on the lowest energy principle, it was proposed that both Zn and P atoms prefer to enter the 96i (FeII/Si) substitution site (Figure 8c). We cannot fully exclude the possibility of partial Zn and P atoms occupying the 8a (La) or 8b (FeI) sites.

4. Conclusions

The phase constitution, microstructure, magnetocaloric effect, and occupation mechanism of Zn/P alloyed LaFe11.6Si1.4 plates were investigated, and the following conclusions were obtained.
(1)
Zn/P elements were mainly distributed in the LaFeSi and La5Si3 phases during centrifugal solidification. After annealing at 1373 K for 72 h, Zn/P elements were homogeneously dispersed in the τ1 matrix and led to slight volume shrinkage of the unit-cell. Both Zn/P atoms prefer to enter the 96i (FeII/Si) substitution site according to the density-functional reconstruction of crystallographic structure.
(2)
A second-order magnetic transition occurred in the annealed LaFe11.6Si1.4 plate, and a first-order transition in both the LaFe11.6Si1.4Zn0.03 and LaFe11.6Si1.4P0.03 plates. The addition of Zn/P decreased the characteristic transition temperature 11–13 K owing to lattice shrinkage.
(3)
P alloying resulted in a striking increase for the maximum magnetic entropy changes from 7.0 to 31.4 J/(kg⋅K) under a magnetic field change of 3 T, while Zn alloying caused a slight decrease to 5.9 J/(kg⋅K). The effective refrigeration capacity of the annealed LaFe11.6Si1.4P0.03 plate reached 189.9 J/kg.

Author Contributions

Conceptualization, H.Z.; methodology, P.J.; formal analysis, P.J., Y.D., Y.L., and Z.X.; writing—original draft preparation, P.J.; writing—review and editing, C.S., H.Z., Q.Z., Z.L., and K.H.; supervision, H.Z.

Funding

This research was funded by the National Natural Science Foundation of China (51474144) and the Shanghai Sailing Program (17YF1405900).

Acknowledgments

The authors are grateful to the National Natural Science Foundation of China and the Shanghai Sailing Program, which enabled the research to be carried out successfully.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wang, G.F.; Zhao, Z.R.; Jing, T.; Li, Y.F.; Ma, Q.; Zhang, X.F. Enhanced magnetocaloric properties in off-stoichiometric LaxFe11.5Si1.5 alloys. Intermetallics 2018, 93, 355–359. [Google Scholar] [CrossRef]
  2. Brown, G.V. Magnetic heat pumping near room temperature. J. Appl. Phys. 1976, 47, 3673–3680. [Google Scholar] [CrossRef]
  3. Provenzano, V.; Shull, R.D.; Kletetschka, G.; Stutzman, P.E. Gd90Co2.5Fe7.5 alloy displaying enhanced magnetocaloric properties. J. Alloy. Compd. 2015, 622, 1061–1067. [Google Scholar] [CrossRef]
  4. Jayaraman, T.V.; Boone, L.; Shield, J.E. Magnetocaloric effect and refrigerant capacity in melt-spun Gd−Mn alloys. J. Magn. Magn. Mater. 2013, 345, 153–158. [Google Scholar] [CrossRef]
  5. Pecharsky, A.O.; Gschneidner, K.A.; Pecharsky, V.K. The giant magnetocaloric effect between 190 and 300 K in the Gd5SixGe4−x alloys for 1.4 ≤ x ≤ 2.2. J. Magn. Magn. Mater. 2003, 267, 60–68. [Google Scholar] [CrossRef]
  6. Gschneidner, K.A.; Pecharsky, V.K. Magnetic refrigeration materials. J. Appl. Phys. 1999, 85, 5365–5368. [Google Scholar] [CrossRef]
  7. Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. A comparison between rare earth and transition metals working as magnetic materials in an AMR refrigerator in the room temperature range. Appl. Therm. Eng. 2015, 91, 767–777. [Google Scholar] [CrossRef]
  8. Tegus, O.; Brück, E.; Buschow, K.H.J.; de Boer, F.R. Transition-metal-based magnetic refrigerants for room-temperature applications. Nature 2012, 415, 150–152. [Google Scholar] [CrossRef]
  9. Yibole, H.; Guillou, F.; Zhang, L.; van Dijk, N.H.; Brück, E. Direct measurement of the magnetocaloric effect in MnFe(P, X) (X = As, Ge, Si) materials. J. Phys. D: Appl. Phys. 2014, 47, 186–187. [Google Scholar] [CrossRef]
  10. Sushmita, D.; Roy, R.K.; Ghosh, M.; Mallick, A.B.; Mitra, A.; Panda, A.K. Enhancement in magnetocaloric properties of NiMnGa alloy through stoichiometric tuned phase transformation and magneto-thermal transitions. J. Magn. Magn. Mater. 2017, 439, 305–311. [Google Scholar] [CrossRef]
  11. Gao, B.; Hu, F.X.; Shen, J.; Wang, J.; Sun, J.R.; Shen, B.G. Field-induced structural transition and the related magnetic entropy change in Ni43Mn43Co3Sn11 alloy. J. Magn. Magn. Mater. 2009, 321, 2571–2574. [Google Scholar] [CrossRef]
  12. Zheng, H.X.; Wang, W.; Xue, S.C.; Zhai, Q.J.; Frenzel, J.; Luo, Z.P. Composition-dependent crystal structure and martensitic transformation in Heusler Ni−Mn−Sn alloys. Acta Mater. 2013, 61, 4648–4656. [Google Scholar] [CrossRef]
  13. Hu, F.X.; Shen, B.G.; Sun, J.R.; Cheng, Z.H.; Rong, G.H.; Zhang, X.X. Influence of negative lattice expansion and metamagnetic transition on magnetic entropy change in the compound LaFe11.4Si1.6. Appl. Phys. Lett. 2001, 78, 3675–3677. [Google Scholar] [CrossRef]
  14. Liu, J.; Krautz, M.; Skokov, K.; Woodcock, T.G.; Gutfleisch, O. Systematic study of the microstructure, entropy change and adiabatic temperature change in optimized La–Fe–Si alloys. Acta Mater. 2011, 59, 3602–3611. [Google Scholar] [CrossRef]
  15. Hamad, M.A. Tailoring Magnetocaloric Effect in La0.7Sr0.3MnO3–TiO2. J. Supercond. Nov. Magn. 2018, 31, 337–340. [Google Scholar] [CrossRef]
  16. Dahal, B.R.; Kyle, S.; Allyn, M.M.; Tackett, R.J.; Huh, Y.; Kharel, P. Near-room-temperature magnetocaloric properties of La1−xSrxMnO3 (x = 0.11, 0.17, and 0.19) nanoparticles. Mater. Res. Express 2018, 5, 106103. [Google Scholar] [CrossRef]
  17. Zehani, K.; Guetari, R.; Mliki, N.; Bessais, L. Study of the Magnetocaloric Effect in (Pr, Dy)2Fe17 and Pr2(Fe, Al)17 Intermetallic Compounds. Phys. Procedia 2015, 75, 1435–1441. [Google Scholar] [CrossRef]
  18. Dahal, B.; Kharel, P.; Ott, T.; Zhang, W.Y.; Valloppilly, A.; Skomski, R.; Sellmyer, D. Magnetic and magnetocaloric properties of Pr2−xNdxFe17 ribbons. AIP Adv. 2019, 9, 035211. [Google Scholar] [CrossRef]
  19. Lyubina, J.; Gutfleisch, O.; Kuz’min, D.M.; Richter, M. La(Fe,Si)13-based magnetic refrigerants obtained by novel processing routes. J. Magn. Magn. Mater. 2009, 320, 2252–2258. [Google Scholar] [CrossRef]
  20. Katter, M.; Zellmann, V.; Reppel, G.W.; Uestuener, K. Magnetocaloric properties of La(Fe,Co,Si)13 bulk material prepared by powder metallurgy. IEEE Trans. Magn. 2008, 44, 3044–3047. [Google Scholar] [CrossRef]
  21. Hansen, B.R.; Kuhn, L.T.; Bahl, C.R.H.; Lundberg, M.; Ancona-Torres, C.; Katter, M. Properties of magnetocaloric La(Fe,Co,Si)13 produced by powder metallurgy. J. Magn. Magn. Mater. 2010, 322, 3447–3454. [Google Scholar] [CrossRef]
  22. Zhong, X.C.; Feng, X.L.; Huang, X.W.; Shen, X.Y.; Liu, Z.W. Structure and magnetocaloric effect of La0.7Ce0.3(Fe0.92Co0.08)11.4Si1.6 bulk alloy prepared by powder metallurgy. J. Alloy. Compd. 2016, 685, 913–916. [Google Scholar] [CrossRef]
  23. Bao, L.H.; Wei, W.; Fan, W.D.; Tegus, O. A novel preparation method and magnetic properties of NaZn13-type La(Fe,Si)13 compounds. J. Alloy. Compd. 2014, 589, 416–419. [Google Scholar] [CrossRef]
  24. Hou, X.L.; Tian, Y.; Xue, Y.; Liu, C.Y.; Xia, W.X.; Xu, H.; Kelley, P.L.; Srikanth, H.; Phan, M.H. Formation of tree-like and vortex magnetic domains of nanocrystalline α-(Fe,Si) in La−Fe−Si ribbons during rapid solidification and subsequent annealing. J. Alloy. Compd. 2016, 669, 205–209. [Google Scholar] [CrossRef]
  25. Blazquez, J.S.; Moreno-Ramírez, L.M.; Ipus, J.J.; Kiss, L.F.; Kaptas, D.; Kemeny, T.; Franco, V.; Conde, A. Effect of α-Fe impurities on the field dependence of magnetocaloric response in LaFe11.5Si1.5. J. Alloy. Compd. 2015, 646, 101–105. [Google Scholar] [CrossRef]
  26. Pulko, B.; Tušek, J.; Moore, J.D.; Weise, B.; Skokov, K.; Mityashkin, O.; Kitanovski, A.; Favero, C.; Fajfar, P.; Gutfleisch, O.; et al. Epoxy-bonded La−Fe−Co−Si magnetocaloric plates. J. Magn. Magn. Mater. 2015, 375, 65–73. [Google Scholar] [CrossRef]
  27. Zhang, H.; Sun, Y.J.; Li, Y.W.; Wu, Y.Y.; Long, Y.; Shen, J.; Hu, F.X.; Sun, J.R.; Shen, B.G. Mechanical properties and magnetocaloric effects in La(Fe,Si)13 hydrides bonded with different epoxy resins. J. Appl. Phys. 2015, 117, 063902. [Google Scholar] [CrossRef]
  28. Zhong, X.C.; Feng, X.L.; Huang, J.H.; Huang, Y.L.; Liu, Z.W.; Ramanujan, R.V. Influence of particle size on the mechanical properties and magnetocaloric effect of La0.8Ce0.2(Fe0.95Co0.05)11.8Si1.2/Sn composites. J. Magn. Magn. Mater. 2018, 463, 23–27. [Google Scholar] [CrossRef]
  29. Zhong, X.C.; Feng, X.L.; Huang, J.H.; Jiao, D.L.; Zhang, H.; Qiu, W.Q.; Liu, Z.W.; Ramanujan, R.V. A bimodal particle size distribution enhances mechanical and magnetocaloric properties of low-temperature hot pressed Sn-bonded La0.8Ce0.2(Fe0.95Co0.05)11.8Si1.2 bulk composites. J. Magn. Magn. Mater. 2019, 469, 133–137. [Google Scholar] [CrossRef]
  30. Dong, X.T.; Zhong, X.C.; Peng, D.R.; Huang, J.H.; Zhang, H.; Jiao, D.L.; Liu, Z.W.; Ramanujan, R.V. La0.8Ce0.2(Fe0.95Co0.05)11.8Si1.2/Sn42Bi58 magnetocaloric composites prepared by low temperature hot pressing. J. Alloy. Compd. 2018, 737, 568–574. [Google Scholar] [CrossRef]
  31. Funk, A.; Freudenberger, J.; Waske, A.; Krautz, M. Getting magnetocaloric materials into good shape: Cold-working of La(Fe,Co,Si)13 by powder-in-tube-processing. Mater. Today Energy 2018, 9, 223. [Google Scholar] [CrossRef]
  32. Wang, Y.X.; Zhang, H.; Liu, E.K.; Zhong, X.C.; Tao, K.; Wu, M.L.; Xing, C.F.; Xiao, Y.N.; Liu, J.; Long, Y. Outstanding comprehensive performance of/In composite with durable service life for magnetic refrigeration. Adv. Electro. Mater. 2018, 4, 1700636. [Google Scholar] [CrossRef]
  33. Dai, Y.T.; Xu, Z.S.; Luo, Z.P.; Han, K.; Zhai, Q.J.; Zheng, H.X. Phase formation kinetics, hardness and magnetocaloric effect of sub-rapidly solidified LaFe11.6Si1.4 plates during isothermal annealing. J. Magn. Magn. Mater. 2018, 454, 356–361. [Google Scholar] [CrossRef]
  34. Fu, S.; Long, Y.; Sun, Y.Y.; Hu, J. Microstructural evolution and phase transition dependent on annealing temperature and carbon content for LaFe11.5Si1.5Cx compounds prepared by arc-melting. Intermetallics 2013, 39, 79–83. [Google Scholar] [CrossRef]
  35. Bez, H.N.; Eggert, B.G.F.; Lozano, J.A.; Bahl, C.R.H.; Barbosa, J.R., Jr.; Teixeira, C.S.; Wendhausen, P.A.P. Magnetocaloric effect and H gradient in bulk La(Fe,Si)13Hy magnetic refrigerants obtained by HDSH. J. Magn. Magn. Mater. 2015, 386, 125–128. [Google Scholar] [CrossRef]
  36. Löwe, K.; Liu, J.; Skokov, K.; Moore, J.D.; Sepehri-Amin, H.; Hono, K.; Katter, M.; Gutfleisch, O. The effect of the thermal decomposition reaction on the mechanical and magnetocaloric properties of La(Fe,Si,Co)13. Acta Mater. 2012, 60, 4268–4276. [Google Scholar] [CrossRef]
  37. Zong, S.T.; Long, Y. The influence of Cr and Ni on the character of magnetic phase transition in LaFe11.52−xMxSi1.48 alloys. AIP Adv. 2018, 8, 048101. [Google Scholar] [CrossRef]
  38. Md Din, M.F.; Wang, J.L.; Zeng, R.; Shamba, P.; Debnath, J.C.; Dou, S.X. Effects of Cu substitution on structural and magnetic properties of La0.7Pr0.3Fe11.4Si1.6 compounds. Intermetallics 2013, 36, 1–7. [Google Scholar] [CrossRef]
  39. Mican, S.; Tetean, R. Magnetic properties and magnetocaloric effect in La0.7Nd0.3Fe13−xSix compounds. J. Solid State Chem. 2012, 187, 238–243. [Google Scholar] [CrossRef]
  40. Chen, X.; Chen, Y.G.; Tang, Y.B.; Xiao, D.Q. Effect of Ce, Co, B on formation of LaCo13-structure phase in La(Fe,Si)13 alloys. Trans. Nonferrous Met. Soc. China 2014, 24, 705–711. [Google Scholar] [CrossRef]
  41. Anh, D.T.K.; Thuy, N.P.; Duc, N.H.; Nhien, T.T.; Nong, N.V. Magnetism and magnetocaloric effect in La1−yNdy(Fe0.88Si0.12)13 compounds. J. Magn. Magn. Mater. 2003, 262, 427–431. [Google Scholar] [CrossRef]
  42. Rosca, M.; Balli, M.; Fruchart, D.; Gignoux, D.; Hlil, E.K.; Miraglia, S.; Ouladdiaf, B.; Wolfers, P. Neutron diffraction study of LaFe11.31Si1.69 and LaFe11.31Si1.69H1.45 compounds. J. Alloy. Compd. 2010, 490, 50–55. [Google Scholar] [CrossRef]
  43. Hai, X.; Mayer, C.; Colin, C.V.; Miraglia, S. In-situ neutron investigation of hydrogen absorption kinetics in La(FexSi1−x)13 magnetocaloric alloys for room-temperature refrigeration application. J. Magn. Magn. Mater. 2016, 400, 344–348. [Google Scholar] [CrossRef]
  44. Bao, L.F.; Hu, F.X.; Chen, L.; Wang, J.; Sun, J.R.; Shen, B.G. Magnetocaloric properties of La(Fe,Si)13-based material and its hydride prepared by industrial mischmetal. Appl. Phys. Lett. 2012, 101, 162406. [Google Scholar] [CrossRef]
  45. Shao, Y.Y.; Lu, B.F.; Zhang, M.X.; Liu, J. An X-ray absorption spectroscopy study of La−Fe−Si−(H) magnetocaloric alloys. Acta Mater. 2018, 150, 206–212. [Google Scholar] [CrossRef]
  46. Liu, J.P.; Fullerton, E.; Gutfleisch, O.; Sellmyer, D.J. Nanoscale Magnetic Materials and Applications; Springer: Boston, MA, USA, 2009; ISBN 978-0-387-85600-1. [Google Scholar]
  47. Phejar, M.; Paul-Boncour, V.; Bessais, L. Investigation on structural and magnetocaloric properties of LaFe13−xSix(H,C)y compounds. J. Solid. State. Chem. 2016, 233, 95–102. [Google Scholar] [CrossRef]
  48. Dai, Y.T.; Li, Y.Q.; Xu, Z.S.; Luo, Z.P.; Han, K.; Zhai, Q.J.; Zheng, H.X. Studying of doping boron and carbon in LaFe11.6Si1.4 magnetocaloric alloy by experimental and density-functional methods. J. Alloy. Compd. 2018, 765, 538–543. [Google Scholar] [CrossRef]
  49. Demuner, A.S.; Takeuchi, A.Y.; Passamani, E.C.; Proveti, J.R.; Larica, C.; Favre-Nicolin, E.; Gomes, A.M. Magnetocaloric properties of the (La−Gd)Fe11.4Si1.6 metamagnetic compound. J. Magn. Magn. Mater. 2009, 321, 1809–1813. [Google Scholar] [CrossRef]
  50. Wu, D.Z.; Xue, S.C.; Frenzel, J.; Eggeler, G.; Zhai, Q.J.; Zheng, H.X. Atomic ordering effect in Ni50Mn37Sn13 magnetocaloric ribbons. Mater. Sci. Eng. A 2012, 534, 568–572. [Google Scholar] [CrossRef]
  51. Li, H.W.; Fang, Y.; Feng, S.T.; Zhai, Q.J.; Luo, Z.P.; Zheng, H.X. Magneto-structural transition behavior in Fe-doped Heusler Mn−Ni−In ribbon materials. J. Magn. Magn. Mater. 2016, 417, 267–271. [Google Scholar] [CrossRef]
  52. Jia, L.; Sun, J.R.; Shen, J.; Dong, Q.Y.; Hu, F.X.; Zhao, T.Y.; Shen, B.G. Magnetic coupling between rare-earth and iron atoms in the La1−xRxFe11.5Si1.5(R = Ce, Pr, and Nd) intermetallics. Appl. Phys. Lett. 2008, 92, 182503. [Google Scholar] [CrossRef]
  53. Fujieda, S.; Fujita, A.; Fukamichi, K.; Hirano, N.; Nagaya, S. Large magnetocaloric effects enhanced by partial substitution of Ce for La in La(Fe0.88Si0.12)13 compound. J. Alloy. Compd. 2006, 408–412, 1165–1168. [Google Scholar] [CrossRef]
  54. Fujieda, S.; Fujita, A.; Fukamichi, K. Enhancements of magnetocaloric effects in La(Fe0.90Si0.10)13 and its hydride by partial substitution of Ce for La. Mater. Trans. 2004, 45, 3228–3231. [Google Scholar] [CrossRef]
  55. Jia, L.; Sun, J.R.; Shen, J.; Dong, Q.Y.; Zou, J.D.; Gao, B.; Zhao, T.Y.; Zhang, H.W.; Hu, F.X.; Shen, B.G. Magnetocaloric effects in the La(Fe,Si)13 intermetallics doped by different elements. J. Appl. Phys. 2009, 105, 07A924. [Google Scholar] [CrossRef]
  56. Balli, M.; Fruchart, D.; Gignoux, D. Optimization of La(Fe,Co)13−xSix based compounds for magnetic refrigeration. J. Phys.: Condens. Matter 2007, 19, 236230. [Google Scholar] [CrossRef]
  57. Wang, F.W.; Kurbakov, A.; Wang, G.J.; Hu, F.X.; Shen, B.G.; Cheng, Z.H. Strong interplay between structure and magnetism in LaFe11.3Co0.6Si1.1: A neutron diffraction study. Phys. B 2006, 385−386, 343–345. [Google Scholar] [CrossRef]
  58. Krautz, M.; Skokov, K.; Gottschall, T.; Teixeira, C.S.; Waske, A.; Liu, J.; Schultz, L.; Gutfleisch, O. Systematic investigation of Mn substituted La(Fe,Si)13 alloys and their hydrides for room-temperature magnetocaloric application. J. Alloy. Compd. 2014, 598, 27–32. [Google Scholar] [CrossRef]
  59. Makarov, S.I.; Krautz, M.; Salamon, S.; Skokov, K.; Teixeira, C.S.; Gutfleisch, O.; Wende, H.; Keune, W. Local electronic and magnetic properties of pure and Mn-containing magnetocaloric LaFe13−xSix compounds inferred from Mössbauer spectroscopy and magnetometry. J. Phys. D Appl. Phys. 2015, 48, 305006. [Google Scholar] [CrossRef]
  60. Bratko, M.; Lovell, E.; Caplin, A.D.; Basso, V.; Barcza, A.; Katter, M.; Cohen, L.F. Determining the first-order character of La(Fe,Mn,Si)13. Phys. Rev. B. 2017, 95, 064411. [Google Scholar] [CrossRef]
  61. Moreno-Ramírez, L.M.; Romero-Muñiz, C.; Law, J.Y.; Franco, V.; Conde, A.; Radulov, I.; Maccari, F.; Skokov, K.P.; Gutfleisch, O. The role of Ni in modifying the order of the phase transition of La(Fe,Ni,Si)13. Acta Mater. 2018, 160, 137–146. [Google Scholar] [CrossRef]
  62. Xu, Z.S.; Dai, Y.T.; Fang, Y.; Luo, Z.P.; Han, K.; Song, C.J.; Zhai, Q.J.; Zheng, H.X. High temperature phase transition behavior and magnetocaloric effect in a sub-rapidly solidified La−Fe−Si plate produced by centrifugal casting. J. Mater. Sci. Technol. 2018, 34, 1337–1342. [Google Scholar] [CrossRef]
  63. Lai, J.W.; Zheng, Z.G.; Zhong, X.C.; Montemayor, R.; Liu, Z.W.; Zeng, D.C. Magnetocaloric effect of nonstoichiometric La1−xFe11.4+xSi1.6 alloys with first-order and second-order magnetic transitions. Intermetallics 2015, 63, 7–11. [Google Scholar] [CrossRef]
  64. Chen, X.; Chen, Y.G.; Tang, Y.B. High-temperature phase transition and magnetic property of LaFe11.6Si1.4 compound. J. Alloy. Compd. 2011, 509, 8534–8541. [Google Scholar] [CrossRef]
  65. Chen, X.; Chen, Y.G.; Tang, Y.B. The influence of different cooling processes on phase, microstructure, and magnetocaloric properties of LaFe11.6Si1.4 compounds. Solid State Commun. 2014, 186, 56–63. [Google Scholar] [CrossRef]
  66. Fujieda, S.; Fukamichi, K.; Suzuki, S. Microstructure and isothermal magnetic entropy change of La(Fe0.89Si0.11)13 in a single-phase formation process by annealing. J. Alloy. Compd. 2013, 566, 196–200. [Google Scholar] [CrossRef]
  67. Shamba, P.; Zeng, R.; Wang, J.L.; Campbell, S.J.; Dou, S.X. Enhancement of the refrigerant capacity in low level boron doped La0.8Gd0.2Fe11.4Si1.6. J. Magn. Magn. Mater. 2013, 331, 102–108. [Google Scholar] [CrossRef]
  68. Gebara, P.; Pawlik, P.; Hasiak, M. Alteration of negative lattice expansion of the La(Fe,Si)13-type phase in LaFe11.14-xCo0.66NixSi1.2 alloys. J. Magn. Magn. Mater. 2017, 422, 61–65. [Google Scholar] [CrossRef]
  69. Zhang, Z.T.; He, C.; Zhang, M.X.; Liu, J. Influence of extra La and annealing temperature on microstructure and magnetocaloric properties of La–Fe–Co–Si alloys. Phys. B. 2015, 476, 167–170. [Google Scholar] [CrossRef]
  70. Goto, T.; Fukamichi, K.; Yamada, H. Itinerant electron metamagnetism and peculiar magnetic properties observed in 3d and 5f intermetallics. Phys. B 2001, 300, 167–185. [Google Scholar] [CrossRef]
  71. Qian, H.Y.; Dahal, B.; Halbritter, L.; Hu, J.; Huh, Y.; Kharel, P. Structural, magnetic and magnetocaloric properties of Ni43Mn46−xFexSn11 (x = 0, 6, 8, 10) alloys. AIP Adv. 2019, 9, 035005. [Google Scholar] [CrossRef]
  72. Law, J.Y.; Franco, V.; Moreno-Ramírez, L.M.; Conde, A.; Karpenkov, D.Y.; Radulov, L.; Skokov, K.P.; Gutfleisch, O. A quantitative criterion for determining the order of magnetic phase transitions using the magnetocaloric effect. Nat. Commun. 2018, 9, 2680. [Google Scholar] [CrossRef]
  73. Inoue, J.; Shimizu, M. Volume dependence of the first-order transition temperature for RCo2 compounds. J. Phys. F Met. Phys. 1982, 12, 1811. [Google Scholar] [CrossRef]
  74. Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef] [Green Version]
  75. Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Erratum: atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1993, 48, 4978. [Google Scholar] [CrossRef]
  76. Slater, J.C. Atomic Radii in Crystals. J. Chem. Phys. 1964, 41, 3199–3204. [Google Scholar] [CrossRef]
  77. Greenwood, N.N.; Earnshaw, A. Chemistry of the Elements, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1997; pp. 944–1226. ISBN 978-0-7506-3365-9. [Google Scholar]
Metals 09 00432 g001 550
Figure 1. Backscatter SEM image of the sub-rapidly solidified LaFe11.6Si1.4 plate (a) and an enlarged image showing the α(Fe), LaFeSi, and La5Si3 phases (b). (c) Backscatter SEM image of LaFe11.6Si1.4Zn0.03 plate and the corresponding La, Fe, Si, and Zn elemental distribution within the area marked by a square in Figure 1c.
Figure 1. Backscatter SEM image of the sub-rapidly solidified LaFe11.6Si1.4 plate (a) and an enlarged image showing the α(Fe), LaFeSi, and La5Si3 phases (b). (c) Backscatter SEM image of LaFe11.6Si1.4Zn0.03 plate and the corresponding La, Fe, Si, and Zn elemental distribution within the area marked by a square in Figure 1c.
Metals 09 00432 g001
Metals 09 00432 g002 550
Figure 2. High-temperature differential scanning calorimetry (DSC) chart of the sub-rapidly solidified LaFe11.6Si1.4 plate with a heating/cooling rate of 20 K/min.
Figure 2. High-temperature differential scanning calorimetry (DSC) chart of the sub-rapidly solidified LaFe11.6Si1.4 plate with a heating/cooling rate of 20 K/min.
Metals 09 00432 g002
Metals 09 00432 g003 550
Figure 3. Backscatter SEM images of the annealed LaFe11.6Si1.4Zn0.03 (a) and LaFe11.6Si1.4P0.03 plates (c). Images (b) and (d) are the corresponding elemental distributions within the areas marked by squares in (a) and (c), respectively.
Figure 3. Backscatter SEM images of the annealed LaFe11.6Si1.4Zn0.03 (a) and LaFe11.6Si1.4P0.03 plates (c). Images (b) and (d) are the corresponding elemental distributions within the areas marked by squares in (a) and (c), respectively.
Metals 09 00432 g003
Metals 09 00432 g004 550
Figure 4. X-ray diffraction (XRD) patterns of the annealed LaFe11.6Si1.4, LaFe11.6Si1.4Zn0.03, and LaFe11.6Si1.4P0.03 plates at room temperature (a), and (b) enlarged τ1(440) peak showing the shift towards higher angle regime with Zn/P alloying.
Figure 4. X-ray diffraction (XRD) patterns of the annealed LaFe11.6Si1.4, LaFe11.6Si1.4Zn0.03, and LaFe11.6Si1.4P0.03 plates at room temperature (a), and (b) enlarged τ1(440) peak showing the shift towards higher angle regime with Zn/P alloying.
Metals 09 00432 g004
Metals 09 00432 g005 550
Figure 5. Magnetization curves measured under a low magnetic field of 0.05 T for annealed LaFe11.6Si1.4 (a), LaFe11.6Si1.4Zn0.03 (b), and LaFe11.6Si1.4P0.03 (c), respectively. Plots (d–f) are the corresponding dM/dT curves upon heating.
Figure 5. Magnetization curves measured under a low magnetic field of 0.05 T for annealed LaFe11.6Si1.4 (a), LaFe11.6Si1.4Zn0.03 (b), and LaFe11.6Si1.4P0.03 (c), respectively. Plots (d–f) are the corresponding dM/dT curves upon heating.
Metals 09 00432 g005
Metals 09 00432 g006 550
Figure 6. Isothermal magnetization curves for the annealed LaFe11.6Si1.4 (a), LaFe11.6Si1.4Zn0.03 (b), and LaFe11.6Si1.4P0.03 (c), respectively. Shadowed areas indicate the magnetic hysteresis. Images (d–f) are the corresponding Arrott plots.
Figure 6. Isothermal magnetization curves for the annealed LaFe11.6Si1.4 (a), LaFe11.6Si1.4Zn0.03 (b), and LaFe11.6Si1.4P0.03 (c), respectively. Shadowed areas indicate the magnetic hysteresis. Images (d–f) are the corresponding Arrott plots.
Metals 09 00432 g006
Metals 09 00432 g007 550
Figure 7. Calculated magnetic entropy changes (ΔSM) under a magnetic field change of 3 T for the annealed LaFe11.6Si1.4 (a), LaFe11.6Si1.4Zn0.03 (b), and LaFe11.6Si1.4P0.03 (c), respectively. Striped area in (a) was taken as an example to indicate the refrigeration capacity.
Figure 7. Calculated magnetic entropy changes (ΔSM) under a magnetic field change of 3 T for the annealed LaFe11.6Si1.4 (a), LaFe11.6Si1.4Zn0.03 (b), and LaFe11.6Si1.4P0.03 (c), respectively. Striped area in (a) was taken as an example to indicate the refrigeration capacity.
Metals 09 00432 g007
Metals 09 00432 g008 550
Figure 8. (010) projection of an ideal crystallographic structure of the LaFe11.6Si1.4 unit-cell (a), where the positions of 8a, 8b, and 96i are occupied by La, FeI, and FeII/Si atoms, respectively. Unit-cell volume (b) and energy change (c) for the original state of LaFe11.6Si1.4 and reconstruction with various Zn/P substitution sites.
Figure 8. (010) projection of an ideal crystallographic structure of the LaFe11.6Si1.4 unit-cell (a), where the positions of 8a, 8b, and 96i are occupied by La, FeI, and FeII/Si atoms, respectively. Unit-cell volume (b) and energy change (c) for the original state of LaFe11.6Si1.4 and reconstruction with various Zn/P substitution sites.
Metals 09 00432 g008

Share and Cite

MDPI and ACS Style

Jin, P.; Li, Y.; Dai, Y.; Xu, Z.; Song, C.; Luo, Z.; Zhai, Q.; Han, K.; Zheng, H. Zn and P Alloying Effect in Sub-Rapidly Solidified LaFe11.6Si1.4 Magnetocaloric Plates. Metals 2019, 9, 432. https://doi.org/10.3390/met9040432

AMA Style

Jin P, Li Y, Dai Y, Xu Z, Song C, Luo Z, Zhai Q, Han K, Zheng H. Zn and P Alloying Effect in Sub-Rapidly Solidified LaFe11.6Si1.4 Magnetocaloric Plates. Metals. 2019; 9(4):432. https://doi.org/10.3390/met9040432

Chicago/Turabian Style

Jin, Pingxia, Yuqiang Li, Yuting Dai, Zhishuai Xu, Changjiang Song, Zhiping Luo, Qijie Zhai, Ke Han, and Hongxing Zheng. 2019. "Zn and P Alloying Effect in Sub-Rapidly Solidified LaFe11.6Si1.4 Magnetocaloric Plates" Metals 9, no. 4: 432. https://doi.org/10.3390/met9040432

APA Style

Jin, P., Li, Y., Dai, Y., Xu, Z., Song, C., Luo, Z., Zhai, Q., Han, K., & Zheng, H. (2019). Zn and P Alloying Effect in Sub-Rapidly Solidified LaFe11.6Si1.4 Magnetocaloric Plates. Metals, 9(4), 432. https://doi.org/10.3390/met9040432

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop