Comparison of Transverse Uniform and Non-Uniform Secondary Cooling Strategies on Heat Transfer and Solidification Structure of Continuous-Casting Billet
Abstract
1. Introduction
2. Brief Description of the Studied Continuous Caster
3. Spraying Nozzle Measurement of Water Flux Distribution
3.1. Experimental Apparatus
3.2. Water Flux Distribution Measurement
4. Numerical Modeling and Validation
4.1. Model Development
4.1.1. Heat Transfer Model
- The heat transfer in casting direction and meniscus was neglected.
- The convective heat transfer was equivalent to the conductive heat transfer by increasing the thermal conductivity of liquid and mushy zone.
- The heat transfer of radiation, contact with the supporting roller, and cooling water in the secondary cooling zone were included by an integrated heat transfer coefficient.
- The water flux distribution along the casting direction of each segment was uniform in the secondary cooling zone.
- The density, solid fraction, and thermal conductivity of the steel were temperature dependent.
- The dimensional change caused by solidification shrinkage was neglected on the analysis of temperature and solidification structure of the billet.
4.1.2. Nucleation Model
4.1.3. Dendritic Tip Growth Model
4.2. Material Properties
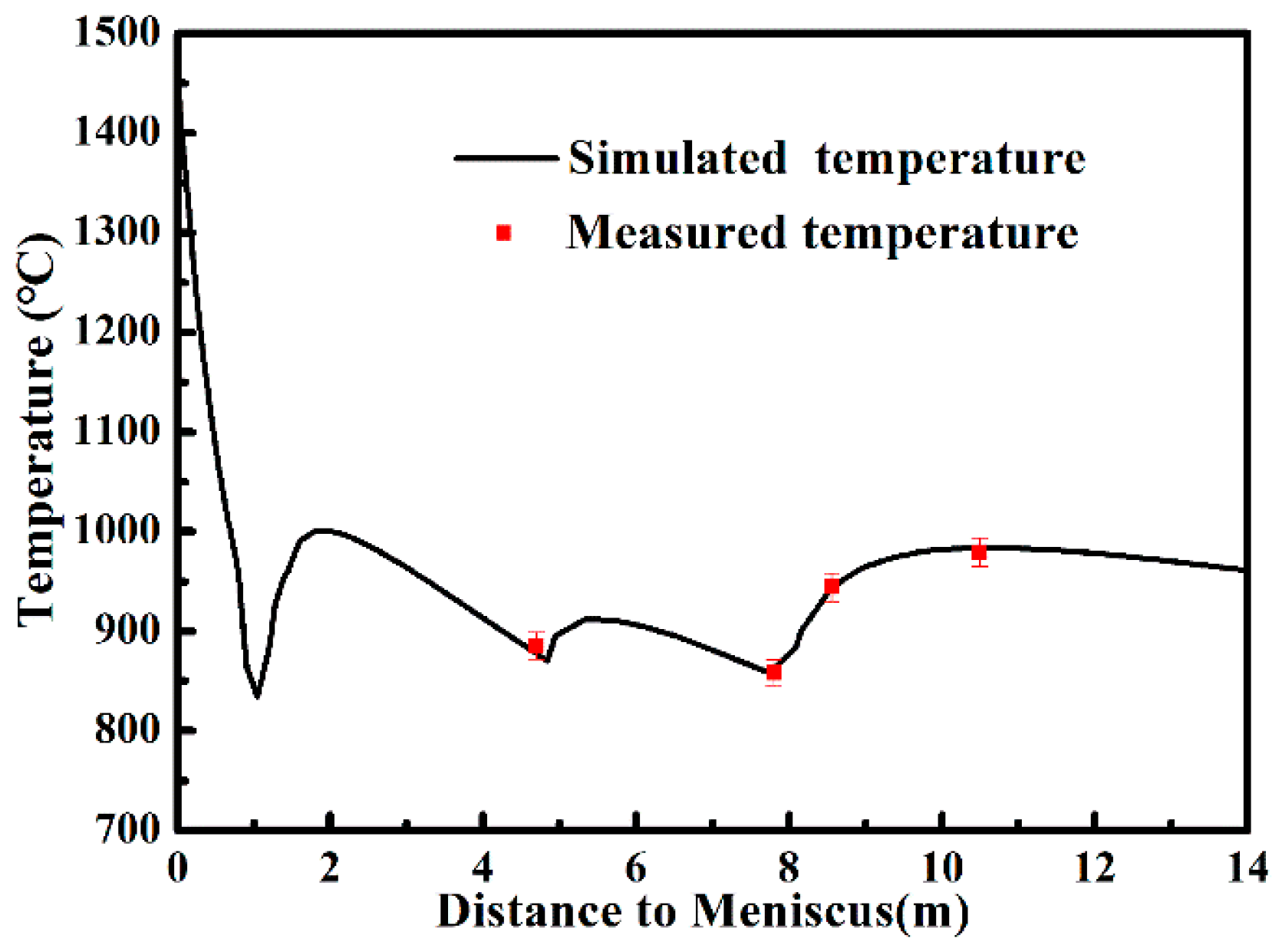
4.3. Model Validation
4.3.1. Casting Parameters
4.3.2. Heat Transfer Model Validation
4.3.3. CAFE Coupling Model Validation
5. Results and Discussion
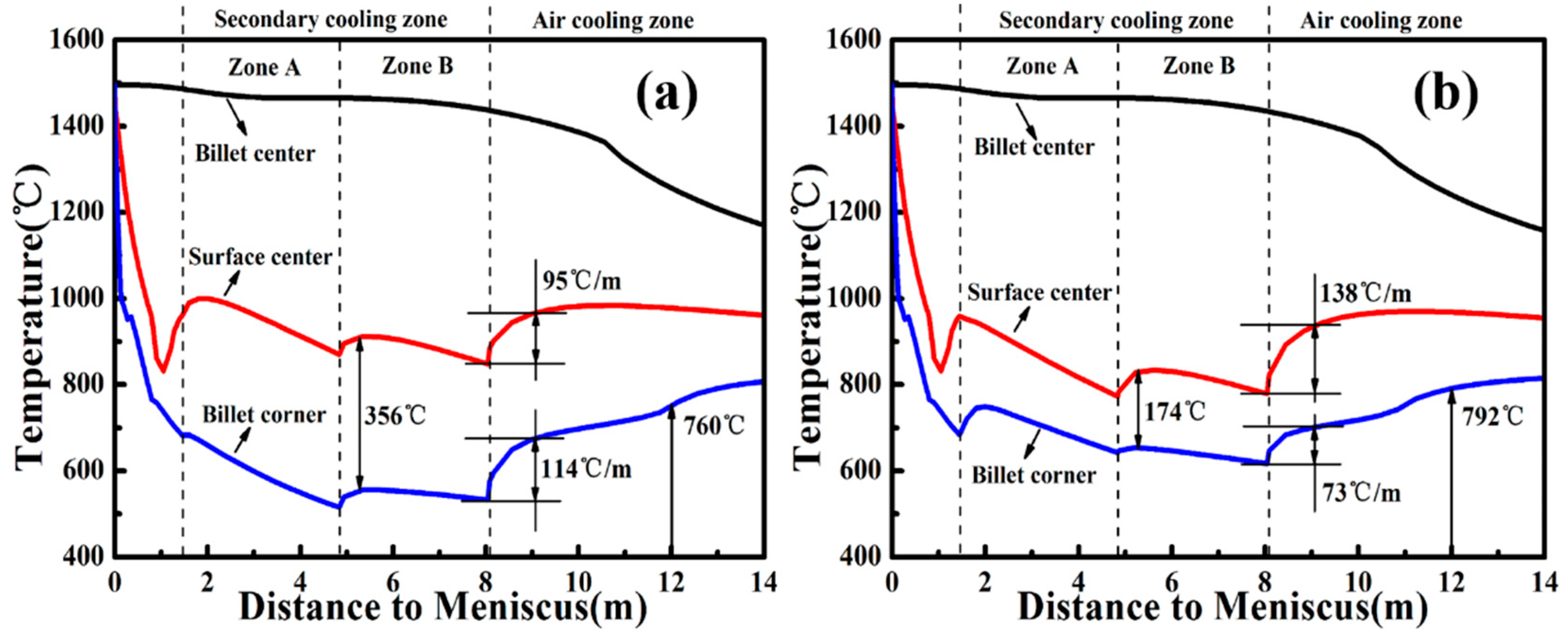
5.1. Comparison of Surface Temperature
5.2. Comparison of Internal Temperature
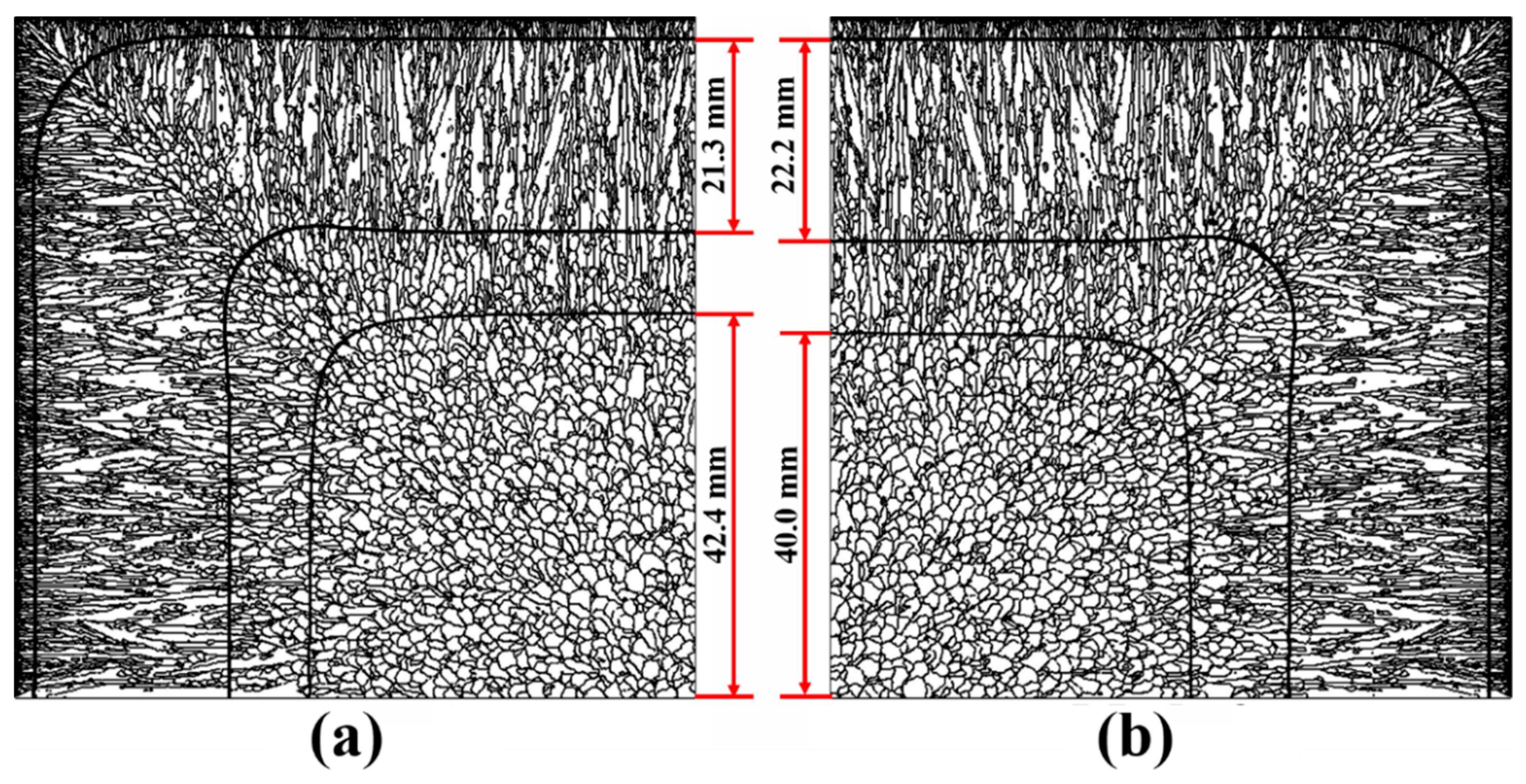
5.3. Comparison of Solidification Structure
5.4. Summary
6. Conclusions
- For a single spraying nozzle, the transverse water flux distribution is non-uniform, and there is more water on the spraying center and less water on the spraying edge. However, a transverse uniform water flux distribution can be obtained in the effective range by adjusting the nozzle collocations.
- The transverse non-uniform secondary cooling water is able to improve the cooling uniformity along the transverse direction. The corner temperature is effectively increased and the transverse temperature difference is reduced. Nevertheless, the reheating rate of the surface center is increased when the billet enters into the air-cooling zone.
- Compared with the uniform cooling strategy, the cooling intensity of the non-uniform strategy on billet is enhanced. The shell thickness at the end of the secondary cooling zone is increased by 1.9 mm and the liquid pool length is decreased by 0.28 m.
- The non-uniform cooling strategy promotes the growth of columnar crystal. The compactness of central equiaxed crystal is increased and the equiaxed crystal ratio is decreased. These effects are equivalent to increasing the secondary cooling intensity.
- The non-uniform cooling strategy is beneficial to improving the surface quality, corner crack, and central segregation of billet, but may result in internal cracks. On the production of C80D steel, the non-uniform strategy is better than the uniform one.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flesch, R.; Bleck, W. Crack susceptibility of medium and high alloyed tool steels under continuous casting conditions. Steel Res. 1998, 69, 292–299. [Google Scholar] [CrossRef]
- Han, Z.; Cai, K.; Liu, B. Prediction and analysis on formation of internal cracks in continuously cast slabs by mathematical models. ISIJ Int. 2001, 41, 1473–1480. [Google Scholar] [CrossRef][Green Version]
- Lu, Y.J.; Wang, Q.; Li, Y.G.; He, S.P.; He, Y.M.; Pan, S.S.; Zhang, J.G.; Hu, B. Prevention of transverse corner cracks in continuously cast steel slabs using asymmetric secondary cooling nozzle. Ironmak. Steelmak. 2011, 38, 561–565. [Google Scholar] [CrossRef]
- Raihle, C.; Fredriksson, H. On the formation of pipes and centerline segregates in continuously cast billets. Metall. Mat. Trans. B 1994, 25, 123–133. [Google Scholar] [CrossRef]
- De Toledo, G.; Lainez, J.; Cirión, J. Model optimization of continuous casting steel secondary cooling. Mater. Sci. Eng. A 1993, 173, 287–291. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, W. Effect of secondary cooling conditions on solidification structure and central macrosegregation in continuously cast high-carbon rectangular billet. High Temp. Mater. Processes 2015, 34, 577–583. [Google Scholar] [CrossRef]
- Dou, K.; Yang, Z.; Liu, Q.; Huang, Y.; Dong, H. Influence of secondary cooling mode on solidification structure and macro-segregation behavior for high-carbon continuous casting bloom. High Temp. Mater. Process. 2017, 36, 741–753. [Google Scholar] [CrossRef]
- Camisani-Calzolari, F.; Craig, I.; Pistorius, P. Speed disturbance compenation in the secondary cooling zone in continuous casting. ISIJ Int. 2000, 40, 469–477. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.; Chen, D.; Wang, S.; Long, M. Compensation control model of superheat and cooling water temperature for secondary cooling of continuous casting. Steel Res. Int. 2011, 82, 213–221. [Google Scholar] [CrossRef]
- Long, M.; Chen, D.; Zhang, L.; Zhao, Y.; Liu, Q. A mathematical model for mitigating centerline macro segregation in continuous casting slab. Met. Int. 2011, 16, 19–33. [Google Scholar]
- Shen, H.; Hardin, R.; MacKenzie, R.; Beckermann, C. Simulation using realistic spray cooling for the continuous casting of multi-component steel. J. Mater. Sci. Technol. 2002, 18, 311–314. [Google Scholar]
- Ramstorfer, F.; Roland, J.; Chimani, C.; Mörwald, K. Investigation of spray cooling heat transfer for continuous slab casting. Mater. Manuf. Process. 2011, 26, 165–168. [Google Scholar] [CrossRef]
- Ji, C.; Luo, S.; Zhu, M.; Sahai, Y. Uneven solidification during wide-thick slab continuous casting process and its influence on soft reduction zone. ISIJ Int. 2014, 54, 103–111. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Q.; Wang, B.; Wang, X.; Qing, J.-S.; Hu, Z.-G.; Sun, Y.H. Optimal control of secondary cooling for medium thickness slab continuous casting. Ironmak. Steelmak. 2011, 38, 552–560. [Google Scholar] [CrossRef]
- Long, M.; Chen, D. Study on Mitigating center macro-segregation during steel continuous casting process. Steel Res. Int. 2011, 82, 847–856. [Google Scholar] [CrossRef]
- Ma, J.; Xie, Z.; Jia, G. Applying of real-time heat transfer and solidification model on the dynamic control system of billet continuous casting. ISIJ Int. 2008, 48, 1722–1727. [Google Scholar] [CrossRef][Green Version]
- Hou, Z.; Jiang, F.; Cheng, G. Solidification structure and compactness degree of central equiaxed grain zone in continuous casting billet using cellular automaton-finite element method. ISIJ Int. 2012, 52, 1301–1309. [Google Scholar] [CrossRef]
- Ma, J.; Wang, B.; Zhang, D.; Song, W. Optimization of secondary cooling water distribution for improving the billet quality for a small caster. ISIJ Int. 2018, 58, 915–920. [Google Scholar] [CrossRef]
- Assuncao, C.; Tavares, R.; Oliveira, G. Comparison of uniform and non-uniform water flux density approaches applied on a mathematical model of heat transfer and solidification for a continuous casting of round billets. Metall. Mat. Trans. B 2015, 46, 366–377. [Google Scholar] [CrossRef]
- Choudhary, S.; Mazumdar, D. Mathematical modelling of fluid flow, heat transfer and solidification phenomena in continuous casting of steel. Steel Res. Int. 1995, 66, 199–205. [Google Scholar] [CrossRef]
- Cai, K.; Yang, J. Investigation of Heat Transfer in the Spray Cooling of Continuous Casting. J. Univ. Sci. Technol. Beijing 1989, 11, 510–515. [Google Scholar]
- Nozaki, T.; Matsuno, J.; Murata, K.; Ooi, H.; Kodama, M. A secondary cooling pattern for preventing surface cracks of continuous casting slab. Trans. Iron Steel Inst. Jpn. 1978, 18, 330–338. [Google Scholar]
- Thevoz, P.; Desbiolles, J.; Rappaz, M. Modeling of equiaxed microstructure formation in casting. Metall. Trans. A 1989, 20, 311–322. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta Metall. 1986, 34, 823–830. [Google Scholar] [CrossRef]
- Kurz, W.; Trivedi, R. Solidification microstructures: Recent developments and future directions. Acta Metall. 1990, 38, 1–17. [Google Scholar] [CrossRef]
- Cornelissen, M. Mathematical-model for solidification of multicomponent alloys. Ironmak. Steelmak. 1986, 13, 204–212. [Google Scholar]
- Jing, C.; Wang, X.; Jiang, M. Study on solidification structure of wheel steel round billet using FE-CA coupling model. Steel Res. Int. 2011, 82, 1173–1179. [Google Scholar] [CrossRef]
- Yamazaki, M.; Natsume, Y.; Harada, H.; Ohsasa, K. Numerical simulation of solidification structure formation during continuous casting in Fe–0.7 mass% C alloy using cellular automaton method. ISIJ Int. 2006, 46, 903–908. [Google Scholar] [CrossRef]
- Brimacombe, J.; Sorimachi, K. Crack formation in the continuous casting of steel. Metall. Trans. B 1977, 8, 489–505. [Google Scholar] [CrossRef]
- Kulkarni, M.; Subash Babu, A. Optimization of continuous casting using simulation. Mater. Manuf. Process. 2005, 20, 595–606. [Google Scholar] [CrossRef]
- M’Hamdi, M.; Combeau, H.; Lesoult, G. Modelling of heat transfer coupled with columnar dendritic growth in continuous casting of steel. Int. J. Numer. Methods Heat Fluid Flow 1999, 9, 296–317. [Google Scholar] [CrossRef]
- Ludlow, V.; Normanton, A.; Anderson, A.; Thiele, M.; Ciriza, J.; Laraudogoitia, J.; Knoop, W. Strategy to minimise central segregation in high carbon steel grades during billet casting. Ironmak. Steelmak. 2005, 32, 68–74. [Google Scholar] [CrossRef]
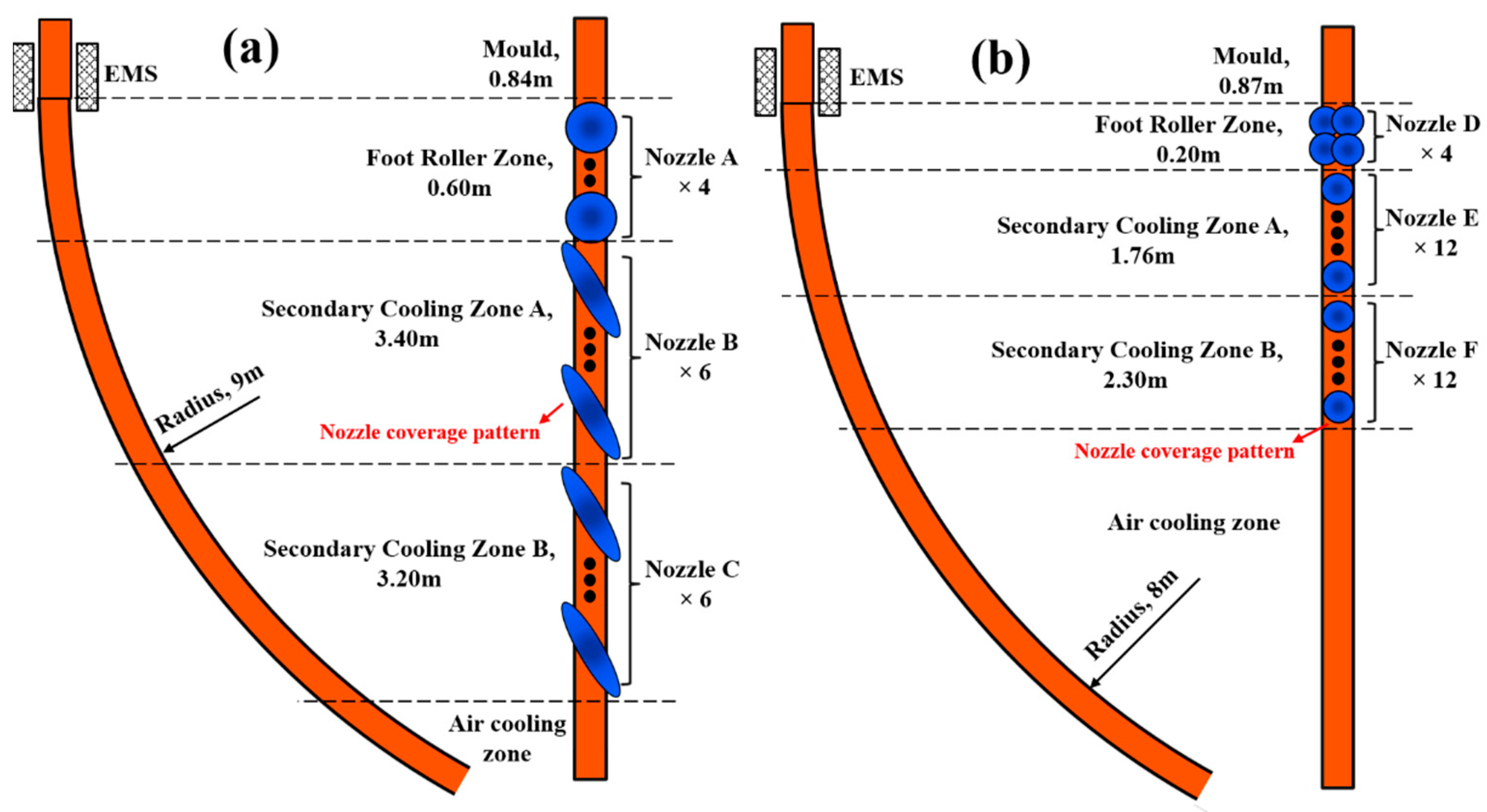

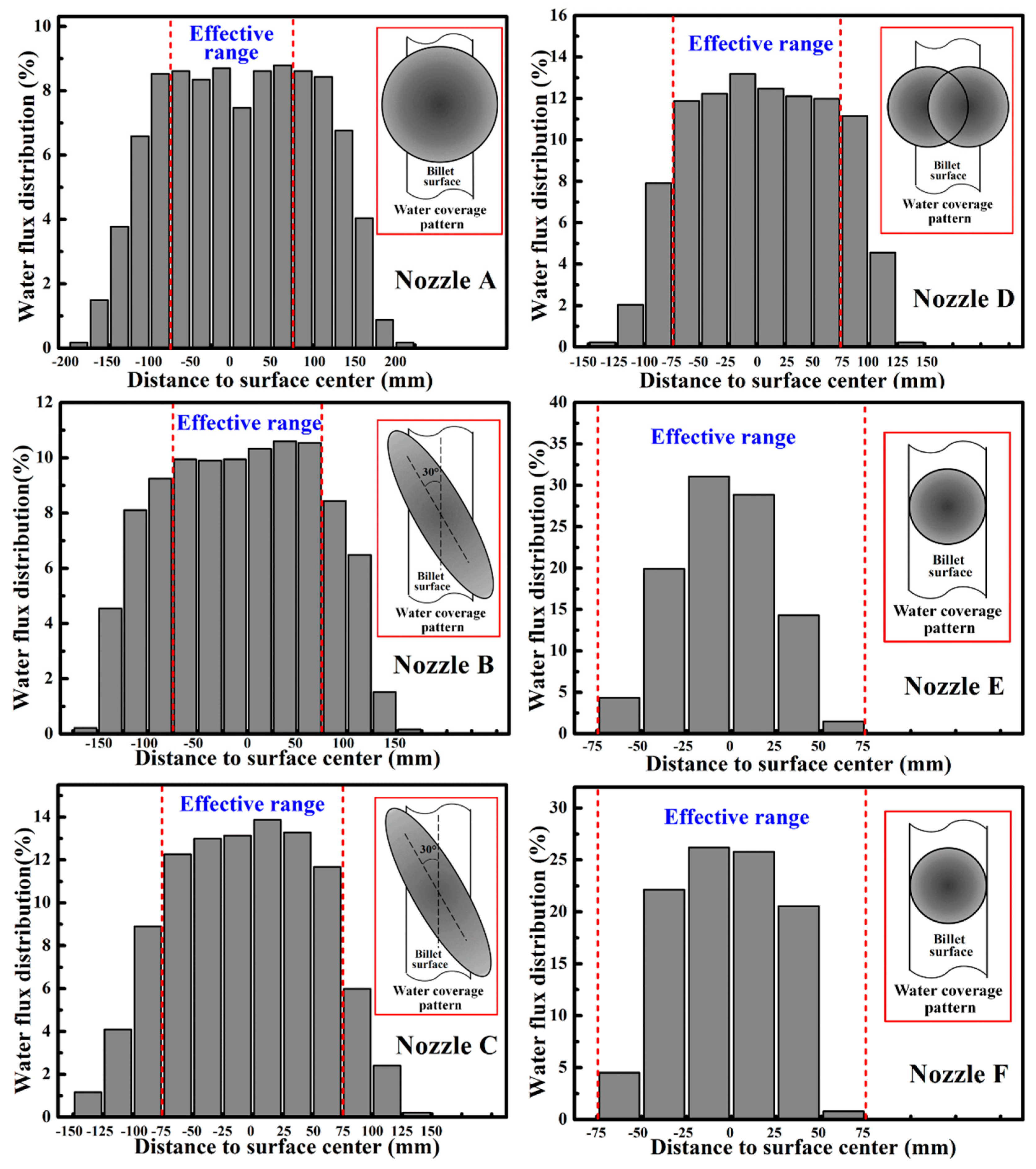







| Nozzle | Type number | Jet type | Pressure/MPa | Jet Distance/mm | Spraying Angle |
|---|---|---|---|---|---|
| Nozzle A | CONCAST 7565L | Full cone | 0.52 | 300 | 60.4° |
| Nozzle B | CONCAST RE2-8-80/28 | Flat | 0.52 | 300 | 87.6°/26.4° |
| Nozzle C | CONCAST RE1-4-80/28 | Flat | 0.52 | 300 | 82.4°/28.4° |
| Nozzle D | ZY3/8PZ72667QZ1 | Full cone | 0.40 | 125 | 61.6° |
| Nozzle E | 3665 | Full cone | 0.80 | 125 | 53.1° |
| Nozzle F | 2265 | Full cone | 0.60 | 125 | 53.5° |
| Zone | Water Flow Rate, m3/h | Boundary Condition | Calculated Formula |
|---|---|---|---|
| Mold | 113 | ||
| Foot-roller zone | 8.06 | ||
| Secondary cooling zone A | 12.96 | ||
| Secondary cooling zone B | 5.76 | ||
| Air-cooling zone | - |
| Composition | C | Si | Mn | P | S |
|---|---|---|---|---|---|
| Mass fraction, % | 0.82 | 0.20 | 0.73 | 0.017 | 0.004 |
| Partition coefficient, k0 | 0.35 | 0.52 | 0.75 | 0.06 | 0.025 |
| Liquidus slope, m | −60 | −8 | −5 | −34 | −40 |
| Diffusivity in liquid, D, m2/s | 2.0 × 10−8 | 2.4 × 10−9 | 2.0 × 10−8 | 4.7 × 10−9 | 4.5 × 10−9 |
| Item | Value |
|---|---|
| Casting speed | 2.4 m/min |
| Pouring temperature | 1485 °C |
| Superheat | 15 °C |
| Water flux of mold cooling | 113 m3/h |
| Temperature difference between inlet and outlet of mold water | 7.9 °C |
| Ambient temperature | 25 °C |
| Cooling Strategy | Equiaxed Crystal Density | Equiaxed Crystal Ratio |
|---|---|---|
| Mode 1 | 0.83 /mm2 | 32.0% |
| Mode 2 | 0.89 /mm2 | 28.4% |
| Item | Uniform | Non-Uniform |
|---|---|---|
| Transverse temperature difference in the secondary cooling zone, °C | 356 | 174 |
| Corner temperature at straightening point, °C | 760 | 792 |
| Maximum reheating rate of surface center, °C/m | 95 | 138 |
| Maximum reheating rate of billet corner, °C/m | 114 | 73 |
| Liquid pool length, m | 10.60 | 10.32 |
| Equiaxed crystal density, /mm2 | 0.83 | 0.89 |
| Equiaxed crystal ratio, % | 32.0 | 28.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Wang, X.; Zhang, J.; Zeng, F.; Chen, J.; Guan, M.; Liu, Q. Comparison of Transverse Uniform and Non-Uniform Secondary Cooling Strategies on Heat Transfer and Solidification Structure of Continuous-Casting Billet. Metals 2019, 9, 543. https://doi.org/10.3390/met9050543
Han Y, Wang X, Zhang J, Zeng F, Chen J, Guan M, Liu Q. Comparison of Transverse Uniform and Non-Uniform Secondary Cooling Strategies on Heat Transfer and Solidification Structure of Continuous-Casting Billet. Metals. 2019; 9(5):543. https://doi.org/10.3390/met9050543
Chicago/Turabian StyleHan, Yanshen, Xingyu Wang, Jiangshan Zhang, Fanzheng Zeng, Jun Chen, Min Guan, and Qing Liu. 2019. "Comparison of Transverse Uniform and Non-Uniform Secondary Cooling Strategies on Heat Transfer and Solidification Structure of Continuous-Casting Billet" Metals 9, no. 5: 543. https://doi.org/10.3390/met9050543
APA StyleHan, Y., Wang, X., Zhang, J., Zeng, F., Chen, J., Guan, M., & Liu, Q. (2019). Comparison of Transverse Uniform and Non-Uniform Secondary Cooling Strategies on Heat Transfer and Solidification Structure of Continuous-Casting Billet. Metals, 9(5), 543. https://doi.org/10.3390/met9050543







