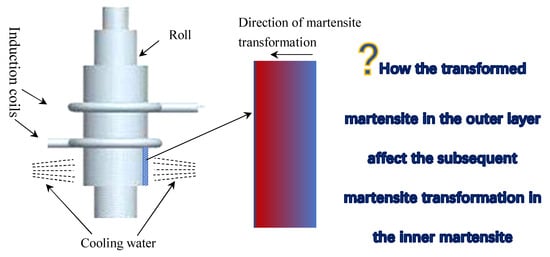
Optimization of Induction Quenching Processes for HSS Roll Based on MMPT Model
Abstract
:1. Introduction
2. Experimental Materials and Methods
2.1. Materials andCooling Tests with Loads
2.2. Quantitative Phase Analysis
2.3. Determinations of Thermophysical Parameters
3. Experimental and Modelling Results
3.1. Results of X-Ray Diffraction
3.2. Establishment of the Martensitic Transformation Model
4. Simulation and Optimization Design of Induction Hardening Processes
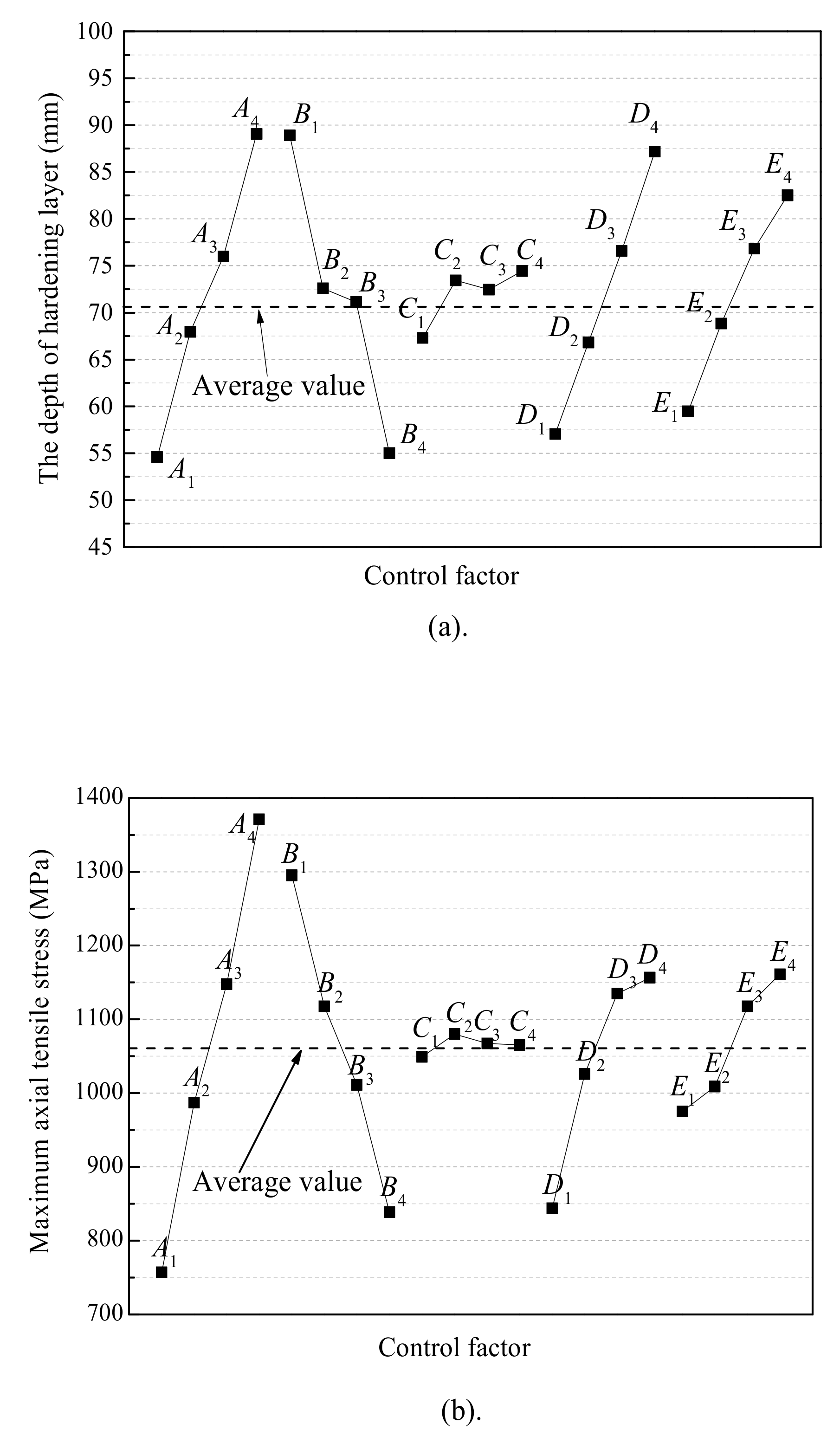
5. Simulated Results and Analyses of Orthogonal Tests
6. Optimization Results Analysis
7. Conclusions
- (1)
- The thermal stress and phase transformation stress can promote the martensite transformation of the tested high carbon roll steel. The modified Magee equation of the tested steel is .
- (2)
- The orthogonal test was designed with the help of five factors four levels orthogonal table to optimize the hardened layer depth and the axial tensile stress in dual frequency induction quenching processes. The optimal combination was found out by the orthogonal analysis. The results show that the effect of preheating temperatures on hardened layer depth and the axial tensile stress is the largest, while the effect of cooling intensity is the least.
- (3)
- The simulation and industrial test studies of the optimized and conventional dual frequency induction quenching processes show that the hardened layer depth is increased by 32.5% and the maximum residual axial tensile stress reaches about 1100MPa in the optimized process, which is acceptable. The simulated and measured depths of the hardened layer coincide with each other, further which indicates the correctness of the phase transition model obtained in this study furtherly.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Chi, H.X.; Ma, D.S.; Yong, Q.L.; Wu, L.Z.; Zhang, Z.P.; Wang, Y.W. Effect of cryogenic treatment on properties of Cr8-type cold work die steel. J. Iron Steel Res. Int. 2010, 17, 43–46. [Google Scholar] [CrossRef]
- Kang, J.Y.; Kim, H.; Son, D.; Kim, C.; Park, S.K.; Lee, T.H. Hot-worked microstructure and hot workability of cold-work tool steels. Mater. Charact. 2018, 135, 8–17. [Google Scholar] [CrossRef]
- Wang, M.J.; Wang, Y.; Sun, F.F. Tempering behavior of a semi-high speed steel containing nitrogen. Mater. Sci. Eng. A 2006, 438–440, 1139–1142. [Google Scholar] [CrossRef]
- Guo, J.; Liu, L.G.; Li, Q.; Sun, Y.L.; Gao, Y.K.; Ren, X.J.; Yang, Q.X. Characterization on carbide of a novel steel for cold work roll during solidification process. Mater. Charact. 2013, 79, 100–109. [Google Scholar] [CrossRef]
- Guo, J.; Liao, B.; Liu, L.G.; Li, Q.; Ren, X.J.; Yang, Q.X. Forging limit of a novel high-speed-steel cold work roll based on ductile fracture criteria by finite element model. Mater. Des. 2013, 52, 1027–1034. [Google Scholar] [CrossRef]
- Šolić, S.; Podgornik, B.; Leskovšek, V. The occurrence of quenching cracks in high-carbon tool steel depending on the austenitizing temperature. Eng. Fail. Anal. 2018, 92, 140–148. [Google Scholar] [CrossRef]
- Wu, H.; Udagawa, Y.; Narukawa, T.; Amaya, M. Crack formation in cladding under LOCA quench conditions. Nucl. Eng. Des. 2016, 303, 25–30. [Google Scholar] [CrossRef]
- Xiong, Z.P.; Jacques, P.J.; Perlade, A.; Pardoen, T. Ductile and intergranular brittle fracture in a two-step quenching and partitioning steel. Scr. Mater. 2018, 157, 6–9. [Google Scholar] [CrossRef]
- Ju, Y.; Koyama, M.; Sawaguchi, T.; Tsuzaki, K.; Noguchi, H. Effects of ε-martensitic transformation on crack tip deformation, plastic damage accumulation, and slip plane cracking associated with low-cycle fatigue crack growth. Int. J. Fatigue 2017, 103, 533–545. [Google Scholar] [CrossRef]
- Montalvo-Urquizo, J.; Liu, Q.; Schmidt, A. Simulation of quenching involved in induction hardening including mechanical effects. Comp. Mater. Sci. 2013, 79, 639–649. [Google Scholar] [CrossRef]
- Tong, D.M.; Gu, J.F.; Yang, F. Numerical simulation on induction heat treatment process of a shaft part: Involving induction hardening and tempering. J. Mater. Process. Technol. 2018, 262, 277–289. [Google Scholar] [CrossRef]
- Fisk, M.; Lindgren, L.E.; Datchary, W.; Deshmukh, V. Modelling of induction hardening in low alloy steels. Finite Elem. Anal. Des. 2018, 144, 61–75. [Google Scholar] [CrossRef]
- Basak, A.; Levitas, V.I. Finite element procedure and simulations for a multiphase phase field approach to martensitic phase transformations at large strains and with interfacial stresses. Comput. Methods Appl. Mech. Eng. 2019, 343, 368–406. [Google Scholar] [CrossRef]
- Yen, H.W.; Ooi, S.W.; Eizadjou, M.; Breen, A.; Huang, C.Y.; Bhadeshia, H.K.D.H.; Ringer, S.P. Role of stress-assisted martensite in the design of strong ultrafine-grained duplex steels. Acta Mater. 2015, 82, 100–114. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.C.; Liu, C.X.; Sommer, F.; Mittemeijer, E.J. Martensite formation kinetics of substitutional Fe-0.7 at.% Al alloy under uniaxial compressive stress. Acta Mater. 2015, 98, 164–174. [Google Scholar] [CrossRef]
- Jiang, B.; Wu, M.; Zhang, M.; Zhao, F.; Zhao, Z.G.; Liu, Y.Z. Microstructural characterization, strengthening and toughening mechanisms of a quenched and tempered steel: Effect of heat treatment parameters. Mater. Sci. Eng. A 2017, 707, 306–314. [Google Scholar] [CrossRef]
- Liu, Q.B.; Liu, H. Experimental study of the laser quenching of 40CrNiMoA steel. J. Mater. Process. Technol. 1999, 88, 77–82. [Google Scholar]
- Gu, S.; Xu, G.Q.; Quan, Y.K.; Yuan, Q.C.; Davies, P.A. Uniform design for the optimization of Al2O3 nanofilms produced by electrophoretic deposition. Surf. Coat. Technol. 2016, 286, 268–278. [Google Scholar]
- Yang, J.; Li, L.; Yang, L.Y.; Li, J.Q. Uniform design for the parameters optimization of pin-fins channel heat sink. Appl. Therm. Eng. 2017, 120, 289–297. [Google Scholar] [CrossRef]
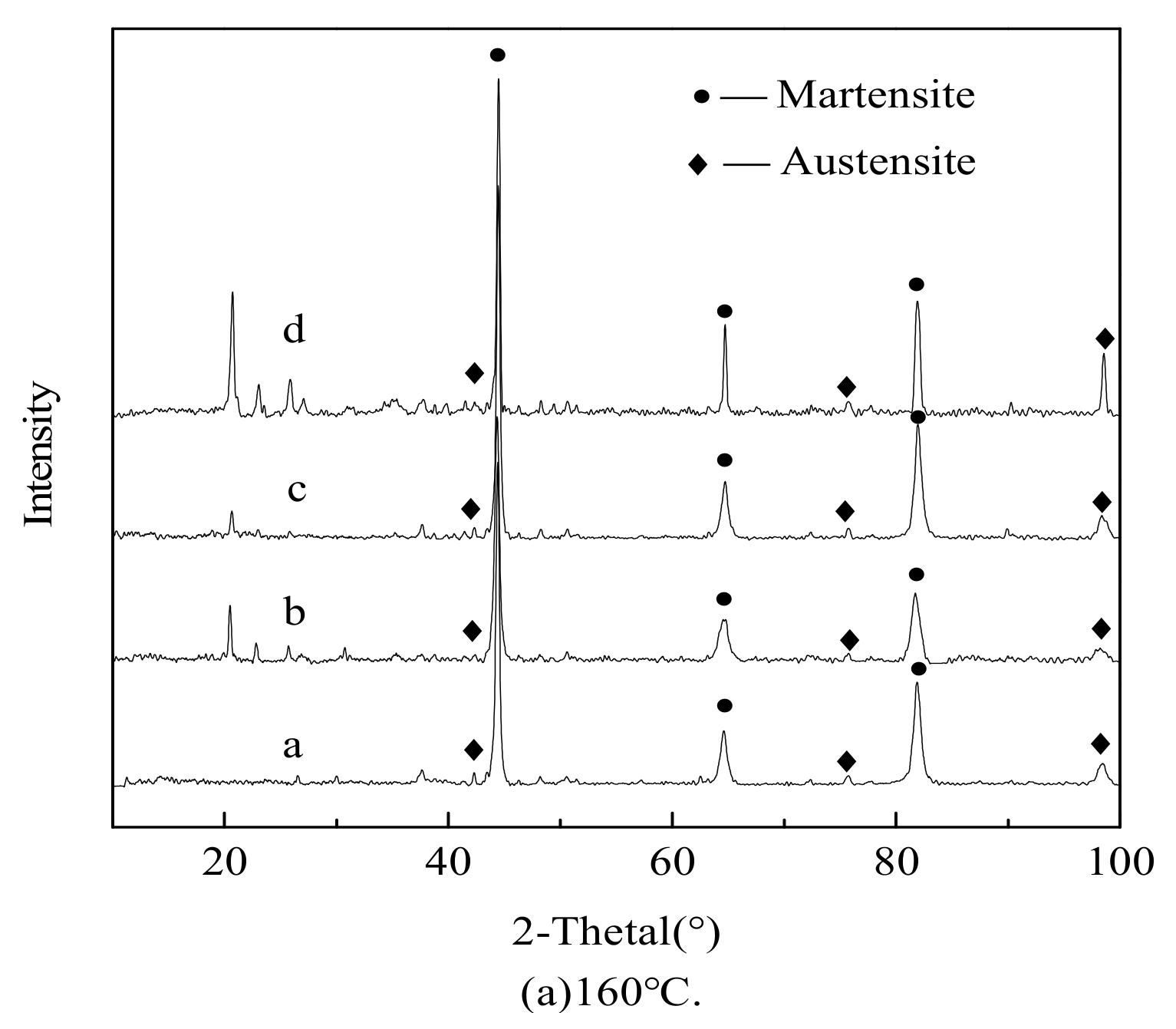
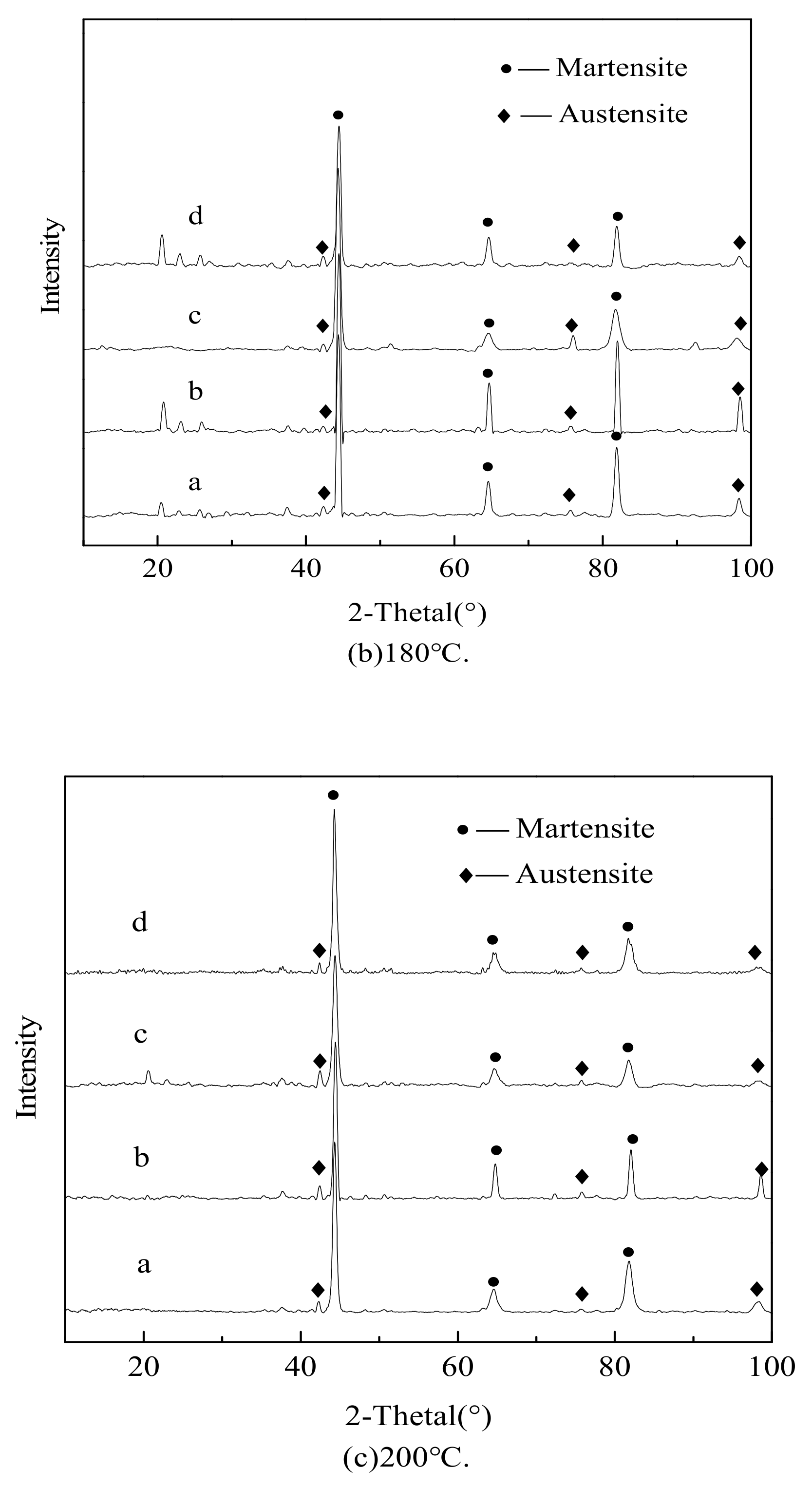




| No. | T(°C) | (Pa) | Calculated | Error (%) | ||
|---|---|---|---|---|---|---|
| 160 °C, 01Rm | 95.46 | 160 | 1.735E8 | 5.78333E7 | 94.66 | 0.83 |
| 160 °C, 02 Rm | 96.65 | 160 | 3.47E8 | 1.15667E8 | 94.73 | 1.98 |
| 160 °C, 03 Rm | 96.60 | 160 | 5.205E8 | 1.735E8 | 95.05 | 1.60 |
| 160 °C, 04 Rm | 96.89 | 160 | 6.94E8 | 2.31333E8 | 95.86 | 1.06 |
| 180 °C, 01 Rm | 90.60 | 180 | 1.702E8 | 5.67333E7 | 89.71 | 0.98 |
| 180 °C, 02 Rm | 93.44 | 180 | 3.404E8 | 1.13467E8 | 90.03 | 3.65 |
| 180 °C, 03 Rm | 95.07 | 180 | 5.106E8 | 1.702E8 | 90.19 | 5.13 |
| 180 °C, 04 Rm | 96.14 | 180 | 6.808E8 | 2.26933E8 | 93.26 | 3.02 |
| 200 °C, 01 Rm | 86.37 | 200 | 1.663E8 | 5.54333E7 | 81.52 | 5.61 |
| 200 °C, 02 Rm | 86.90 | 200 | 3.326E8 | 1.10867E8 | 82.34 | 5.20 |
| 200 °C, 03 Rm | 87.52 | 200 | 4.989E8 | 1.663E8 | 82.67 | 5.55 |
| 200 °C, 04 Rm | 88.63 | 200 | 6.652E8 | 2.21733E8 | 83.63 | 5.65 |
| Levels | A | B | C | D | E |
|---|---|---|---|---|---|
| Preheating Temperatures (°C) | Speeds (mm·s−1) | Cooling Intensity (W·m−2·°C−1) | Frequency of Coil Ⅰ(Hz) | Frequency of Coil Ⅱ(Hz) | |
| 1 | 300 | 0.6 | 4000 | 60 | 100 |
| 2 | 400 | 0.7 | 6000 | 65 | 150 |
| 3 | 500 | 0.8 | 8000 | 70 | 200 |
| 4 | 600 | 1 | 10,000 | 75 | 250 |
| T(°C) | 20 | 100 | 300 | 500 | 700 | 900 | 1100 |
|---|---|---|---|---|---|---|---|
| c (J/kg·K) | 501 | 515 | 562 | 660 | 827 | 695 | 528 |
| λ(W/m·K) | 36.58 | 35.77 | 34.16 | 31.09 | 26.95 | 26.1 | 26.1 |
| a (10−6/K) | 10.13 | 11.80 | 13.38 | 14.01 | 14.12 | 16.37 | 20.24 |
| Rm (MPa) | 2062 | 1827 | 1510 | 963 | 671 | 207 | 124 |
| Rel (MPa) | 1740 | 1552 | 1283 | 818 | 570 | 162 | 98 |
| ν | 0.3 | 0.3 | 0.3 | 0.304 | 0.31 | 0.33 | 0.33 |
| E (103 MPa) | 205 | 196 | 180 | 159 | 97 | 48 | 26 |
| No. | level | Simulated results | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | Depth of Hardened Layer (mm) | Maximum Axial Tensile Stress (MPa) | |
| 1 | 1 | 1 | 1 | 1 | 1 | 42.05 | 635 |
| 2 | 1 | 2 | 2 | 2 | 2 | 48.63 | 727 |
| 3 | 1 | 3 | 3 | 3 | 3 | 63.94 | 825 |
| 4 | 1 | 4 | 4 | 4 | 4 | 63.77 | 840 |
| 5 | 2 | 1 | 2 | 3 | 4 | 101.77 | 1395 |
| 6 | 2 | 2 | 1 | 4 | 3 | 86.57 | 1245 |
| 7 | 2 | 3 | 4 | 1 | 2 | 49.40 | 676 |
| 8 | 2 | 4 | 3 | 2 | 1 | 34.08 | 633 |
| 9 | 3 | 1 | 3 | 4 | 2 | 105.73 | 1515 |
| 10 | 3 | 2 | 1 | 3 | 1 | 69.09 | 1200 |
| 11 | 3 | 3 | 4 | 2 | 4 | 78.49 | 1110 |
| 12 | 3 | 4 | 2 | 1 | 3 | 50.71 | 765 |
| 13 | 4 | 1 | 4 | 2 | 3 | 106.08 | 1635 |
| 14 | 4 | 2 | 3 | 1 | 4 | 86.04 | 1298 |
| 15 | 4 | 3 | 2 | 4 | 1 | 92.63 | 1433 |
| 16 | 4 | 4 | 1 | 3 | 2 | 71.53 | 1118 |
| Level Analyses | Depth of Hardened Layer(mm) | Maximum Axial Tensile Stress (MPa) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | A | B | C | D | E | |
| Ti1 | 218.39 | 355.63 | 269.24 | 228.20 | 237.85 | 3027 | 5180 | 4198 | 3374 | 3901 |
| Ti2 | 271.82 | 290.33 | 293.74 | 267.28 | 275.29 | 3949 | 4469 | 4319 | 4105 | 4035 |
| Ti3 | 304.02 | 284.46 | 289.79 | 306.33 | 307.30 | 4590 | 4043 | 4271 | 4538 | 4470 |
| Ti4 | 356.28 | 220.09 | 297.74 | 348.70 | 330.07 | 5483 | 3353 | 4261 | 5033 | 4643 |
| 54.60 | 88.91 | 67.31 | 57.05 | 59.46 | 757 | 1295 | 1049 | 844 | 975 | |
| 67.96 | 72.58 | 73.44 | 66.82 | 68.82 | 987 | 1118 | 1080 | 1026 | 1009 | |
| 76.00 | 71.12 | 72.45 | 76.58 | 76.83 | 1148 | 1011 | 1067 | 1135 | 1118 | |
| 89.07 | 55.02 | 74.44 | 87.18 | 82.52 | 1371 | 839 | 1065 | 1157 | 1161 | |
| R | 34.47 | 33.89 | 7.13 | 30.13 | 23.06 | 614 | 457 | 76 | 313 | 186 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Yu, H.; Yang, Z.; Zhao, C.; Zhai, T. Optimization of Induction Quenching Processes for HSS Roll Based on MMPT Model. Metals 2019, 9, 663. https://doi.org/10.3390/met9060663
Liu L, Yu H, Yang Z, Zhao C, Zhai T. Optimization of Induction Quenching Processes for HSS Roll Based on MMPT Model. Metals. 2019; 9(6):663. https://doi.org/10.3390/met9060663
Chicago/Turabian StyleLiu, Ligang, Hui Yu, Zhiqiang Yang, Chunmei Zhao, and Tongguang Zhai. 2019. "Optimization of Induction Quenching Processes for HSS Roll Based on MMPT Model" Metals 9, no. 6: 663. https://doi.org/10.3390/met9060663
APA StyleLiu, L., Yu, H., Yang, Z., Zhao, C., & Zhai, T. (2019). Optimization of Induction Quenching Processes for HSS Roll Based on MMPT Model. Metals, 9(6), 663. https://doi.org/10.3390/met9060663