On the Influence of Loading Order in Nanostructural Fatigue Crack Propagation in BCC Iron—A Molecular Dynamics Study
Abstract
1. Introduction
2. Simulation Method
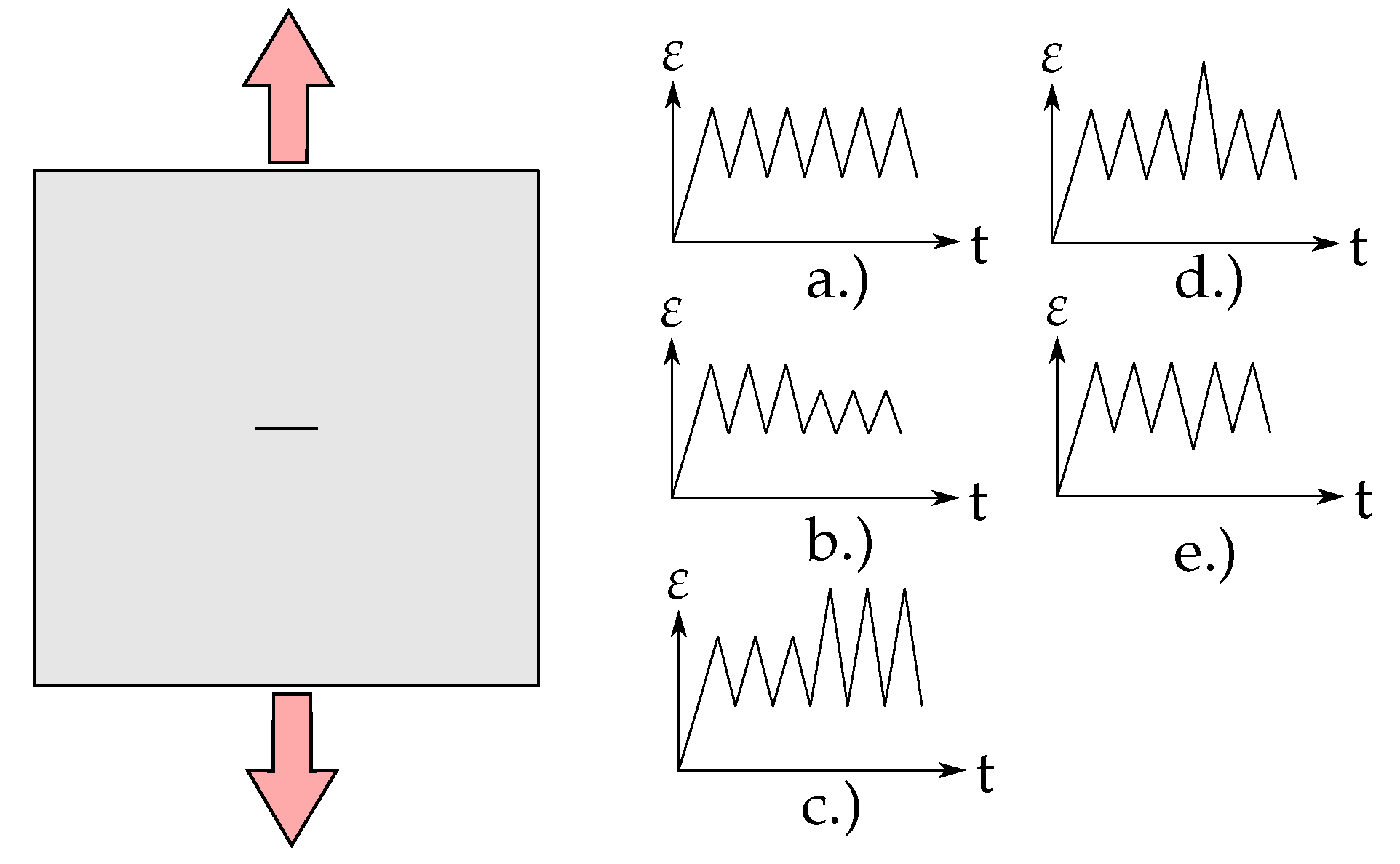
3. Simulation Setup
4. Results
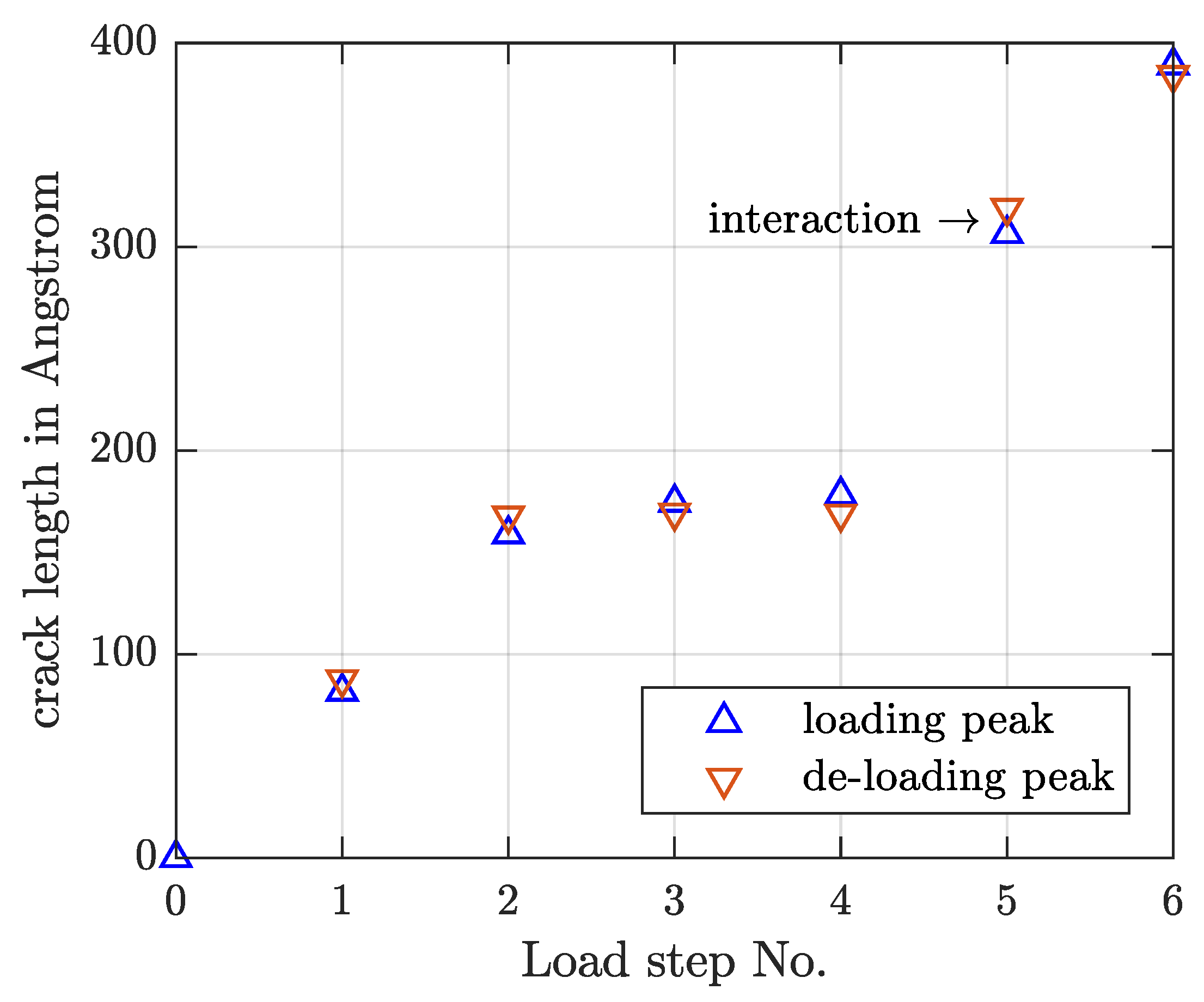
4.1. Determination of Crack Length
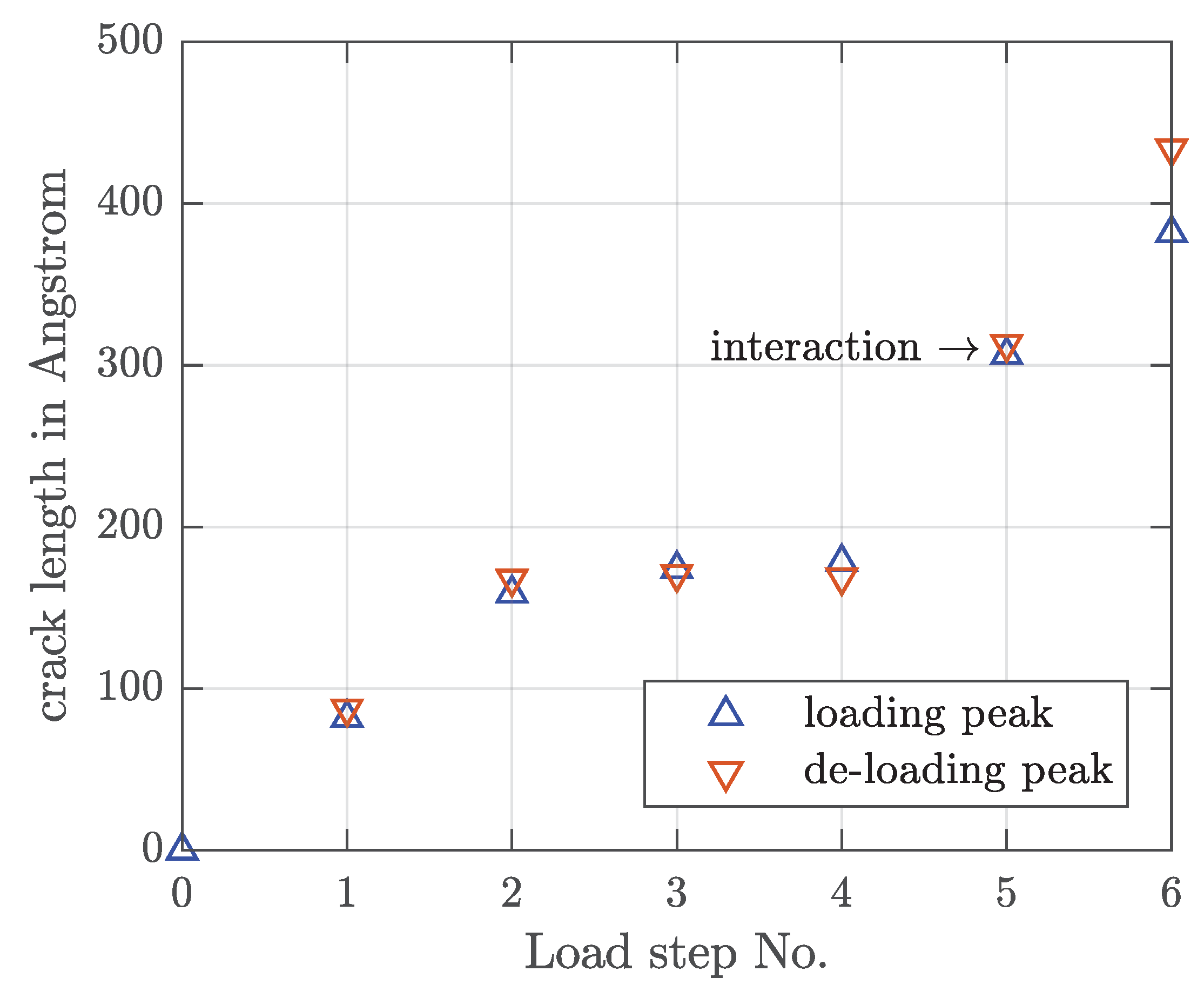
4.2. Constant Strain Amplitude
4.3. High-Low and Low-High Loading
4.3.1. High-Low
4.3.2. Low-High
4.4. Single Under- and Over-Load
4.4.1. Single Under-Load
4.4.2. Single Over-Load
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MD | Molecular dynamics |
| S-N | Stress life approach to fatigue |
| -N | Strain life approach to fatigue |
| LEFM | Linear elastic fracture mechanics |
| da | Increment increase of crack length |
| dN | Increment increase of cycles |
| C, m | Material parameters for the Paris equation |
| Range of stress intensity factor | |
| Maximum stress intensity factor | |
| Minimum stress intensity factor | |
| Threshold value for fatigue crack propagation | |
| Damage sum according to Miner’s rule | |
| Number of cycles occurring at the stress range i | |
| Number of cycles to failure at the stress range i | |
| EAM | Embedded atom method |
| EAM potential | |
| Scalar distance between atoms | |
| Pairwise additive contributions to the potential | |
| Electron density | |
| Initial crack length | |
| H | Height of the specimen |
| W | Width of the specimen |
| a | Lattice constant |
| Strain | |
| bcc | Body centered cubic crystal structure |
| fcc | Face centered cubic crystal structure |
| hcp | Hexagonal closed packed crystal structure |
| t | Time |
| SOL | Single overload |
| SUL | Single underload |
| Mode I | Crack opening perpendicular to the crack plane |
| Mode II | In plane sliding of the crack |
References
- Sander, M. Sicherheit und Betriebsfestigkeit von Maschinen und Anlagen: Konzepte und Methoden zur Lebensdauer-Vorhersage, 1st ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Hobbacher, A. The use of fracture mechanics in the fatigue analysis of welded joints. In Fracture and Fatigue of Welded Joints and Structures; Elsevier: Amsterdam, The Netherlands, 2011; pp. 91–112. [Google Scholar]
- Hobbacher, A. (Ed.) Recommendations for Fatigue Design of Welded Joints and Components, 2nd ed.; IIW Collection, Springer: Berlin, Germany, 2016. [Google Scholar]
- Berger, C.; Blauel, J.G.; Hodulak, L.; Pyttel, B.; Varfolomeev, I. Bruchmechanischer Festigkeitsnachweis für Maschinenbauteile, 4th ed.; FKM-Richtlinie, VDMA-Verl.: Frankfurt am Main, Germany, 2018. [Google Scholar]
- Kuna, M. Finite Elements in Fracture Mechanics: Theory–Numerics–Applications; Solid Mechanics and Its Applications; Springer: Dordrecht, The Netherlands; New York, NY, USA, 2013. [Google Scholar]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Chowdhury, P.; Sehitoglu, H. Mechanisms of fatigue crack growth—A critical digest of theoretical developments. Fatigue Fract. Eng. Mater. Struct. 2016, 1–23. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; reprint ed.; Cambridge Univ. Press: Cambridge, UK, 2004. [Google Scholar]
- Potirniche, G.P.; Horstemeyer, M.F. On the growth of nanoscale fatigue cracks. Philos. Mag. Lett. 2006, 86, 185–193. [Google Scholar] [CrossRef]
- Davidson, D.L. Characterizing small fatigue cracks in metallic alloys. Metall. Mater. Trans. A 2004, 35, 7–14. [Google Scholar] [CrossRef]
- Hussain, K. Short fatigue crack behaviour and analytical models: A review. Eng. Fract. Mech. 1997, 58, 327–354. [Google Scholar] [CrossRef]
- Miller, K.J. (Ed.) Short Fatigue Cracks: [Papers Read at the ESIS Conference on Short Fatigue Cracks Held at Sheffield in December 1990]; Volume 13: ESIS Publication; Mechanical Engineering Publ: London, UK, 1992. [Google Scholar]
- Hobson, P.D. The formulation of a crack growth equation for short cracks. Fatigue Fract. Eng. Mater. Struct. 1982, 5, 323–327. [Google Scholar] [CrossRef]
- Endo, M.; Mcevily, A. Prediction of the Behavior of Small Fatigue Cracks. Mater. Sci. Eng. A 2007, 468, 51–58. [Google Scholar] [CrossRef]
- Zerbst, U.; Madia, M.; Schork, B.; Hensel, J.; Kucharczyk, P.; Ngoula, D.; Tchuindjang, D.; Bernhard, J.; Beckmann, C. Fatigue and Fracture of Weldments; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Miner, M.A. Cumulative damage in fatigue. Trans. ASME J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar]
- Radaj, D.; Sonsino, C.M.; Fricke, W. Fatigue Assessment of Welded Joints by Local Approaches, 2nd ed.; Woodhead Publishing in Materials, Woodhead: Cambridge, UK, 2006. [Google Scholar]
- Fatemi, A.; Yang, L. Cumulative fatigue damage and life prediction theories: A survey of the state of the art for homogeneous materials. Int. J. Fatigue 1998, 20, 94. [Google Scholar] [CrossRef]
- Leung, K.W.K.; Pan, Z.L.; Warner, D.H. Kohn–Sham density functional theory prediction of fracture in silicon carbide under mixed mode loading. Model. Simul. Mater. Sci. Eng. 2016, 24, 035004. [Google Scholar] [CrossRef]
- Bitzek, E.; Kermode, J.R.; Gumbsch, P. Atomistic aspects of fracture. Int. J. Fract. 2015, 191, 13–30. [Google Scholar] [CrossRef]
- Farkas, D.; Selinger, R.L.B. Atomistics of Fracture. In Handbook of Materials Modeling; Yip, S., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 839–853. [Google Scholar]
- Horstemeyer, M.F.; Farkas, D.; Kim, S.; Tang, T.; Potirniche, G. Nanostructurally small cracks (NSC): A review on atomistic modeling of fatigue. Int. J. Fatigue 2010, 32, 1473–1502. [Google Scholar] [CrossRef]
- Nishimura, K.; Miyazaki, N. Molecular dynamics simulation of crack growth under cyclic loading. Comput. Mater. Sci. 2004, 31, 269–278. [Google Scholar] [CrossRef]
- Ma, L.; Xiao, S.; Deng, H.; Hu, W. Molecular dynamics simulation of fatigue crack propagation in bcc iron under cyclic loading. Int. J. Fatigue 2014, 68, 253–259. [Google Scholar] [CrossRef]
- Ma, L.; Xiao, S.; Deng, H.; Hu, W. Atomic simulation of fatigue crack propagation in Ni3Al. Appl. Phys. A 2015, 118, 1399–1406. [Google Scholar] [CrossRef]
- Uhnáková, A.; Machová, A.; Hora, P. 3D atomistic simulation of fatigue behaviour of a ductile crack in bcc iron. Int. J. Fatigue 2011, 33, 1182–1188. [Google Scholar] [CrossRef]
- Uhnáková, A.; Pokluda, J.; Machová, A.; Hora, P. 3D atomistic simulation of fatigue behaviour of a ductile crack in bcc iron loaded in mode II. Comput. Mater. Sci. 2012, 61, 12–19. [Google Scholar] [CrossRef]
- Potirniche, G.P.; Horstemeyer, M.F.; Gullett, P.M.; Jelinek, B. Atomistic modelling of fatigue crack growth and dislocation structuring in FCC crystals. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2006, 462, 3707–3731. [Google Scholar] [CrossRef]
- Zhou, X.; Li, X.; Chen, C. Atomistic mechanisms of fatigue in nanotwinned metals. Acta Mater. 2015, 99, 77–86. [Google Scholar] [CrossRef]
- Potirniche, G.; Horstmeyer, M.; Jelinek, B.; Wagner, G. Fatigue damage in nickel and copper single crystals at nanoscale. Int. J. Fatigue 2005, 27, 1179–1185. [Google Scholar] [CrossRef]
- Tang, T.; Kim, S.; Horstemeyer, M.F. Fatigue crack growth in magnesium single crystals under cyclic loading: Molecular dynamics simulation. Comput. Mater. Sci. 2010, 48, 426–439. [Google Scholar] [CrossRef]
- White, P. Molecular dynamic modelling of fatigue crack growth in aluminium using LEFM boundary conditions. Int. J. Fatigue 2012, 44, 141–150. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, E. Peridynamic Theory and Its Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Lee, J.G. Computational Materials Science: An Introduction, 2nd ed.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2017. [Google Scholar]
- Tadmor, E.B.; Miller, R.E. Modeling Materials: Continuum, Atomistic and Multiscale Techniques; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- LeSar, R. Introduction to Computational Materials Science: Fundamentals to Applications; Materials Research Society, Cambridge Univ. Press: Cambridge, UK, 2013. [Google Scholar]
- Möller, J.J.; Bitzek, E. Comparative study of embedded atom potentials for atomistic simulations of fracture in α -iron. Model. Simul. Mater. Sci. Eng. 2014, 22, 045002. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Bürgel, R.; Richard, H.A.; Riemer, A. Werkstoffmechanik: Bauteile Sicher Beurteilen und Werkstoffe Richtig Einsetzen, 2nd ed.; Springer Vieweg: Wiesbaden, Germany, 2014. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Verlet, L. Computer “Experiments” on Classical Fluids. II. Equilibrium Correlation Functions. Phys. Rev. 1968, 165, 201–214. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Skorupa, M. Load interaction effects during fatigue crack growth under variable amplitude loading-a literature review. Part I: Empirical trends. Fatigue Fract. Eng. Mater. Struct. 1998, 21, 987–1006. [Google Scholar] [CrossRef]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ladinek, M.; Hofer, T. On the Influence of Loading Order in Nanostructural Fatigue Crack Propagation in BCC Iron—A Molecular Dynamics Study. Metals 2019, 9, 684. https://doi.org/10.3390/met9060684
Ladinek M, Hofer T. On the Influence of Loading Order in Nanostructural Fatigue Crack Propagation in BCC Iron—A Molecular Dynamics Study. Metals. 2019; 9(6):684. https://doi.org/10.3390/met9060684
Chicago/Turabian StyleLadinek, Markus, and Thomas Hofer. 2019. "On the Influence of Loading Order in Nanostructural Fatigue Crack Propagation in BCC Iron—A Molecular Dynamics Study" Metals 9, no. 6: 684. https://doi.org/10.3390/met9060684
APA StyleLadinek, M., & Hofer, T. (2019). On the Influence of Loading Order in Nanostructural Fatigue Crack Propagation in BCC Iron—A Molecular Dynamics Study. Metals, 9(6), 684. https://doi.org/10.3390/met9060684




