On the Influence of Loading Order in Nanostructural Fatigue Crack Propagation in BCC Iron—A Molecular Dynamics Study
Abstract
:1. Introduction
2. Simulation Method
3. Simulation Setup
4. Results
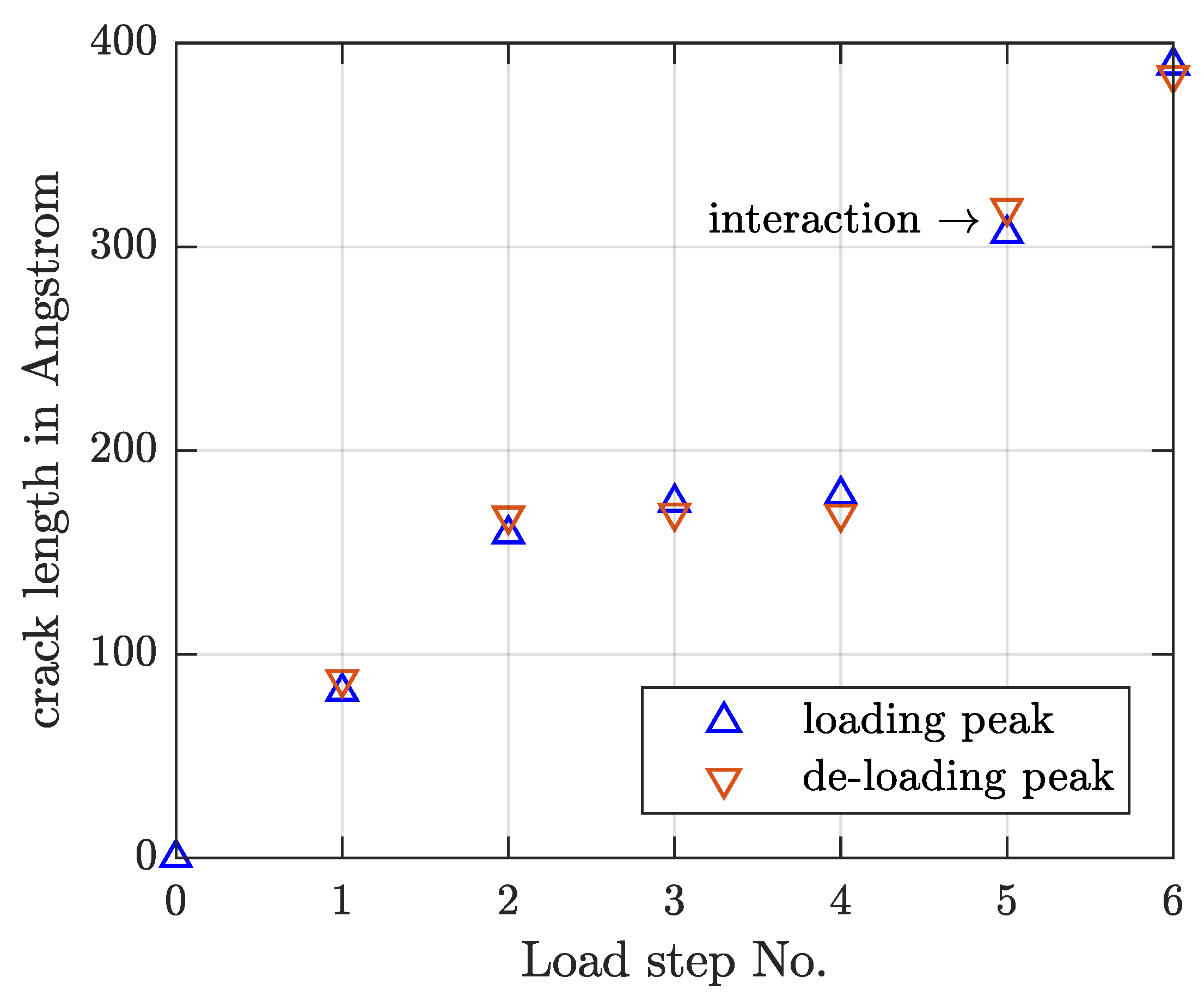
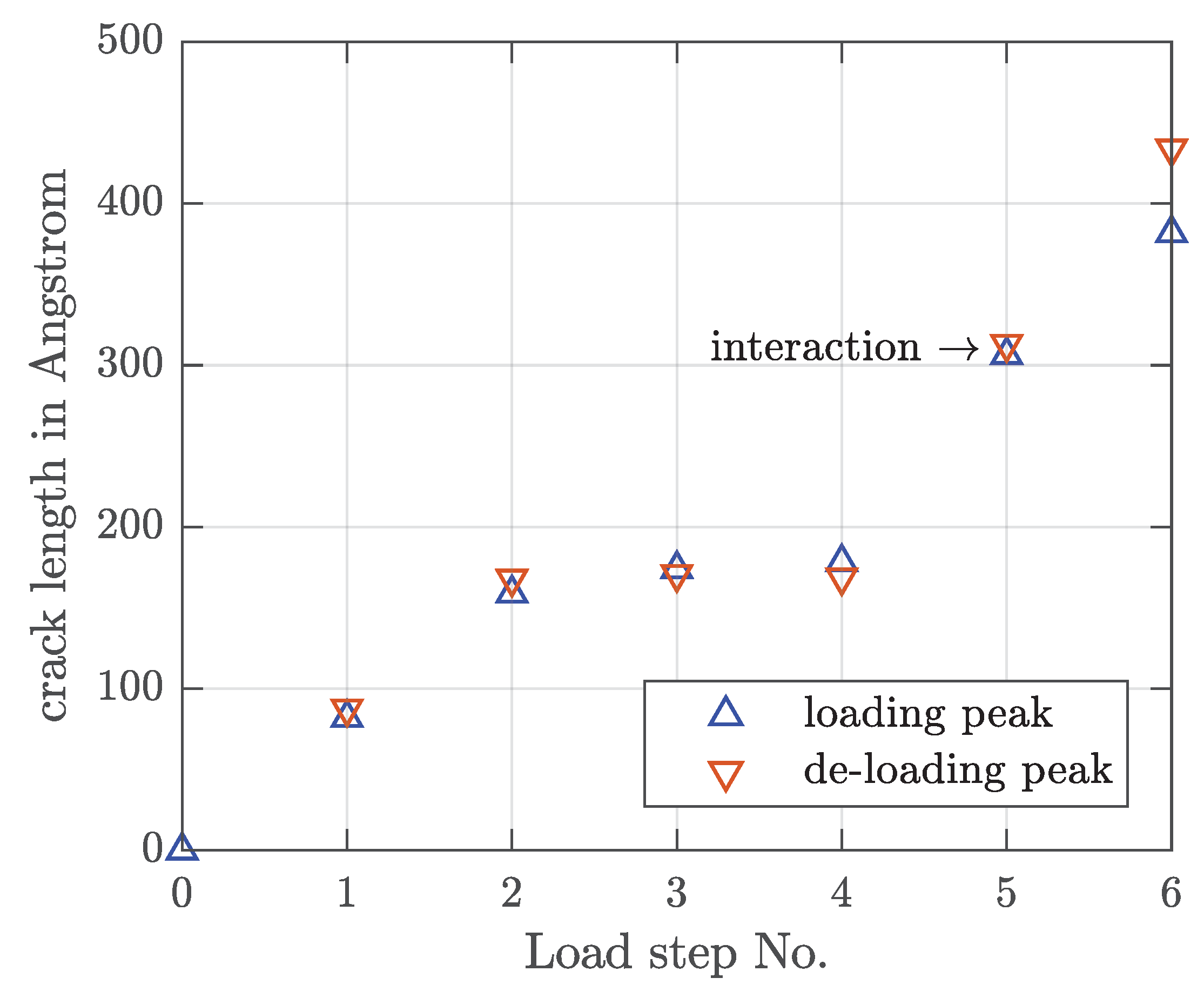
4.1. Determination of Crack Length
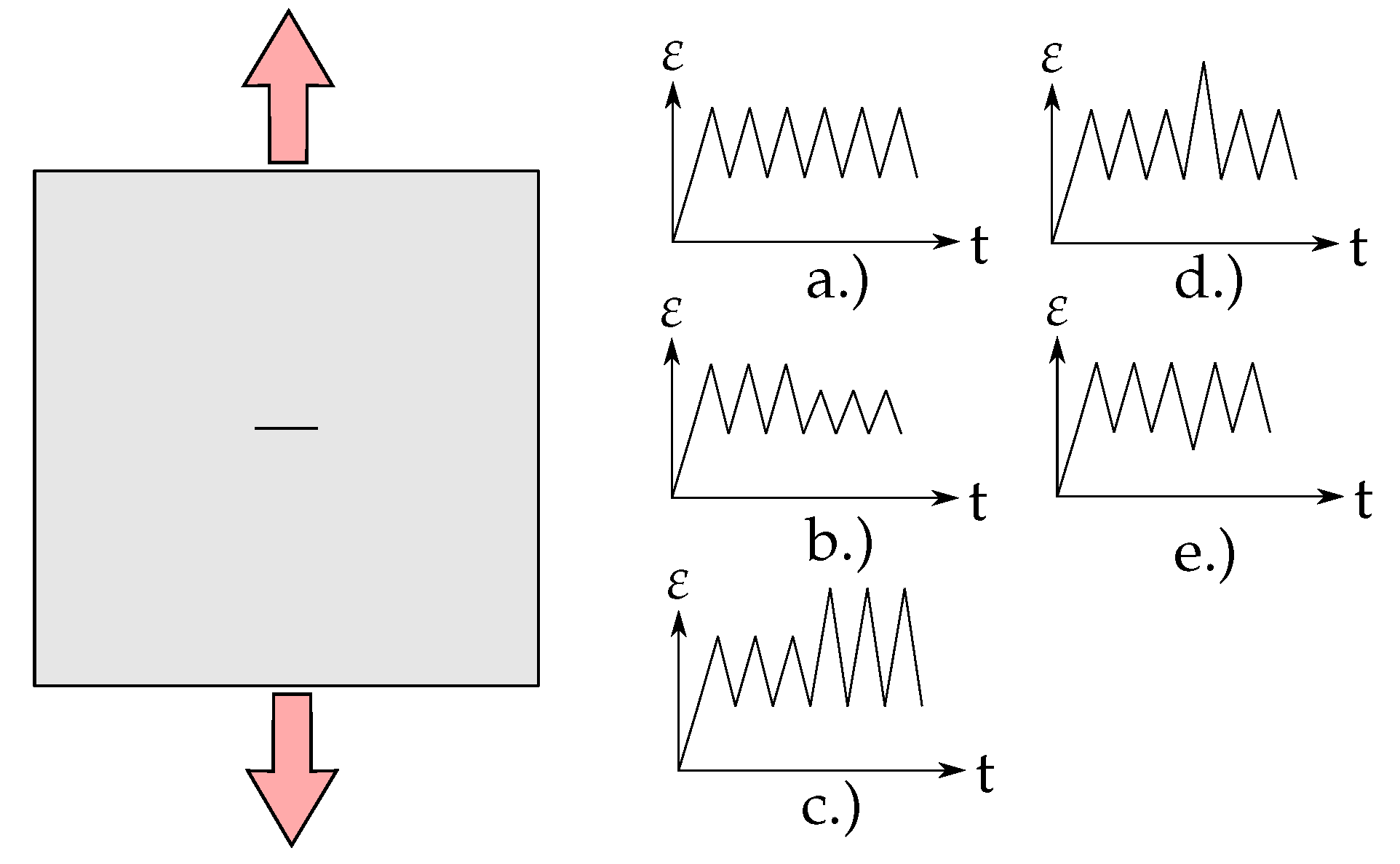
4.2. Constant Strain Amplitude
4.3. High-Low and Low-High Loading
4.3.1. High-Low
4.3.2. Low-High
4.4. Single Under- and Over-Load
4.4.1. Single Under-Load
4.4.2. Single Over-Load
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MD | Molecular dynamics |
| S-N | Stress life approach to fatigue |
| -N | Strain life approach to fatigue |
| LEFM | Linear elastic fracture mechanics |
| da | Increment increase of crack length |
| dN | Increment increase of cycles |
| C, m | Material parameters for the Paris equation |
| Range of stress intensity factor | |
| Maximum stress intensity factor | |
| Minimum stress intensity factor | |
| Threshold value for fatigue crack propagation | |
| Damage sum according to Miner’s rule | |
| Number of cycles occurring at the stress range i | |
| Number of cycles to failure at the stress range i | |
| EAM | Embedded atom method |
| EAM potential | |
| Scalar distance between atoms | |
| Pairwise additive contributions to the potential | |
| Electron density | |
| Initial crack length | |
| H | Height of the specimen |
| W | Width of the specimen |
| a | Lattice constant |
| Strain | |
| bcc | Body centered cubic crystal structure |
| fcc | Face centered cubic crystal structure |
| hcp | Hexagonal closed packed crystal structure |
| t | Time |
| SOL | Single overload |
| SUL | Single underload |
| Mode I | Crack opening perpendicular to the crack plane |
| Mode II | In plane sliding of the crack |
References
- Sander, M. Sicherheit und Betriebsfestigkeit von Maschinen und Anlagen: Konzepte und Methoden zur Lebensdauer-Vorhersage, 1st ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Hobbacher, A. The use of fracture mechanics in the fatigue analysis of welded joints. In Fracture and Fatigue of Welded Joints and Structures; Elsevier: Amsterdam, The Netherlands, 2011; pp. 91–112. [Google Scholar]
- Hobbacher, A. (Ed.) Recommendations for Fatigue Design of Welded Joints and Components, 2nd ed.; IIW Collection, Springer: Berlin, Germany, 2016. [Google Scholar]
- Berger, C.; Blauel, J.G.; Hodulak, L.; Pyttel, B.; Varfolomeev, I. Bruchmechanischer Festigkeitsnachweis für Maschinenbauteile, 4th ed.; FKM-Richtlinie, VDMA-Verl.: Frankfurt am Main, Germany, 2018. [Google Scholar]
- Kuna, M. Finite Elements in Fracture Mechanics: Theory–Numerics–Applications; Solid Mechanics and Its Applications; Springer: Dordrecht, The Netherlands; New York, NY, USA, 2013. [Google Scholar]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Chowdhury, P.; Sehitoglu, H. Mechanisms of fatigue crack growth—A critical digest of theoretical developments. Fatigue Fract. Eng. Mater. Struct. 2016, 1–23. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; reprint ed.; Cambridge Univ. Press: Cambridge, UK, 2004. [Google Scholar]
- Potirniche, G.P.; Horstemeyer, M.F. On the growth of nanoscale fatigue cracks. Philos. Mag. Lett. 2006, 86, 185–193. [Google Scholar] [CrossRef]
- Davidson, D.L. Characterizing small fatigue cracks in metallic alloys. Metall. Mater. Trans. A 2004, 35, 7–14. [Google Scholar] [CrossRef]
- Hussain, K. Short fatigue crack behaviour and analytical models: A review. Eng. Fract. Mech. 1997, 58, 327–354. [Google Scholar] [CrossRef]
- Miller, K.J. (Ed.) Short Fatigue Cracks: [Papers Read at the ESIS Conference on Short Fatigue Cracks Held at Sheffield in December 1990]; Volume 13: ESIS Publication; Mechanical Engineering Publ: London, UK, 1992. [Google Scholar]
- Hobson, P.D. The formulation of a crack growth equation for short cracks. Fatigue Fract. Eng. Mater. Struct. 1982, 5, 323–327. [Google Scholar] [CrossRef]
- Endo, M.; Mcevily, A. Prediction of the Behavior of Small Fatigue Cracks. Mater. Sci. Eng. A 2007, 468, 51–58. [Google Scholar] [CrossRef]
- Zerbst, U.; Madia, M.; Schork, B.; Hensel, J.; Kucharczyk, P.; Ngoula, D.; Tchuindjang, D.; Bernhard, J.; Beckmann, C. Fatigue and Fracture of Weldments; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Miner, M.A. Cumulative damage in fatigue. Trans. ASME J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar]
- Radaj, D.; Sonsino, C.M.; Fricke, W. Fatigue Assessment of Welded Joints by Local Approaches, 2nd ed.; Woodhead Publishing in Materials, Woodhead: Cambridge, UK, 2006. [Google Scholar]
- Fatemi, A.; Yang, L. Cumulative fatigue damage and life prediction theories: A survey of the state of the art for homogeneous materials. Int. J. Fatigue 1998, 20, 94. [Google Scholar] [CrossRef]
- Leung, K.W.K.; Pan, Z.L.; Warner, D.H. Kohn–Sham density functional theory prediction of fracture in silicon carbide under mixed mode loading. Model. Simul. Mater. Sci. Eng. 2016, 24, 035004. [Google Scholar] [CrossRef]
- Bitzek, E.; Kermode, J.R.; Gumbsch, P. Atomistic aspects of fracture. Int. J. Fract. 2015, 191, 13–30. [Google Scholar] [CrossRef]
- Farkas, D.; Selinger, R.L.B. Atomistics of Fracture. In Handbook of Materials Modeling; Yip, S., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 839–853. [Google Scholar]
- Horstemeyer, M.F.; Farkas, D.; Kim, S.; Tang, T.; Potirniche, G. Nanostructurally small cracks (NSC): A review on atomistic modeling of fatigue. Int. J. Fatigue 2010, 32, 1473–1502. [Google Scholar] [CrossRef]
- Nishimura, K.; Miyazaki, N. Molecular dynamics simulation of crack growth under cyclic loading. Comput. Mater. Sci. 2004, 31, 269–278. [Google Scholar] [CrossRef]
- Ma, L.; Xiao, S.; Deng, H.; Hu, W. Molecular dynamics simulation of fatigue crack propagation in bcc iron under cyclic loading. Int. J. Fatigue 2014, 68, 253–259. [Google Scholar] [CrossRef]
- Ma, L.; Xiao, S.; Deng, H.; Hu, W. Atomic simulation of fatigue crack propagation in Ni3Al. Appl. Phys. A 2015, 118, 1399–1406. [Google Scholar] [CrossRef]
- Uhnáková, A.; Machová, A.; Hora, P. 3D atomistic simulation of fatigue behaviour of a ductile crack in bcc iron. Int. J. Fatigue 2011, 33, 1182–1188. [Google Scholar] [CrossRef]
- Uhnáková, A.; Pokluda, J.; Machová, A.; Hora, P. 3D atomistic simulation of fatigue behaviour of a ductile crack in bcc iron loaded in mode II. Comput. Mater. Sci. 2012, 61, 12–19. [Google Scholar] [CrossRef]
- Potirniche, G.P.; Horstemeyer, M.F.; Gullett, P.M.; Jelinek, B. Atomistic modelling of fatigue crack growth and dislocation structuring in FCC crystals. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2006, 462, 3707–3731. [Google Scholar] [CrossRef]
- Zhou, X.; Li, X.; Chen, C. Atomistic mechanisms of fatigue in nanotwinned metals. Acta Mater. 2015, 99, 77–86. [Google Scholar] [CrossRef]
- Potirniche, G.; Horstmeyer, M.; Jelinek, B.; Wagner, G. Fatigue damage in nickel and copper single crystals at nanoscale. Int. J. Fatigue 2005, 27, 1179–1185. [Google Scholar] [CrossRef]
- Tang, T.; Kim, S.; Horstemeyer, M.F. Fatigue crack growth in magnesium single crystals under cyclic loading: Molecular dynamics simulation. Comput. Mater. Sci. 2010, 48, 426–439. [Google Scholar] [CrossRef]
- White, P. Molecular dynamic modelling of fatigue crack growth in aluminium using LEFM boundary conditions. Int. J. Fatigue 2012, 44, 141–150. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, E. Peridynamic Theory and Its Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Lee, J.G. Computational Materials Science: An Introduction, 2nd ed.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2017. [Google Scholar]
- Tadmor, E.B.; Miller, R.E. Modeling Materials: Continuum, Atomistic and Multiscale Techniques; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- LeSar, R. Introduction to Computational Materials Science: Fundamentals to Applications; Materials Research Society, Cambridge Univ. Press: Cambridge, UK, 2013. [Google Scholar]
- Möller, J.J.; Bitzek, E. Comparative study of embedded atom potentials for atomistic simulations of fracture in α -iron. Model. Simul. Mater. Sci. Eng. 2014, 22, 045002. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Bürgel, R.; Richard, H.A.; Riemer, A. Werkstoffmechanik: Bauteile Sicher Beurteilen und Werkstoffe Richtig Einsetzen, 2nd ed.; Springer Vieweg: Wiesbaden, Germany, 2014. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Verlet, L. Computer “Experiments” on Classical Fluids. II. Equilibrium Correlation Functions. Phys. Rev. 1968, 165, 201–214. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Skorupa, M. Load interaction effects during fatigue crack growth under variable amplitude loading-a literature review. Part I: Empirical trends. Fatigue Fract. Eng. Mater. Struct. 1998, 21, 987–1006. [Google Scholar] [CrossRef]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ladinek, M.; Hofer, T. On the Influence of Loading Order in Nanostructural Fatigue Crack Propagation in BCC Iron—A Molecular Dynamics Study. Metals 2019, 9, 684. https://doi.org/10.3390/met9060684
Ladinek M, Hofer T. On the Influence of Loading Order in Nanostructural Fatigue Crack Propagation in BCC Iron—A Molecular Dynamics Study. Metals. 2019; 9(6):684. https://doi.org/10.3390/met9060684
Chicago/Turabian StyleLadinek, Markus, and Thomas Hofer. 2019. "On the Influence of Loading Order in Nanostructural Fatigue Crack Propagation in BCC Iron—A Molecular Dynamics Study" Metals 9, no. 6: 684. https://doi.org/10.3390/met9060684




